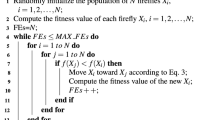Keywords

1 Introduction

Typical “real world” decision-making involves complex problems that possess design requirements which are frequently very difficult to incorporate into their supporting mathematical programming formulations and tend to be riddled with competing performance objectives [3, 11, 13]. While optimal solutions provide provably best solutions to the mathematical constructions, they are generally not the best solutions to the underlying real problems as there are invariably unquantified issues and unmodelled objectives not apparent during the model formulation phase [3, 11, 12]. Hence, it is generally considered desirable to generate a reasonable number of very different alternatives that provide multiple, contrasting perspectives to the specified problem [16]. These alternatives should preferably all possess good (i.e. near-optimal) measures with respect to all of the modelled objective(s), but be as fundamentally different as possible from each other in terms of the system structures characterized by their decision variables. Several approaches collectively referred to as modelling-to-generate-alternatives (MGA) have been developed in response to this multi-solution creation requirement [2, 7,8,9,10, 12, 16].

The primary motivation behind MGA is to produce a manageably small set of alternatives that are good with respect to all known objective(s) yet are as different as possible from each other within the decision space. The resulting set of alternatives should provide diverse approaches that all perform similarly with respect to the known modelled objectives, yet very differently with respect to any unmodelled issues [7, 13]. Clearly the decision-makers must conduct subsequent evaluations to ascertain which alternatives are most applicable to their specific circumstances. Therefore, MGA methods must necessarily be regarded as decision support processes in contrast to the explicit solution determination methods of optimization.

In this chapter, it is shown how to simultaneously generate sets of maximally different alternatives by implementing a modified version of the nature-inspired Firefly Algorithm (FA) [14, 15] by extending previous concurrent MGA approaches [5,6,7,8,9,10]. For optimization, it has been demonstrated that the FA is more computationally efficient than such metaheuristics as enhanced particle swarm optimization, simulated annealing, and genetic algorithms [4, 15]. The MGA procedure extends the earlier efforts of Imanirad et al. [5,6,7,8,9,10] to now permit the simultaneous generation of the desired number of alternatives in a single computational run. This new simultaneous FA-based MGA procedure is extremely computationally efficient. This chapter illustrates the efficacy of the new FA approach for simultaneously constructing multiple, good-but-very-different solution alternatives on a 100-peak multimodal optimization test problem [12].

2 Firefly Algorithm for Optimization

While this section provides only an abridged outline of the steps involved in the FA process [4,5,6], more comprehensive explanations appear in [14, 15]. The FA is a biologically-inspired, population-based metaheuristic. Each firefly in the population represents one potential solution to a problem and the population of fireflies should initially be distributed uniformly and randomly throughout the solution space. The solution approach employs three idealized rules. (i) All fireflies within the population are considered “unisex”, so that any one firefly could potentially be attracted to any other firefly irrespective of their sex. (ii) The brightness of a firefly is determined by the overall landscape of the objective function. Namely, for a maximization problem, the brightness is simply considered to be proportional to the value of the objective function. (iii) The relative attractiveness between any two fireflies is directly proportional to their respective brightness. This implies that for any two flashing fireflies, the less bright firefly will always be inclined to move towards the brighter one. However, attractiveness and brightness both decrease as the relative distance between the fireflies increases. If there is no brighter firefly within its visible neighborhood, then the particular firefly will move about randomly. Based upon these three rules, the basic operational steps of the FA can be summarized within the following pseudo-code [15].

In the FA, there are two important issues to resolve: the variation of light intensity and the formulation of attractiveness. For simplicity, it can always be assumed that the attractiveness of a firefly is determined by its brightness which in turn is associated with its encoded objective function value. In the simplest case, the brightness of a firefly at a particular location X would be its calculated objective value F(X). However, the attractiveness, β, between fireflies is relative and will vary with the distance r ij between firefly i and firefly j. In addition, light intensity decreases with the distance from its source, and light is also absorbed in the media, so the attractiveness needs to vary with the degree of absorption. Consequently, the overall attractiveness of a firefly can be defined as

$$\beta = \beta_{0} \exp ( - \gamma r^{2} )$$

where β 0 is the attractiveness at distance r = 0 and γ is the fixed light absorption coefficient for the specific medium. If the distance r ij between any two fireflies i and j located at X i and X j , respectively, is calculated using the Euclidean norm, then the movement of a firefly i that is attracted to another more attractive (i.e. brighter) firefly j is determined by

$$\varvec{X}_{i} = \varvec{X}_{i} + \beta_{0} \exp \,( - \gamma (r_{ij} )^{2} )\,(\varvec{X}_{i} {-}\varvec{X}_{j} ) + a\varvec{\varepsilon}_{i} .$$

In this expression of movement, the second term is due to the relative attraction and the third term is a randomization component. Yang [15] indicates that α is a randomization parameter normally selected within the range [0,1] and ε i is a vector of random numbers drawn from either a Gaussian or uniform (generally [−0.5,0.5]) distribution. It should be explicitly noted that this expression represents a random walk biased toward brighter fireflies and if β 0 = 0, it becomes a simple random walk. The parameter γ characterizes the variation of the attractiveness and its value determines the speed of the algorithm’s convergence. For most applications, γ is typically set between 0.1 to 10 [4, 15]. For all computational approaches for the FA considered in this study, the variation of attractiveness parameter γ was fixed at 5 while the randomization parameter α was initially set at 0.6, but is then gradually decreased to a value of 0.1 as the procedure approaches its maximum number of iterations (see [15]).

In any given optimization problem, for a very large number of fireflies n >> k, where k is the number of local optima, the initial locations of the n fireflies should be distributed relatively uniformly throughout the entire search space. As the FA proceeds, the fireflies begin to converge into all of the local optima (including the global ones). Hence, by comparing the best solutions among all these optima, the global optima can easily be determined. Yang [15] proves that the FA will approach the global optima when n → ∞ and the number of iterations t, is set so that t ≫1. In reality, the FA has been found to converge extremely quickly with n set in the range 20–50 [4, 14].

Two important limiting or asymptotic cases occur when γ → 0 and when γ → ∞. For γ → 0, the attractiveness is constant β = β 0, which is equivalent to having a light intensity that does not decrease. Thus, a firefly would be visible to every other firefly anywhere within the solution domain. Hence, a single (usually global) optima can easily be reached. If the inner loop for j in the pseudo-code is removed and X j is replaced by the current global best G*, then this implies that the FA reverts to a special case of the accelerated particle swarm optimization (PSO) algorithm. Subsequently, the computational efficiency of this special FA case is equivalent to that of enhanced PSO. Conversely, when γ → ∞ , the attractiveness is essentially zero along the sightline of all other fireflies. This is equivalent to the case where the fireflies randomly roam throughout a very thick foggy region with no other fireflies visible and each firefly roams in a completely random fashion. This case corresponds to a completely random search method. As the FA operates between these two asymptotic extremes, it is possible to adjust the parameters α and γ so that the FA can outperform both a random search and the enhanced PSO algorithms [4].

The computational efficiencies of the FA will be exploited in the subsequent MGA solution approach. As noted, within the two asymptotic extremes, the population in the FA can determine both the global optima as well as the local optima concurrently. This concurrency of population-based solution procedures holds huge computational and efficiency advantages for MGA purposes [16]. An additional advantage of the FA for MGA implementation is that the different fireflies essentially work independently of each other, implying that FA procedures are better than PSO and genetic algorithms for MGA because the fireflies will tend to aggregate more closely around each local optimum [4, 15]. Consequently, with a judicious selection of parameter settings, the FA will simultaneously converge extremely quickly into both local and global optima [4, 14, 15].

3 Modelling to Generate Alternatives

Most optimization methods appearing in the mathematical programming literature have focused almost entirely on the production of single optimal solutions to single-objective problem formulations or, equivalently, on the generation of noninferior sets of solutions to multi-objective instances [2, 5, 6, 11, 13]. While such algorithms may efficiently generate solutions to the derived complex mathematical models, whether these outputs actually establish “best” approaches to the underlying real problems is debatable [2, 3, 11, 12]. In most “real world” applications, there are innumerable system requirements and objectives that are never included or apparent in the decision formulation stage [3, 13]. Furthermore, it may never be possible to explicitly incorporate all of the subjective components because there are frequently many incompatible, competing, design interpretations and, perhaps, adversarial stakeholders involved. Therefore most of the subjective aspects of a problem necessarily remain unquantified and unmodelled in the construction of the resultant decision models. This occurs frequently in situations where final decisions are constructed based not only upon clearly stated and modelled objectives, but also upon more fundamentally subjective socio-political-economic goals and stakeholder preferences [16]. Numerous “real world” examples describing these types of incongruent modelling dualities are discussed in [1, 2, 12, 17].

When unquantified objectives and unmodelled issues are suspected, then non-conventional approaches should be undertaken that not only search the feasible region for noninferior solutions, but also explore the feasible region for obviously inferior alternatives to the formulated problem. In particular, any search for good alternatives to problems known or suspected to contain unmodelled objectives must focus not only on the non-inferior solution set, but also necessarily on an explicit exploration of the problem’s inferior decision space.

To illustrate the implications of an unmodelled objective on a decision search, assume that the optimal solution for a quantified, single-objective, maximization decision problem is X* with corresponding objective value Z1*. Now suppose that there exists a second, unmodelled, maximization objective Z2 that subjectively reflects some unquantifiable “political acceptability” component. Let the solution X a, belonging to the noninferior, 2-objective set, represent a potential best compromise solution if both objectives could somehow have been simultaneously evaluated by the decision-maker. While X a might be viewed as the best compromise solution to the real problem, it would appear inferior to the solution X* in the quantified mathematical model, since it must be the case that Z1 a ≤ Z1*. Consequently, when unmodelled objectives are factored into the decision making process, mathematically inferior solutions for the modelled problem can prove optimal to the underlying real problem. Therefore, when unmodelled objectives and unquantified issues might exist, different solution approaches are needed in order to not only search the decision space for the noninferior set of solutions, but also to simultaneously explore the decision space for inferior alternative solutions to the modelled problem. Population-based solution methods such as the FA permit concurrent searches throughout a feasible region and thus prove to be particularly adept procedures for searching through a problem’s decision space.

The primary motivation behind MGA is to produce a manageably small set of alternatives that are quantifiably good with respect to the known modelled objectives yet are as different as possible from each other in the decision space. The resulting alternatives are likely to provide truly different choices that all perform somewhat similarly with respect to the modelled objective(s) yet very differently with respect to any unknown unmodelled issues. By generating a set of good-but-different solutions, the decision-makers can explore desirable qualities within the alternatives that may prove to satisfactorily address the various unmodelled objectives to varying degrees of stakeholder acceptability.

In order to properly motivate an MGA search procedure, it is necessary to supply a more mathematically formal definition of the goals of the MGA process [7, 12, 16]. Suppose the optimal solution to an original mathematical model is X* with objective value Z* = F(X*). The following model can then be solved to generate an alternative solution, X, that is maximally different from X *:

$$\begin{array}{*{20}c} {\text{Maximize}} \hfill & {\Delta (\varvec{X},\varvec{X}^{*} )=\sum\limits_{i} {\left| {X_{i} - X_{i}^{*} } \right|} } \hfill \\ {{\text{Subject}}\, : {\text{to}}} \hfill & {\begin{array}{*{20}c} {\varvec{X} \in D} \hfill \\ {\left| {F(\varvec{X}) - \varvec{Z}^{*} } \right| \le T} \hfill \\ \end{array} } \hfill \\ \end{array}$$
([P1])

where ∆ represents some difference function (for clarity, shown as an absolute difference in this instance) and T is a targeted tolerance value specified relative to the problem’s original optimal objective Z*. T is a user-supplied value that determines how much of the inferior region is to be explored in the search for acceptable alternative solutions. This difference function concept can be extended into a measure of difference between a set of alternatives by replacing X * in the objective of [P1] and calculating the overall sum (or some other function) of the differences of the pairwise comparisons between each pair of alternatives—subject to the condition that each alternative is feasible and falls within the specified tolerance constraint.

4 FA-Based Simultaneous MGA Computational Algorithm

The MGA method to be introduced produces a pre-determined number of near-optimal, maximally different alternatives, by modifying the value of the bound T in [P1] and using an FA to solve the corresponding, maximal difference problem. Each solution within the FA’s population contains one potential set of p different alternatives. By exploiting the co-evolutionary solution structure within the population of the algorithm, the Fireflies collectively evolve each solution toward sets of different local optima within the solution space. In this process, each desired solution alternative undergoes the common search procedure of the FA. However, the survival of solutions depends not only upon how well the solutions perform with respect to the modelled objective(s), but also by how far away they are from all of the other alternatives generated in the decision space.

A direct process for generating alternatives with the FA is to iteratively solve the maximum difference model [P1] by incrementally updating the target T whenever a new alternative needs to be created and then re-running the algorithm. This iterative approach parallels the seminal Hop, Skip, and Jump (HSJ) MGA algorithm [2] in which, once an initial problem formulation has been optimized, supplementary alternatives are systematically produced one-by-one via an incremental adjustment of the target constraint to force the sequential generation of suboptimal solutions. While this approach is straightforward, it requires a recurrent execution of the optimization algorithm [5, 6, 16].

To improve upon the stepwise alternative approach of the HSJ algorithm, a concurrent MGA technique was subsequently designed based upon the concept of co-evolution [5,6,7, 9]. In the co-evolutionary approach, pre-specified stratified subpopulation ranges within the algorithm’s overall population were established that collectively evolved the search toward the creation of the stipulated number of maximally different alternatives. Each desired solution alternative was represented by each respective subpopulation and each subpopulation underwent the common processing operations of the FA. The survival of solutions in each subpopulation depended simultaneously upon how well the solutions perform with respect to the modelled objective(s) and by how far away they are from all of the other alternatives. Consequently, the evolution of solutions in each subpopulation toward local optima is directly influenced by those solutions contained in all of the other subpopulations, which forces the concurrent co-evolution of each subpopulation towards good but maximally distant regions within the decision space according to [P1] [16].

By employing this co-evolutionary concept, it became possible to implement an MGA procedure that concurrently produced alternatives possessing objective function bounds analogous to those created by the sequential, iterative HSJ-styled approach. In contrast, while each alternative produced by an HSJ procedure is maximally different only from the overall optimal solution (together with its bound on the objective value which is at least x% different from the best objective (i.e. x = 1%, 2%, etc.)), the concurrent procedure generated alternatives that are no more than x% different from the overall optimal solution but with each one of these solutions being as maximally different as possible from every other generated alternative that was produced. Co-evolution is also much more efficient than sequential HSJ in that it exploits the inherent population-based searches of FA procedures to concurrently create its entire set of maximally different solutions using only a single population [7, 9].

While a concurrent approach exploits the population-based nature of the FA’s solution approach, the co-evolution process occurs within each of the stratified subpopulations. The maximal differences between solutions in different subpopulations is based upon aggregate subpopulation measures. Conversely, in the following simultaneous MGA algorithm, each solution in the population contains exactly one entire set of alternatives and the maximal difference is calculated only for that particular solution (i.e. the specific alternative set contained within that solution in the population). Hence, by the evolutionary nature of the FA search procedure, in the subsequent approach, the maximal difference is simultaneously calculated for the specific set of alternatives considered within each specific solution—and the need for concurrent subpopulation aggregation measures is circumvented.

The steps in the simultaneous co-evolutionary alternative generation algorithm are as follows:

Initialization Stage: In this preliminary step, solve the original optimization problem to determine the optimal solution, X*. As with prior solution approaches [5]–[10] and without loss of generality, it is entirely possible to forego this step and construct the algorithm to find X* as part of its solution processing. However, such a requirement increases the number of computational iterations of the overall procedure and the initial stages of the processing focus upon finding X* while the other elements of each population solution remain essentially “computational overhead”. Based upon the objective value F(X*), establish P target values. P represents the desired number of maximally different alternatives to be generated within prescribed target deviations from the X*.

Note: The value for P has to have been set a priori by the decision-maker.

  1. Step 1.

    Create the initial population of size K in which each solution is divided into P equally-sized partitions. The size of each partition corresponds to the number of variables for the original optimization problem. A p represents the pth alternative, p = 1,…,P, in each solution.

  2. Step 2.

    In each of the K solutions, evaluate each A p , p = 1,…,P, with respect to the modelled objective. Alternatives meeting their target constraint and all other problem constraints are designated as feasible, while all other alternatives are designated as infeasible. A solution can only be designated as feasible if all of the alternatives contained within it are feasible.

  3. Step 3.

    Apply an appropriate elitism operator to each solution to rank order the best individuals in the population. The best solution is the feasible solution containing the most distant set of alternatives in the decision space (the distance measure is defined in Step 5). Note: Because the best solution to date is always retained in the population throughout each iteration of the FA, at least one solution will always be feasible. A feasible solution for the first step can always consists of P repetitions of X*.

This step simultaneously selects a set of alternatives that respectively satisfy different values of the target T while being as far apart as possible (i.e. maximally different as defined in [P1]) from the other solutions generated. By the co-evolutionary nature of the FA, the alternatives are simultaneously generated in one pass of the procedure rather than the P implementations suggested by the necessary increments to T in problem [P1].

  1. Step 4.

    Stop the algorithm if the termination criteria (such as maximum number of iterations or some measure of solution convergence) are met. Otherwise, proceed to Step 5.

  2. Step 5.

    For each solution k = 1,…, K, calculate D k , a distance measure between all of the alternatives contained within solution k.

As an illustrative example for determining a distance measure, calculate

$$D_{k} = \sum\limits_{i = 1\,to\,P} {\sum\limits_{j = 1\,to\,P} {\Delta (A_{i} ,A_{j} )} } .$$

This represents the total distance between all of the alternatives contained within solution k. Alternatively, the distance measure could be calculated by some other appropriately defined function.

  1. Step 6.

    Rank the solutions according to the distance measure D k objective—appropriately adjusted to incorporate any constraint violation penalties for infeasible solutions. The goal of maximal difference is to force alternatives to be as far apart as possible in the decision space from the alternatives of each of the partitions within each solution. This step orders the specific solutions by those solutions which contain the set of alternatives which are most distant from each other.

  2. Step 7.

    Apply appropriate FA “change operations” to the each of the solutions and return to Step 2.

5 Computational Testing of Simultaneous MGA Algorithm

As alluded to in the earlier sections, non-mathematically orientated, “real world” planners generally prefer to be able to select from a set of “near-optimal” alternatives that significantly differ from each other in terms of the system structures characterized by their decision variables. The ability of the FA MGA procedure to simultaneously produce such maximally different alternatives will be demonstrated using a non-linear optimization problem taken from [12]. The mathematical formulation for this multimodal problem is:

$$\begin{array}{*{20}c} {\text{Maximize}}\,F(x,y) = \sin (19\pi x) + \frac{x}{1.7} + \sin (19\pi y) + \frac{y}{1.7} + 2 \\ {\begin{array}{*{20}l} {0.0 \le x \le 1.0} \hfill & {0.0 \le y \le 1.0} \hfill \\ \end{array} } \\ \end{array}$$

The non-linear, feasible region contains 100 peaks separated by valleys in which the amplitudes of both the peaks and valleys increase as the values of the decision variables increase from the (0,0) toward (1,1). For the design parameters employed in this formulation, the best solution of F(x, y) = 5.146 occurs at point (x, y) = (0.974, 0.974) [12].

In order to create the set of different alternatives, extra target constraints that varied the value of T by up to 1.5% between successive alternatives were placed into the original formulation in order to force the generation of solutions maximally different from the initial optimal solution (i.e. the values of the bound were set at 1.5, 3, 4.5%, etc. for the respective alternatives). The MGA maximal difference algorithm described in the previous section was run to produce the optimal solution and the 10 maximally different solutions shown in Table 1 and illustrated in Fig. 1.

Table 1 Objective values and solutions for the 11 maximally different alternatives
Full size table
Fig. 1
figure 1

Dispersion of the maximally different alternatives throughout the decision space

Full size image

As described earlier, most “real world” optimization applications tend to be riddled with incongruent performance requirements that are exceedingly difficult to quantify. Consequently, it is preferable to create a set of quantifiably good alternatives that provide very different perspectives to the potentially unmodelled performance design issues during the policy formulation stage. The unique performance features captured within these dissimilar alternatives can result in very different system performance with respect to the unmodelled issues, hopefully thereby addressing some of the unmodelled issues into the actual solution process.

The example in this section underscores how a co-evolutionary MGA modelling perspective can be used to simultaneously generate multiple alternatives that satisfy known system performance criteria according to the prespecified bounds and yet remain as maximally different from each other as possible in the decision space. In addition to its alternative generating capabilities, the FA component of the MGA approach simultaneously performs extremely well with respect to its role in function optimization. It should be explicitly noted that the cost of the overall best solution produced by the MGA procedure is indistinguishable from the one determined in [12].

The computational example has demonstrated several important findings with respect to the simultaneous FA-based MGA method: (i) The co-evolutionary capabilities within the FA can be exploited to generate more good alternatives than planners would be able to create using other MGA approaches because of the evolving nature of its population-based solution searches; (ii) By the design of the MGA algorithm, the alternatives generated are good for planning purposes since all of their structures will be maximally different from each other (i.e. these differences are not just simply different from the overall optimal solution as in an HSJ-style approach to MGA); and, (iv) The approach is computationally efficient since it need only be run a single time in order to generate its entire set of multiple, good solution alternatives (i.e. to generate n solution alternatives, the MGA algorithm needs to run exactly once irrespective of the value of n).

6 Conclusions

“Real world” decision-making problems generally possess multidimensional performance specifications that are compounded by incompatible performance objectives and unquantifiable modelling features. These problems usually contain incongruent design requirements which are very difficult—if not impossible—to capture at the time that supporting decision models are formulated. Consequently, there are invariably unmodelled problem facets, not apparent during the model construction, that can greatly impact the acceptability of the model’s solutions to those end users that must actually implement the solution. These uncertain and competing dimensions force decision-makers to integrate many conflicting sources into their decision process prior to final solution construction. Faced with such incongruencies, it is unlikely that any single solution could ever be constructed that simultaneously satisfies all of the ambiguous system requirements without some significant counterbalancing involving numerous tradeoffs. Therefore, any ancillary modelling techniques used to support decision formulation have to somehow simultaneously account for all of these features while being flexible enough to encapsulate the impacts from the inherent planning uncertainties.

In this chapter, an MGA procedure was presented that demonstrated how the population structures of a computationally efficient FA could be exploited to simultaneously generate multiple, maximally different, near-best alternatives. In this MGA capacity, the approach produces numerous solutions possessing the requisite structural characteristics, with each generated alternative guaranteeing a very different perspective to the problem. Since FA techniques can be modified to solve a wide variety of problem types, the practicality of this MGA approach can clearly be extended into numerous disparate planning applications. These extensions will be studied in future research.