Keywords

1 Introduction

In recent years, the areas of physics and swarm intelligence have generated a large number of algorithms, many of which have been effective and efficient in solving complex optimization problems. Examples of these algorithms are Ant Colony Optimization [8], Firefly Algorithm [17], Gravitational Search Algorithm [14], Cuckoo Search Algorithm [18], Particle Swarm Optimization [9]. Many of these algorithms have the characteristic that the movement of the particles are performed in a continuous space. On the other hand, combinatorial problems arise in many areas of computer science and application domains. For example in protein structure prediction, grouping routing, planning, scheduling and timetabling problems. It is natural to try to apply algorithms inspired by physics and swarm intelligence in these combinatorial problems [4]. In the process of adaptation a series of difficulties arise when moving from continuous spaces to discrete spaces. Examples of these difficulties are spacial disconnect, hamming cliffs, loss of precision and the curse of dimension [12]. This has the consequence that binarizations are not always effective and efficient [11].

In this paper, a general binarization technique called Percentile Transition Ranking Algorithm (PTRA) is proposed to binarize continuous swarm intelligence metaheuristics. The main operator corresponds to the percentile ranking transition operator. This operator performs the binarization using percentiles grouping process and it is complemented with local search and perturbation operators. The main goal of this work corresponds to evaluate our algorithm when dealing with an NP-hard combinatorial optimization problem such as the MKP. To develop the evaluation, we used the metaheuristic Cuckoo Search. The metaheuristic Cuckoo Search was chosen because it is a swarm intelligence continuous metaheuristic that has been widely used in combinatorial problems [5, 15].

Experiments were developed that shed light on the contribution of the different operators to the effectiveness of the algorithm. Moreover, our algorithm was compared with recent algorithms that use transfer functions as binarization method. For this purpose we use tests problems from the OR-Library.Footnote 1 We compared our framework with the Binary Artificial Algae Algorithm (BAAA) published by [19]. The numerical results show that PTRA achieves highly competitive results.

The remainder of this paper is organized as follows. Section 2 briefly introduces the Knapsack problem. In Sect. 3 we explain the transition ranking binarization algorithm. The results of numerical experiments are presented in Sect. 4. Finally we provide the conclusions of our work.

2 KnapSack Problem

The MKP is a combinatorial problem that has multiple applications in science and engineering. For example capital budgeting and project selection applications. The MKP has also been introduced to model problems like cutting stock, loading problems, allocation of processors in a distributed data processing [7], and delivery in vehicles with multiple compartments [3].

Numerous methods have been developed to solve the MKP. The exact methods were applied in the 80’s to solve MKP. They generate a variety of methods including dynamic programming, branch-and-bound, network approach and reduction schemes. The exact methods have made possible the solution of middle size MKP instances. The major drawback of these methods remains the temporal complexity when dealing with large instances. Therefore, many researchers focus on heuristic and meta-heuristic search methods which can produce solutions of good qualities in a reasonable amount of time. In recent years, many bio-inspired and physics based algorithms, such Swarm Optimization [2], Firefly algorithm [1], Binary Black Hole [6] and Binary Fruitfly [16] have been proposed to solve large instances of the MKP.

The MKP problem belongs to the class of NP-hard problems. MKP corresponds to a model of resource allocation, whose objective is to select a subset of objects that produce the greatest benefit considering certain capacity constraints. Each object j consumes a different amount of resources in each dimension. Also each object has a profit associated. Formally the MKP can be set as:

$$\begin{aligned} \text{ maximize } \sum _{j=1}^n p_jx_j \end{aligned}$$
(1)
$$\begin{aligned} \text{ subjected } \text{ to } \sum _{j=1}^n c_{ij}x_j \le b_i \text{, } i \in \{1,...,m\} \end{aligned}$$
(2)
$$\begin{aligned} \text{ with } x_j \in \{0,1\} \text{, } j \in \{1,...,n\} \end{aligned}$$
(3)

where \(p_j\) is the profit for the item j, \(c_{ij}\) corresponds to the consumption of resources of item j in the dimension i, and \(b_i\) is the capacity constraint of each dimension i. The representation of a solution of the problem is modelled naturally in binary form where 0 in the j-th position means that the j item is not included in the Knapsack and 1 indicates that j is included.

3 Percentile Transition Ranking Algorithm

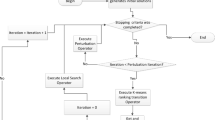
The first step of PTRA corresponds to the initialization of the feasible solutions Sect. 3.2. Once the initialization of the particles is performed, it is consulted if the detention criterion is satisfied. This criterion includes a maximum of iterations. Subsequently, if the criterion is not satisfied, the percentile transition ranking operator is executed (Sect. 3.2). This operator is responsible for performing the iteration of solutions. Once the transitions of the different solutions are made, we compare the resulting solutions with the best solution previously obtained. In the event that a superior solution is found, this replaces the previous one. When a replacement occurs, the new solution is subjected to a local search operator. Finally, having met a number of iterations where there has not been a replacement for the best solution, a perturbation operator is used. The general algorithm scheme is detailed in Fig. 1. In the following subsection we will explain in detail the initialization method, the percentile transition ranking operator and the repair operator. The explanation of the other operators will be left for an extended version.

Fig. 1.
figure 1

Flowchart of the percentile transition ranking algorithm.

Full size image

3.1 Initialization and Element Weighting

PTRA uses a binarization of swarm-intelligence metaheuristics to try to find the optimum. Each of these possible solutions, is generated as follows: First we select an item randomly. Subsequently we consulted the constraints of our problem if there are other elements that can be incorporated. The list of possible elements to be incorporated is obtained, the weight for each of these elements is calculated and the best element is selected. The procedure continues until no more elements can be incorporated. The initialization algorithm is detailed in Fig. 2.

Several techniques were proposed in the literature, to calculate the weight of each element. For example [13] introduced the pseudo-utility in the surrogate duality approach. The pseudo-utility of each variable was given in Eq. 4. The variable \(w_j\) is the surrogate multiplier between 0 and 1 which can be viewed as shadow prices of the j-th constraint in the linear programming (LP) relaxation of the original MKP

$$\begin{aligned} \delta _i = \frac{p_i}{\sum _{j=1}^m w_jc_{ij}} \end{aligned}$$
(4)

Another more intuitive measure is proposed by [10]. This measure is focused on the average occupancy of resources. Its equation is shown in 5.

$$\begin{aligned} \delta _i = \frac{\sum _{j=1}^m \frac{c_{ij}}{mb_j}}{p_i} \end{aligned}$$
(5)

In this paper, we propose a variation of this last measure focused on the average occupation. However this variation considers the elements that exist in backpacks to calculate the average occupancy. In each iteration depending on the selected items in the solution the measure is calculated again. The equation of this new measure is shown in Eq. 6.

$$\begin{aligned} \delta _i = \frac{\sum _{j=1}^m \frac{c_{ij}}{m (b_j - \sum _{i \in S}c_{ij})}}{p_i} \end{aligned}$$
(6)
Fig. 2.
figure 2

Flowchart of generation of a new solution.

Full size image

3.2 Percentile Transition Ranking Operator

Considering that our metaheuristic is a continuous and swarm intelligence. Due to its iterative nature, it needs to update the position of particles at each iteration. When the metaheuristic is continuous, this update is performed in \(\mathbb {R}^n\) space. In Eq. 7, the position update is presented in a general form. The \(x_{t+1}\) variable represents the x position of the particle at time t+1. This position is obtained from the position x at time t plus a \(\varDelta \) function calculated at time t+1. The function \(\varDelta \) is proper to each metaheuristic and produces values in \(\mathbb {R}^n\). For example in Cuckoo Search \(\varDelta (x) = \alpha \oplus Levy(\lambda )(x)\), in Black Hole \(\varDelta (x) = \text{ rand } \times (x_{bh}(t) - x(t))\) and in the Firefly, Bat and PSO algorithms \(\varDelta \) can be written in simplified form as \(\varDelta (x) = v(x)\).

$$\begin{aligned} x_{t+1} = x_{t} + \varDelta _{t+1}(x(t)) \end{aligned}$$
(7)

In the percentile transition ranking operator, we considering the movements generated by the metaheuristic in each dimension for all particles. \(\varDelta ^i(x)\) corresponds to the magnitude of the displacement \(\varDelta (x)\) in the i-th dimension for the particle x. Subsequently these displacement are grouped using \(\varDelta ^i(x)\), the magnitude of the displacement. This grouping is done using the percentile list. In our case the percentile list used the values {20, 40, 60, 80, 100}.

The percentile operator has as entry the parameters percentile list (percentileList) and the list of values (valuesList). Given an iteration, the list of values corresponds to the magnitude \(\varDelta ^i\) of all particles in all dimensions. As a first step the operator uses the valueList and obtains the values of the percentiles given in the percentileList. Later, each value in the valueList is assigned the group of the smallest percentile to which the value belongs. Finally, the list of the percentile to which each value belongs is returned (percentileGroupValue).

A transition probability through the function \(P_{tr}\) is assigned to each element of the valueList. This assignment is done using the percentile group assigned to each value (percentileGroupValue). For the case of this study, we particularly use the Step function given in rule 8.

$$\begin{aligned} \small P_{tr}(x^i)= \left\{ \begin{array}{@{}ccc@{}} 0.1 , &{}\text{ if } x^i \in \text{ group } \{0,1\} \\ 0.5 , &{} \text{ if } x^i \in \text{ group } \{2,3,4\} \end{array}\right. \end{aligned}$$
(8)

Afterwards the transition of each particle is performed. In the case of Cuckoo search the rule 9 is used to perform the transition, where \(\hat{x}^i\) is the complement of \(x^i\). Finally, each solution is repaired using the repair operator. The algorithm is shown in 1.

$$\begin{aligned} x^i(t+1) := \left\{ \begin{array}{@{}ccc@{}} \hat{x}^i(t) , &{}\text{ if } rand < P_{tg}(x^i) \\ x^i(t) , &{} \text{ otherwise } \end{array}\right. \end{aligned}$$
(9)
figure a

3.3 Repair Operator

In each movement performed by operators: transition ranking, local search and perturbation, it is possible to generate solutions that are infeasible. Therefore, each candidate solution must be checked and modified to meet every constraint. This verification and subsequent repairing is performed using the measure defined in Sect. 3.1 Eq. 6. The procedure is shown in Algorithm 2. As input the repair operator receives the solution \(S_{in}\) to repair, and the output of the repair operator gives the repaired solution \(S_{out}\). As a first step, the repair algorithm asks whether the solution needs to be repaired. In the case that the solution needs repair, a weight is calculated for each element of the solution using the measure defined in Eq. 6. The element of the solution with the largest measure is returned and removed from the solution. This element is named \(s_{max}\). This process is iterated until our solution does not require repair. The next step is to improve the solution. The Eq. 6 is again used for obtaining the element with the smallest measure that meets the constraints \(s_{min}\) and add \(s_{min}\) to the solution. In the case of absence of elements, empty is returned. The algorithm iterates until there are no elements that satisfy the constraints.

figure b

4 Results

4.1 Insight of PTRA Algorithm

In this section we investigated some important ingredients of PTRA to get insight into the behavior of the proposed algorithm. To carry out this comparison the first 10 problems of the set cb.5.250 of the OR library were chosen. The contribution of the percentile transition ranking operator on the final performance of the algorithm was studied. The contribution of the perturbation and local search operators will be developed in an extended version. To compare the distributions of the results of the different experiments we use violin Chart. The horizontal axis X corresponds to the problems, while Y axis uses the measure % - Gap defined in Eq. 10

$$\begin{aligned} \%-Gap = 100\frac{Best Known - SolutionValue}{Best Known} \end{aligned}$$
(10)

Furthermore, a non-parametric test, Wilcoxon signed-rank test is carried out to determine if the results of PTRA with respect to other algorithms have significant difference or not. The parameter settings and browser ranges are shown in Table 1.

Table 1. Setting of parameters for Cuckoo Search Algorithm.
Full size table

Evaluation of Percentile Transition Ranking Operator. To evaluate the contribution of the percentile transition ranking operator to the final result. We designed a random operator. This random operator executes the transition with a fixed probability (0.5) without considering the ranking of the particle in each dimension. Two scenarios were established. In the first one the perturbation and local search operators are included. In the second one these operators are excluded. PTRA corresponds to our standard algorithm. 05.pe is the random variant that includes the perturbation and local search operators. wpe corresponds to the version with percentile transition operator without perturbation and local search operators. Finally 05.wpe describes the random algorithm without perturbation and local search operators.

Fig. 3.
figure 3

Evaluation of percentile transition operator with perturbation and Local Search operators

Full size image
Table 2. Evaluation of percentile transition ranking operator
Full size table
Fig. 4.
figure 4

Evaluation of percentile transition operator without perturbation and Local Search operators

Full size image

When we compared the Best Values between PTRA and 05.pe which are shown in Table 2. PTRA outperforms to 05.pe. However the Best Values between both algorithms are very close. In the Average comparison, PTRA outperforms 05.pe in all problems. The comparison of distributions is shown in Fig. 3. We see the dispersion of the 05.pe distributions are bigger than the dispersions of PTRA. In particular this can be appreciated in the problems 1, 4, 5, 6, and 9. Therefore, the percentile transition ranking operator together with perturbation and local search operators, contribute to the precision of the results. Finally, the PTRA distributions are closer to zero than 05.pe distributions, indicating that PTRA has consistently better results than 05.pe. When we evaluate the behaviour of the algorithms through the Wilcoxon test, this indicates that there is a significant difference between the two algorithms.

Table 3. OR-Library benchmarks MKP cb.5.500
Full size table

Our next step is trying to separate the contribution of local search and perturbation operator from the percentile transition operator. For this, we compared the algorithms wpe and 05.wpe.

When we check the Best Values shown in the Table 2, we note that wpe performs better than 05.wpe in all problems except 3 and 7. However the results are quite close. In the case of the average indicator, wpe outperforms in all problems to 05.wpe. The Wilcoxon test indicates that the difference is significant. This suggests that wpe is consistently better than 05.wpe. In the violin chart shown n the Fig. 4 it is further observed that the dispersion of the solutions for the case of 05.wpe is much larger than in the case of wpe. This indicates that the operator percentile transition ranking plays an important role in the precision of the results.

4.2 PTRA Compared with BAAA

In this section we evaluate the performance of our PTRA with the algorithm BAAA developed in [19]. BAAA uses transfer functions as a general mechanism of binarization. In particular BAAA used the \(\tanh = \frac{e^{\tau |x|}-1}{e^{\tau |x|}+1}\) function to perform the transference. The parameter \(\tau \) of the \(\tanh \) function was set to a value 1.5. Additionally, a elite local search procedure was used by BAAA to improve solutions. As maximum number of iterations BAAA used 35000. The computer configuration used to run the BAAA algorithm was: PC Intel Core(TM) 2 dual CPU Q9300@2.5GHz, 4GB RAM and 64-bit Windows 7 operating system. In our PTRA algorithm, the configurations are the same used in the previous experiments. These are described in the Table 1.

The results are shown in Table 3. The comparison was performed for the set cb.5.500 of the OR-library. The results for PTRA were obtained from 30 executions for each problem. In black, the best results are marked for both indicators the Best Value and the Average. In the Best Value indicator, BAAA was higher in eight instances and PTRA in twenty two. In the averages indicator BAAA was higher in two instances, and PTRA in eighteen. We should also note that the standard deviation in most problems was quite low, indicating that PTRA has good accuracy.

5 Conclusions and Future Work

In this article, we proposed a algorithm whose main function is to binarize continuous swarm intelligence metaheuristics. To evaluate the performance of our algorithm, the multidimensional Knapsack problem was used together with the Cuckoo Search metaheuristic. The contribution of the main operator of the algorithm was evaluated, finding that the percentile transition ranking operator contributes significantly to improve the precision of the solutions. Finally, in comparison with state of the art algorithms our algorithm showed a good performance.

As a future works we want to investigate the behaviour of other metaheuristics. Furthermore, the algorithm must be verified with other NP-hard problems. Moreover to simplify the choice of the appropriate configuration, it is important to explore adaptive techniques. From an understanding point of view of how the framework performs binarization, it is interesting to understand how the algorithm alters the properties of exploration and exploitation. Also is interesting to study how the velocities and positions generated by continuous metaheuristics are mapped to positions in the discrete space.