Abstract
Outline We consider quantitative game models for the design of reactive systems working in resource-constrained environment. The game is played on a finite weighted graph where some resource (e.g., battery) can be consumed or recharged along the edges of the graph.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Outline. We consider quantitative game models for the design of reactive systems working in resource-constrained environment. The game is played on a finite weighted graph where some resource (e.g., battery) can be consumed or recharged along the edges of the graph.
In mean-payoff games, the resource usage is computed as the long-run average resource consumption. In energy games, the resource usage is the initial amount of resource necessary to maintain the resource level always positive.
We review fundamental results about mean-payoff games that show the existence of memoryless optimal strategies, and the equivalence of mean-payoff games with finite-duration reachability games, as well as with energy games (which can also be viewed as safety games). These results provide conceptually simple backward-induction algorithms for solving mean-payoff games, and for constructing memoryless optimal strategies. It follows that mean-payoff games can be solved in NP \(\cap \) coNP.
Then we consider games with multiple mean-payoff conditions for systems using multiple resources. In multi-dimension mean-payoff games, memory is necessary for optimal strategies, and the previous equivalence results with reachability and energy (safety) games no longer hold. First, infinite memory is necessary in general for optimal strategies. With infinite memory, the limit of the long-run average resource consumption may not exist, and it is necessary to distinguish between the limsup and the liminf of the long-run average resource consumption. Second, the equivalence with a multi-dimensional version of energy games holds only if the players are restricted to use finite-memory strategies, and in that case the limsup- and the liminf-value coincide.
The complexity of solving multi-dimension mean-payoff games is as follows, depending on which class of strategies is given to the player: NP-complete for memoryless strategies, coNP-complete for finite-memory strategies, NP \(\cap \) coNP for infinite-memory strategies and a conjunction of limsup objectives, and coNP-complete for infinite-memory strategies and a conjunction of liminf objectives.
Games. We consider two-player games of infinite duration, as a model of non-terminating reactive systems with controllable and uncontrollable actions. Such models have applications in the verification and synthesis of reactive systems [3, 36, 38], and fundamental connections with many areas of computer science, such as logic and automata [24, 27, 37].
The game is played for infinitely many rounds, on a finite graphs \(\langle V,E \rangle \) with vertices \(V = V_1 \uplus V_2\) partitioned into player-1 and player-2 vertices. Initially a token is placed on a designated vertex \(v_0 \in V\). In each round the player owning the vertex \(v_i\) where the token lies moves the token to a successor vertex \(v_{i+1}\) along an edge \((v_i,v_{i+1}) \in E\) of the graph. The outcome of the game is an infinite path \(v_0,v_1,\dots \) called a play. In the traditional qualitative analysis, plays are classified as either winning or losing (for player 1). An objective is a set \(\varOmega \subseteq V^{\omega }\) of winning plays. The goal of player 1 is to achieve a winning play: the central qualitative question is to decide if there exists a strategy for player 1 such that for all strategies of player 2 the outcome is a winning play in \(\varOmega \). Sets of winning plays defined by \(\omega \)-regular conditions are central in verification and synthesis of reactive systems [36, 38] and have been extensively studied [10, 18, 26].
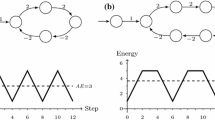
Mean-Payoff and Energy Games. For the design of reactive systems working in resource-constrained environment, we consider weighted graphs \(\langle V,E,w \rangle \) where \(w: E \rightarrow {\mathbb Z}\) is a weight function that assigns a resource consumption to each edge of the graph. The limit-average value (or mean-payoff value) of a play  is defined in two variants, the limsup-average
is defined in two variants, the limsup-average

and the liminf-average

The goal of player 1 is to maximize the mean-payoff value, and the associated decision problem is to decide, given a threshold value \(\nu \in {\mathbb Q}\), whether there exists a winning strategy for player 1 for the mean-payoff objective  (or,
(or,  ) with a mean-payoff value at least \(\nu \). In the sequel we only consider the case \(\nu = 0\), which can be obtained by shifting all weights in the graph by the given value \(\nu \) (and scaling them to get integers).
) with a mean-payoff value at least \(\nu \). In the sequel we only consider the case \(\nu = 0\), which can be obtained by shifting all weights in the graph by the given value \(\nu \) (and scaling them to get integers).
Memoryless strategies are sufficient to win mean-payoff games [23] and the associated decision problem lies in NP \(\cap \) coNP [32, 43]. The solution of mean-payoff games is more intuitive by considering the class of energy games [6, 11] where the objective of player 1 is to maintain the accumulated resource level (i.e., the energy level) always nonnegative, given an initial credit value \(c_0 \in \mathbb N\). The energy level of a finite path with initial credit \(c_0\) is defined by
and the energy objective is
The associated decision problem asks whether there exists \(c_0\) such that player 1 has a winning strategy for the energy objective with initial credit \(c_0\). It is important that the initial credit \(c_0\) is not fixed to obtain the equivalence with mean-payoff games (see next paragraph). For fixed initial credit we get a variant of energy games (see Related Work). Note that the energy condition is a safety condition [1]: if a finite prefix of a play violates the energy condition, then every continuation violates the energy condition.
Memoryless Determinacy and Equivalence Results. Intuitively, player 1 wins the energy game if he can ensure that whenever a cycle is formed in the play, the cycle has nonnegative sum of weights. The converse is also true [6, 39]. Consider a finite-duration game played analogously to the games we considered so far, but that stops whenever a cycle is formed, and declared won by player 1 if and only if the cycle is nonnegative. If player 1 wins the finite-duration game, then we can use his strategy to play the energy game and ensure that all cycles that are formed are nonnegative and therefore a finite initial credit \(c_0\) is sufficient to survive along acyclic portions of the play (thus \(c_0 \le |V| \cdot W\) is sufficient, where W is the largest absolute weight in the graph). Conversely, if player 1 cannot avoid that a negative cycle is formed in the finite-duration game, then it is easy to show that player 2 can fix a strategy to ensure that only negative cycles are formed in the energy game, which would exhaust any arbitrary finite initial credit. Thus player 1 cannot win the energy game.
This argument reduces energy games to a reachability game in the finite tree obtained by unfolding the original graph and stopping a branch whenever a cycle is formed. Each leaf corresponds to the closing of a cycle, and the leaves associated with a positive cycle define the target nodes of a reachability objective for player 1. Using backward induction on the tree it is easy to establish that from all nodes where player 1 has a winning strategy for the reachability objective, finite initial credit is sufficient for the energy objective.
Finally, to establish the equivalence with mean-payoff games [6, 23], it is easy to see that if player 1 can ensure that only nonnegative cycles are formed along a play, than the mean-payoff value is nonnegative (both for the limsup and the liminf variants), and otherwise player 2 can ensure that only negative cycles are formed, and the mean-payoff value is negative. It follows that mean-payoff games are determined (i.e., if player 1 does not have a winning strategy for \(\overline{\mathsf{MP}}^{\ge 0}\), then player 2 has a winning strategy for the complement \(V^{\omega } \setminus \overline{\mathsf{MP}}^{\ge 0}\)). Moreover, viewing energy games as a safety game it is easy to show that memoryless strategies are sufficient to win energy games, and that the same strategy can be used for the mean-payoff objective, showing the memoryless determinacy of mean-payoff games.
We can solve mean-payoff games in NP by guessing a memoryless strategy for player 1 and checking that it induces only nonnegative reachable cycles in the graph game, which can be done in polynomial time using shortest-path algorithms. By memoryless determinacy, a coNP algorithm can guess a memoryless winning strategy for player 2. Hence mean-payoff games are in NP \(\cap \) coNP [32, 43], which can be improved to UP \(\cap \) coUP [30]. Mean-payoff games can be solved in \(O(|V| \cdot |E| \cdot W)\), thus in P for weights encoded in unary [9]. It is a long-standing open question to know whether mean-payoff games can be solved in polynomial time for weights encoded in binary.
Multi-Dimension Mean-Payoff Games. In multi-dimension mean-payoff games, the weight function \(w: E \rightarrow {\mathbb Z}^k\) assigns a vector of resource consumption to each edge of the graph. The objective of player 1 is to ensure the mean-payoff objective in each dimension \(1, \dots ,k\), thus a conjunction of k one-dimension mean-payoff objectives with threshold 0. Hence for player 2 the objective is a disjunction of mean-payoff objectives. Simple examples show that infinite memory may be necessary for player 1, for both the limsup and the liminf variants [42]. Moreover, the conjunction of mean-payoff objectives is not equivalent to a conjunction of energy conditions (which requires to maintain the accumulated resource level always nonnegative in every dimension, for some vector of finite initial credit).
Since infinite memory may be necessary for player 1, we consider the problem of deciding the existence of a winning strategy with the following memory restrictions: memoryless strategies, finite-memory strategies, and the general case of infinite-memory strategies [42]. With memoryless strategies, the decision problem is NP-complete. With finite-memory strategies, multi-dimension mean-payoff games are equivalent to energy games, in both the limsup and the liminf variants; memoryless strategies are sufficient for player 2 and the problem is coNP-complete. In the general case with infinite-memory strategies, the problem is in NP \(\cap \) coNP for conjunctions of limsup-average, and coNP-complete for conjunctions of liminf-average. In both cases memoryless strategies are sufficient for player 2. Thus in all cases player 2 does not need memory, but the proofs of the memoryless results rely on different techniques (see next paragraph).
Memoryless Strategies in Mean-Payoff Games. In the results presented above, it is crucial to establish that memoryless strategies are sufficient for one player (and sometimes for both). We emphasize that different techniques can be used to prove those memorylessness results.
Edge induction and shuffling. A general technique is to use edge induction [25, 34]: to prove that a player is memoryless, consider for example a vertex v owned by that player with two outgoing edges, and consider the game \(G_1\) obtained by removing the first outgoing edge, and the game \(G_2\) obtained by removing the second outgoing edge. By induction we argue that memoryless strategies are sufficient for the player owning v in the games \(G_1\) and \(G_2\), and we need to show that no (arbitrary) strategy in the original game can achieve a better value than either the optimal (memoryless) strategy in \(G_1\) or in \(G_2\). Thus switching between the two outgoing transitions when visiting the vertex v does not give a better play (for the owner of v). Roughly, such a play can be decomposed into the appropriate shuffling of a play in \(G_1\) and a play in \(G_2\), and essentially it suffices to show (in case the owner of v is a minimizer, i.e., player 2) that the mean-payoff value of a shuffle of two plays is not smaller than the min of the values of the two plays, which holds for liminf-average (but not for limsup-average [33, 42]). Dually, in case the owner of v is a maximizer, i.e., player 1, we need to show that the mean-payoff value of a shuffle of two plays is not greater than the max of the values of the two plays.
This technique can be used to show that player 2 is memoryless in multi-dimension energy games, and in the liminf-average variant of mean-payoff games.
Backward induction. To show memorylessness in one-dimension energy games, a simpler proof uses a monotonicity property that if an outgoing edge is a good choice from a vertex v when the current accumulated resource level is x, then the same outgoing edge is a good choice in v for all accumulated resource levels \(x' > x\). Therefore in every vertex there exists a choice of outgoing edge that is independent of the current resource level and defines a memoryless winning strategy. This argument is similar to the proof that safety games admit memoryless winning strategies: to win a safety game it is sufficient to always choose a successor vertex that lies in the winning set.
Nested memoryless objectives. As the edge-induction technique does not work to show that player 2 is memoryless in limsup-average mean-payoff games, we use a specific result, based on nested (iterated) elimination of losing vertices: if from a given vertex v player 1 cannot win for one of the limsup-average mean-payoff objective, then v is a losing vertex for player 1 (and player 2 can use a memoryless strategy to win). Given a set \(L \subseteq V\) of such losing vertices, all vertices from which player 2 can ensure to reach L are also losing for player 1. Note that player 2 can use a memoryless strategy to reach L. As long as such losing vertices (for player 1) exist, the above argument shows that player 2 has a memoryless strategy to win. The conclusion of the argument is to show that if no losing vertex remains (for any of the one-dimension objectives), then player 1 wins for the multi-dimension objective from every remaining vertex [42].
Related Work. We give pointers to the literature related to multiple mean-payoff conditions in graphs and games. Deriving a deterministic algorithm from the coNP result for multi-dimension mean-payoff games gives an algorithm that is exponential in the number of vertices. The hyperplane separation technique gives an algorithm that is polynomial for fixed dimension k and bounded weights [21]. The technique has been extended to obtain a pseudo-polynomial algorithm for solving multi-dimension energy games of fixed dimension with a fixed initial credit [31]. Strategy synthesis is studied in [20] showing that exponential memory is sufficient for winning strategies in multi-dimension energy games (and thus in multi-dimension mean-payoff games under finite-memory strategies). Finitary variants of mean-payoff objectives have been considered in [17].
The vector of Pareto-optimal thresholds for multi-dimension mean-payoff games is studied in [8], showing that deciding if there exists a vector of threshold in a given polyhedron that can be ensured by player 1 is complete for \(\text {NP}{}^\text {NP}\). Games with a Boolean combination of mean-payoff objectives are undecidable [41], and their restriction to finite-memory strategies is inter-reducible with Hilbert’s tenth problem over the rationals [40]. Mean-payoff conditions have been used to define quantitative specification frameworks with appealing expressiveness and closure properties [2, 15]. The special case of a Boolean combination of mean-payoff objectives defined by a one-dimension weight function gives rise to interval objectives, solvable in NP \(\cap \) coNP [29].
We discuss three directions to extend the model of two-player mean-payoff games. First, the mean-payoff objective has been combined with Boolean objectives such as the parity condition, a canonical form to express \(\omega \)-regular conditions, in one dimension [13, 19] and in multiple dimensions [5, 20]. Note that parity games can be reduced to (one-dimension) mean-payoff games [30], which can be reduced to discounted-sum games, themselves reducible to simple stochastic games [43]. Second, the mean-payoff objective has been considered in Markov decision processes [7, 12] and stochastic games [4, 14], in combination with parity condition [16] and under finite-memory strategies [14]. Third, mean-payoff and energy games (in single dimension) with partial observation have been shown undecidable [22, 28]. Special assumptions on the structure of the game lead to decidable subclasses [28]. Partial-observation energy games with fixed initial credit are Ackermann-complete [35].
References
Alpern, B., Demers, A.J., Schneider, F.B.: Safety without stuttering. Inform. Process. Lett. 23(4), 177–180 (1986)
Alur, R., Degorre, A., Maler, O., Weiss, G.: On omega-languages defined by mean-payoff conditions. In: Alfaro, L. (ed.) FoSSaCS 2009. LNCS, vol. 5504, pp. 333–347. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00596-1_24
Alur, R., Henzinger, T.A., Kupferman, O.: Alternating-time temporal logic. J. ACM 49, 672–713 (2002)
Basset, N., Kwiatkowska, M., Topcu, U., Wiltsche, C.: Strategy synthesis for stochastic games with multiple long-run objectives. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 256–271. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46681-0_22
Bohy, A., Bruyère, V., Filiot, E., Raskin, J.-F.: Synthesis from LTL specifications with mean-payoff objectives. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013. LNCS, vol. 7795, pp. 169–184. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36742-7_12
Bouyer, P., Fahrenberg, U., Larsen, K.G., Markey, N., Srba, J.: Infinite runs in weighted timed automata with energy constraints. In: Cassez, F., Jard, C. (eds.) FORMATS 2008. LNCS, vol. 5215, pp. 33–47. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85778-5_4
Brázdil, T., Brožek, V., Chatterjee, K., Forejt, V., Kučera, A.: Markov decision processes with multiple long-run average objectives. Logical Meth. Comput. Sci.10(1:13) (2014)
Brenguier, R., Raskin, J.-F.: Pareto curves of multidimensional mean-payoff games. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9207, pp. 251–267. Springer, Cham (2015). doi:10.1007/978-3-319-21668-3_15
Brim, L., Chaloupka, J., Doyen, L., Gentilini, R., Raskin, J.-F.: Faster algorithms for mean-payoff games. Formal Meth. Syst. Des. 38(2), 97–118 (2011)
Büchi, J.R., Landweber, L.H.: Solving sequential conditions by finite-state strategies. Trans. Am. Math. Soc. 138, 295–311 (1969)
Chakrabarti, A., Alfaro, L., Henzinger, T.A., Stoelinga, M.: Resource interfaces. In: Alur, R., Lee, I. (eds.) EMSOFT 2003. LNCS, vol. 2855, pp. 117–133. Springer, Heidelberg (2003). doi:10.1007/978-3-540-45212-6_9
Chatterjee, K.: Markov decision processes with multiple long-run average objectives. In: Arvind, V., Prasad, S. (eds.) FSTTCS 2007. LNCS, vol. 4855, pp. 473–484. Springer, Heidelberg (2007). doi:10.1007/978-3-540-77050-3_39
Chatterjee, K., Doyen, L.: Energy parity games. In: Abramsky, S., Gavoille, C., Kirchner, C., Meyer auf der Heide, F., Spirakis, P.G. (eds.) ICALP 2010. LNCS, vol. 6199, pp. 599–610. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14162-1_50
Chatterjee, K., Doyen, L.: Perfect-information stochastic games with generalized mean-payoff objectives. In: Proceedings of LICS: Logic in Computer Science, pp. 247–256. ACM (2016)
Chatterjee, K., Doyen, L., Edelsbrunner, H., Henzinger, T.A., Rannou, P.: Mean-payoff automaton expressions. In: Gastin, P., Laroussinie, F. (eds.) CONCUR 2010. LNCS, vol. 6269, pp. 269–283. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15375-4_19
Chatterjee, K., Doyen, L., Gimbert, H., Oualhadj, Y.: Perfect-information stochastic mean-payoff parity games. In: Muscholl, A. (ed.) FoSSaCS 2014. LNCS, vol. 8412, pp. 210–225. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54830-7_14
Chatterjee, K., Doyen, L., Randour, M., Raskin, J.-F.: Looking at mean-payoff and total-payoff through windows. In: Hung, D., Ogawa, M. (eds.) ATVA 2013. LNCS, vol. 8172, pp. 118–132. Springer, Cham (2013). doi:10.1007/978-3-319-02444-8_10
Chatterjee, K., Henzinger, T.A.: A survey of stochastic \(\omega \)-regular games. J. Comput. Syst. Sci. 78(2), 394–413 (2012)
Chatterjee, K., Henzinger, T.A., Jurdziński, M.: Mean-payoff parity games. In: Proceedings of LICS: Logic in Computer Science, pp. 178–187. IEEE Computer Society (2005)
Chatterjee, K., Randour, M., Raskin, J.-F.: Strategy synthesis for multi-dimensional quantitative objectives. Acta Inf. 51, 129–163 (2014)
Chatterjee, K., Velner, Y.: Hyperplane separation technique for multidimensional mean-payoff games. In: D’Argenio, P.R., Melgratti, H. (eds.) CONCUR 2013. LNCS, vol. 8052, pp. 500–515. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40184-8_35
Degorre, A., Doyen, L., Gentilini, R., Raskin, J.-F., Toruńczyk, S.: Energy and mean-payoff games with imperfect information. In: Dawar, A., Veith, H. (eds.) CSL 2010. LNCS, vol. 6247, pp. 260–274. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15205-4_22
Ehrenfeucht, A., Mycielski, J.: Positional strategies for mean payoff games. Int. J. Game Theory 8(2), 109–113 (1979)
Emerson, E.A., Jutla, C.: Tree automata, mu-calculus and determinacy. In: Proceedings of FOCS: Foundations of Computer Science, pp. 368–377. IEEE (1991)
Gimbert, H., Zielonka, W.: When can you play positionally? In: Fiala, J., Koubek, V., Kratochvíl, J. (eds.) MFCS 2004. LNCS, vol. 3153, pp. 686–697. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28629-5_53
Mazala, R.: Infinite games. In: Grädel, E., Thomas, W., Wilke, T. (eds.) Automata Logics, and Infinite Games. LNCS, vol. 2500, pp. 23–38. Springer, Heidelberg (2002). doi:10.1007/3-540-36387-4_2
Gurevich, Y., Harrington, L.: Trees, automata, and games. In: Proceedings of STOC: Symposium on Theory of Computing, pp. 60–65. ACM Press (1982)
Hunter, P., Pérez, G.A., Raskin, J.-F.: Mean-payoff games with partial-observation. In: Ouaknine, J., Potapov, I., Worrell, J. (eds.) RP 2014. LNCS, vol. 8762, pp. 163–175. Springer, Cham (2014). doi:10.1007/978-3-319-11439-2_13
Hunter, P., Raskin, J.-F.: Quantitative games with interval objectives. In: Proceedings of FSTTCS: Foundation of Software Technology and Theoretical Computer Science, vol. 29 of LIPIcs, pp. 365–377. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2014)
Jurdziński, M.: Deciding the winner in parity games is in UP \(\cap \) co-UP. Inf. Process. Lett. 68(3), 119–124 (1998)
Jurdziński, M., Lazić, R., Schmitz, S.: Fixed-dimensional energy games are in pseudo-polynomial time. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015. LNCS, vol. 9135, pp. 260–272. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47666-6_21
Karzanov, A.V., Lebedev, V.N.: Cyclical games with prohibitions. Math. Program. 60, 277–293 (1993)
Kelmendi, E.: Two-Player Stochastic Games with Perfect and Zero Information. Ph.D. thesis, Université de Bordeaux (2016)
Kopczyński, E.: Half-positional determinacy of infinite games. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006. LNCS, vol. 4052, pp. 336–347. Springer, Heidelberg (2006). doi:10.1007/11787006_29
Pérez, G.A.: The fixed initial credit problem for partial-observation energy games is Ack-complete. Inform. Process. Lett. 118, 91–99 (2017)
Pnueli, A., Rosner R.: On the synthesis of a reactive module. In: Proceedings of POPL, pp. 179–190. ACM Press (1989)
Rabin, M.O.: Automata on Infinite Objects and Church’s Problem. American Mathematical Society, Boston (1972)
Ramadge, P.J., Wonham, W.M.: The control of discrete event systems. Proc. IEEE 77, 81–98 (1989)
Raskin, J.-F.: A tutorial on mean-payoff and energy games. Dependable Softw. Syst. Eng. 45, 179–201 (2016)
Velner, Y.: Finite-memory strategy synthesis for robust multidimensional mean-payoff objectives. In Proceedings of CSL-LICS: Joint Meeting of Computer Science Logic (CSL) and Logic in Computer Science (LICS), pp. 79:1–79:10. ACM (2014)
Velner, Y.: Robust multidimensional mean-payoff games are undecidable. In: Pitts, A. (ed.) FoSSaCS 2015. LNCS, vol. 9034, pp. 312–327. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46678-0_20
Velner, Y., Chatterjee, K., Doyen, L., Henzinger, T.A., Rabinovich, A.M., Raskin, J.-F.: The complexity of multi-mean-payoff and multi-energy games. Inf. Comput. 241, 177–196 (2015)
Zwick, U., Paterson, M.: The complexity of mean payoff games on graphs. Theor. Comput. Sci. 158(1&2), 343–359 (1996)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Doyen, L. (2017). The Multiple Dimensions of Mean-Payoff Games. In: Hague, M., Potapov, I. (eds) Reachability Problems. RP 2017. Lecture Notes in Computer Science(), vol 10506. Springer, Cham. https://doi.org/10.1007/978-3-319-67089-8_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-67089-8_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-67088-1
Online ISBN: 978-3-319-67089-8
eBook Packages: Computer ScienceComputer Science (R0)