Equilibrium Fluctuations for the Slow Boundary Exclusion Process

Abstract

We prove that the equilibrium density fluctuations of the symmetric simple exclusion process in contact with slow boundaries is given by an Ornstein–Uhlenbeck process with Dirichlet, Robin or Neumann boundary conditions depending on the range of the parameter that rules the slowness of the boundaries.

1 Introduction

The study of nonequilibrium behavior of interacting particle systems is one of the most challenging problems in the field and it has only been completely solved in very particular cases. The toy model for the study of a system in a nonequilibrium scenario is the symmetric simple exclusion process (SSEP) whose dynamics is rather simple to explain and it already captures many features of more complicated systems.

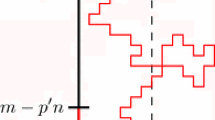
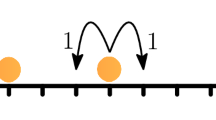
The dynamics of this model can be described as follows. We fix a scaling parameter n and we consider the SSEP evolving on the discrete space $\Sigma _n=\{1,\ldots , n-1\}$ to which we call the bulk. To each pair of bonds $\{x,x+1\}$ with $x=1,\ldots , n-2$ we associate a Poisson process $N_{x,x+1}(t)$ of rate 1. Now we artificially add two end points at the bulk, namely, we add the sites $x=0$ and $x=n$ and we superpose the exclusion dynamics with a Glauber dynamics which has only effect at the boundary points of the bulk, namely at the sites $x=1$ and $x=n-1$. For that purpose, we add extra Poisson processes at the bonds $\{0,1\}$ and $\{n-1,n\}$. In each one of these bonds there are two Poisson processes: $N_{0,1}(t)$ with parameter $\alpha n^{-\theta }$, $N_{1,0}(t)$ with parameter $(1-\alpha )n^{-\theta }$, $N_{n-1,n}(t)$ with parameter $\beta n^{-\theta }$ and $N_{n,n-1}(t)$ with parameter $(1-\beta )n^{-\theta }$. All the Poisson processes are independent. Above $\alpha , \beta \in (0,1)$ and $\theta \ge 0$ is a parameter that rules the slowness of the boundary dynamics. Below in the figure we colored the Poisson clocks associated to the bonds in the bulk in the blue color, while the Poisson clocks associated to the bonds at the boundary are colored in the gray and pink colors, to emphasize that they have different rates.

Now that the clocks are fixed we can explain the dynamics. For that purpose, initially we place particles in the bulk according to some probability measure and we denote this configuration of particles and holes by $\eta =(\eta (1),\ldots , \eta (n-1))$, so that for $x\in \Sigma _n$, $\eta (x)=1$ if there is a particle at the site x and $\eta (x)=0$ if the site x is empty. Now, if a clock rings for a bond $\{x,x+1\}$ in the bulk, then we exchange the coordinates x and $x+1$ of $\eta$, that is we exchange $\eta (x)$ with $\eta (x+1)$ at rate 1. If the clock rings for the bond at the boundary as, for example, from the Poisson process $N_{0,1}(t)$ then a particle gets into the bulk through the site 1 at rate $\alpha n^{-\theta }$ if and only if there is no particle at the site 1, otherwise nothing happens. If the clock rings from the Poisson process $N_{1,0}(t)$ and there is a particle at the site 1, then it exits the bulk from the site 1 at rate $(1-\alpha )n^{-\theta }$. Note that the higher the value of $\theta$ the slower is the dynamics at the boundaries. For a display of the description above, see the figure below.

The dynamics just described is Markovian and can be completely characterized in terms of its infinitesimal generator given below in (1). We note that the space state of this Markov process is $\varOmega _n:=\{0,1\}^{\Sigma _n}$. Observe that the bulk dynamics preserves the number of particles and our interest is to describe the space-time evolution of this conserved quantity as a solution of some partial differential equation called the hydrodynamic equation.

Note that for the choice $\alpha =\beta =\rho$ a simple computation shows that the Bernoulli product measure of parameter $\rho$ given by: $\nu ^n_{\rho }(\eta \in \varOmega _n:\eta (x)=1)=\rho$ is invariant under the dynamics. For this choice of the parameters the boundary reservoirs have the same intensity and we do not see any induced current on the system. Nevertheless, in the case $\alpha \ne \beta$, let us say for example $\alpha <\beta$, there is a tendency to have more particles entering into the bulk from the right reservoir and leaving the system from the left reservoir. This is a current which is induced by the difference of the density at the boundary reservoirs. Note that in the bulk the dynamics is symmetric. In the case $\alpha \ne \beta$, since we have a finite state Markov process, there is only one stationary measure that we denote by $\mu _n^{ss}$ which is no longer a product measure as in the case $\alpha =\beta$. By using the matrix ansatz method developed by [3, 10, 11] and references therein, it is possible to compute the correlation function in the stationary state and an important problem is to analyze the behavior of the system starting from this non-equilibrium stationary state.

We note that the hydrodynamic limit of this model was studied in [1] and the hydrodynamic equations consist in the heat equation with different types of boundary conditions depending on the range of the parameter $\theta$. More precisely, for $0\le \theta <1$ the heat equation has Dirichlet boundary conditions which fix the value of the density profile at the points 0 and 1 to be $\alpha$ and $\beta$, respectively. In this case we do not see any difference at the macroscopic level with respect to the case $\theta =0$. Nevertheless, for $\theta =1$ the boundary dynamics is slowed enough in such a way that macroscopically the Dirichlet boundary conditions are replaced by a type of Robin boundary conditions. These Robin boundary conditions state that the rate at which particles are injected into the system through the boundary points, is given by the difference of the density at the bulk and the boundary. Finally for $\theta >1$, the boundaries are sufficiently slowed so that the Robin boundary conditions are replaced by Neumann boundary conditions stating that macroscopically there is no flux of particles from the boundary reservoirs.

We emphasize that there are many similar models to the one studied in these notes which we summarize as follows. In [7,8,9], the authors consider a model where removal of particles can only occur at an interval around the left boundary and the entrance of particles is allowed only at an interval around the right boundary. Their model presents a current exchange between the two reservoirs and shows some similarities with our model for the choice $\theta =1$. Another case already studied in the literature (see [12, 19]) is when the boundary is not slowed, that corresponds to our model for the choice $\theta =0$. As mentioned above, the hydrodynamic equation of this model has Dirichlet boundary conditions, see [12] or the Eq. (7). A similar model, whose hydrodynamic equation has both Dirichlet boundary conditions and Neumann boundary conditions, was studied in [6]. The main difference, at the macroscopic level, is that the end points of the boundary conditions vary with time. The microscopic dynamics there is given by the SSEP evolving on ${\mathbb Z}$ with additional births and deaths restricted to a subset of configurations where there is a leftmost hole and a rightmost particle. In this situation, at a fixed rate j birth of particles occur at the position of the leftmost hole and at the same rate, independently, the rightmost particle dies. Another model which has a current is considered in [4]. The dynamics evolves on the discrete torus ${\mathbb Z}/n{\mathbb Z}$ without reservoirs, but has a surprising phenomenon: a “battery effect”. This effect produces a current of particles through the system and is due to a single abnormal bond, where the rates to cross from left to right and from right to left are different. Finally, another model which has similarities with the model we consider in these notes is the SSEP with a slow bond, which was studied in [13,14,15]. The dynamics evolves on the discrete torus ${\mathbb Z}/n{\mathbb Z}$, and particles exchange positions between nearest neighbor bonds at rate 1, except at one particular bond, where the exchange occurs at rate $n^{-\beta }$. In this case $\beta >0$ is a parameter that rules the slowness of the bond and for that reason the bond is called the slow bond. The similarity between the slow bond model and the slow boundary model considered in these notes is that if we “open” the discrete torus exactly at the position of the slow bond, then the slow bond gives rise to a slow boundary. In [13, 15] different hydrodynamic behaviors were obtained, depending on the range of the parameter $\beta$, more precisely, the hydrodynamic equation is, in all cases, the heat equation but the boundary conditions vary with the value of $\beta$, exhibiting three different regimes as for the slow boundary model, see [1].

Our interest in these notes is to go beyond the hydrodynamical behavior, analyzing the fluctuations around the hydrodynamical profile. To accomplish this, we restrict ourselves to the case $\alpha =\beta =\rho$ and starting from the stationary measure $\nu _\rho ^n$ defined above. Our result states that the fluctuations starting from $\nu _\rho ^n$ are given by an Ornstein–Uhlenbeck process solution of

$$\begin{aligned} d\mathcal {Y}_t=\varDelta _\theta \mathcal {Y}_tdt+\sqrt{2\chi (\rho )t}\,\nabla _\theta \, d{\mathcal W}_t\,, \end{aligned}$$

where $\chi (\rho )$ is the variance of $\eta (x)$ with respect to $\nu _\rho ^n$, ${\mathcal W}_t$ is a space-time white noise of unit variance and $\varDelta _\theta$ and $\nabla _\theta$ are, respectively, the Laplacian and derivative operators defined on a space of test functions with different types of boundary conditions depending on the value of $\theta$. We note that the case $\theta =0$ was studied in [19] and the case $\theta =1$ was studied in [16]. In those articles, the nonequilibrium fluctuations were obtained starting from general initial measures, which include the equilibrium case $\nu ^n_\rho$ treated here. We note however, that the case $\theta \ne 1$ is quite difficult to attack at the nonequilibrium scenario since we need to establish a local replacement (see Lemma 3) in order to close the martingale problem, which we can only prove starting the system from the equilibrium state. In a future work, we will dedicate to extending this result to the nonequilibrium situation as, for example, starting the system from the steady state when $\alpha \ne \beta$.

Here follows an outline of these notes. In Sect. 2 we give the definition of the model, we recall from [1] the hydrodynamic limit and in Sect. 3 we state our main result, namely, Theorem 3. In Sect. 4 we characterize the limit process by means of a martingale problem. Tightness is proved in Sect. 5 and in Sect. 6 we prove the Replacement Lemma which is the most technical part of these notes.

2 Statement of Results

2.1 The Model

For $n\ge {1}$, we denote by $\Sigma _n$ the set $\{1,\ldots ,n-1\}$, which will be referred by the expression bulk. The symmetric simple exclusion process with slow boundaries is a Markov process $\{\eta _t:\,t\ge {0}\}$ with state space $\varOmega _n:=\{0,1\}^{\Sigma _n}$. The slowness of the boundaries is ruled by a parameter that we denote by $\theta \ge 0$. If $\eta$ is a configuration of the state space $\varOmega$, then for $x\in \Sigma _n$, the random variable $\eta (x)$ can take only two values, namely 0 or 1. If $\eta (x)=0$, it means that the site x is vacant, while $\eta (x)=1$ means that the site x is occupied. The dynamics of this model can be described as follows. In the bulk particles move according to continuous time random walks, but whenever a particle wants to jump to an occupied site, the jump is suppressed. At the left boundary, particles can be created (resp. removed) at rate $\alpha n^{-\theta }$ (resp. $(1-\alpha ) n^{-\theta }$). At the right boundary, particles can be created (resp. removed) at rate $\beta n^{-\theta }$ (resp. $(1-\beta ) n^{-\theta }$).

Fix now a finite time horizon T. The Markov process $\{\eta _t(x): x\in \Sigma _n ; t\in [0,T]\}$ can be characterized in terms of its infinitesimal generator that we denote by ${\mathcal L}_{n}^\theta$ and is defined as follows. For a function $f:\varOmega _n\rightarrow {\mathbb R}$, we have that

$$\begin{aligned} ({\mathcal L}_{n}^{\theta }f)(\eta )\;=\;&\left[ \frac{\alpha }{n^\theta }(1-\eta (1))+\frac{(1-\alpha )}{n^\theta }\eta (1)\right] \left( f( \eta ^{1})-f(\eta )\right) \nonumber \\ +&\left[ \frac{\beta }{n^\theta }(1-\eta (n-1))+\frac{(1-\beta )}{n^\theta }\eta (n-1)\right] \left( f(\eta ^{n-1})-f(\eta )\right) \\ +&\sum _{x=1}^{n-2}\left( f(\sigma ^{x,x+1}\eta )-f(\eta )\right) \,, \nonumber \end{aligned}$$

(1)

where $\sigma ^{x,x+1}\eta$ is the configuration obtained from $\eta$ by exchanging the occupation variables $\eta (x)$ and $\eta (x+1)$, that is,

$$\begin{aligned} (\sigma ^{x,x+1}\eta )(y)=\left\{ \begin{array}{cl} \eta (x+1),&{} \text{ if }\,\,\, y=x\,,\\ \eta (x),&{} \text{ if } \,\,\,y=x+1\,,\\ \eta (y),&{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

(2)

and for $x=1,n-1$ $\eta ^x$ is the configuration obtained from $\eta$ by flipping the occupation variable $\eta (x)$:

$$\begin{aligned} (\eta ^x)(y)=\left\{ \begin{array}{cl} 1-\eta (y),&{} \text{ if }\,\,\, y=x\,,\\ \eta (y),&{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

(3)

Let ${\mathcal D}([0,T],\varOmega _n)$ be the space of trajectories which are right continuous and with left limits, taking values in $\varOmega _n$. Denote by ${\mathbb P}_{\mu _{n}}^{\theta ,n}$ the probability on ${\mathcal D}([0,T],\varOmega _n)$ induced by the Markov process with generator $n^2{\mathcal L}_n^\theta$ and the initial measure $\mu _n$ and denote by ${\mathbb E}_{\mu _n}^{\theta ,n}$ the expectation with respect to ${\mathbb P}_{\mu _n}^{\theta ,n}$.

2.2 Stationary Measures

The stationary measure $\mu _n^{ss}$ for this model when $\alpha =\beta =\rho \in (0,1)$ is the Bernoulli product measure given by

$$\nu ^n_\rho \Big (\eta \in \varOmega _n:\eta (x)=1\Big )=\rho \,.$$

But in the general case, where $\alpha \ne \beta$, the stationary measure $\mu _n^{ss}$ does not have independent marginals, see [10]. What we can say about the stationary behavior of this model is that the density of particles has a behavior very close to a linear profile, which depends on the range of $\theta$ in the sense of the following definition:

Definition 1

Let $\gamma : [0,1] \rightarrow [0,1]$ be a measurable profile. A sequence $\{\mu _n\}_{n\in {\mathbb N}}$ is said to be associated to $\gamma$ if, for any $\delta >0$ and any continuous function $f: [0,1]\rightarrow {\mathbb R}$ the following limit holds:

$$\begin{aligned} \lim _{n\rightarrow \infty } \mu _{n} \left( \, \eta :\, \left| \frac{1}{n} \sum _{x = 1}^{n\!-\!1} f(\genfrac{}{}{}1{x}{n})\, \eta (x) - \int f(u)\, \gamma (u)\, du \right| > \delta \,\right) \;=\; 0\,. \end{aligned}$$

For $\mu _{n}$ equal to the stationary measure $\mu ^{ss}_n$, the limit above is called the hydrostatic limit.

Theorem 1

(Hydrostatic Limit, [1]) Let $\mu _n^{ss}$ be the stationary probability measure in $\varOmega _n$ wrt the Markov process with infinitesimal generator $n^2 {\mathcal L}_n^\theta$, defined in (1). The sequence $\{\mu _n^{ss}\}_{n\in \mathbb {N}}$ is associated (in the sense of Definition 1) to the profile $\overline{\rho }: [0,1]\rightarrow \mathbb R$ given by

$$\begin{aligned} \overline{\rho }(u)\;=\; {\left\{ \begin{array}{ll} (\beta - \alpha )u+\alpha , &{} \text {if }\,\theta \in [0,1), \\ \frac{\beta - \alpha }{3}u + \alpha +\frac{\beta -\alpha }{3}, &{} \text {if }\,\theta = 1, \\ \frac{\beta + \alpha }{2}, &{} \text {if }\,\theta \in (1,\infty ), \end{array}\right. } \end{aligned}$$

(4)

for all $u\in [0,1]$.

Another feature that we can say about the stationary state of the model studied in this paper is that the profiles in (4) are very close to the mean of $\eta (x)$ taken with respect to the stationary measure $\mu _n^{ss}$. To state this result properly, we start by defining for an initial measure $\mu _n$ in $\varOmega _n$, for $x\in \Sigma _n$ and for $t\ge 0$ the empirical mean given by

$$\begin{aligned} \rho ^n_t(x):={\mathbb E}_{\mu _n}^{\theta ,n}[\eta _t(x)]\,. \end{aligned}$$

(5)

If in the expression above $\mu _n=\mu _n^{ss}$, then $\rho ^n_t(x)$ does not depend on t, so that $\rho ^n_t(x)=\rho ^n(x)$. From [1], we have that $\rho ^n(x)$ satisfies the following recurrence relations:

$$\begin{aligned} {\left\{ \begin{array}{ll} 0 =[\rho ^n(x+1)-\rho ^n(x)]+[\rho ^n(x-1)-\rho ^n(x)],\quad \text{ if } \;\;\;x\in \{2,\ldots ,n\!-\!2\},\\ 0 =[\rho ^n(2)-\rho ^n(1)]+n^{-\theta }[\alpha - \rho ^n(1)], \\ 0 =n^{-\theta }[\beta - \rho ^n(n\!-\!1)]+[\rho ^n(n\!-\!2)-\rho ^n(n\!-\!1)]. \end{array}\right. } \end{aligned}$$

A simple computation shows that $\rho ^n(x)$ is given by $\rho ^n(x)=a_nx+b_n,$ for all $x\in \Sigma _n,$ where $a_n=\frac{\beta -\alpha }{2n^\theta +n\!-\!2}$ and $b_n=\alpha + a_n(n^\theta -1).$ Moreover, we conclude that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Big (\max _{x\in \Sigma _n}\big |\rho ^n(x)-\overline{\rho }(\genfrac{}{}{}1{x}{n})\big |\Big )=0. \end{aligned}$$

2.3 Hydrodynamic Limit

In [1] it was established the hydrodynamic limit of the model for any $\theta \ge 0$. For completeness we recall that result now. Fix a measurable density profile $\rho _0: [0,1] \rightarrow [0,1 ]$ and for each $n \in {\mathbb N}$, let $\mu _n$ be a probability measure on $\varOmega _n$.

Theorem 2

(Hydrodynamic Limit, [1]) Suppose that the sequence $\{\mu _n\}_{n\in {\mathbb N}}$ is associated to a profile $\rho _0(\cdot )$ in the sense of Definition 1. Then, for each $t \in [0,T]$, for any $\delta >0$ and any continuous function $f:[0,1]\rightarrow {\mathbb R}$,

$$\begin{aligned} \lim _{ n \rightarrow +\infty } {\mathbb P}_{\mu _{n}}^{\theta ,n} \left[ \eta _{\cdot } : \left| \frac{1}{n} \sum _{x =1}^{n-1} f(\genfrac{}{}{}1{x}{n})\, \eta _{tn^2}(x) - \int f(u)\, \rho (t,u)\, du\, \right| > \delta \right] \;=\; 0, \end{aligned}$$

where $\rho (t,\cdot )$ is the unique weak solution of the heat equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t \rho (t,u)= \partial _u^2 \rho (t,u)\,, &{} \text {for } t>0\,,\, u\in (0,1),\\ \rho (0,u)=\rho _0(u)\,,&{} u\in [0,1]. \end{array}\right. } \end{aligned}$$

(6)

with boundary conditions that depend on the range of $\theta$, which are given by:

$$\begin{aligned}&\text {For } \theta <1, \;\partial _u \rho (t,0) = \alpha \text { and } \partial _u \rho (t,1) = \beta , \text { for } t>0. \end{aligned}$$

(7)

$$\begin{aligned}&\text {For } \theta =1,\; \partial _u \rho (t,0) = \rho (t,0)-\alpha \text { and } \partial _u \rho (t,1) = \beta -\rho (t,1), \text { for } t>0.\end{aligned}$$

(8)

$$\begin{aligned}&\text {For }\theta>1, \;\partial _u \rho (t,0) = \partial _u \rho (t,1) =0, \text { for }t>0. \end{aligned}$$

(9)

Remark 1

We note that the profiles in (4) are stationary solutions of the heat equation with the corresponding boundary conditions given above.

3 Density Fluctuations

3.1 The Space of Test Functions

The space $C^\infty ([0,1])$ is the space of functions $f:[0,1]\rightarrow {\mathbb R}$ such that f is continuous in [0, 1] as well as all its derivatives.

Definition 2

Let $\mathcal S_{\theta }$ denote the set of functions $f\in C^\infty ([0,1])$ such that for any $k\in \mathbb {N}\cup \{0\}$ it holds that

• (1) for $\theta <1$: $\partial _u^{2k} f(0)=\partial _u^{2k} f(1)=0.$

• (2) for $\theta =1$: $\partial _u^{2k+1} f(0)= \partial _u^{2k}f(0)$ and $\partial _u^{2k+1} f(1)=- \partial _u^{2k}f(1).$

• (3) for $\theta >1$: $\partial _u^{2k+1} f(0)=\partial _u^{2k+1} f(1)=0.$

Definition 3

For $\theta \ge 0$, let $-\varDelta _\theta$ be the positive operator, self-adjoint on $L^2{[0,1]}$, defined on $f\in {\mathcal S}_\theta$ by

$$\begin{aligned} \varDelta _\theta f(u)\;=\;\left\{ \begin{array}{cl} \partial _u^2 f(u)\,,&{} \text{ if }\,\,\,u\in (0,1),\\ \partial _u^2 f(0^+)\,,&{} \text{ if } \,\,\,u=0,\\ \partial _u^2 f(1^-)\,,&{} \text{ if } \,\,\,u=1.\\ \end{array} \right. \end{aligned}$$

(10)

Above, $\partial _u^2 f(a^\pm )$ denotes the side limits at the point a. Analogously, let  $\nabla _\theta : {\mathcal S}_\theta \rightarrow C^\infty ([0,1])$ be the operator given by

$$\begin{aligned} \nabla _\theta f(u)\;=\;\left\{ \begin{array}{cl} \partial _u f(u)\,,&{} \text{ if }\,\,\,u\in (0,1),\\ \partial _u f(0^+)\,,&{} \text{ if } \,\,\,u=0,\\ \partial _u f(1^-)\,,&{} \text{ if } \,\,\,u=1.\\ \end{array} \right. \end{aligned}$$

(11)

Definition 4

Let $T_t^\theta :{{\mathcal S}}_\theta \rightarrow {\mathcal S}_\theta$ be the semigroup associated to (6) with the corresponding boundary conditions for the case $\alpha =\beta =0$. That is, given $f\in {\mathcal S}_\theta$, by $T_t^\theta f$ we mean the solution of the homogeneous version of (6) with initial condition f.

Definition 5

Let ${\mathcal S}'_{\theta }$ be the topological dual of ${\mathcal S}_{\theta }$ with respect to the topology generated by the seminorms

$$\begin{aligned} \Vert f\Vert _{k}=\sup _{u\in [0,1]}|\partial _u^kf(u)|\,, \end{aligned}$$

(12)

where $k\in \mathbb {N}\cup \{0\}$. In other words, ${\mathcal S}'_\theta$ consists of all linear functionals $f:{\mathcal S}_\theta \rightarrow {\mathbb R}$ which are continuous with respect to all the seminorms $\Vert \cdot \Vert _k$.

Let ${\mathcal D}([0,T],{\mathcal S}'_\theta )$ (resp. ${\mathcal C}([0,T], {\mathcal S}'_\theta )$) be the space of trajectories which are right continuous and with left limits (resp. continuous), taking values in ${\mathcal S}'_\theta$.

The expression for $T_t^\theta$, $\theta \ge 0$, is presented in the next proposition:

Proposition 1

Let $\theta \ge 0$. Suppose that $\rho _0\in L^2[0,1]$. Then

$$\begin{aligned} (T_t^\theta \rho _0)(u) \;:=\; \sum _{n=1}^\infty a_n\,e^{-\lambda _n t}\,\Psi _n(u)\,, \end{aligned}$$

(13)

where $\{\Psi _n\}_{n\in {\mathbb N}}$ is an orthonormal basis of $L^2[0,1]$ constituted by eigenfunctions of the associated Regular Sturm-Liouville Problem (concerning the operator $\varDelta _\theta$) and $a_n$ are the Fourier coefficients of $\rho _0$ in the basis $\{\Psi _n\}_{n\in {\mathbb N}}$.

• For $\theta <1$, the corresponding orthonormal basis of $L^2[0,1]$ is

  $$ {\left\{ \begin{array}{ll} \Psi _n(u)\;=\; \sqrt{2}\sin (n\pi u)\,,\; &{} \text { for }n\in {\mathbb N}\,,\\ \Psi _0(u)\;\equiv \; 1\,. \end{array}\right. } $$

  The eigenvalues of the associated Regular Sturm-Liouville Problem (concerning the operator $\varDelta _\theta$) are given by $\lambda _n= n^2\pi ^2$.

• For $\theta =1$, the corresponding orthonormal basis of $L^2[0,1]$ is a linear combination of sines and cosines, namely,

  $$\Psi _n(u)\;=\; A_n\sin (\sqrt{\lambda _n} u)+A_n\sqrt{\lambda _n}\cos (\sqrt{\lambda _n} u)\,,\; \text { for }n\in {\mathbb N}\cup \{0\}\,, $$

  where $A_n$ is a normalizing constant. The eigenvalues $\lambda _n$ do not have an explicit formula, but it can verified that $\lambda _n\sim n^2\pi ^2$.

• For $\theta >1$, the corresponding orthonormal basis of $L^2[0,1]$ is

  $$ {\left\{ \begin{array}{ll} \Psi _n(u)\;=\; \sqrt{2}\cos (n\pi u)\,,\; &{} \text { for }n\in {\mathbb N}\,,\\ \Psi _0(u)\;\equiv \; 1\,. \end{array}\right. } $$

The eigenvalues of the associated Regular Sturm-Liouville Problem (concerning the operator $\varDelta _\theta$) are given by $\lambda _n= n^2\pi ^2$.

Proof

For $\theta =1$ the expression for $T_t^\theta$ has been obtained in [16]. For the case $\theta \ne 1$, as in [16], we state the associated Regular Sturm-Liouville Problem (for details on this subject we refer to [2], for instance):

$$\begin{aligned} \text{ For } ~\theta <1:\quad {\left\{ \begin{array}{ll}&{}\Psi ''(u)+\lambda \Psi (u) \;=\; 0\,, \quad u\in (0,1)\,, \\ &{} \Psi (0)\;=\;0\,, \quad \Psi (1)\;=\;0\,; \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \text{ For } ~\theta \ge 1:\quad {\left\{ \begin{array}{ll}&{}\Psi ''(u)+\lambda \Psi (u) \;=\; 0\,, \quad u\in (0,1)\,, \\ &{} \Psi '(0)\;=\;0\,, \quad \Psi '(1)\;=\;0\,. \end{array}\right. } \end{aligned}$$

The solution of each one of the problems above (the eigenvalues $\lambda _n$ and the eigenfunctions $\Psi _n$) can be found in Chap. 10 of [5].

As a consequence, the series (13) converges exponentially fast, implying that $(T_t^\theta \rho _0)(u)$ is smooth in space and time for any $t>0$. This observation implies a property of $T_t^\theta :{\mathcal S}_\theta \rightarrow {\mathcal S}_\theta$ stated in the next corollary.

Corollary 1

If $f\in {\mathcal S}_\theta$, then for any $t>0$, $T_t^\theta f \in {\mathcal S}_\theta$ and $\varDelta _\theta T_t^\theta f\in {\mathcal S}_\theta$.

We observe that the previous result is needed in the proof of uniqueness of the corresponding Ornstein–Uhlenbeck process (which is defined in the next section). Its proof is a consequence of the formula (13), see [16] for more details.

3.2 Ornstein–Uhlenbeck Process

Fix $\rho \in (0,1)$. Based on [17, 18], we give here a characterization of the generalized Ornstein–Uhlenbeck process which is a solution of

$$\begin{aligned} d\mathcal {Y}_t=\varDelta _\theta \mathcal {Y}_tdt+\sqrt{2\chi (\rho )t}\,\nabla _\theta \, d{\mathcal W}_t\,, \end{aligned}$$

(14)

where ${\mathcal W}_t$ is a space-time white noise of unit variance and $\chi (\rho )=\int (\eta (x)-\rho )^2d\nu ^n_\rho =\rho (1-\rho )$, in terms of a martingale problem. We will see below that this process governs the equilibrium fluctuations of the density of particles of our model. In spite of having a dependence of $\mathcal {Y}_t$ on $\theta$, we do not index on it to not overload notation. Denote by $\mathbf Q_\rho ^{\theta }$ the distribution of $\mathcal {Y}_\cdot$ and $\mathbf E_{\mathbf {Q}_\rho ^{\theta }}$ the expectation with respect to $\mathbf Q_\rho ^{\theta }$.

Define the inner product between the functions $f,g:[0,1]\rightarrow {\mathbb R}$ by

$$\begin{aligned} \langle f,\,g\rangle _{L^{2,\theta }_{\rho }}=2\chi (\rho )\Bigg [\int _{0}^1f(u)\,g(u) \,du+\Big (f(0)g(0)+ f(1)g(1)\Big )\mathbf 1 _{\theta =1}\Bigg ], \end{aligned}$$

where $\mathbf 1 _{\cdot }$ is the indicator function. Then, $L^{2,\theta }_{\rho }([0,1])$ is the space of functions $f:[0,1]\rightarrow {\mathbb {R}}$ with $\Vert f\Vert _{L^{2,\theta }_{\rho }}<\infty$, where

$$\begin{aligned} \Vert f\Vert _{L^{2,\theta }_{\rho }}^2=\langle f,\,f\rangle _{L^{2,\theta }_{\rho }}. \end{aligned}$$

(15)

Proposition 2

There exists an unique random element ${\mathcal Y}$ taking values in the space ${\mathcal C}([0,T],\mathcal {S}'_{\theta })$ such that:

• (i) For every function $f \in \mathcal {S}_{\theta }$, ${\mathcal M}_t(f)$ and ${\mathcal N}_t(f)$ given by

  $$\begin{aligned}&{\mathcal M}_t(f)= {\mathcal Y}_t(f) -{\mathcal Y}_0(f) - \int _0^t {\mathcal Y}_s(\varDelta _\theta f)ds\,,\nonumber \\&{\mathcal N}_t(f)=\big ({\mathcal M}_t(f)\big )^2 - 2\chi (\rho ) \; t\,\Vert \nabla _\theta f\Vert _{L^{2,\theta }_{\rho }}^2 \end{aligned}$$

  (16)

  are ${\mathcal F}_t$-martingales, where for each $t\in {[0,T]}$, ${\mathcal F}_t:=\sigma ({\mathcal Y}_s(f); s\le t, f \in \mathcal {S}_{\theta })$.

• (ii) ${\mathcal Y}_0$ is a Gaussian field of mean zero and covariance given on $f,g\in {\mathcal {S}_{\theta }}$ by

  $$\begin{aligned} \mathbf E_{\mathbf {Q}_\rho ^{\theta }}\big [ {\mathcal Y}_0(f) {\mathcal Y}_0(g)\big ] = \langle f,\,g\rangle _{L^{2,\theta }_{\rho }} \end{aligned}$$

  (17)

Moreover, for each $f\in {\mathcal S}_\theta$, the stochastic process $\{\mathcal {Y}_t(f)\,;\,t\ge 0\}$ is Gaussian, being the distribution of $\mathcal {Y}_t(f)$ conditionally to ${\mathcal F}_s$, for $s<t$, normal of mean $\mathcal {Y}_s(T_{t-s}^\theta f)$ and variance $\int _0^{t-s}\Vert \nabla _\theta T_{r}^\theta f\Vert ^2_{L^{2,\theta }_{\rho }}\,dr$, where $T_t^\theta$ was given in Definition 4.

The random element ${\mathcal Y}_\cdot$ is called the generalized Ornstein–Uhlenbeck process of characteristics $\varDelta _\theta$ and $\nabla _\theta$. From the second equation in (16) and Lévy’s Theorem on the martingale characterization of Brownian motion, for each $f\in \mathcal S_\theta$, the process

$$\begin{aligned} {\mathcal M}_t(f)\Big (2\chi (\rho )t\Vert \nabla _\theta f\Vert ^2_{L^{2,\theta }_{\rho }}\Big )^{-1/2} \end{aligned}$$

(18)

is a standard Brownian motion. Therefore, in view of Proposition 2, it makes sense to say that $\mathcal {Y}_\cdot$ is the formal solution of (14).

3.3 The Density Fluctuation Field

We define the density fluctuation field ${\mathcal Y}^n_\cdot$ as time-trajectory of the linear functional acting on functions $f\in \mathcal S_\theta$ as

$$\begin{aligned} {\mathcal Y}^n_t(f)\;=\;\frac{1}{\sqrt{n}}\sum _{x=1}^{n-1}f\Big (\frac{x}{n}\Big )\Big (\eta _{tn^2}(x)-\rho ^n_t(x)\Big ),\quad \text{ for } \text{ all } t\ge 0, \end{aligned}$$

(19)

where $\rho ^n_t$ was defined in (5). Our results are given for the case $\alpha =\beta =\rho$ and for $\mu _n$ being equal to $\nu ^n_\rho$, that is, the Bernoulli product measure with parameter $\rho \in (0,1)$, so that $\rho ^n_t(x)=\rho ,$ for all $x\in \Sigma _n$ and $t\ge 0$. Let ${\mathcal Q}_\rho ^{\theta ,n}$ be the probability measure on ${\mathcal D}([0,T],{\mathcal S}'_{\theta })$ induced by the density fluctuation field $\mathcal {Y}^n_{\cdot }$ and $\nu _{\rho }^n$. We note that since we will consider only the initial measure $\mu _n$ as $\nu _\rho ^n$, we will simplify the notations ${\mathbb P}_{\nu _\rho ^n}^{\theta ,n}$ and ${\mathbb E}_{\nu _\rho ^n}^{\theta ,n}$ as ${\mathbb P}_{\rho }^{\theta ,n}$ and ${\mathbb E}_{\rho }^{\theta ,n}$, respectively. Our main result is the following theorem.

Theorem 3

(Ornstein–Uhlenbeck limit) For $\alpha =\beta =\rho \in (0,1)$, if we take the initial measure to be $\nu _\rho ^n$, namely, the Bernoulli product measure with parameter $\rho$, then, the sequence $\{{\mathcal Q}_\rho ^{\theta ,n}\}_{ n\in \mathbb {N}}$ converges, as $n\rightarrow \infty$, to a generalized Ornstein–Uhlenbeck (O.U.) process, which is the formal solution of equation (14). As a consequence, the variance of the limit field $\mathcal {Y}_t$ is given on $f\in {{\mathcal S}_\theta }$ by

$$\begin{aligned} \mathbf E_{\mathbf {Q}_\rho ^{\theta }}\,[\mathcal {Y}_t(f)\mathcal {Y}_s(f)]\;=\;\chi (\rho )\int _0^1 \,(f(u))^2\,du+\int _0^s\Vert T_{t-r}^\theta f\Vert ^2_{L^{2,\theta }_{\rho }}dr\,, \end{aligned}$$

(20)

where $\Vert \cdot \Vert ^2_{L^{2,\theta }_{\rho }}$ was defined in (15).

4 Proof of Theorem 3

4.1 Characterization of Limit Points

Fix a test function f. By Dynkin’s formula, we have that

$$\begin{aligned} M^n_t(f)={\mathcal Y}_t^n(f)-{\mathcal Y}_0(f)-\int _{0}^t(\partial _s+n^2{\mathcal L}_n^\theta ){\mathcal Y}_s^n(f)ds, \end{aligned}$$

(21)

$$\begin{aligned} N^n_t(f)=(M_t^n(f))^2-\int _{0}^tn^2{\mathcal L}_n^\theta {\mathcal Y}_s^n(f)^2-2{\mathcal Y}_s^n(f)n^2{\mathcal L}_n^\theta {\mathcal Y}_s^n(f)ds \end{aligned}$$

(22)

are martingales with respect to the natural filtration ${\mathcal F}_t:=\sigma (\eta _s:\, s\le t)$. To simplify notation we denote $\varGamma _s^n(f):=(\partial _s+n^2{\mathcal L}_n^\theta ){\mathcal Y}_s^n(f)$. A long but elementary computation shows that

$$\begin{aligned} \varGamma _s^n(f)=&\frac{1}{\sqrt{n}}\sum _{x=1}^{n-1}\varDelta _n f\Big (\tfrac{x}{n}\Big )(\eta _s(x)-\rho )\nonumber \\ +&\sqrt{n} \nabla _n^+f(0)(\eta _s(1)-\rho )-\sqrt{n} \nabla _n^-f({n})(\eta _s(n-1)-\rho )\\ -&\frac{n^{3/2}}{n^\theta }f\Big (\tfrac{1}{n}\Big )(\eta _s(1)-\rho )-\frac{n^{3/2}}{n^\theta }f\Big (\tfrac{n-1}{n}\Big )(\eta _s(n-1)-\rho ). \nonumber \end{aligned}$$

(23)

Above

$$\begin{aligned} \varDelta _nf(x):=n^2\Big [f\Big (\tfrac{x+1}{n}\Big )+f\Big (\tfrac{x-1}{n}\Big )-2f\Big (\tfrac{x}{n}\Big )\Big ]\,, \end{aligned}$$

$$\begin{aligned} \nabla _n^+f(x):=n\Big [f\Big (\tfrac{x+1}{n}\Big )-f\Big (\tfrac{x}{n}\Big )\Big ] \end{aligned}$$

and

$$\begin{aligned} \nabla _n^-f(x):=n\Big [f\Big (\tfrac{x}{n}\Big )-f\Big (\tfrac{x-1}{n}\Big )\Big ]\,. \end{aligned}$$

We note that for the choice $\theta =0$, using the fact that $f(0)=0=f(1)$, the expression (23) reduces to

$$\begin{aligned} \varGamma _s^n(f)=\frac{1}{\sqrt{n}}\sum _{x=1}^{n-1}\varDelta _n f\Big (\tfrac{x}{n}\Big ) (\eta _s(x)-\rho )\,, \end{aligned}$$

(24)

which is ${\mathcal Y}_s^n(\varDelta _n f).$

Now, we close the Eq. (23) for each regime of $\theta$. The goal is to show that we can rewrite (23) as (24) plus a term which vanishes as $n\rightarrow \infty$.

$\bullet$ The case $\theta <1$: we note that since $f\in {\mathcal S_\theta }$ we can write $\varGamma _s^n(f)$ as

$$\begin{aligned} {\mathcal Y}_s^n(\varDelta _n f)+ \sqrt{n}(1-n^{-\theta })\Big \{ \nabla _n^+f(0)(\eta _s(1)-\rho )- \nabla _n^-f(n)(\eta _s(n-1)-\rho )\Big \}. \end{aligned}$$

In order to close the equation for the martingale we need to show that:

$$\begin{aligned} \lim _{n\rightarrow \infty }\mathbb {E}_{\rho }^{\theta ,n}\left[ \left( \int _{0}^t\sqrt{n}(\eta _{s}(x)-\rho ) \, ds\right) ^2\right] =0,\quad \text{ for } x=1,n-1, \end{aligned}$$

(25)

which is a consequence of Lemma 3, see Remark 2.

$\bullet$ The case $\theta =1$: we can write $\varGamma _s^n(f)$ as

$$\begin{aligned}&{\mathcal Y}_s^n(\varDelta _n f)+ \sqrt{n} \Big ( \partial _uf(0)-f(0)\Big )(\eta _s(1)-\rho )\\&+\sqrt{n} \Big (\partial _u f(1)+f(1)\Big )(\eta _s(n-1)-\rho )+O\left( \frac{1}{\sqrt{n}}\right) . \end{aligned}$$

Since $f\in {\mathcal S_\theta }$ the last expression equals to ${\mathcal Y}_s^n(\varDelta _n f).$

$\bullet$ The case $\theta >1$: we can repeat the computations above and since $f\in {\mathcal S_\theta }$, $\varGamma _s^n(f)$ can be rewritten as

$$\begin{aligned} {\mathcal Y}_s^n(\varDelta _n f) -\frac{n^{3/2}}{n^\theta }f\Big (\tfrac{1}{n}\Big )(\eta _s(1)-\rho )-\frac{n^{3/2}}{n^\theta }f\Big (\tfrac{n-1}{n}\Big )(\eta _s(n-1)-\rho )+O\left( \frac{1}{\sqrt{n}}\right) . \end{aligned}$$

Then, in order to close the equation for the martingale term we need to show that

$$\begin{aligned} \lim _{n\rightarrow \infty }\mathbb {E}^{\theta ,n}_{\rho }\left[ \left( \int _{0}^t\frac{ n^{3/2}}{n^\theta }(\eta _s(x)-\rho ) \, ds\right) ^2\right] =0, \quad \text{ for } x=1,n-1\,, \end{aligned}$$

(26)

which is a consequence of Lemma 3, see Remark 2.

From the previous observations, for each regime of $\theta$ we can rewrite (23) as (24) plus a negligible term.

Lemma 1

For all $\theta \ge 0$, $t>0$ and $f\in {\mathcal S}_\theta$ it holds that

$$\begin{aligned} \lim _{n\rightarrow \infty } \mathbb {E}_{\rho }^{\theta ,n}[|M_{t}^{n}(f)|^{2}]= t \Vert \nabla _\theta f\Vert _{L^{2,\theta }_{\rho }}, \end{aligned}$$

where the norm above was defined in (15).

Proof

A simple computation shows that the integral part of the martingale $N_t^n(f)$ can be written as

$$\begin{aligned} n^2{\mathcal L}_n^\theta {\mathcal Y}_s^n(f)^2- 2{\mathcal Y}_s^n(f)n^2&{\mathcal L}_n^\theta {\mathcal Y}_s^n(f)=\frac{1}{n}\sum _{x=1}^{n-2}\Big (\nabla ^+_n f\Big (\tfrac{x}{n}\Big )\Big )^2 \Big (\eta _s(x)-\eta _s(x+1)\Big )^2\\ +&\frac{n}{n^\theta }\, \Big (f\big (\genfrac{}{}{}1{1}{n}\big )\Big )^2\Big (\rho -2\rho \eta _s(1)+\eta _s(1)\Big )\\ +&\frac{n}{n^\theta }\, \Big (f\big (\genfrac{}{}{}1{n-1}{n}\big )\Big )^2\Big (\rho -2\rho \eta _s(n-1)+\eta _s(n-1)\Big ), \end{aligned}$$

from where we get that

$$\begin{aligned}&\mathbb {E}_{\rho }^{\theta ,n}\big [|M_{t}^{n}(f)|^{2}\big ]\nonumber \\&=2\chi ( \rho )\;t\,\Bigg \{\frac{1}{n}\sum _{x=1}^{n-2}\Big (\nabla ^+_n f\Big (\tfrac{x}{n}\Big )\Big )^2 +\frac{n}{n^\theta }\, \Bigg (\Big (f\big (\genfrac{}{}{}1{1}{n}\big )\Big )^2+ \Big (f\big (\genfrac{}{}{}1{n-1}{n}\big )\Big )^2\Bigg )\Bigg \}. \end{aligned}$$

(27)

Let $f\in {{\mathcal S_\theta }}$. The first term at the right hand side of the previous expression converges to $2\chi ( \rho )\int _0^1\Big (\nabla _\theta f(u)\Big )^2\,du$, for all $\theta \ge 0$. The second term at the right hand side of last expression has to be analyzed for each case of $\theta$ separately:

$\bullet$ The case $\theta <1$: since $f(0)=0=f(1)$, the second term at the right hand side of (27) can be rewritten as $2\chi ( \rho )\,t$ times

$$ \frac{n}{n^\theta }\, \Bigg (\Big (f\big (\genfrac{}{}{}1{1}{n}\big )\Big )^2+ \Big (f\big (\genfrac{}{}{}1{n-1}{n}\big )\Big )^2\Bigg )=\frac{1}{n^{1+\theta }}\, \Bigg (\Big (\nabla _n^+f(0)\Big )^2+ \Big (\nabla _n^-f(n)\Big )^2\Bigg ), $$

which goes to zero as $n\rightarrow \infty$.

$\bullet$ The case $\theta =1$: the second term at the right hand side of (27) converges, as $n\rightarrow \infty$, to

$$2\chi ( \rho )\, t\,\Big (f^2\big (0\big )+ f^2\big (1\big )\Big ). $$

Recalling that $f(0)=\partial _u f(0)$ and $f(1)=-\partial _u f(1)$, the proof ends.

$\bullet$ The case $\theta >1$: since $f\in {{\mathcal S_\theta }}$ and $\frac{n}{n^\theta }\rightarrow 0$, as $n\rightarrow \infty$, the second term at the right hand side of (27) converges to zero when $n\rightarrow \infty$.

We have just proved that the quadratic variation of the martingale converges in mean. In the next Lemma we state the stronger convergence of the martingales to a Brownian motion.

Lemma 2

For $f\in {\mathcal S}_\theta$, the sequence of martingales $\{M^n_t(f);t\in [0,T]\}_{n\in {\mathbb N}}$ converges in the topology of ${\mathcal D}([0,T], {\mathbb R})$, as $n\rightarrow \infty$, towards a Brownian motion $\mathcal {W}_t(f)$ of quadratic variation given by $t\Vert \nabla _\theta f\Vert _{L^{2,\theta }_{\rho }}$ where $\Vert \cdot \Vert _{L^{2,\theta }_{\rho }}$ was defined in (15).

Proof

We can repeat here the same proof of [14, p. 4170], which is based on Lemma 1 and the fact that a limit in distribution of a uniformly integrable sequence of martingales is a martingale. We leave the details to the interested reader.

4.2 Convergence at Initial Time

Proposition 3

The sequence $\{{\mathcal Y}^n_0\}_{n\in \mathbb {N}}$ converges in distribution to ${\mathcal Y}_0$, where ${\mathcal Y}_0$ is a Gaussian field with mean zero and covariance given by (17).

Proof

We first claim that, for every $f\in \mathcal {S}_\theta$ and every $t>{0}$,

$$\begin{aligned} \lim _{n\rightarrow {{+\infty }}}\log \,\mathbb {E}_\rho ^{\theta ,n}\Big [\exp \{i\lambda {\mathcal {Y}^n_{0}(f)}\}\Big ]=-\frac{\lambda ^2}{2} \chi (\rho )\int _{0}^1 f^2(u)\,du\,. \end{aligned}$$

Since $\nu ^n_\rho$ is a Bernoulli product measure,

$$\begin{aligned} \log \,\mathbb {E}_\rho ^{\theta ,n}[\exp \{i\lambda \mathcal {Y}^n_{0}(f)\}]&= \log \int \left[ \exp \left\{ \frac{i\lambda }{\sqrt{n}}\sum _{x \in {\Sigma _n}}\; (\eta _0(x)-\rho )\,f\left( \frac{x}{n}\right) \right\} \right] d{\nu _{\rho }^{n}}\\&=\sum _{x\in {\Sigma _n}}\log \int \left[ \exp \left\{ \frac{i\lambda }{\sqrt{n}}\; (\eta _0(x)-\rho )\,f\left( \frac{x}{n}\right) \right\} \right] {d\nu _{\rho }^{n}}\,. \end{aligned}$$

Since f is smooth and using Taylor’s expansion, the right hand side of last expression is equal to

$$\begin{aligned} -\frac{\lambda ^2}{2n}\sum _{x\in {\Sigma _n }}f^{2}\left( \frac{x}{n}\right) \chi (\rho )+O\left( \frac{1}{\sqrt{n}}\right) \,. \end{aligned}$$

Taking the limit as $n\rightarrow {+\infty }$ and using the continuity of f, the proof of the claim ends. Replacing f by a linear combination of functions and recalling the Cramér-Wold device, the proof finishes.

5 Tightness

Now we prove that the sequence of processes $\{{\mathcal Y}_t^n; t \in [0,T]\}_{n \in {\mathbb N}}$ is tight. Recall that we have defined the density fluctuation field on test functions $f\in {\mathcal S}_\theta$. Since we want to use Mitoma’s criterium [20] for tightness, we need the following property from the space $\mathcal S_\theta$.

Proposition 4

The space ${\mathcal S}_\theta$ endowed with the semi-norms given in (12) is a Fréchet space.

Proof

The definition of a Fréchet space can be found, for instance, in [21]. Since $C^{\infty }([0,1])$ endowed with the semi-norms (12) is a Fréchet space, and a closed subspace of a Fréchet space is also a Fréchet space, it is enough to show that ${\mathcal S}_\theta$ is a closed subspace of $C^\infty ([0,1])$, which is a consequence of the fact that uniform convergence implies point-wise convergence.

As a consequence of Mitoma’s criterium [20] and Proposition 4, the proof of tightness of the ${\mathcal S}'_\theta$ valued processes $\{{\mathcal Y}_t^n; t \in [0,T]\}_{n \in {\mathbb N}}$ follows from tightness of the sequence of real-valued processes $\{{\mathcal Y}_t^n(f); t \in [0,T]\}_{n \in {\mathbb N}}$, for $f\in {{\mathcal S}_\theta }$.

Proposition 5

(Mitoma’s criterium, [20]) A sequence of processes $\{x_t;t \in [0,T]\}_{n \in {\mathbb N}}$ in ${\mathcal D}([0,T],{\mathcal S_\theta }')$ is tight with respect to the Skorohod topology if, and only if, the sequence $\{x_t(f);t \in [0,T]\}_{n \in {\mathbb N}}$ of real-valued processes is tight with respect to the Skorohod topology of ${\mathcal D}([0,T], {\mathbb R})$, for any $f \in {\mathcal S_\theta }$.

Now, to show tightness of the real-valued process we use the Aldous’ criterium:

Proposition 6

A sequence $\{x_t; t\in [0,T]\}_{n \in {\mathbb N}}$ of real-valued processes is tight with respect to the Skorohod topology of ${\mathcal D}([0,T],{\mathbb R})$ if:

• (i) $\displaystyle \lim _{A\rightarrow {+\infty }}\;\limsup _{n\rightarrow {+\infty }}\;\mathbb {P}_{\mu _n}\Big (\sup _{0\le {t}\le {T}}|x_{t } |>A\Big )\;=\;0\,,$

• (ii) for any $\varepsilon >0\,,$ $\displaystyle \lim _{\delta \rightarrow 0} \;\limsup _{n \rightarrow {+\infty }} \;\sup _{\lambda \le \delta } \;\sup _{\tau \in {\mathcal T}_T}\; \mathbb {P}_{\mu _n}(| x_{\tau +\lambda }- x_{\tau }| >\varepsilon )\; =\;0\,,$

where ${\mathcal T}_T$ is the set of stopping times bounded by T.

Fix $f\in {{\mathcal S}_\theta }$. By (21), it is enough to prove tightness of $\{{\mathcal Y}_0^n(f)\}_{n \in {\mathbb N}}$, $\{ \int _{0}^t\varGamma _s^n(f)\, ds; t \in [0,T]\}_{n \in {\mathbb N}}$, and $\{{\mathcal M}_t^n(f ); t \in [0,T]\}_{n \in {\mathbb N}}$.

5.1 Tightness at the Initial Time

This follows from Proposition 3.

5.2 Tightness of the Martingales

By Lemma 2, the sequence of martingales converges. In particular, it is tight.

5.3 Tightness of the Integral Terms

The first claim of Aldous’ criterium can be easily checked for the integral term $\int _{0}^t\varGamma _s^n(f)\, ds$, where the expression for $\varGamma _s^n(f)$ can be found in (23). Let $f\in {{\mathcal S_\theta }}$.

• The case $\theta <1$: by Young’s inequality and Cauchy-Schwarz’s inequality we have that

  $$\begin{aligned} {\mathbb E}_{\rho }^{\theta ,n}\Bigg [\sup _{t\le {T}}\Bigg (&\int _{0}^t\varGamma _s^n(f)\, ds\Bigg )^2\Bigg ]\\ {}&\le CT \int _{0}^T \mathbb {E}^{\theta ,n}_{\rho }\Bigg [\Bigg (\frac{1}{\sqrt{n}}\sum _{x=1}^{n-1}\varDelta _n f(\tfrac{x}{n})(\eta _{sn^2}(x)-\rho )\Bigg )^2\Bigg ]\, ds\\&+C\,(\nabla _n^+f(0))^2\,T \int _{0}^T \mathbb {E}^{\theta ,n}_{\rho }\Big [\Big (\sqrt{n}(\eta _{sn^2}(1)-\rho )\Big )^2\Big ]\, ds\\&+C\,(\nabla _n^-f({1}))^2\,T \int _{0}^T \mathbb {E}^{\theta ,n}_{\rho }\Big [\Big (\sqrt{n}(\eta _{sn^2}(n-1)-\rho )\Big )^2\Big ]\, ds. \end{aligned}$$

  Since $f\in {\mathcal S}_\theta$ and by (25), the second and third terms at the right hand side of the previous expression go to zero, as $n\rightarrow \infty$. Then there exists $C>0$ such that these two terms are bounded from above by CT. The first term at the right hand side of last expression is bounded from above by $T^2$ times

  $$\begin{aligned} \frac{1}{{n}}\sum _{x=1}^{n-1}\big (\varDelta _n f(\tfrac{x}{n})\Big )^2\chi (\rho ) \,. \end{aligned}$$

  (28)

  Now, since $f\in {\mathcal S}_\theta$ last expression is bounded from above by a constant. Now we need to check the second claim of Aldous’ criterium. For that purpose, fix a stopping time $\tau \in {\mathcal T}_T$. By Chebyshev’s inequality together with (28), we get that

  $$\begin{aligned} {\mathbb P}_{\rho }^{\theta ,n}\Big (\Big | \int _{\tau }^{\tau +\lambda }\!\!\varGamma ^n_s(f)\, ds\;\Big | >\varepsilon \Big ) \le \frac{1}{\varepsilon ^2}{\mathbb E}_{\rho }^{\theta ,n}\Big [ \Big ( \int _{\tau }^{\tau +\lambda }\!\!\varGamma ^n_s(f)\; ds \;\Big )^2\Big ] \le \frac{\delta C}{\varepsilon ^2}\,, \end{aligned}$$

  which vanishes as $\delta \rightarrow {0}$.

• The case $\theta =1$: we note that it was treated in [16].

• The case $\theta >1$: as in the case $\theta <1$, we have that

  $$\begin{aligned} {\mathbb E}_{\rho }^{\theta ,n}\Bigg [\sup _{t\le {T}}\Bigg (&\int _{0}^t\varGamma _s^n(f)\, ds\Bigg )^2\Bigg ]\\ {}&\le CT \int _{0}^T \mathbb {E}^{\theta ,n}_{\rho }\Bigg [\Bigg (\frac{1}{\sqrt{n}}\sum _{x=1}^{n-1}\varDelta _n f(\tfrac{x}{n})(\eta _{sn^2}(x)-\rho )\Bigg )^2\Bigg ]\, ds\\&+C\,f^2\Bigg (\tfrac{1}{n}\Bigg )\,T \int _{0}^T \mathbb {E}^{\theta ,n}_{\rho }\Bigg [\Bigg (\frac{n^{3/2}}{n^\theta }(\eta _{sn^2}(1)-\rho )\Bigg )^2\Bigg ]\, ds\\&+C\,f^2\Bigg (\tfrac{n-1}{n}\Bigg )\,T \int _{0}^T \mathbb {E}^{\theta ,n}_{\rho }\Bigg [\Bigg (\frac{n^{3/2}}{n^\theta }(\eta _{sn^2}(n-1)-\rho )\Bigg )^2\Big ]\, ds\,, \end{aligned}$$

  plus a term of order $\frac{1}{\sqrt{n}}$. To bound the first term at the right hand side of the previous inequality we repeat the same computations as in the case $\theta <1$. In order to bound the second and the third terms at the right hand side of the previous inequality, we use (26) and the proof follows as in the case $\theta <1$.

6 Replacement Lemma

This section is devoted to estimate the expectations (25) and (26). In order to do this we start introducing some notations. Let $\mu$ be an initial measure. For $x=0,1,\ldots ,n-1$, define

$$\begin{aligned} I_{x,x+1}(f,\mu )\;:=\; \int r_{x,x+1}(\eta )\left( {f(\sigma ^{x,x+1}\eta )}-{f(\eta )}\right) ^{2} d\mu \,, \end{aligned}$$

where $\sigma ^{x,x+1}\eta$ was defined in (2), for $x=1,\ldots ,n-2$, $\sigma ^{0,1}\eta :=\eta ^{1}$, $\sigma ^{n-1,n}\eta :=\eta ^{n-1}$ (the configurations $\eta ^{1}$ and $\eta ^{n-1}$ were defined in (3)), and the rates are given by

$$\begin{aligned} r_{0,1}(\eta )\;&:=\;r_{\alpha }(\eta ):=\frac{\alpha }{n^\theta }(1-\eta (1)) + \frac{1-\alpha }{n^\theta }\eta (1)\,,\\ r_{n-1,n}(\eta )&\;:=\;r_{\beta }(\eta ):=\frac{\beta }{n^\theta }(1-\eta (n-1)) +\frac{1-\beta }{n^\theta }\eta (n-1)\,,\\ r_{x,x+1}(\eta )&\;:=\;1,\; \text { if } x=1,\ldots ,n-2\,. \end{aligned}$$

Define the quantity:

$$\begin{aligned} \mathcal D_{n}(f,\mu )\;:=\sum _{x=0}^{n-1}I_{x,x+1}(f,\mu )\;= \sum _{x=0}^{n-1}\int r_{x,x+1}(\eta )\left( {f(\sigma ^{x,x+1}\eta )}-{f(\eta )}\right) ^{2} d\mu \,. \end{aligned}$$

(29)

The Dirichlet form is defined by $\langle -\mathcal L_{n}^\theta {f},{f} \rangle _{\mu }$, where we can rewrite for short the infinitesimal generator as

$$\begin{aligned} \mathcal L_{n}^\theta f(\eta )\;:=\;\sum _{x=0}^{n-1}L_{x,x+1}f(\eta )\;:=\;\sum _{x=0}^{n-1}r_{x,x+1}(\eta )(f(\sigma ^{x,x+1}\eta )-f(\eta ))\,.\end{aligned}$$

Now, we recall that we consider the case $\alpha =\beta =\rho \in {(0,1)}$, so that the measure $\nu _\rho ^n$ (the Bernoulli product measure) is invariant for this process and it satisfies

$$\begin{aligned} r_{x,x+1}(\eta )\,\nu _\rho ^n(\eta )=r_{x,x+1}(\sigma ^{x,x+1}\eta )\, \nu _\rho ^n(\sigma ^{x,x+1}\eta )\,, \end{aligned}$$

(30)

for all $x\in \{0,1,\ldots ,n-1\}$. Let us check this equality in the case $x=0$, the case $x=n-1$ is similar and the others are also very simple to check. Note that

$$\begin{aligned} r_{0,1}(\sigma ^{0,1}\eta )\, \frac{\nu _\rho ^n(\sigma ^{0,1}\eta )}{\nu _\rho ^n(\eta )}= \Bigg [\frac{\rho }{n^\theta }(1-\eta ^1(1)) + \frac{1-\rho }{n^\theta }\eta ^1(1)\Bigg ]\frac{\nu _\rho ^n(\eta ^1)}{\nu _\rho ^n(\eta )}. \end{aligned}$$

(31)

Since

$$\begin{aligned} \frac{\nu _\rho ^n(\eta ^1)}{\nu _\rho ^n(\eta )}=\mathbf 1 _{\eta (1)=1}\frac{1-\rho }{\rho }+\mathbf 1 _{\eta (1)=0}\frac{\rho }{1-\rho }\,, \end{aligned}$$

(32)

then (31) becomes

$$\mathbf 1 _{\eta (1)=1}\;\Bigg [\frac{\rho }{n^\theta }\Bigg ]\;\frac{1-\rho }{\rho }\; + \mathbf 1 _{\eta (1)=0}\;\Bigg [\frac{1-\rho }{n^\theta }\Bigg ]\;\frac{\rho }{1-\rho }\;=r_{0,1}(\eta )\,.$$

Thus, using (30), we get

$$\begin{aligned} \langle -\mathcal L_{n}^\theta {f},{f} \rangle _{\nu _\rho ^n} =\frac{1}{2}\mathcal D_{n}(f,\nu _\rho ^n)\,.\end{aligned}$$

(33)

Lemma 3

(Replacement Lemma) Let $x=1,n-1$ and $t>0$ fixed. Then

$$\begin{aligned} {\mathbb E}_{\rho }^{\theta ,n}\Bigg [\Bigg (\int _0^t c_n\big (\eta _s(x)-\rho \big )\, ds\Bigg )^2\Bigg ]\;\le \; C\frac{c_n^2n^\theta }{n^2}. \end{aligned}$$

Remark 2

Recall that for $\theta <1$ we have in (25) $c_n=\sqrt{n}$, so that the error above becomes $n^\theta /n$, which vanishes as $n\rightarrow \infty$. Recall that for $\theta >1$ we have in (26) $c_n=n^{3/2}/n^\theta$, so that the error above becomes $n/n^\theta$, which vanishes as $n\rightarrow \infty$.

Proof

The proof follows by a classical argument combining both the Kipnis–Varadhan’s inequality (see [18, p. 333, Lemma 6.1]) with Young’s inequality. For that purpose let $x=1$ (the other case is completely analogous) and note that the expectation in the statement of the lemma can be bounded from above by

$$\begin{aligned} \sup _{f\in L^2_{\nu ^n_\rho }}\Big \{ \int c_n(\eta (1)-\rho )f(\eta )\,d\nu _\rho ^n+ {n^2}\langle \mathcal L_{n}^\theta {f},{f} \rangle _{\nu _\rho ^n}\Big \}, \end{aligned}$$

(34)

where $L^2_{\nu ^n_\rho }$ is the space of functions f such that $\int f^2(\eta )\,d\nu _\rho ^n<+\infty$. We start by writing the integral $\int c_n(\eta (1)-\rho )f(\eta )d\nu _\rho ^n$ as twice its half and in one of the terms we make the exchange $\eta \rightarrow \eta ^1$ to have

$$\begin{aligned} \frac{1}{2}\int c_n(\eta (1)-\rho )f(\eta )\,d\nu ^n_\rho + \frac{1}{2}\int c_n(1-\eta (1)-\rho )f(\eta ^1) \frac{\nu _\rho ^n(\eta ^1)}{\nu _\rho ^n(\eta )}\,d\nu ^n_\rho \,, \end{aligned}$$

see (32) to get the expression of $\frac{\nu _\rho ^n(\eta ^1)}{\nu _\rho ^n(\eta )}$. A simple computation shows that the integral at the right hand side of last expression is equal to

$$\begin{aligned} - \frac{1}{2}\int c_n(\eta (1)-\rho )f(\eta ^1)\,d\nu ^n_\rho \,, \end{aligned}$$

so that the display above is equal to

$$\begin{aligned} \frac{1}{2}\int c_n(\eta (1)-\rho )(f(\eta )-f(\eta ^1))\,d\nu ^n_\rho . \end{aligned}$$

By Young’s inequality we can bound the previous expression by

$$\begin{aligned} B\int c_n^2(\eta (1)-\rho )^2d\nu ^n_\rho + \frac{1}{4B}\int ({f(\eta )}-{f(\eta ^1)})^2\,d\nu ^n_\rho \,. \end{aligned}$$

Now, remember the notation $\eta ^1=\sigma ^{0,1}\eta$ and multiply and divide by $r_{0,1}(\eta )$ the integrand function inside the second integral above. We can do it, because there exists $\tilde{C}_\rho$ such that $\frac{\tilde{C}_\rho }{n^\theta }\le r_{0,1}(\eta )\le \frac{C_\rho }{n^\theta }$. Then we can bound the previous expression from above by

$$\begin{aligned}&B\int c_n^2(\eta (1)-\rho )^2\,d\nu ^n_\rho + \frac{n^\theta }{4B\tilde{C}_\rho }\int r_{0,1}(\eta )\,({f(\sigma ^{0,1}\eta )}-{f(\eta )})^2\,d\nu ^n_\rho \,. \end{aligned}$$

Using (29) the second integral in the last expression is bounded from above by $\mathcal D_{n}({f},\nu _\rho ^n)$. Recalling (33), we get

$$\begin{aligned} \int c_n(\eta (1)-\rho )f(\eta )\,d\nu _\rho ^n\le&\,B\,c_n^2\int (\eta (1)-\rho )^2\,d\nu ^n_\rho + \frac{n^\theta }{2B\tilde{C}_\rho }\langle -\mathcal L^\theta _{n}{f},{f} \rangle _{\nu _\rho ^n}\,. \end{aligned}$$

Putting this inequality in (34) and choosing $B=n^{\theta -2}/2\tilde{C}_\rho$, the term at the right hand side of the last expression cancels with $n^2\langle \mathcal L_{n}^\theta {f},{f} \rangle _{\nu _\rho ^n}$. Therefore, the expectation appearing in the statement of the lemma is bounded from above by

$$\begin{aligned} \frac{c_n^2n^\theta }{2\tilde{C}_\rho n^2}\int (\eta (1)-\rho )^2\,d\nu ^n_\rho \,. \end{aligned}$$

Since $\eta$ is bounded the proof ends.