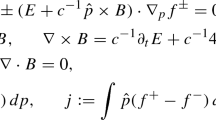On a Vlasov–Poisson Plasma with Infinite Charge and Velocities

Abstract

In this article I will overview some recent results on the Vlasov and the Vlasov–Poisson equations, for a given initial particle distribution which is not $L^1$ in space and has infinite support in the velocities.

1 Introduction

We consider a one-species, positively charged plasma whose time evolution is ruled by the following Vlasov equations

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \partial _t f(x,v,t) +v\cdot \nabla _x f(x,v,t)+ \left( E(x,t)+F(x,v)\right) \cdot \nabla _v f(x,v,t)=0 \\ \displaystyle E(x,t)=\int \frac{x-y}{|x-y|^3} \ \rho (y,t) \, dy \\ \displaystyle \rho (x,t)=\int f(x,v,t) \, dv \\ \displaystyle f(x,v,0)=f_0(x,v) \end{array} \right. \end{aligned}$$

(1)

where f(x, v, t) represents the plasma density, that is the distribution of charged particles at the point of the phase space $(x,v)\in \mathbb {R}^3\times \mathbb {R}^3$ at time t, $\rho (x,t)$ is the charge in x at time t, E is the self-induced electric field and F is an external force acting on the system. Notice that for $F=0$ we get the usual Vlasov–Poisson equation.

Equation (1) is a conservation equation for the density f along the characteristics of the system, that is the solutions to the following problem:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \dot{X}(t)= V(t)\\ \displaystyle \dot{V}(t)= E(X(t),t)+F((X(t), V(t)) \\ \displaystyle ( X(0), V(0))=(x,v), \end{array} \right. \end{aligned}$$

(2)

where $(X(t),V(t))=(X(x,v,t),V(x,v,t))$ denote position and velocity of a particle starting at time $t=0$ from (x, v) and the particles are initially distributed by $f_0(x,v).$

Since f is time-invariant along this motion, it is:

$$\begin{aligned} \Vert f(t)\Vert _{L^\infty }=\Vert f_0\Vert _{L^\infty }=C. \end{aligned}$$

(3)

As it is well known, solutions of (2) produce weak solutions of Eq. (1), which become classical solutions whenever f(x, v, 0) is assumed smooth.

The above equations have been widely studied in the case $F=0$ and $f_0\in L^1,$ and the problem of the existence and uniqueness of its solutions is completely solved, as it can be seen in many papers (we quote [7,8,9] and a nice review of many such results in [6] for all). The subsequent problem of a spatial density not belonging to $L^1$ has been investigated since many years by many authors, but here we only quote papers [1,2,3], which will be discussed in our exposition. All the results in these papers have been obtained in the hypothesis that the density has compact support in the velocities, which actually seems somewhat unphysical. For this reason, in very recent times the same authors have faced also the problem of a plasma whose particles may have infinite velocities, even if “with low probability”, that is having the density a sufficiently strong decay in the velocities. This has been done in papers [4, 5], and our aim here is to briefly describe the problems and the results in both situations, of infinite charge and of infinite velocities. This will be done in subsequent Sects. 2 and 3 in which we will illustrate the results in papers [2,3,4,5] respectively. In the spirit of a review, we will only sketch the proofs of the results, which can be found in extensive form in the papers.

2 The Case with Infinite Charge

In [2] and in [3] we have considered an infinitely extended plasma, confined in a cylinder by an external magnetic field ($F\ne 0$) and in the whole space respectively ($F=0$). In both cases the density is assumed to have compact support in the velocities, while the spatial density is not supposed to be in $L^1.$ In this case it is of primary relevance to achieve a good position of the equations, since the electric field could be infinite even at time $t=0$. To avoid this problem, we have assumed that the spatial density, even if not integrable, is slightly decaying at infinity. Another problem coming from the infinite charge of the plasma is that the total energy of the system, usually employed to get estimates on the spatial density, is infinite. We bypass this difficulty by introducing the $local \ energy,$ which is defined as follows.

For $\mu \in \mathbb {R}$ and $R>0$ we introduce the function,

$$\begin{aligned} \varphi ^{\mu ,R}( x)=\varphi \Bigg (\frac{| x-\mu |}{R}\Bigg ) \end{aligned}$$

(4)

with $\varphi$ a smooth function such that:

$$\begin{aligned} \varphi (r)=1 \ \ \hbox {if} \ \ r\in [0,1] \end{aligned}$$

(5)

$$\begin{aligned} \varphi (r)=0 \ \ \hbox {if} \ \ r\in [2,+\infty ) \end{aligned}$$

(6)

$$\begin{aligned} -2\le \varphi '(r)\le 0. \end{aligned}$$

(7)

Then the local energy is defined as

$$\begin{aligned} W( \mu ,R,t)= & {} \frac{1}{2} \int d x\ \varphi ^{\mu ,R}( x)\int d v \ |v|^2 f( x, v,t) \nonumber \\&+\, \frac{1}{2}\int d x \ \varphi ^{\mu ,R}( x)\rho ( x,t)\int dy \frac{ \rho ( y,t)}{ | x- y|}. \end{aligned}$$

(8)

Notice that the function W can be seen as a sort of energy of a bounded region, which however takes into account the whole interaction with the rest of the particles. We will make assumptions on $f_0$ such that it will be finite at time $t=0,$ and this will enable us to prove, in both papers, the existence and uniqueness of the solution globally in time, for initial data which are not $L^1$ in space.

2.1 A Magnetically Confined Plasma

In [2] the equation we consider is (2), in which we have chosen the external force F to be a magnetic Lorentz force, confining the plasma in an infinite cylinder, that is, if $x=(x_1,x_2,x_3)$ then

$$\begin{aligned} F(x,v)=v \wedge B(x) \end{aligned}$$

(9)

with

$$\begin{aligned} B = \left( h(x_2^2+x_3^2),0,0\right) .\end{aligned}$$

(10)

The function h is defined in the cylinder

$$\begin{aligned} D=\left\{ x\in \mathbb {R}^3: -\infty<x_1< +\infty , \ 0\le \sqrt{x_2^2+x_3^2}< L\right\} \end{aligned}$$

(11)

and it is assumed to be non negative, smooth in D and diverging together with its primitive as $\sqrt{x_2^2+x_3^2}\rightarrow L$.

We consider a cylinder $D_0 \subset D$

$$\begin{aligned} D_0=\left\{ x\in \mathbb {R}^3: -\infty<x_1< +\infty , \ 0\le \sqrt{x_2^2+x_3^2}\le L_0 \right\} \end{aligned}$$

(12)

for some $L_0<L$ and define the set

$$\begin{aligned} S_0=\Big \{(x,v): x\in D_0, \ |v|\le { \mathscr {V}}_0\Big \} \end{aligned}$$

(13)

with $\mathscr {V}_0$ a positive constant. Moreover, for any $\alpha >0$ we define the following family of states:

$$\begin{aligned} {\mathscr {F}}^\alpha = \Big \{\rho : D_0\rightarrow \mathbb {R}^+\ \hbox {such that}\ \ M_i \le C |i|^{-\alpha } \Big \} \end{aligned}$$

(14)

with C a positive constant, $i\in \mathbb {Z}/\{0\}$ and

$$\begin{aligned} M_i= \int _{i\le x_1\le i+1} \rho (x) \, dx. \end{aligned}$$

(15)

In the following we set

$$ \rho _0(x)=\int f_0(x,v)\,dv. $$

Notice that, if we restrict the domain of $\rho _0(x)$ in $D_0,$ then the magnetic field at time $t=0$ is bounded.

Now we have all the ingredients to state the main result in [2].

Theorem 1

Let us fix an arbitrary positive time T. Let $f_0\in L^{\infty }$ be supported on the set $S_0$ defined in (13) and $\rho _0\in {\mathscr {F}}^\alpha$ with $\alpha >0$ arbitrary. Then there exists a solution to system (2) in [0, T] and continuous functions ${ \mathscr {V}}(t)$ and L(t) from $[0,T]\rightarrow {\mathbb {R}^+},$ satisfying ${ \mathscr {V}}(0)={ \mathscr {V}}_0,$ $L(0)=L_0$ and $0\le \sup _{t\in [0,T]}L(t)< L$ such that, for all times $t\in [0,T],$ f(t) is supported on the set:

$$\begin{aligned} S_t= \{(x,v): x\in D_t, \ |v|\le { \mathscr {V}}(t)\}\end{aligned}$$

(16)

with

$$\begin{aligned} D_t=\left\{ x\in \mathbb {R}^3: -\infty<x_1< +\infty , \ 0\le \sqrt{x_2^2+x^2_3}\le L(t)\right\} \end{aligned}$$

(17)

and moreover $\rho (t)\in { \mathscr {F}}^\alpha _t$ where

$$\begin{aligned} { \mathscr {F}}^\alpha _t = \Big \{\rho : D_t\rightarrow \mathbb {R}^+\ \hbox {such that}\ \ M_i \le C |i|^{-\alpha } \Big \}. \end{aligned}$$

(18)

This solution is unique in the class of the characteristics distributed with $f( t) \in L^\infty ,$ supported on $S_t$ and belonging to ${ \mathscr {F}}^\alpha _t \ \forall t\in [0,T].$

Remark 1

The assumption for $\rho _0$ to belong to the class (14) makes the electric field E finite at time $t=0.$ It can be satisfied in case that the spatial density, even being not integrable, has a suitable decay at infinity, but also whenever $\rho _0(x)$ is constant, or has an oscillatory character, provided it has suitable support properties. Hence this hypothesis allows for spatial densities which possibly do not belong to any $L^p$ space.

The theorem is proved by considering a cut-off system, obtained by putting in Eq. (1) the initial condition

$$\begin{aligned} f_0^N(x,v)=f_0(x,v)\chi _{D_0^N}(x), \end{aligned}$$

(19)

being $\chi _{{\mathscr {A}}}$ the characteristic function of the set ${\mathscr {A}}$ and

$$D_0^N=D_0\cap \{x\in \mathbb {R}^3:|x_1|\le N\}.$$

Let us set $\left( X^N(x,v,t),V^N(x,v,t)\right)$ to indicate the time evolved characteristics of system (2) with initial distribution $f_0^N.$ Then existence and uniqueness of solutions to (2), together with property (18) are ensured, being the spatial support of $f_0^N$ compact. Moreover one can see that, provided we have a bound on the velocities, then the confinement in the cylinder comes automatically. The following argument proves this fact. For simplicity we omit the index N, which would indicate that we are considering the time evolution of the cut-off system.

We put $l(t)=\sqrt{X_2^2(t)+X^2_3}.$ Writing by components Eq. (2) with initial datum (44), after elementary calculation we get:

$$ (V_2X_2+V_3X_3)h(l^2)=\dot{V}_2X_3-\dot{V}_3X_2+X_2E_3-X_3E_2. $$

Denoting by H a primitive of h and integrating in time we obtain,

$$\begin{aligned}&\displaystyle {\frac{1}{2}\int _0^t \frac{d}{ds} H(l^2(s))ds} \nonumber \\&\quad =\frac{1}{2} \left[ H(l^2(t))-H(l^2(0))\right] \nonumber \\&\quad =\int _0^t ds \Big [ \dot{V}_2(s)X_3(s)-\dot{V}_3(s)X_2(s)+X_2(s)E_3(s) -X_3(s)E_2(s)\Big ]. \end{aligned}$$

(20)

$H(l^2(0))$ is bounded by the hypotheses on $f_0^N,$ while the assumptions on h imply that $H(l^2(t))\rightarrow \infty$ as $l\rightarrow L.$ Hence, the left hand side in Eq. (20) goes to infinity as $l\rightarrow L.$ On the other hand, by integrating by parts the right hand side we have,

$$\begin{aligned}&\displaystyle \int _0^t ds \left[ \dot{V}_2(s)X_3(s)-\dot{V}_3(s)X_2(s)+X_2(s)E_3(s)-X_3(s)E_2(s)\right] \nonumber \\&\quad = \left[ V_2(s)X_3(s)-V_3(s)X_2(s)\right] _0^t \nonumber \\&\qquad \qquad +\displaystyle \int _0^t\left[ X_2(s)E_3(X(s),s)-X_3(s)E_2(X(s),s)\right] ds. \end{aligned}$$

(21)

If one has a bound on the velocities over the time interval [0, T], it can be proven that also the field E is bounded, so that by (21) the latter term in (20) is bounded. Hence, not to get an absurd, the plasma does remain confined in a cylinder properly contained in D, as stated before.

The previous argument shows that the main effort has to be done to find a bound on the particle velocities, which is independent of the cut-off N. To this aim an important role is played by the local energy. Putting $W^N$ for the function defined in (8) relative to the evolution of the cut-off system, and setting

$$\begin{aligned} Q^N(R,t)=\max \left\{ 1, \sup _{\mu \in {\mathbb {R}} }W^N( \mu ,R,t)\right\} \end{aligned}$$

(22)

$$\begin{aligned} {\mathscr {V}}^N(t)= \sup _{s\in [0,t]}\sup _{(x,v)\in D\times {\mathbb {R}^3}}|V^N(x,v,s)| \end{aligned}$$

(23)

and

$$\begin{aligned} R^N(t)= 1 +\int _0^t {\mathscr {V}}^N(s)ds \end{aligned}$$

(24)

we can state the following result:

Proposition 1

There exists a constant C independent of N such that

$$ Q^N(R^N(t),t)\le CQ^N(R^N(t),0). $$

Since the assumptions on $f_0^N$ ensure that the function $Q^N$ is finite at time $t=0,$ the above proposition shows that it remains finite at later times, and enables us to get estimates on the spatial density $\rho (x,t)$ and consequently on the electric field E(x, t). This is sufficient to prove the theorem.

2.2 The Vlasov–Poisson Plasma in $\mathbb {R}^3$

In this case we consider a plasma in the whole of $\mathbb {R}^3$ and its time evolution given by the Vlasov–Poisson equation, that is Eq. (1) in which $F=0.$ In analogy with the preceding case, we define W as in (8) and we set

$$\begin{aligned} Q(R,t)=\max \left\{ 1, \sup _{\mu \in {\mathbb {R}} }W( \mu ,R,t)\right\} . \end{aligned}$$

(25)

As before, for any $\alpha >0$ we define the following family of states:

$$\begin{aligned} \mathscr {F}^\alpha (C)=\Big \{\rho : \mathbb {R}^3\rightarrow \mathbb {R}^+\ \hbox {such that}\ \ M_i \le C|i|^{-\alpha } \Big \} \end{aligned}$$

(26)

with C a positive constant, $i\in \mathbb {Z}^3/\{0\}$ and

$$\begin{aligned} M_i= \int _{|i-x|\le 1} \rho (x) \, dx. \end{aligned}$$

(27)

Theorem 2

Let us fix an arbitrary positive time T. Let $f_0\in L^{\infty }$ be supported on the set

$$\begin{aligned} S_0=\Big \{(x,v): x\in {\mathbb {R}}^3, \quad |v|\le {\mathscr {V}}_0 \Big \} \end{aligned}$$

(28)

with ${\mathscr {V}}_0$ a positive constant. Moreover assume that $\rho _0\in {\mathscr {F}}^{1+\varepsilon }(C_0),$ with $\varepsilon$ arbitrary and positive, and that for any $R>1$

$$\begin{aligned} Q(R,0)\le C R^\beta , \qquad \beta < \frac{7}{5} \end{aligned}$$

(29)

with C a positive constant. Then there exists a solution to system (2) in [0, T]. Moreover this solution is unique among those distributed according to $f(t)\in L^\infty ,$ which enjoys the following properties: it is supported at any time $t\in [0,T]$ on the set

$$ S_t= \Big \{(x,v): x\in {\mathbb {R}}^3, \quad |v|\le {\mathscr {V}}(t) \Big \}, $$

$\rho (t)\in {\mathscr {F}}^{1+\varepsilon }(C(t))$ with $\varepsilon$ arbitrary and positive, being ${\mathscr {V}}(t)$ and C(t) positive continuous functions on [0, T] such that ${\mathscr {V}}(0)={\mathscr {V}}_0$ and $C(0)=C_0$ and finally, for any $R>1$

$$\begin{aligned} Q(R,t)\le C R^\beta \qquad \beta < \frac{7}{5} \end{aligned}$$

(30)

with C a positive constant.

3 The Case with Infinite Charge and Velocities

In this section we illustrate some results obtained removing, in the two preceding systems, the assumption for the density to be compactly supported in the velocities. More precisely, we consider a plasma having infinite charge and velocities, and we assume that its density is slowly decaying in space (not integrably) and Gaussian in the velocities. As in the previous cases, these hypotheses allow to well pose the problem, and make the local energy bounded at time $t=0.$ Because of this new setup, we will look for bounds on the velocity of any single particle, for a fixed initial (x, v), over an arbitrary time interval [0, T].

3.1 A Magnetically Confined Plasma

In [4] we have considered the same model as in [2]. In order to have the confinement of the plasma we have to assume that the magnetic field is sufficiently strongly diverging on the walls of the cylinder. More precisely, we define as before

$$ F(x,v)=v\wedge B(x) $$

$$\begin{aligned} B = \left( h(x_2^2+x_3^2),0,0\right) . \end{aligned}$$

(31)

but we ask for the function h to satisfy

$$\begin{aligned} h(r^2)=\frac{1}{(L^2-r^2)^\theta }\quad \quad \quad \hbox {with} \quad \quad \theta >2 \end{aligned}$$

(32)

where $r=\sqrt{x_2^2+x_3^2}.$ As before we consider a plasma initially confined in a cylinder $D_0\subset D,$ in order to have a finite magnetic field at time $t=0,$ and we introduce the family of states (14). We prove the following result:

Theorem 3

Let us fix an arbitrary positive time T. Assume that the field B satisfies (31). Let $f_0(x,v)$ be supported on $D_0\times \mathbb {R}^3$ and satisfy the two following hypotheses:

$$\begin{aligned} 0\le f_0(x,v)\le C_0 e^{- \lambda |v|^2} \end{aligned}$$

(33)

$$\begin{aligned} \rho _0(x)\in { \mathscr {F}}^\alpha \quad \quad \quad \alpha >\frac{5}{9} \end{aligned}$$

(34)

for some positive constants $C_0$ and $\lambda .$

Then there exists a solution to system (2) in [0, T] such that, for any $(x,v)\in D_0\times \mathbb {R}^3$, $\sup _{0\le t\le T}\sqrt{X_2(t)^2+X_3(t)^2}<L.$ Moreover

$$\begin{aligned} 0\le f(x,v,t)\le Ce^{-\bar{\lambda }|v|^2} \end{aligned}$$

(35)

for some positive constants C and $\bar{\lambda }$ and, for any $i\in {\mathbb {Z}}/{\{0\}}$,

$$\begin{aligned} \int _{i\le x_1\le i+1}\rho (x,t)\ dx \le C\frac{\log (1+ |i|)}{|i|^{\alpha }}. \end{aligned}$$

(36)

This solution is unique in the class of those satisfying (35) and (36).

3.2 The Vlasov–Poisson Plasma in $\mathbb {R}^3$

In [5] we prove the following two theorems.

Theorem 4

Let us fix an arbitrary positive time T. Let $f_0$ satisfy the following hypotheses:

$$\begin{aligned} 0\le f_0(x,v)\le C_0 e^{- \lambda |v|^2}g(|x|) \end{aligned}$$

(37)

where is g a bounded, continuous function satisfying, for any $i\in {\mathbb {Z}}^3/{\{0\}},$

$$\begin{aligned} \int _{|i-x|\le 1}g(|x|)\ dx \le C\frac{1}{|i|^{2+\varepsilon }} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \forall \ \varepsilon >1/15 \end{aligned}$$

(38)

being $\lambda ,$ $C_0$ and C positive constants. Then there exists a solution to Eq. (2) on [0, T] and positive constants C and $\bar{\lambda }$ such that

$$\begin{aligned} 0\le f(x,v,t)\le Ce^{-\bar{\lambda }|v|^2} \end{aligned}$$

(39)

and for any $i\in {\mathbb {Z}}^3/{\{0\}}$

$$\begin{aligned} \int _{|i-x|\le 1}\rho (x,t)\ dx \le C\frac{\log ^\frac{3}{2} (1+ |i|)}{|i|^{2+\varepsilon }}. \end{aligned}$$

(40)

This solution is unique in the class of those satisfying (39) and (40).

Remark 2

Making the more strict assumption on the spatial density to be point-wise decreasing for large |x| in place of hypothesis (38), allows us to improve the thesis of Theorem 4. Indeed, we are able to show that at any time $t\in [0,T]$ $\rho (t)$ keeps the same decreasing property, which is the object of the next theorem.

Theorem 5

Let us fix an arbitrary positive time T. Let $f_0$ satisfy the following hypotheses:

$$\begin{aligned} 0\le f_0(x,v)\le C_0 e^{- \lambda |v|^2}g(|x|) \end{aligned}$$

(41)

where is g a bounded, continuous, not increasing function such that, for $|x|\ge 1$

$$\begin{aligned} g(|x|) \le C\frac{1}{|x|^{2+\varepsilon }} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \forall \ \varepsilon >1/15 \end{aligned}$$

(42)

being $\lambda ,$ $C_0$ and C positive constants. Then there exists a solution to Eq. (2) on [0, T] and positive constants C and $\bar{\lambda }$ such that

$$\begin{aligned} 0\le f(x,v,t)\le Ce^{-\bar{ \lambda } |v|^2}g(|x|). \end{aligned}$$

(43)

This solution is unique in the class of those satisfying (43).

3.3 Proof of Theorem 5

We want to briefly sketch the proof of this theorem, as a paradigm of the kind of proofs of Theorems 3 and 4.

We introduce a cut-off system, obtained by putting in Eq. (1) the initial condition

$$\begin{aligned} f_0^N(x,v)=f_0(x,v)\chi \{|v|\le N\}. \end{aligned}$$

(44)

We consider Eq. (2) for the characteristics, with initial distribution $f_0^N,$ and set $(X^N(t),V^N(t))$ for position and velocity in this dynamics of a point particle which is in (x, v) at time $t=0.$ The solutions for such system are known to exist by the preceding results in Sect. 2, being the velocity support of the density compact. From now on all the functions relative to this dynamics will be indexed by N.

The main job is to get a fine bound on the electric field. Recalling the definition

$$ {\mathscr {V}}^N(t)= \sup _{s\in [0,t]}\sup _{(x,v)\in {\mathbb {R}^3}\times {\mathbb {R}^3}}|V^N(x,v,s)| $$

by means of the local energy we can prove the following estimate:

Proposition 2

There exists a positive constant C such that, for any $t\in [0,T]:$

$$ \int _0^t|E^N(x,s)|ds\le C \left[ {\mathscr {V}}^N(t)\right] ^\alpha \quad \quad \frac{5-\varepsilon }{9}<\alpha <\frac{2}{3} $$

being $\varepsilon$ the one in (38).

The proof of this proposition is quite lengthy and involved, and is devoted to find the exponent $\alpha ,$ which is suited for our purposes. A consequence of this result is the following

Corollary 1

$$\begin{aligned} {\mathscr {V}}^N(T) \le C N \end{aligned}$$

(45)

$$\begin{aligned} \rho ^N(x, t) \le C N^{3\alpha } \end{aligned}$$

(46)

$$\begin{aligned} Q^N(R^N(t), t)\le CN^{1-\varepsilon }. \end{aligned}$$

(47)

At this point we consider the time evolved of the point (x, v) in the phase space, in the N-th and in the $(N+1)$-th dynamics, that is we consider $\left( X^N(t), V^N(t)\right)$ and $\left( X^{N+1}(t), V^{N+1}(t)\right) ,$ the solutions to Eq. (2) with initial condition $f_0^N$ and $f_0^{N+1}$ respectively given by (44). We set

$$ \delta ^N(t) = \sup _{(x,v)\in \mathbb {R}^3 \times B(0,N)} |X^N(t)-X^{N+1}(t)| $$

where $B(0,N)=\{v:|v|\le N\},$ and we prove the following result:

Proposition 3

For any $t\in [0,T]$ it holds

$$\begin{aligned} \delta ^N(x,v,t)\le C\int _0^tdt_1\int _o^{t_1}dt_2 \left[ N^{3\alpha }\delta ^N(t_2)\left( \left| \log \delta ^N(t_2)\right| +1\right) +e^{-\frac{\lambda }{2} N^2}\right] . \end{aligned}$$

(48)

We do not give its proof, but the above result enables us to prove what follows. Put

$$ \eta ^N(t)= \sup _{(x,v)\in \mathbb {R}^3 \times B(0,N)} |V^N(t)-V^{N+1}(t)| $$

and

$$ \sigma ^N(t)= \max \{\delta ^N(t),\eta ^N(t)\}. $$

Hence we have

Proposition 4

There exists a positive constant C such that

$$\begin{aligned} \sup _{t\in [0,T]}\sigma ^N(t)\le C^{-CN}. \end{aligned}$$

(49)

This result is obviously conclusive for the proof of Theorem 5.

We prove the proposition for the quantity $\delta ^N(t),$ being the proof for $\eta ^N(t)$ similar and easier.

Notice that estimate (48) is not linear in $\delta ^N(t),$ while we would like to iterate it in time. However, it is easily seen that if $r\in (0,1),$ for any $a\in (0,1)$ the following inequality holds by convexity:

$$ r(|\log r|+1)\le r|\log a|+a. $$

Hence, for $\delta ^N(t)< 1,$ Proposition 3 gives us, for any $a<1,$

$$\begin{aligned} \delta ^N(x,v,t) \le C \int _0^t dt_1 \int _0^{t_1} dt_2\left[ N^{3\alpha } \left( \delta ^N(t_2)|\log a|+a\right) +e^{-\frac{\lambda }{2} N^2}\right] . \end{aligned}$$

(50)

On the other side, in case $\delta ^N(t)\ge 1,$ it easily seen that estimate (48) would be linear, that is

$$\begin{aligned} \delta ^N(t)\le C \int _0^t dt_1 \int _0^{t_1} dt_2\left[ N^{3\alpha }\delta ^N(t_2)+e^{-\frac{\lambda }{2} N^2}\right] . \end{aligned}$$

(51)

Hence, in case $\delta ^N(t)< 1,$ choosing $a =e^{-\frac{\lambda }{2} N^2}$ in (50), we get

$$\begin{aligned} \delta ^N(t)\le \, C \int _0^t dt_1 \int _0^{t_1} dt_2\left[ N^{3\alpha +2}\delta ^N(t_2)+e^{-\frac{\lambda }{4} N^2}\right] . \end{aligned}$$

(52)

Now we are in condition to iterate inequality (48), by inserting in the integral the same estimate for $\delta ^N(t_2).$ We make k iterations up to time $t_{k}$ and at the last step we use the estimate $\sup _{t\in [0,T]}\delta ^N(t)\le CN,$ which comes from (45). Notice that at any step we get a double factorial at the denominator, due to the double time integration, obtaining

$$\begin{aligned} \delta ^N(t)\le CNe^{-\frac{\lambda }{4} N^2}\sum _{i=1}^{k-1}\frac{C^iN^{(3\alpha +2)i}T^{2i}}{(2i)!}+\frac{C^kN^{(3\alpha +2)k}T^{2k}}{(2k)!} \end{aligned}$$

(53)

where C stands as ever for a positive constant. The latter term is exponentially vanishing as $N\rightarrow \infty ,$ provided $k>N^{(3\alpha +2)}.$ For the former term we have

$$\begin{aligned} \sum _{i=1}^{k-1}\frac{C^iN^{(3\alpha +2)i}T^{2i}}{(2i)!}\le e^{\sqrt{CT}N^{\left( \frac{3}{2}\alpha +1\right) }}. \end{aligned}$$

(54)

Hence

$$\begin{aligned} \delta ^N(t)\le CNe^{-\frac{\lambda }{4} N^2}e^{\sqrt{CT}N^{\left( \frac{3}{2}\alpha +1\right) }}+C^{-N}. \end{aligned}$$

(55)

Since in Proposition 2 we have found the “right” exponent, that is $\frac{3}{2}\alpha +1< 2,$ we have

$$\begin{aligned} \delta ^N(t)\le C^{-CN}. \end{aligned}$$

(56)