From the N-Body Schrödinger Equation to the Vlasov Equation

Abstract

This paper describes a method for obtaining an estimate of the convergence rate for the joint mean-field and semiclassical limit of the N-particle Schrödinger equation leading to the Vlasov equation. The interaction force is assumed to be Lipschitz continuous. This is an account of a recent work in collaboration with T. Paul [Arch. Rational Mech. Anal. https://doi.org/10.1007/s00205-016-1031-x].

1 Introduction

The Vlasov equation is a mean-field model in the kinetic theory of charged/massive particles. Vlasov equations are used in plasma physics to describe the dynamics of charged particles, or in cosmology to describe the collective motion of massive celestial bodies.

In the case where the interaction force between elementary constituents (ions or electrons in plasma physics, for instance) are Lipschitz continuous, the Vlasov equation has been derived from the N-body problem of classical mechanics in the large N, small coupling constant limit (see the works of Neunzert–Wick [26], Braun–Hepp [8] and Dobrushin [11]).

In the present paper, we shall investigate the following natural problem.

Problem: Is it possible to derive the Vlasov equation from the quantum N-body problem by a joint semiclassical ($\hbar \rightarrow 0$) and mean-field ($N\rightarrow \infty$) limit¹?

This problem has received the attention of several authors: see for instance the works of Graffi–Martinez–Pulvirenti [16], Pezzotti–Pulvirenti [28], and the more recent paper by Benedikter–Porta–Saffirio–Schlein [7], which discusses the Vlasov limit for a gas of fermions described by the Hartree–Fock equations. (The mean-field limit in the case of fermions involves an equivalent Planck constant of order $N^{-1/3}$, and therefore shares some features with the semiclassical limit.)

The interest for the mean-field limit in the quantum N-body problem in quantum mechanics can be explained as follows. In many applications, the particle number N is very large (typically, from $10^2$ to $10^{23}$ or more...)

Now, the N-body problem in classical mechanics involves a phase space of dimension 6N (i.e. 3 degrees of freedom for the position and 3 degrees of freedom for the momentum for each point particle). On the other hand, the N-body problem in quantum mechanics involves wave functions defined on a configuration space of dimension 3N. This explains the need for a reduced description, in the single-particle phase-space $\mathbf {R}^6$ in the case of classical mechanics, and in the single-particle configuration space $\mathbf {R}^3$ in the case of quantum mechanics.

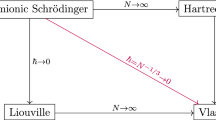
This situation can be summarized by the following diagram.

In this diagram, the horizontal arrows correspond to the mean-field limit (i.e. the limit as $N\rightarrow \infty$). Thus, the Hartree equation is the mean-field limit of the N-body Schrödinger equation in quantum mechanics, in the same way as the Vlasov equation is the mean-field limit of the N-body Liouville equation in classical mechanics. The vertical arrows correspond to the semiclassical limit (i.e. the limit as $\hbar \rightarrow 0$). The Liouville equation can be obtained as the semiclassical limit of the Schrödinger equation, while the Vlasov equation can be likewise obtained as the semiclassical limit of the Hartree equation.

The semiclassical limit of quantum mechanics is an old and distinguished subject, on which there is a huge body of literature. The reader is referred to Chap. VII of [19] for an introduction to the subject aimed at physicists, and Appendix 11 of [2] or Theorem 5.1 in [1] for a mathematical statement. Both [1, 2] refer to Maslov’s treatise [25] for a proof of the semiclassical limit; an alternate, perhaps simpler proof of the same result, based on the Laptev–Sigal parametrix [20], can be found in [5].

The limit discussed in the present paper corresponds to the diagonal arrow — i.e. to the simultaneous mean-field ($N\rightarrow \infty$) and semiclassical ($\hbar \rightarrow 0$) limits. Obviously, the validity of this limit is a consequence of the uniformity as $\hbar \rightarrow 0$ of the mean-field limit in quantum mechanics (the upper horizontal arrow), and of the semiclassical limit of the Hartree equation, leading to the Vlasov equation. The semiclassical limit of the Hartree equation has been studied for instance by Lions–Paul [24] in terms of Wigner measures (see Theorem IV.2 in [24]). Interestingly, their result applies to singular potentials, including the Coulomb potential, which is of great interest for applications (see Theorem IV.5 in [24]). The uniformity as $\hbar \rightarrow 0$ of the mean-field limit in quantum mechanics has been recently obtained in [13], and formulated in terms of some quantum analogue of the Monge–Kantorovich (or Kantorovich-Rubinshtein, or Vasershtein) distances, following the work of Dobrushin [11] in classical mechanics. The main result in [13] applies to the case of Lipschitz continuous interaction forces.

Independently of this question of uniformity, there is an important body of literature on the mean-field limit in quantum mechanics. Most of these results use the formalism of BBGKY hierarchies: [3, 31] in the case of bounded potentials, [12] in the case of the Coulomb potential. The problem of estimating the convergence rate for this limit has been studied in [30] (notice that this reference does not use the formalism of BBGKY hierarchies). More recently, a much simpler method, also avoiding the use of BBGKY hierarchies has been proposed in [29]. This new method applies to singular interaction forces, with significant restrictions on the limiting solution (which has to be a pure state). All these estimates involve either the trace norm or the operator norm, and therefore cannot be uniform as $\hbar \rightarrow 0$.

The results described in this paper have been obtained in collaboration with T. Paul [14].

2 Quantum Versus Classical Dynamics

2.1 The Vlasov Equation

The unknown of the Vlasov equation is $f\equiv f(t,x,\xi )$, the particle distribution function, which is a time-dependent probability density on the single particle phase space $\mathbf {R}^d\times \mathbf {R}^d$: in other words, f is measurable and

$$ f\ge 0\hbox { a.e. on }\mathbf {R}_+\times \mathbf {R}^d\times \mathbf {R}^d\,,\quad \iint _{\mathbf {R}^d\times \mathbf {R}^d}f(t,x,\xi )dxd\xi =1\,. $$

The Vlasov equation is a mean-field kinetic equation governing the dynamics of a gas of identical particles interacting via the potential V:

$$ {\partial }_tf+\xi \cdot {\nabla }_xf-{\nabla }V_f(t,x)\cdot {\nabla }_\xi f=0\,,\quad x,\xi \in \mathbf {R}^d\,,\quad t\ge 0\,. $$

The potential V is an even, real-valued function whose regularity will be discussed later.

This equation is obviously Hamiltonian: the left hand side is indeed of the form

$$ ({\partial }_t\,{+}\,\xi \cdot {\nabla }_x\,{-}\,{\nabla }V_f(t,x)\cdot {\nabla }_\xi )f(t,x,\xi )\,{=}\,{\partial }_tf(t,x,\xi )+\{H_f(t,x,\xi ),f(t,x,\xi )\}\,, $$

where the mean-field, self-consistent potential and Hamiltonian are given by the formulas

$$ \left\{ \begin{aligned}{}&V_f(t,x):=\iint _{\mathbf {R}^d\times \mathbf {R}^d}V(x-y)f(t,y,\xi ) dyd\xi \,, \\ \\&H_f(t,x,\xi ):=\tfrac{1}{2}|\xi |^2+V_f(t,x)\,, \end{aligned}\right. $$

while the Poisson bracket is defined by the prescription

$$ \{x_m,x_n\}=\{\xi _m,\xi _n\}=0\,,\qquad \{\xi _m,x_n\}={\delta }_{mn}\,,\quad m,n=1,\ldots ,d\,. $$

2.2 The N-Body Schrödinger Equation

The unknown of the N-body Schrödinger equation is the N-body wave function $\varPsi _N\equiv \varPsi _N(t,x_1,\ldots ,x_N)\in \mathbf {C}$, where $x_j$ is the position of the j-th particle for each $j=1,\ldots ,N$. The N-body configuration space is $\mathfrak {H}_N:=\mathfrak {H}^{\otimes N}\simeq L^2((\mathbf {R}^d)^N)$, with $\mathfrak {H}:=L^2(\mathbf {R}^d)$.

The Schrödinger equation is written in terms of the quantum N-body Hamiltonian

$$ \mathscr {H}_N:=\sum _{j=1}^N-\tfrac{1}{2}\hbar ^2{\varDelta }_{x_j}+\frac{1}{N}\sum _{1\le j<k\le N}V(x_j-x_k)\,, $$

which involves the real-valued, even interaction potential V. The quantum Hamiltonian is viewed as an unbounded operator acting on $\mathfrak {H}_N$, and the Schrödinger equation takes the form

$$\begin{aligned} \begin{aligned}i\hbar {\partial }_t\varPsi _N=\mathscr {H}_N\varPsi _N:=\sum _{j=1}^N-\tfrac{1}{2}\hbar ^2{\varDelta }_{x_j}\varPsi _N+\frac{1}{N}\sum _{1\le j<k\le N}V(x_j-x_k)\varPsi _N\,, \\ x_1,\ldots ,x_N\in \mathbf {R}^d\,. \end{aligned}\end{aligned}$$

(1)

Observe the 1/N coupling constant in front of the potential. It is chosen so that the kinetic energy of the N-particle system, i.e.

$$ \sum _{j=1}^N-\tfrac{1}{2}\hbar ^2{\varDelta }_{x_j} $$

which involves a N-term summation, is of the same order of magnitude as its potential energy

$$ \frac{1}{N}\sum _{1\le j<k\le N}V(x_j-x_k) $$

involving a $N^2$-term summation. The 1/N coupling constant is typical of the mean-field limit for particles which do not satisfy the Pauli exclusion principle — in other words, one should keep in mind that the mean-field scaling for fermions is completely different (see [6] on p. 1089).

2.3 The N-Body Heisenberg Equation

Let $\rho (t)$ be the $\mathfrak {H}_N$-orthogonal projection on the complex line $\mathbf {C}\varPsi _N(t,\cdot )\subset \mathfrak {H}_N$. Adopting Dirac’s notation involving “bras” and “kets” (see Chap. I.6 in [10])

$$ \rho _{N}(t):=|\varPsi _N(t,\cdot )\rangle \langle \varPsi _N(t,\cdot )|\,. $$

If $\varPsi _N$ satisfies the Schrödinger equation (1), then $\rho _N(t)$ satisfies the Heisenberg equation

$$ i\hbar {\partial }_t\rho _N(t)=\mathscr {H}_N\rho _N(t)-\rho _N(t)\mathscr {H}_N=:[\mathscr {H}_N,\rho _N(t)]\,, $$

since the N-body quantum Hamiltonian $\mathscr {H}_N$ is self-adjoint on $\mathfrak {H}_N$.

More generally, the Heisenberg equation defines a dynamics on the set of density operators on $\mathfrak {H}_N$.

A density operator on $\mathfrak {H}_N$ is a linear operator $\rho$ on $\mathfrak {H}_N$ satisfying

$$ \rho =\rho ^*\ge 0\,,\quad {\text {tr}}_{\mathfrak {H}_N}(\rho )=1\,. $$

The set of density operators on $\mathfrak {H}_N$ is henceforth denoted $\mathscr {D}(\mathfrak {H}_N)$.

3 Comparing Quantum and Classical Densities

3.1 Monge–Kantorovich(-Rubinshtein)/Vasershtein Distance

Let $\mu ,\nu$ be Borel probability measures on $\mathbf {R}^d$ with bounded p-th order moments, where $p\ge 1$.

A coupling of $\mu ,\nu$ is a Borel probability measure $\pi$ on $\mathbf {R}^d\times \mathbf {R}^d$ with 1st and 2nd marginals $\mu$ and $\nu$ respectively. In other words, for all $\phi ,\psi \in C_b(\mathbf {R}^d)$, one assumes that

$$ \iint _{\mathbf {R}^d\times \mathbf {R}^d}(\phi (x)+\psi (y))\pi (dxdy)=\int _{\mathbf {R}^d}\phi (x)\mu (dx)+\int _{\mathbf {R}^d}\psi (y)\nu (dy)\,. $$

The set of couplings of $\mu ,\nu$ is denoted $\varPi (\mu ,\nu )$.

The Monge–Kantorovich distance of exponent p between $\mu$ and $\nu$ is defined as

$$ {\text {dist}}_{MK,p}(\mu ,\nu ):=\inf _{\pi \in \varPi (\mu ,\nu )}\left( \iint _{\mathbf {R}^d\times \mathbf {R}^d}|x-y|^p\pi (dxdy)\right) ^{1/p}\,. $$

This distance is often referred to as the “Vasershtein (or Wasserstein) distance” and sometimes as the “Kantorovich–Rubinshtein distance” (the latter terminology being used mostly in the case $p=1$). An excellent reference for this class of distances is Chap. 7 of [32]. (Even the fact that the expression above satisfies the triangle inequality is far from obvious: see Sect. 1 in Chap. 7 of [32].)

Perhaps the most important result on Monge–Kantorovich distances for the purpose of our study is that the Monge–Kantorovich distance of exponent p metrizes the weak topology of probability measures with bounded moments of order p (see Sect. 2 in Chap. 7 of [32]).

The following elementary computations show that the Monge–Kantorovich distance between probability measures is well suited for measuring the proximity/stability of particle trajectories — at variance with the distance defined by the total variation.

Example 1

Let $a,b\in \mathbf {R}^d$; then

$$ {\text {dist}}_{MK,p}({\delta }_a,{\delta }_b)=|a-b|\,, $$

whereas

$$ \Vert {\delta }_a-{\delta }_b\Vert _{TV}=\left\{ \begin{aligned}2\quad \hbox { if }a\not =b\,,\\ 0\quad \hbox { if }a=b\,.\end{aligned}\right. $$

The essence of the semiclassical limit is that the dynamics of the quantum density operators concentrates on particle trajectories in phase space. Therefore, it is natural to expect that a uniform in $\hbar$ convergence rate estimate for the mean-field limit in quantum mechanics should involve some analogue of a Monge–Kantorovich distance. Indeed, Monge–Kantorovich distances metrize the weak topology of probability measures (with additional moment bounds). These distances are particularly well adapted to estimating the difference between a smooth density and a probability measure concentrated on a lower dimensional set, such as a Dirac measure. This was the rationale for introducing the “pseudo-distance” $MK_2^\hbar$ in [13]. The reader is referred to (4) below for a precise definition of this quantity, which is obviously analogous to the quadratic Monge–Kantorovich distance ${\text {dist}}_{MK,2}$ on the set of Borel probability measures in phase space.

3.2 Coupling Quantum and Classical Densities

Next we seek to define a notion of “pseudo-distance” between a quantum and a classical density. This pseudo-distance is constructed by analogy with the Monge–Kantorovich distance of exponent 2, following Dobrushin’s 1979 derivation of the Vlasov equation in [11].

As a first step we need to define a notion of coupling of a quantum and of a classical density.

Definition 1

Let $\rho \in \mathscr {D}(\mathfrak {H})$ and let p be a Borel probability density on $\mathbf {R}^d\times \mathbf {R}^d$. A coupling of $\rho$ and p is an operator-valued function $(x,\xi )\mapsto Q(x,\xi )$ defined on $\mathbf {R}^d\times \mathbf {R}^d$ such that

$$ \left\{ \begin{aligned}{}&(x,\xi )\mapsto Q(x,\xi )=Q(x,\xi )^*\in \mathscr {L}(\mathfrak {H})\quad \hbox { s.t. } Q(x,\xi )\ge 0\,, \\&{\text {tr}}(Q(x,\xi ))=p(x,\xi )\,,\qquad \quad \iint _{\mathbf {R}^d\times \mathbf {R}^d}Q(x,\xi )dxd\xi =\rho \,. \end{aligned}\right. $$

The set of all couplings of the densities $\rho$ and p is denoted $\mathscr {C}(p,\rho )$.

Example 2

The set $\mathscr {C}(p,\rho )$ is obviously nonempty, since the map

$$ p\otimes \rho :\,(x,\xi )\mapsto p(x,\xi )\rho \qquad \hbox { belongs to }\mathscr {C}(p,\rho )\,. $$

3.3 Pseudo-distance Between Quantum and Classical Densities

Next we introduce a cost function comparing classical and quantum “coordinates” (i.e. position and momentum). This cost function is defined as follows:

$$ c_\hbar (x,\xi ):=|x-y|^2+|\xi +i\hbar {\nabla }_y|^2\,. $$

The reason for considering a quadratic cost function is that quadratic polynomials are quantized exactly as second order differential operators. In other words, $c_\hbar$ is the quantization of the cost-function $|x-y|^2+|\xi -\eta |^2$ defined on the 2-body phase space $\mathbf {R}^6_{x,\xi }\times \mathbf {R}^6_{y,\eta }$.

Definition 2

Let $\rho \in \mathscr {D}(\mathfrak {H})$ and let p be a Borel probability density on $\mathbf {R}^d\times \mathbf {R}^d$. We define

$$ E_\hbar (p,\rho ):=\inf _{Q\in \mathscr {C}(p,\rho )}\sqrt{\iint _{\mathbf {R}^d\times \mathbf {R}^d}{\text {tr}}(c_\hbar (x,\xi )Q(x,\xi ))dxd\xi }\,. $$

This pseudo-distance² is obviously analogous to the Monge–Kantorovich distance with exponent 2.

Remark 1

The integrand in the expression defining $E_\hbar (p,\rho )$ may not be defined, since $c_\hbar (x,\xi )Q(x,\xi )$ may fail in general to be a trace-class operator on $\mathfrak {H}$. In fact this integrand should be thought of as being defined by the following formula:

$$ {\text {tr}}(c_\hbar (x,\xi )Q(x,\xi )):={\text {tr}}(Q(x,\xi )^{1/2}c_\hbar (x,\xi )Q(x,\xi )^{1/2})\in [0,\infty ]\,. $$

Indeed, the right hand side above always defines an element of $[0,+\infty ]$ since $Q(x,\xi )^{1/2}c_\hbar (x,\xi )Q(x,\xi )^{1/2}$ is a self-adjoint nonnegative operator for a.e. $x,\xi \in \mathbf {R}^d$. (This is analogous to the integral of a nonnegative measurable function, which always defines an element of $[0,+\infty ]$.)

Unfortunately, the pseudo-distance defined by the expression above is a slightly mysterious object. In the sequel, we seek to compare it to more familiar quantities.

3.4 Husimi Transform and Lower Bound for $E_\hbar$

First we recall the notions of Wigner and Husimi transforms of a density operator on a Hilbert space.

Definition 3

Let $\rho \in \mathscr {D}(\mathfrak {H})$. The Wigner transform at scale $\hbar$ of the density operator $\rho$ is the function defined on the phase space $\mathbf {R}^d_x\times \mathbf {R}^d_\xi$ by the formula

$$ W_\hbar [\rho ](x,\xi ):=\tfrac{1}{(2\pi )^d}\int _{\mathbf {R}^d}e^{-i\xi \cdot y}\rho (x+\tfrac{1}{2}\hbar y,x-\tfrac{1}{2}\hbar y)dy\,. $$

The Husimi transform at scale $\hbar$ of the density operator $\rho$ is the function on the phase space $\mathbf {R}^d_x\times \mathbf {R}^d_\xi$ defined in terms of the Wigner function by the formula

$$ \widetilde{W}_\hbar [\rho ]:=e^{\hbar {\varDelta }_{x,\xi }/4}W_\hbar [\rho ]\,. $$

The Wigner function of a density operator $\rho \in \mathscr {D}(\mathfrak {H})$ satisfies

$$ W_\hbar [\rho ](x,\xi )\in \mathbf {R}\quad \hbox { for a.e. }x,\xi \in \mathbf {R}^d\,. $$

However, $W_\hbar [\rho ]$ is in general not a.e. nonnegative. In other words, the Wigner transform does not map the set $\mathscr {D}(\mathfrak {H})$ of (quantum) density operators on configuration space into the set of (classical) probability densities on phase space.

On the other hand, the Husimi transform satisfies

$$ \widetilde{W}_\hbar [\rho ](x,\xi )\ge 0\quad \hbox { for a.e. }x,\xi \in \mathbf {R}^d\,. $$

The next result establishes a lower bound for the pseudo-distance $E_\hbar$ in terms of the quadratic Monge–Kantorovich distance between the classical probability density and the Husimi transform of the quantum density.

Theorem 1

Let p be a probability density on $\mathbf {R}^d\times \mathbf {R}^d$ s.t.

$$ \iint _{\mathbf {R}^d\times \mathbf {R}^d}(|x|^2+|\xi |^2)p(x,\xi )dxd\xi <\infty \,. $$

For each $\rho \in \mathscr {D}(\mathfrak {H})$, one has

$$ E_\hbar (p,\rho )^2\ge \max \left( d\hbar \,,\,\mathrm{dist}_{\mathrm{MK},2}(p,\widetilde{W}_\hbar [\rho ])^2-d\hbar \right) \,. $$

See Theorem 2.4 (2) in [14] for a proof of this result. Notice in particular that $E_\hbar (p,\rho )>0$ for all p and $\rho$.

3.5 Töplitz Quantization and Upper Bound for $E_\hbar$

In this section, we first define the notion of Töplitz quantization, which can be thought of as the reciprocal of the Husimi transform, up to an error term of order $O(\hbar )$.

Given $q,p\in \mathbf {R}^d$, we define the coherent state $|q+ip,\hbar \rangle$, which is the wave function given by the formula

$$ |q+ip,\hbar \rangle (x):=(\pi \hbar )^{-d/4}e^{-|x-q|^2/2\hbar }e^{ip\cdot x/\hbar }\,. $$

This wave function consists of a plane wave in the direction of p, modulated with a Gaussian amplitude centered at q. See Figs. 1 and 2 for a graphic representation of the modulus of $|q+ip,\hbar \rangle$.

The coherent state $|q,p\rangle$ is the quantum analogue of the perfectly localized phase space density ${\delta }_{q,p}$ on $\mathbf {R}^6_{x,\xi }$. Of course, this state is not perfectly localized in position and momentum because of Heisenberg’s uncertainty principle. The Gaussian localization is known to saturate the Heisenberg uncertainty principle: see Theorem 226 in [17], which is quoted as “Weyl’s inequality”.

Fig. 1

With $\hbar =8\cdot 10^{-5}$, $Z =\,$real part of coherent state centered at $q=(0,0)$ with momentum $p=(1,0)$ with space variable $(X,Y)\in \mathbf {R}^2$

Fig. 2

Oscillating structure of a Gaussian coherent state. This is the section of the graph in Fig. 1 in the plane of equation $x=0$

Definition 4

For each positive Borel measure $\mu$ on $\mathbf {C}^d$, the Töplitz operator with symbol $\mu$ is

$$ {\text {OP}}^T_\hbar (\mu ):=\tfrac{1}{(2\pi \hbar )^d}\int _{\mathbf {C}^d}|z,\hbar \rangle \langle z,\hbar |\,\mu (dz)\ge 0\,. $$

For instance, an elementary computation shows that ${\text {OP}}^T_\hbar (1)=I_\mathfrak {H}$.

The relation between the Töplitz quantization and the Husimi transform is explained by the following formula:

$$ \tilde{W}_\hbar [{\text {OP}}^T_\hbar (\mu )]=\tfrac{1}{(2\pi \hbar )^d}e^{\hbar {\varDelta }_{x,\xi }/2}\mu \,. $$

(See formula (51) in [13].) In other words, the Husimi transform of a Töplitz operator is equal to its symbol up to a smoothing operator which is an $O(\hbar )$ perturbation of the identity.

Theorem 2

Under the same assumptions as in Theorem 1, let $\mu$ be a Borel probability measure on $\mathbf {C}^d$. Then ${\text {OP}}^T_\hbar ((2\pi \hbar )^d\mu )\in \mathscr {D}(\mathfrak {H})$ and

$$ E_\hbar (p,{\text {OP}}^T_\hbar ((2\pi \hbar )^d\mu ))^2\le \mathrm{dist}_{\mathrm{MK},2}(p,\mu )^2+d\hbar \,. $$

See Theorem 2.4 (1) in [14] for a proof of this result.

4 From the N-Body Heisenberg Equation to the Vlasov Equation

4.1 Indistinguishable Particles and Symmetries

Henceforth, we use the following notation for N-tuples of positions or momenta:

$$ X_N:=(x_1,\ldots ,x_N)\,,\qquad \varXi _N:=(\xi _1,\ldots ,\xi _N)\,. $$

We also need the following representation of the symmetric group $\mathfrak {S}_N$ in $\mathfrak {H}_N$. For each ${\sigma }\in \mathfrak {S}_N$ and each $\varPsi \in \mathfrak {H}_N$, we define $U_{\sigma }\in \mathscr {L}(\mathfrak {H}_N)$ by the following formula:

$$ U_{\sigma }\varPsi (X_N):=\varPsi ({\sigma }\cdot X_N)\,,\qquad \hbox { where }{\sigma }\cdot X_N:=(x_{{\sigma }^{-1}(1)},\ldots ,x_{{\sigma }^{-1}(N)})\,. $$

Obviously

$$ U^*_{\sigma }=U_{\sigma }^{-1}(=U_{{\sigma }^{-1}})\,; $$

in other words, $U_{\sigma }$ is a unitary operator on $\mathfrak {H}_N$.

With this, we define a notion of symmetric quantum N-body density operator. A density operator $\rho \in \mathscr {D}(\mathfrak {H}_N)$ is said to be symmetric if

$$ U_{\sigma }\rho _NU_{\sigma }^*=\rho _N\,,\qquad \hbox { for all }{\sigma }\in \mathfrak {S}_N\,. $$

The set of symmetric density operators on $\mathfrak {H}_N$ is denoted $\mathscr {D}^s(\mathfrak {H}_N)$. Since the N particles under consideration are indistinguishable, their density operator is obviously symmetric.

This symmetry property is propagated by Heisenberg’s equation, in the following sense. If $\rho _N(t)$ is a solution of Heisenberg’s equation, then

$$ \rho _N(0)\in \mathscr {D}^s(\mathfrak {H}_N)\Rightarrow \rho _N(t)\in \mathscr {D}^s(\mathfrak {H}_N)\,,\quad \hbox { for all }t\in \mathbf {R}\,. $$

4.2 Symmetric Densities and $k-$Particle Marginals

For each symmetric N-particle density operator $\rho _N\in \mathscr {D}^s(\mathfrak {H}_N)$, its k-particle marginal is the symmetric density operator $\rho ^\mathbf {k}_N\in \mathscr {D}^s(\mathfrak {H}_k)$ such that

$$ {\text {tr}}_{\mathfrak {H}_k}(A\rho ^\mathbf {k}_N)={\text {tr}}_{\mathfrak {H}_N}((A\otimes I_{\mathfrak {H}_{N-k}})\rho _N) $$

for each $A\in \mathscr {L}(\mathfrak {H}_k)$.

Example 3

For each $\rho \in \mathscr {D}(\mathfrak {H})$ and all $N\ge k\ge 1$, one has

$$ \rho _N:=\rho ^{\otimes N}\Rightarrow \rho _N^\mathbf {k}=\rho ^{\otimes k}\,. $$

4.3 From the N-Body Heisenberg Equation to the Vlasov Equation

The main result in this paper is the following theorem (which is Theorem 2.6 in [14]).

Theorem 3

Let $f^{in}\equiv f^{in}(x,\xi )\in L^1((|x|^2+|\xi |^2)dxd\xi )$ be a probability density on $\mathbf {R}^d\times \mathbf {R}^d$, and let $\rho ^{in}_{N,\hbar }\in \mathscr {D}^s(\mathfrak {H}_N)$. Let f and $\rho _{N,\hbar }$ be the solutions of the Vlasov and the Heisenberg equation with initial data $f^{in}$ and $\rho ^{in}_{N,\hbar }$ respectively. Let $\varGamma$ be given by the formula

$$ \varGamma :=2+4\max (1,{\text {Lip}}({\nabla }(V))^2\,. $$

(1) Then, for each $t\ge 0$ one has

$$ E_\hbar (f(t),\rho _{\hbar , N}^\mathbf {1}(t))^2\!\le \!\frac{1}{N}E_\hbar ((f^{in})^{\otimes N},\rho ^{in}_{\hbar , N})^2e^{\varGamma t}\!+\!\frac{8\Vert {\nabla }V\Vert _{L^\infty }^2}{N-1}\frac{e^{\varGamma t}\!-\!1}{\varGamma }\,. $$

(2) If moreover $\rho _{\hbar ,N}^{in}={\text {OP}}^T_\hbar [(2\pi \hbar )^{dN}(f^{in})^{\otimes N}]$, then

$$ \mathrm{dist}_{\mathrm{MK},2}(f(t),\widetilde{W}_\hbar [\rho _{\hbar , N}^\mathbf {1}(t)])^2\le d\hbar (1+e^{\varGamma t})+\frac{8\Vert {\nabla }V\Vert _{L^\infty }^2}{N-1}\frac{e^{\varGamma t}-1}{\varGamma }\,. $$

An example of initial bosonic state satisfying the assumption of Theorem 3 (2) is

$$ \rho _{\hbar ,N}^{in}={\text {OP}}^T_\hbar [(2\pi \hbar )^{dN}{\delta }_{(q,p)}^{\otimes N}]\quad \hbox { for some }q,p\in \mathbf {R}^d\,. $$

In other words, $\rho _{\hbar ,N}^{in}$ is the density operator associated to the factorized N-body wave function

$$ \varPsi ^{in}_{\hbar ,N}(x_1,\ldots ,x_N)=\prod _{k=1}^N|q+ip,\hbar \rangle (x_k)\,. $$

Actually, one can replace the Gaussian profile in the definition of the wave packet $|q+ip,\hbar \rangle$ with any other real-valued function $a\in \mathscr {S}(\mathbf {R}^d)$. This would lead to an initial state defined in terms of the factorized N-body wave function

$$ \varPsi ^{in}_{\hbar ,N}(x_1,\ldots ,x_N)=\prod _{k=1}^Na\left( \frac{x_k-q}{\sqrt{\hbar }}\right) e^{ip\cdot x_k/\hbar }\,. $$

With this modification, the inequality in Theorem 3 (2) remains unchanged, except for the first term on the right hand side, which should be replaced with $\hbar (d+H[a]e^{\varGamma t})$, where H[a] is a positive constant depending on the function a only. The interested reader is referred to the forthcoming publication [15] for a detailed discussion on this matter.

We shall not insist further on this issue, since we are concerned with the joint mean-field and semiclassical limit of the quantum dynamics of N-particle systems. Indeed, the influence of the quantum statistics (i.e. the difference between bosons and fermions) disappears in the semiclassical limit.

5 Proof of Theorem 3

The core of the proof is based on an Eulerian analogue of Dobrushin’s argument in [11], which was based on following particle trajectories. In addition, Dobrushin used the following essential feature of the N-particle dynamics in classical mechanics: the phase-space empirical measure built on a solution of Newton’s system of motion equations is an exact (weak) solution of the Vlasov equation. No analogue of this property is known in quantum mechanics to this date. Our analysis uses instead the N-particle Heisenberg equation, which is the quantum analogue of the Liouville equation in classical mechanics.

5.1 Dynamics of Couplings

Our first task is to write an equation defining a dynamics on the set of couplings of the N-fold tensor product of the Vlasov solution and of the N-particle Heisenberg solution. This idea follows [13] — see also [9, 27] which used a similar idea in a rather different context (specifically, for nonlinear diffusion equations viewed as gradient flows in the sense of Otto). However, the procedure used in [13] and in [14] — described below — for propagating couplings of solutions of the Heisenberg and of the Vlasov–Poisson equations differs significantly from the method used in [9, 27]. We shall not insist further on this point, which is rather subtle; suffice it to say that the argument in [9, 27] uses tools from optimal transport — specifically, the Benamou–Brenier variational formula for the quadratic Monge–Kantorovich distance (formula (7.34) in [33]), specialized to gradient fields. There does not seem to be any obvious analogue of this method in the case considered below and in [14], which uses a completely different procedure.

Let $Q^{in}_{N,\hbar }\in \mathscr {C}((f^{in})^{\otimes N},\rho ^{in}_{N,\hbar })$; solve the classical+quantum transport equation

$$\begin{aligned} \left\{ \begin{aligned}{}&{\partial }_tQ_{N,\hbar }(t,X_N,\varXi _N)+\left\{ \sum _{j=1}^NH_f(t,x_j,\xi _j),Q_{N,\hbar }(t,X_N,\varXi _N)\right\} _N \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad +\frac{i}{\hbar }[\mathscr {H}_N,Q_{N,\hbar }(t,X_N,\varXi _N)]=0\,, \\ \\&Q_{N,\hbar }{\big |}_{t=0}=Q^{in}_{N,\hbar }\,, \end{aligned}\right. \end{aligned}$$

(2)

where we recall that

$$ \left\{ \begin{aligned}{}&\mathscr {H}_N:=\sum _{j=1}^N-\tfrac{1}{2}\hbar ^2{\varDelta }_{y_j}+\frac{1}{N}\sum _{1\le j<k\le N}V(y_j-y_k)\,, \\ \\&H_f(t,x,\xi ):=\tfrac{1}{2}|\xi |^2+\iint _{\mathbf {R}^d\times \mathbf {R}^d}V(x-z)f(t,z,\zeta )dzd\zeta \,. \end{aligned}\right. $$

The notation $\{\cdot ,\cdot \}_N$ designates the N-body Poisson bracket, defined by

$$ \{x_{j,m},x_{k,n}\}_N=\{\xi _{j,m},\xi _{k,n}\}_N=0\,,\quad \{\xi _{j,m},x_{k,n}\}_N={\delta }_{jk}{\delta }_{mn}\,, $$

with $j,k=1,\ldots ,N$ and $m,n=1,\ldots ,d$. In other words, the Eq. (2) describes the joint dynamics of N quantum, indistinguishable particles and of N associated classical, independent particles.

This mixed system of particles satisfies the following symmetry property.

Definition 5

Let $\rho _N\in \mathscr {D}^s(\mathfrak {H}_N)$. A coupling $Q_N$ of $f^{\otimes N}$ and $\rho _N$ is said to be a symmetric coupling if

$$ U_{\sigma }Q_N({\sigma }\cdot X_N,{\sigma }\cdot \varXi _N)U_{\sigma }^*=Q_N(X_N,\varXi _N)\qquad \hbox { for all }{\sigma }\in \mathfrak {S}_N\,, $$

for a.e. $X_N,\varXi _N\in (\mathbf {R}^d)^N$.

In other words, the classical particles are exchanged by the same permutation as their quantum associates.

Not surprisingly, this symmetry property is propagated by (2).

Lemma 1

Let $Q_{N,\hbar }$ be the solution of (2).

(1) For each $t\ge 0$, one has

$$ Q_{N,\hbar }(t)\in \mathscr {C}(f(t)^{\otimes N},\rho _{N,\hbar }(t))\,. $$

(2) If $Q^{in}_{N,\hbar }$ is a symmetric coupling, then, for all $t\ge 0$, the coupling $Q_{N,\hbar }(t)$ is symmetric.

This is Lemma 5.1 in [14], to which we refer for a proof. The key idea in the proof of statement (1) is the following: elementary computations show that the ${\text {tr}}_{\mathfrak {H}_N}(Q(t,X_N,\varXi _N))$ is a classical N-body probability density which satisfies the same equation as

$$ \prod _{j=1}^nf(t,x_j,\xi _j)\,. $$

Likewise

$$ \int _{(\mathbf {R}^d\times \mathbf {R}^d)^N}Q(t,X_N,\varXi _N)dX_Nd\varXi _N\in \mathscr {D}(\mathfrak {H}_N) $$

and satisfies the N-body Heisenberg equation. By uniqueness of the solution of the Vlasov and of the Heisenberg equation, this implies statement (1). Statement (2) follows from observing that $Q_N$ and

$$ (t,X_N,\varXi _N)\mapsto U_{\sigma }Q_N(t,{\sigma }\cdot X_N,{\sigma }\cdot \varXi _N)U_{\sigma }^* $$

are both solutions of the Cauchy problem (2) with the same initia data.

5.2 The Functional D(t)

For each symmetric coupling that is a solution of (2), define

$$ D(t):=\frac{1}{N}\!\iint _{(\mathbf {R}^d\times \mathbf {R}^d)^N}\sum _{k=1}^N{\text {tr}}_{\mathfrak {H}_N}(c_{\hbar }(x_j,\xi _j,y_j,{\nabla }_{y_j})Q_{N,\hbar }(t,X_N,\varXi _N))dX_Nd\varXi _N\,. $$

Lemma 2

For each $t\ge 0$, one has

$$ D(t)\ge E_\hbar (f(t),\rho ^\mathbf {1}_{N,\hbar }(t))^2\,. $$

Proof

First $Q^\mathbf {1}_{N,\hbar }(t)\in \mathscr {C}(f(t),\rho ^\mathbf {1}_{N,\hbar }(t))$, and by symmetry of $Q_{N,\hbar }$

$$ \begin{aligned}D(t)=\!\iint _{(\mathbf {R}^d\times \mathbf {R}^d)^N}{\text {tr}}_{\mathfrak {H}_N}(c_{\hbar }(x_1,\xi _1,y_1,{\nabla }_{y_1})Q_{N,\hbar }(t,X_N,\varXi _N))dX_Nd\varXi _N&\\ =\!\iint _{(\mathbf {R}^d\times \mathbf {R}^d)}{\text {tr}}_{\mathfrak {H}}(c_{\hbar }(x_1,\xi _1,y_1,{\nabla }_{y_1})Q^\mathbf {1}_{N,\hbar }(t,x_1,\xi _1))dx_1d\xi _1&\\ \ge E_\hbar (f(t),\rho ^\mathbf {1}_{N,\hbar }(t))^2&\end{aligned}$$

by definition of $E_\hbar$.

5.3 The Evolution of D

Apply the cost operator $c_\hbar (x_1,\xi _1,y_1,{\nabla }{y_1})$ to both sides of the equation for $Q_{N,\hbar }$, integrate by parts in the classical variables and use the identity

$$ {\text {tr}}([A,S]T)=-{\text {tr}}([A,T]S)\,, $$

which is in some sense analogous to “integration by parts in the quantum variables”.

We thus arrive at the differential equality

$$ \begin{aligned}\dot{D}\!=\!\!\iint \!{\text {tr}}_\mathfrak {H}\left( (\{\tfrac{1}{2}|\xi _1|^2,c_\hbar \}\!-\![\tfrac{i\hbar }{2}{\varDelta }_{y_1},c_\hbar ])(x_1,\xi _1,y_1,{\nabla }{y_1})Q^\mathbf {1}_{N,\hbar }(t,x_1,\xi _1)\right) dx_1d\xi _1&\\ +\frac{i}{\hbar }\iint {\text {tr}}_{\mathfrak {H}_2}\left( \tfrac{N-1}{N}[V(y_1-y_2),c_\hbar (x_1,\xi _1,y_1,{\nabla }{y_1})]Q^\mathbf {2}_{N,\hbar }(t,X_2,\varXi _2)\right) dX_2d\varXi _2&\\ +\iint \!{\text {tr}}_\mathfrak {H}\left( \{V_f,c_\hbar \}(x_1,\xi _1,y_1,{\nabla }{y_1})Q^\mathbf {1}_{N,\hbar }(t,x_1,\xi _1)\right) dx_1d\xi _1&\,. \end{aligned}$$

At this point, we denote the symmetric operator product as follows

$$ A\vee B:=AB+BA\,, $$

and use the inequality

$$\begin{aligned} A^*B+B^*A\le A^*A+B^*B\,,\quad \hbox { for all }A,B\in \mathscr {L}(\mathfrak {H}_N)\,. \end{aligned}$$

(3)

(Indeed $A^*A+B^*B-A^*B-B^*A=(A^*-B^*)(A-B)\ge 0$.)

Then, one has

$$ \{\tfrac{1}{2}|\xi _1|^2,c_\hbar \}\!-\![\tfrac{i\hbar }{2}{\varDelta }_{y_1},c_\hbar ]=(\xi _1+i\hbar {\nabla }_{y_1})\vee (x_1-y_1)\le c_\hbar \,. $$

Since $Q_{N,\hbar }\ge 0$, this inequality and the equality above for $\dot{D}$ imply that

$$ \begin{aligned}\dot{D}\le D-\tfrac{N-1}{N}\int {\text {tr}}_{\mathfrak {H}_2}(Q^\mathbf {2}_{N,\hbar }(\xi _1+i\hbar {\nabla }_{y_1})\vee \mathscr {W}(X_2,Y_2))dX_2d\varXi _2&\\ -\int {\text {tr}}_{\mathfrak {H}_N}(Q_{N,\hbar }(\xi _1+i\hbar {\nabla }_{y_1})\vee \tfrac{1}{N-1}\sum _{j=2}^N\mathscr {V}(t,x_1,x_j))dX_Nd\varXi _N&\,, \end{aligned}$$

using again the symmetry of $Q_{N,\hbar }$ in the last term, and denoting

$$ \begin{aligned}{}&\mathscr {V}(t,x_1,x_j)\!:={\nabla }V\star f(t,x_1)-\tfrac{N-1}{N}{\nabla }V(x_1-x_j)\,, \\&\mathscr {W}\,(X_2,Y_2)\,:={\nabla }V(x_1-x_2)-{\nabla }V(y_1-y_2)\,. \end{aligned}$$

Indeed

$$ {\text {tr}}_{\mathfrak {H}_N}(Q_{N,\hbar }(A^*B+B^*A))\le {\text {tr}}_{\mathfrak {H}_N}(Q_{N,\hbar }(A^*A+B^*B))\,, $$

since

$$ \begin{aligned}{\text {tr}}_{\mathfrak {H}_N}(Q_{N,\hbar }(A^*A+B^*B))-{\text {tr}}_{\mathfrak {H}_N}(Q_{N,\hbar }(A^*B+B^*A))&\\ ={\text {tr}}_{\mathfrak {H}_N}(Q_{N,\hbar }^{1/2}(A^*-B^*)(A-B)Q_{N,\hbar }^{1/2})\ge 0&\,. \end{aligned}$$

Therefore

$$ \dot{D}\le (3+2L^2)D+\int _{(\mathbf {R}^d\times \mathbf {R}^d)^N}\left| \tfrac{1}{N-1}\sum _{k=2}^N\mathscr {V}(t,x_1,x_k)\right| ^2f^{\otimes N}dX_Nd\varXi _N\,. $$

Expand the square in the last term on the right hand side, and observe that

$$ j\not =k\Rightarrow \int \mathscr {V}(t,x_1,x_j)\cdot \mathscr {V}(t,x_1,x_k)f^{\otimes N}dX_Nd\varXi _N=0\,. $$

Therefore, the last term on the right hand side of the last inequality is equal to

$$ \begin{aligned}\int \tfrac{1}{(N-1)^2}\sum _{j=2}^N|\mathscr {V}(t,x_1,x_k)|^2f^{\otimes N}dX_Nd\varXi _N&\\ =\int \tfrac{1}{N-1}|\mathscr {V}(t,x_1,x_2)|^2f^{\otimes 2}dX_2d\varXi _2&=O(1/N)\,. \end{aligned}$$

One concludes with the Gronwall inequality.

6 Final Remarks and Perspectives

The core of the convergence rate estimate in the proof of Theorem 3 involves a stability inequality and a consistency estimate, as in Lax’s equivalence theorem [21] in numerical analysis.

The stability part of the analysis (leading to the exponential amplification by Gronwall’s inequality) can be seen at the level of the first equation in the BBGKY hierarchy. Because the cost function in D is a sum of quantities depending on $x_j,y_j,\xi _j$, there is a “localization in degree” effect in the BBGKY hierarchy. In particular, there is no bound à la Cauchy–Kowalevsky when estimating D.

The consistency part of the analysis requires distributing the interaction term $\mathscr {V}$ on all the particles. Since the $\mathscr {V}$ term depends on the $X_N$ variables only, and the $X_N$ marginal of $Q_{N,\hbar }$ is the N-fold tensor power of the Vlasov solution, one concludes by (a trivial quantitative variant of the) law of large numbers.

The quantity $E_\hbar$ introduced in [14] and Definition 2 can also be used to prove quantitative estimate of the convergence rate for the semiclassical limit of the Hartree equation, leading to the Vlasov equation. Likewise, one can also prove the semiclassical limit of the N-body Heisenberg equation leading to the N-body Liouville equation, and obtain a uniform in N estimate for the convergence rate in terms of the $E_\hbar$ pseudo-distance. These results are stated as Theorems 2.5 and 2.7 respectively in [14]. Both proofs assume that ${\nabla }V$ is Lipschitz continuous on $\mathbf {R}^d$, as in the derivation of the Vlasov equation from the N-body Heisenberg equation discussed here. While the semiclassical limit has been known for a long time, it is perhaps not without interest to compare the existing results in the literature with Theorems 2.5 and 2.7 in [14].

The traditional method for describing the semiclassical limit is the WKB ansatz (see Chap. VII in [19], especially Sect. 46). Controling the propagation of the WKB ansatz puts severe regularity requirements on the potential (which should be $C^\infty$), and on the initial phase function (assumed to be $C^m$ with $m>6d+5$): see [5]. The formulation of the semiclassical limit in [24] requires much less on the potential (which should be of class $C^{1,1}$, as in [14] and the present work), and essentially nothing on the family of initial density operators indexed by $\hbar$. The quantitative result in [14] only requires that the phase space moments of order 2 of the initial family of density operators should be bounded as $\hbar \rightarrow 0$. However, obtaining a precise description of the structure of the propagated Wigner measure in the semiclassical limit seems to require additional regularity properties on the initial condition. The propagation of the Wigner measure associated to a WKB ansatz in the semiclassical limit has been studied in detail in [4] with the tools of geometric measure theory. One of the conclusions to be drawn from the discussion in [4] is that the basic structure of the propagated WKB ansatz, especially as regards the notion of “caustic”, may differ dramatically if the regularity of the initial phase function falls below some regularity threshold. However, this does not affect the validity of the semiclassical limit and the convergence rate for this limit in terms of the pseudo-distance $E_\hbar$. In other words, one can argue that the pseudo-distance $E_\hbar$ considered in [14] and in the present paper is probably the most appropriate tool for propagating convergence rate estimates in the semiclassical limit under minimal regularity assumptions.

We conclude this paper with a (very incomplete) list of open problems related to the ones considered in [14].

Problem 1. Can one generalize Theorem 3 to the case of the Coulomb potential $V=1/r$? This would lead to a rigorous justification of the Vlasov–Poisson system from the quantum mechanics of a large number of identical particles. Deriving the Vlasov–Poisson system from the classical N-point dynamics with Coulomb interaction is still an outstanding open problem. There has been some recent progress on this problem. The best result with point particles at the time of this writing is due tu Hauray and Jabin [18]; it can handle singular interaction forces of order $O(r^{-{\alpha }})$ with ${\alpha }<1$ in terms of the inter-particle distance r. The Hauray–Jabin method falls short of treating the Coulomb interaction even in the most favorable space dimension 2.

Problem 2. Another class of results assumes that the interacting particles have a positive radius, vanishing as the number of particles $N\rightarrow \infty$. This suggests considering a mollified potential V, with a regularizing effect that is gradually removed as $N\rightarrow \infty$: see [22, 23] for the best results in that direction, leading ultimately to the Vlasov–Poisson system. Is it possible to obtain a similar result starting from the quantum N-body problem, and viewing $\hbar$ as a regularization parameter analogous to the particle radius in the classical case, with some asymptotic ordering of $\hbar$ and 1 / N?

Problem 3. It could be interesting to explore more thoroughly the properties of $E_\hbar$ and of the pseudo-distance $MK_2^\hbar$ used in [13]. Let us briefly recall the definition of $MK_2^\hbar$. Let $\mathfrak {H}:=L^2(\mathbf {R}^d)$ and let $\rho _1,\rho _2\in \mathscr {D}(\mathfrak {H})$. A coupling of $\rho _1$ and $\rho _2$ is a density operator $R\in \mathscr {D}(\mathfrak {H}\otimes \mathfrak {H})$ such that

$$ {\text {tr}}_{\mathfrak {H}_2}(R(A\otimes I))={\text {tr}}_\mathfrak {H}(\rho _1A)\,,\quad {\text {tr}}_{\mathfrak {H}_2}(R(I\otimes A))={\text {tr}}_\mathfrak {H}(\rho _2A)\,. $$

Denoting by $\varPi (\rho _1,\rho _2)$ the set of couplings of $\rho _1,\rho _2$, one defines

$$\begin{aligned} MK_2^\hbar (\rho _1,\rho _2):=\inf _{R\in \varPi (\rho _1,\rho _2)}\sqrt{{\text {tr}}_{\mathfrak {H}_2}((|x_1-x_2|^2-|{\nabla }_{x_1}-{\nabla }_{x_2}|^2)R)}\,. \end{aligned}$$

(4)

We do not know whether $MK^\hbar _2$ satisfies the triangle inequality — at least none of the two proofs of the triangle inequality for the Monge–Kantorovich distances proposed in Chap. 7, Sect. 1 of [32], seems to have any obvious analogue for $MK^\hbar _2$.

Similarly, one can study the following question: let p be a probability density on $\mathbf {R}^d\times \mathbf {R}^d$ such that

$$ \iint _{\mathbf {R}^d\times \mathbf {R}^d}(|x|^2+|\xi |^2)p(x,\xi )dxd\xi <\infty \,, $$

and let $\rho _1,\rho _2\in \mathscr {D}(\mathfrak {H})$. Does one have

$$ E_\hbar (p,\rho _2)\le E_\hbar (p,\rho _1)+MK_2^\hbar (\rho _1,\rho _2)? $$

If such an inequality was known, one could immediately deduce Theorem 3 from Theorem 2.4 in [13] and from the convergence rate for the semiclassical limit obtained in Theorem 2.5 in [14].