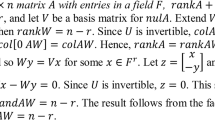The Learning and Teaching of Linear Algebra Through the Lenses of Intellectual Need and Epistemological Justification and Their Constituents

Abstract

Intellectual need and epistemological justification are two central constructs in a conceptual framework called DNR-based instruction in mathematics. This is a theoretical paper aiming at analyzing the implications of these constructs and their constituent elements to the learning and teaching of linear algebra. At the center of these analyses are classifications of intellectual need and epistemological justification in mathematical practice along with their implications to linear algebra curriculum development and instruction. Two systems of classifications for intellectual need are discussed. The first system consists of two subcategories, global need and local need; and the second system consists of five categories of needs: need for certainty, need for causality, need for computation, need for communication, and formalization, and need for structure. Epistemological justification is classified into three categories: sentential epistemological justification (SEJ), apodictic epistemological justification (ASJ), and meta epistemological justification (MEJ).

DNR-based instruction in mathematics (DNR, for short; Harel, 1998, 2000, 2008a, b, c, 2013a, b) is a theoretical framework for the learning and teaching of mathematics—a framework that provides a language and tools to formulate and address critical curricular and instructional concerns. DNR can be thought of as a system consisting of three categories of constructs: premises—explicit assumptions underlying the DNR concepts and claims; concepts—constructs defined and oriented within these premises; and claims—statements formulated in terms of the DNR concepts, entailed from the DNR premises, and supported by empirical studies.

The main goal of this paper is to discuss cognitive and pedagogical aspects of linear algebra through the lenses of two central DNR concepts: intellectual need and epistemological justification . As the above list of references indicates, DNR has been discussed extensively elsewhere, and so in this paper we only reiterate briefly the definitions of these concepts along with their essential constituent elements: the concepts of ways of understanding and ways of thinking and four out of the eight premises of DNR.

We begin in Sect. 1 with the concepts of ways of understanding and ways of thinking. Following this, in Sect. 2, we discuss the four DNR premises. With these concepts and premises in hand, we turn, in Sect. 3, to the definition of intellectual need and epistemological justification . The fourth and fifth sections present, respectively, more refined analyses into various categories of the latter two concepts. The sixth, and last, section concludes with reflections and research questions. In each section, the discussion is accompanied with observations made in teaching experiments in linear algebra we have conducted during the years. In this respect, this is a theoretical, not empirical, paper. That is, the purpose of the paper is to theorize and illustrate the role and function of intellectual need and epistemological justification and their constituent elements in the learning and teaching of linear algebra.

To help the reader navigate through the various DNR terms introduced in this paper, we end each section with a figure depicting the network of terms accrued up to that section. Figure 1, for example, depicts the three categories of constructs comprising DNR outlined in this introduction. The rest of the figures in the paper will be expansions of this figure.

Fig. 1

DNR’s three categories of constructs

1 Ways of Understanding and Ways of Thinking

The notions of way of understanding and way of thinking have technical definitions (see Harel, 2008c). However, for the purpose of this paper it is sufficient to think of them as two different categories of knowledge, the first refers to one’s conceptualization of “subject matter,” such as the way one interprets particular definitions, theorems, proofs, problems and their solutions; and the second refers to “conceptual tools,” such as deductive reasoning, empirical reasoning, attention to structure and precision, and problem-solving approaches (e.g., heuristics). One of the central claims of DNR, called the duality principle, asserts that (a) one’s ways of thinking impacts her or his ways of understanding; and, (b) it is the acquisition of appropriate ways of understanding that brings about a change and development in one’s ways of thinking.

To illustrate, consider the following example. A mathematically mature student who possesses definitional reasoning—the way of thinking by which one examines concepts and proves assertions in terms of well-defined statements—is likely to understand the concept of dimension of a subspace as intended—the number of vectors in a basis of the subspace—but he or she would also realize that such a definition is meaningless without answering the question whether all bases of a subspace have the same number of vectors. Another student, for whom definitional reasoning has not yet reached full maturity, may have the same understanding without realizing the need to settle this question. Yet another student whose conceptualization of mathematics is principally action-based (in the sense of APOS theory),¹ is likely to understand the concept of dimension in terms of a rule applied to n-tuples. For such a student, the dimension of a span of a set of vectors in $R^{n}$ amounts to carrying out a procedure of, for example, setting up these vectors as the columns of a matrix, row reducing the matrix, and determining, accordingly, the number of pivot columns the matrix has. We observed each of these three conceptualizations among students on various occasions, even in upper division linear algebra courses. And scenarios corresponding to these three conceptualizations have occurred throughout our teaching experiments when attention to a well-defined concept was called for. For example, when the instructor concluded that the projection matrix onto a subspace $V$ of $R^{n}$ is the matrix $P = W(W^{T} W)^{ - 1} W^{T}$, where $W$ is a basis matrix² of $V$, there were a few students who fully understood, and some even independently raised, the concern that $P$ might be dependent on the choice of $W$. For most of the students, however, the conclusion engendered no concern.

The implication of the second part of the duality principle is that students acquire a particular way of thinking only by repeatedly dealing with specific ways of understanding associated with that way of thinking. For example, students develop definitional reasoning not by preaching but by repeatedly using definitions in the process of mathematical argumentations and by dealing in a multitude of contexts with the question whether a concept is well defined.

The examples of ways of thinking we have listed above are general—they pertain to mathematics as a discipline. Different areas or sub-areas of mathematics, however, can be branded by ways of thinking specific to them. The conceptualizations of matrix theory and the theory of general vector spaces share ways of thinking (e.g., axiomatic proof schemes (Harel & Sowder, 1998) and structural reasoning (Harel & Soto, 2016), and yet each is branded by a set of ways of thinking unique to it. For example, while thinking in terms of row reduction and block matrices is part of elementary matrix theory, it is often not applicable to coordinate-free, vector spaces.

Problem-solving approaches are instances of ways of thinking (Harel, 2008c). Therefore, “reasoning in terms of __ in solving problems” is an instance of a way of thinking. For example, reasoning in terms functions, reasoning in terms of row reduction, reasoning in terms of block matrices, reasoning in terms of linear combinations are all problem-solving approaches, and hence are ways of thinking. In our experience, the acquisition and application of such ways of thinking is difficult for students. Consider, for example, reasoning in terms of block matrices (known also as partitioned matrices) and linear combination. It is one thing applying block-matrices rules to multiply matrices; it is another using block matrices to represent and solve problems. Typically, students are able to perform at the level of action conception (ala APOS theory) algebraic operations using block matrices, but they experience major difficulties when block matrices are constructed to represent relations and prove theorems. Consider the simple case of the product $A_{m \times n} x_{n \times 1}$ as a linear combination of the columns of $A$. We repeatedly observed students having difficulties representing a common statement such as “$v_{1}, v_{2}, \ldots, v_{k} \in span(u_{1}, u_{2}, \ldots, u_{m} ) \subseteq R^{n}$” in a matrix form: $\left[ {\begin{array}{*{20}c} {v_{1} } & {v_{2} } & \ldots & {v_{k} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & \ldots & {u_{m} } \\ \end{array} } \right]Q$ for some $Q_{m \times k}$.

This difficulty manifested itself on numerous occasions, for example in comprehending the following proof of the theorem, “Any set of $m$ linearly independent vectors in an $m$-dimensional subspace $H$ of $R^{n}$ spans $H$”. The proof presented in class was an elaboration of the following lines:

Let $u_{1} ,u_{2} , \ldots ,u_{m}$ be linearly independent vectors in $H$, and set $U = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & \ldots & {u_{m} } \\ \end{array} } \right]$. Let $V = \left[ {\begin{array}{*{20}c} {v_{1} } & {v_{2} } & \ldots & {v_{m} } \\ \end{array} } \right]$ be a basis matrix of $H$. There exists a matrix $Q_{m \times m}$ such that $U = VQ$. Since the columns of $U$ are linearly independent, $Q$ is invertible, and so $UQ^{ - 1} = V$. Hence $u_{1} ,u_{2} , \ldots ,u_{m}$ span $H$.

We point to two obstacles students typically encounter in comprehending this proof. The first revolves around the equation $U = VQ$; students indicate that they do not understand where the matrix $Q$ came from, even after they are presented with an explanation by their group mates or the instructor. A possible conceptual basis for this difficulty is that the construction of $Q$ requires performance at the level of process conception (ala APOS theory), a form of abstraction known to be cognitively demanding (Dubinsky, 1991). Specifically, one needs to construct, successively and in thought, each column of $Q$ out of the coefficients of the expression representing its corresponding column of $U$ as a linear combination of the columns of $V$ (i.e., $Q_{i} = \left[ {\begin{array}{*{20}c} {q_{i1} } & {q_{i2} } & \ldots & {q_{im} } \\ \end{array} } \right]^{T}$, where $U_{i} = \sum\nolimits_{j = 1}^{m} {q_{ij} V_{i} }$, $i = 1,2, \ldots ,m$). Even students who overcome this difficulty express discomfort with the claim that the result $UQ^{ - 1} = V$ completes the proof. At the heart of this claim, and the difficulty, is the fact that linear combination of linear combinations is a linear combination—that since each vector in $H$ is a linear combination of the columns of $V$ and each column of $V$ is a linear combination of the columns of $U$, by $UQ^{ - 1} = V$, $ColU = H$. Here too performance at the level of process conception seems essential, in that one has to carry out this chain of relations in thought in order to fully bring oneself to a firm conviction about the validity of the claim.

Figure 2 expands Fig. 1 to include the DNR constructs discussed in this section.

Fig. 2

Two of the DNR concepts: Ways of understanding and ways of thinking—

2 DNR Premises

DNR has eight premises; they are philosophical stands appropriated from existing theories, such as the Piagetian theory of equilibration (Piaget, 1985), Brousseau’s (1997) theory of didactical situation, and Aristotle. Relevant to this paper are four of these premises; they are: the knowledge of mathematics premise, the knowing premise, the knowledge-knowing linkage premise, and the subjectivity premise.

The knowledge of mathematics premise states: knowledge of mathematics consists of two related but different categories of knowledge: the ways of understanding and ways of thinking that have been institutionalized throughout history.³ The significance of this premise to mathematics instruction is that while knowledge of and focus on ways of understanding is indispensable for quality teaching, it is not sufficient. Mathematics instruction should also attend to ways of thinking. With this instructional view one would teach, for example, row reduction not only as a tool to solve systems of linear equations but be cognizant of and explicit about the value of this tool in analyzing and answering theoretical questions. In accordance to the duality principle stated earlier, the development of such a way of thinking is facilitated by instruction that persistently models it in proving theorems and solving problems, as the following episode illustrates.

The episode occurred in an elementary linear algebra class. The instructor defined column rank and row rank. It turned out that the class as a whole dealt with these concepts in an add-on Matlab component to the course (entirely not coordinated with the instructional pace of the course), where the students have used the fact that ${ \dim }\,ColA = { \dim }\,RowA$ without proof. Before the instructor turned to prove this statement, one of the students in the class exclaimed publically that she found this fact fascinating—that for any array of numbers, “no matter what” (her words), the maximum number of linearly independent columns equals the maximum number of linearly independent rows. Then she added: “I kept thinking about it for some time until I found why”. In response to the instructor’s question, “What was the explanation you have found?” she said: “… by reducing the matrix into $rref$ … I always bring up $rref$ … it helps me solve the homework problems”. Then she proceeded by explaining how in $rrefA$ the number of columns with a leading 1 is necessarily equal to the number of rows with a leading 1, from which she concluded that ${ \dim }\,ColA = { \dim }\,RowA$, using the previously proved facts that row reduction preserves dependence/independence of the columns of $A$ as well as $RowA$.

We posit that the instructor’s explicit and persistent effort to present row reduction as a conceptual tool in proving theorems and solving problems contributed to conceptualizations as the one articulated by this student.

The next two premises are inextricably linked; one is about knowing and the other about the linkage between knowing and knowledge. The knowing premise states: The means of knowing is the process of assimilation and accommodation. According to Piaget (1985), disequilibrium, or perturbation, is a mental state when one fails to assimilate. Equilibrium, on the other hand, is a state in which one perceives success in assimilating. In Piaget’s terms, equilibrium occurs when one has successfully modified her or his viewpoint (accommodation) and is able, as a result, to integrate new ideas toward obtaining a solution of a problem (assimilation). The knowing - knowledge linkage premise states: Any piece of knowledge humans know is an outcome of their resolution of a problematic situation (Brousseau, 1997; Piaget, 1985). This premise is an extension of the knowing premise. While the knowing premise is about the mechanism of learning, the knowing-knowledge linkage premise guarantees that row material for the operation of that mechanism (i.e., a problematic situation from the engagement of which knowledge is constructed) exist. Collectively, the last two premises constitute a theoretical foundation for, respectively, the essentiality and viability of problem-solving based curricula. Namely, these curricula are essential because the only way to construct knowledge is by resolution to problematic situations (by the knowing-knowledge premise); and they are viable because such situations exist (by the knowing premise).

The implication for instruction of the view articulated by the last two premises is the necessity principle, which states: For students to learn what we intend to teach them, they must have a need for it, where ‘need’ refers to intellectual need . Relevant to curriculum design, the necessity principle entails that new concepts and skills should emerge from problems understood and appreciated as such by the students, and these problems should demonstrate to the student the intellectual benefit of the concept at the time of its introduction.

The problematic situations referred to in this premise may or may not be historic. For example, matrices did not grow out of the need to solve systems of linear equations, as typically is done in elementary linear algebra textbooks, but out of the need to develop determinants (in 1848 by J.J. Sylvester). According to Tucker (1993), “array of coefficients led mathematicians to develop determinants, not matrices. Leibniz … used determinants in 1693 about hundred and fifty years before the study of matrices …” (p. 5). Also, most problems studied in linear algebra are not introduced in the context of the field in which they originated initially. For example, Gauss elimination is typically introduced in textbooks in an application-free context, but it initially emerged in the field of geodesy and for years was considered part of the development of this field (Tucker, 1993).

The subjectivity premise states: Any observations humans claim to have made are due to what their mental structure attributes to their environment. This premise orients our interpretations of the actions and views of the learner. It cautions us—teachers—that what might be problematic for one individual or a community may not be so for others. A situation might trigger a mental perturbation with one person and be accepted by another. To illustrate, we continue the discussion about the concept of dimension we started in Sect. 1. In one of our teaching experiments, the instructor deliberately defined “dimension” as the number of vectors in a basis without first stating the theorem that all bases of a subspace have the same number of vectors. Following this, he asked the students to discuss in their working groups whether the definition is sound. A while later, when no productive response came from the students, he made the task more explicit by asking whether there is a need to establish a particular property of bases in a subspace for the definition to be meaningful. None of the students found any fault with the definition as stated. Following this, the instructor asked the class to comment on the following hypothetical scenario:

Two students, John and Mary, are asked to determine the dimension of a particular subspace of a vector space. John identifies a basis of the subspace, counts the number of its elements, and reports that the dimension is 5. Mary identifies a different basis of the subspace, counts the number of its elements, and reports that the dimension is 7.

While some of the students responded as expected—that there is a need to establish that all bases of the subspace have the same number of vectors—astonishingly, there were students who responded by saying something to the effect that for John the dimension of the subspace is 5, and for Mary the dimension is 7. Presumably, these students did not possess the definitional way of thinking, and so the scenario described by their instructor did not cause them the desirable perturbation—their response was an outcome of their current schemes.

The subjectivity premise also cautions us, teachers, that learners’ current ways of thinking may lead them to independently generalize faulty knowledge from a correct one. For example, student may, and typically do, erroneously conclude that row reduction preserves the column space, as it does with row space. Furthermore, often due to the level of robustness of certain ways of thinking students possess counterexamples to such faulty generalizations may not be effective (Harel & Sowder, 2007). For example, in our experience, students continue to hold this generalization true even after they are shown counterexamples to the contrary [e.g., for any matrix whose entries are all 1s, $ColA \ne Col(rrefA)$]. Many scholars (e.g., Confrey, 1991; Dubinsky, 1991; Steffe, Cobb, & Glasersfeld, 1988; Steffe & Thompson, 2000) have articulated essential implications of the subjectivity premise to mathematics curriculum and instruction, even if they have not given it an axiomatic status as we do.

Figure 3 expands Fig. 2 to include the DNR constructs discussed in this section.

Fig. 3

Three of the eight DNR premises and two of DNR foundational principles

3 Intellectual Need and Epistemological Justification

With these premises at hand, we now present the definitions of intellectual need and its associated concept, epistemological justification , as formerly introduced in Harel (2013a), with minor modifications.

[Let] K be a piece of knowledge possessed by an individual or community, then, by the knowing-knowledge linkage premise, there exists a problematic situation S out of which K arose. S (as well as K) is subjective, by the subjectivity premise, in the sense that it is a perturbational state resulting from an individual’s encounter with a situation that is incompatible with, or presents a problem that is unsolvable by, her or his current knowledge. Such a problematic situation S, prior to the construction of K, is referred to as an individual’s intellectual need : S is the need to reach equilibrium by learning a new piece of knowledge. Thus, intellectual need has to do with disciplinary knowledge being created out of people’s current knowledge through engagement in problematic situations conceived as such by them. One may experience S without succeeding to construct K. That is, intellectual need is only a necessary condition for constructing an intended piece of knowledge. Methodologically, intellectual need is observed when we see that (a) one’s engagement in the problematic situation S has led her or him to construct the intended piece of knowledge K and (b) one sees how K resolves S. The latter relation between S and K is crucial, in that it constitutes the genesis of mathematical knowledge—the perceived reasons for its birth in the eyes of the learner. We call this relation epistemological justification .

Intellectual need and epistemological justification are two sides of the same coin—they are different but inextricably related constructs. Their occurrence is entirely dependent on one’s background knowledge. Consider the question: What is a generator for the ideal of polynomials annihilating a given operator $T$ over an n-dimensional vector space? Clearly, such a question wouldn’t occur unless one possesses a cluster of ways of understanding for the concepts: ideal, generator of an ideal, operator annihilating ideal etc. Less trivial is the question, what ways of thinking facilitate the emergence of such a question with an individual? Or put in another way, how can we educate students to develop the habit of mind of asking such questions? A critical claim of this paper is that attention to epistemological justifications in generating definitions and proving theorems may pave the road to such habit of minds, as we will see in the next sections.

Even if such a question is raised, its answer hinges upon one’s understanding and appreciation of the most foundational concept of linear algebra: linear combination. Thinking in terms of this concept and its derivative concepts of linear independence and linear dependence, one may recognize that the ideal of polynomials annihilating an operator $T$ over an n-dimensional vector space is not empty, since it contains an annihilator polynomial of degree $n^{2}$. This may not end here if this individual continues to ask: What is a generator for this ideal? And since the degree of such a polynomial is not greater than $n^{2}$, can it be $n$? Is there a polynomial of degree n that annihilates $T$? If the search for an answer to this question leads the individual, independently or with the help of an expert, to Cayley-Hamilton Theorem (“Any linear operator on a finite-dimensional vector space is annihilated by its characteristic polynomial”), then by definition, the individual has constructed an epistemological justification for the theorem. An epistemological justification for the proof of the theorem—how the proof might be elicited—is a different matter. Such a proof may require additional or different networks of ways of understanding and ways of thinking.

It is important to highlight two points concerning intellectual need and epistemological justification . First, we iterate a point we made earlier, these constructs are not historical; rather, they are pedagogical (and research) tools. Namely, the need which has originally necessitated a particular concept may not—and is usually not—the one used in a curriculum. For example, in one of our teaching experiment, the concept of linear independence was necessitated through the question, When does Gaussian Elimination lead to “loss” of equations (i.e., zero equations in a system obtained through the application of elementary operations)?; and in another experiment through the question, When does a consistent system of linear equation have a unique solution? Historically, this concept emerged from generalizations of spatial relationships by Grassmann (Li, 2008).

Second, while problems outside the fields of mathematics can serve as intellectual need for particular mathematical concepts and ideas, as we know from history, intellectual need is not synonymous with application. Cognitively, the term “application” refers to problematic situations aiming at helping students solidify mathematical knowledge they have already constructed or are in the process of constructing. Intellectual need , on the other hand, aims at eliciting knowledge students are yet to learn.

Figure 4 expands Fig. 3 to include the DNR constructs discussed in this section.

Fig. 4

Two additional foundational DNR concepts: Intellectual need and epistemological justification

4 Categories of Intellectual Need

We offer two systems of classifications of intellectual need , each with a particular role in curriculum development and instruction; in this paper, they are instantiated in the context of the learning and teaching of linear algebra. The first system of classification rests on the distinction between local need and global need; it pertains to the structure of a mathematics curriculum. The second system of classification is more refined, in that it identifies specific types of intellectual needs that emerge in mathematical practice; they are: need for certainty, need for causality, need for computation, need for communication, and need for structure. These two systems of classifications will be discussed in turn in the next two sections. (For a discussion on the cognitive origins of these needs, see Harel, 2013a.)

4.1 Local Need Versus Global Need

Consider an elementary course in linear algebra structured around a series of investigations, each aimed at answering a particular central question. The course begins with the question: (1) What is linear algebra? And it immediately discusses one of its branches: systems of linear equations, both systems in which the unknowns are scalars in a particular field (linear systems of scalar equations) and systems in which the unknowns are functions (linear systems of differential equations). Attending first to linear systems of scalar equations, the course then progressively proceeds by investigating, in this order, the questions: (2) Why is the focus on linear systems? (3) What exactly is the elimination process (which typically students are familiar with its basic form from their high-school mathematics)? (4) Why does the process of elimination work? (5) Why are equations “lost” in the elimination process? (6) Is there an algorithm to solve linear (scalar) systems? (7) What does the reduced echelon form (rref) tell us about the solution set of a system? This is a partial sequence of central questions aimed at helping the students build a coherent global image of the purposes of the study of systems of linear equations. Collectively, not individually, such questions represent a global intellectual need for the study of a particular area of mathematics.

An investigation into each of such questions generates specific problems manifesting local intellectual need —the need for the construction of particular concepts and ideas. A probe into some of the above questions, generate, for example, the concepts of linear combination, equivalent systems, linear independence, and basis, for the purpose of advancing the overarching investigation. To illustrate, consider, for example, Question 4—Why does the process of elimination work? In linear-algebraic terms, this question can be formulated as: Why elementary operations preserve the solution set of a system? A probe into the nature of these operations elicits the need for the creation of concepts and ideas. It begins with the following central idea:

Let $S$ be an $m \times n$ system, with equations $\varepsilon_{1} ,\varepsilon_{2} , \ldots ,\varepsilon_{m}$. For any $m$ scalars $c_{1} ,c_{2} , \ldots ,c_{m}$, any solution of system $S$ is a solution of the equation $\varepsilon_{\varSigma } = c_{1} \varepsilon_{1} + c_{1} \varepsilon_{1} + \ldots + c_{m} \varepsilon_{m}$.

In turn, this idea elicits the foundational concept of linear combination (i.e., the equation $\varepsilon_{\varSigma }$ is a linear combination of the equations, $\varepsilon_{1} ,\varepsilon_{2} , \ldots ,\varepsilon_{m}$), and with it, the following conclusion, which gives rise to the concept of equivalent systems:

Given two systems $S_{1}$ and $S_{2}$ of the same size, if each equation of $S_{1}$ is a linear combination of equations of $S_{2}$ and each equation of $S_{2}$ is a linear combination of $S_{1}$, then the two systems have same solution set.

Thus,

Two systems of equal size are equivalent if each equation in one system is a linear combination of the equations in the second system, and vice versa.

And so:

If two systems are equivalent, then they have the same solution set.

These results, then, lay the foundation for the question under consideration (Question 4), which now can be stated as: Do elementary operations preserve equivalency?

The second half of the course turns to linear systems of differential equations (i.e., $Y^{\prime}(t) = AY(t)$, $Y(0) = C$) where eigen theory is then introduced through the global need to investigate the question, How to solve such systems? This question leads to local needs, as will be discussed in the next section.

Figure 5 expands Fig. 4 to include the DNR constructs discussed in this section.

Fig. 5

First classification of intellectual need

4.2 Intellectual Need in Mathematical Practice

Based on cognitive and historical analyses, we offered in Harel (2013a) five categories of intellectual needs : (1) need for certainty, (2) need for causality, (3) need for computation, (4) need for communication, and (5) need for structure.

The first two needs are complementary to each other: understanding cause brings about certainty, and certainty might trigger the need to determine cause. The need for certainty is the need to prove—to remove doubts. One’s certainty is achieved when one determines, by whatever means he or she deems appropriate, that an assertion is true. The need for causality, on the other hand, is the need to explain—to determine a cause of a phenomenon, to understand what makes a phenomenon the way it is. A student might be certain that a particular assertion is true because a teacher or textbook said so or because he or she verified the assertion empirically. The student might even reach certainty on the basis of a proof, and yet lack an insight as to what makes the assertion true—the proof may not be explanatory for her or him. In the next section, we will discuss explanatory proofs in the context of epistemological justification .

The third need is the need for computation. It is the need to quantify or calculate values of quantities and relations among them by means of symbolic algebra. For example, the need to quantify the “size” of a solution set of a linear system $Ax = b$ may be addressed by the concept of rank: the smaller the rank of a matrix $A$ is the “larger” the solution set of a consistent system $Ax = b$ becomes. Likewise, the need to reduce the data storage of a digitized image without compromising significantly the quality of the image through its electronic transmission may be responded to by decomposing the matrix representing the gray values of the image into a particular sum of rank-1 matrices, what is known as singular value decomposition ($svd$; see below for more discussion on this decomposition).

The fourth need is the need for communication. This need consists in two reflexive needs: the need for formulation—the need to transform strings of spoken language into algebraic expressions—and the need for formalization—the need to externalize the exact meaning of ideas and concepts and the logical justification for arguments. It is common that students experience difficulties formalizing a mathematical statement into a symbolic form. For example, students may understand that to find a least square solution to an inconsistent system $Ax = b$, one needs to replace $b$ by $\hat{b}$, such that $\hat{b}$ is the “closest” to $ColA$. The challenge for students is two-fold: first, they have to reformulate this goal into mathematical statements, verbally or symbolically, such as $\hat{b} \in ColA$ and $b - \hat{b} \bot ColA$; and second they have to express these statements in terms of equation-based expressions, $\hat{b} = Ac$ for some vector $c$ and $A^{T} (b - \hat{b}) = 0$. This latter step is typically challenging for students. Likewise, students may have an intuitive idea of what dimension is—usually in the context of 2- and 3-dimensional Euclidean spaces, but experience difficulty understanding the formalization of their intuition into a well-defined mathematical concept.

The fifth, and final, need is the need for structure. The common meaning of the term structure is something made up of a number of parts that are held or put together in a particular way. In mathematics the way these “parts” are held together are relations one conceives among different objects. For example, the expression $Ab = 0$ constitutes a structure for a person when he or she is conceives it as a string of symbols put together in a particular way to convey a particular meaning, such as 0 is a linear combination of the columns of $A$ with the entries of $b$ being the weights of the combination; or $b$ is orthogonal to the row space of $A$.

In mathematics, in general, the need for structure manifests itself as a need to encapsulate (in the sense of APOS theory) occurrences of phenomena. For example, one might encapsulate a series of empirical observations concerning products of square matrices into the patterns, $\det (AB) = \det (A)\det (B)$ or $tr(AB) = tr(BA)$; another may derive such patterns through deduction or may observe them empirically but see a need to establish them deductively. In linear algebra, there is the critical need to encapsulate different structures into a single representation: a vector space over the reals as a single representation of all $n$-tuples of real number, of all polynomials of degree less or equal to $n$ with real coefficients, of all $m \times n$ matrices with real entries, etc. This process of encapsulation assumes, of course, that members of each of these spaces are conceived as conceptual entities (in the sense of APOS theory and Greeno, 1992)) in, respectively, an $n$-dimensional, $n + 1$-dimensional, and $mn$-dimensional vector space.

Figure 6 expands Fig. 5 to include the DNR constructs discussed in this section.

Fig. 6

Second classification of intellectual need

5 Categories of Epistemological Justification

We distinguish among three categories of epistemological justifications : sentential, apodictic, and meta. While the distinction among these types of epistemological justification is sufficiently clear, as we will now see, it should be noted that they are not mutually exclusive.

5.1 Sentential Epistemological Justification

Sentential epistemological justification (SEJ) refers to a situation when one is aware of how a definition, axiom, or proposition was born out of a need to resolve a problematic situation. It is called so because it pertains to sentences with objective and logical meaning. To illustrate, consider how linear algebra textbooks typically introduce the pivotal concepts of “eigenvalue,” “eigenvector,” and “matrix diagonalization”. A widely used linear algebra textbook motivates these concepts by saying that the concepts of “eigenvalue” and “eigenvector” are needed to deal with the problem of factoring an $n \times n$ matrix $A$ into a product of the form $XDX^{ - 1}$, where $D$ is diagonal, and that this factorization would provide important information about $A$, such as its rank and determinant. Such an introductory statement aims at pointing out to the student an important problem. While the problem is intellectually intrinsic to its poser (a university instructor), it is most likely to be alien to a student in an elementary linear algebra course, who is unlikely to realize from such a statement the true nature of the problem, its mathematical importance, and the role the concepts to be taught (“eigenvalue,” “eigenvector,” and “diagonalization”) play in solving it.

One of the alternative approaches to this presentation, based particularly on students’ intellectual need for computation, is through linear systems of differential equations, which has been experimented successfully several times. In this approach, one begins with an initial-value problem (e.g., a mixture problem) involving a sequence of rate of change functions, $f_{1}^{{\prime }} (t),f_{2}^{{\prime }} (t), \ldots ,f_{n}^{{\prime }} (t)$, each is a linear combination of the original position functions, $f_{1} (t),f_{2} (t), \ldots ,f_{n} (t)$. This leads to a linear system of differential equations of the form:

$$\left\{ {\begin{array}{*{20}l} {AY(t) = Y^{{\prime }} (t)} \hfill \\ {Y(0) = C} \hfill \\ \end{array} } \right.$$

(1)

where $A$ is a real square matrix. Students are asked to analogize system (*) to the scalar case:

$$\left\{ {\begin{array}{*{20}l}{ay(t) = y^{\prime } (t)} \hfill \\ {y(0) = c} \hfill \\ \end{array} } \right.$$

(2)

At first, students’ typically propose a solution to system (1) that is symbolically analogous to the solution of system (2), which they are familiar with from calculus; that is, corresponding to the symbolic structure of $y(t) = ce^{at}$, students offer $Y(t) = Ce^{At}$ (sic). A discussion of the meaning of the latter expression leads the students to (a) revise the expression $At$ into $tA$ and (b) probe into the definition of the concept of “$e$ to the power of a square matrix.” This question is resolved by, again, analogizing $e^{B}$, where $B$ is a square matrix, to $e^{b}$ where $b$ is a scalar, resulting in the definition, $e^{B} = \sum\nolimits_{i = 0}^{\infty } {(1/i!)B^{i} }$.⁴ By considering the sizes of the matrices involved in the product $Ce^{tA}$ in their proposed solution, students come to realize that there is a need to perform a third revision, from $Y(t) = Ce^{tA}$ to $Y(t) = e^{tA} C$. Once the students have verified that their revised proposed solution works, the instructor returns to the solution in its expansion form, $Y(t) = e^{tA} C = \sum\nolimits_{i = 0}^{\infty } {(t^{i} /i!)} A^{i} C$, and points out the following critical observation: If it so happens that there is a relationship between the condition vector $C$ and the coefficient matrix $A$ in the form of $AC = \lambda C$ for some scalar $\lambda$, then the solution to system (1) would be easily computable: $Y(t) = e^{\lambda t} C$. This observation necessitates attention to the relation $AC = \lambda C$, and due to its perceived significance it deserves a name: $C$ is called an eigenvector of $A$ and $\lambda$ its corresponding eigenvalue. Thus, students learn a sentential epistemological justification for the emergence of these central linear algebraic concepts; the concepts do not emerge out of the blue, as is typically the case in textbooks.

Following a few examples of solving system (1), the instructor (and in many cases the students themselves) raises the question about the computability of the solution in cases where the condition vector is not an eigenvector of the coefficient matrix. This leads, in turn, to the observation that whenever the condition vector $C$ is a linear combination of eigenvectors of $A$, the solution is still easily computable: $Y(t) = e^{tA} C = \sum\nolimits_{i = 1}^{k} {a_{i} e^{{\lambda_{i} t}} v_{i} }$, where $C = \sum\nolimits_{i = 1}^{k} {a_{i} v_{i} }$ and $Av_{i} = \lambda_{i} v_{i}$.

With this background, the instructor turns to the special case where $A$ has a basis of eigenvectors, in which case the solution is easily computable for any choice of $C$. For a more advanced linear algebra course, the proceeding discussion continues the investigation of the computability of the solution to system (1), leading up in a long journey to Jordan Theorem (and its related Canonical Form); namely, that remarkably system (1) is always easily computable since each vector is a linear combination of generalized eigen vectors.

We see here an example of how content presentation in linear algebra can be structured in a way that students develop sentential epistemological justifications for the birth of concepts through intellectual need , whereby students become partners in knowledge development, not passive receivers of ready-made knowledge.

5.2 Apodictic Epistemological Justification (AEJ)

The second category is apodictic epistemological justification (AEJ). This pertains to the process of proving; hence, the term apodictic. It is when one views a particular logical implication, $\alpha \Rightarrow \beta$, in causality, or explanatory, terms—how $\alpha$ causes $\beta$ to happen; that is, how $\alpha$ explains the presence of $\beta$. Consider, for example, the Spectral Theorem: Any $n \times n$ real symmetric matrix $A$ is orthogonally diagonalizable (i.e., $A = V\Lambda V^{T}$, where $V$ is orthogonal and $\Lambda$ diagonal). An apodictic epistemological justification of this assertion is present with a student when he or she exhibits an understanding of how the combined features of being real and symmetric are “responsible” for the matrix to be orthogonally diagonalizable—how specifically the absence of one of these features would derail the proof of the assertion. The central characteristic of AEJ is that the student is aware of the role that the various conditions in the hypothesis of an assertion play in its proof. The student, however, does not necessarily cognizant of the way the proof was conceived—that is a characteristic of the meta epistemological justification which we will discuss in the next section.

AEJ is a way of thinking not addressed sufficiently in mathematics instruction. It is acquired through repeated experience of probing into the specific role the conditions comprising a hypothesis of an assertion play in the proof. We conjecture that through the acquisition of this way of thinking students’ ability to produce proofs is advanced. Consider the following episode.

In a matrix-based linear algebra course, a particular attention was paid to epistemological justifications (as well as to other ways of thinking—thinking in terms of block matrices is one of them). At one point during the first half of the course, the instructor presented what is known as the Basis Theorem.

Let ${\rm H}$ be a $p$-dimensional subspace of $R^{n}$, and let $v_{1} ,v_{2} , \ldots ,v_{p}$ be vectors in ${\rm H}$.

• 1. If $v_{1} ,v_{2} , \ldots ,v_{p}$ span ${\rm H}$, then they are linearly independent.

• 2. If $v_{1} ,v_{2} , \ldots ,v_{p}$ are linearly independent, then they span ${\rm H}$.

As was the standard practice in this course, the students were asked to work in groups on comprehending the theorem, not necessarily proving it. After about 12 min, the instructor initiated a classroom discussion about the theorem. One of the students said something to the effect that she and her working mate thought that for Claim (1) there is a need to express two facts: that ${\rm H}$ is a $p$-dimensional subspace of $R^{n}$ and that $v_{1} ,v_{2} , \ldots ,v_{p}$ span ${\rm H}$, and so, she continued, they let $U = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & \ldots & {u_{p} } \\ \end{array} } \right]$ be a matrix basis for ${\rm H}$ and $U = VA$ for some matrix $A$, where $V = \left[ {\begin{array}{*{20}c} {v_{1} } & {v_{2} } & \ldots & {v_{p} } \\ \end{array} } \right]$. By this time, we should mention, the class as a whole got accustom to the approach of representing relationship in terms of matrix equations. After some further discussion, the instructor asked what other sufficient conditions in Claim 1 has not been expressed. Another student in the class responded that the fact that the columns of $U$ are linearly independent hasn’t been used. With help from the instructor to consider the sizes of the matrices involved in the equation $U = VA$, one of students declared that $A$ must be a square matrix ($p \times p$) and that since the columns of $U$ are linearly independent $A$ must be invertible (a fact which was previously proved and used on several occasions during the course). Following additional time for the students to collaborate on completing the proof, one of the working groups came to the board and completed the proof, saying something to the effect that since $U = VA$ and $A$ is invertible, $V = UA^{ - 1}$. And since the columns of $A^{ - 1}$ are linearly independent, the columns of $V$ are linearly independent, as was required.

It is interesting and important to add that this student also indicated at the end of his presentation that he used ideas he learned from the proof of the Dimension Theorem (All bases of a subspace ${\rm H}$ of $R^{n}$ have the same number of vectors), which the instructor presented a week earlier. Indeed the proof just presented includes considerations similar to those made in the proof of the Dimension Theorem. The latter proof began by setting two basis matrices $U = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & \ldots & {u_{k} } \\ \end{array} } \right]$ and $V = \left[ {\begin{array}{*{20}c} {v_{1} } & {v_{2} } & \ldots & {v_{r} } \\ \end{array} } \right]$, aiming at showing that $k = r$. The similar considerations are that since $U$ and $V$ are basis matrices, their columns span ${\rm H}$, and therefore there exist two matrices $M$ and $N$ such that $U = VM$ and $V = UN$. By considering the sizes of the matrices involved, it was concluded that $M$ is an $r \times k$ matrix and $N$ is a $k \times r$ matrix. But since the columns of each of these matrices are linearly independent, $r \ge k$ and $k \ge r$, respectively, and hence $k = r$.

5.3 Meta Epistemological Justification (MEJ)

The third, and final, category is meta epistemological justification (MEJ). This refers to a situation when one not only views a proof in explanatory terms but also one is aware of how the proof came into being. To illustrate, consider the Singular Value Decomposition (SVD) Theorem. We reviewed the proof of this theorem in five commonly used linear textbooks. In each case the proof is presented with virtually no epistemological justification . Generally, the proof commences with the observation that for any $m \times n$ real matrix $A$ (without loss of generality, $m \ge n$), $A^{T} A$ is symmetric, and then abruptly the textbook offer three ready-made matrices $V$, $\Sigma$, and $U$ for the decomposition $A = U\Sigma V^{T}$. In this presentation, even students who fully understand the proof are unlikely to gain an insight as to how the proof might have come into light—students are not partners in figuring out possible sources of the proof ideas.

The following is an alternative presentation used in our classes. Its ultimate goal was not just to prove the SVD theorem, but to help students acquire an MEJ for the proof. Of course, the theorem itself was first necessitated through a suitable SEJ for its statement. We introduced the theorem in the context of the need to reduce the amount of data in transmitting a digitized image without affecting significantly the quality of the image, by expressing the matrix representing the array of the gray levels of the image’s pixels as a sum of rank-1 matrices, i.e., $A = \sigma_{1} u_{1} {{v_{1}}^{T}} + \sigma_{2} u_{2} {{v_{2}}^{T}} + \cdots + \sigma_{n} u_{n} {{v_{n}}^{T}}$, where $\sigma_{1} \ge \sigma_{2} \ge \cdots \ge \sigma_{n}$, and then curtailing a certain number of addends in the tail of the sum.⁵ Following this, the proof evolved through the MEJ outlined below:

• 1. At this stage of the course, the students have witnessed the utility of matrix representations in solving problems and proving theorems (e.g., representing a set of differential equations emerging from application problems, such as mixture problems, in terms of matrix equations (see Sect. 5.1) or the Dimension Theorem and Basis Theorem (see Sect. 5.2), and so the students seemed receptive to the idea to represent the desired equation, $A = \sigma_{1} u_{1} {{v_{1}}^{T}} + \sigma_{2} u_{2} {{v_{2}}^{T}} + \cdots + \sigma_{n} u_{n} {{v_{n}}^{T}}$, in the form of the matrix equation, $A = U\Sigma V^{T}$, where $U = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & \ldots & {u_{m} } \\ \end{array} } \right]$, $(\Sigma )_{ij} = \sigma_{i}$ if $i = j$ and $(\Sigma )_{ij} = 0$ if $i \ne j$ for $1 \le i,\,j \le m$, and $V = \left[ {\begin{array}{*{20}c} {v_{1} } & {v_{2} } & \ldots & {v_{n} } \\ \end{array} } \right]$.

• 2. Students were then told that we have here an equation with three unknowns, $U$, $\Sigma$, and $V$, and that the goal is to try to eliminate one of the unknowns. We note that students are well familiar with eliminating unknowns as a strategy to solve equations, so this proposed approach by the instructor is unlikely to have been foreign to them.

• 3. The instructor then wrote $A^{T} = V\Sigma U^{T}$ on the board and asked if they can offer an idea as to how to eliminate one of the unknowns. After about 8 min of consultation among students in their working groups, one of the students indicated something to the effect that if $U$ were orthogonal, it would be eliminated in the product $A^{T} A$. But, he then added, “we do not know that $U$ is orthogonal”. The observation that the product of an orthogonal matrix and its transpose disappears in computing various expressions was well familiar to students at this point of the course; for example, in calculating the power of a diagonalizable matrix, and in computing a $UR$-factorization using the Gram-Schmidt process.

• 4. The instructor then responded: “Let see what happens if we assume that the unknown matrix $U$ is orthogonal”. It is important to point out that this last dialogue between one of the students and the instructor represents a significant way of thinking in mathematical practice, that a desired mathematical result is conditioned a priori by a particular hypothesis. The instructor then pursued the student’s proposal to obtain, $A^{T} A = V(\Sigma ^{T}\Sigma )V^{T} = V\Sigma _{1} V^{T}$, where $\varSigma_{1}$ is a diagonal matrix with ${{\sigma_{1}}^{2}} \cdot {{\sigma_{2}}^{2}} , \ldots, {{\sigma_{n}}^{2}}$ on its diagonal.

• 5. With no further responses from the students as to how to proceed, the instructor drew students’ attention to the fact that $A^{T} A$ is symmetric, urging them to recall a major result obtained previously in class about symmetric matrices. This, pleasingly, prompted another student to offer taking the missing matrix $V$ as an orthogonal diagonalizing matrix of $A^{T} A$, whose existence is guaranteed by the Spectral Theorem.

• 6. None of the students raised the concern that the proposed $V$ entails that the eigenvalues of $A^{T} A$ must be non-negative. This concern was raised by the instructor, which he then resolved by showing that indeed—remarkably—this was the case. Thus, in collaboration with the students two of the three unknown matrices $V$ and $\Sigma$ were successfully constructed.

• 7. These results then paved the path for the construction of $U$: that the first $r$ columns of $U$ are necessarily $u_{i} = \frac{1}{{\sigma_{i} }}Av_{i}$, members of $ColA$ and corresponding to the $r$ positive values $\sigma_{1} ,\sigma_{2} , \ldots ,\sigma_{r}$ (the singular values), and the rest are to be any orthonormal vectors in $(ColA)^{ \bot } = NulA^{T}$. The fact that the vector $u_{i} = \frac{1}{{\sigma_{i} }}Av_{i}$ turned out to be orthonormal, as needed, fascinated some students.

Surely the reader is familiar with the proof of the SVD Theorem—and all the other proofs, concepts, and ideas discussed in this paper, for that matter. Their appearance in the paper aimed at demonstrating how they can be introduced from the perspective of intellectual need and epistemological justification .

We conclude that students’ success in acquiring and applying desirable ways of understanding and ways of thinking in our courses has been correlated with, and therefore, attributed to, the persistent application of DNR-based instruction, with particular attention to intellectual need and epistemological justification in their various manifestations. A critical principle of this instruction, beyond the application of the duality principle and the necessity principle we discussed earlier, is the repeated-reasoning principle, which states: Students must practice reasoning in order to internalize, organize, and retain ways of understanding and ways of thinking. Research has shown that repeated experience is a critical factor in these cognitive processes (Cooper, 1991). Repeated reasoning, not mere drill and practice of routine problems, is essential to the process of internalization—a conceptual state where one is able to apply knowledge autonomously and spontaneously—and reorganization of knowledge. The sequence of problems must continually call for reasoning through the situations and solutions, and they must respond to the students’ changing intellectual needs .

Consonant with the repeated-reasoning principle, we typically keep the number of theorems presented in elementary linear algebra courses to a minimum, letting students reason and re-reason about various relations and claims (e.g., in terms of row reduction when relevant), rather than stating them as theorems ready to be used. Once a claim is stated as a theorem and proved, there is little incentive for the students to reason about the underlying ideas of its proof (Harel & Sowder, 1998). It should be clear, however, that we are not advocating eliminating theorems from the course; rather, we are advocating preserving the title “theorem” to truly “non-trivial” assertions. For example, the claim “A system $Ax = b$ is consistent iff an echelon form of the augmented matrix $\left[ {A\left| b \right.} \right]$ does not have a row of the form $\left[ {\begin{array}{*{20}c} 0 & 0 & \ldots & 0 \\ \end{array} \left| c \right.} \right]$, where $c \ne 0$ does not deserve the title theorem, for a brief inspection of the meaning of such a row should be sufficient to conclude that the system is inconsistent. On the other hand, the claim “Eigenvectors corresponding to distinct eigenvalues are linearly independent” is relatively not trivial and so it entitled to the label “theorem”. This pedagogical approach is generally antithetical to the approach taken in many current linear algebra textbooks, where even simple claims are stated as propositions or theorems (see for example, the “Invertible Matrix Theorem” with its 25 logically equivalent statements in the widely used linear algebra textbook by Lay, Lay, and McDonald (2016).

Figure 7 expands Fig. 6 to include the DNR constructs discussed in this section.

Fig. 7

Classification of epistemological justification and the third foundational principle of DNR

6 Summary

In this paper we theorized and illustrated the role and function of intellectual need and epistemological justification and their constituents in the learning and teaching of linear algebra. We presented two systems of classifications for intellectual need . The first system consists of two subcategories, global need and local need; and the second system consists of five categories of needs: need for certainty, need for causality, need for computation, need for communication, and formalization, and need for structure. We also presented a classification of epistemological justification into three categories: sentential epistemological justification (SEJ), apodictic epistemological justification (ASJ), and meta epistemological justification (MEJ). The main constituent elements for intellectual need and epistemological justification presented in this paper are the concepts of ways of understanding and ways of thinking and four out of the eight premises of DNR: the mathematical knowledge premise, the knowing premise, the knowledge-knowing linkage premise, and the subjectivity premise. Figure 7 depicts this web of the DNR concepts discussed in this paper. The three foundational principles that articulate best the essence of DNR-based instruction are the duality principle, the necessity principle, and the repeated reasoning principle, also depicted in Fig. 7.

The central focus of the paper, however, is the instantiations and role of this network of DNR cognitive and epistemological concepts in the learning and teaching of linear algebra. We illustrated how certain ways of thinking (e.g., definitional reasoning) play a critical role in the ways students understand fundamental linear algebraic concepts (e.g., the concept of dimension and projection matrix), claiming that the acquisition and internalization of desirable linear algebraic ways of understanding and ways of thinking can only take place by positioning the intellectual need of the student in the center of the instructional effort (the necessity principle), by instruction being cognizant of and explicit about the role and function of ways of thinking in solving problems (the duality principle), and by providing the students with opportunity to reason repeatedly about problematic situations that call for the application of such ways of understanding and ways of thinking (the repeated-reasoning principle).

We also illustrated how successful students can be in linear algebra when such an instructional approach is applied. We posited that a persistent instructional effort to, for example, present row reduction and block matrices as conceptual tools to represent and solve problems contribute to the emergence of sophisticated linear algebraic conceptualizations among students (e.g., the proofs provided by students for the theorem $\dim ColA = \dim RowA$ and the Basis Theorem).

The underlying approach of focusing on both ways of understanding and ways of thinking, not only the former as is typically the case in traditional linear algebra curricula, is the knowledge premise, which provides equal status to these two categories of knowledge in the mathematics discipline. (For a fuller discussion, see Harel, 2008c.) The focus on intellectual need and epistemological justification is theoretically entailed from the knowing-knowledge linkage premise, which collectively assert that knowledge construction is (a) possible only through intellectual perturbation and (b) that resolutions of such perturbations always exist for an individual or community who possess suitable mental structures. Entailed from the subjectivity premise is that intellectual need and epistemological justification , as well as ways of understanding and ways of thinking, are not fixed; rather, their origin and acquisition vary across individuals and communities. Furthermore, they typically are not historical.

The various classifications of intellectual need aimed at addressing different roles in curriculum development and instruction. While global need pertains to the structure of a mathematics curriculum, as we have demonstrated through an outline of a part of a DNR-based elementary course in matrix theory, local need pertains to elicitation of specific concepts and ideas, as we have shown for the concepts of linear combination, equivalent systems, linear independence, basis, eigen value, eigen vector, and diagonalization.

Ways of understanding and ways of thinking emerge in a variety of mathematical practices, when mathematicians encounter a need to be certain, to determine cause, to compute, to communicate, and to structure. Humans seem to have been endowed with cognitive primitive (pre-conceptualizations whose function is to orient us to the intellectual needs we experience when we learn mathematics; see Harel, 2013a), but in essence these are learned needs. We have illustrated the difficulties students encounter in acquiring and applying some of these needs (e.g., the need to formulate the notion of “closest” in terms of linear algebraic equations and the need formalize the intuitive concept of dimension).

Lastly, epistemological justification represents a higher level of mathematical knowledge—not only does one possess a desirable way of understanding of a particular concept, but also is being aware of how that concept was born out of a need to resolve a problematic situation (sentential epistemological justification —SEJ); not only does one understand the proof of an implication, but also understands the proof in terms of cause (apodictic epistemological justification —AEJ); and not only does one understand a proof of logical implications in terms of cause but also is aware of how the construction of the proof might have come about (meta epistemological justification —MEJ). We have demonstrated the application of each of these categories of epistemological justification in the context linear algebra.

We hope that the analyses presented in this paper will generate interest on the part of mathematics education researchers whose research focus is the learning and teaching of linear algebra to test empirically the central theoretical claim made in this paper: Does instruction that is organized around intellectual need and epistemological justification and their constituent elements, as were articulated in this paper, result in advanced performance by students in linear algebra courses? Elsewhere we discussed the development, application, and utility of DNR-based curricula in linear algebra (Harel, in press a), complex numbers (Harel, 2013b), geometry (Harel, 2014), proof (Harel & Sowder, 1998), and mathematical practice (Harel, in press b; Harel & Soto, in press).