Virtual Small Cell Selection Schemes Based on Sum Rate Analysis in Ultra-Dense Network

Abstract

Ultra-Dense Network (UDN) is regarded as a major development trend in the evolution of future networks, due to its ability to provide larger sum rate to the whole system and meet higher users’ Quality of Service (QoS). Different from the existing heterogeneous network, UDN has a smaller cell radius and a new network structure. The core concept of UDN is to deploy the low power Base Stations (BSs), i.e. Virtual Small Cells (VSCs). First, we derive an ergodic sum rate expression. To acquire the maximum ergodic sum rate of all the users, then we adopt the selection mode based on minimum distance. Due to the consideration of the computation complexity of the above VSC selection scheme, we finally propose a novel VSC selection scheme based on pattern search. The simulation results demonstrate the correctness of the ergodic sum rate expression and show the lower computation complexity of the proposed VSC selection scheme comparing with the above reference scheme.

1 Introduction

Current heterogeneous network is consisted of macro-cells and small cells. This network structure could not be able to meet the traffic demand which is increasing rapidly in the future 5th Generation (5G). In [1], it is predicted that the traffic demand would increase at least a 1000x network capacity in 2020. To meet the more traffic demand, enhanced technologies are essential. So far, there are some potential candidates in [2], such as UDN, massive Multiple-Input Multiple-Output (MIMO), and Non-Orthogonal Multiple Access (NOMA). This paper focuses on UDN which is seen as a major development trend in the evolution of future networks, due to its ability to provide larger sum rate to the whole system and meet higher users’ QoS. In recent years, UDN attracts many researchers in colleges and workers in industries. Both the industry and academia are working together, e.g. Mobile and wireless communications Enablers for the 2020 Information Society (METIS) and 5th Generation Non-Orthogonal Waveforms (5GNOW), to meet the capacity demand of the 5G mobile communication systems [3, 4].

Different from the existing heterogeneous network, UDN has a smaller cell radius and a new network structure. In urban areas, there exist many potential hot spots, such as conference halls, hospitals, and schools. In these areas, users are more easily to aggregate in a small place. At the same time, many users require high data transmission rate to support kinds of multimedia business. To meet the demand, VSC is presented in [5]. The core concept of UDN is to deploy the low power Base Stations (BSs) in the network, and the number of BSs is even larger than the number of Mobile Stations (MSs) [6]. We regard each low-power BS as a VSC.

There have been some researches of the VSC in UDN. Recently, [7] analyzes radius of VSC based large-scale distributed antenna system, and proves that the number of BSs and MSs has an impact on the downlink rate. [8] proposes a novel Resource Allocation (RA) scheme which is based on the sectoring of VSC. Its main idea is to reuse the Physical Resource Blocks (PRBs) of sectoring and improve the system capacity. [9] draws attention to the sum-rate maximization, and they develop a new formulation of the beamforming problem for sum-rate maximization in VSC and analyze the structure of its optimal solutions. Different from the existing single cell serving mode, [10, 11] present the concept of VSC clustering in UDN. [10] utilizes VSC clustering technique to maximize energy saving gain. [11] studies orthogonal training resource allocation problem for VSC cooperative network through a graph-theoretic approach aiming at minimizing the overall training overhead and then demonstrates that the proposed low complexity algorithm performs closely to the optimal solution.

This paper aims to maximize ergodic sum rate of all the users in UDN with low computation complexity. In this paper, the following tasks are completed: we first derive an ergodic sum rate expression. Second, due to the consideration of the computation complexity of the VSC selection scheme based on minimum distance, we propose a novel VSC selection scheme based on pattern search. Also, the two schemes can acquire almost the same maximum ergodic sum rate of all the users. The simulation results demonstrate the correctness of the ergodic sum rate expression and show the lower computation complexity of the proposed VSC selection scheme comparing with the reference scheme.

The remainder of this paper is organized as follows: In Sect. 2, we present the system model of VSC with multi-user environment. Section 3 derives an ergodic sum rate expression. In Sect. 4, we propose VSCs selection schemes based on maximum sum rate analysis. We provide simulation results in Sect. 5. Finally, conclusions are provided in Sect. 6.

2 System Model

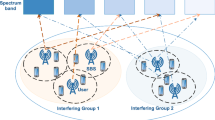
We consider the downlink transmission in UDN with $K$ MSs and $N$ VSCs. Both of them are equipped with a single antenna. As shown in Fig. 1, nine VSCs and four MSs uniformly and randomly are distributed in the area, and the number of VSCs is larger than the number of MSs $\left( {K\, < \,N} \right)$. In our analysis, the total available power of VSCs is $P$. We assume each VSC has the same power constraint, i.e. the $j_{th}$ VSC transmitted power is $P_{j} = P/N$, $(j = 1,2,3 \ldots N)$. The transmitted signal to noise power ratio for all VSCs is $\gamma_{0} = \frac{P}{{N\sigma_{n}^{2} }}$. If the $j_{th}$ VSC is turned off, $P_{j} = 0$. A principal goal of this paper is to determine the pairings of $N$ VSCs and their supporting MSs which maximize the ergodic sum rate. Let us denote the transmission mode

$$ X = [u_{1} ,u_{2} , \ldots ,u_{N} ] $$

(1)

as the MS index of $N$ VSCs where $u_{n} \in \{ 0,1, \ldots ,K\}$, $(n = 1,2, \ldots N)$ represents the MS index supported by the $n_{th}$ VSC. If $n_{th}$ VSC turns off, we define $u_{n} = 0$. From (1), let us define $G_{i,S} (x) = \{ n|u_{n} = i,n \in \{ 1,2, \ldots ,N\} \}$ as the set of VSC indices supporting the $i_{th}$ MS, and $G_{i,I} (x) = \{ n|u_{n} \ne i,u_{n} \ne 0,n \in \{ 1,2, \ldots ,N\} \}$ as the set of VSC indices supporting other MSs except $i_{th}$ MS. For MS $i$, the signal from VSCs in $G_{i,S}$ is regarded as the useful signal, while the signal transmitted from VSCs in $G_{i,I}$ is treated as interference. In Fig. 1, the transmission mode $X = [1,1,3,2,1,3,2,4,0]$. For $1_{th}$ MS, the useful signal is from $G_{1,S}$, i.e. $1_{th}$ VSC, $2_{th}$ VSC and $5_{th}$ VSC, and the interference information is from $3_{th}$ VSC, $4_{th}$ VSC, $6_{th}$ VSC, $7_{th}$ VSC and $8_{th}$ VSC.

Fig. 1.

Structure of UDN with four MSs and nine VSCs $\left( {K = 4, \, N = 9} \right)$.

The received signal of $i_{th}$ MS is

$$ y_{i} = \sum\limits_{j = 1}^{N} {\sqrt {P_{j} } g_{i,j} x_{j} + n_{i} } ,(i = 1,2, \ldots ,K) $$

(2)

where $x_{j} (j = 1,2, \ldots ,N)$ is the transmitted symbol from the VSC $j$ with the average power ${\text{E}}[|x_{j} |^{2} ] = 1$, $P_{j}$ is the power allocated to VSC $j$, $g_{i,j}$ denotes the channel gain from $i_{th}$ MS to $j_{th}$ VSC, and $n_{i}$ represents the additive white Gaussian noise with variance $\sigma_{n}^{2}$ for the $i_{th}$ MS. The channel gain is $g_{i,j} = \sqrt {Cd_{i,j}^{ - \alpha } s_{i,j} } h_{i,j}$, where $C$ is a constant, $d_{i,j}$ is the distance from $i_{th}$ MS to $j_{th}$ VSC, $\alpha$ is the path loss factor, $s_{i,j}$ denotes shadow fading, and $h_{i,j}$ is the independent and identically distributed complex Gaussian random variable. Let $10\lg s_{i,j}$ represent zero mean Gaussian random variable, and its standard deviation equals 1. Also the mean value of $h_{i,j}$ is 0, and standard deviation of $h_{i,j}$ is 1.

3 Ergodic Sum Rate Analysis

In this paper, inter-MS interference is regarded as the Gaussian noise since it can be interpreted as the worst effect that the measurement noise can have [12]. We use $\Omega _{i,j}$ to represent $Cd_{i,j}^{ - \alpha } s_{i,j}$, i.e. $\Omega _{i,j} = Cd_{i,j}^{ - \alpha } s_{i,j}$. Then we can do the following theoretical derivations. And the Signal to Interference plus Noise power Ratio (SINR) of the $i_{th}$ MS is generally represented as

$$ \begin{aligned} & \rho_{i} = \frac{{\sum\limits_{{l \in G_{i,S} }} {(\frac{P}{N})\Omega _{i,l} \left| {h_{i,l} } \right|}^{2} }}{{\sum\limits_{{k \in G_{i,I} }} {(\frac{P}{N})\Omega _{i,k} \left| {h_{i,k} } \right|}^{2} + \sigma_{n}^{2} }} = \frac{{\sum\limits_{{l \in G_{i,S} }} {(\frac{{d_{i,l} }}{R})^{ - \alpha } s_{i,l} \left| {h_{i,l} } \right|}^{2} }}{{\sum\limits_{{k \in G_{i,I} }} {(\frac{{d_{i,k} }}{R})^{ - \alpha } s_{i,k} \left| {h_{i,k} } \right|}^{2} + \frac{{NR^{\alpha } }}{{CP/\sigma_{n}^{2} }}}} \\ & = \frac{{\sum\limits_{{l \in G_{i,S} }} {\gamma_{i,l} } }}{{\sum\limits_{{k \in G_{i,I} }} {\gamma_{i,k} + \beta } }} = \frac{{\gamma_{i,S} }}{{\gamma_{i,I} + \beta }} \\ \end{aligned} $$

(3)

where $\gamma_{i,l} = (\frac{{d_{i,l} }}{R})^{ - \alpha } s_{i,l} \left| {h_{i,l} } \right|^{2}$ is the logarithmic normal distributed random variable, $\beta$ represents $\frac{{NR^{\alpha } }}{{CP/\sigma_{n}^{2} }}$, and $R$ is the normalized distance.

In the following, we consider the Probability Density Function (PDF) of $\rho_{i}$ to derive a closed form of the ergodic sum rate. The corresponding PDF of $\rho_{i}$ can be expressed as [13]

$$ f_{{\gamma_{i,l} }} (x) = \int_{0}^{\infty } {\frac{1}{\omega }\exp ( - \frac{x}{\omega })\frac{\xi }{{\sqrt {2\pi } \sigma_{i,l} \omega }}\exp [ - \frac{{(10\lg \omega - \mu_{i,l} )^{2} }}{{2\sigma_{i,l}^{2} }}]} d\omega $$

(4)

where $\mu_{i,l} = 10\lg [(d_{i,l} /R)^{ - \alpha } ]$, $\sigma_{i,l}$ is the standard deviation of $10\lg s_{i,l}$, and $\xi = 10/{\ln} 10$ is a constant. The moment-generating function of $\gamma_{i,l}$ can be expressed as follows [13]

$$ \Psi _{{\gamma_{i,l} }} (s) \approx \frac{1}{\sqrt \pi }\sum\limits_{p = 1}^{M} {W_{p} [1 - 10^{{0.1(\sqrt 2 \sigma_{i.l} Z_{p} + \mu_{i.l} )}} s]^{ - 1} } $$

(5)

where $Z_{p}$ and $W_{p}$ are the $p_{th}$ root of $M$ order Hermite polynomial and the corresponding integral weighted coefficient respectively.

Let us regard $\gamma_{i,S} = \sum {\gamma_{i,l} }$ as the sum of several independent random variable. Its moment-generating function is

$$ \Psi _{{\gamma_{i,S} }} (s) = \prod\limits_{{l \in G_{i,S} }} {\varPsi_{{\gamma_{i,l} }} (s)} . $$

(6)

$\gamma_{i,S}$ can approximatively be expressed by a logarithmic normal distributed random variable, so the PDF of $\gamma_{i,S}$ is denoted as [14]

$$ f_{{\gamma_{i,S} }} (x) = \frac{\xi }{{\sqrt {2\pi } \sigma_{i,S} x}}\exp [ - \frac{{(10\lg x - \mu_{i,S} )^{2} }}{{2\sigma_{i,s}^{2} }}](x \ge 0). $$

(7)

The corresponding moment-generating function of $\gamma_{i,S}$ is [13]

$$ \Psi _{{\gamma_{i,S} }} (s) \approx \frac{1}{\sqrt \pi }\sum\limits_{p = 1}^{M} {W_{p} \exp [10^{{0.1(\sqrt 2 \sigma_{i,S} Z_{p} + \mu_{i,S} )}} s]} . $$

(8)

Here, the Eq. (6) is equal to the Eq. (8), i.e.

$$ \prod\limits_{{l \in G_{i,S} }} {\Psi _{{\gamma_{i,l} }} (s)} = \frac{1}{\sqrt \pi }\sum\limits_{p = 1}^{M} {W_{p} \exp [10^{{0.1(\sqrt 2 \sigma_{i,S} Z_{p} + \mu_{i,S} )}} s]} . $$

(9)

When there are two different values for variable $s$, we can get binary equation groups of $\mu_{i,S}$ and $\sigma_{i,S}$. The equation groups can be solved by numerical method. So $\gamma_{i,S}$ can be approximatively expressed as a logarithmic normal distributed random variable through the parameter $(\mu_{i,S} ,\sigma_{i,S} )$.

In the same way, $\gamma_{i,I} + \beta$ can be approximatively expressed as a logarithmic normal distributed random variable, and its PDF is

$$ f_{{\gamma_{i,I} + \beta }} (y) = \frac{\xi }{{\sqrt {2\pi } \sigma_{i,I} (y - \beta )}}\exp [ - \frac{{(10\lg (y - \beta ) - \mu_{i,I} )^{2} }}{{2\sigma_{i,I}^{2} }}](y \ge \beta ). $$

(10)

From (3), SINR of the $i_{th}$ MS $\rho_{i}$ is the radio between $\gamma_{i,S}$ and $\gamma_{i,I} + \beta$, so the PDF of $\rho_{i}$ is denoted as

$$ \begin{array}{*{20}l} {f_{{\rho_{i} }} (\rho ) = \int_{\beta }^{\infty } {yf_{{\gamma_{i,S} }} (\rho y)} f_{{\gamma_{i,I + \beta } }} (y)dy = \frac{{\xi^{2} }}{{2\pi \sigma_{i,S} \sigma_{i,I} \rho }} \cdot } \hfill \\ {\int_{0}^{\infty } {\frac{1}{x}} \exp - \frac{{\{ 10\lg [\rho (x + \beta )] - \mu_{i,S} \}^{2} }}{{2\sigma_{i,S}^{2} }} \cdot \exp [ - \frac{{(10\lg x - \mu_{i,I} )^{2} }}{{2\sigma_{i,I}^{2} }}]dx(y - \beta \to x).} \hfill \\ \end{array} $$

(11)

From the above, we can denote ergodic rate of $i_{th}$ MS as

$$ \begin{array}{*{20}l} {{\text{E}}[R_{i} ] = \int_{0}^{\infty } {\log_{2} (1 + \rho )f_{{\rho_{i} }} (\rho )d\rho } } \hfill \\ { = \frac{{\xi^{2} }}{{2\pi \sigma_{i,S} \sigma_{i,I} \rho }} \cdot \int_{0}^{\infty } {\frac{1}{x}} \exp ( - \frac{{(10\lg x - \mu_{i,I} )^{2} }}{{2\sigma_{i,I}^{2} }})\int_{0}^{\infty } {\frac{{\log_{2} (1 + \rho )}}{\rho } \cdot } } \hfill \\ {\exp ( - \frac{{\{ 10\lg [\rho (x + \beta )] - \mu_{i,S} \}^{2} }}{{2\sigma_{i,S}^{2} }})d\rho dx.} \hfill \\ \end{array} $$

(12)

We can get the following equation through the Gauss-Hermite integration

$$ {\text{E}}[R_{i} ] \, = \frac{1}{\pi }\sum\limits_{q = 1}^{M} {W_{q} \cdot } [\sum\limits_{p = 1}^{M} {W_{p} \log_{2} (1 + \frac{{10^{{0.1(\sqrt 2 \sigma_{i,S} Z_{p} + \mu_{i,S} )}} }}{{10^{{0.1(\sqrt 2 \sigma_{i,I} Z_{p} + \mu_{i,I} )}} + \beta }})} ] $$

(13)

where $Z_{p}$ and $W_{p}$ are the $p_{th}$ root of $M$ order Hermite polynomial and the corresponding integral weighted coefficient respectively. So the ergodic sum rate of $K$ MSs is

$$ R_{sum} = \sum\limits_{i = 1}^{K} {{\text{E}}[R_{i} ]} . $$

(14)

4 Analysis on VSC Selection Schemes

In this section, we study the VSC selection scheme based on minimum distance and propose a novel VSC selection scheme for the ergodic sum rate maximization using the derived expression in the previous section.

4.1 VSC Selection Scheme Based on Minimum Distance

We introduce a VSC selection scheme based on the minimum distance where the number of mode candidates increases dramatically for large $N$. For $N$ VSCs and $K$ MSs, we can define all mode candidates as ${\mathcal{X}}$. The size of the set of mode candidates ${\mathcal{X}}$ is given as $2^{N} - N$ [15].

In this scheme, we first set $X_{0} = [u_{1} ,u_{2} , \ldots ,u_{N} ]$ as the mode where each VSC serves its nearest MS with turning on all the VSCs. Then, we turn off VSCs in this transmission mode one by one with $2^{N} - 1$ distinct combinations, and generate a mode candidate by replacing the corresponding user indices to 0. Then, all these $2^{N} - 1$ candidates are added to the mode candidate set ${\mathcal{X}}$. Finally, after evaluating the ergodic sum rate for each candidate mode in ${\mathcal{X}}$ using the expressions derived in Sect. 3, we select the best mode which exhibits the maximum rate.

4.2 VSC Selection Scheme Based on Pattern Search

In this subsection, we propose a novel transmission mode selection scheme which reduces the computation complexity comparing with VSC selection scheme based on minimum distance. This scheme is based on pattern search. The objective function is

$$ f_{obj} (X) = R_{sum} . $$

(15)

Our objection is searching the $X_{opt} = \mathop {\arg \hbox{max} }\limits_{{X \in {\mathcal{X}}}} R_{sum}$. The mode selection procedure is described in Table 1, where $I_{N} (i,*)$ means the $i$ row of the $N$ order identity matrix.

Table 1. VSC selection sheme based on pattern search.

5 Simulation Results and Analysis

In this section, we demonstrate the correctness of the ergodic sum rate expression. And we also evaluate computation complexity of the proposed VSC selection scheme comparing with the selection mode based on minimum distance by a system level simulator. The results of simulation with the method of Monte Carlo are given. In this simulation, we use wrap-around to have reliable interference calculation. The number of generated channel realizations is equivalent to 5000. More specific parameter is shown in Table 2 in detail.

Table 2. Basic parameters of simulation scenario.

In Fig. 2, each VSC chooses the nearest MS to serve with all VSCs turned on, and the two pairing lines are almost overlap with different $K$. So it can demonstrate the correctness of the ergodic sum rate expression. With the increasing of $K$ or the transmitted signal to noise power ratio $\gamma_{0}$, the ergodic sum rate is increasing.

Fig. 2.

Ergodic sum rate with different $K$.

In Fig. 3, the ergodic sum rate by VSC selection scheme based on pattern search is similar to the result of VSC selection scheme based on minimum distance. However, the proposed scheme has lower computation complexity than VSC selection scheme based on minimum distance. From Fig. 4, the computation complexity of VSC selection scheme based on minimum distance is a constant value with different number of MSs $K$. Because the computation complexity of VSC selection scheme based on minimum distance is only related to the number of VSCs $N$. However, the computation complexity of VSC selection scheme based on pattern search is much lower than the computation complexity of VSC selection scheme based on minimum distance with different $K$ $(K < N)$. When $N$ is given, the computation complexity of VSC selection scheme based on pattern search increases with $K$ and then start to change little. This is because when $K$ is closed to $N$, there are almost the same number of times the objective function is called.

Fig. 3.

The ergodic sum rate comparison between VSC selection scheme based on minimum distance and VSC selection scheme based on pattern search.

Fig. 4.

The comparison of compute times about two VSC selection scheme with different $K$ $(K \,<\, N,N = 9)$.

6 Conclusions

In this paper, we have studied the multi-MSs downlink VSC and have derived an ergodic sum rate expression using the PDF of MSs’ SINR. The simulation result demonstrates the correctness of the ergodic sum rate expression. Through the derived expressions, we have proposed the VSC selection scheme based on pattern search to maximize the ergodic sum rate of whole MSs. In the proposed scheme, the ergodic sum rate is similar to the result of VSC selection scheme based on minimum distance. However, simulation results show that the VSC selection scheme based on pattern search has lower computation complexity than VSC selection scheme based on minimum distance. So the proposed scheme can get desired ergodic sum rate with lower computation complexity.