Keywords

1 Introduction

Many physical systems can be represented by a class of second-order nonlinear model, including inertia wheel pendulums (Chen and Chen 2010; Iriarte et al. 2017), robotic manipulators (Eksin et al. 2017), magnetic levitation systems (Yang et al. 2017), and pneumatic muscle actuators (Lilly 2017). Various model-based control methods have been proposed for the second-order nonlinear model by researchers. The main difficulty is that the available mathematical models are usually imprecise due to parameter uncertainties and the external disturbances, which are usually unmeasurable, commonly exists in practice. To deal with the problem, many strategies have been proposed, for example, robust fuzzy method (Xiang et al. 2017). Besides the above problem, what is specially considered in this paper is, in case the actuator force becomes excessively large, which may do harm to the environment, even to the human body in some special cases, overdamped dynamics of the system is desired. This is the so-called safety problem in (Kikuuwe and Fujimoto 2006), which can not be solved by conventional stiff positional control when the robustness and tracking accuracy are required simultaneously. For example, the PID control can possess an overdamped and smooth recovery without overshoot from large positional errors by using a very high velocity feedback gain, which guarantees the safety of the actuator, but this can magnify the noise, which will deteriorate the tracking accuracy.

Sliding mode control (SMC) has been applied in many non-linear systems due to its design simplicity and robustness against matched disturbances and parameter uncertainties. Theoretically, the SMC can produce the control signal which will force the state variables to the sliding surface, and the system state can be robustly constrained to the surface and convergent to zero in finite time. Besides, the magnitude limit of the control signal can be set arbitrarily by the controller. Therefore, in an ideal condition, the tracking accuracy and overdamped dynamics can be both obtained by using SMC. However, it is just due to the purpose to account for the presence of modelling imprecision and of disturbances, the discontinuous function (e.g. signum-type function) need to be introduced across the sliding surface. The implementation of the proposed control method is imperfect, because the switching of signum function can not be infinite fast in practice, and the value of sliding mode is not known with infinitely precision. This will lead to undesired phenomenon, chattering. Chattering can excite high frequency dynamics to the system and may produce excessively large control signal when big positional error occurs, which can do damage to physical systems. To reduce the chattering phenomenon in SMC, two main approaches are commonly used. One method is introducing a boundary layer so that the control law is linear in the vicinity of the sliding surface (Slotine and Li 1991). In this method, the selection of an appropriate value for the boundary thickness is very important. The chattering can not be solved with too narrow boundary layer while the tracking performance and robustness will be deteriorated if the value is too large. Therefore, it is obvious that this method can not guarantee both the safety and the accuracy with large position error in the system. The other is using higher order sliding mode control (John 2005) in which the derivative of the state variable can not be measured. Thus, the observer is needed to be designed to estimate that variable. Whereas, the high order SMC requires more complex calculation than normal SMC.

Proxy-based Sliding Mode Control (PSMC), introduced by Kikuuwe and Fujimoto in 2006, can be viewed as a modified version of SMC, and also an extension of the force limited PID control, which achieves the chattering free target from another perspective. Thus, both the safety and the tracking accuracy can be guaranteed by using the PSMC. We can notice from the above that the root of the chattering problem is the existence of the signum-type function in the control law. An imaginary proxy object is introduced in PSMC to remove the signum-type function out of the closed loop of the controller. By this way, the signum-type function can be algebraically transferred to the saturation function, which eliminates the chattering in essence. Therefore, this control method can achieve overdamped recovery when big positional error occurs and accurate tracking performance during normal operation.

At the same time, it should be noted that the stability problem of PSMC is not well addressed so far. The stability analysis of PSMC in (Kikuuwe et al. 2010) is based on a conjecture of the local passivity of the well-tuned PID control, which, however, remains an issue to study in the future. In this paper, we proposed a model-based PSMC for a class of second-order nonlinear systems, and its stability analysis based on Lyapunov stability theory is also given.

The rest of the paper is organized as follows. A class of second-order nonlinear system is described in Sect. 2. Based on the PSMC, a newly designed model-based controller is also derived for the system in this section. The stability analysis is given in Sect. 3. Experiments on pneumatic muscle system are carried out to demonstrate the validity of the designed controller in Sect. 4. Finally a conclusion is given in Sect. 5.

2 System Formulation and Controller Design

2.1 System Description

Consider a single-input second-order nonlinear system defined as following differential equation:

$$\begin{aligned} \ddot{q} = f(q,\dot{q},t) + b(q,\dot{q},t)u(t) + d(t) \end{aligned}$$
(1)

where q denotes the actuator position. u is the control input signal. f is the nonlinear dynamic. b is the control gain and d(t) is the lumped disturbance containing the model uncertainties and external disturbances.

2.2 Design of Model-Based PSMC

To generate overdamped response when big tracking error occurs, without sacrificing accurate, responsive tracking ability during normal operations, chattering need to be eliminated. From the above, we know that chattering problem is caused by the existence of discontinuous function \( {\mathop {\text {sgn}}}(\cdot )\). When the \( {\mathop {\text {sgn}}}(\cdot )\) is enclosed in the feedback loop which passes through the physical devices, time delay is inevitable. To solve the problem, we need to put closed loop containing the \( {\mathop {\text {sgn}}}(\cdot )\) in the control software. For this purpose, an imaginary object called “proxy” is introduced to the control scheme. A proxy is a virtual object which is supposed to be connected to the physical actuator, and the connection between actuator and proxy is the so-called virtual coupling. Then, the ideal SMC can be thought to control the proxy which does not contain any physical object, so that the chattering can be eliminated since no time delay exists. On the other hand, the virtual coupling is supposed to maintain its length to be zero, which means the error between actuator position and proxy position is going to be convergent to zero. The physical model of PSMC is illustrated in Fig. 1. For the stability of the system, in this paper, we proposed a new control method to control the proxy which can be seen as an extension of the classical SMC. The sliding manifold is defined as:

$$\begin{aligned} \sigma _p = \dot{q}_d - \dot{p} + H(q_d - p) \end{aligned}$$
(2)
$$\begin{aligned} \sigma _q = \dot{q}_d - \dot{q} + H(q_d - q) \end{aligned}$$
(3)

where H is a positive constant. p denotes the proxy position. \(q_d \) denotes the desired position. The newly designed sliding mode controller produces the force \(f_p\), which is applied to the proxy, as follows

$$\begin{aligned} \begin{array}{ll} f_p &{}= \varGamma {\mathop {\text {sgn}}} \left( {\sigma _p } \right) - m_p H\dot{p} - K_P \left( {p - q} \right) \\ &{}\quad \mathrm{{ }} - K_D \left( {\dot{p} - \dot{q}} \right) + m_p \ddot{q}_d + m_p H\dot{q}_d \\ &{}\quad \mathrm{{ + }}\frac{1}{b}( - f + K_P \left( {p - q} \right) + K_D \left( {\dot{p} - \dot{q}} \right) \\ &{}\quad \mathrm{{ }} - H\dot{q} + H\dot{q}_d + \ddot{q}_d ) \\ \end{array} \end{aligned}$$
(4)

where q denotes the actuator position. \(m_p \) denotes the proxy mass. \(K_P \) and \(K_D \) are positive constants which represent the proportional and differential gains. \( {\mathop {\text {sgn}}}(\cdot )\) is the signum function which is defined by

$$\begin{aligned} {\mathop {\text {sgn}}} (x) = \left\{ {\begin{array}{*{20}c} {1,\begin{array}{*{20}c} {} &{} {} &{} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} &{} {} \\ \end{array}} &{} {x > 1} \\ \end{array}} \\ \end{array}} \\ {[ - 1,1],\begin{array}{*{20}c} {} &{} {} &{} {x = 1} \\ \end{array}} \\ { - 1,\begin{array}{*{20}c} {\begin{array}{*{20}c} {} &{} {} \\ \end{array}} &{} {} &{} {x < 1} \\ \end{array}} \\ \end{array}} \right. \end{aligned}$$
(5)

The virtual coupling, which is designed to make convergent to, can be selected in many ways. In (Kikuuwe and Fujimoto 2006), a PID-type virtual coupling is adopted; in (Kashiri and Jinoh 2016), a PD-type is used. In this paper, the virtual coupling is defined as:

$$\begin{aligned} \begin{array}{ll} f_c &{}= \frac{1}{b}(K_P \left( {p - q} \right) + K_D \left( {\dot{p} - \dot{q}} \right) \\ &{}\quad \mathrm{{ }} - f - H\dot{q} + H\dot{q}_d + \ddot{q}_d ) \\ \end{array} \end{aligned}$$
(6)

The force \(f_c\) is directly applied to the physical controlled actuator, and its reaction force is applied to the proxy. Thus, the dynamics of the proxy can be described as:

$$\begin{aligned} \begin{array}{ll} m_p \ddot{p} &{}= f_p - f_c \\ \mathrm{{ }} &{}= \varGamma {\mathop {\text {sgn}}} \left( {\sigma _p } \right) - m_p H\dot{p} - K_P \left( {p - q} \right) \\ &{}\quad \mathrm{{ }} - K_D \left( {\dot{p} - \dot{q}} \right) + m_p \ddot{q}_d + m_p H\dot{q}_d \\ \end{array} \end{aligned}$$
(7)
Fig. 1.
figure 1

Principle of PSMC

Full size image

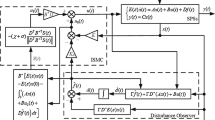
Figure 2 is a block-diagram representation of the controller. From Fig. 2, we know that the feedback loop containing the signum function does not pass through the physical controlled object. It should be noticed that the proxy is a virtual object whose mass can be set to 0. Then (7) can be rewritten as:

$$\begin{aligned} \dot{p} + Xw = Y{\mathop {\text {sgn}}} (z - Z\dot{p}) \end{aligned}$$
(8)

where

$$\begin{aligned} \left\{ \begin{array}{l} Xw = \frac{{K_P (p - q) - K_D \dot{q}}}{{K_D }} \\ Y = \frac{\varGamma }{{K_D }} \\ z = \dot{q}_d + H(q_d - p) \\ Z = 1 \\ \end{array} \right. \end{aligned}$$
(9)
$$\begin{aligned} \begin{array}{l} y + Xw = Y{\mathop {\text {sgn}}} (z - Zy) \\ \Leftrightarrow y = - Xw + Ysat(\frac{{z/Z + Xw}}{Y}) \\ \end{array} \end{aligned}$$
(10)

By (10), in a similar way to that in (Kikuuwe et al. 2010), (8) can be rewritten as:

$$\begin{aligned} \dot{p} = - Xw + Ysat(\frac{{z/Z + Xw}}{Y}) \end{aligned}$$
(11)

In this way, the \( {\mathop {\text {sgn}}}(\cdot )\) function is rolled out as a sat function. (8) and (11) are algebraically equivalent, which implies that (8) is actually a saturated controller. This is really different from simply substituting the \( {\mathop {\text {sgn}}}(\cdot )\) by \( {\mathop {\text {sat}}}(\cdot )\) approximately. Therefore, the proposed control scheme doesn’t cause chattering.

Fig. 2.
figure 2

Block diagram of PSMC

Full size image

3 Stability Analysis

The stability analysis in Theorem 1 is based on the case of free motion, i.e. \(d(t) = 0\). The passivity of the system in the presence of the lumped disturbance, i.e. \(d(t) \ne 0\) is considered in Theorem 2.

Theorem 1

Consider the second-order nonlinear system (1) with \(d(t) = 0\). The stability of the system can be guaranteed by using the controller (6), whose dynamics is defined by (7).

Proof

We choose a Lyapunov candidate as

$$\begin{aligned} V = V_1 + V_2 + V_3 \end{aligned}$$
(12)

where

$$\begin{aligned} V_1 = \frac{1}{2}m_p \sigma _p ^2 \end{aligned}$$
(13)
$$\begin{aligned} V_2 = \frac{1}{2}\sigma _q ^2 \end{aligned}$$
(14)
$$\begin{aligned} V_3 = \frac{1}{2}\left( {K_P + HK_D } \right) \left( {p - q} \right) ^2 \end{aligned}$$
(15)

Apparently,

$$\begin{aligned} \begin{array}{l} V > 0,x_e \ne 0 \\ V = 0,x_e = 0 \\ \end{array} \end{aligned}$$
(16)

is satisfied, where \(x_e = [\sigma _p ,\sigma _q ,p - q]\). Differentiating both sides of \(V_1\) and substitute (7) and (2) into it, we have:

$$\begin{aligned} \begin{array}{ll} \dot{V}_1 &{}= \sigma _p m_p \dot{\sigma }_p = \sigma _p \left( {m_p \ddot{q}_d - m_p \ddot{p} + m_p H\dot{q}_d - m_p H\dot{p}} \right) \\ &{}= \sigma _p \left( { - \varGamma {\mathop {\text {sgn}}} \left( {\sigma _p } \right) + K_P \left( {p - q} \right) + K_D \left( {\dot{p} - \dot{q}} \right) } \right) \\ &{}= - \varGamma \left| {\sigma _p } \right| + K_P (\dot{q}_d - \dot{p})\left( {p - q} \right) + K_P H(q_d - p)\left( {p - q} \right) \\ &{}\quad \mathrm{{ }} + K_D (\dot{q}_d - \dot{p})\left( {\dot{p} - \dot{q}} \right) + K_D H(q_d - p)\left( {\dot{p} - \dot{q}} \right) \\ \end{array} \end{aligned}$$
(17)

Differentiating both sides of \(V_2\) and substitute (1), (3) and (6) into it, we have:

$$\begin{aligned} \begin{array}{ll} \dot{V}_2 &{}= \sigma _q \dot{\sigma }_q = \sigma _q \left( {\ddot{q}_d - \ddot{q} + H\dot{q}_d - H\dot{q}} \right) \\ &{}= \sigma _q ( - K_P \left( {p - q} \right) - K_D \left( {\dot{p} - \dot{q}} \right) + H\dot{q} - H\dot{q}_d - \ddot{q}_d \\ &{}\quad + \ddot{q}_d + H\dot{q}_d - H\dot{q}) \\ &{}= - K_P (\dot{q}_d - \dot{q})\left( {p - q} \right) - HK_P (q_d - q)\left( {p - q} \right) \\ &{}\quad \mathrm{{ }} - K_D (\dot{q}_d - \dot{q})\left( {\dot{p} - \dot{q}} \right) - HK_D (q_d - q)\left( {\dot{p} - \dot{q}} \right) \\ \end{array} \end{aligned}$$
(18)

Differentiating both sides of \(V_3\), we have:

$$\begin{aligned} \begin{array}{ll} \dot{V}_3 &{}= \left( {K_P + HK_D } \right) \left( {p - q} \right) \left( {\dot{p} - \dot{q}} \right) \\ &{}= K_P \left( {p - q} \right) \left( {\dot{p} - \dot{q}} \right) + HK_D \left( {p - q} \right) \left( {\dot{p} - \dot{q}} \right) \\ \end{array} \end{aligned}$$
(19)

Thus, the derivation of the Lyapunov candidate is given by:

$$\begin{aligned} \begin{array}{ll} \dot{V} &{}= \dot{V}_1 + \dot{V}_2 + \dot{V}_3 \\ &{}= - \varGamma \left| {\sigma _p } \right| - K_D \left( {\dot{p} - \dot{q}} \right) \left( {\dot{p} - \dot{q}} \right) \\ &{}\quad - HK_P \left( {p - q} \right) \left( {p - q} \right) \\ &{}\le 0 \\ \end{array} \end{aligned}$$
(20)

From (16) and (20), we know that V is a positive-definite function and \(\dot{V}\) is a negative semi-definite function. Thus, The stability of the system around the equilibrium \([\sigma _p ,\sigma _q ,p - q] = 0\) is proven in the sense of Lyapunov.

Theorem 2

The second-order nonlinear system

$$\begin{aligned} \begin{array}{l} \ddot{q} = f(q,\dot{q},t) + b(q,\dot{q},t)u(t) + d(t) \\ y = - \sigma _q \\ \end{array} \end{aligned}$$
(21)

mapping d(t) to y is passive.

Proof

We choose the storage function as same as (12). With \(d(t) \ne 0\), \(\dot{V}_1\) and \(\dot{V}_3\) are calculated as the same as (17) and (19), while \(\dot{V}_2\) is calculated as follows:

$$\begin{aligned} \begin{array}{ll} \dot{V}_2 &{}= \sigma _q \dot{\sigma }_q = \sigma _q \left( {\ddot{q}_d - \ddot{q} + H\dot{q}_d - H\dot{q}} \right) \\ &{}= \sigma _q ( - K_P \left( {p - q} \right) - K_D \left( {\dot{p} - \dot{q}} \right) + H\dot{q} - H\dot{q}_d \\ &{}\quad - \ddot{q}_d - d + \ddot{q}_d + H\dot{q}_d - H\dot{q}) \\ &{}= - K_P (\dot{q}_d - \dot{q})\left( {p - q} \right) - HK_P (q_d - q)\left( {p - q} \right) \\ &{}\quad \mathrm{{ }} - K_D (\dot{q}_d - \dot{q})\left( {\dot{p} - \dot{q}} \right) - HK_D (q_d - q)\left( {\dot{p} - \dot{q}} \right) + yd \\ \end{array} \end{aligned}$$
(22)

Therefore, we have:

$$\begin{aligned} \begin{array}{ll} \dot{V} &{}= \dot{V}_1 + \dot{V}_2 + \dot{V}_3 \\ &{}= - \varGamma \left| {\sigma _p } \right| - K_D \left( {\dot{p} - \dot{q}} \right) \left( {\dot{p} - \dot{q}} \right) \\ &{}\quad - HK_P \left( {p - q} \right) \left( {p - q} \right) + yd \\ &{}\le yd \\ \end{array} \end{aligned}$$
(23)

which satisfied the necessary condition for the passivity of the system. This completes the stability proof with the condition \(d(t) \ne 0\).

4 Example

To verify the proposed control method, the experiments on Pneumatic Muscle Actuators (PMAs) system, which is a typical second order nonlinear system, are carried out.

PMA is widely used as the actuator in human muscle-like application due to its similarity with human muscle in size, weight and power output. The dynamic equation is based on the three elements model proposed by Reynolds (Reynolds et al. 2003). In this model, as shown in Fig. 3, the dynamics of the PMA is regarded as being composed of a contraction element, a spring element and a damping element in parallel, and the coefficients of the three elements depend on the magnitude of the input air pressure. The dynamic model of PMA is given by:

$$\begin{aligned} M\ddot{x} - B(P)\dot{x} - K(P)x = F(P) - Mg \end{aligned}$$
(24)
$$\begin{aligned} \begin{array}{l} K(P) = K_0 + K_1 P \\ F(P) = F_0 + F_1 P \\ B(P) = \left\{ \begin{array}{l} B_{0i} + B_{1i} P\mathrm{{ (inflation)}} \\ B_{0d} + B_{1d} P\mathrm{{ (deflation)}} \\ \end{array} \right. \\ \end{array} \end{aligned}$$
(25)

where M is the mass. g is the acceleration of gravity. x is the axial contraction length and P is the system input, the air pressure. B(P) and K(P) denote the damping coefficient and spring coefficient respectively. F(P) is the effective force generated by the contractile element. According to (1), the dynamics of PMA system is actually described as:

$$\begin{aligned} \begin{array}{l} \ddot{x} = f + bP \\ f = \frac{1}{M}(F_0 - Mg - B_0 \dot{x} - K_0 x) \\ b = \frac{1}{M}(F_1 - B_\mathrm{{1}} \dot{x} - K_\mathrm{{1}} x) \\ \end{array} \end{aligned}$$
(26)

Then we can apply the propose control method on PMA conveniently.

Fig. 3.
figure 3

Three elements model.

Full size image

The PMA system experiment platform is shown in Fig. 4. It consists of a pneumatic muscle, a displacement sensor, a force sensor, a baroceptor, an air compressor and an xPC target system. After getting the real time sensory data of the PMA system, the computer computes the control signal according to the control algorithm. The output is then fed into the electromagnetic proportion valve to adjust the air pressure. Then the pneumatic muscle can be stretched to drive the load. The xPC Target from MATLAB is used in our experiment. In this environment, a desktop PC is used as a host computer to run SIMULINK models and the second PC compiler system is used as a target computer to generate the code which can executes in real-time.

Based on three elements model, the extended PSMC control strategy is carried out on real PMA system to evaluate its control performance. The coefficients are chosen as \(K_P = 31000,K_D = 0.1,H = 0.0005,F = 100000\). To make a comparison, the experiment using SMC is also carried out. The position tracking result of two control strategy is shown in Fig. 5. The corresponding tracking error result is shown in Fig. 6. The SMC can hardly achieve in tracking reference when the peak value occurs, and the chattering is obvious. Besides, the tracking error of PSMC is smaller.

Fig. 4.
figure 4

PMA system experiment platform.

Full size image
Fig. 5.
figure 5

Trajectory tracking control result of the model.

Full size image
Fig. 6.
figure 6

Comparison of the tracking error using PSMC and SMC.

Full size image

5 Conclusion

The PSMC is proposed to guarantee both safety and tracking accuracy. It has already been verified experimentally (e.g. (Van Damme et al. 2009; Kikuuwe et al. 2008)), while the theoretical stability analysis is not well addressed. In this paper, we proposed an extended PSMC where a new type of virtual coupling between proxy and actuator is adopted. In this way, stability of the system is proven based on Lyapunov theory. Experiments on PMA system are also carried out to show the validity of the proposed scheme. The future study will focus on model-free PSMC by using neural network.