Continuous-time Lyapunov stability analysis and systematic parametrization of robust adaptive sliding mode controller for systems with matched and unmatched dynamics

Abstract

This paper presents the development of a continuous-time robust adaptive sliding mode controller using the model reference adaptive control philosophy. The stability analysis of the controller considering a system subjected to matched and unmatched dynamics is provided using the Lyapunov stability criterion. This control strategy can be applied to plants that are partially modeled, systems with uncertain parameters, or unmodeled dynamics. The stability analysis elucidates the controller constraints and proves that the tracking error tends to a small residual value, even in the presence of unmodeled dynamics (matched or unmatched). In addition, a systematic controller parametrization procedure based on the sine–cosine algorithm is presented to automate this task. Simulation results of the robust adaptive continuous-time sliding mode controller applied to an unstable non-minimum-phase system are presented. A comparison of this controller with a robust model reference adaptive controller is also presented, where the benefits of the adaptive sliding mode controller stand out, obtaining a superior performance that reduces relevantly the error metrics of 56.28%, 28.57%, and 14.79% for mean absolute error, mean squared error, and root mean squared error, respectively. Furthermore, a processor-in-the-loop experiment considering a complex real-world engineering problem is also provided to corroborate the controller performance and discuss its robustness, demonstrating its feasibility.

1 Introduction

Adaptive control emerged in the 1950 s as a class of controllers that allowed its behavior to be modified in response to changes in process dynamics and external perturbations. In the 1980 s, adaptive control gained new impetus with the development of microelectronics, which made it possible to implement adaptive control laws with more complex structures in practice. One decade later, this control philosophy was expanded to nonlinear systems. Currently, adaptive control is the subject of intense research, focusing on robustness improvements of the original algorithms, new adaptation mechanisms, as well as the combination of multiple strategies to improve transient performance, with application in several areas, such as aerospace [1,2,3,4], satellite [5, 6], cruise control [7, 8], robotics [9,10,11,12], multi-agent systems [13,14,15], biomedical [16,17,18], and renewable energies [19,20,21,22].

Model reference adaptive control (MRAC), developed by Whitaker [23], is considered one of the main adaptive control methods. In this approach, the controller aims to approximate the system response with the model reference output. The challenge of this method consists in the determination of an adaptation mechanism for ensuring the matching between the real and the desired response, while maintaining the system’s global stability in the presence of unmodeled dynamics (matched or unmatched). Taking this into consideration, modifications to the MRAC algorithm have been proposed with the aim of making it more robust and with better transient responses. Although MRAC can present fast reference model output tracking, its transient response can be a concern while the gains do not converge to a solution set, resulting in unsatisfactory performance during the adaptation of the gains. In the past, some strategies were adopted to enhance the controller’s performance, such as error estimation [24], mean square tracking error criterion, and the L$_{\infty }$ tracking error bound criterion [25]. However, they lack robustness and may cause local instabilities, called bursting phenomena [26]. Nowadays, there is a tendency to combine control techniques to improve the transient regime while maintaining global stability, ensuring tracking error elimination, or making it tend to a residual set, such as a proportional-integral-derivative (PID) controller and its variants [27,28,29,30,31,32,33] and predictive controller [34,35,36].

Sliding mode control (SMC) strategies stand out due to their satisfactory performance in regulating complex systems [37,38,39]. This kind of controller has been receiving relevant attention from adaptive control researchers, who have recently proposed several combinations of SMC and adaptation algorithms, such as [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. Therefore, adaptive SMC is a trending topic in the control area, thanks to its insensitivity to plant parameters and robust characteristics, making it feasible to deal with real systems. However, many of the proposed controllers do not have their stability proof well established. The Lyapunov criterion is recurrently used for stability analysis of the controllers. This kind of investigation is an important step in providing reliability for adaptive controllers because it gives the mathematical background to identify the constraints that delimit the set of controller parameters for ensuring the system’s global stability while minimizing the tracking error.

Adaptive SMCs have been proposed in the literature. However, there are several formulations of SMC structure. These variations commonly aim to reduce chattering by increasing the controller order, modifying the sliding surface, or integrating it into other control algorithms. In this sense, several adaptive variable structure control strategies are grounded in fuzzy systems such as [55,56,57] or neural networks [58,59,60,61]. These approaches use inference rules or networks with non-interpretable information flow through their layers. In a different approach, the adaptive SMC based on MRAC is grounded in strong mathematical background. However, most works in the literature propose the union of SMC and MRAC in multi-loop control structures, where some MRAC is used to reject exogenous disturbance, while a fixed-gain SMC algorithm forces the closed-loop system to track the reference signal, such as [62, 63]. In a sophisticated approach, an MRAC-based SMC was presented in [64], where a gradient algorithm updated the SMC gains. However, this controller did not incorporate robustness terms. Thus, as can be seen, there is a gap in the literature on adaptive SMC based on robust MRAC. Furthermore, it is fundamental to prove the global stability of the resulting adaptive control structure formed by MRAC and SMC to provide a certificate of its reliability.

The purpose of this paper is to present the stability proofs of a continuous-time robust model reference adaptive sliding mode controller (RMRAC-SM) and its design using the sine–cosine optimization algorithm. The RMRAC-SM explores the best from each technique: The RMRAC provides robustness and fast reference tracking, while the adaptive SMC acts on transient regimes, improving transient response but tending to zero when the system achieves a steady state for mitigation of chattering effects. However, it is not trivial to design because there are several parameters and initial gains to choose. Direct adaptive controllers are often designed based on the control designer experience, lacking systematic methodologies. In this sense, the automation of this task by an optimization procedure saves the designer time while enhancing the overall controller response. The stability proof of the controller is developed based on [65] and [66]. The analysis considers plants subject to unmodeled dynamics (match and unmatched dynamics), using a Lyapunov candidate function with the aim of showing that internal signals of the closed-loop system are bounded, and the tracking error tends to a small residual set in the order of chattering. Therefore, the contributions of this work are:

• Stability analysis and design of a continuous-time RMRAC-SM using the Lyapunov criterion, considering the plant subject to unmodeled dynamics;

• A simplified methodology for automatic parametrization of the RMRAC-SM using the sine–cosine optimization algorithm.

The structure of this work is organized as follows: Sect. 2 introduces plant and reference model descriptions and assumptions, control law, error equation development, and parameters adaptation algorithm. Section 3 provides the development of stability proof and robustness analysis of the identifier. Section 4 introduces a procedure for controller parametrization. Next, Sect. 5 presents a numerical example of the application of the developed controller in an unstable, non-minimum-phase system to corroborate controller performance and robustness, and a comparison to other similar adaptive controller. In addition, Section 6 presents the results of a processor-in-the-loop experiment of a complex real-world engineering problem dealt with the presented controller. Section 7 discusses the final considerations for this work.

2 Mathematical background of RMRAC-SM

This section presents the fundamental theory for plant and reference model assumptions, as well as the controller algorithm and the development of the error equation.

2.1 Assumptions of plant and reference model

Consider a continuous-time single-input single-output plant, G(s), as

$$\begin{aligned} y=G(s)u=\left[ \ G_{0}(s)(1+\mu _1 \Delta _{m}(s))+\mu _2 \Delta _{a}(s)\ \right] u, \end{aligned}$$

(1)

where u and y are the input and output of G(s), respectively. Besides, $\Delta _{m}(s)$ and $\Delta _{a}(s)$ are multiplicative and additive unmodeled dynamics, respectively. Moreover, $\mu$ is a positive parameter that, with no loss of generality, can be equal for both dynamics $\mu _1=\mu _2=\mu$ [65]. This assumption is adopted in this work to facilitate controller stability analysis. The nominal part of the plant, $G_0(s)$, is given by

$$\begin{aligned} G_{0}(s)=k_p \frac{Z_{0}(s)}{R_{0}(s)}, \end{aligned}$$

(2)

where $k_p$, $Z_0(s)$, and $R_0(s)$ are plant gain, monic polynomial with order m, and monic polynomial with order n, respectively.

In accordance with [65], for a direct adaptive controller, $G_0(s)$ must satisfy the following assumptions:

A-I: $R_0(s)$ is a monic polynomial, Hurwitz with degree n;

A-II: $Z_0(s)$ is a monic polynomial with degree m, and $m \le (n-1)$;

A-III: The sign of $k_p$ and the relative degree of $G_0(s)$ are known.

The assumptions for G(s) are:

A-IV: $\Delta _{a}(s)$ is a strictly proper transfer function;

A-V: $\Delta _{m}(s)$ is a proper transfer function.

Remark 1

It is important to highlight that $G_0(s)$ has to be a minimum phase transfer function. However, it does not imply that the overall plant, G(s), cannot present non-minimum phase zeros because they are treated as unmodeled dynamics. In addition, the relative degree of G(s) and the system parameters can be completely unknown, which means that the overall system can also be unstable.

Remark 2

$\mu$ is a small scalar, such that $|\mu \Delta _m(j\omega )|$ is small at low frequencies. However, since $\Delta _m(s)$ can be non-proper for relative degree $n^*$ greater than 1 $(n_p - m_p > 1)$, then $|\mu \Delta _m(j\omega )|$ may be large for high frequencies, which is $|\mu \Delta _m(j\omega )|\xrightarrow []{} \infty$ when $|\omega |\xrightarrow []{} \infty$ even when $\mu$ is very small [67].

The only a priori information required about $\Delta _{a}(s)$ and $\Delta _{m}(s)$ is a lower limit for the stability margin of their poles. In the case of fast unmodeled dynamics, p has an order of $\dfrac{1}{\varepsilon }$, where $0<\varepsilon<<1$, and, consequently, a lower bound $p_0$ can be found out [65], satisfying assumption A-V.

Regarding the reference model $W_m(s)$, it follows

$$\begin{aligned} y_m=W_m(s)r=\frac{k_m}{R_m(s)}r, \end{aligned}$$

(3)

where $y_m$ and r are the reference model output and a uniformly limited reference signal, respectively. Furthermore, $k_m$ and $R_m(s)$ are reference model gain and a monic stable polynomial with a relative degree of $n^*=n-m>0$, respectively.

The reference model needs to satisfy only one assumption:

A-VI: The relative degree of $W_m(s)$ is the same as the relative degree of $G_0(s)$.

2.2 Control law

The control law of the continuous-time RMRAC-SM is developed as an expansion of RMRAC, incorporating SMC into its structure. Therefore, it can be described using a conventional matrix form as follows:

$$\begin{aligned} \varvec{\theta }^{T}\varvec{\omega }+r=0, \end{aligned}$$

(4)

where $\varvec{\omega }$ is the auxiliary vector, composed by

$$\begin{aligned} \varvec{\omega }^{T}=[\ {\varvec{\omega }_1}^{T}\ \ {\varvec{\omega }_2}^{T}\ \ y\ \ u\ \ \nu \ ], \end{aligned}$$

(5)

where ${\varvec{\omega }_1}^{T}$ and ${\varvec{\omega }_2}^{T}$ are internal filters, $\nu =sgn(e_1)$, being $e_1$ the tracking error, defined by $e_1=y-y_m$. The internal filters are designed as

$$\begin{aligned} \begin{aligned} {\varvec{\omega }_1}=(s{{\textbf {I}}}-{{\textbf {F}}})^{-1}{\varvec{q}}u\\ {\varvec{\omega }_2}=(s{{\textbf {I}}}-{{\textbf {F}}})^{-1}{\varvec{q}}y \end{aligned} \end{aligned}$$

(6)

where ${{\textbf {F}}}$ is a stable matrix with order $(n-1)\times (n-1)$ and the pair $({{\textbf {F}}},{{\textbf {q}}})$ is controllable. Variables ${\varvec{\omega }_1}^{T}, \ {\varvec{\omega }_2}^{T}, \ y\ \text {and}\ u$ in $\varvec{\omega }^T$ are related to the RMRAC, while $\nu$ is originated from SMC, whose sliding surface is $e_1$.

Adaptive gains are straightforwardly related to the variables into an auxiliary vector $\varvec{\omega }$, from the gains vector $\varvec{\theta }$,

$$\begin{aligned} \varvec{\theta }^{T}=[\ {\varvec{\theta }_1}^{T}\ \ {\varvec{\theta }_2}^{T}\ \ {\theta _3}\ \ {\theta _4} \ \ {\theta _{SM}}\ ]. \end{aligned}$$

(7)

From (4), (5) and (7), the control law can be written as

$$\begin{aligned} u=\frac{-{\varvec{\theta }_1}^{T}{\varvec{\omega }_1}-{\varvec{\theta }_2}^{T}{\varvec{\omega }_2}-{\theta _3}y-{\theta _{SM}}\nu - r}{{\theta _4}}, \end{aligned}$$

(8)

or yet,

$$\begin{aligned} u=u_{RMRAC}+u_{SM}, \end{aligned}$$

(9)

where $u_{RMRAC}=-{\varvec{\theta }}_1^{T}\varvec{\omega }_1-{\varvec{\theta }}_2^{T}\varvec{\omega }_2-{\theta }_3y-{\theta }_rr$ and $u_{SM}=-{\theta }_{SM}\nu$, being $u_{RMRAC}$ the control action referring to continuous-time RMRAC and $u_{SM}$ the contribution of adaptive SMC.

The objective of the controller is to force the plant output y to track the reference model output $y_m$ as close as possible, even in the presence of unmodeled dynamics. Moreover, for $\mu ^* > 0$ and any $\mu \in [0, \mu ^*)$, the controller ensures the global stability of the closed-loop system.

2.3 Development of error equation

Lemma 1

The tracking error $e_1$ is given by the difference between plant output and model reference output. Thus,

$$\begin{aligned} y-y_m=e_1=W_m(s)\phi ^{T}\varvec{\omega } +\mu \eta , \end{aligned}$$

(10)

where $\eta =\eta _1+\eta _2$, being $\eta _1=\Delta _1(s)u$, $\eta _2=\Delta _2(s)\nu$, and $\nu =sgn(e_1)$, where $\Delta _1(s)$ and $\Delta _2(s)$ are strictly proper transfer functions and sgn represents the sign function.

Proof

The parametric error vector $\varvec{\phi }$ is $\varvec{\phi }=\varvec{\theta }-\varvec{\theta }^{*}$, where $\varvec{\theta }^{*}$ is the desired gains vector, given by ${\varvec{\theta }}^{*T}=[\ {\varvec{\theta }}_{1}^{*T}, {\varvec{\theta }}_{2}^{*T},{\theta }_{3}^{*},{\theta }_{4}^{*},{\theta }_{SM}^{*}\ ]$. Therefore, (4) can be written as

$$\begin{aligned} \varvec{\phi }^{T}\varvec{\omega }+r=-\varvec{\theta }^{*T}\varvec{\omega }, \end{aligned}$$

(11)

which, with the replacement of ${\varvec{\theta }}^{*T}$, ${\varvec{\omega }_1}^{T}$, and ${\varvec{\omega }_2}^{T}$, results in

$$\begin{aligned}{} & {} \varvec{\phi }^{T}\varvec{\omega }+ r= -[ \varvec{\theta } {{_{_{1}}^{*}}^{T}}{{(s{{\textbf {I}}}-{{\textbf {F}}})}^{-1}}{{\textbf {q}}}u+\varvec{\theta } {{_{_{2}}^{*}}^{T}}{{(s{{\textbf {I}}}-{{\textbf {F}}})}^{-1}}{{\textbf {q}}}G(s)u\nonumber \\{} & {} \quad +\, {{\theta }_{3}}^{*}(G(s)u)+ {{\theta }_{4}}^{*}u+\theta _{SM}^{*}\nu ]. \end{aligned}$$

(12)

Defining ${f_1(s)} = {(s{{\textbf {I}}} - {{\textbf {F}}})^{ - 1}}{{\textbf {q}}}$ follows

$$\begin{aligned} {\varvec{\phi } ^T}\varvec{\omega } + r= & {} - [ \varvec{\theta } {{_{_1}^*}^T}{f_1(s)}u + \varvec{\theta } {{_{_2}^*}^T}{f_1(s)}G(s)u\nonumber \\{} & {} +\,{\theta _3}^*G(s)u + {\theta _4}^*u + \theta _{SM}^*\nu ]. \end{aligned}$$

(13)

Due to the controllability of the plant, it can be affirmed that there is a vector $\varvec{\theta }=\varvec{\theta }^{*}$ such that $\varvec{\phi }=[{\varvec{0}}]$, and then, (13) can be written as

$$\begin{aligned} \begin{aligned}&r =- [ \varvec{\theta } {{_{_1}^*}^T}{f_1}(s)u + \varvec{\theta } {{_{_2}^*}^T}{f_1}(s){G_0}(s)u\\&\qquad + {\theta _3}^*{G_0}(s)u +{\theta _4}^*u + \theta _{SM}^*\nu ]. \end{aligned} \end{aligned}$$

(14)

The controller’s objective is to track the reference model’s output. Therefore, when $y=y_m$, it is true that

$$\begin{aligned} r = {W_m}{(s)^{ - 1}}{G_0}(s)u. \end{aligned}$$

(15)

Equaling (14) and (15), it follows

$$\begin{aligned} G_0(s)u= & {} -W_m(s)[ \varvec{\theta }_1^{*T}{f_1}(s)u + \varvec{\theta } {{_{_2}^*}^T}{f_1}(s){G_0}(s)u \nonumber \\{} & {} +\, {\theta _3}^*{G_0}(s)u + {\theta _4}^*u + \theta _{SM}^{*}\nu ]. \end{aligned}$$

(16)

Besides, as the plant output is given by

$$\begin{aligned} y = G(s)u = {G_0}(s)\left[ {1 + \mu {\Delta _m}(s)} \right] u + \mu {\Delta _a}(s)u, \end{aligned}$$

(17)

and replacing (16) into (17), it is obtained

$$\begin{aligned} y= & {} - {W_m}(s)[\varvec{\theta }_{1}^{*T}{f_1}(s)u + (\varvec{\theta }_{2}^{*T}{f_1}(s) + {\theta _3}^*){G_0}(s)u\nonumber \\{} & {} +{\theta _4}^*u + \theta _{SM}^*\nu ][1 + \mu {\Delta _m}(s)] \mu {\Delta _a}(s)u. \end{aligned}$$

(18)

Defining ${f_2}(s) = \varvec{\theta } {_{_2}^{*T}}{f_1}(s) + {\theta _3}^*$, (18) is rewritten as

$$\begin{aligned}{} & {} y = - {W_m}(s)[\varvec{\theta }{_1^{*T}}{f_1}(s)u + {f_2}(s){G_0}(s)u + {\theta _4}^*u+\theta _{SM}^*\nu ]\nonumber \\{} & {} \qquad \qquad [1 + \mu {\Delta _m}(s)] + \mu {\Delta _a}(s)u. \end{aligned}$$

(19)

Moreover, adding and subtracting ${W_m}(s){f_2}(s)G(s)\left[ {1 + \mu {\Delta _m}(s)} \right] u(s)$ on (19) follows

$$\begin{aligned}{} & {} y = - {W_m}(s)[\varvec{\theta } {_1^{*T}}{f_1}(s)u + {f_2}(s)G(s)u + {\theta _4}^*u + \theta _{SM}^*\nu ]\nonumber \\{} & {} \qquad \qquad \! \left[ {1 \!+\! \mu {\Delta _m}(s)}\! \right] \!+\! {W_m}(s){f_2}(s)G(s)\left[ {1 \!+\! \mu {\Delta _m}(s)}\! \right] u \nonumber \\{} & {} \qquad \qquad -\, {W_m}(s){f_2}(s){G_0}(s)\left[ {1 \!+\! \mu {\Delta _m}(s)} \right] u + \mu {\Delta _a}(s)u.\nonumber \\ \end{aligned}$$

(20)

Thereby, from (13) and (20), it follows

$$\begin{aligned}{} & {} y = {W_m}(s)[{\varvec{\phi } ^T}\varvec{\omega } + r] - \mu {\Delta _m}(s){W_m}(s)[\varvec{\theta } {_1^{*T}}{f_1}(s)u\nonumber \\{} & {} \qquad \qquad +\,{\theta _4}^*u + \theta _{SM}^*\nu ] + {W_m}(s){f_2}(s)G(s)u\nonumber \\{} & {} \qquad \qquad - \,{W_m}(s){f_2}(s){G_0}(s) \left[ {1 + \mu {\Delta _m}(s)} \right] u + \mu {\Delta _a}(s)u. \end{aligned}$$

(21)

Replacing (1) on (21), it results in

$$\begin{aligned} y{} & {} = {W_m}(s)[{\varvec{\phi } ^T}\varvec{\omega } + r]\nonumber \\{} & {} \quad - \mu {\Delta _m}(s){W_m}(s)[\varvec{\theta } {_1^{*T}}{f_1}(s)u + {\theta _4}^*u + \theta _{SM}^*\nu ] \nonumber \\{} & {} \quad + {W_m}(s){f_2}(s)[{G_0}(s)\left[ {1 + \mu {\Delta _m}(s)} \right] \nonumber \\{} & {} \quad + \mu {\Delta _a}(s)]u-{W_m}(s){f_2}(s){G_0}(s)\nonumber \\{} & {} \quad \left[ {1 + \mu {\Delta _m}(s)} \right] u + \mu {\Delta _a}(s)u, \end{aligned}$$

(22)

which, after simplification, is

$$\begin{aligned} y{} & {} = {W_m}(s)[{\varvec{\phi }^T}\varvec{\omega } + r] + \mu [ - {\Delta _m}(s){W_m}(s)\varvec{\theta } {_1^{*T}}{f_1}(s) \nonumber \\{} & {} \quad -{\Delta _m}(s){W_m}(s){\theta _4}^* + {W_m}(s){f_2}(s){\Delta _a}(s)\nonumber \\{} & {} \quad + \,{\Delta _a}(s)]u - \mu {\Delta _m}(s){W_m}(s)\theta _{SM}^*\nu , \end{aligned}$$

(23)

or yet,

$$\begin{aligned} y = {W_m}(s)[{\varvec{\phi } ^T}\varvec{\omega } + r] + \mu {\Delta _1}(s)u + \mu {\Delta _2}(s)\nu , \end{aligned}$$

(24)

where

$$\begin{aligned} \begin{aligned} {\Delta _1}(s)&= - {\Delta _m}(s){W_m}(s)\varvec{\theta } {_1^{*T}}{f_1}(s) - {\Delta _m}(s){W_m}(s){\theta _4}^*\\&\quad +{W_m}(s){f_2}(s){\Delta _a}(s) + {\Delta _a}(s), \end{aligned} \end{aligned}$$

(25)

and

$$\begin{aligned} {\Delta _2}(s) = - {\Delta _m}(s){W_m}(s)\theta _{SM}^*. \end{aligned}$$

(26)

As the reference model output is given by ${y_m} = {W_m}(s)r$, (24) can be rewritten as

$$\begin{aligned} {e_1} = y - {y_m} = {W_m}(s){\varvec{\phi } ^T}\varvec{\omega } + \mu {\eta _1} + \mu {\eta _2}, \end{aligned}$$

(27)

with ${\eta _1} = {\Delta _1}(s)u$ and ${\eta _2} = {\Delta _2}(s)\nu$. Thereby, (27), which represents the tracking error, can also be written as

$$\begin{aligned} {e_1} = {W_m}(s){\varvec{\phi } ^T}\varvec{\omega } + \mu \eta , \end{aligned}$$

(28)

where $\eta = {\eta _1} + {\eta _2}$.

From (28) and the following equality

$$\begin{aligned} {\varvec{\theta } ^T}{W_m}(s)\varvec{\omega } - {W_m}(s){\varvec{\theta } ^T}\varvec{\omega } = {\varvec{\phi } ^T}{W_m}(s)\varvec{\omega } - {W_m}(s){\varvec{\phi } ^T}\varvec{\omega },\nonumber \\ \end{aligned}$$

(29)

the augmented error can be determined as

$$\begin{aligned} \varepsilon = {e_1} + {\varvec{\theta } ^T}\varvec{\xi } - {W_m}(s){\nu _1} = {\varvec{\phi } ^T}\varvec{\xi } + \mu \eta , \end{aligned}$$

(30)

where $\varvec{\xi } = {W_m}(s)\varvec{\omega }$, and ${\nu _1} = {\varvec{\theta } ^T}\varvec{\omega }$.

It is stated that

$$\begin{aligned} \varepsilon = {\varvec{\phi } ^T}\varvec{\xi } + \mu \eta , \end{aligned}$$

(31)

is developed only for mathematical proof purposes, while

$$\begin{aligned} \varepsilon = {e_1} + {\varvec{\theta } ^T}\varvec{\xi } - {W_m}(s){\nu _1}, \end{aligned}$$

(32)

is the implementable augmented error.

$\square$

2.4 Algorithm for adaptation of controller parameters

In this work, a modified gradient algorithm is implemented to adjust the gains of the controller. This parametric adaptation law is

$$\begin{aligned} \dot{\varvec{\theta }} = - \sigma \varvec{\Gamma } \varvec{\theta } - \frac{\gamma {\Gamma \varvec{\xi } \varepsilon }}{{{m^2}}}, \end{aligned}$$

(33)

where $\varvec{\Gamma }$ is a square symmetric positive defined matrix with compatible order. Furthermore, $\varvec{\xi }$ is the regressor vector defined by $\varvec{\xi } = {W_m}(s)\varvec{\omega }$, and $\varepsilon$ is the augmented error defined on (32). Moreover, m is a majorant signal, similar to the majorant signal used on [68], which guarantees robustness to the identifier, expressed as

$$\begin{aligned} m^2= {\bar{m}}^2+{\varvec{\xi }}^T{\varvec{\Gamma }}{\varvec{\xi }}, \end{aligned}$$

(34)

where

$$\begin{aligned} \dot{{\bar{m}}} = - {\delta _0}{\bar{m}} + {\delta _1}\left( {1 + |u |+ |y |} \right) , \end{aligned}$$

(35)

with initial condition, $m(0) \ge \dfrac{{{\delta _1}}}{{{\delta _0}}}$ being ${\delta _1} > {\delta _0}$. Moreover, ${\delta _1}$ and ${\delta _0} \in {R^ + }$. In addition, $\sigma$-modification is incorporated into the parametric adaptation law to avoid parameter drifting [65], defined as

$$\begin{aligned} \sigma (t) = \left\{ \begin{matrix} 0 &{} \text {if}&{} \!\!\left\| {{\bar{\varvec{\theta }}}} \right\| \le {M_0}\\ {\sigma _0}\left( {\dfrac{{\left\| \bar{ \varvec{\theta }} \right\| }}{{{M_0}}} - 1} \right) &{} \text {if}&{}\qquad \quad {M_0}< \left\| {{\bar{ \varvec{\theta }}}} \right\| < 2{M_0},\\ {\sigma _0} &{} \text {if}&{} \!\! \left\| {{\bar{ \varvec{\theta }}}} \right\| \ge 2{M_0} \end{matrix} \right. \end{aligned}$$

(36)

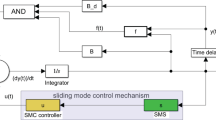
where $M_0$ and $\sigma _{0}$ are design parameters, and $||\varvec{\theta }||$ is the Euclidean norm of the parameter vector. It is highlighted that $M_0$ can be oversized, as $\bar{{\varvec{\theta }}}^*$ are unknown [69]. Figure 1 shows the block diagram of RMRAC-SM. Besides, the steps to implement the continuous-time RMRAC-SM controller are:

Fig. 1

Block diagram of continuous-time RMRAC-SM

The logic flow to implement this control technique is:

• 1. Update of reference, r;

• 2. Update of reference model output, $y_m$;

• 3. Update of auxiliary vector, ${\varvec{\omega }}$;

• 4. Update of regressor vector, $\varvec{\xi }$;

• 5. Update of gains norm, $||{\varvec{\theta }}||$;

• 6. Update of $\sigma$-modification, $\sigma$;

• 7. Update of tracking error, $e_1$;

• 8. Update of augmented error, $\epsilon$;

• 9. Update of majorant signal, $m^2$;

• 10. Update of adaptive gains, ${\varvec{\theta }}$;

• 11. Update of control action, u.

3 Stability analysis

Theorem 1

Consider the plant defined by (1) and (2) subjected to the assumptions A-I to A-V, and the reference model described on (3) subjected to assumption A-VI. In addition, consider the control action given by (4), and the parametric adaptation algorithm determined from (33) to (36). Then, the closed-loop control system is robust, and the tracking error $e_1$ shown on (28) tends to zero when the system tends to a steady state (${t\rightarrow \infty }$), even in the presence of unmodeled dynamics.

Proof

Suppose initially $\mu =0$ on (30), or yet

$$\begin{aligned} \varepsilon = {e_1} + {\varvec{\theta } ^T}\varvec{\xi } - {W_m}(s){\nu _1} = {\varvec{\phi } ^T}\varvec{\xi }. \end{aligned}$$

(37)

Then, let $V = {\varvec{\phi } ^T}{\varvec{\Gamma } ^{ - 1}}\varvec{\phi }$ be a Lyapunov function candidate, then deriving V, it is obtained

$$\begin{aligned} \dot{V} = 2\varvec{\phi }^T\varvec{\Gamma }^{-1}\dot{ \varvec{\phi } }. \end{aligned}$$

(38)

From (33), it also follows

$$\begin{aligned} \dot{\varvec{\phi }} = \dot{\varvec{\theta }} = - \sigma \varvec{\Gamma } \varvec{\theta } - \frac{\gamma \varvec{\Gamma } \varvec{\xi } \varepsilon }{m^2}, \end{aligned}$$

(39)

and replacing (39) into (38) follows

$$\begin{aligned} \dot{V}= & {} 2{{\varvec{\phi }} ^T}{{\varvec{\Gamma }} ^{-1}}\left( { - \sigma \varvec{\Gamma } \varvec{\theta } - \frac{{\gamma \varvec{\Gamma } \varvec{\xi } \varepsilon }}{{{m^2}}}} \right) \nonumber \\= & {} - 2\sigma {\varvec{\phi } ^T}\varvec{\theta } - \frac{{2\gamma {\varvec{\phi } ^T}\varvec{\xi } \varepsilon }}{{{m^2}}}. \end{aligned}$$

(40)

Next, replacing (37) into (40) results in

$$\begin{aligned} \dot{V} = - 2\sigma {\varvec{\phi } ^T}\varvec{\theta } - \frac{{2\gamma {{({\varvec{\phi } ^T}\varvec{\xi } )}^2}}}{{{m^2}}} \le 0. \end{aligned}$$

(41)

Using Lemma 2, presented in Appendix A, it follows $2\sigma {\varvec{\phi } ^T}\varvec{\theta } \ge 0$. Thereby, it is concluded that $\dot{V} \le 0$ when $\mu = 0$. Moreover, $\varvec{\phi } = \varvec{\theta } - {\varvec{\theta } ^*} \rightarrow 0$ when $t \rightarrow \infty$ and therefore $\varvec{\theta } \rightarrow {\varvec{\theta } ^*}$ when $t \rightarrow \infty$. Analyzing (37) also follows

$$\begin{aligned} \varepsilon = {e_1} + {\varvec{\theta } ^T}\varvec{\xi } - {W_m}(s){\nu _1} = {\varvec{\phi } ^T}\varvec{\xi } \rightarrow 0, \end{aligned}$$

(42)

and therefore ${\varvec{\phi } ^T}\varvec{\xi } - {W_m}(s){\nu _1} \rightarrow 0$. Thus, $\varepsilon = {e_1} \rightarrow 0$ when $t \rightarrow \infty$.

When $\mu \ne 0$, the augmented error $\varepsilon$ and the tracking error $e_1$ are not zero. Assuming $e_1$ is in the unmodeled dynamics’ magnitude order, then it can be written

$$\begin{aligned} {e_1} = {\alpha _1}\mu \eta . \end{aligned}$$

(43)

From definition, $\eta = {\eta _1} + {\eta _2}$, where ${\eta _1} = {\Delta _1}(s)u$ and ${\eta _2} = {\Delta _2}(s)\nu$, ${\Delta _1}(s)$ is assumed to be an unmodeled dynamics of first order. Therefore, it follows

$$\begin{aligned} \eta = \left( {\frac{{{\beta _1}}}{{s + {\beta _2}}}} \right) u + {\varvec{\xi } _1} + {\eta _2}, \end{aligned}$$

(44)

where ${\varvec{\xi _1}}$ is an additional first-order disturbance to the unmodeled dynamics with ${\beta _1}$ and ${\beta _{2\mathrm{{ }}}} \in \mathrm{{ }}{\mathrm{{R}}^ + }$. Thereby, (44) can be rewritten as

$$\begin{aligned} \eta = \left( {\frac{{{\beta _1}}}{{s + {\beta _2}}}} \right) u + {\varvec{\xi }_2}, \end{aligned}$$

(45)

where ${\varvec{\xi }_2} = {\varvec{\xi }_1} + {\eta _2}$. From (45), it follows ${\dot{\eta }} = - {\beta _2}\eta + {\beta _1}u + {\varvec{\xi }_3}$, or, equivalently,

$$\begin{aligned} \mu {\dot{\eta }} = - \mu {\beta _2}\eta + \mu {\beta _1}u + \mu {\varvec{\xi } _3}. \end{aligned}$$

(46)

Deriving (43) and replacing it on (46), it is obtained

$$\begin{aligned} {\dot{e}_1} = - {\beta _2}{e_1} + \mu {\beta _3}u + {\alpha _1}\mu {\varvec{\xi } _3}, \end{aligned}$$

(47)

where ${\beta _3} = {\alpha _1}{\beta _1}$. Using (9) in (47) follows

$$\begin{aligned} {\dot{e}_1} = - {\beta _2}{e_1} + \mu {\beta _3}{u_1} + \mu {\beta _3}{u_{SM}} + {\alpha _1}\mu {\varvec{\xi } _3}. \end{aligned}$$

(48)

For the stability proof, considering the condition $\mu \ne 0$, let $V = {\varvec{\phi } ^T}{\varvec{\Gamma } ^{ - 1}}\varvec{\phi } + {e_1}^2$ a Lyapunov function candidate. The derivative of V is

$$\begin{aligned} \dot{V} = 2{\varvec{\phi } ^T}{\varvec{\Gamma } ^{ - 1}}\dot{\varvec{\phi }} + 2{e_1}{\dot{e}_1}, \end{aligned}$$

(49)

and replacing (39) on (49) follows

$$\begin{aligned}{} & {} \dot{V} = 2{\varvec{\phi } ^T}{\varvec{\Gamma } ^{-1}}\left( { - \sigma \varvec{\Gamma } \varvec{\theta } - \frac{\gamma {\varvec{\Gamma } \varvec{\xi } \varepsilon }}{{{m^2}}}} \right) + 2{e_1}\dot{e_1} \nonumber \\{} & {} \quad - 2\sigma {\varvec{\phi } ^T}\varvec{\theta } -\frac{{2\gamma {\varvec{\phi } ^T}\varvec{\xi } \varepsilon }}{{{m^2}}} + 2{e_1}{\dot{e_1}}. \end{aligned}$$

(50)

Besides, using (30) into (50), it is obtained

$$\begin{aligned} \dot{V} = - 2\sigma {\varvec{\phi } ^T}\varvec{\theta } - \frac{{2\gamma {{({\varvec{\phi } ^T}\varvec{\xi } )}^2}}}{{{m^2}}} - \frac{{2\gamma {\varvec{\phi } ^T}\varvec{\xi } \mu \eta }}{{{m^2}}} + 2{e_1}{\dot{e}_1}. \end{aligned}$$

(51)

Next, adding and subtracting $\dfrac{{{{\left( {\mu \eta } \right) }^2}}}{{{m^2}}}$ on (51), and replacing (48), it results in

$$\begin{aligned} \dot{V}= & {} - 2\sigma {\varvec{\phi } ^T}\varvec{\theta } - \dfrac{{{{\gamma ({\varvec{\phi } ^T}\varvec{\xi } )}^2}}}{{{m^2}}} - \dfrac{{{{\gamma ({\varvec{\phi } ^T}\varvec{\xi } + \mu \eta )}^2}}}{{{m^2}}} + \dfrac{{{{(\mu \eta )}^2}}}{{{m^2}}} \nonumber \\{} & {} + 2{e_1}( - {\beta _2}{e_1} + \mu {\beta _3}{u_1} + \mu {\beta _3}{u_{SM}} + {\alpha _1}\mu . {\varvec{\xi }_3}). \end{aligned}$$

(52)

Replacing $u_{SM}=-{\bar{\theta }}_{SM}\nu$ into (52) results in

$$\begin{aligned} \dot{V}= & {} - 2\sigma {\varvec{\phi } ^T}\varvec{\theta } - \dfrac{{{{\gamma ({\varvec{\phi } ^T}\varvec{\xi } )}^2}}}{{{m^2}}}\nonumber \\{} & {} - \dfrac{{{{\gamma ({\varvec{\phi } ^T}\varvec{\xi } + \mu \eta )}^2}}}{{{m^2}}} + \dfrac{{{{(\mu \eta )}^2}}}{{{m^2}}} \nonumber \\{} & {} - 2{\beta _2}{e_1}^2 + 2\mu {e_1}({\beta _3}{u_1} + {\alpha _1}{\varvec{\xi } _3}) \nonumber \\{} & {} - 2\mu {e_1}{\beta _3}{{\bar{\varvec{\theta }} }_{SM}}{\mathop {\textrm{sgn}}} ({e_1}). \end{aligned}$$

(53)

Defining ${\xi _4} = ({\beta _3}{u_1} + {\alpha _1}{\xi _3})$ follows

$$\begin{aligned} \dot{V}= & {} - 2\sigma {\varvec{\phi } ^T}\varvec{\theta } - \dfrac{{{{\gamma ({\varvec{\phi } ^T}\varvec{\xi } )}^2}}}{{{m^2}}} \nonumber \\{} & {} - \dfrac{{{{\gamma ({\varvec{\phi } ^T}\varvec{\xi } + \mu \eta )}^2}}}{{{m^2}}} + \dfrac{{{{(\mu \eta )}^2}}}{{{m^2}}}\nonumber \\{} & {} - 2{\beta _2}{e_1}^2 + 2\mu {e_1}{\varvec{\xi } _4} - 2\mu {\beta _3}{\bar{\varvec{\theta }} _{SM}}|{{e_1}} |. \end{aligned}$$

(54)

From (54), it follows $\forall$ $\mathrm{{ }}{\varvec{\xi } _4}$,

$$\begin{aligned} {\dot{V}} \frac{{{{(\mu \eta )}^2}}}{{{m^2}}} - 2{\beta _2}{e_1}^{2} - 2\mu {\beta _3}{\bar{\varvec{\theta }} _{SM}}|{{e_1}} |+ 2\mu {e_1}{\varvec{\xi }_4}. \end{aligned}$$

(55)

Replacing (43) on (55), it is obtained

$$\begin{aligned} \dot{V} \le \!-\! \left( {2{\beta _2}\alpha _1^2 \!-\! \dfrac{1}{{{m^2}}}} \right) {\mu ^2}{\eta ^2} - 2\mu {\beta _3}{\bar{\varvec{\theta }}_{SM}}|{{e_1}} |+ 2\mu {e_1}{\varvec{\xi }_4}.\nonumber \\ \end{aligned}$$

(56)

According to (35), it is notable that $m^2$ tends to a high value; thereby, $\dfrac{1}{m^2}$ tends to zero. Then, $2{\beta _2}\alpha _1^2 \ge \dfrac{1}{{{m^2}}}$ is easily satisfied. In addition, (56) has to accomplish $2\mu \left( { - {\beta _3}{{\bar{\varvec{\theta }} }_{SM}}|{{e_1}} |+ {e_1}{\varvec{\xi }_4}} \right) \le 0$,

or yet, ${\beta _3}{\bar{\varvec{\theta } }_{SM}}|{{e_1}} |\ge {e_1}{\varvec{\xi } _4}$,

which is equivalent to

$$\begin{aligned} {\beta _3}{\bar{\varvec{\theta }} _{SM}} \ge {\varvec{\xi } _4}{\mathop {\textrm{sgn}}} ({e_1}), \end{aligned}$$

(57)

or yet,

$$\begin{aligned} |{{\beta _3}{{\bar{\varvec{\theta }} }_{SM}}} |\ge {\varvec{\xi } _4}{\mathop {\textrm{sgn}}} ({e_1}). \end{aligned}$$

(58)

Therefore, (58) needs to be satisfied to ensure $\dot{V} \le 0$, with $\mu$ and ${\beta _{3}} \in {R^ + }$. Thereby, $\dot{V}$, defined on (49), turns negative or at maximum equal to zero. Thus, Theorem 1 is proved, and consequently, the control algorithm stability is verified.

$\square$

4 Procedure for controller parametrization

The parametrization of adaptive controllers is a complex task because it is not intuitive, such as a PID controller configuration. In general, the choice of parameters and initial gains is dependent on designer experience. However, it can be a tiring and extensive process. Thus, a systematic procedure to parametrize adaptive controllers can bring several benefits, such as automating the controller parametrization, reducing time spent on this task, and optimizing controller performance with less dependency on designer experience. In this sense, we propose using a stochastic optimization algorithm to perform this task. The sine–cosine algorithm (SCA) [70] is proposed to design the controller’s convergence parameters and the initial gains. These elements have the highest influence on the closed-loop system’s performance. The SCA was chosen because it is one of the most successful stochastic optimization algorithms in the recent literature and has been used to solve several optimization problems.

Stochastic optimization algorithms have two stages: exploration and exploitation. In the first one, the algorithm generates random solutions to find the promising regions of the search space (exploration). Next, it generates a new solution with gradual changes relevantly smoother than the first phase to locate the global optima (exploitation). In the SCA, the position of the solution in the search space for both stages is given by

$$\begin{aligned} X_i^{t+1}={\left\{ \begin{array}{ll} X_i^{t}+r_1 \times \sin (r_2)\times |r_3P_i^t-X_i^t|, \ \ \ r_4<0.5\\ X_i^{t}+r_1 \times \cos (r_2)\times |r_3P_i^t-X_i^t|, \ \ \ r_4\ge 0.5 \end{array}\right. },\nonumber \\ \end{aligned}$$

(59)

where $X_i^{t}$ is the position of the current solution in the i-th dimension at the t-th iteration, $r_1$ to $r_3$ are random numbers, $P_i$ is the position of the destination point in the i-th dimension, and $r_4$ is a random number that belongs to [0, 1]. In summary, $r_1$ drives the movement direction of the solution in the search space, $r_2$ determines how far the current solution can go (toward or outward the destination), $r_3$ gives a random weight to the destination (emphasize: $r_3>1$ or deemphasize: $r_3<1$), and $r_4$ switches between sine and cosine components. Stochastic optimization algorithms must contain a proper balance between exploration and exploitation to find a global solution. Thus, $r_1$ changes to allow it, as follows:

$$\begin{aligned} r_1 = a \left( 1 - \frac{t}{T} \right) , \end{aligned}$$

(60)

where t is the current iteration, T is the maximum number of iterations, and a is a constant.

Now, relating the variables with controller parameters, this optimization process turns more comprehensible. As aforementioned, $X_i$ represents the position of the best current solution in the search space. Therefore, $X_i$ are the controller parameters and gains. Naturally, the search space is the range that contains the minimum and maximum values of each parameter or gain. Each individual variable can be a specific range. Furthermore, the optimization process requires a function to minimize or maximize. In our study, the function is system emulation, where the SCA aims to minimize the tracking error. Therefore, the cost function uses the tracking error information to drive the solutions generated iteratively by SCA. Here, the mean absolute tracking error is used as the cost function (or fitness, as the cost function is commonly named in the stochastic optimization literature).

Table 1 Controller parameters and initial gains obtained using SCA

5 Simulation results

The developed controller is applied to an unstable non-minimum-phase system to evaluate its performance and robustness. The system is

$$\begin{aligned} G(s) = \frac{1-\lambda s}{ (s-1)(1+\lambda s) }, \end{aligned}$$

(61)

where $\lambda = 0.02$. As can be noted, this system contains a non-minimum-phase zero, located at Laplace’s right half-plane.

Discretizing G(s) with a sampling period of 0.0001 s, the discrete-time system G(z) is

$$\begin{aligned} G(z) = \frac{-0.005774 z + 0.009729}{ z^2 - 1.617 z + 0.6126}. \end{aligned}$$

(62)

Remark 3

Given that the reference signal frequency (0.1 Hz) is significantly lower than the sampling frequency (100000 times slower), and considering the use of a zero-order hold (ZOH) method with a very small sampling time, it is reasonable to expect that the discretization effects will be minimal. This allows for a meaningful comparison between the continuous-time and discrete-time algorithms. However, it is important to remain vigilant about potential discrepancies that may arise due to discretization, even with such a small sampling time. Small discrepancies in system behavior or performance can still occur, especially in complex systems or under specific conditions. In this way, this and the next demonstration (Section 5.1) are useful for demonstration purposes of the continuous-time algorithm presented in this paper. Nevertheless, it is crucial to verify the validity of the discrete-time implementation through rigorous testing and comparison with the continuous-time algorithm to ensure its effectiveness and correctness.

The relative degree of the reference model must be the same as the nominal part of the plant, $G_0(s)$. Therefore, the system model for controller design disregards the dynamics of non-minimum-phase zero, aiming to reduce the complexity of the controller structure. In this sense, the controller has to deal with this zero as an unmodeled dynamic, which is an unmatched dynamic. As the relative degree of $W_m(s)$ increases, so does the quantity of controller parameters. As the developed controller is robust enough to deal with unmodeled dynamics, this simplification can be done during its design. Naturally, the resulting controller is evaluated on the complete system model. Therefore, the nominal part of the system is considered as

$$\begin{aligned} G(s) = \frac{1}{ s-1 }, \end{aligned}$$

(63)

which has a relative degree of one. Then, the reference model can be a first-order plant, chosen as

$$\begin{aligned} W_m(s) = \frac{3}{ s-3 }. \end{aligned}$$

(64)

When the relative degree of the reference model is one, there are no internal filters $\omega _1$ and $\omega _2$, and, consequently, the vector of gains is ${{\varvec{\theta }}}=[\ \theta _3 \ \theta _4 \ \theta _{SM}\ ]$.

The control problem is defining the convergence parameters $\Gamma$ and $\gamma$, as well as the initial gains $\theta _3(0)$, $\theta _4(0)$, and $\theta _{SM}(0)$. Although there are fewer parameters due to the adopted strategy, a bad choice of these parameters can make the closed-loop system response too slow or present unacceptable transient regime performance. Thus, the SCA is used to set these parameters, reducing the dependency on designer experience and saving time in this process.

The controller parametrization using SCA considers the same events as the simulation. The reference is a sinusoidal signal with an amplitude of 10 and a frequency of 0.1 Hz. When time reaches 100 s, the reference amplitude changes to 20. A parametric variation test is also performed to evaluate the robustness of the developed controller. When time reaches 50 s, the system parameter $\lambda$ is modified from 0.02 to 0.1, which is a relevant modification to the zeros and poles of the system. The aim of this event is to show how the controller deals with a matched dynamic, which is the parametric variation.

The other controller parameters are not optimized because they are similar to other direct adaptive controllers from literature. However, they can be easily included in the SCA routine to be determined by the algorithm. Naturally, the inclusion of the parameters impacts in the time spent in the optimization process. But, it runs offline, and therefore, could be optimized too with no additional requirements. In this work, the other controller parameters are: $\delta _0 = 0.7$, $\delta _1 = 1$, $m^2(0) = 5$, $M_0 = 15$, $\sigma _0 = 0.1$.

The SCA was run 10 times to verify its ability to optimize the developed controller. The used cost function in this optimizer is the mean of the absolute tracking error. We opt not to include any penalizations for overshoot or duration of transient regimes or violation of controller’s constraints. It can be done in a simple way, just adding some conditional at the end of the algorithm and summing a high value to the fitness if the condition of penalization is satisfied. However, we would like to show that just applying the simplest form of a heuristic optimization algorithm to the controller parametrization problem already provides satisfactory solutions. When the system is a real-world problem, it is possible to include hardware constraints as penalizations, such as the maximum control actuation, safety values to maintain the integrity of the hardware (e.g., current or voltage of an electrical system), duration of transient regimes, and maximum overshoot or undershoot. For the showcase discussed in this work, we just pass the search space to the algorithm, which has the minimum and maximum values for each parameter that SCA optimizes. Therefore, considering the outputs of SCA, ${\textbf{K}}^0 = [ ~ \Gamma ~~ \gamma ~~ \theta _3(0) ~~ \theta _4(0) ~~ \theta _{SM}(0) ~ ]$. Then, the lower search limit is $K_{inf} = [ ~ 1 ~~ 1 ~~ -10 ~~ -10 ~~ -10 ~ ]$, and the upper search limit is $K_{sup} = [ ~ 100 ~~ 100 ~~ 10 ~~ 10 ~~ 10 ~ ]$. It is important to provide a large space search for the SCA to avoid a biased solution. The SCA parameters are the number of search agents, which was set as 30, and the maximum number of iterations, which was configured as 1000. Table 1 shows the SCA outputs for the 10 optimizations performed along with the best fitness.

All solutions provided by SCA ensure high performance in the control of the unstable non-minimum-phase system. The most relevant benefit of using it is the absence of overshoot in the initial transient regime. In general, the initial transient regime of direct adaptive controllers presents some overshoot because the gains need to converge to a solution from a defined value by the designer. Here, the stochastic optimization algorithm evaluates a large set of candidate solutions and returns the set that minimizes the tracking error. Furthermore, no overshoot occurs when the reference amplitude changes or even when the parametric variation occurs. It indicates that all solutions are feasible, and the proposed systematic parametrization procedure is reliable to configure the developed adaptive controller.

As aforementioned, all solutions provided by SCA to parametrize the controller demonstrated high performance. Therefore, three error metrics are considered to decide what the best solution set is: mean absolute error (MAE), mean squared error (MSE), and root-mean-squared error (RMSE). Table 2 shows these metrics, where the best solution is highlighted in bold.

Table 2 Evaluated metrics obtained using SCA

The general performance obtained with all solutions can be considered equivalent. Note that MAE varies from 0.0163 to 0.0172 in the best and worst performances, respectively. However, the difference in absolute error is 0.0009, which is negligible. For MSE, the difference is even smaller (only 0.0006). On the other hand, RMSE varies from 0.0553 to 0.0603, which is also a small difference but more relevant than other metrics. (It varied 0.05 from the best to the worst solution.) Therefore, the solution elected as the best one is the one that minimizes the higher quantity of error metrics. In this sense, the fourth solution stands out.

Figure 2 shows the model reference output tracking. As can be seen, there is no overshoot in any transient regime. In fact, the SCA provides a satisfactory solution for this control problem since the transient regime duration is very short. Moreover, as the duration of the transient regime related to the parametric variation test and reference amplitude change are both short, it means that the convergence of the gains is fast, which indicates that $\Gamma$ and $\gamma$ were properly designed by SCA.

Fig. 2

Model reference output tracking using RMRAC-SM

Figure 3 presents the tracking error. From this figure, some interesting information is inferred. First, the tracking error during the initial transient regime is practically zero because the gains are set close to a perfect solution set, which would make the tracking error zero from the first instant. Naturally, a perfect parametrization is impossible in practice, even for a designer with decades of experience, because any real system suffers from the influence of unmodeled dynamics in the real world. Thus, the initial gains obtained provided satisfactory tracking error minimization. Second, there is a more relevant error at the beginning of each transient regime. It is natural because when the system is disturbed, the controller needs to adjust all gains to compensate for the new condition. In this instant, the controller must be robust to maintain closed-loop stability while maintaining the proper tracking task. As can be seen, the tracking errors in these transient regimes are small in comparison with the reference amplitude, which means that the controller acts fast and makes the tracking error converge to a residual value, which has the same magnitude as the chattering in steady state. In this showcase, these values are 1$\times 10^{-4}$, 1$\times 10^{-3}$, and 1$\times 10^{-3}$ for the first, second, and third steady regimes, respectively. Moreover, despite the control algorithm being in continuous-time, it was validated using a discretization time of 10kHz, as explained before and outlined in Remark 3. In this sense, some chattering resulting from the discretization process is still present. Additionally, as noted in [37], usually there is no significant observable chattering improvement for sampling times higher than 10 kHz, which helps to validate the presented results.

Fig. 3

Tracking error of RMRAC-SM

Figure 4 shows the control actions of the RMRAC and adaptive SMC.

Fig. 4

Control actions of RMRAC-SM

Notably, the effort of the RMRAC contribution is greater than that of adaptive SMC. In fact, the adaptive SMC acts more intensively during transient regimes. When the system reaches a steady state, it tends to reduce the actuation, which helps to reduce the chattering. Although the contribution of adaptive SMC is small in the total control action, it acts to compensate for matched and unmatched dynamics.

Figure 5 presents the convergence of the gains. As can be noted, the gains are continuously adapting thanks to the modified gradient algorithm used in the controller. However, as the gains are initialized properly, there are small changes during the overall test. The most relevant adjustments occur at the beginning of each transient regime. At a steady state, the gains are accommodated to maintain the system’s stability and performance.

Fig. 5

Adaptive gains of RMRAC-SM

Fig. 6

Model reference output tracking using RMRAC

5.1 Comparison to a robust model reference adaptive controller

This subsection presents a comparison of the SCA-based designed RMRAC-SM with a well-known RMRAC. The RMRAC structure is similar to the RMRAC-SM since both are developed from model reference adaptive control (MRAC) theory. The main difference between both structures is that RMRAC does not have the adaptive sliding mode contribution. In other words, the RMRAC structure uses (4) and (32) to (36), but $\varvec{\omega }$ is composed by

$$\begin{aligned} \varvec{\omega }=[\ {\varvec{\omega }_1}^{T}\ \ {\varvec{\omega }_2}^{T}\ \ y\ \ u\ \ ], \end{aligned}$$

(65)

where ${\varvec{\omega }_1}^{T}$ and ${\varvec{\omega }_2}^{T}$ are internal filters described by (6). Therefore, the adaptive gains are

$$\begin{aligned} \varvec{\theta }=[\ {\varvec{\theta }_1}^{T}\ \ {\varvec{\theta }_2}^{T}\ \ {\theta _3}\ \ {\theta _4} \ \ ]^{T}, \end{aligned}$$

(66)

and, consequently, the control law is

$$\begin{aligned} u=\frac{-{\varvec{\theta }_1}^{T}{\varvec{\omega }_1}-{\varvec{\theta }_2}^{T}{\varvec{\omega }_2}-{\theta _3}y- r}{{\theta _4}}. \end{aligned}$$

(67)

More information regarding the RMRAC structure can be found in [69, 71].

The simulation consists of the same steps discussed previously. The RMRAC parameters were also obtained using the SCA, which results in $\Gamma =$ 23.8372, $\gamma =$ 99.966382, $\theta _3(0)=$ $-$0.213507300493765, and $\theta _4(0)=$ $-$1.35238782031892. The other parameters were maintained the same used on RMRAC-SM, which are $\delta _0 = 0.7$, $\delta _1 = 1$, $m^2(0) = 5$, $M_0 = 15$, $\sigma _0 = 0.1$. Figure 6 shows the model reference output tracking using RMRAC. At first look, RMRAC is able to regulate the system properly. In fact, it can keep the system stable and forces the system output to track the reference model output closely. However, it has a persistent tracking error that does not tend to zero in the steady state throughout the simulation. This is more clearly depicted in the tracking error graph.

Figure 7 presents the tracking error from RMRAC structure. Here, it is clear that the adaptive sliding mode term present in the RMRAC structure makes the RMRAC-SM superior to RMRAC in terms of regulation dynamics. As can be seen, there is a persistent error during the overall simulation. It is more expressive when there are reference changes and parametric variations. Furthermore, this tracking error does not converge to a small residual value during the first steady state. A similar behavior is observed after reference changes at 50 s. The third transient regime is related to parametric variation, and it starts at 100 s. In this case, the controller can reduce the tracking error, but not eliminate it. The error metrics using RMRAC are MAE = 0.03729, MSE = 0.0042, and RMSE = 0.0649. These values are all greater than those obtained with RMRAC-SM, which are MAE = 0.0163, MSE = 0.0030, and RMSE = 0.0553. Therefore, it can be affirmed that RMRAC-SM can provide a reduction of 56.28%, 28.57%, and 14.79% for MAE, MSE, and RMSE, respectively. Thus, the RMRAC-SM provides a satisfactory enhancement in the controller’s performance for this specific scenario.

Fig. 7

Tracking error of RMRAC

Figure 8 shows the control action of RMRAC.

Fig. 8

Control action of RMRAC

In general, the control action is very similar to what was observed using RMRAC-SM. Naturally, there are more efforts when the system suffers from matched dynamics because it changes completely the location of the poles and zeros. However, no relevant differences are observed in this dynamic.

Figure 9 presents the convergence of the adaptive gains for the RMRAC. Differently from the RMRAC-SM gains, the RMRAC gains are very stressed to control this system, even optimized with SCA. After some instants in the transients, the gains were slowly changing, which explains the persistent tracking error observed in the simulation. The better dynamics response from the proposed controller is expected because the adaptive sliding mode term was incorporated into the RMRAC structure with the aim of enhancing the controller robustness during transients.

Fig. 9

Adaptive gains of RMRAC

Hence, these results validate one of the controller’s primary objectives, demonstrating satisfactory improvements in the transient regimes and robustness against matched and unmatched dynamics.

6 Processor-in-the-loop experiment: application of the controller in a real-world engineering problem

This section presents the application of the presented controller in the current regulation of a three-phase grid-tied power inverter with an LCL filter, which is a plant common to renewable energy systems. This experiment consists of high-fidelity simulations in processor-in-the-loop software. Processor-in-the-loop simulations consist in embedding the code in the microcontroller language and emulating the system elements with highly reliable virtual system [72]. Here, it was used the PSIM software, and the controller code runs in a DSP (Digital Signal Processor), a TMS320F28335 Delfino microcontroller from Texas Instruments. Furthermore, a Kalman filter-based phase-locked loop to synchronize the inverter and the electrical grid [73], as well as the space vector modulation [74], used to synthesize the control actions, are also implemented to make the experiment equivalent to the experimental setup. Figure 10 shows the circuit of the grid-tied three-phase inverter with an LCL filter, where the filter elements are inverter-side inductor $L_c$, capacitor $C_f$, and grid-side inductor $L_{g}$, whose inductors have parasitic resistances represented by $r_c$ and $r_g$ for $L_c$ and $L_g$, respectively. The electrical grid is denoted by the voltage source $v_g$, the inductance $L_{g2}$ and the parasitic resistance $r_{g2}$. Furthermore, $i_{Lg2}$ is the grid-injected current, which is regulated by the developed control strategy. Moreover, $i_{Lc}$, $i_{Cf}$, and $i_{Lg}$ are the inverter-side, capacitor branch, and grid-side currents. Furthermore, $V_d(ab)$ and $V_d(bc)$ are voltage sensors, $i_{ca}$, $i_{cb}$, and $i_{cc}$ are the current sensors at inverter-side, and $i_{ga}$, $i_{gb}$, and $i_{gc}$ are the current sensors at grid-side. In addition, $S_1$ to $S_6$ indicate the inverter switches that synthesizes the control actions, “EN” is trigger that enables the inverter connection to the grid, and “Par. var.” represents the switch that forces a parametric variation in the grid-side impedance.

Fig. 10

Schematic of the grid-tied three-phase inverter with an LCL filter at PSIM software for the processor-in-the-loop experiment

As grid voltage is inaccessible in practice, it is measured at the point of common coupling (PCC), between the inverter and the grid. According to [75], the LCL transfer function is given by

$$\begin{aligned} G(s)=\dfrac{i_{Lg}(s)}{{\bar{v}}_{ab}(s)}=\frac{1}{a_1s^3+a_2s^2+a_3s+a_4}, \end{aligned}$$

(68)

where ${\bar{v}}_{ab}(s)$ is the voltage synthesized by the inverter, $a_1=L_gL_cC$, $a_2=(R_gL_c+R_cL_g)C$, $a_3=L_c+L_g+R_gR_cC$, and $a_4=R_g+R_c$.

Developing a control strategy for a tightly integrated system like a grid-connected inverter with an LCL filter, described in the abc coordinate system, presents a significant challenge [76, 77]. This challenge is amplified when the system faces uncertainties and variations in parameters. The utilization of the Clarke transform in the abc model serves to simplify control design complexity by converting the three-phase interconnected model into two equivalent independent single-phase models in $\alpha \beta 0$ coordinates. Besides, the LCL filter is a third-order transfer function with a relative degree equal to three. Due to this, a direct adaptive controller requires a reference model with a relative degree equal to three, which is a high-order system. However, the LCL filter can be approximated to a first-order transfer function for controller design if the control algorithm is robust enough to deal with neglected dynamics while maintaining the global stability of the closed-loop system in the face of disturbance rejection, parametric variations, and load changes [78].

The elements of the LCL filter were designed following the steps of [79, 80], which results in $L_c=1$ mH, $C_f=62\ \mu$F, and $L_g=0.3$ mH, considering $r_c=r_g=50$ m${\Omega }$ for a power inverter with $P_{in} = 2.245$ kW$_{pk}$ per phase, DC bus voltage set as 500 V, and an electrical grid with 127 V. A simplification of the LCL filter model is adopted for controller design, where the capacitor dynamics are disregarded, reducing the LCL filter model to a first-order transfer function, as proposed in [19], only for the purpose of designing the controller. In this sense, this simplification allows the choice of a first-order reference model, but it requires a controller robust enough to deal with neglected dynamics in practice, because the capacitor dynamics are relevant. Thus, the neglected capacitor dynamic is considered as an unmodeled dynamic for the controller. The resulting model is

$$\begin{aligned} G_{0}(s)= \dfrac{1}{(L_c+L_g)s+R_c+R_g}. \end{aligned}$$

(69)

The LCL filter model considering the system parameters is

$$\begin{aligned} G_0(s)= \frac{769.257}{s+76.9257} \end{aligned}$$

(70)

As electrical grid dynamics are ignored during LCL modeling to obtain the $G_0(s)$, a periodic disturbance rejection term is integrated into the control law, as detailed in [81]. Therefore, the control action for disturbance rejection is given by

$$\begin{aligned} u_D=-\dfrac{\theta _c}{\theta _1}V_c-\dfrac{\theta _s}{\theta _1}V_s, \end{aligned}$$

(71)

where $\theta _c$ and $\theta _s$ are adaptive gains that update their values in response to the phase ($V_s$) and quadrature ($V_c$) components of the exogenous disturbance (electrical grid voltage), respectively. So, the ${\varvec{\omega }}$ and ${\varvec{\theta }}$ vectors now contain 2 additional parameters. Therefore, the complete control action is given by the sum of $u_d$ and (9). It is important to note that $u_D$ is not considered in stability analysis because the grid dynamics are periodic, stable, and limited, which is rejected by estimation using the PCC voltages [36].

The reference model, whose controller aims to track output, is

$$\begin{aligned} W_m(s) = \frac{8300}{s+8300}. \end{aligned}$$

(72)

The discretization of the plant and reference model are performed using the ZOH, considering a sample time, $T_s$, equal to 198 $\mu$s. When discretized, the plant presents a non-minimum-phase zero, which also requires robustness from the controller.

The parameters for the controller are set as follows: $\Gamma =200$, $\gamma =1000$, $\sigma _0=0.1$, $M_0=15$, $\bar{m}^{2}=4$, $\delta _0=0.7$, $\delta _1=1$. The initial controller gains for the $\alpha$ and $\beta$ coordinates were established as $\theta {(0)}=[-1 \quad 0 \quad 0 \quad 0 \quad 0 \quad 0]$. In pursuit of enhancing the performance during the initial transient period, the gains obtained at the end of the first simulation were adopted as the starting gains for the subsequent simulation. These gains are $\varvec{\theta }_{ \alpha }(0)=\left[ -0.73 \hspace{0.13cm} -0.06 \hspace{0.13cm} -0.0035 \hspace{0.13cm} 0.16 \hspace{0.13cm} 0.07 \right]$ and $\varvec{\theta }_ {\beta }(0)=\left[ -0.72 \hspace{0.15cm} -0.87 \hspace{0.15cm} -0.021 \hspace{0.15cm} 0.0093 \hspace{0.15cm} 0.07 \hspace{0.15cm} 0.92 \right]$. Naturally, this controller can be optimized with SCA as shown previously. However, this experiment aims to show the feasibility of the RMRAC-SM applied to a complex real-world system.

The processor-in-the-loop experiment consists of the following steps:

• At $t=0$ s, the synchronization of the inverter with the grid is initialized;

• At $t=0.05$s, the inverter starts the operation with active power reference current;

• At $t=0.15$ s, a parametric variation is forced into the system, varying the grid-side resistance $r_{g2}$ from 50 $m\Omega$ to 100 m$\Omega$, and the grid-side inductance $L_{g2}$ from 0.3 mH to 1.3 mH;

• The reference signal is maintained as a sinusoidal waveform with an amplitude of 20 A, a frequency of 60 Hz, and a phase angle of $0^{\circ }$ until 0.25 s;

• At $t=0.25$ s, an active power step changes the current reference from 20 A to 25 A;

• At 0.35 s, the simulation ends.

Figure 11 presents an overview of the current reference tracking. As can be seen, the grid-injected currents ($y_{\alpha }$ and $y_{\beta }$) are very close to their references ($y_{m\alpha }$ and $y_{m\beta }$, respectively). Furthermore, the current tracking errors are small in both coordinates at each transient regime because the control system is capable of ensuring fast convergence and stability during all the experiment.

Fig. 11

Processor-in-the-loop results: reference model and plant outputs currents in $\alpha$ and $\beta$ coordinates (overall experiment)

Figure 12 shows the initial transient regime.

Fig. 12

Processor-in-the-loop results: reference model and plant outputs currents in $\alpha$ and $\beta$ coordinates (initial transient regime)

Notably, it takes less than one grid cycle, which is satisfactory for this kind of application. A fast response is desired in renewable generation systems because these systems aim for maximum power generation continuously. About the performance, the simulation reveals a more pronounced variation in the $\beta$ coordinates than in the $\alpha$. The maximum overshoot in the initial transient is 28.09A in $\beta$ coordinate. Although there is an overshoot in the system startup, it does not surpass 35 A, which is the maximum current supported by considered inverter. It is highlighted that the current observed in both coordinates is in the form of short steps due to space vector modulation, which is required in a real system to implement the controller.

Figure 13 presents the control system response to parametric variation. There is a brief transient during the adaptive gains’ settling phase. However, the system quickly converges due to the controller’s robustness, ensuring that the plant’s output follows the reference model’s output. Here, a small overshoot/undershoot occurs, with the amplitude of 2.38 A and 2.90 A in $\alpha$ and $\beta$ coordinates, respectively. Again, it is not a concern, and both currents are corrected fast, converging to the steady state around 1 grid cycle.

Fig. 13

Processor-in-the-loop results: reference model and plant outputs currents in $\alpha$ and $\beta$ coordinates (parametric variation response)

Fig. 14

Processor-in-the-loop results: reference model and plant outputs currents in $\alpha$ and $\beta$ coordinates (power step variation)

Additionally, a load variation is performed in the system, changing the reference from $20A_{pk}$ to $25A_{pk}$ at $t=0.25s$. Figure 14 shows this event. As can be observed, the controller exhibits low or almost no transient response to this type of condition. If compared to other transient regimes, it is even reduced and the overshoot is yet smaller, whose amplitudes are 1.10 A and 1.56 A for $\alpha$ and $\beta$ coordinates, respectively. Figure 15 presents the system behavior in steady state at maximum current amplitude tracking. This figure shows that the system remains stable after all the imposed disturbances, showcasing the adaptive control algorithm’s effectiveness.

Fig. 15

Processor-in-the-loop results: reference model and plant outputs currents in $\alpha$ and $\beta$ coordinates (steady-state response)

Figure 16 depicts the tracking errors in $\alpha$ and $\beta$ coordinates. This figure corroborates the previous discussion. Here, it is important to highlight that a persistent error in each steady state is related to the modulation technique used to synthesize the control action. It happens in all pulse width modulated control strategies. Thus, it can be affirmed that the controller exhibits visibly close current reference tracking, making the errors converge to small values in the steady state. In addition, there is a transient period due to inverter synchronization with the grid at the beginning of the experiment. During the first 0.05 s, the inverter is not grid-tied, and, consequently, the controller is not actuating. It is necessary for the Kalman filter to estimate the grid voltages. However, after the connection, a strong disturbance is applied instantaneously, making a greater initial current tracking error. Despite that, the controller compensates for disturbance rejection quickly, maintaining the global stability of the closed-loop system.

Fig. 16

Processor-in-the-loop results: tracking errors in $\alpha$ and $\beta$ coordinates

Figure 17 shows the control action required to maintain the current adequately regulated while ensuring the global stability of the system. As can be seen, the voltage synthesized by the inverter is far from the DC bus voltage, making it securely implementable. Moreover, no excessive voltage is required when the system is disturbed. Thus, it can be affirmed that the controller is feasible to deal with matched and unmatched dynamics in complex real-world systems.

Fig. 17

Processor-in-the-loop results: $V_{CC}$ and control actions

Figure 18 presents the sliding mode control action. As can be observed, there is a continuous adaptation of the SMC term for the controller of this system differently from the simulation. It is natural since the space vector modulation imposes a time delay to synthesize the control action, which is the reason for the tracking error not achieving zero in the steady state. In this sense, the adaptive SMC control action is always acting, with a more expressive action during the transient regimes. Moreover, it is possible to observe a squared shape-based waveform, originated from the sgn function present in $u_{SM}$ (9).

Fig. 18

Processor-in-the-loop results: sliding mode control action in $\alpha$ and $\beta$ coordinates

Figures 19 and 20 present the adaptation gains over the entire experimental test. In these figures, it is notable that there are slight fluctuations in transient behavior because the gradient algorithm is changing the values of the gains. However, these modifications are smooth, which do not impact relevantly on the control actions. After each transient regime, the gains are maintained at nearly constant values until the next system disturbance.

Fig. 19

Processor-in-the-loop results: adaptive gains in $\alpha$ coordinate

Fig. 20

Processor-in-the-loop results: adaptive gains in $\beta$ coordinate

Fig. 21

Processor-in-the-loop results: three-phase currents

Finally, Fig. 21 shows the three-phase currents injected into the grid for the overall processor-in-the-loop experiment. As expected, these currents achieve the desired values (20 A and next 25 A) because the $\alpha \beta$ currents are well controlled. The transient regimes in three-phase are very similar to those discussed for $\alpha \beta$ coordinates for all events (initial transient regime, parametric variation transient regime and power step transient regime). It is natural, since the three-phase currents are obtained by simply applying the inverse Clarke transformation to the $\alpha \beta$ currents. In this sense, there is no need to discuss the behavior of the grid-injected currents again.

Therefore, this section corroborates the feasibility of using the described controller in a complex real-world engineering control problem through a processor-in-the-loop experiment, considering all implementation aspects necessary to describe a high-fidelity simulation.

7 Conclusion

This paper presented the stability analysis of a continuous-time robust model reference adaptive sliding mode controller using the Lyapunov criterion. The presented controller is robust in relation to unmodeled dynamics, which can be additive or multiplicative. Due to this, the controller can be applied to non-minimum-phase plants if the non-minimum-phase zeros are treated as unmodeled dynamics in the controller design. Furthermore, through the presented analysis, it can be verified that in the presence of unmodeled dynamics, the tracking error converges to a small residual value in order to mitigate chattering, which is reduced by the adaptive algorithm incorporated into the controller. From this analysis, controller design constraints were also obtained, and the parametrization was carried out using a stochastic optimization algorithm known as SCA. The simulation results of the continuous-time RMRAC-SM applied to an unstable non-minimum-phase system validate the robustness of the control strategy, with the SCA providing satisfactory parametrization across all tests. Consequently, the SCA can be confidently employed to automate the controller parametrization process, thereby saving time and ensuring optimized gains for the controller. Furthermore, a comparison of this controller with a similar adaptive control structure, an RMRAC, highlighted the superiority of the presented controller. Notably, it significantly reduced error metrics by 56.28%, 28.57%, and 14.79% for MAE, MSE, and RMSE, respectively. Additionally, processor-in-the-loop results of a real-world control engineering problem were included, confirming the feasibility and high robustness of the presented controller. These results demonstrate its ability to effectively manage complex systems with both matched and unmatched dynamics.

Appendix A - Lemma 2

This appendix presents Lemma 2, which contains useful results for the stability analysis of the continuous-time RMRAC-SM.

Lemma 2

The value of $2\sigma \varvec{\phi } \varvec{\theta }$ is greater or, at maximum, equal to zero.

Proof

Let

$$\begin{aligned} {\left\| {{\varvec{\theta } ^*}} \right\| ^2}{} & {} = {\varvec{\theta } ^*}^T{\varvec{\theta } ^*} = {(\;\varvec{\theta } - \varvec{\phi } )^T}(\varvec{\theta } - \varvec{\phi } )\; \nonumber \\ {}{} & {} = \;{\varvec{\theta } ^T}\varvec{\theta } - 2{\varvec{\phi } ^T}\varvec{\theta } + {\varvec{\phi } ^T}\varvec{\phi }, \end{aligned}$$

(73)

or yet,

$$\begin{aligned} 2{\varvec{\phi } ^T}\varvec{\theta } = \;\;{\left\| \varvec{\theta } \right\| ^2}\; + \;{\left\| \varvec{\phi } \right\| ^2}\;\; - \;{\left\| {{\varvec{\theta } ^*}} \right\| ^2}. \end{aligned}$$

(74)

From (74), it is written as the following inequality, $2{\varvec{\phi } ^T}\varvec{\theta } \ge {\left\| \varvec{\theta } \right\| ^2} - {\left\| {{\varvec{\theta } ^*}} \right\| ^2}$, which can be expressed as

$$\begin{aligned} 2\sigma {\varvec{\phi } ^T}\varvec{\theta } \ge \sigma \left( {{{\left\| \varvec{\theta } \right\| }^{2}} - {{\left\| {{\varvec{\theta } {^*}}} \right\| }^{2}}} \right) . \end{aligned}$$

(75)

From (36) and (75), it can be concluded

$$\begin{aligned} \left\{ \begin{matrix} 2\sigma {{\bar{\varvec{\phi }} }^T}\bar{\varvec{\theta }}> 0&{}\mathrm{{ if }} &{}\left\| {\bar{\varvec{\theta }} } \right\| \ge 2{M_0}\\ 2\sigma {{\bar{\varvec{\phi }} }^T}\bar{\varvec{\theta }} > 0&{}\mathrm{{ if }}&{}{M_0}\mathrm{{< }}\left\| {\bar{\varvec{\theta }} } \right\| < 2{M_0}.\\ 2\sigma {{\bar{\varvec{\phi }} }^T}\bar{\varvec{\theta }} = 0&{}\mathrm{{ if }}&{}\left\| {\bar{\varvec{\theta }} } \right\| \le {M_0} \end{matrix} \right. \end{aligned}$$

(76)

Therefore, $2\sigma {\varvec{\phi } ^T}\varvec{\theta } \ge 0$.

$\square$