Robust Incremental Nonlinear Dynamic Inversion Controller of Hexapod Flight Simulator Motion System

Abstract

This paper presents a motion control strategy for a hexapod flight simulator based on a novel incremental nonlinear dynamics inversion methodology. By using the feedback of the motion base acceleration measurement in joint space, this strategy is capable of achieving accurate system linearisation in existence of model inaccuracies which will significantly degrade the performance of a typical inverse dynamics approach. The proposed control scheme is not sensitive to model and parametric mismatch, hence is robust to model uncertainties. This feature is very helpful for a nonlinear simulator motion system without accurate model, while high performance is generally required. The robustness feature of this strategy allows the use of simplified model and state set-points, instead of full model and state feedback, to invert the nonlinear dynamics, which will reduce the computation burden. The performance and robustness of the proposed scheme is validated by numerical simulations.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

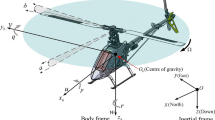
The Stewart platforms, also known as hexapod systems, are most commonly used as motion bases for modern flight simulators. In this configuration, a moving upper platform is driven by six linear actuators connected to the stationary base to provide motion in 6 degree-of-freedom(DOF), as shown in Fig. 1. Commonly an Universal-Prismatic-Spherical(UPS) structure is designed in such systems, in which the lower and upper platforms are connected to the legs through passive universal joints and spherical joints and the two parts of each leg are connected by a prismatic joint where electrical or hydraulic actuation force is acted on. The parallel structure provide higher rigidity and accuracy compared with its serial robot counterparts. A typical example of such a system is the SIMONA research simulator (SRS) in Delft University of Technology as shown in Fig. 1 [18].

Fig. 1

A Stewart platform based motion system SRS at TU Delft and it’s schematic drawing [6]

The main goal of the flight simulator motion systems is to track the reference motion calculated by aircraft aerodynamics model and pilot input as accurate as possible. Different from industrial applications, the pilot-in-the-loop flight simulators require high performance motion systems to enhance the fidelity of simulation flight. Typical PID controller is hardly eligible for the high performance requirement due to the highly nonlinear dynamics of the parallel manipulator. Thus more advanced control techniques have been studied intensively [5].

Nonlinear dynamics inversion [9, 13] (NDI) is capable of exactly linearise the nonlinear dynamics and is also referred to as computed torque control [12] in the field of robot control. However, it’s well known that NDI is seriously dependent on the accuracy of the model that for a complex flight simulator system, any model parametric uncertainty, unmodelled dynamics and disturbances such as joint friction will significantly degrade the performance [1]. Thus NDI is rarely used directly in parallel robot motion control. Adaptive control is a possible technique to deal with parametric uncertainties and has been proposed for similar applications [4, 11, 12]. Nevertheless, the computational burden of adaption motion controller based on a well modeled system is significant that real-time application is hard to achieve. Robust control which is also capable of overcoming model uncertainties, is studied by only a few papers addressing the studied control system [1, 7, 8] and a sliding mode methodology is commonly used that may lead to chattering problem.

The Incremental Nonlinear Dynamic Inversion (INDI) is a sensor-based control technique for nonlinear systems which is much more robust than NDI [14, 15]. By computing the incremental input commands using the acceleration measurement instead of calculating the total inputs, the controller need less model information and is not sensitive to model mismatches while proving a high performance. These features are useful for a parallel flight simulator which suffers from model uncertainties or even load-varying mechanics due to change of pilots.

In this paper the application of INDI methodology to a 6-DOF hexapod flight simulator outer-loop motion control is presented, parametric uncertainties and unmodelled dynamics are introduced to model dynamics to simplify the controller design and reduce computational burden. This is the first time that INDI is proved to be suitable for a parallel robot motion control, and the fact that an important assumption, i.e. time scale separation principle, holds for the dynamics of such systems. This work hires a detailed flight simulator model with consideration of actuator inertial and joint friction based on SIMONA Research Simulator in Delft University of Technology. The actuator dynamics are not considered in order to focus on the INDI controller performance on the parallel robotic dynamics. In future work with practical implementation of proposed control, the influences of actuator dynamics will be included and considered.

This paper is organized as follows. In Sect. 2, the kinematics and dynamics of the 6-DOF hexapod motion system are briefly derived. Section 3 presents the motion control system design based on INDI technique in detail and simulation results are given in Sect. 4. The main conclusions are summarized in Sect. 5.

2 System Kinematics and Dynamics

A schematic drawing of a hexapod motion system is shown in Fig. 1. The Newton–Euler approach [2, 3] is used to derive the system dynamic equations in Cartesian space. The platform position and velocity are defined as

$$\begin{aligned} \mathbf sx&=\left[ \mathbf c ^{T}, \varvec{\varPhi }^{T}\right] ^{T} \nonumber \\ \dot{\mathbf{x }}&=\left[ \dot{\mathbf{c }}^{T}, \varvec{\omega }_{p}^{T}\right] ^{T} \end{aligned}$$

(1)

where $\mathbf c$ denotes the translation vector of the upper platform in inertial frame $E_b$, $\varvec{\varPhi }$ is the Euler angles between the body fixed frame$E_a$ and $E_b$ and $\varvec{\omega }_p$ is the angular velocity of the upper platform.

Different from serial manipulators, the inverse kinematics of parallel robots are very simple, which can be given by calculating the leg vector $\mathbf S$ in Fig. 1 as

$$\begin{aligned} \begin{aligned} \mathbf S&=\mathbf c +T_{ba}{} \mathbf p -\mathbf b \\&=\mathbf c +\mathbf q _p-\mathbf b \end{aligned} \end{aligned}$$

(2)

where $\mathbf p$ and $\mathbf q _p$ are upper universal joint locations in reference frames $E_a$ and $E_b$ respectively, and $T_{ba}$ the rotational matrix between them.

In terms of the platform dynamics, the dynamics of a single leg is derived in literature [3] by combining Euler’s equation of the entire leg and Newton’s equation of the moving rod as

$$\begin{aligned} -\mathbf F _{s}=\mathbf Q \ddot{\mathbf{c }}-\mathbf Q \tilde{\mathbf{q }}_p\dot{\varvec{\omega }}_{p}+\mathbf V -F\mathbf s \end{aligned}$$

(3)

where $\mathbf F _s$ is the force vector acting on the upper universal joint, F is the actuation force generated on the prismatic joint, $\mathbf s$ is the unit vector to $\mathbf S$, and $\mathbf Q$ and $\mathbf V$ are matrix depending on leg inertial and dynamics properties.

Similarly, the dynamics of the upper moving platform is described by writing the Newton and Euler’s equation as

$$\begin{aligned} \sum \limits _{n=1}^{6}\left( \mathbf F _{s}\right) _{i}+M_{p}{} \mathbf g =M_{p}{} \mathbf a _{p} \end{aligned}$$

(4)

and

$$\begin{aligned} \sum \limits _{n=1}^{6}\left( \mathbf q _{p}\times \mathbf F _{s}\right) _{i}+M_{p}{} \mathbf R \times \mathbf g =M_{p}{} \mathbf R \times \mathbf a _{p}+\mathbf I _{p}\dot{\varvec{\omega }}_{p}+\varvec{\omega }_{p}\times \mathbf I _{p}\varvec{\omega }_{p} \end{aligned}$$

(5)

Combining Eqs. 3, 4 and 5, the closed form of Stewart platform dynamic equation is obtained as [3, 6]

$$\begin{aligned} \mathbf M \left( \mathbf{sx }\right) \ddot{\mathbf{x }}+\varvec{\eta }\left( \dot{\mathbf{x }},\mathbf{sx }\right) =\mathbf H \left( \mathbf{sx }\right) \mathbf F \end{aligned}$$

(6)

where

$$ \mathbf M =\left[ \begin{array}{cc} M\mathbf E _3 &{} -M\tilde{\mathbf{R }} \\ M\tilde{\mathbf{R }} &{} \mathbf I _{p}+M\left( R^2\mathbf E _{3}-\mathbf R {} \mathbf R ^T\right) \end{array}\right] +\sum \limits _{n=1}^{6}\left[ \begin{array}{cc} \mathbf Q _{i} &{} -\mathbf Q _{i}\tilde{\mathbf{q }}_{i} \\ \tilde{\mathbf{q }}_{i}{} \mathbf Q _{i} &{} -\tilde{\mathbf{q }}_{i}{} \mathbf Q _{i}\tilde{\mathbf{q }}_{i} \end{array}\right] $$

$$ \varvec{\eta }=\left[ \begin{array}{cc} M\lbrace \varvec{\omega }_{p}\times \left( \varvec{\omega }_{p}\times \mathbf R \right) -\mathbf g \rbrace \\ \varvec{\omega }_{p}\times \mathbf I _{p} +M\mathbf R \times \lbrace \left( \varvec{\omega }_{p}\cdot \mathbf R \right) \varvec{\omega }_{p}-\mathbf g \rbrace \end{array}\right] +\sum \limits _{n=1}^{6}\left[ \begin{array}{cc} \mathbf V _{i} \\ \mathbf q _{i}\times \mathbf V _{i} \end{array}\right] $$

$\mathbf F$ is the actuation forces of all actuators

$$ \mathbf F =\left[ F_{1}\quad F_{2}\quad F_{3}\quad F_{4}\quad F_{5}\quad F_{6}\right] $$

and $\mathbf H$ is

$$ \mathbf H = \left[ \begin{array}{cccccc} \mathbf s _1 &{} \mathbf s _2 &{} \mathbf s _3 &{} \mathbf s _4 &{} \mathbf s _5 &{} \mathbf s _6 \\ \mathbf q _{p1}\times \mathbf s _1 &{} \mathbf q _{p2}\times \mathbf s _2 &{} \mathbf q _{p3}\times \mathbf s _3 &{} \mathbf q _{p4}\times \mathbf s _4 &{} \mathbf q _{p5}\times \mathbf s _5 &{} \mathbf q _{p6}\times \mathbf s _6 \end{array}\right] $$

It is now clear that matrix $\mathbf H$ is actually the transpose matrix [16] of the Jacobian matrix relating leg length velocity $\dot{\mathbf{L }}$ with platform velocity $\dot{\mathbf{x }}$ that

$$\begin{aligned} \dot{\mathbf{L }}=\mathbf J _{l,x}\dot{\mathbf{x }}=\mathbf H ^T\dot{\mathbf{x }} \end{aligned}$$

(7)

Take time derivative of Eq. 7 we have

$$\begin{aligned} \ddot{\mathbf{L }}=\mathbf{H }^T\ddot{\mathbf{x }}+\dot{\mathbf{H }}^T\dot{\mathbf{x }}=\mathbf H ^T\ddot{\mathbf{x }}+\mathbf{U }(\mathbf{sx },{\dot{\mathbf{x }}}) \end{aligned}$$

(8)

Thus

$$\begin{aligned} \ddot{\mathbf{x }}=\mathbf H ^{-T}[\ddot{\mathbf{L }}-\mathbf U {(\dot{\mathbf{x }},\mathbf{sx })}] \end{aligned}$$

(9)

Substituting Eq. 9 into Eq. 6 one gets

$$\begin{aligned} \ddot{\mathbf{L }}=\mathbf H ^{T}{} \mathbf M ^{-1}{} \mathbf H {} \mathbf F -\mathbf H ^{T}{} \mathbf M ^{-1}\varvec{\eta }{({\dot{\mathbf{x }},\mathbf{sx }})}+\mathbf U {(\dot{\mathbf{x }},\mathbf{sx })} \end{aligned}$$

(10)

At this point we have the dynamic equations of Stewart platform both in operation space as given in Eq. 6 and partly in joint space with Eq. 10. For a motion control system, the actuation forces $\mathbf {F}$ are the system inputs. The matrix on the right hand side of Eq. 10 still depend on operation space states $\mathbf {sx}$ and $\dot{\mathbf {x}}$ and the cumbersome forward kinematics of parallel robots are required in a model based feedback control approach like NDI. However, it will be shown in the following chapters that this problem is inherently solved with INDI approach, thus Eq. 10 should be enough for INDI based controller design in joint space.

3 Motion System Controller Design

The application of INDI strategy on a hexapod flight simulator is previously mentioned in [5] by the author. The basic idea is to calculate the required incremental control inputs at the given moment to achieve a linearized relation. To do this, consider system dynamic equation Eq. 10, a first-order Taylor series estimation of the right hand side is given by

$$\begin{aligned} \begin{aligned} \ddot{\mathbf{L }}&=\left( \mathbf H ^{T}{} \mathbf M ^{-1}{} \mathbf H \right) _\mathbf{sx _0}{} \mathbf F _0-\left( \mathbf H ^{T}{} \mathbf M ^{-1}\right) _\mathbf{sx _0}\varvec{\eta }\left( \dot{\mathbf{x }}_0,\mathbf{sx }_0\right) +\mathbf U \left( \dot{\mathbf{x }}_0,\mathbf{sx }_0\right) \\&+\left( \mathbf H ^{T}{} \mathbf M ^{-1}{} \mathbf H \right) _\mathbf{sx _0}\left( \mathbf F -\mathbf F _0\right) \\&+\frac{\partial }{\partial \dot{\mathbf{x }}}\left[ -\mathbf H ^{T}{} \mathbf M ^{-1}\varvec{\eta }\left( \dot{\mathbf{x }},\mathbf{sx }\right) +\mathbf U \left( \dot{\mathbf{x }},\mathbf{sx }\right) \right] _{\dot{\mathbf{x }}_0}\left( \dot{\mathbf{x }}-\dot{\mathbf{x }}_0\right) \\&+\frac{\partial }{\partial \mathbf{sx }}\left[ \mathbf H ^{T}{} \mathbf M ^{-1}{} \mathbf H {} \mathbf F -\mathbf H ^{T}{} \mathbf M ^{-1}\varvec{\eta }\left( \dot{\mathbf{x },\mathbf{sx }}\right) +\mathbf U \left( \dot{\mathbf{x },\mathbf{sx }}\right) \right] _\mathbf{sx _0}\left( \mathbf{sx -\mathbf sx }_0\right) \end{aligned} \end{aligned}$$

(11)

where subscribe 0 denotes the time point around which the Taylor series expansion is taken.

For a nonlinear system, the first-order estimation is accurate enough within a very small time increment. The first terms on the right hand side of the equation is actually $\ddot{\mathbf{L }}_0$, i.e.

$$\begin{aligned} \ddot{\mathbf{L }}_0=\left( \mathbf H ^{T}{} \mathbf M ^{-1}{} \mathbf H \right) _\mathbf{sx _0}{} \mathbf F _0-\left( \mathbf H ^{T}{} \mathbf M ^{-1}\right) _\mathbf{sx _0}\varvec{\eta }\left( \dot{\mathbf{x }}_0,\mathbf{sx _0}\right) +\mathbf U \left( \dot{\mathbf{x }}_0,\mathbf{sx _0}\right) \end{aligned}$$

(12)

Which is leg length acceleration which can be obtained by sensor measurement. In case of SIMONA flight simulator motion system, leg length are measured by Temposonics sensors, thus the acceleration information should be obtained by numerical differentiation. The INDI based controller is sensitive to sensor measurement, thus is is also considered a sensor-based approach.

Now consider the other terms in Eq. 11. The last two terms are considered much smaller than the second term according to the time scale separation principle [14, 15, 17]. This is explained as the change of actuation forces $\delta \mathbf F$ has a direct effect on the system acceleration change, which is represented by the left hand side of Eq. 11. The system velocity only change by integrating the system acceleration and the position change is even integrated by the velocity. Thus when the integration sample time is very small, these two terms are also small while the input change can be significantly large. This indicates that the dynamics of system input is faster than system velocity and position. It is noted that this assumption only holds with very small sample time and very fast actuator dynamics. According to the aforementioned analysis, Eq. 11 is finally simplified as

$$\begin{aligned} \ddot{\mathbf{L }}=\ddot{\mathbf{L }}_0+\left( \mathbf H ^{T}{} \mathbf M ^{-1}{} \mathbf H \right) _\mathbf{sx _0}\left( \mathbf F -\mathbf F _0\right) \end{aligned}$$

(13)

Equation 13 is the incremental form of the system dynamic equation given by Eq. 10, which is actually a linear approximation around system states in zero time for a small time increment. By comparing these two equations we can see that nonlinear terms, $\mathbf U$ and $\varvec{\eta }$ which consists of Coriolis/centripetal effects and gravity, disappeared from the original equation. This indicates that the INDI controller designed based on the incremental form system dynamics is not dependent on that part of the model. However, the dynamics of the neglected part of the model is still compensated by INDI since the leg length acceleration measurement already contain those information. Thus it is already clear now that INDI is not sensitive to model and parametric uncertainties in non-control-related parts in Eq. 6, e.g. gravity and Coriolis effect terms.

Based on Eq. 13, typical procedure of NDI can be designed by inverting the dynamics if the coupling matrix is invertible, hence the INDI control law is given in incremental form as

$$\begin{aligned} \delta \mathbf F =\left( \mathbf H ^{-1}{} \mathbf M {} \mathbf H ^{-T}\right) _\mathbf{sx _0}\left( \varvec{\nu }-\ddot{\mathbf{L }}_0\right) \end{aligned}$$

(14)

where $\varvec{\nu }$ is the virtual control and the control input as the required actuation force is given by

$$\begin{aligned} \mathbf u =\mathbf F =\mathbf F _0+\delta \mathbf F \end{aligned}$$

(15)

Substituting Eq. 14 into Eq. 15, the full linearisation is achieved and the system is turned into a double integrator:

$$\begin{aligned} \varvec{\nu }=\ddot{\mathbf{L }} \end{aligned}$$

(16)

Simple linear controller can be designed for the double integrator, for example

$$\begin{aligned} \varvec{\nu }=\ddot{\mathbf{L }}_d+\mathbf K _p\left( \mathbf L _d-\mathbf L \right) +\mathbf K _d\left( \dot{\mathbf{L }}_d-\dot{\mathbf{L }}\right) \end{aligned}$$

(17)

where subscript d denotes the reference trajectory given by the host to be tracked by the motion system. In case of SIMONA simulator, the reference trajectory is given in operation space, which means inverse kinematics are required for the proposed joint space controller.

The state feedback used in INDI control law Eq. 13 is another problem for parallel robots. It is well known that the forward kinematic problem of 6-DOF does not have an analytic solution. The mass matrix $\mathbf M \left( \mathbf sx \right)$ and Jacobian matrix $\mathbf H \left( \mathbf sx \right)$ are given in the operation space while the measurement of system states is performed in joint space. That means numerical iteration are required to calculate system states in Cartesian space as well as the mass matrix and the Jacobian matrix, which will largely add the computational burden. However, as will be discussed as follows, this problem is inherently tackled by the robustness feature of INDI controller.

Assuming ideal sensor measurements, define the control related matrix in Eq. 13 as the control effectiveness matrix as

$$\begin{aligned} \mathbf G \left( \mathbf{sx }\right) =\mathbf H ^{T}\left( \mathbf{sx }\right) \mathbf M ^{-1}\left( \mathbf{sx }\right) \mathbf H \left( \mathbf{sx }\right) \end{aligned}$$

(18)

In existence of model inaccuracies in the effectiveness matrix, for instance mass mismatch due to modification of flight cockpit or different pilot numbers, the system dynamics is then written as

$$\begin{aligned} \ddot{\mathbf{L }}=\ddot{\mathbf{L }}_0+\left[ \mathbf G _n\left( \mathbf{sx }_0\right) +\varDelta \mathbf G \left( \mathbf{sx }_0\right) \right] \left( \mathbf F -\mathbf F _0\right) \end{aligned}$$

(19)

where the subscript n denotes the nominal condition.

Since only nominal part of the system is known, the following control law is actually applied according to Eq. 14:

$$\begin{aligned} \delta \mathbf F =\mathbf G ^{-1}_n\left( \mathbf sx _0\right) \left( \varvec{\nu }-\ddot{\mathbf{L }}_0\right) \end{aligned}$$

(20)

Substituting Eq. 20 into Eq. 19, the system under control yields

$$\begin{aligned} \ddot{\mathbf{L }}=\varvec{\nu }+\varDelta \mathbf G \left( \mathbf sx _0\right) \mathbf G ^{-1}_n\left( \mathbf sx _0\right) \left( \varvec{\nu }-\ddot{\mathbf{L }}_0\right) \end{aligned}$$

(21)

Again, using the assumption that very high sampling rate is used in INDI, the change of leg length acceleration during one small sample time is very small that $\ddot{\mathbf{L }}\approx \ddot{\mathbf{L }}_0$ holds and Eq. 21 yields

$$\begin{aligned} \mathbf A \ddot{\mathbf{L }}=\mathbf A \varvec{\nu } \end{aligned}$$

(22)

where

$$\begin{aligned} \mathbf A =\mathbf I _{6\times 6}+\varDelta \mathbf G \left( \mathbf sx _0\right) \mathbf G ^{-1}_n\left( \mathbf sx _0\right) \end{aligned}$$

(23)

This result indicates that with relative high sampling rate, the linearized relation still holds with INDI controller in existence of model uncertainties in control effectiveness matrix. This also imply that the INDI based controller is not sensitive to almost all kinds of model inaccuracies in mass matrix, gravity effect terms as well as the Coriolis/centripetal effect terms. Thus the proposed control scheme is robust to model uncertainties of a hexapod parallel robot.

Taking advantage of the robustness of INDI methodology to model inaccuracies, tow important modification can be made to simplify the controller design. First, the complicated forward kinematics of parallel robot can be removed from the control structure. As the controller is robust to control effectiveness matrix inaccuracies, the trajectory set-points can be used to calculate the mass matrix $\mathbf M$ and Jacobian matrix $\mathbf H ^{T}$ instead of system position feedback, since they are considered to be very close if the motion controller works. Second, simplified mass matrix can be used by neglecting less important parts like the mass of legs, which will largely reduce the computation burden. By doing that, the INDI control law Eq. 14 can be simplified to

$$\begin{aligned} \delta \mathbf F =\left( \mathbf H ^{-1}{} \mathbf M _s\mathbf H ^{-T}\right) _\mathbf{sx _{d}}\left( \varvec{\nu }-\ddot{\mathbf{L }}_0\right) \end{aligned}$$

(24)

where $\mathbf M _s$ is the simplified mass matrix and $\mathbf sx _{d}$ is the system position trajectory set-points.

The proposed motion control system is presented in Fig. 2. The input of the INDI controller is the virtual control $\varvec{\nu }$ which is subtracted by actuator acceleration measurement and the output is the calculated actuation force required to track the motion. The virtual control is calculated by a linear controller which hire state feedback and inverse kinematics of Stewart platform. The reference trajectory set-points are used to calculate the control effectiveness matrix. Using the aforementioned two simplifications, the controller share the advantage of a feed forward control scheme, i.e. the avoidance of forward kinematics and availability of simplified model, while still offer a full system linearisation just as a typical NDI did with precise model information.

Fig. 2

INDI based motion controller architecture

The proposed INDI based motion controller is robust to model uncertainties at a cost of sensitivity to sensor measurement. It is note that the INDI technique is based on three main assumptions: high sampling rate, fast actuator dynamics and ideal sensor measurement. The performance of proposed control system will be tested with simulation in the following chapter.

Fig. 3

SRS top view [6]

Table 1 Geometric and inertial parameters

Fig. 4

Position tracking performance with nominal INDI controller

Fig. 5

Position tracking error with nominal INDI controller

4 Simulation Results

The performance of the proposed controller is verified by numerical simulations, the leg length tracking performance is presented since the controller is designed in the joint space. A detailed model of flight simulator motion system based on SIMONA Research Simulator(SRS) in Delft University of Technology is previously introduced in literature [6] and is used for simulations in this work, only the actuators are set to be ideal force generators. The simulations are performed in MATLAB/Simulink environment and the fourth-order Runge–Kutta integration is used to solve the system dynamic equation. The geometry of SRS simulator motion system is shown in Fig. 3 while the geometric and inertial parameters are given in Table 1. For all the simulations, the sampling rate is set to 1000 Hz, which is the same with the current controller implemented on SRS simulator.

Motion tracking tasks are performed in all the simulations. The motion profile of a state reconstruction experiment [6, 10] performed on the SRS is used to give reference trajectory in operation space. The origin of the upper platform moves in a horizontal circular path with a radius of 0.5 m with a period of 5 s.

Fig. 6

Position tracking error with simplified INDI controller

Figure 4 presents the tracking performance of each leg under nominal condition while real state feedback is used to calculate matrix $\mathbf M$ and $\mathbf H$. The leg length tracking errors are shown in Fig. 5. It is shown that the controller gives stable and good tracking performance, with a maximum tracking error limited within $2\times 10^{-3}$m. This result is already a verification of robustness of INDI controller to model inaccuracies in gravity and Coriolis related terms, since that part of the model is not used in the controller.

Figure 6 gives tracking errors when the system position set-point, instead of the real state feedback, are used to calculate the control effectiveness matrix. In this simulation the modified control law Eq. 24 is used. It is shown that the performance almost remain intact. This result verified that the INDI controller is not sensitive to model mismatch in the control effectiveness matrix, and the proposed simplified control law will provide similar performance as a complete state feedback approach will do.

In order to further test the robustness of the proposed controller, a significant model mismatch is set for the system. In Fig. 7 the position tracking error of each leg when there is $50\%$ mismatch in the upper platform mass is presented, which is generally beyond what we expect in reality. It is indicated that the performance is almost intact again. This result verifies that INDI is very robust to parameter mismatch in the control effectiveness matrix, hence the validation of using a simplified mass matrix $\mathbf M _s$ is also enhanced.

Fig. 7

Position tracking error with simplified INDI controller with $50\%$ mass mismatch

The previous simulation results verify that at least at an practical sampling rate, the time scale separation principle assumption holds for a hexapod flight simulator motion system. The INDI technique is a promising approach for the studied motion system and a wider range of parallel or serial robots to overcome model uncertainties with simple design procedure and small computational burden.

5 Conclusion

Incremental nonlinear dynamic inversion is a promising approach for parallel robot motion control. The time scale separation principle, which is the base of INDI technique, holds for the studied system at a practical sampling rate. The INDI based controller is not sensitive to almost all kinds of model and parametric inaccuracies, which allows for an accurate system linearization without precise model information. Furthermore, the robustness of INDI to model uncertainties allows for trajectory set-points to be used with simplified mass matrix, which will largely reduce the computational burden. Since INDI technique depends on accurate sensor measurement and fast actuator dynamics, the influence of measurement noise and bias, as well as actuator dynamics should be investigated as future work before the proposed control scheme is implemented to a promising real world application.