Fuzzy Portfolio Selection Models for Dealing with Investor’s Preferences

Abstract

This chapter provides an overview of the authors’ previous work about dealing with investor’s preferences in the portfolio selection problem. We propose a fuzzy model for dealing with the vagueness of investor preferences on the expected return and the assumed risk, and then we consider several modifications to include additional constraints and goals.

1 Introduction

H.M. Markowitz won the 1990 Nobel Price for his work in the foundation of modern portfolio theory (MPT) [27, 28], which has become a main tool in portfolio management as well as in other economic theories, such as asset pricing [33]. MPT is a deep theory which can hardly be described in a few words (see [11] for a comprehensive account), but, roughly speaking, it aims to determine the best portfolio we can form from a given set of possible assets on the basis of two characteristics. The first one is the expected return. In order to measure it, the return of each asset is considered as a random variable and the expected return is often measured by its mean, which in practice is estimated by the arithmetical mean of the historical returns. The expected return of a portfolio is defined as the weighted sum of the expected returns of its assets.

Here we should face the critical question: to what extent can we trust that the future return of a portfolio will be similar to the expected return calculated from its past returns? This leads to the second characteristic to be considered in order to select a portfolio to invest in: the risk. It tries to estimate the difference between the expected return and the real future return of a portfolio.

Whereas the theoretical relevance of MPT is not questioned, several criticisms about its real world applicability have arisen [38]. However there are also renowned specialists supporting it [18, 30, 33]. Assuming that the expected return and an adequate measure of the risk are reliable, MPT establishes that a rational investor should select an efficient portfolio, i.e., a portfolio providing the least possible risk for a given expected return or, what is essentially the same, providing the greatest expected return for a maximum allowable risk.

The original (classical) Markowitz model is also called the mean-variance model since it takes as indicators of the expected return and the risk of a portfolio the mean and the quadratic form associated to the variance-covariance matrix of the returns of the assets, respectively, which in practice are estimated from the historical data by standard statistical techniques assuming that they are normally distributed.

However, several alternative ways for measuring the risk of a portfolio have been proposed. Value at Risk (VaR) is widely used (see [36] for a discussion of this concept, or also [16]). Konno and Yamazaki [21] propose a linear model which dramatically simplifies the computational aspects of the portfolio selection problem. Some other possibilities arose from the fact that many risk measures become high when there is a high probability that the return will be far from the expected return, but they do not distinguish whether the difference is positive (higher return than expected) or negative (less return than expected). Since aversion to having more benefits than expected is questionable, some asymmetric measures for the so-called downside risk that take into account only the risk of having less return than expected, have been proposed. The first downside risk measure appeared in Roy’s “safety-first” model [31, 32]. See also [8, 9, 25, 26, 35]. Other asymmetric measures of risk take into account higher statistical moments: skewness, kurtosis [15, 17, 20]. For more advanced models taking into account the dynamics of the variance see for instance [10].

2 The Classical Portfolio Selection Problem

Thus, the original Markowitz Portfolio Selection Model is formulated as

$$\begin{aligned} \begin{aligned}&\text{ Min. }\, \mathbf x^tVx\\&\, \, \, \text{ s.a }\, \, \mathbf{e}^t\mathbf{x}\ge r\\&\qquad \, \, \mathbf{1}^t\mathbf{x}=1\\&\qquad \, \, \mathbf{x}\ge 0 \end{aligned} \end{aligned}$$

(1)

where the vector $\mathbf x$ contains the weights of the assets in the portfolio (i.e. the proportion of each asset in the total invested fund), $\mathbf e$ is the vector of expected returns, measured by the means of the historical data and $\mathbf V$ is the variance-covariance matrix of such data, so that R estimates the risk of the portfolio and r is the minimum expected return specified by the investor.

Alternatively, a dual form of the problem consists of maximizing the expected return and imposing a maximum admissible risk:

$$\begin{aligned} \begin{aligned}&\text{ Max. }\, \mathbf{e}^t\mathbf{x}\\&\, \, \, \, \text{ s.a } \, \, \mathbf{x}^t\mathbf{Vx}\le R\\&\qquad \, \, \, \mathbf{1}^t\mathbf{x}=1\\&\qquad \, \, \, \mathbf{x}\ge 0 \end{aligned} \end{aligned}$$

(2)

In fact, the portfolio selection problem is better understood as a bi-objective problem aiming both maximizing the expected return and minimizing the risk. The minimizing formulation is the most widely used in the literature, mainly because by being a quadratic problem it is more easily handled from a mathematical point of view. However, we will also deal with (2) since it is more realistic to ask an investor what risk he considers acceptable rather than forcing him to fix a minimum return without having any reference about the risk it carries. In fact, it is the usual practice for small investors [see for instance (http://www.santander.com)].

The original Markowitz Portfolio Selection Model included just linear constraints, mainly because computers could not handle more difficult instances. However, nowadays the available computational power is much greater and hence more sophisticated models can be dealt with, looking for efficient portfolios satisfying also additional constraints. There are many contexts in which such constraints become necessary. Some of them are related to the mutual fund management. Fund managers must comply contractual requirements determined by the prospectus as well as legal requirements, such as the 5–10–40-constraint imposed by the §60(1) of the German investment law [2], which establishes that securities of the same issuer are allowed to amount to up to 5% of the net asset value of the mutual fund, but they are allowed to 10% if the total of all of these assets is less than 40% of the net asset value. It is also usual to include buy-in thresholds to reduce transaction costs. This means not allowing the stocks of a mutual fund in a given asset to be less than a certain amount. A third typical example is that managers often impose upper bounds to the total number of assets in a mutual fund also to reduce transaction costs, as well as lower bounds in order to diversificate the investment. See [13] for the computational aspects associated to these additional constraints. This leads to the model

$$\begin{aligned} \begin{aligned}&\text{ Min. } \,\mathbf{x}^t\mathbf{Vx}\\&\, \, \, {\text{ s.t. }} \, \, \mathbf{e}^t \mathbf{x} \ge r\\&\qquad \, \, \, \mathbf{1}^t \mathbf{x} = 1\\&\qquad \, \, \, \mathbf{l}\le \mathbf{x} \le \mathbf{u}, \end{aligned} \end{aligned}$$

(3)

where $\mathbf{l}$ and $\mathbf{u}$ are the vectors of lower and upper bounds for each weight. However, in many cases the investor does not really wish to force each asset to have a minimum weight in the portfolio but, in order to avoid an artificially imposed excess of diversification in the optimal portfolio, he may just wish to require a minimum weight only for those assets actually appearing in it. This leads to the incorporation of semicontinuous variable constraints into the model, which means that each variable $x_i$ is allowed either to be 0 or to vary in the rank $[l_i, u_i]$. Such constraints can be expressed with the help of binary variables $y_i$ taking the value 1 if the i-th asset appears in the portfolio and 0 otherwise. The resulting model is:

$$\begin{aligned} \begin{aligned}&\text{ Min. } \, R = \mathbf{x}^t\mathbf{Vx}\\&\text{ s.t. } \, \, \, \, \mathbf{e}^t \mathbf{x} \ge r\\&\qquad \, \, \, \mathbf{1}^t \mathbf{x} = 1\\&\qquad \, \, \, l_iy_i\le x_i\le u_iy_i, \, 1\le i\le n,\\&\qquad \, \, \, y_i\in \{0,1\}. \end{aligned} \end{aligned}$$

(4)

In any portfolio selection problem, the set of optimal pairs (r, R) consisting of the minimal risk R providing a given expected return r, or, equivalently, the maximum expected return provided by a portfolio that does not exceed a maximum level of risk R, is known as the efficient frontier of the problem. In the simplest case where even the sign constraints are removed, it consists just of a branch of parabola [6, 11]. However, in the last decades, computation techniques have been developed to solve large and more sophisticated instances of the portfolio selection problem including many different kinds of constraints, making it more realistic (see [12, 37]).

3 A Fuzzy Formulation of the Portfolio Selection Problem

Obviously, the portfolio selection, like most financial problems, is related with uncertainty because it consists of taking a decision about future events. Moreover, it is not easy to model the investor’s preferences. After the seminal work by Markowitz, attention has been given to the study of alternative models [22, 25] which try to deal more efficiently with the uncertainty of the data. Most of these models are based on probability distributions, which are used to characterize risk and return. However, another way of dealing with uncertainty is to work with models based on soft computing. Watada [41] solves this problem by using imprecise aspiration levels for an expected biobjective approach, where the membership functions of the goals are of a logistic-type. In 2000, Tanaka et. al. [39] propose using possibility distributions to model uncertainty on the expected returns and to incorporate the knowledge of financial experts by means of a possibility degree of similarity between the future state of financial markets and the state in previous periods [14]. Multiobjective programming has also been used to design fuzzy models of portfolio selection, either for compromise solutions [29] or by introducing multi-indices [1]. Specific methods have even been proposed for dealing with the unfeasibility provoked by conflict between the expected return and the investor’s diversification requirements [23, 24].

However, in this section we will consider a very different class of vagueness related to the portfolio problem, namely the vagueness of the invertor’s criteria for selecting a satisfactory trade off between the risk he considers acceptable and the return he wishes to obtain. In other words, the investor must choose a point at the efficient frontier of the problem. From a theoretical point of view, the investor’s preferences are usually formalized by means of utility functions, so that the final choice is that efficient portfolio maximizing a given utility function, but when we try to reflect the preferences of a real specific investor we must ask him directly for a point in the efficient frontier. Nevertheless, it is obvious that the investor’s preferences are essentially vague, so that it is unnatural to force him to choose a specific point. In practice, he could only determine a zone or a fuzzy point on it.

This leads to the fuzzy model proposed by the authors in [5]. The main idea is to consider partially feasible solutions involving slightly greater risk than that fixed by the decision-maker, and to study the possibilities that they offer in order to improve the expected return.

A fuzzy set $\tilde{S}$, of partially feasible solutions, is defined so that the membership degree of a given portfolio depends on how much its risk exceeds the risk $R_0$ fixed by the investor. On the other hand, a second fuzzy set $\tilde{G}$ is defined, whose membership function reflects the improvement on the return provided by a partially feasible solution with respect to the optimal crisp return $z^*$. In practice, we consider piecewise linear membership functions

$$ \mu _{\tilde{S}}(x) =\left\{ \begin{array}{lll} 1&{} \qquad &{}\text{ if } r \le R_0,\\ 1-\frac{r-R_0}{p_f}&{} &{} \text{ if } R_0<r<R_0+p_f,\\ 0&{} &{}\text{ if } r\ge R_0+p_f, \end{array}\right. $$

$$\mu _{\tilde{G}}(x) =\left\{ \begin{array}{lll} 0&{}\qquad &{}\text{ if } z \le z^*,\\ \frac{z-z^*}{p_g}&{} &{}\text{ if } z^*<z<z^*+p_g,\\ 1&{} &{}\text{ if } z\ge z^*+p_g, \end{array}\right. $$

where r and z are the risk and the return provided by the portfolio x (which is assumed to satisfy the constraints of (MV), except the second one); the parameter $p_f$ is the maximum increment in the risk that the decision-maker can accept, and $p_g$ is the increment on the return that the decision-maker would consider completely satisfactory. From this, we can define a global degree of satisfaction

$$ \lambda (x) = \min \{\mu _{\tilde{G}}(x), \mu _{\tilde{S}}(x)\}, $$

which is the membership degree for the fuzzy intersection of $\tilde{S}\cap \tilde{G}$. The fuzzy portfolio model becomes

$$\begin{aligned} \begin{aligned}&\text{(FMV) } \, \, \text{ Max. } \, \lambda (x)\\&\text{ s.t. }\, x\in \tilde{S}. \end{aligned} \end{aligned}$$

(5)

In [3] exact and heuristic procedures for solving this problem are described. In order to illustrate the main idea on which the model is based we consider five assets from the historical data introduced by Markowitz [28]. Table 1 shows the returns of American Tobacco, AT&T, United States Steel, General Motors and Atcheson & Topeka & Santa Fe.

Table 1 Returns on five assets

We have fixed a risk level $R = 0.03$. The optimal crisp portfolio is formed by assets AmT, ATT, GM, ATS and provides an optimal return $z^* = 0.103926$. For the fuzzy model, we have fixed $p_f = 0.02$, $p_g = 0.02$. By explicitly solving the Kuhn-Tucker conditions associated to the model, we can calculate the optimal return for a given risk R, which happens to be

$$ F(R) = \frac{-0.02355 + 52.6832 R + 2.6136\sqrt{-0.77841 + 52.6832 R}}{9.09494 \times 10^{-13} R + 33.84051\sqrt{-0.77841 + 52.6832 R}} $$

Computations are valid for risks in the interval $I=[0.025826, 0.083341]$. The functions $\mu _f(R)$ and $\mu _g(R)$ are shown in Fig. 1. They intersect at $R^*= 0.041381$, corresponding to $\lambda = 0.430977$. The return on the fuzzy portfolio is 0.112545, whereas the crisp return was 0.103926.

Fig. 1

Membership functions for the degree feasibility and degree of improvement on the expected return

We observe that the global degree of satisfaction is low. This means that the risk is increased much more than the return of the asset. The higher value of $\lambda$, the more preferable the alternative fuzzy portfolio is. High fuzzy satisfaction levels are more usual when additional constraints are considered making the efficient frontier more irregular, as we will see in the next section.

4 Portfolio Selection with Semi-continuous Variable and Cardinality Constraints

As we have already noticed, real world investments require incorporating many additional constraints into the portfolio selection model, many of which can be expressed as mathematically simple linear constraints, but some others are more complex from a mathematical point of view since they transform the model into a mixed integer one. To illustrate this fact we will consider semicontinuous variable and cardinality constraints, although any set of linear constraints could be considered in addition. Hence, our starting point is now the model (4).

Let us call X the set defined by the constraints imposed on the problem when the minimum return constraint is relaxed, which will be handled separately. The constraint and goal set will be fuzzy subsets of the (crisp) universe set X. The fuzzy constraint set $\tilde{C}$ must be such that the value $\mu _{\tilde{C}}(\mathbf{x})$ is high when the expected return on the portfolio $\mathbf{x}\in X$ is not much less than $r_0$ and the risk is not much greater than $R_0$. This means that $\tilde{C}$ can be defined as the fuzzy intersection of two fuzzy sets $\tilde{C}_r$ and $\tilde{C}_R$, such that the degree of membership of each portfolio $\mathbf{x}\in X$ is given by $\mu _{\tilde{C}_r}(\mathbf{x}) := f_1(r(\mathbf{x}))$ and $\mu _{\tilde{C}_R}(\mathbf{x}) := g_1(R(\mathbf{x}))$, where $r(\mathbf{x})$ and $R(\mathbf{x})$ are the expected return and risk of the portfolio $\mathbf x$, $f_1: \mathrm{I\!R}\longrightarrow [0,1]$ is a non-decreasing function such that $f_1(r_0)=1$ and $g_1: \mathrm{I\!R}\longrightarrow [0,1]$ is a non-increasing function such that $g_1(R_0)=1$. The specific choice of $f_1$ and $g_1$ will depend on the available information about the investor’s preferences regarding risk and return. Hence the membership function to the fuzzy feasible set $\tilde{C} := \tilde{C}_r\cap \tilde{C}_R$ is given by the membership function $\mu _{\tilde{C}}(\mathbf{x}):=\min \{\mu _{\tilde{C}_r}(\mathbf{x}),\mu _{\tilde{C}_R}(\mathbf{x})\}$, which is of the form $\mu _{\tilde{C}}(\mathbf{x}) = h_1(r(\mathbf{x}), R(\mathbf{x}))$, where $h_1(r,R):= \min \{f_1(r),g_1(R)\}$ generally has the shape shown in Fig. 2a.

Fig. 2

Membership functions to $\tilde{C}$ and $\tilde{G}$

On the other hand, the degree of membership of the goal set $\tilde{G}$ of the fuzzy problem must be high for portfolios whose expected return is much greater than $r_0$ or the risk is much less than $R_0$. Hence, $\tilde{G}$ is the fuzzy union of the fuzzy sets $\tilde{G}_r$ and $\tilde{G}_R$ whose membership functions are of the form $\mu _{\tilde{G}_r}(\mathbf{x}) := f_2(r(\mathbf{x}))$ and $\mu _{\tilde{G}_R}(\mathbf{x}) := g_2(R(\mathbf{x}))$, where $f_2:\mathrm{I\!R}\longrightarrow [0,1]$ is a non-decreasing function such that $f_2(r_0)=0$ and $g_2:\mathrm{I\!R}\longrightarrow [0,1]$ is a non-increasing function such that $g_2(R_0)=0$. Notice that in this case $\tilde{G}$ is a fuzzy union and not a fuzzy intersection, since improving the crisp optimal portfolio means improving the risk or improving the expected return, but both cases cannot occur simultaneously. The fuzzy intersection would be the empty set.

Thus, the membership function of the fuzzy goal set $\tilde{G}=\tilde{G}_r\cup \tilde{G}_R$ (which can be called the degree of improvement of the goal) is given by

$$ \mu _{\tilde{G}}(\mathbf{x}) := \max \{\mu _{\tilde{G}_r}(\mathbf{x}),\mu _{\tilde{G}_R}(\mathbf{x)}\} = h_2(r(\mathbf{x}), R(\mathbf{x})), $$

where $h_2(r, R) := \max \{f_2(r), g_2(R)\}$ has the shape shown in Fig. 2b.

Fig. 3

Degree of global satisfaction and the efficient frontier. The surface represents the degree of global satisfaction for each pair (R, r) of expected risk and desired return. The dotted line is the efficient frontier and the continuous line is its lifting to the graph

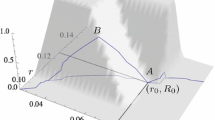
Now, following Delgado et al. [7], we consider the fuzzy decision set of our problem, defined as the fuzzy intersection $\tilde{D} := \tilde{C}\cap \tilde{G}$, which has the shape shown in Fig. 3. The degree of membership of a portfolio $\mathbf x$ to $\tilde{D}$ is called its degree of global satisfaction: $\lambda (\mathbf{x}) := \min \{\mu _{\tilde{C}}(\mathbf{x}),\mu _{\tilde{G}}(\mathbf{x})\}$. In Fig. 3 we have represented a possible (simplified) efficient frontier of the crisp problem (SCP) and the pair $(r_0, R_0)$ chosen by the investor as the starting point for the fuzzy model. We see that its degree of feasibility is 1 but its degree of improvement of the goal is 0, and so the degree of global satisfaction is 0. We can also see the lifting of the efficient frontier to the graph of the degree of global satisfaction. In order to choose a specific solution from the fuzzy decision set $\tilde{D}$ we maximize its degree of global satisfaction, i.e. we find the optimal fuzzy portfolio by solving the program:

$$ \begin{array}{rl} \text{(FSC) } \text{ Max. }&{}\lambda (\mathbf{x})\\ \text{ s.t. }&{}\mathbf{x}\in X\ \end{array} $$

In Fig. 3 we can see that the degree of global satisfaction has two local maxima on the efficient frontier, the best of which is the optimal solution of the fuzzy model we are introducing.

The problem of choosing membership functions suitable for modelling a real uncertain situation is a very subtle issue in fuzzy set theory. Here, in the absence of specific preferences, we will consider the simplest case. Notice that we intend to compare possible variations of the expected return with possible variations of the risk, and what is really comparable with a variation of the expected return is not a variation of its variance but a variation of its typical deviation. The difference between the variance and the typical deviation is just a square root, which is irrelevant when minimizing the risk, but it must be incorporated into our membership functions. In other words, the natural way to express the investor’s preferences on the trade-off between variations in the expected return and variations in the risk is in terms of the mean and the typical deviation instead of the mean and the variance. In the absence of more specific criteria, we will assume a piecewise linear dependence on r and $\sqrt{R}$; namely, we take

$$ f_1(r) := \left\{ \begin{array}{ll}0&{}\text{ if } r< r_0-p_{f_1},\\ 1-\frac{r_0-r}{p_{f_1}}&{}\text{ if } r_0-p_{f_1}\le r\le r_0,\\ 1&{}\text{ if } r_0<r, \end{array}\right. \ \ g_1(R) := \left\{ \begin{array}{ll}1&{}\scriptstyle \text{ if } \sqrt{R}<\sqrt{ R_0},\\ 1-\frac{\sqrt{R}-\sqrt{R_0}}{p_{g_1}}&{}\scriptstyle \text{ if } \sqrt{ R_0}\le \sqrt{R}\le \sqrt{R_0}+p_{g_1},\\ 0&{}\scriptstyle \text{ if } \sqrt{R}>\sqrt{R_0}+p_{g_1}, \end{array}\right. $$

$$ f_2(r) := \left\{ \begin{array}{ll}0&{}\text{ if } r< r_0,\\ \frac{r-r_0}{p_{f_2}}&{}\text{ if } r_0\le r\le r_0+p_{f_2},\\ 1&{}\text{ if } r_0+p_{f_2}<r, \end{array}\right. \ \ g_2(R) := \left\{ \begin{array}{ll}1&{}\scriptstyle \text{ if } \sqrt{R}< \sqrt{R_0}-p_{g_2},\\ \frac{\sqrt{R_0}-\sqrt{R}}{p_{g_2}}&{}\scriptstyle \text{ if } \sqrt{R_0}-p_{g_2}\le \sqrt{R} \le \sqrt{R_0},\\ 0&{}\scriptstyle \text{ if } \sqrt{R_0}<\sqrt{R}. \end{array}\right. $$

Fig. 4

Left Membership function to the feasible set and to the goal set as functions of the expected return. Right The efficient frontier around the crisp expected return

Table 2 Comparison between the crisp and the fuzzy solutions of Example 1

In [5] we show how to handle this fuzzy model. As an illustration, we consider the same data set considered in the previous section, but now we incorporate semicontinuous variables with vectors of bounds $\mathbf{l} = (0.2,0.3,0.2,0.3,0.2)$ and $\mathbf{u} = (0.6,0.6,0.6,0.6,0.6)$, as well as a cardinality constraint with $m = 2$ and $M = 5$.

Let us consider an investor that has chosen an expected return $r_0 = 0.125$, whose corresponding risk is $R_0 = 0.0742$. In order to interpret this variance, we will calculate the standard deviation $\sqrt{R_0} =0.272$. We can consider the later as a quite high risk, and so we assume that the investor would be interested in reducing it. In this sense, a reduction of $p_{g_2}=0.06$ would be considered as totally satisfactory. On the other hand, an increment greater than $p_{g_1}=0.01$ would not be acceptable in any case. We assume that the investor would accept variations on the expected return with tolerances $p_{f_1}=p_{f_2}=0.02$.

Figure 4 left shows the degrees of membership to the feasible and the goal sets as functions of the expected return on a given efficient portfolio. We can compare it with the piece of the efficient frontier around $r_0$ within the tolerance levels, which is shown at the right.

There we can see that near $r_0$ there are two horizontal jumps below and a vertical one above. In Fig. 4 we have highlighted the two local maxima of the degree of global satisfaction. Specifically, they correspond to the efficient portfolios described in Table 2, which also includes the crisp efficient portfolio. Both in the figure and in the table we can see that the fuzzy optimal solution is the left-hand one with a degree of global satisfaction $\lambda = 0.71$. Notice that the three portfolios shown in Table 2 have different compositions.

In Table 2 we can also appreciate the interest of the fuzzy alternative: by changing from the crisp portfolio to the fuzzy one, we reduce the risk of the investment by a bit more than $1\%$ at the cost of reducing the expected return by just 0.0058. The significantly lower degree of global satisfaction of the right fuzzy solution is reasonable since the increment on the expected return is far less than the increment on the risk.

5 Portfolio Selection with Non-financial Goals

The Social Investment Forum in its new 2012 Trends Report in US [40] finds that 11.23% of all assets under professional management in the United States at the end of 2011 applied various environmental social, governance and ethical criteria in their investment analysis. Investors practicing Socially Responsible Investment (SRI) strategies held $3.74 trillion out of $33.3 trillion of investment assets. This represents an increase of 22% since 2009 and reflects the “growing investors’ interest in considering environmental, community, other societal or corporate governance (ESG) issues to refine how they make decisions as they select and manage their portfolios or raise their voices as shareholders” [40].

This growth of SRI strategies all around the world has stimulated in turn the rise of many entities working in the rating of assets with regard to their social responsibility. This poses two mathematical problems: how to evaluate assets’ social responsibility which is by its nature a vague an imprecise concept and how to aggregate in a final rating a great amount of relevant but imprecise information about firms and/or funds.

Nevertheless, and although investors could be provided with highly processed non-financial information from the experts, in order to select a portfolio, they must elicit their preferences. The simplest way would be to restrict the feasible set of investments to those being “acceptable” for the investor from a SRI point of view. However this would mean to completely subordinate the financial goals to the non-financial ones and in fact, in practice most of the SRI assets first apply financial screens and then social screens. This clearly reflects that actually most of socially responsible investors consider SRI as a secondary goal with regard to maximizing the financial return and minimizing the financial risk.

In this section a fuzzy portfolio selection problem is proposed in which a secondary goal besides the financial ones is considered in such a way that no potentially interesting solution with regard to the risk and the return is discarded by the constraints. Specifically, the constraints of the model do not mention the secondary goal, which appears just in the objective function, in such a way that all the feasible portfolios within given ranges of risk and return are taken into consideration. Thus, the investor can be aware of what is being exactly missed as a result of the improvement of the additional non-financial goal.

Our starting point is again the model (4), and hence each portfolio is determined by a pair $(\mathbf{x}, \mathbf{y})$ of weights and binary variables. We measure the Social Responsibility of a portfolio as the degree of membership of a fuzzy set $\tilde{S}$, say $\mu _{\tilde{S}}(\mathbf{x}, \mathbf{y})$. See [4] for a way of defining such a fuzzy set.

Now we take as fuzzy feasible set the fuzzy subset of the set of all portfolios satisfying the hard constraints of (4) (i.e., all but the first one), defined as $\tilde{C} = \tilde{C}_r\cap \tilde{C}_R$, where the membership functions of the fuzzy sets $\tilde{C}_r$ and $\tilde{C}_R$ are given by:

$$ \mu _{\tilde{C}_r}(x,y)= \left\{ \begin{array}{ll} 1&{}\text{ if } r\ge r_0,\\ \frac{r-r_0+s_r}{s_r}&{}\text{ if } r_0-s_r<r<r_0,\\ 0&{}\text{ if } r\le r_0-s_r, \end{array}\right. $$

$$ \mu _{\tilde{C}_R}(x,y)= \left\{ \begin{array}{ll} 1&{}\text{ if } R\le R_0,\\ \frac{R_0+s_R-R}{s_R}&{}\text{ if } R_0<R<R_0+s_R,\\ 0&{}\text{ if } R\ge R_0+s_R, \end{array}\right. $$

where r y R are respectively the expected return and the risk of the portfolio (x, y) and the values $r_0$, $R_0$, $s_r$ and $s_R$ are determined from the investor’s preferences. This means that $r_0$ and $R_0$ are an expected return and a risk that the investor considers as completely acceptable, but he would accept worse values until reaching the tolerances $s_r$ and $s_R$ if this provides better results for the secondary goal.

Next we define a fuzzy goal set $\tilde{G}$ from two auxiliary fuzzy sets $\tilde{E}$ and $\tilde{S}$, the first one defining the “efficient enough” portfolios and the second one defining the “good enough” ones with regard to the secondary goal (always according to the investor’s preferences). The set $\tilde{E}$ will express what we are loosing by accepting a non-efficient portfolio, and so efficient portfolios will be now the totally efficient portfolios, i.e. those having degree of membership of $\tilde{E}$ equal to 1.

First we define efficiency with regard to the expected return and then, the efficiency with regard to the risk by means of two fuzzy sets $\tilde{E}_r$ and $\tilde{E}_R$. The membership of $\tilde{E}_r$ is:

$$ \mu _{\tilde{E}_r}(x,y)=\left\{ \begin{array}{ll} 1-\frac{r_\mathrm{ef}(R)-r}{t_r}&{}\text{ if } r\ge r_{ef}(R)-t_r,\\ 0&{}\text{ otherwise, } \end{array}\right. $$

where $t_r$ is a tolerance determined from the investor’s preferences and $r_\mathrm{ef}(R)$ is the efficient expected return corresponding to the risk R of the portfolio (x, y). This means that the degree of efficiency with regard to the expected return reaches the value 0 when the difference between the expected return r of the portfolio and $r_\mathrm{ef}(R)$ exceeds a tolerance fixed by the investor.

Analogously, we define the membership function of $\tilde{E}_R$ as

$$ \mu _{\tilde{E}_R}(x,y)=\left\{ \begin{array}{ll} 1-\frac{R-R_\mathrm{ef}(r)}{t_R}&{}\text{ if } R\le R_{ef}(r)+t_R,\\ 0&{}\text{ otherwise, } \end{array}\right. $$

which means that the degree of efficiency of a portfolio with regard to the risk is 1 for efficient portfolios and reaches the value 0 when the difference between the risk R of the portfolio and the efficient risk $R_\mathrm{ef}(r)$ for its return r exceeds a given tolerance $t_R$.

Now we define $\tilde{E}=\tilde{E}_r\cap \tilde{E}_R$, where the membership function of the fuzzy intersection is defined as the minimum of the previously defined membership functions. Hence the set $\tilde{E}$ allows us to speak about partially efficient portfolios in such a way that efficient portfolios in the usual sense are now the totally efficient ones, but a portfolio close enough to the efficient frontier is considered as “almost efficient” in the fuzzy sense.

Finally, we define our fuzzy goal set $\tilde{G}$ by means of the membership function as a weighted sum

$$ \mu _{\tilde{G}}(x,y)= w\mu _{\tilde{S}}(x,y)+(1-w)\mu _{\tilde{E}}(x,y), $$

where the weight w expresses the importance of the secondary goal for the investor with regard to efficiency. So, a high value for w means that the investor is willing to go relatively far from the efficient frontier in order to obtain higher values of $\mu _{\tilde{S}}$, whereas a small value of w means that the investor wishes to stay near the efficient frontier. In any case, recall we have defined the feasible set in such a way that only good enough solutions with regard to the financial goals are under consideration, and so the financial goals are always the main goals of the problem. More specifically, a large value for w means that, among the acceptable solutions with regard to the financial goals, those best with regard to $\tilde{S}$ are preferred, and only for similar values with regard to $\tilde{S}$ the degree of efficiency becomes relevant.

All in all, the degree of membership of the decision set is given by

$$ \mu _{\tilde{D}}(x,y) =\min \{\mu _{\tilde{C}}(x,y),w\mu _{\tilde{S}}(x,y)+(1-w)\mu _{\tilde{E}}(x,y)\} $$

and the fuzzy problem (6) is the problem determined by this decision set, whose optimal solutions are those with maximum degree of membership of $\tilde{D}$:

$$\begin{aligned} \begin{aligned}&\text{ Max. }{\min \{\mu _{\tilde{C}}(x,y),w\mu _{\tilde{S}}(x,y)+(1-w)\mu _{\tilde{E}}(x,y)\}}\\&\,\, \, \,\, \text{ s.t. }1x=1\\&\qquad \, \, m\le \sum \nolimits _i y_i\le M\\&\qquad \, \, l_iy_i\le x_i\le u_i y_i, \qquad i=1,\ldots , n\\&\qquad \, \, x_i\ge 0,\ y_i\in \{0,1\} \, \quad i=1,\ldots , n \end{aligned} \end{aligned}$$

(6)

In order to illustrate this model, we consider the 10 mutual funds listed in Table 3. The first five have positive SRI degree, whereas the last five are conventional funds with null SRI degree. The variance-covariance matrix and the vector of expected returns are calculated from the weekly data from 31-12-2006 to 31-12-2007 provided by Morningstar Ltd. Assume we wish to select a portfolio consisting of a minimum of 3 and of a maximum of 6 funds in such a way that each non-zero weight is at least 0.05. As upper bounds for the weights, we fix 0.25 for the first five (the socially responsible ones) and 0.15 for the conventional ones. These weights allow up to a $75\%$ of conventional funds and up to a $100\%$ of socially responsible funds in each feasible portfolio.

Table 3 Selected funds

Table 4 The six best solutions for different portfolio compositions

By observing the efficient frontier, the investor can choose the zone of the plane risk-return he is interested in. Formally, this means to determine the fuzzy set $\tilde{C}$. For this, we fix $(r_0, R_0) = (0.26,1.98)$ with tolerances $(s_r,s_R) = (0.01,0.02)$.

To determine an instance of the problem (6), we need to fix the weight w for the social responsibility degree in the goal function. Let us set a quite high value, namely $w=0.8$ to favor those portfolios being quite far from the efficient frontier if they are good with regard to SRI.

The optimal solution of (6) is the portfolio N1 in Table 4, whose degree of membership of the decision set is 0.6262. With this solution, the investor gets an expected return $r=0.258$, with a risk $R=1.98$ and a social responsibility degree $s=0.3808$. It is interesting to compare this optimal solution with other alternatives, and therefore Table 4 contains the six best portfolios that are optimal with regard to the portfolios with the same composition. Notice that this does not mean that portfolio N2 is the second best solution of (FP), since there are infinitely many portfolios near to N1 that are better than N2. What we can say is that, if we look for a portfolio with a composition different from that of N1, the best possibility is N2, and so on.

Figure 5 shows the position of the portfolios appearing in Table 4 in the risk-return plane. We see that N2 is completely efficient. When compared to N1, it has a similar expected return, a substantially better risk, but a significantly lower social responsibility degree. By contrast, portfolio N3 is again a good solution with regard to social responsibility (it has the second best SRD), but it is worse than N1 because of its SRD, and worse than N2 because of its significantly lower degree of efficiency.

In general, when applying a heuristical procedure for solving a larger instance of (6), it is useful to save not only the best portfolio along the search process, but the best portfolio found for each composition. Hence, in the end we can present the investor not only the optimal portfolio, but a list of alternatives for different compositions. These alternatives are ordered a priori according to his own preferences. In this way the investor is given a last chance to decide which portfolio suits better his preferences with regard to the trade off between risk, return and social responsibility.

With this proposal, the investor knows exactly what he is missing with respect to the financial goals by accepting the solution of (6), and if he considers the financial cost excessive, he has the possibility of choosing a more conservative alternative among the proposed list or even solving again (FP) with a lower value for the weight of the social responsibility degree.

Fig. 5

Location on the plane risk-return of the best solutions

6 Conclusion

In this chapter we have seen how fuzzy techniques can be applied to the portfolio selection problem in order to deal with different issues related to the subjectivity of the investor’s preferences: on one hand, the integrality constraints considered in Sect. 4 make the problem very sensitive to small changes of the risk and return preferences, and our proposed model look for the best solution taking into account that those preferences are soft ones and, hence, the investor will accept slight variations if they provide a reasonable improvement of the solution. On the other hand, when considering non-financial goals as in Sect. 5, our model provides a precise way of prioritizing the financial behavior of the selected portfolio without disregarding its non-financial properties. Of course, it would not be reasonable to expect that a single model would be suitable for reflecting the preferences of every investor (even if it has some adjustable parameters to this end), and hence any other investor’s profiles will need essentially different models involving new ideas, and this leaves a rich field for future research.