Abstract
The Web Ontology Language (OWL) has gained serious attraction since its foundation in 2004, and it is heavily used in applications requiring representation of as well as reasoning with knowledge. It is the language of the Semantic Web, and it has a strong logical underpinning by means of so-called Description Logics (DLs). DLs are a family of conceptual languages suitable for knowledge representation and reasoning due to their strong logical foundation, and for which the decidability and complexity of common reasoning problems are widely explored. In particular, the reasoning tasks allow for the deduction of implicit knowledge from explicitly stated facts and axioms, and plenty of appropriate algorithms were developed, optimized, and implemented, e.g., tableaux algorithms and completion algorithms. In this document, we present a technique for the acquisition of terminological knowledge from social networks. More specifically, we show how OWL axioms, i.e., concept inclusions and role inclusions in DLs, can be obtained from social graphs in a sound and complete manner. A social graph is simply a directed graph, the vertices of which describe the entities, e.g., persons, events, messages, etc.; and the edges of which describe the relationships between the entities, e.g., friendship between persons, attendance of a person to an event, a person liking a message, etc. Furthermore, the vertices of social graphs are labeled, e.g., to describe properties of the entities, and also the edges are labeled to specify the concrete relationships. As an exemplary social network we consider Facebook, and show that it fits our use case.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction and Problem Description
In the last years, a rapidly increasing amount of data was collected and recorded in so-called triple stores. Basically, those triple stores are databases of a special kind, allowing for storing data in the form of triples (s, p, o) which express that the subject s is related to the object o via the (binary) predicate p. For example, it is possible to say that an individual x is a human by means of the triple (x, rdf: type, some−namespace: human). As another example, with the triple (x, foaf: hasFriend, y) we can denote that individual x is a friend of the individual y. The vocabulary used in the triples can be freely chosen such that it best fits the application’s needs. Please note that there are plenty of vocabularies available, which could be used without requiring to invent one’s own vocabulary from scratch. The most famous examples are, of course, the vocabularies from RDF/RDFS and OWL which allow for the expression of very basic and logical facts. Further vocabularies specifically tailored to certain use cases are, e.g., Friend-of-a-Friend (FOAF) and others. It is easy to see that those triple datasets can also be represented as labeled directed graphs, the vertices of which are the elements occurring as subjects or objects, and each triple (s, p, o) induces an edge from s to o with label p. Labels of vertices are induced by triples of the form (s, rdf:type, c), and in particular for each such triple, the vertex s is labeled with c.
The Web Ontology Language (OWL) was founded in 2004 as an improvement of the Resource Description Framework (RDF) and the corresponding RDF Schema (RDFS). OWL and its successor OWL2 have various dialects providing different expressibility and complexity such that always one can be chosen that best fits the user’s purpose. Most of the dialects, and in particular the dialects OWL DL, OWL2 DL, and OWL2 EL, have a strong logical underpinning by means of Description Logics (DLs). DLs are a family of logical languages for knowledge representation and reasoning, for which the decidability and complexity of common reasoning problems are widely explored. Those reasoning tasks allow for the deduction of implicit knowledge from explicitly given facts and axioms, and a vast amount of algorithms for solving those reasoning problems were developed, optimized, and implemented—the most popular ones are the tableaux algorithms and the completion algorithms.
An interesting problem in the field of Description Logics is the problem of learning, a specific instance of which is the acquisition of terminological knowledge from a given set of assertional facts. So far there are several techniques for achieving this, and some of them utilize the algorithmic solutions of the problem of computing implication bases in the field of Formal Concept Analysis, or utilize the Attribute Exploration algorithm that is capable of handling incomplete data by incorporating an expert in the domain of interest which is able to answer questions correctly and thus enables the algorithm to process axioms the validity of which is either not answerable within the input dataset, or is not refuted due to the non-existence of a counterexample. A famous work in this direction was published by Baader and Distel [2, 3, 16] who generalized the computation, or exploration, respectively, of implication bases for formal contexts to the computation, or exploration, respectively, of bases of concept inclusions (CIs) valid in a given interpretation and expressible in the description logic \(\mathcal{EL}^{\!\perp }\). Furthermore, Borchmann [10, 11] defined the notion of confidence of a CI within an interpretation, a measure indicating which fraction of the individuals in the interpretation fulfill a certain CI. He then developed a technique for the construction of a base of CIs the confidence of which exceeds a pre-defined threshold in [0, 1]. His work is particularly useful for datasets occuring in practical use cases where it cannot be ruled out that there is some noise, i.e., errors, in the dataset to be analyzed. Borchmann then also investigated and constituted an explorative method for the axiomatization of confident CIs, which also needs an interpretation as input, and furthermore an expert that is capable of correctly answering questions in the domain of interest.
We consider social networks that are encoded as description graphs, i.e., as directed graphs the vertices and edges of which are labeled. The aim is to extract terminological axioms, so-called concept inclusions, from the graph in order to describe the logical structure of the social network. Furthermore, we assume that the underlying graph to be analyzed is complete and error-free, i.e., fully describes all persons and entities in the social network as well as their connections. It is straightforward that description graphs and interpretations are isomorphic—we will later elaborate on this fact. In particular, we consider a social network that is given in form of an interpretation \(\mathcal{I}\), which we indeed may assume for the aforementioned reason. Our aim now is to formulate terminological axioms that are valid in \(\mathcal{I}\), i.e., we are searching for CIs C ⊑ D that are valid in \(\mathcal{I}\). Furthermore, we shall do this in a complete manner. However, it is easy to see that the number of concept inclusions that are expressible over a given signature is infinite; and in case of a restricted role depth and a finite signature there are only finitely many concept inclusions. By some simple observations, one can verify that the number of concept descriptions with a role depth of δ + 1 is exponential in the number of concept descriptions with a role depth of δ. Consequently, it would certainly not be a good idea to enumerate all valid concept inclusions of \(\mathcal{I}\). We should rather try to find a base for the valid CIs of \(\mathcal{I}\), as it has been first investigated by Baader and Distel in [2, 16] with respect to greatest fixpoint semantics, and later by Borchmann, Distel, and Kriegel, in [12] with respect to descriptive semantics (the default semantics). A base of CIs for \(\mathcal{I}\) is a TBox \(\mathcal{B}\) such that for each concept inclusion C ⊑ D, \(\mathcal{I}\models C \sqsubseteq D\) if, and only if, \(\mathcal{B}\models C \sqsubseteq D\). A slight generalization of the notion of a base for an interpretation has been introduced in [29], which allows for the incorporation of existing knowledge.
In this chapter we in particular provide a generalization of the aforementioned means for constructing bases of CIs in the more expressive description logic \(\mathcal{MH}\), and also demonstrate how the technique can be applied to social graphs. This chapter is structured as follows. In Sect. 2 the notion of a social graph is defined, and it is shown that the data model of Facebook induces a social graph. Section 3 gives a short introduction to the Web Ontology Language (OWL), and the following Sect. 4 presents the description logic \(\mathcal{MH}\) which is a monotonous fragment of the DL \(\mathcal{SROIQ}\) underlying the second version of OWL. Then in Sect. 5 we investigate the lattice induced by the \(\mathcal{M}\)-concept descriptions. Section 6 gives a brief introduction to Formal Concept Analysis. In Sect. 7 we show that each interpretation in the description logic \(\mathcal{MH}\) induces a Galois connection between the set of \(\mathcal{MH}\)-concept descriptions and the powerset of the interpretation’s domain; in particular Sect. 8 justifies the existence of the aforementioned Galois connection by providing a construction for so-called role-depth-bounded model-based most specific concept descriptions in the DL \(\mathcal{M}\). Section 9 generalizes the notion of a concept lattice from formal contexts to \(\mathcal{MH}\)-interpretations. Furthermore, Sect. 10 presents an important connection between Formal Concept Analysis and \(\mathcal{MH}\)-interpretations, which is then utilized in Sect. 11 to develop a construction method for knowledge bases of \(\mathcal{MH}\)-interpretations. Eventually, Sect. 12 gives a short overview on description logics the expressivity of which is below \(\mathcal{MH}\) and that may also be used as a language for axiomatizing terminological knowledge. The chapter closes with Sect. 13.
2 Social Networks and Social Graphs
A social graph is a directed graph the vertices and edges of which are labeled. The vertices represent the entities, e.g., persons, events, messages, etc., and the edges represent relationships between the entities, e.g., friendship between persons, attendance of a person to an event, a person liking a message, etc. Formally, we describe social networks as follows. First, fix a set N V of vertex labels as well as a set N E of edge labels. Then, a social graph over (N V, N E) is a tuple \(\mathcal{G}\,:=\,(V,E,L_{V },L_{E})\) where
-
1.
V is a set of vertices,
-
2.
E ⊆ V × V is a set of directed edges,
-
3.
 is a vertex labeling function, and
is a vertex labeling function, and -
4.
 is an edge labeling function.
is an edge labeling function.
A toy example of a social graph is shown in Fig. 1. It contains two persons, Alice and Bob, which are friends. Furthermore, Alice attends a concert and publishes a message which Bob likes. Bob publishes a message, too.
As an exemplary social network we consider Facebook [19], which is the most popular social network as of 2017. It has been founded by Mark Zuckerberg, and its website was launched in 2004. In the beginning it was limited to students from Harvard, but was later opened stepwise to a broader audience. In 2006 everybody with an age of at least 13 was allowed to create an account on Facebook. Since its beginning it has successfully evolved to a networking platform, which allows its users to publish messages, share photos, etc., and interact with each other, e.g., by liking other’s activities, communicating with private messages, connecting by (digital) friendship, etc. Facebook’s data is available via the Facebook Graph API, cf. [20]. Its data model fits well for our use case—it is accessible as a directed graph with labeled vertices and edges. In general the Facebook graph consists of nodes, edges, and fields. The nodes represent entities, like persons, photos, comments, events, etc.; the edges represent connections between the entities, e.g., an edge could link a photo to a person, or express that two persons are virtual friends; the fields represent information about the entities, e.g., a person’s name, a person’s birthday, the publish date of a comment, etc. In terms of description logics, those field values can be expressed by appropriate values in concrete domains. We will not go into detail here, and rather refer the interested reader to [20].
3 The Web Ontology Language (OWL)
The Web Ontology Language (OWL) was introduced in its first version in 2004 as an extension of the Resource Description Framework (RDF) and RDF Schema (RDFS) in order to provide a well-founded semantics and to increase the expressibility of the language. There were some language constructs expressible in RDF/RDFS leading to inconsistencies or undecidability that are not expressible in OWL anymore, i.e., OWL resolved this issue. Later in 2009, a more expressive second version OWL2 was founded.
However, RDF was not fully replaced, but remained a storage format for OWL, besides other formats, e.g., XML, Manchester Syntax, etc. A new vocabulary was defined, which allowed for the expression of the language constructs of OWL, e.g., the predicate owl:isA for assigning types to individuals (similar to rdf:type), the predicate owl:subClassOf for expressing subclass relationships, etc. For a full reference, the reader is referred to [46]—in the sequel of this chapter we only consider some of the provided language constructs. In particular, we will leave out concrete domains, disjunctions and negations, and others. Additionally, plenty of information including interesting examples and use cases can be found in the book [26] of Hitzler, Krötzsch, and Rudolph. OWL and its dialects are used for the Semantic Web and for Linked Data, e.g., in the medical domain (SNOMED ontology), and in DBpedia as well as Wikidata (structured machine-readable derivations of Wikipedia).
The logical underpinning of OWL and some of its dialects is provided by Description Logics (DLs), which are a family of conceptual languages suitable for knowledge representation and reasoning that have a strong logical foundation for which the decidability and complexity of common reasoning problems is widely explored. In particular, the reasoning tasks allow for deduction of implicit knowledge from explicitly stated facts and axioms, and plenty of appropriate algorithms were developed and implemented, e.g., tableaux algorithms and completion algorithms. In particular, the full first version of the Web Ontology Language corresponds to the description logic \(\mathcal{SHOIN}\), and the full second version of the Web Ontology Language is covered by the description logic \(\mathcal{SROIQ}\). In the next Sect. 4, we shall focus on (a fragment of) the description logic \(\mathcal{SROIQ}\), which is suitable for terminological learning, i.e., which allows for a certain degree of abstraction and not only rewrites given assertional data into terminological axioms. In particular, this implies that we shall not make use of neither negation, nor disjunction, nor nominals, nor other constructors that can emulate the aforementioned.
4 The Description Logic \(\mathcal{MH}\)
This section presents the description logic  , which is a fragment of \(\mathcal{SROIQ}\), and allows for conjunctions, primitive negations, value restrictions, qualified at-least restrictions, unqualified at-most restrictions, and existential self restrictions. Furthermore, we will not focus on the implementation details of OWL, and do not present any of the different syntaxes of OWL, but rather use the theoretical notations that are used in the field of description logics. The considered description logic
, which is a fragment of \(\mathcal{SROIQ}\), and allows for conjunctions, primitive negations, value restrictions, qualified at-least restrictions, unqualified at-most restrictions, and existential self restrictions. Furthermore, we will not focus on the implementation details of OWL, and do not present any of the different syntaxes of OWL, but rather use the theoretical notations that are used in the field of description logics. The considered description logic  is abbreviated as \(\mathcal{M}\), which encodes the monotonicity of all allowed constructors.
is abbreviated as \(\mathcal{M}\), which encodes the monotonicity of all allowed constructors.
Consider a finite signature Σ : = (N
C, N
R), that is, N
C is a finite set of concept names, and N
R is a finite set of role names. Then an \(\mathcal{M}\)-concept description over Σ can be constructed according to the following inductive rule where A ∈ N
C, r ∈ N
R, and  .
.

The semantics are model-theoretic, that is, they are defined by means of so-called interpretations. An interpretation
\(\mathcal{I}\) over Σ = (N
C, N
R) is a pair \((\varDelta ^{\mathcal{I}},\cdot ^{\mathcal{I}})\) consisting of a non-empty set \(\varDelta ^{\mathcal{I}}\) which is called domain, and an extension function  that maps concept names A ∈ N
C to subsets \(A^{\mathcal{I}} \subseteq \varDelta ^{\mathcal{I}}\), and role names r ∈ N
R to binary relations \(r^{\mathcal{I}} \subseteq \varDelta ^{\mathcal{I}} \times \varDelta ^{\mathcal{I}}\). The extension function is then canonically extended to all \(\mathcal{M}\)-concept descriptions according to the following recursive definitions.
that maps concept names A ∈ N
C to subsets \(A^{\mathcal{I}} \subseteq \varDelta ^{\mathcal{I}}\), and role names r ∈ N
R to binary relations \(r^{\mathcal{I}} \subseteq \varDelta ^{\mathcal{I}} \times \varDelta ^{\mathcal{I}}\). The extension function is then canonically extended to all \(\mathcal{M}\)-concept descriptions according to the following recursive definitions.

Of course, we may emulate existential restrictions, the expressibility of which is symbolized by the letter \(\mathcal{E}\) within the description logic’s name, by using the abbreviation  , i.e., both \(\mathcal{M}\) and
, i.e., both \(\mathcal{M}\) and  denote essentially the same logic. It is readily verified that the following equation for the extension of existential restrictions is satisfied.
denote essentially the same logic. It is readily verified that the following equation for the extension of existential restrictions is satisfied.

Informally, the role depth of a concept description is defined as the maximal number of nestings of role quantifiers. More specifically, we define the role depth rd(C) of an \(\mathcal{M}\)-concept description C recursively as follows.

The set of all \(\mathcal{M}\)-concept descriptions over a signature Σ is symbolized as \(\mathcal{M}(\varSigma )\), and for a role-depth bound  , we denote by \(\mathcal{M}(\varSigma )\upharpoonright _{\delta }\) the set of all \(\mathcal{M}\)-concept descriptions over Σ with a role depth not exceeding δ.
, we denote by \(\mathcal{M}(\varSigma )\upharpoonright _{\delta }\) the set of all \(\mathcal{M}\)-concept descriptions over Σ with a role depth not exceeding δ.
A concept inclusion (abbr. CI) is an expression C ⊑ D where both C and D are concept descriptions. A terminological box (abbr. TBox) is a finite set of concept inclusions. A CI C ⊑ D is valid in \(\mathcal{I}\) if \(C^{\mathcal{I}} \subseteq D^{\mathcal{I}}\). We then also refer to \(\mathcal{I}\) as a model of C ⊑ D, and denote this by \(\mathcal{I}\models C \sqsubseteq D\). Furthermore, \(\mathcal{I}\) is a model of a TBox \(\mathcal{T}\), symbolized as \(\mathcal{I}\models \mathcal{T}\), if each CI in \(\mathcal{T}\) is valid in \(\mathcal{I}\). The entailment relation is lifted to TBoxes as follows: A CI C ⊑ D is entailed by a TBox \(\mathcal{T}\), denoted as \(\mathcal{T}\models C \sqsubseteq D\), if each model of \(\mathcal{T}\) is a model of C ⊑ D, too. We then also say that C is subsumed by D with respect to \(\mathcal{T}\). A TBox \(\mathcal{T}\) entails a TBox \(\mathcal{U}\), symbolized as \(\mathcal{T}\models \mathcal{U}\), if \(\mathcal{T}\) entails each CI in \(\mathcal{U}\), or equivalently if each model of \(\mathcal{T}\) is also a model of \(\mathcal{U}\). Two \(\mathcal{M}\)-concept descriptions C and D are equivalent with respect to \(\mathcal{T}\), and we shall write \(\mathcal{T}\models C \equiv D\), if  . In case \(\mathcal{T} =\emptyset\) we may omit the prefix “∅⊧”. However, then we have to carefully interpret an expression C ⊑ D—it either just denotes a concept inclusion, i.e., an axiom, without stating where it is valid; or it expresses that C is subsumed by D (w.r.t. ∅), i.e., \(C^{\mathcal{I}} \subseteq D^{\mathcal{I}}\) is satisfied in all interpretations \(\mathcal{I}\). An analogous hint applies to concept equivalences C ≡ D.
. In case \(\mathcal{T} =\emptyset\) we may omit the prefix “∅⊧”. However, then we have to carefully interpret an expression C ⊑ D—it either just denotes a concept inclusion, i.e., an axiom, without stating where it is valid; or it expresses that C is subsumed by D (w.r.t. ∅), i.e., \(C^{\mathcal{I}} \subseteq D^{\mathcal{I}}\) is satisfied in all interpretations \(\mathcal{I}\). An analogous hint applies to concept equivalences C ≡ D.
To justify the choice of the abbreviation \(\mathcal{M}\) for  , we remark that each of the constructors is monotonous, i.e., it holds true that for all \(\mathcal{M}\)-concept descriptions C, D, E, all role names r ∈ N
R, and all natural numbers
, we remark that each of the constructors is monotonous, i.e., it holds true that for all \(\mathcal{M}\)-concept descriptions C, D, E, all role names r ∈ N
R, and all natural numbers  ,
,

A role inclusion (abbr. RI) is an expression r ⊑ s where r, s ∈ N R are role names. A relational box (abbr. RBox) is a finite set of role inclusions. For an interpretation \(\mathcal{I}\), we say that r ⊑ s is valid in \(\mathcal{I}\), denoted as \(\mathcal{I}\models r \sqsubseteq s\), if \(r^{\mathcal{I}} \subseteq s^{\mathcal{I}}\). Furthermore, an RBox \(\mathcal{R}\) is valid in \(\mathcal{I}\), symbolized as \(\mathcal{I}\models \mathcal{R}\), if each role inclusion in \(\mathcal{R}\) is valid in \(\mathcal{I}\). In case a description logic allows for the usage of these role inclusions, then its name contains the letter \(\mathcal{H}\). In what follows we are going to merely consider the description logic \(\mathcal{MH}\).
In order to decide entailment, the well-known tableaux algorithm [5, Sect. 3.4] can be utilized. It takes as input a knowledge base \((\mathcal{T},\mathcal{A})\) consisting of a TBox and an ABox, and tries to construct a model of the knowledge base. It was shown that the tableaux algorithm is sound (i.e., the output is indeed a model), complete (i.e., if a model exists, then a model is constructed and returned), and terminates (i.e., for finite input yields a result after a finite amount of time). These are the following common reasoning problems, cf. [5, Sect 3.2.2].
-
1.
Knowledge Base Consistency: Given a knowledge base \(\mathcal{K}\), is there a model of \(\mathcal{K}\)?
-
2.
Concept Satisfiability: Given a concept description C, and a knowledge base \(\mathcal{K}\), is there a model of \(\mathcal{K}\) in which C has a non-empty extension?
-
3.
Concept Subsumption: Given two concept descriptions C and D, and a knowledge base \(\mathcal{K}\), does \(\mathcal{I}\models C \sqsubseteq D\) hold true for all models \(\mathcal{I}\) of \(\mathcal{K}\)?
-
4.
Concept Equivalence: Given two concept descriptions C and D, and a knowledge base \(\mathcal{K}\), does \(\mathcal{I}\models C \equiv D\) hold true for all models \(\mathcal{I}\) of \(\mathcal{K}\)?
-
5.
Instance Checking: Given an individual a, a concept description C, and a knowledge base \(\mathcal{K}\), does \(\mathcal{K}\) entail
 ?
? -
6.
Role Instance Checking: Given two individuals a and b, a role name r, and a knowledge base \(\mathcal{K}\), does \(\mathcal{K}\) entail
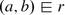 ?
?
There is a strong correspondence between interpretations and directed labeled graphs, and in particular it is easy to translate between both formalisms. We start with defining a description graph, which is very similar to a social graph as introduced in Sect. 2. A description graph over a signature (N C, N R) is a tuple \(\mathcal{G}\,:=\,(V,E,L_{V },L_{E})\) that satisfies the following conditions.
-
1.
(V, E) is a directed graph, i.e., V is a set of vertices, and E ⊆ V × V is a set of directed edges,
-
2.
 is a vertex labelling, and
is a vertex labelling, and -
3.
 is an edge labelling.
is an edge labelling.
Please note that in some works description graphs are defined to have a distinguished root vertex—however, this is not necessary for our purposes.
Each interpretation induces a directed labeled graph as follows: let \(\mathcal{I}\,:=\,(\varDelta ^{\mathcal{I}},\cdot ^{\mathcal{I}})\) be an interpretation over the signature (N C, N R). Then, define the description graph \(\mathcal{G}(\mathcal{I})\,:=\,(V,E,L_{V },L_{E})\) over (N C, N R) that consists of the directed graph (V, E) with the components

and the corresponding labeling functions

Note that \(\mathcal{G}(\mathcal{I})\) just formalizes the natural graphical representation of interpretations as they are usually drawn in toy examples.
Vice versa, if \(\mathcal{G}\,:=\,(V,E,L_{V },L_{E})\) is a description graph over (N C, N R), then its induced interpretation is \(\mathcal{I}(\mathcal{G})\,:=\,(\varDelta ^{\mathcal{I}(\mathcal{G})},\cdot ^{\mathcal{I}(\mathcal{G})})\) the components of which are defined in the following way.

It is readily verified that the two transformations are mutually inverse, and this justifies that we do not have to distinguish between interpretations and description graphs (or social graphs) in the sequel of this document.
5 The Lattice of \(\mathcal{M}\)-Concept Descriptions
It is readily verified that the subsumption ⊑ with respect to the empty TBox ∅ constitutes a quasi-order on the set \(\mathcal{M}(\varSigma )\) of all \(\mathcal{M}\)-concept descriptions over the signature Σ = (N C, N R), i.e., the following conditions are satisfied.
-
1.
⊑ w.r.t. ∅ is reflexive, i.e., for all \(\mathcal{M}\)-concept descriptions C, ∅⊧C ⊑ C, and
-
2.
⊑ w.r.t. ∅ is transitive, i.e., for all \(\mathcal{M}\)-concept descriptions C, D, E, it holds true that ∅⊧C ⊑ D and ∅⊧D ⊑ E implies ∅⊧C ⊑ E.
Of course, then the equivalence ≡ with respect to ∅ is an equivalence relation, i.e., the following statements hold true.
-
1.
≡ w.r.t. ∅ is reflexive, i.e., for all \(\mathcal{M}\)-concept descriptions C, ∅⊧C ≡ C,
-
2.
≡ w.r.t. ∅ is transitive, i.e., for all \(\mathcal{M}\)-concept descriptions C, D, E, we have that ∅⊧C ≡ D and ∅⊧D ≡ E implies ∅⊧C ≡ E, and
-
3.
≡ w.r.t. ∅ is symmetric, i.e., for all \(\mathcal{M}\)-concept descriptions C, D, it holds true that ∅⊧C ≡ D implies ∅⊧D ≡ C.
By definition it follows that it is the induced equivalence relation of ⊑, i.e., ∅⊧C ≡ D if, and only if, ∅⊧C ⊑ D as well as ∅⊧D ⊑ C. Hence, the quotient of \((\mathcal{M}(\varSigma ),\sqsubseteq )\) with respect to the induced equivalence ≡ w.r.t. ∅ is a partially ordered set (a poset). It consists of all equivalence classes \(\left [C\right ]_{\equiv }\) for \(\mathcal{M}\)-concept descriptions C, which are defined by

Furthermore, for an equivalence class \(\left [C\right ]_{\equiv }\), we say that C is a representative of it. We can then define a partial order on the classes which is induced by the subsumption between their representatives, i.e., for all \(\mathcal{M}\)-concept descriptions C, D,
This partial order enjoys all properties of a quasi-order as stated above, and furthermore is anti-symmetric, i.e., for all \(\mathcal{M}\)-concept descriptions C, D,
For the sake of simplicity, we will not distinguish between the equivalence classes and their representatives in the sequel of this chapter. The poset \((\mathcal{M}(\varSigma ),\sqsubseteq )/\!\equiv \) is even a bounded lattice. Of course, ⊥ is the smallest element, and ⊤ is the greatest element. It is easy to see that the (finitary) conjunction  corresponds to the finitary infimum operation, since for all finite sets \(\mathcal{C}\) of \(\mathcal{M}\)-concept descriptions over Σ, it holds that the conjunction
corresponds to the finitary infimum operation, since for all finite sets \(\mathcal{C}\) of \(\mathcal{M}\)-concept descriptions over Σ, it holds that the conjunction  is the greatest lower bound (w.r.t. ⊑ ) of all concept descriptions in \(\mathcal{C}\), i.e.,
is the greatest lower bound (w.r.t. ⊑ ) of all concept descriptions in \(\mathcal{C}\), i.e.,  for all \(C \in \mathcal{ C}\), and for all \(\mathcal{M}\)-concept descriptions D with ∅⊧D ⊑ C for all \(C \in \mathcal{ C}\), it holds true that
for all \(C \in \mathcal{ C}\), and for all \(\mathcal{M}\)-concept descriptions D with ∅⊧D ⊑ C for all \(C \in \mathcal{ C}\), it holds true that  . However, what is missing is a supremum operation. Of course, in description logics allowing for disjunction, we can easily prove that the disjunction is the supremum operation. For the general case, the notion of a smallest upper bound is rather called least common subsumer in the field of description logics, and is defined as follows.
. However, what is missing is a supremum operation. Of course, in description logics allowing for disjunction, we can easily prove that the disjunction is the supremum operation. For the general case, the notion of a smallest upper bound is rather called least common subsumer in the field of description logics, and is defined as follows.
Definition 5.1
Let C, D be \(\mathcal{M}\)-concept descriptions over the signature Σ. Then a concept description \(E \in \mathcal{ M}(\varSigma )\) is called a least common subsumer (abbr. LCS) of C and D if the following conditions are fulfilled.
-
1.
E subsumes both C and D, i.e., ∅⊧C ⊑ E and ∅⊧D ⊑ E.
-
2.
Whenever F is a common subsumer of C and D, then F subsumes E, i.e., for all concept descriptions \(F \in \mathcal{ M}(\varSigma )\),
 implies ∅⊧E ⊑ F.
implies ∅⊧E ⊑ F.
It follows that least common subsumers are always unique up to equivalence. Hence, we can speak of the LCS of two concept descriptions, and furthermore we denote it by C ∨ D. The definition can be canonically extended to an arbitrary number of concept descriptions, and we then write \(\bigvee \mathcal{C}\) for the least common subsumer of a set \(\mathcal{C}\) of \(\mathcal{M}\)-concept descriptions over Σ. It is readily verified that the conjunction is a categorical product, cf. Fig. 2, and dually the least common subsumer is a categorical coproduct, cf. Fig. 3.
The conjunction is a product in the category the objects of which are concept descriptions and the morphisms of which are subsumptions, cf. [38, p. 69]
The least common subsumer is a coproduct in the category the objects of which are concept descriptions and the morphisms of which are subsumptions, cf. [38, p. 63]
It was shown that least common subsumers always exist in several description logics, e.g., in \(\mathcal{EL}\), \(\mathcal{FLE}\), and \(\mathcal{ALE}\), as shown in [4] by Baader, Küsters, and Molitor; in \(\mathcal{ALQ}\) and \(\mathcal{ALENR}\) as shown in [40, 41] by Mantay; in \(\mathcal{ALEN}\) as shown in [33] by Küsters and Molitor; in \(\mathcal{ALEHIN}_{\!R^{+}}\) as shown in [18] by Donini, Colucci, Di Noia, and Di Sciascio; in \(\mathcal{EL}_{\mathsf{gfp}}\), i.e., \(\mathcal{EL}\) interpreted with greatest fixpoint semantics, as shown in [1] by Baader; in \(\mathcal{FLE}_{\mathsf{gfp}}\) as shown in [14] by Distel; and in \(\mathcal{EL}_{\mathsf{gfp}}^{\!\perp }\) as shown by Distel in [16].
As a practical means for ensuring the existence of least common subsumers, we could also apply a bound on the role depth of the concept descriptions under consideration. For the case of \(\mathcal{EL}^{\!\perp }\) this has been done in [12] by Borchmann, Distel, and Kriegel. However, this result also applies to all other description logics equipped with a bound on the role depths—in particular, we know that then for all concept descriptions C and D, there are only finitely many concept descriptions that satisfy the role depth bound, use only concept names and role names occuring in C or D, and that only include numbers in at-least or at-most restrictions not exceeding those occuring in C or D. Denote the conjunction of these three properties by ∗. Then, we can infer that

holds true and is a well-defined formula as the set  must be finite, and thus its conjunction indeed exists. Note that this is a rather theoretical argument showing the existence, but not allowing for a practical computation of least common subsumers.
must be finite, and thus its conjunction indeed exists. Note that this is a rather theoretical argument showing the existence, but not allowing for a practical computation of least common subsumers.
It is easy to see that the equivalence ≡ is compatible with both ⊓ and ∨. In the sequel of this chapter, we shall denote this bounded lattice by  , and accordingly
, and accordingly  symbolizes the bounded lattice of (equivalence classes of) \(\mathcal{M}\)-concept descriptions the role depth of which is bounded by δ. Note that
symbolizes the bounded lattice of (equivalence classes of) \(\mathcal{M}\)-concept descriptions the role depth of which is bounded by δ. Note that  is indeed complete if the underlying signature Σ is finite, since then there are only finitely many \(\mathcal{M}\)-concept descriptions over Σ with a role depth of at most δ. Eventually, the dual
is indeed complete if the underlying signature Σ is finite, since then there are only finitely many \(\mathcal{M}\)-concept descriptions over Σ with a role depth of at most δ. Eventually, the dual  of the lattice
of the lattice  is obtained by simply reversing the order relation, and an analogous notion applies to the lattice
is obtained by simply reversing the order relation, and an analogous notion applies to the lattice  .
.
6 Formal Concept Analysis
This section briefly introduces the standard notions of Formal Concept Analysis (abbr. FCA) [24]. A formal context  consists of a set G of objects (Gegenstände in German), a set M of attributes (Merkmale in German), and an incidence relation I ⊆ G × M. For a pair (g, m) ∈ I, we say that g has m. The derivation operators of
consists of a set G of objects (Gegenstände in German), a set M of attributes (Merkmale in German), and an incidence relation I ⊆ G × M. For a pair (g, m) ∈ I, we say that g has m. The derivation operators of  are the mappings
are the mappings  and
and  such that for each object set A ⊆ G, the set A
I contains all attributes that are shared by all objects in A, and dually for each attribute set B ⊆ M, the set B
I contains all those objects that have all attributes from B. Formally, we define the derivation operators as follows.
such that for each object set A ⊆ G, the set A
I contains all attributes that are shared by all objects in A, and dually for each attribute set B ⊆ M, the set B
I contains all those objects that have all attributes from B. Formally, we define the derivation operators as follows.

For singleton sets, we may also use the abbreviations  for all objects g ∈ G, as well as
for all objects g ∈ G, as well as  for all attributes m ∈ M.
for all attributes m ∈ M.
It is well-known [24] that both derivation operators constitute a so-called Galois connection between the powersets  and
and  , i.e., the following statements hold true for all subsets A, A
1, A
2 ⊆ G and B, B
1, B
2 ⊆ M.
, i.e., the following statements hold true for all subsets A, A
1, A
2 ⊆ G and B, B
1, B
2 ⊆ M.
For obvious reasons, formal contexts can be represented as binary tables the rows of which are labeled with the objects, the columns of which are labeled with the attributes, and the occurrence of a cross × in the cell at row g and column m indicates that the object g has the attribute m.
An intent of  is an attribute set B ⊆ M with B = B
II. The set of all intents of
is an attribute set B ⊆ M with B = B
II. The set of all intents of  is denoted by
is denoted by  . An implication over M is an expression X → Y where X, Y ⊆ M. It is valid in
. An implication over M is an expression X → Y where X, Y ⊆ M. It is valid in  , denoted as
, denoted as  , if X
I ⊆ Y
I, i.e., if each object of
, if X
I ⊆ Y
I, i.e., if each object of  that possesses all attributes in X also has all attributes in Y. An implication set \(\mathcal{L}\) is valid in
that possesses all attributes in X also has all attributes in Y. An implication set \(\mathcal{L}\) is valid in  , denoted as
, denoted as  , if all implications in \(\mathcal{L}\) are valid in
, if all implications in \(\mathcal{L}\) are valid in  . Furthermore, the relation ⊧ is lifted to implication sets as follows: an implication set \(\mathcal{L}\) entails an implication X → Y, symbolized as \(\mathcal{L}\models X \rightarrow Y\), if X → Y is valid in all formal contexts in which \(\mathcal{L}\) is valid. More specifically, ⊧ is called the semantic entailment relation.
. Furthermore, the relation ⊧ is lifted to implication sets as follows: an implication set \(\mathcal{L}\) entails an implication X → Y, symbolized as \(\mathcal{L}\models X \rightarrow Y\), if X → Y is valid in all formal contexts in which \(\mathcal{L}\) is valid. More specifically, ⊧ is called the semantic entailment relation.
A model of X → Y is an attribute set Z ⊆ M such that X ⊆ Z implies Y ⊆ Z, and we shall then write Z⊧X → Y. Of course, then an implication X → Y is valid in  if, and only if, for each object g ∈ G, the object intent g
I is a model of X → Y. It is furthermore straightforward to verify that the following statements are equivalent.
if, and only if, for each object g ∈ G, the object intent g
I is a model of X → Y. It is furthermore straightforward to verify that the following statements are equivalent.
-
1.
X → Y is valid in
 .
. -
2.
Each object intent of
 is a model of X → Y.
is a model of X → Y. -
3.
Each intent of
 is a model of X → Y.
is a model of X → Y. -
4.
Y ⊆ X II.
The equivalence between the first and the last statement indicates that X
II is the largest consequence of X in  , i.e., X → X
II is valid in
, i.e., X → X
II is valid in  , and for each strict superset \(Z \supsetneq X^{II}\), the implication X → Z is not valid in
, and for each strict superset \(Z \supsetneq X^{II}\), the implication X → Z is not valid in  .
.
Consider an implication set  . A model of \(\mathcal{L}\) is an attribute set which is a simultaneous model of each implication in \(\mathcal{L}\). In particular, each model Z of \(\mathcal{L}\) satisfies the following: for each implication \(X \rightarrow Y \in \mathcal{ L}\), X ⊆ Z implies Y ⊆ Z, i.e., Z is a fixed point of the operator
. A model of \(\mathcal{L}\) is an attribute set which is a simultaneous model of each implication in \(\mathcal{L}\). In particular, each model Z of \(\mathcal{L}\) satisfies the following: for each implication \(X \rightarrow Y \in \mathcal{ L}\), X ⊆ Z implies Y ⊆ Z, i.e., Z is a fixed point of the operator

The smallest model \(Z^{\mathcal{L}}\) of \(\mathcal{L}\) that contains Z is obtained by successive exhaustive application of the operator \(\cdot ^{\mathcal{L}(1)}\), i.e.,  where \(Z^{\mathcal{L}(n+1)}\,:=\,(Z^{\mathcal{L}(1)})^{\mathcal{L}(n)}\) for all n ≥ 1. Additionally, the following statements are equivalent.
where \(Z^{\mathcal{L}(n+1)}\,:=\,(Z^{\mathcal{L}(1)})^{\mathcal{L}(n)}\) for all n ≥ 1. Additionally, the following statements are equivalent.
-
1.
\(\mathcal{L}\) entails X → Y.
-
2.
Each model of \(\mathcal{L}\) is a model of X → Y.
-
3.
X → Y is valid in all those formal contexts with attribute set M in which \(\mathcal{L}\) is valid.
-
4.
\(Y \subseteq X^{\mathcal{L}}\).
We then infer that \(X^{\mathcal{L}}\) is the largest consequence of X with respect to the implication set \(\mathcal{L}\), i.e., \(\mathcal{L}\) entails \(X \rightarrow X^{\mathcal{L}}\), and for all supersets \(Y \supsetneq X^{\mathcal{L}}\), the implication X → Y does not follow from \(\mathcal{L}\).
It was shown that entailment can also be decided syntactically by applying deduction rules to the implication set \(\mathcal{L}\) without the requirement to consider all formal contexts in which \(\mathcal{L}\) is valid, or all models of \(\mathcal{L}\), respectively. Recall that an implication X → Y is syntactically entailed by an implication set \(\mathcal{L}\), denoted by \(\mathcal{L} \vdash X \rightarrow Y\), if X → Y can be constructed from \(\mathcal{L}\) by the application of inference axioms, cf. [39, p. 47], which are described as follows.

In the inference axioms above the symbols X, Y, Z, and W denote arbitrary subsets of the considered set M of attributes. Formally, we define \(\mathcal{L} \vdash X \rightarrow Y\) if there is a finite sequence of implications X 0 → Y 0, …, X n → Y n such that the following conditions hold.
-
1.
For each
 , there is a subset
, there is a subset  such that \(\mathcal{L}_{i} \vdash X_{i} \rightarrow Y _{i}\) matches one of the Axioms F1–F6.
such that \(\mathcal{L}_{i} \vdash X_{i} \rightarrow Y _{i}\) matches one of the Axioms F1–F6. -
2.
X n → Y n = X → Y.
Often, the Axioms F1, F2, and F6 are referred to as Armstrong’s axioms. These three axioms constitute a complete and independent set of inference axioms for entailment, i.e., from it the other Axioms F3–F5 can be derived, and none of them is derivable from the others.
The semantic entailment and the syntactic entailment coincide, i.e., an implication X → Y is semantically entailed by an implication set \(\mathcal{L}\) if, and only if, \(\mathcal{L}\) syntactically entails X → Y, cf. [39, Theorem 4.1 on Page 50] as well as [24, Proposition 21 on Page 81]. Consequently, we do not have to distinguish between both entailment relations ⊧ and ⊢ when it is up to decide whether an implication follows from a set of implications.
The data encoded in a formal context can be visualized as a line diagram of the corresponding concept lattice, which we shall shortly describe. A formal concept of a formal context  is a pair (A, B) consisting of a set A ⊆ G of objects as well as a set B ⊆ M of attributes such that A
I = B and B
I = A. We then also refer to A as the extent, and to B as the intent, respectively, of (A, B). Another characterization of a formal concept is as follows: (A, B) is a formal concept of
is a pair (A, B) consisting of a set A ⊆ G of objects as well as a set B ⊆ M of attributes such that A
I = B and B
I = A. We then also refer to A as the extent, and to B as the intent, respectively, of (A, B). Another characterization of a formal concept is as follows: (A, B) is a formal concept of  if, and only if, A ⊆ G, B ⊆ M, and both A and B are maximal with respect to the property A × B ⊆ I, i.e., for each strict superset \(C \supsetneq A\), C × B ⊈ I, and accordingly for each strict superset \(D \supsetneq B\), A × D ⊈ I. In the denotation of
if, and only if, A ⊆ G, B ⊆ M, and both A and B are maximal with respect to the property A × B ⊆ I, i.e., for each strict superset \(C \supsetneq A\), C × B ⊈ I, and accordingly for each strict superset \(D \supsetneq B\), A × D ⊈ I. In the denotation of  as a cross table, those formal concepts are the maximal rectangles full of crosses (modulo reordering of rows and columns). Then, the set of all extents of
as a cross table, those formal concepts are the maximal rectangles full of crosses (modulo reordering of rows and columns). Then, the set of all extents of  is symbolized as
is symbolized as  , and the set of all formal concepts of
, and the set of all formal concepts of  is denoted as
is denoted as  , which is ordered by defining (A, B) ≤ (C, D) if, and only if, A ⊆ C. It was shown that this order always induces a complete lattice
, which is ordered by defining (A, B) ≤ (C, D) if, and only if, A ⊆ C. It was shown that this order always induces a complete lattice  , called the concept lattice of
, called the concept lattice of  , cf. [24, 48], in which the infimum and the supremum operation satisfy the equations
, cf. [24, 48], in which the infimum and the supremum operation satisfy the equations

and where ⊤ = (∅I, ∅II) is the greatest element, and where ⊥ = (∅II, ∅I) is the smallest element, respectively. The number of formal concepts can be exponential in the size of the formal context. Kuznetsov shows that determining this number is a #P-complete problem, cf. [34]. Furthermore, the problems of existence of a formal concept with restrictions on the size of the extent, intent, or both, respectively, are investigated in [34]—Kuznetsov demonstrates that the existence of a formal concept (A, B) such that | A | = k, | B | = k, or | A | + | B | = k, respectively, are NP-complete problems; the similar problems with ≥ are all in P; and the problems with ≤ are also in P, except the problem where | A | + | B | ≤ k is NP-complete.
Furthermore, the concept lattice of  can be nicely represented as a line diagram as follows: each formal concept is depicted as a vertex. Furthermore, there is an upward directed edge from each formal concept to its upper neighbors, i.e., to all those formal concepts which are greater with respect to ≤, but for which there is no other formal concept in between. The nodes are labeled as follows: an attribute m ∈ M is an upper label of the attribute concept (m
I, m
II), and an object g ∈ G is a lower label of the object concept (g
II, g
I). Then, the extent of the formal concept represented by a vertex consists of all objects which label vertices reachable by a downward directed path, and dually the intent is obtained by gathering all attribute labels of vertices reachable by an upward directed path.
can be nicely represented as a line diagram as follows: each formal concept is depicted as a vertex. Furthermore, there is an upward directed edge from each formal concept to its upper neighbors, i.e., to all those formal concepts which are greater with respect to ≤, but for which there is no other formal concept in between. The nodes are labeled as follows: an attribute m ∈ M is an upper label of the attribute concept (m
I, m
II), and an object g ∈ G is a lower label of the object concept (g
II, g
I). Then, the extent of the formal concept represented by a vertex consists of all objects which label vertices reachable by a downward directed path, and dually the intent is obtained by gathering all attribute labels of vertices reachable by an upward directed path.
Let  . A pseudo-intent of a formal context
. A pseudo-intent of a formal context  relative to an implication set \(\mathcal{L}\) is an attribute set P ⊆ M which is no intent of
relative to an implication set \(\mathcal{L}\) is an attribute set P ⊆ M which is no intent of  , but is a model of \(\mathcal{L}\), and satisfies Q
II ⊆ P for all pseudo-intents \(Q \subsetneq P\). The set of all those pseudo-intents is symbolized by
, but is a model of \(\mathcal{L}\), and satisfies Q
II ⊆ P for all pseudo-intents \(Q \subsetneq P\). The set of all those pseudo-intents is symbolized by  . Then the implication set
. Then the implication set

constitutes an implication base of  relative to \(\mathcal{L}\), i.e., for each implication X → Y over M, the following equivalence is satisfied.
relative to \(\mathcal{L}\), i.e., for each implication X → Y over M, the following equivalence is satisfied.

 is called the canonical base of
is called the canonical base of  relative to \(\mathcal{L}\). It can be shown that it is a minimal implication base of
relative to \(\mathcal{L}\). It can be shown that it is a minimal implication base of  relative to \(\mathcal{L}\), i.e., there is no implication base of
relative to \(\mathcal{L}\), i.e., there is no implication base of  relative to \(\mathcal{L}\) with smaller cardinality. Further information is given in [21, 23, 25, 45]. The most prominent algorithm for computing the canonical base is certainly NextClosure developed by Ganter [21, 23]. Bazhanov and Obiedkov propose an optimized version of NextClosure in [8] which speeds up the computation of the lectically next closure, and furthermore they then perform some benchmarks to compare both versions. Additionally, they also utilize three different algorithms for computing closures with respect to implication sets, i.e., firstly the already presented and straightforward algorithm which computes the (least) fixed point of the operator \(X\mapsto X^{\mathcal{L}(1)}\), see also [39], secondly the LinClosure algorithm [9], which computes \(X^{\mathcal{L}}\) in linear time, and thirdly Wild’s Closure algorithm [47], which is essentially an improved version of LinClosure. Please note that LinClosure is not always faster than computing the least fixed point of \(X\mapsto X^{\mathcal{L}(1)}\), due to its initialization overhead. Furthermore, Obiedkov and Duquenne constitute an attribute-incremental algorithm for constructing the canonical base, cf. [42]. A parallel algorithm called NextClosures is also available [28, 32], and an implementation is provided in Concept Explorer FX [27]; its advantage is that its processing time scales almost inverse linear with respect to the number of available CPU cores.
relative to \(\mathcal{L}\) with smaller cardinality. Further information is given in [21, 23, 25, 45]. The most prominent algorithm for computing the canonical base is certainly NextClosure developed by Ganter [21, 23]. Bazhanov and Obiedkov propose an optimized version of NextClosure in [8] which speeds up the computation of the lectically next closure, and furthermore they then perform some benchmarks to compare both versions. Additionally, they also utilize three different algorithms for computing closures with respect to implication sets, i.e., firstly the already presented and straightforward algorithm which computes the (least) fixed point of the operator \(X\mapsto X^{\mathcal{L}(1)}\), see also [39], secondly the LinClosure algorithm [9], which computes \(X^{\mathcal{L}}\) in linear time, and thirdly Wild’s Closure algorithm [47], which is essentially an improved version of LinClosure. Please note that LinClosure is not always faster than computing the least fixed point of \(X\mapsto X^{\mathcal{L}(1)}\), due to its initialization overhead. Furthermore, Obiedkov and Duquenne constitute an attribute-incremental algorithm for constructing the canonical base, cf. [42]. A parallel algorithm called NextClosures is also available [28, 32], and an implementation is provided in Concept Explorer FX [27]; its advantage is that its processing time scales almost inverse linear with respect to the number of available CPU cores.
There are some important complexity problems related to the pseudo-intents and canonical bases. Kuznetsov, and later together with Obiedkov, has proven in [35–37] that the number of pseudo-intents can be exponential in  as well as in
as well as in  or in
or in  , and determining this number is #P-hard, furthermore that recognizing a pseudo-intent is in coNP, and that determining the number of non-pseudo-intents is #P-complete. Sertkaya and Distel demonstrated in [15, 17, 43, 44] that the number of intents can be exponential in the number of pseudo-intents, i.e., the set of pseudo-intents cannot be enumerated in output-polynomial time by utilizing one of the existing algorithms, which all enumerate the closure system of both intents and pseudo-intents, and that the lectically first pseudo-intent can be computed in polynomial time, but recognizing the first n pseudo-intents is coNP-complete. Consequently, the pseudo-intents of a given formal context cannot be enumerated in the lectic order with polynomial delay, unless P = NP. Enumeration of pseudo-intents (in an arbitrary order) was also investigated, but concrete complexity results are outstanding. Babin and Kuznetsov showed in [6, 7] that recognizing a pseudo-intent is coNP-complete, and furthermore that recognizing the lectically largest pseudo-intent is coNP-hard. Hence, computing pseudo-intents in the dual lectic order is also intractable, i.e., not possible with polynomial delay, unless P = NP. As a corollary Babin and Kuznetsov conclude that the maximal pseudo-intents cannot be enumerated with polynomial delay, unless P = NP. Further consequences which they found are, for example, that premises of minimal implication bases cannot be tractably recognized, since this problem is coNP-complete, and that there cannot be an algorithm that outputs a random pseudo-intent in polynomial time, unless NP = coNP.
, and determining this number is #P-hard, furthermore that recognizing a pseudo-intent is in coNP, and that determining the number of non-pseudo-intents is #P-complete. Sertkaya and Distel demonstrated in [15, 17, 43, 44] that the number of intents can be exponential in the number of pseudo-intents, i.e., the set of pseudo-intents cannot be enumerated in output-polynomial time by utilizing one of the existing algorithms, which all enumerate the closure system of both intents and pseudo-intents, and that the lectically first pseudo-intent can be computed in polynomial time, but recognizing the first n pseudo-intents is coNP-complete. Consequently, the pseudo-intents of a given formal context cannot be enumerated in the lectic order with polynomial delay, unless P = NP. Enumeration of pseudo-intents (in an arbitrary order) was also investigated, but concrete complexity results are outstanding. Babin and Kuznetsov showed in [6, 7] that recognizing a pseudo-intent is coNP-complete, and furthermore that recognizing the lectically largest pseudo-intent is coNP-hard. Hence, computing pseudo-intents in the dual lectic order is also intractable, i.e., not possible with polynomial delay, unless P = NP. As a corollary Babin and Kuznetsov conclude that the maximal pseudo-intents cannot be enumerated with polynomial delay, unless P = NP. Further consequences which they found are, for example, that premises of minimal implication bases cannot be tractably recognized, since this problem is coNP-complete, and that there cannot be an algorithm that outputs a random pseudo-intent in polynomial time, unless NP = coNP.
Eventually, in case a given formal context is not complete in the sense that it does not contain enough objects to refute invalid implications, i.e., only contains some observed objects in the domain of interest, but one aims at exploring all valid implications over the given attribute set, a technique called Attribute Exploration can be utilized, which guides the user through the process of axiomatizing an implication base for the underlying domain in a way the number of questions posed to the user is minimal. For a sophisticated introduction as well as for theoretical and technical details, the interested reader is rather referred to [21–23, 31, 45]. A parallel variant of the Attribute Exploration also exists, cf. [28, 31], which is implemented in Concept Explorer FX [27].
For transferring and extending the results on canonical bases from Formal Concept Analysis to Description Logics, there are two key observations, namely that in the simple description logic \(\mathcal{L}_{0}\), which only allows for ⊤ and ⊓, there is a one-to-one correspondence between interpretations over the signature (M, ∅) and formal contexts with attribute set M, and furthermore that implications over M can be represented as concept inclusions over (M, ∅), and vice versa. In particular, an attribute subset X ⊆ M then corresponds to the conjunction  , and accordingly an implication X → Y corresponds to the CI
, and accordingly an implication X → Y corresponds to the CI  . These observations were successfully used in [2, 12, 16], among others. All of the aforementioned papers have in common that they provide a certain extension of the method for axiomatizing bases of implications from formal contexts. In particular, each of the methods makes heavy use of the canonical base. We will later elaborate on that, and provide results specifically tailored to our considered description logic \(\mathcal{MH}\).
. These observations were successfully used in [2, 12, 16], among others. All of the aforementioned papers have in common that they provide a certain extension of the method for axiomatizing bases of implications from formal contexts. In particular, each of the methods makes heavy use of the canonical base. We will later elaborate on that, and provide results specifically tailored to our considered description logic \(\mathcal{MH}\).
7 The Galois Connection of an Interpretation
In Sect. 6 we have seen that in Formal Concept Analysis the pair of the derivation operators  and
and  of a formal context
of a formal context  constitutes a Galois connection. In Description Logics however, for an interpretation \(\mathcal{I}\,:=\,(\varDelta ^{\mathcal{I}},\cdot ^{\mathcal{I}})\) we only have an extension mapping
constitutes a Galois connection. In Description Logics however, for an interpretation \(\mathcal{I}\,:=\,(\varDelta ^{\mathcal{I}},\cdot ^{\mathcal{I}})\) we only have an extension mapping  , which is defined recursively on the structure of concept descriptions, cf. Sect. 4. As a short repetition on Galois connections between posets, the interested reader is referred to [13, Definition 7.23] and [13, Lemma 7.26]. However, we will later formulate corresponding notions specifically tailored to our use case.
, which is defined recursively on the structure of concept descriptions, cf. Sect. 4. As a short repetition on Galois connections between posets, the interested reader is referred to [13, Definition 7.23] and [13, Lemma 7.26]. However, we will later formulate corresponding notions specifically tailored to our use case.
By definition the extension mapping  preserves finitary joins, i.e., we have that
preserves finitary joins, i.e., we have that  for all finite families
for all finite families  of \(\mathcal{M}\)-concept descriptions over Σ. When imposing a role-depth bound δ on the concept descriptions, then we know that there are only finitely many concept descriptions in case of a finite signature, and thus the extension mapping
of \(\mathcal{M}\)-concept descriptions over Σ. When imposing a role-depth bound δ on the concept descriptions, then we know that there are only finitely many concept descriptions in case of a finite signature, and thus the extension mapping  preserves arbitrary joins—then [13, 7.34] yields that there is another mapping
preserves arbitrary joins—then [13, 7.34] yields that there is another mapping  , which together with \(\cdot ^{\mathcal{I}}\) constitutes a Galois connection, and in terms of lattice theory this mapping is called the upper adjoint of the extension mapping \(\cdot ^{\mathcal{I}}\). In [2, 12, 16] this upper adjoint is rather called model-based most specific concept description mapping, and in each of the references it was shown that the pair of this mapping together with the extension mapping forms a Galois connection. Furthermore, [13, 7.33] then states that this other mapping can be found as
, which together with \(\cdot ^{\mathcal{I}}\) constitutes a Galois connection, and in terms of lattice theory this mapping is called the upper adjoint of the extension mapping \(\cdot ^{\mathcal{I}}\). In [2, 12, 16] this upper adjoint is rather called model-based most specific concept description mapping, and in each of the references it was shown that the pair of this mapping together with the extension mapping forms a Galois connection. Furthermore, [13, 7.33] then states that this other mapping can be found as  ,Footnote 1 i.e., the mapping which assigns to each subset \(X \subseteq \varDelta ^{\mathcal{I}}\) its role-depth-bounded model-based most specific concept description (or, to be formally correct, its equivalence class) which is characterized by the following definition.
,Footnote 1 i.e., the mapping which assigns to each subset \(X \subseteq \varDelta ^{\mathcal{I}}\) its role-depth-bounded model-based most specific concept description (or, to be formally correct, its equivalence class) which is characterized by the following definition.
Definition 7.1
Let \(\mathcal{I}\) be an interpretation over the signature Σ = (N
C, N
R), and let  be a role-depth bound. Then, for a subset \(X \subseteq \varDelta ^{\mathcal{I}}\), a concept description \(C \in \mathcal{ M}(\varSigma )\upharpoonright _{\delta }\) is called role-depth-bounded model-based most specific concept description (abbr. RMMSC) of X in \(\mathcal{I}\) with respect to δ if it satisfies the following conditions.
be a role-depth bound. Then, for a subset \(X \subseteq \varDelta ^{\mathcal{I}}\), a concept description \(C \in \mathcal{ M}(\varSigma )\upharpoonright _{\delta }\) is called role-depth-bounded model-based most specific concept description (abbr. RMMSC) of X in \(\mathcal{I}\) with respect to δ if it satisfies the following conditions.
-
1.
rd(C) ≤ δ,
-
2.
\(X \subseteq C^{\mathcal{I}}\), and
-
3.
for all \(\mathcal{M}\)-concept descriptions D over Σ with a role depth not exceeding δ, it holds true that ∅⊧C ⊑ D if \(X \subseteq D^{\mathcal{I}}\).
We shall denote the set of all RMMSCs in \(\mathcal{I}\) w.r.t. δ by \(\mathsf{Mmsc}(\mathcal{I},\delta )\).
Firstly, all role-depth-bounded model-based most specific concept descriptions of X in \(\mathcal{I}\) with respect to δ are equivalent, and a representative of the equivalence class is hence denoted as \(X^{\mathcal{I}(\delta )}\). Secondly, we can easily convince us that \(X^{\mathcal{I}(\delta )}\) always exists—provided that the underlying signature is finite. This is due to the fact that for a finite signature, only finitely many concept descriptions with a role depth of at most δ exist. Consequently, in order to construct \(X^{\mathcal{I}(\delta )}\) we may just build the (finite) conjunction of all those concept descriptions the role depth of which does not exceed δ and the extension of which contains X as a subset. Of course, this does not yield a practical means for the construction of role-depth-bounded model-based most specific concept descriptions, but we will investigate an appropriate computation method later in Sect. 8.
Lemma 7.2
Let \(\mathcal{I}\) be an interpretation over the signature Σ = (N
C, N
R),  be a family of subsets \(X_{t} \subseteq \varDelta ^{\mathcal{I}}\)
, and
be a family of subsets \(X_{t} \subseteq \varDelta ^{\mathcal{I}}\)
, and  a family of concept descriptions \(C_{s} \in \mathcal{ M}(\varSigma )\)
. Then, the following statements hold.
a family of concept descriptions \(C_{s} \in \mathcal{ M}(\varSigma )\)
. Then, the following statements hold.
-
1.

-
2.

Proof
-
1.
Let
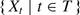 be a family of subsets \(X_{t} \subseteq \varDelta ^{\mathcal{I}}\). Then we can show that
be a family of subsets \(X_{t} \subseteq \varDelta ^{\mathcal{I}}\). Then we can show that  is indeed a role-depth-bounded model-based most specific concept description of
is indeed a role-depth-bounded model-based most specific concept description of  . (It would also be possible to dually prove that
. (It would also be possible to dually prove that  is a least common subsumer of the concept descriptions \(X_{t}^{\mathcal{I}(\delta )}\) for t ∈ T.)
is a least common subsumer of the concept descriptions \(X_{t}^{\mathcal{I}(\delta )}\) for t ∈ T.)First, we prove that
 is a subset of the extension
is a subset of the extension  . By definition, it holds that \(X_{t} \subseteq X_{t}^{\mathcal{I}(\delta )\mathcal{I}}\) for all t ∈ T. Furthermore, every RMMSC \(X_{t}^{\mathcal{I}(\delta )}\) is subsumed by the LCS
. By definition, it holds that \(X_{t} \subseteq X_{t}^{\mathcal{I}(\delta )\mathcal{I}}\) for all t ∈ T. Furthermore, every RMMSC \(X_{t}^{\mathcal{I}(\delta )}\) is subsumed by the LCS  . It then immediately follows that each X
t must be a subset of the extension
. It then immediately follows that each X
t must be a subset of the extension  .
.Second, we have to show that whenever C is a concept description the extension of which contains
 , then C subsumes
, then C subsumes  with respect to the empty TBox ∅. By definition of RMMSCs then we infer that each \(X_{t}^{\mathcal{I}(\delta )}\) is subsumed by C, and hence by definition of LCS,
with respect to the empty TBox ∅. By definition of RMMSCs then we infer that each \(X_{t}^{\mathcal{I}(\delta )}\) is subsumed by C, and hence by definition of LCS,  must be subsumed by C, too.
must be subsumed by C, too. -
2.
holds true by definition of the semantics of conjunctions. □
Lemma 7.3
Let \(\mathcal{I}\) be an interpretation over the signature Σ = (N
C, N
R), and  be a role-depth bound. Then, the extension mapping \(\cdot ^{\mathcal{I}}\) and the MMSC-mapping \(\cdot ^{\mathcal{I}(\delta )}\) constitute a Galois connection between the powerset lattice of the domain \(\varDelta ^{\mathcal{I}}\) and the dual of the concept description lattice
be a role-depth bound. Then, the extension mapping \(\cdot ^{\mathcal{I}}\) and the MMSC-mapping \(\cdot ^{\mathcal{I}(\delta )}\) constitute a Galois connection between the powerset lattice of the domain \(\varDelta ^{\mathcal{I}}\) and the dual of the concept description lattice  .
.
In particular, the following statements hold true for all subsets \(X,Y \subseteq \varDelta ^{\mathcal{I}}\) , and for all \(\mathcal{M}\) -concept descriptions C, D over Σ with a role-depth not exceeding δ.
Proof
It suffices to prove the first statement, since the others are then obtained as consequences, cf. [13, Definition 7.23 and Lemma 7.26]. Hence, assume that \(X \subseteq C^{\mathcal{I}}\). Then by Statement 3 of Definition 7.1 we conclude that \(\emptyset \models X^{\mathcal{I}(\delta )} \sqsubseteq C\). Vice versa, if \(X^{\mathcal{I}(\delta )}\) is subsumed by C with respect to the empty TBox ∅, then in particular it follows that \(X^{\mathcal{I}(\delta )\mathcal{I}} \subseteq C^{\mathcal{I}}\). An application of Statement 2 of Definition 7.1 then yields \(X \subseteq X^{\mathcal{I}(\delta )\mathcal{I}} \subseteq C^{\mathcal{I}}\). □
From the preceding lemma we conclude that the composition of the extension mapping and the MMSC mapping yields a closure operator in the dual of  , and it furthermore holds true that the implications which are valid in \(\cdot ^{\mathcal{I}\mathcal{I}(\delta )}\) are exactly those concept inclusions which are valid in \(\mathcal{I}\) and the subsumee and the subsumer of which have a role depth not exceeding δ. Furthermore, we infer that each implication base, of \(\cdot ^{\mathcal{I}\mathcal{I}(\delta )}\) is a base of CIs for \(\mathcal{I}\) and δ. Further information on implications that are valid in closure operators can be found in [30, Sect. 3].
, and it furthermore holds true that the implications which are valid in \(\cdot ^{\mathcal{I}\mathcal{I}(\delta )}\) are exactly those concept inclusions which are valid in \(\mathcal{I}\) and the subsumee and the subsumer of which have a role depth not exceeding δ. Furthermore, we infer that each implication base, of \(\cdot ^{\mathcal{I}\mathcal{I}(\delta )}\) is a base of CIs for \(\mathcal{I}\) and δ. Further information on implications that are valid in closure operators can be found in [30, Sect. 3].
8 Computation of Role-Depth-Bounded Model-Based Most Specific Concept Descriptions
In this section we are going to develop a method for the computation of RMMSCs in \(\mathcal{M}\). By definition of the \(\mathcal{M}\)-concept descriptions in Sect. 4, it follows that each such \(\mathcal{M}\)-concept description is essentially a conjunction of other \(\mathcal{M}\)-concept descriptions, i.e., for each \(C \in \mathcal{ M}(\varSigma )\), there is a finite set \(\mathsf{Conj}(C) \subseteq \mathcal{ M}(\varSigma )\) such that  Footnote 2 is satisfied and Conj(C) does not contain any elements of the form D ⊓ E. We call the elements in Conj(C) the top-level conjuncts of C. Furthermore, we can distinguish between the different possible types of these top-level conjuncts, i.e., if \(\mathcal{X} \subseteq \mathcal{ M}(\varSigma )\), then \(\mathsf{Conj}(C,\mathcal{X})\,:=\,\mathsf{Conj}(C) \cap \mathcal{ X}\). If A ⊆ N
C, R ⊆ N
R,
Footnote 2 is satisfied and Conj(C) does not contain any elements of the form D ⊓ E. We call the elements in Conj(C) the top-level conjuncts of C. Furthermore, we can distinguish between the different possible types of these top-level conjuncts, i.e., if \(\mathcal{X} \subseteq \mathcal{ M}(\varSigma )\), then \(\mathsf{Conj}(C,\mathcal{X})\,:=\,\mathsf{Conj}(C) \cap \mathcal{ X}\). If A ⊆ N
C, R ⊆ N
R,  , and \(\mathbf{C} \subseteq \mathcal{ M}(\varSigma )\), then define the following sets.
, and \(\mathbf{C} \subseteq \mathcal{ M}(\varSigma )\), then define the following sets.

It is readily verified that then for every \(\mathcal{M}\)-concept description C,

i.e., C must be of the following form.

We conclude that for the construction of an RMMSC we have to investigate which conjuncts of the different types must occur in the RMMSC. In particular, we investigate a technique for the construction of an RMMSC \(X^{\mathcal{I}(\delta )}\) of a subset \(X \subseteq \varDelta ^{\mathcal{I}}\) within a given interpretation \(\mathcal{I}\) and with respect to a pre-defined bound  on the role depths. We start by considering the smallest bound δ = 0. It is then readily verified that the RMMSC must have the form
on the role depths. We start by considering the smallest bound δ = 0. It is then readily verified that the RMMSC must have the form

where

Now assume that δ > 0. We have already argued that for a finite signature Σ, which we can always assume for practical cases, the RMMSC \(X^{\mathcal{I}(\delta )}\) must exist, and furthermore must then be of the following form.

For the first three parts, we can, of course, utilize the results from the case δ = 0. Furthermore, we can immediately see that

For analyzing the remaining parts, we repeat the definitions of extensions of some of the corresponding \(\mathcal{M}\)-concept descriptions as follows.

If we denote the set of all r-successors of an element \(d \in \varDelta ^{\mathcal{I}}\) by \(\mathsf{suc}_{\mathcal{I}}(d,r)\), i.e., if we set  , then we can rewrite the equations given above as follows.
, then we can rewrite the equations given above as follows.

Consequently, when lifting the equations from a characterization of elements of the extensions to subsets of the extensions, we get the following equivalences.

Further define

i.e., n(x, r) denotes the number of r-successors of x in \(\mathcal{I}\), and n(X, r) is the smallest n such that  . Then, of course it holds true that
. Then, of course it holds true that

We can then collect all subsets of the interpretation’s domain the extension of which serves as a filler for the appropriate constructors, and in particular we set

Obviously, then

and applying Statement 1 of Lemma 7.3 yields that

The connection between the sets CSuc(…) and Suc(…) is as follows.
-
1.
For all
 it holds true that
it holds true that  .
. -
2.
For all
 it holds true that
it holds true that  .
.
Continuing the way towards a construction of the RMMSC of a subset \(X \subseteq \varDelta ^{\mathcal{I}}\), we can see that it must satisfy the following subsumption.

It is easy to see that for the construction of the RMMSC it suffices to consider the minimal successors, and hence we explicitly define them as follows.

Definition 8.1
Let \(\mathcal{I}\) be a finite interpretation over a finite signature Σ : = (N
C, N
R), \(X \subseteq \varDelta ^{\mathcal{I}}\) with X ≠ ∅ be a subset of the domain, and  be a role-depth bound. Then, the syntactic RMMSC of X in \(\mathcal{I}\) with respect to δ is the concept description \(\mathsf{mmsc}(X,\mathcal{I},\delta )\) which is defined by induction on the role depth as follows.
be a role-depth bound. Then, the syntactic RMMSC of X in \(\mathcal{I}\) with respect to δ is the concept description \(\mathsf{mmsc}(X,\mathcal{I},\delta )\) which is defined by induction on the role depth as follows.

Furthermore, we define \(\mathsf{mmsc}(\emptyset,\mathcal{I},\delta )\,:=\,\perp \) for all  .
.
Lemma 8.2
Let C
1, …, C
m and D
1, …, D
n be \(\mathcal{M}\)
-concept descriptions over the signature Σ : = (N
C, N
R). Then  if for each
if for each  , there is an
, there is an  such that∅⊧C
i ⊑ D
j.
such that∅⊧C
i ⊑ D
j.
Proof
Obviously, it holds true that  for all indices
for all indices  . We conclude that for each
. We conclude that for each  , the subsumption
, the subsumption  is satisfied, and thus
is satisfied, and thus  . □
. □
Theorem 8.3
Let \(\mathcal{I}\) be a finite interpretation over a finite signature Σ : = (N
C, N
R), \(X \subseteq \varDelta ^{\mathcal{I}}\) a subset of the domain, and  a role-depth bound. Then, the concept description \(\mathsf{mmsc}(X,\mathcal{I},\delta )\) is the role-depth-bounded model-based most-specific concept description of X in \(\mathcal{I}\) with respect to δ, i.e., \(\emptyset \models X^{\mathcal{I}(\delta )} \equiv \mathsf{mmsc}(X,\mathcal{I},\delta )\).
a role-depth bound. Then, the concept description \(\mathsf{mmsc}(X,\mathcal{I},\delta )\) is the role-depth-bounded model-based most-specific concept description of X in \(\mathcal{I}\) with respect to δ, i.e., \(\emptyset \models X^{\mathcal{I}(\delta )} \equiv \mathsf{mmsc}(X,\mathcal{I},\delta )\).
Proof
The case X = ∅ is obvious. Hence, consider a non-empty subset \(X \subseteq \varDelta ^{\mathcal{I}}\). It is easy to see that for a finite interpretation \(\mathcal{I}\), it always holds true that  for all numbers
for all numbers  and all role names r ∈ N
R. Consequently \(\mathsf{mmsc}(X,\mathcal{I},\delta )\) consists of finitely many conjunctions, and thus is indeed a well-defined \(\mathcal{M}\)-concept description.
and all role names r ∈ N
R. Consequently \(\mathsf{mmsc}(X,\mathcal{I},\delta )\) consists of finitely many conjunctions, and thus is indeed a well-defined \(\mathcal{M}\)-concept description.
We now show the three properties of Definition 7.1 by simultaneous induction on the role-depth bound δ.
- (δ = 0):
-
- 1.:
-
Since concept names and their negations possess a role depth of 0, it obviously follows that \(\mathsf{mmsc}(X,\mathcal{I},0)\) must have a role-depth of 0, too.
- 2.:
-
Since for each concept name A ∈ N C occurring in \(\mathsf{mmsc}(X,\mathcal{I},0)\), it is true that \(X \subseteq A^{\mathcal{I}}\), and furthermore for each primitive negation ¬A for an A ∈ N C which is a top-level conjunct in \(\mathsf{mmsc}(X,\mathcal{I},0)\), we have that \(X \subseteq \varDelta ^{\mathcal{I}}\setminus A^{\mathcal{I}}\), we can easily conclude that \(X \subseteq \mathsf{mmsc}(X,\mathcal{I},0)^{\mathcal{I}}\).
- 3.:
-
Assume that D is an \(\mathcal{M}\)-concept description over Σ with a role depth of 0, i.e., D consists only of a conjunction of concept names and primitive negations, and let \(X \subseteq D^{\mathcal{I}}\). Then, for concept name A ∈ N C occurring in D, it certainly holds that \(X \subseteq A^{\mathcal{I}}\), and hence A is a top-level conjunct in \(\mathsf{mmsc}(X,\mathcal{I},0)\), too. Analogously, for a primitive negation ¬A in D, we know that \(X \subseteq (\neg A)^{\mathcal{I}}\) must be satisfied, and so also ¬A is contained in the top-level conjunction of \(\mathsf{mmsc}(X,\mathcal{I},0)\). We just showed that each conjunct in D also occurs in \(\mathsf{mmsc}(X,\mathcal{I},0)\), and hence \(\emptyset \models \mathsf{mmsc}(X,\mathcal{I},0) \sqsubseteq D\).
- (δ > 0):
-
- 1.:
-
Note that
 for δ > 0. By induction hypothesis, \(\mathsf{rd}(\mathsf{mmsc}(Y,\mathcal{I},\delta -1)) \leq \delta -1\), and hence it follows that \(\mathsf{rd}(\mathsf{mmsc}(X,\mathcal{I},\delta )) \leq \delta\).
for δ > 0. By induction hypothesis, \(\mathsf{rd}(\mathsf{mmsc}(Y,\mathcal{I},\delta -1)) \leq \delta -1\), and hence it follows that \(\mathsf{rd}(\mathsf{mmsc}(X,\mathcal{I},\delta )) \leq \delta\). - 2.:
-
Let δ > 0, and consider a top-level conjunct
 occurring in \(\mathsf{mmsc}(X,\mathcal{I},\delta )\), i.e.,
occurring in \(\mathsf{mmsc}(X,\mathcal{I},\delta )\), i.e.,  . By induction hypothesis, Y is a subset of \(\mathsf{mmsc}(Y,\mathcal{I},\delta -1)^{\mathcal{I}}\). We continue with a case distinction on the quantifier
. By induction hypothesis, Y is a subset of \(\mathsf{mmsc}(Y,\mathcal{I},\delta -1)^{\mathcal{I}}\). We continue with a case distinction on the quantifier  .
. -
 :
: -
By definition of the successor sets, it holds true that all elements in Y are r-successors of some element in X, since \(Y \subseteq \mathsf{suc}_{\mathcal{I}}(X,r)\). Furthermore, Y satisfies the condition that for each element x ∈ X, the cardinality of the intersection \(\mathsf{suc}_{\mathcal{I}}(x,r) \cap Y\) is at least n, i.e., each element x ∈ X has n or more r-successors in Y. Consequently,
 .
. -
 :
: -
In this case, we have that \(Y = \mathsf{suc}_{\mathcal{I}}(X,r)\). Consider an arbitrary x ∈ X. If \(y \in \varDelta ^{\mathcal{I}}\) and \((x,y) \in r^{\mathcal{I}}\), then y ∈ Y, and so
 .
.
-
- 3.:
-
Consider δ > 0, and let E be a conjunct on the top-level of D. Of course, it then holds true that \(X \subseteq E^{\mathcal{I}}\). We proceed with a case distinction on E, and prove that there is always a top-level conjunct in \(\mathsf{mmsc}(X,\mathcal{I},\delta )\) which is subsumed by E with respect to the empty TBox ∅. As a consequence then Lemma 8.2 yields that \(\emptyset \models \mathsf{mmsc}(X,\mathcal{I},\delta ) \sqsubseteq D\).
-
 :
: -
Since
 , we infer that each r-successor of each element in X is in the extension \(F^{\mathcal{I}}\), i.e.,
, we infer that each r-successor of each element in X is in the extension \(F^{\mathcal{I}}\), i.e.,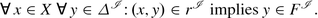
As the set \(\mathsf{suc}_{\mathcal{I}}(X,r)\) contains all r-successors of any element in X and no additional elements, we conclude that \(\mathsf{suc}_{\mathcal{I}}(X,r) \subseteq F^{\mathcal{I}}\). Applying Statement 1 of Lemma 7.3 yields \(\emptyset \models (\mathsf{suc}_{\mathcal{I}}(X,r))^{\mathcal{I}(\delta -1)} \sqsubseteq F\). An application of the induction hypothesis implies that \(\emptyset \models (\mathsf{suc}_{\mathcal{I}}(X,r))^{\mathcal{I}(\delta -1)} \equiv \mathsf{mmsc}(\mathsf{suc}_{\mathcal{I}}(X,r),\mathcal{I},\delta -1)\). Eventually, it follows that

-
(
 ):
): -
By assumption, we have that
 , i.e., every element x ∈ X has n or more r-successors which are in the extension of F. Thus,
, i.e., every element x ∈ X has n or more r-successors which are in the extension of F. Thus,  for all x ∈ X, and consequently there is a set
for all x ∈ X, and consequently there is a set  such that \(Y \subseteq F^{\mathcal{I}}\). By applying Statement 1 of Lemma 7.3 we conclude that \(\emptyset \models Y ^{\mathcal{I}(\delta -1)} \sqsubseteq F\), and since the induction hypothesis yields that \(\emptyset \models Y ^{\mathcal{I}(\delta -1)} \equiv \mathsf{mmsc}(Y,\mathcal{I},\delta -1)\), it eventually follows that
such that \(Y \subseteq F^{\mathcal{I}}\). By applying Statement 1 of Lemma 7.3 we conclude that \(\emptyset \models Y ^{\mathcal{I}(\delta -1)} \sqsubseteq F\), and since the induction hypothesis yields that \(\emptyset \models Y ^{\mathcal{I}(\delta -1)} \equiv \mathsf{mmsc}(Y,\mathcal{I},\delta -1)\), it eventually follows that 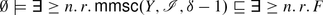 where the subsumee is a top-level conjunct in \(\mathsf{mmsc}(X,\mathcal{I},\delta )\).
where the subsumee is a top-level conjunct in \(\mathsf{mmsc}(X,\mathcal{I},\delta )\). -
(
 ):
): -
The set inclusion
 yields that for every element x ∈ X, the number of r-successors of x does not exceed n. It is readily verified that then n(X, r) ≤ n, and thus
yields that for every element x ∈ X, the number of r-successors of x does not exceed n. It is readily verified that then n(X, r) ≤ n, and thus  . Of course,
. Of course,  is contained as a top-level conjunct in \(\mathsf{mmsc}(X,\mathcal{I},\delta )\).
is contained as a top-level conjunct in \(\mathsf{mmsc}(X,\mathcal{I},\delta )\). -
(
 ):
): -
From
 it follows that each element x ∈ X is an r-successor of itself, i.e.,
it follows that each element x ∈ X is an r-successor of itself, i.e.,  . By definition, \(\mathsf{mmsc}(X,\mathcal{I},\delta )\) then also contains
. By definition, \(\mathsf{mmsc}(X,\mathcal{I},\delta )\) then also contains  as a top-level conjunct. □
as a top-level conjunct. □
-
9 Concept Lattices of Interpretations
Let \(\mathcal{I}\) be an interpretation over Σ : = (N
C, N
R), and assume that  is a role depth bound. A formal concept of \(\mathcal{I}\) with respect to the role depth bound δ is a pair (X, [C] ≡) such that its extent X is a subset of \(\varDelta ^{\mathcal{I}}\), its intent [C] ≡ is an equivalence class of \(\mathcal{M}\)-concept descriptions over Σ, and \(X^{\mathcal{I}(\delta )} = [C]_{\equiv }\) as well as \(C^{\mathcal{I}} = X\) are satisfied. For the sake of simplicity, we denote the formal concept (X, [C] ≡) simply as (X, C). Then we may furthermore define an ordering of formal concepts by (X, C) ≤ (Y, D) if X ⊆ Y. In case (X, C) ≤ (Y, D) we say that (X, C) is a subconcept of (Y, D), and vice versa that (Y, D) is a superconcept of (X, C). Using the Galois properties from Lemma 7.3, it is easy to prove that (X, C) ≤ (Y, D) if, and only if, ∅⊧C ⊑ D. The set of all formal concepts of \(\mathcal{I}\) w.r.t. δ is denoted by \(\mathfrak{B}(\mathcal{I},\delta )\), and the set of all extents is symbolized as \(\mathsf{Ext}(\mathcal{I},\delta )\).
is a role depth bound. A formal concept of \(\mathcal{I}\) with respect to the role depth bound δ is a pair (X, [C] ≡) such that its extent X is a subset of \(\varDelta ^{\mathcal{I}}\), its intent [C] ≡ is an equivalence class of \(\mathcal{M}\)-concept descriptions over Σ, and \(X^{\mathcal{I}(\delta )} = [C]_{\equiv }\) as well as \(C^{\mathcal{I}} = X\) are satisfied. For the sake of simplicity, we denote the formal concept (X, [C] ≡) simply as (X, C). Then we may furthermore define an ordering of formal concepts by (X, C) ≤ (Y, D) if X ⊆ Y. In case (X, C) ≤ (Y, D) we say that (X, C) is a subconcept of (Y, D), and vice versa that (Y, D) is a superconcept of (X, C). Using the Galois properties from Lemma 7.3, it is easy to prove that (X, C) ≤ (Y, D) if, and only if, ∅⊧C ⊑ D. The set of all formal concepts of \(\mathcal{I}\) w.r.t. δ is denoted by \(\mathfrak{B}(\mathcal{I},\delta )\), and the set of all extents is symbolized as \(\mathsf{Ext}(\mathcal{I},\delta )\).
Lemma 9.1
Let
\(\mathcal{I}\)
be a finite interpretation over the signature Σ, and
 a role-depth bound.
a role-depth bound.
-
1.
For all formal concepts (X, C) and (Y, D) of \(\mathcal{I}\) w.r.t. δ, it is true that
$$\displaystyle{\begin{array}{c} (X,C) \leq (Y,D)\mathit{\text{ if, and only if, }}X \subseteq Y \mathit{\text{ if, and only if, }}\emptyset \models C \sqsubseteq D.\end{array} }$$ -
2.
The relation ≤ is an order on \(\mathfrak{B}(\mathcal{I},\delta )\).
Proof
-
1.
The first equivalence holds by definition. Assume that X is a subset of Y, then from Statement 4 of Lemma 7.3 it follows that \(\emptyset \models X^{\mathcal{I}(\delta )} \sqsubseteq Y ^{\mathcal{I}(\delta )}\). Finally, since (X, C) and (Y, D) are description concepts we conclude \(\emptyset \models C \equiv X^{\mathcal{I}(\delta )} \sqsubseteq Y ^{\mathcal{I}(\delta )} \equiv D\). The other direction can be shown analogously, as also the extension mapping is monotonous, cf. Statement 7 of Lemma 7.3.
-
2.
It is well-known that the subset inclusion is an order relation, hence also ≤ must be reflexive and transitive. □
Furthermore, \(\mathfrak{B}(\mathcal{I},\delta )\) is in fact a lattice, in which the infimum and the supremum of a finite family  of formal concepts satisfy the following equations.
of formal concepts satisfy the following equations.

The lattice is bounded by the smallest formal concept (∅, ⊥ ), and by the greatest formal concept \((\varDelta ^{\mathcal{I}},(\varDelta ^{\mathcal{I}})^{\mathcal{I}})\). We denote this lattice by \(\underline{\mathfrak{B}}(\mathcal{I},\delta )\,:=\,(\mathfrak{B}(\mathcal{I},\delta ),\leq )\). Note that in case of finiteness of the interpretation \(\mathcal{I}\), the concept lattice is complete.
10 Induced Formal Contexts
In this section we are going to consider the notion of induced formal contexts, which has first been defined and utilized by Baader and Distel [2, 16], and later also by Borchmann [11], for the description logic \(\mathcal{EL}_{\mathsf{gfp}}^{\!\perp }\). Similar results were found by Borchmann, Distel, and Kriegel, cf. [12], for the description logic \(\mathcal{EL}^{\!\perp }\) where the role depth of the considered concept descriptions is restricted. In the sequel of this section, we extend the previous definitions and results to the more expressive description logic \(\mathcal{M}\).
Consider a set \(\mathcal{C}\) of \(\mathcal{M}\)-concept descriptions over the signature Σ : = (N C, N R). Then, we define a projection \(\pi _{\mathcal{C}}\) with respect to \(\mathcal{C}\) as follows.

Furthermore, we say that an \(\mathcal{M}\)-concept description C over Σ is expressible in terms of \(\mathcal{C}\) if there is a subset \(\mathcal{X} \subseteq \mathcal{ C}\) such that  . It turns out that the projection \(\pi _{\mathcal{C}}\) is a counterpart for the conjunction
. It turns out that the projection \(\pi _{\mathcal{C}}\) is a counterpart for the conjunction  such that their pair constitutes a Galois connection between the lattice
such that their pair constitutes a Galois connection between the lattice  and the powerset
and the powerset  , i.e., the statements in the following lemma hold true.
, i.e., the statements in the following lemma hold true.
Lemma 10.1
Let \(\mathcal{C}\) be a set of \(\mathcal{M}\) -concept descriptions over Σ. Then for all subsets \(\mathcal{X},\mathcal{Y } \subseteq \mathcal{ C}\) and all concept descriptions \(C,D \in \mathcal{ M}(\varSigma )\) , the following statements are valid.
-
1.
\(\mathcal{X} \subseteq \pi _{\mathcal{C}}(C)\) if, and only if,

-
2.
\(\mathcal{X} \subseteq \mathcal{ Y }\) implies

-
3.

-
4.
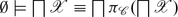
-
5.
∅⊧C ⊑ D only if \(\pi _{\mathcal{C}}(C) \supseteq \pi _{\mathcal{C}}(D)\)
-
6.

-
7.

Proof
It suffices to show Statement 1. Then the other statements are obtained as a consequence. We can easily see that the following equivalences hold.

□
In the case of \(\mathcal{EL}_{\mathsf{gfp}}^{\!\perp }\), Baader and Distel showed that each (unbounded) MMSC of an interpretation \(\mathcal{I}\) can be expressed in terms of  . Similarly, for the role-depth-bounded case, Borchmann, Distel, and Kriegel showed that each RMMSC of \(\mathcal{I}\) w.r.t. δ is expressible in terms of
. Similarly, for the role-depth-bounded case, Borchmann, Distel, and Kriegel showed that each RMMSC of \(\mathcal{I}\) w.r.t. δ is expressible in terms of  . As a straightforward extension to \(\mathcal{M}\), we can infer from Theorem 8.3 that each RMMSC is expressible in terms of
. As a straightforward extension to \(\mathcal{M}\), we can infer from Theorem 8.3 that each RMMSC is expressible in terms of

i.e., the set \(\mathcal{C}(\mathcal{I},\delta )\) is  -dense in the set \(\mathsf{Mmsc}(\mathcal{I},\delta )\) of all RMMSCs of \(\mathcal{I}\) with respect to δ.
-dense in the set \(\mathsf{Mmsc}(\mathcal{I},\delta )\) of all RMMSCs of \(\mathcal{I}\) with respect to δ.
Definition 10.2
Let \(\mathcal{I}\) be an interpretation, and let \(\mathcal{C}\) be a set of \(\mathcal{M}\)-concept descriptions, both over the same signature Σ. Then, the induced formal context of \(\mathcal{I}\) and \(\mathcal{C}\) is defined as  the incidence of which is defined by (d, C) ∈ I if, and only if, \(d \in C^{\mathcal{I}}\). Furthermore, the induced formal context
the incidence of which is defined by (d, C) ∈ I if, and only if, \(d \in C^{\mathcal{I}}\). Furthermore, the induced formal context  of \(\mathcal{I}\) and a role-depth bound
of \(\mathcal{I}\) and a role-depth bound  is defined as the induced formal context of \(\mathcal{I}\) and \(\mathcal{C}(\mathcal{I},\delta )\). The projection \(\pi _{\mathcal{C}(\mathcal{I},\delta )}\) with respect to \(\mathcal{C}(\mathcal{I},\delta )\) is simply denoted as \(\pi _{\mathcal{I},\delta }\).
is defined as the induced formal context of \(\mathcal{I}\) and \(\mathcal{C}(\mathcal{I},\delta )\). The projection \(\pi _{\mathcal{C}(\mathcal{I},\delta )}\) with respect to \(\mathcal{C}(\mathcal{I},\delta )\) is simply denoted as \(\pi _{\mathcal{I},\delta }\).
Lemma 10.3
Let  be an induced formal context such that \(\mathcal{C} \subseteq \mathcal{ M}(\varSigma )\upharpoonright _{\delta }\) for a role depth bound
be an induced formal context such that \(\mathcal{C} \subseteq \mathcal{ M}(\varSigma )\upharpoonright _{\delta }\) for a role depth bound  . Then, for all subsets \(X \subseteq \varDelta ^{\mathcal{I}}\)
, all subsets \(\mathcal{X} \subseteq \mathcal{ C}\)
, and all \(\mathcal{M}\)
-concept descriptions \(C \in \mathcal{ M}(\varSigma )\)
, the following statements hold true.
. Then, for all subsets \(X \subseteq \varDelta ^{\mathcal{I}}\)
, all subsets \(\mathcal{X} \subseteq \mathcal{ C}\)
, and all \(\mathcal{M}\)
-concept descriptions \(C \in \mathcal{ M}(\varSigma )\)
, the following statements hold true.
-
1.
\(\pi _{\mathcal{C}}(X^{\mathcal{I}(\delta )}) = X^{I}\)
-
2.

-
3.
\(C^{\mathcal{I}} \subseteq \pi _{\mathcal{C}}(C)^{I}\)
-
4.

Furthermore, if C is expressible in terms of \(\mathcal{C}\) , then also the following statements are satisfied.
-
5.

-
6.
\(C^{\mathcal{I}} = (\pi _{\mathcal{C}}(C))^{I}\)
Eventually, if \(\mathcal{X}\) is an intent of  , then the following equality is valid, too.
, then the following equality is valid, too.
-
7.
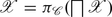
Proof
-
1.
Let \(X \subseteq \varDelta ^{\mathcal{I}}\). Then we have

where the equality (∗) follows from Statement 1 of Lemma 7.3.
-
2.
Let \(\mathcal{X} \subseteq \mathcal{ C}\). Then it holds that

-
3.
Let \(C \in \mathcal{ M}(\varSigma )\) be a concept description. Then we have

-
4.
Let \(\mathcal{X} \subseteq \mathcal{ C}\) be a set of concept descriptions from \(\mathcal{C}\). Then it holds that

Now let furthermore C be a concept description that is expressible in terms of \(\mathcal{C}\). Then we know that there is a subset \(\mathcal{X} \subseteq \mathcal{ C}\) such that  .
.
-
5.
By an application of Statement 4 of Lemma 10.1 we immediately conclude that

-
6.
The equality follows from the former Statements 2 and 5—in particular, from
 we deduce that
we deduce that  .
.
Finally consider an intent \(\mathcal{X}\) of  .
.
-
7.
We have the following equations which follow from Statement 4 and Statement 7 of Lemma 10.1:

□
Lemma 10.4
Let  be an induced formal context. Then for all subsets \(\mathcal{X},\mathcal{Y } \subseteq \mathcal{ C}\)
, the concept inclusion
be an induced formal context. Then for all subsets \(\mathcal{X},\mathcal{Y } \subseteq \mathcal{ C}\)
, the concept inclusion  is valid in \(\mathcal{I}\) if, and only if, the implication \(\mathcal{X} \rightarrow \mathcal{ Y }\) is valid in
is valid in \(\mathcal{I}\) if, and only if, the implication \(\mathcal{X} \rightarrow \mathcal{ Y }\) is valid in  .
.
Proof
It is readily verified that the following equivalences hold true.

□
Definition 10.5
Let \(\mathcal{I}\) be an interpretation over the signature Σ, let  be a role depth bound, and assume that C is an \(\mathcal{M}\)-concept description over Σ. Then the lower approximation of C with respect to \(\mathcal{I}\) and δ is defined as the concept description
be a role depth bound, and assume that C is an \(\mathcal{M}\)-concept description over Σ. Then the lower approximation of C with respect to \(\mathcal{I}\) and δ is defined as the concept description

Lemma 10.6
Let \(\mathcal{I}\) be an interpretation over the signature Σ, and assume that  is a role depth bound. Then, for all concept descriptions \(C,D \in \mathcal{ M}(\varSigma )\)
, all role names r ∈ N
R
, and all natural numbers
is a role depth bound. Then, for all concept descriptions \(C,D \in \mathcal{ M}(\varSigma )\)
, all role names r ∈ N
R
, and all natural numbers  , the following statements hold true.
, the following statements hold true.
-
1.
\((C \sqcap D)^{\mathcal{I}} = (C^{\mathcal{I}\mathcal{I}(\delta )} \sqcap D)^{\mathcal{I}}\)
-
2.

-
3.

Proof
Beforehand observe that according to Statement 6 of Lemma 7.3, for all \(\mathcal{M}\)-concept descriptions C over Σ, it holds true that \(\emptyset \models C^{\mathcal{I}} \equiv C^{\mathcal{I}\mathcal{I}(\delta )\mathcal{I}}\).
-
1.
It holds true that \((C \sqcap D)^{\mathcal{I}} = C^{\mathcal{I}} \cap D^{\mathcal{I}} = C^{\mathcal{I}\mathcal{I}(\delta )\mathcal{I}} \cap D^{\mathcal{I}} = (C^{\mathcal{I}\mathcal{I}(\delta )} \sqcap D)^{\mathcal{I}}\).
-
2.
It holds true that

-
3.
It holds true that

□
Lemma 10.7
Let \(\mathcal{I}\) be an interpretation over Σ. Then for every \(\mathcal{M}\) -concept description C over Σ the role depth of which does not exceed δ, it holds true that

Proof
We know that \(\emptyset \models D^{\mathcal{I}\mathcal{I}(\delta -1)} \sqsubseteq D\) for all concept descriptions D over Σ with rd(D) ≤ δ − 1, and since value restrictions as well as qualified greater-than restrictions are monotonous in its concept argument, we have that  and
and  is satisfied for all role names r ∈ N
R and all natural numbers
is satisfied for all role names r ∈ N
R and all natural numbers  . Hence, we conclude that the lower approximation
. Hence, we conclude that the lower approximation  is subsumed by C with respect to the empty TBox ∅.
is subsumed by C with respect to the empty TBox ∅.
Furthermore, we infer the following equivalences, in particular the equality (∗) follows by applying Lemma 10.6.

Eventually, it follows that  and using Statement 1 of Lemma 7.3 we infer that
and using Statement 1 of Lemma 7.3 we infer that  . □
. □
Lemma 10.8
Let \(\mathcal{I}\) be an interpretation and  be a role depth bound. Then every model-based most specific concept description of \(\mathcal{I}\) with role depth bound δ is expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\).
be a role depth bound. Then every model-based most specific concept description of \(\mathcal{I}\) with role depth bound δ is expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\).
Proof
Let C be a model-based most specific concept description in \(\mathcal{I}\) with respect to the role depth δ. Then Statement 3 of Lemma 7.3 yields that \(\emptyset \models C \equiv C^{\mathcal{I}\mathcal{I}(\delta )}\). Using the previous Lemma 10.7, we then know that C is equivalent to its lower approximation w.r.t. \(\mathcal{I}\). Obviously, C is then expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\). □
Lemma 10.9
Let
 be an induced formal context. Then, for all subsets
\(\mathcal{X} \subseteq \mathcal{ C}(\mathcal{I},\delta )\)
and all
\(\mathcal{M}\)
-concept descriptions C
over Σ, the following statements hold true.
be an induced formal context. Then, for all subsets
\(\mathcal{X} \subseteq \mathcal{ C}(\mathcal{I},\delta )\)
and all
\(\mathcal{M}\)
-concept descriptions C
over Σ, the following statements hold true.
-
1.

-
2.
If \(\mathcal{X}\) is an intent of
 , then
, then  is a model-based most specific concept description of \(\mathcal{I}\) with role-depth bound δ.
is a model-based most specific concept description of \(\mathcal{I}\) with role-depth bound δ.
-
3.
If C is a model-based most specific concept description of \(\mathcal{I}\) with role-depth bound δ, then \(\pi _{\mathcal{I},\delta }(C)\) is an intent of
 .
.
Proof
-
1.
We already know that
 holds, cf. Statement 4 of Theorem 10.3, and thus also
holds, cf. Statement 4 of Theorem 10.3, and thus also  . Furthermore, from Lemma 10.8 it follows that
. Furthermore, from Lemma 10.8 it follows that  is expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\), i.e., Statement 5 of Lemma 10.3 implies
is expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\), i.e., Statement 5 of Lemma 10.3 implies  .
. -
2.
Let \(\mathcal{X} =\mathcal{ X}^{II}\) be an intent. Then it follows that
 , and Lemma 10.3 yields
, and Lemma 10.3 yields  , i.e.,
, i.e.,  is a RMMSC.
is a RMMSC. -
3.
Conversely, let C be an RMMSC, i.e., \(\emptyset \models C \equiv C^{\mathcal{I}\mathcal{I}(\delta )}\). Then Statement 5 of Lemma 10.3 implies
 . Furthermore, it follows that
. Furthermore, it follows that  . In particular then
. In particular then  holds, and according to Lemma 10.1 this is equivalent to \(\pi _{\mathcal{I},\delta }(C)^{II} \subseteq \pi _{\mathcal{I},\delta }(C)\). Of course, the inverse set inclusion also holds, i.e., eventually \(\pi _{\mathcal{I},\delta }(C)\) is an intent. □
holds, and according to Lemma 10.1 this is equivalent to \(\pi _{\mathcal{I},\delta }(C)^{II} \subseteq \pi _{\mathcal{I},\delta }(C)\). Of course, the inverse set inclusion also holds, i.e., eventually \(\pi _{\mathcal{I},\delta }(C)\) is an intent. □
Corollary 10.10
The concept lattice of  is isomorphic to the concept lattice of \(\mathcal{I}\) and δ. A complete overview on the corresponding isomorphisms is shown in Fig.
4
.
is isomorphic to the concept lattice of \(\mathcal{I}\) and δ. A complete overview on the corresponding isomorphisms is shown in Fig.
4
.
11 Knowledge Bases of Interpretations
In Sect. 4 we introduced the notion of a concept inclusion. In particular, a CI C ⊑ D is valid in an interpretation \(\mathcal{I}\) if \(C^{\mathcal{I}} \subseteq D^{\mathcal{I}}\) is satisfied. We denote the set of all valid CIs of \(\mathcal{I}\) by \(\mathcal{T}(\mathcal{I})\). In contrast to formal contexts, where there are only finitely many valid implications in case of a finite attribute set, the set \(\mathcal{T}(\mathcal{I})\) is infinite, even for finite interpretations over finite signatures. As an example, consider the CI ⊤ ⊑ ⊤, which is valid in all interpretations. Furthermore, if a CI C ⊑ D is valid in \(\mathcal{I}\), then so is  . We conclude that \(\mathcal{T}(\mathcal{I})\) always contains at least countably infinitely many CIs, provided that there is at least one role name. An important question now is, whether there is a finite base of CIs for \(\mathcal{I}\), i.e., a (finite) TBox \(\mathcal{B}(\mathcal{I})\) such that \(\mathcal{B}(\mathcal{I})\models \mathcal{T}(\mathcal{I})\) as well as \(\mathcal{T}(\mathcal{I})\models \mathcal{B}(\mathcal{I})\). Baader and Distel found an affirmative answer in [2, 16] for the case of finite interpretations over finite signatures in the description logic \(\mathcal{EL}^{\!\perp }\), where they take an elegant detour over \(\mathcal{EL}_{\mathsf{gfp}}^{\!\perp }\), i.e., \(\mathcal{EL}^{\!\perp }\) interpreted with greatest fixpoint semantics, and later Borchmann, Distel, and Kriegel found a positive answer in [12] for finite interpretations over finite signatures in the description logic \(\mathcal{EL}^{\!\perp }\) restricted by a role depth bound, which is easier to apply and implement, since the descriptive semantics are utilized for which plenty of reasoners already exist. Furthermore, it was investigated how the technique of construction of a base of CIs can be iterated for taking into account input interpretations which can be observed on a daily basis, and similarly taking into account existing knowledge in form of a TBox, cf. [29].
. We conclude that \(\mathcal{T}(\mathcal{I})\) always contains at least countably infinitely many CIs, provided that there is at least one role name. An important question now is, whether there is a finite base of CIs for \(\mathcal{I}\), i.e., a (finite) TBox \(\mathcal{B}(\mathcal{I})\) such that \(\mathcal{B}(\mathcal{I})\models \mathcal{T}(\mathcal{I})\) as well as \(\mathcal{T}(\mathcal{I})\models \mathcal{B}(\mathcal{I})\). Baader and Distel found an affirmative answer in [2, 16] for the case of finite interpretations over finite signatures in the description logic \(\mathcal{EL}^{\!\perp }\), where they take an elegant detour over \(\mathcal{EL}_{\mathsf{gfp}}^{\!\perp }\), i.e., \(\mathcal{EL}^{\!\perp }\) interpreted with greatest fixpoint semantics, and later Borchmann, Distel, and Kriegel found a positive answer in [12] for finite interpretations over finite signatures in the description logic \(\mathcal{EL}^{\!\perp }\) restricted by a role depth bound, which is easier to apply and implement, since the descriptive semantics are utilized for which plenty of reasoners already exist. Furthermore, it was investigated how the technique of construction of a base of CIs can be iterated for taking into account input interpretations which can be observed on a daily basis, and similarly taking into account existing knowledge in form of a TBox, cf. [29].
Definition 11.1
Let \(\mathcal{I}\) be an interpretation over a signature Σ, and assume that  is a role depth bound. Then, a knowledge base for \(\mathcal{I}\) and δ is a pair \(\mathcal{K}\,:=\,(\mathcal{T},\mathcal{R})\) consisting of a TBox \(\mathcal{T}\) and an RBox \(\mathcal{R}\) such that for all concept inclusions α the role depth of the subsumee of which, and of the subsumer of which, respectively, does not exceed δ, and also for all role inclusions α, it holds true that
is a role depth bound. Then, a knowledge base for \(\mathcal{I}\) and δ is a pair \(\mathcal{K}\,:=\,(\mathcal{T},\mathcal{R})\) consisting of a TBox \(\mathcal{T}\) and an RBox \(\mathcal{R}\) such that for all concept inclusions α the role depth of the subsumee of which, and of the subsumer of which, respectively, does not exceed δ, and also for all role inclusions α, it holds true that
A knowledge base \(\mathcal{K}\) is non-redundant if none of the axioms is entailed by the others, i.e., if for each \(\alpha \in \mathcal{ T} \cup \mathcal{ R}\), it holds true that  . Furthermore, a knowledge base for \(\mathcal{I}\) and δ is minimal if there is no knowledge base for \(\mathcal{I}\) and δ of a smaller cardinality.
. Furthermore, a knowledge base for \(\mathcal{I}\) and δ is minimal if there is no knowledge base for \(\mathcal{I}\) and δ of a smaller cardinality.
By means of the results of the previous sections we are now ready to formulate a knowledge base for an interpretation \(\mathcal{I}\), or for a description graph \(\mathcal{G}\), respectively. Beforehand, we inspect the interplay of role and concept inclusions, and we list some trivial concept inclusions that are valid in all interpretations.
Lemma 11.2
Let  be non-negative integers with n < m, r ∈ N
R be a role name, and C, D be \(\mathcal{M}\)
-concept descriptions. Then, the following concept inclusions hold in every interpretation \(\mathcal{I}\).
be non-negative integers with n < m, r ∈ N
R be a role name, and C, D be \(\mathcal{M}\)
-concept descriptions. Then, the following concept inclusions hold in every interpretation \(\mathcal{I}\).

Proof
Most of the concept inclusions are obviously valid. We are only going to explain the validity of the penultimate concept inclusion. If a domain element has at least  r-successors in C, then especially it must be an r-successor of itself, hence be in C and in
r-successors in C, then especially it must be an r-successor of itself, hence be in C and in  . Furthermore, there cannot be any further r-successors, and so all r-successors must be in C. □
. Furthermore, there cannot be any further r-successors, and so all r-successors must be in C. □
Please note that there are no direct subsumptions between existential restrictions  and value restrictions
and value restrictions  , i.e., both
, i.e., both  and
and  do not hold. There is also a crossover between both which is denoted by
do not hold. There is also a crossover between both which is denoted by  , and has the semantics
, and has the semantics  , i.e., a domain element is in the extension of
, i.e., a domain element is in the extension of  if, and only if, there is an r-successor in C, and all r-successors are in C. Furthermore, there is also a reversed value restriction
if, and only if, there is an r-successor in C, and all r-successors are in C. Furthermore, there is also a reversed value restriction  with the semantics
with the semantics  . However, we do not use either of them for our mining technique.
. However, we do not use either of them for our mining technique.
The next two lemmas show us which concept inclusions can be inferred from known role inclusions.
Lemma 11.3
Let \(\mathcal{I}\) be a model of the role inclusion r ⊑ s, as well as of the concept inclusion C ⊑ D, and furthermore let m ≤ n be natural numbers. Then \(\mathcal{I}\) is also a model of the following concept inclusions.

Proof
Assume that m ≤ n, and let \(\mathcal{I}\) be an interpretation such that \(r^{\mathcal{I}} \subseteq s^{\mathcal{I}}\) and \(C^{\mathcal{I}} \subseteq D^{\mathcal{I}}\).
- ( ≥ ):
-
Then we have that

-
 :
: -
For the existential self restrictions we can infer the following.

-
 :
: -
Furthermore, consider a concept inclusion
 . We can infer the following.
. We can infer the following.
- ( ≤ ):
-
Finally, it holds true that

□
First, we want to extract a minimal RBox \(\mathcal{R}(\mathcal{I})\) from the interpretation that entails all role inclusions valid in \(\mathcal{I}\). We therefore define an equivalence relation \(\equiv _{\mathcal{I}}\) on the role names as follows: \(r \equiv _{\mathcal{I}}s\) if, and only if, \(r^{\mathcal{I}} = s^{\mathcal{I}}\). Then let \(N_{R}^{\mathcal{I}}\) be a set of representatives of this equivalence relation, i.e.,  for all role names r ∈ N
R. If
for all role names r ∈ N
R. If  is an enumeration of the equivalence class of r, then add the following role equivalence axioms to \(\mathcal{R}(\mathcal{I})\).
is an enumeration of the equivalence class of r, then add the following role equivalence axioms to \(\mathcal{R}(\mathcal{I})\).

Furthermore, define an order relation \(\sqsubseteq _{\mathcal{I}}\) on the representatives \(N_{R}^{\mathcal{I}}\) by \(r \sqsubseteq _{\mathcal{I}}s\) if, and only if, \(r^{\mathcal{I}} \subseteq s^{\mathcal{I}}\). Let \(\prec _{\mathcal{I}}\) be the neighborhood relation of \(\sqsubseteq _{\mathcal{I}}\), then add the role inclusion axioms r ⊑ s for each pair \(r \prec _{\mathcal{I}}s\) to the RBox \(\mathcal{R}(\mathcal{I})\). Obviously, the constructed RBox is minimal w.r.t. the property to entail all valid role inclusion axioms holding in the interpretation \(\mathcal{I}\). Eventually, the RBox is defined as follows.

Proposition 11.4
Let \(\mathcal{I}\) be an interpretation. Then the RBox \(\mathcal{R}(\mathcal{I})\) as defined above is a base for the role inclusions which are valid in \(\mathcal{I}\) , i.e., for each role inclusion r ⊑ s, the following equivalence holds true.
In particular, \(\mathcal{R}(\mathcal{I})\) is non-redundant, i.e., for every role inclusion \(r \sqsubseteq s \in \mathcal{ R}(\mathcal{I})\)
, it holds true that  .
.
Proof
The statements are immediate consequences of the construction of \(\mathcal{R}(\mathcal{I})\) preceding the proposition. □
Lemma 11.5
Let \(\mathcal{I}\) be an interpretation over a signature Σ, let C and D be \(\mathcal{M}\)
-concept descriptions over Σ, and further assume that  is a role depth bound. If the CI C ⊑ D is valid in \(\mathcal{I}\)
, and both C and D have a role depth not exceeding δ, then the CI \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\) is valid in \(\mathcal{I}\) too, and furthermore, C ⊑ D follows from \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\).
is a role depth bound. If the CI C ⊑ D is valid in \(\mathcal{I}\)
, and both C and D have a role depth not exceeding δ, then the CI \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\) is valid in \(\mathcal{I}\) too, and furthermore, C ⊑ D follows from \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\).
Proof
For the concept description C it follows by an application of Statement 6 of Lemma 7.3 that \(C^{\mathcal{I}} = C^{\mathcal{I}\mathcal{I}(\delta )\mathcal{I}}\), i.e., the CI \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\) is always valid in \(\mathcal{I}\).
Now consider a model \(\mathcal{J}\) of the CI \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\). Since \(\mathcal{I}\models C \sqsubseteq D\), it follows that \(C^{\mathcal{I}} \subseteq D^{\mathcal{I}}\), and by Statement 1 of Lemma 7.3 we conclude that \(\emptyset \models C^{\mathcal{I}\mathcal{I}(\delta )} \sqsubseteq D\). In particular, then the last CI is also valid in \(\mathcal{J}\), and hence \(\mathcal{J}\models C \sqsubseteq D\). Since \(\mathcal{J}\) was an arbitrary model, we conclude that  . □
. □
Proposition 11.6
Let \(\mathcal{I}\) be a finite interpretation, and let  be a role depth bound. Then, the following TBox is sound and complete for the CIs which satisfy the role depth bound δ and are valid in \(\mathcal{I}\).
be a role depth bound. Then, the following TBox is sound and complete for the CIs which satisfy the role depth bound δ and are valid in \(\mathcal{I}\).

Proof
For the sake of improving the readability, denote the above given TBox as \(\mathcal{T}\). Since for all \(\mathcal{X} \subseteq \mathcal{ C}(\mathcal{I},\delta )\), the implication \(\mathcal{X} \rightarrow \mathcal{ X}^{II}\) trivially holds in the induced formal context  , it immediately follows by an application of Lemma 10.4 that the CI
, it immediately follows by an application of Lemma 10.4 that the CI  is valid in \(\mathcal{I}\). Consequently, we have just proven the soundness of \(\mathcal{T}\).
is valid in \(\mathcal{I}\). Consequently, we have just proven the soundness of \(\mathcal{T}\).
Consider a CI C ⊑ D which is valid in \(\mathcal{I}\), and where both C and D possess a role depth of at most δ. Then Lemma 11.5 yields that the CI \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\) is also valid in \(\mathcal{I}\), and furthermore the entailment  holds true. Hence, it suffices to show that our TBox \(\mathcal{T}\) entails all CIs of the form \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\). For this purpose, consider an arbitrary model \(\mathcal{J}\) of \(\mathcal{T}\) as well as an arbitrary concept description \(C \in \mathcal{ M}(\varSigma )\upharpoonright _{\delta }\)—we are now going to prove that the CI \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\) is valid in \(\mathcal{J}\), too. Beforehand, note that for the right-hand sides of the CIs it holds true that
holds true. Hence, it suffices to show that our TBox \(\mathcal{T}\) entails all CIs of the form \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\). For this purpose, consider an arbitrary model \(\mathcal{J}\) of \(\mathcal{T}\) as well as an arbitrary concept description \(C \in \mathcal{ M}(\varSigma )\upharpoonright _{\delta }\)—we are now going to prove that the CI \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\) is valid in \(\mathcal{J}\), too. Beforehand, note that for the right-hand sides of the CIs it holds true that  , cf. Statement 1 of Lemma 10.9. Furthermore, we also know that each CI \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\) where C is expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\) is valid in \(\mathcal{J}\). We prove this as follows: if C is expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\), then there is a subset \(\mathcal{X} \subseteq \mathcal{ C}(\mathcal{I},\delta )\) such that
, cf. Statement 1 of Lemma 10.9. Furthermore, we also know that each CI \(C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\) where C is expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\) is valid in \(\mathcal{J}\). We prove this as follows: if C is expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\), then there is a subset \(\mathcal{X} \subseteq \mathcal{ C}(\mathcal{I},\delta )\) such that  . Since
. Since  , we can immediately conclude that \(\mathcal{J}\models C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\).
, we can immediately conclude that \(\mathcal{J}\models C \sqsubseteq C^{\mathcal{I}\mathcal{I}(\delta )}\).
We proceed with a proof by induction on the structure of C.
Let C = ⊥. Since \(\perp \in \mathcal{ C}(\mathcal{I},\delta )\), we may immediately conclude that \(\mathcal{J}\models \perp \sqsubseteq \perp ^{\mathcal{I}\mathcal{I}(\delta )}\).
Assume that C = ⊤. From  it follows that \(\mathcal{J}\models \top \sqsubseteq \top ^{\mathcal{I}\mathcal{I}(\delta )}\).
it follows that \(\mathcal{J}\models \top \sqsubseteq \top ^{\mathcal{I}\mathcal{I}(\delta )}\).
For a concept name C = A ∈ N C, we have that \(A \in \mathcal{ C}(\mathcal{I},\delta )\), and hence \(\mathcal{J}\models A \sqsubseteq A^{\mathcal{I}\mathcal{I}(\delta )}\).
For a primitive negation C = ¬A, it follows that \(\neg A \in \mathcal{ C}(\mathcal{I},\delta )\), and so we conclude that \(\mathcal{J}\models \neg A \sqsubseteq (\neg A)^{\mathcal{I}\mathcal{I}(\delta )}\).
Consider a conjunction C = D ⊓ E. By induction hypothesis it holds true that \(\mathcal{J}\models D \sqsubseteq D^{\mathcal{I}\mathcal{I}(\delta )}\) as well as \(\mathcal{J}\models E \sqsubseteq E^{\mathcal{I}\mathcal{I}(\delta )}\). Consequently,
The second subsumption follows from the fact that the concept description \(D^{\mathcal{I}\mathcal{I}(\delta )} \sqcap E^{\mathcal{I}\mathcal{I}(\delta )}\) is expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\), and the last subsumption is a consequence of Statement 5 of Lemma 7.3.
Assume that  is a value restriction. Then the following subsumptions hold true in \(\mathcal{J}\).
is a value restriction. Then the following subsumptions hold true in \(\mathcal{J}\).

The first subsumption is a consequence of the induction hypothesis and the fact that value restrictions are monotonous. For the second subsumption, observe that \(D^{\mathcal{I}\mathcal{I}(\delta -1)}\) certainly satisfies that \(\mathsf{rd}(D^{\mathcal{I}\mathcal{I}(\delta -1)}) \leq \delta\) as well as \(D^{\mathcal{I}} \subseteq D^{\mathcal{I}\mathcal{I}(\delta -1)\mathcal{I}}\), and so an application of Statement 3 of Definition 7.1 yields that \(\emptyset \models D^{\mathcal{I}\mathcal{I}(\delta )} \sqsubseteq D^{\mathcal{I}\mathcal{I}(\delta -1)}\). Since  is contained in \(\mathcal{C}(\mathcal{I},\delta )\), it must in particular be expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\), and this justifies the validity of the third subsumption. Again, the last subsumption follows from Statement 5 of Lemma 7.3.
is contained in \(\mathcal{C}(\mathcal{I},\delta )\), it must in particular be expressible in terms of \(\mathcal{C}(\mathcal{I},\delta )\), and this justifies the validity of the third subsumption. Again, the last subsumption follows from Statement 5 of Lemma 7.3.
Now let  be a qualified greater-than restriction, and first assume that
be a qualified greater-than restriction, and first assume that  . Then, we may argue similarly as for the value restrictions that the following subsumptions hold true in \(\mathcal{J}\).
. Then, we may argue similarly as for the value restrictions that the following subsumptions hold true in \(\mathcal{J}\).

For the remaining case where  , we argue as follows:
, we argue as follows:

and hence the concept descriptions ⊥ and  are equivalent in \(\mathcal{J}\). Since we have already proven above that \(\perp \sqsubseteq \perp ^{\mathcal{I}\mathcal{I}(\delta )}\) is valid in \(\mathcal{J}\), also the CI
are equivalent in \(\mathcal{J}\). Since we have already proven above that \(\perp \sqsubseteq \perp ^{\mathcal{I}\mathcal{I}(\delta )}\) is valid in \(\mathcal{J}\), also the CI  is valid in \(\mathcal{J}\).
is valid in \(\mathcal{J}\).
Assume that  is an unqualified less-than restriction, and let
is an unqualified less-than restriction, and let  . Of course, then
. Of course, then  certainly holds true, since
certainly holds true, since  . In case
. In case  , then
, then  and ⊤ are equivalent in \(\mathcal{J}\), and the validity of
and ⊤ are equivalent in \(\mathcal{J}\), and the validity of  follows from \(\mathcal{J}\models \top \sqsubseteq \top ^{\mathcal{I}\mathcal{I}(\delta )}\), which we have shown above.
follows from \(\mathcal{J}\models \top \sqsubseteq \top ^{\mathcal{I}\mathcal{I}(\delta )}\), which we have shown above.
Eventually, consider an existential self restriction  . Obviously,
. Obviously,  is contained in \(\mathcal{C}(\mathcal{I},\delta )\), and so the CI
is contained in \(\mathcal{C}(\mathcal{I},\delta )\), and so the CI  is valid in \(\mathcal{J}\). □
is valid in \(\mathcal{J}\). □
As final step we use the trivial concept inclusions and concept inclusions that are entailed by valid role inclusions to define some background knowledge for the computation of the canonical implication base of the induced concept context which is trivial in terms of Description Logics, but not for Formal Concept Analysis, due to their different semantics.
Theorem 11.7
Let
\(\mathcal{I}\)
be an interpretation over the signature Σ, and
 a role-depth bound. Furthermore, assume that
\(\mathcal{L}\)
is an implication base of the induced formal context
a role-depth bound. Furthermore, assume that
\(\mathcal{L}\)
is an implication base of the induced formal context
 with respect to the background knowledge
with respect to the background knowledge

Then
 where
where

is a knowledge base for \(\mathcal{I}\) and δ. In particular, the canonical knowledge base for \(\mathcal{I}\) and δ is defined as

Proof
It is obvious that

and hence it suffices to prove that for each implication base \(\mathcal{L}\) of  with respect to the background knowledge \(\mathcal{S}(\mathcal{I},\delta )\), the pair
with respect to the background knowledge \(\mathcal{S}(\mathcal{I},\delta )\), the pair  is a knowledge base for \(\mathcal{I}\).
is a knowledge base for \(\mathcal{I}\).
It is obvious that \(\mathcal{I}\models \mathcal{K}\), i.e., \(\mathcal{K}\) is sound. We proceed with proving completeness. Completeness for role inclusions follows immediately from Proposition 11.4. In Proposition 11.6 we have proven that the TBox

is complete for the concept inclusions which are valid in \(\mathcal{I}\) and satisfy the role depth bound δ, and thus it suffices to show that for each subset \(\mathcal{X} \subseteq \mathcal{ C}(\mathcal{I},\delta )\),

Consider a model \(\mathcal{J}\) of \(\mathcal{K}\). We divide the remaining part of this proof in three steps:
-
1.
First, we show that all implications in \(\mathcal{L}\) are also valid in the induced formal context
 the incidence relation of which we denote as J.
the incidence relation of which we denote as J. -
2.
Then, we prove that the background knowledge \(\mathcal{S}(\mathcal{I},\delta )\) is valid in the induced formal context
 , too.
, too. -
3.
Finally, we show that \(\mathcal{J}\) is a model of the CI
 .
.
From the last step, we then immediately conclude that \(\mathcal{J}\) is also a model of the TBox from Proposition 11.6. Since \(\mathcal{J}\) was chosen arbitrarily, then \(\mathcal{K}\) must be complete.
W.l.o.g. we may assume that \(\mathcal{L}\) only contains implications of the form \(\mathcal{X} \rightarrow \mathcal{ X}^{II}\). Hence, let \(\mathcal{X} \rightarrow \mathcal{ X}^{II} \in \mathcal{ L}\), then it follows that

i.e., the implication \(\mathcal{X} \rightarrow \mathcal{ X}^{II}\) is valid in  .
.
Now consider an implication  in \(\mathcal{S}(\mathcal{I},\delta )\), i.e., it holds true that \(C_{1},\ldots,C_{\ell},D \in \mathcal{ C}(\mathcal{I},\delta )\) and \(\mathcal{R}(\mathcal{I})\models C_{1} \sqcap \ldots \sqcap C_{\ell} \sqsubseteq D\). Since \(\mathcal{J}\) is a model of \(\mathcal{R}(\mathcal{I})\), the aforementioned CI is valid in \(\mathcal{J}\). Lemma 10.4 then justifies that the considered implication must be valid in the induced formal context
in \(\mathcal{S}(\mathcal{I},\delta )\), i.e., it holds true that \(C_{1},\ldots,C_{\ell},D \in \mathcal{ C}(\mathcal{I},\delta )\) and \(\mathcal{R}(\mathcal{I})\models C_{1} \sqcap \ldots \sqcap C_{\ell} \sqsubseteq D\). Since \(\mathcal{J}\) is a model of \(\mathcal{R}(\mathcal{I})\), the aforementioned CI is valid in \(\mathcal{J}\). Lemma 10.4 then justifies that the considered implication must be valid in the induced formal context  .
.
As the last step, we consider an arbitrary CI  where \(\mathcal{X} \subseteq \mathcal{ C}(\mathcal{I},\delta )\), and prove that it is valid in \(\mathcal{J}\). Since the implication set \(\mathcal{L} \cup \mathcal{ S}(\mathcal{I},\delta )\) is sound and complete for
where \(\mathcal{X} \subseteq \mathcal{ C}(\mathcal{I},\delta )\), and prove that it is valid in \(\mathcal{J}\). Since the implication set \(\mathcal{L} \cup \mathcal{ S}(\mathcal{I},\delta )\) is sound and complete for  , and \(\mathcal{X} \rightarrow \mathcal{ X}^{II}\) is trivially valid in
, and \(\mathcal{X} \rightarrow \mathcal{ X}^{II}\) is trivially valid in  , it holds true that \(\mathcal{X} \rightarrow \mathcal{ X}^{II}\) is entailed by \(\mathcal{L} \cup \mathcal{ S}(\mathcal{I},\delta )\). Consequently, since
, it holds true that \(\mathcal{X} \rightarrow \mathcal{ X}^{II}\) is entailed by \(\mathcal{L} \cup \mathcal{ S}(\mathcal{I},\delta )\). Consequently, since  is a model of both \(\mathcal{L}\) and \(\mathcal{S}(\mathcal{I},\delta )\), it follows that \(\mathcal{X} \rightarrow \mathcal{ X}^{II}\) is valid in
is a model of both \(\mathcal{L}\) and \(\mathcal{S}(\mathcal{I},\delta )\), it follows that \(\mathcal{X} \rightarrow \mathcal{ X}^{II}\) is valid in  , too. By Lemma 10.4 we conclude that the CI
, too. By Lemma 10.4 we conclude that the CI  is valid in \(\mathcal{J}\). □
is valid in \(\mathcal{J}\). □
12 Other Description Logics
If only a lower expressivity of the underlying description logic is necessary, then one could also use \(\mathcal{EL}\), \(\mathcal{FL}_{0}\), \(\mathcal{FLE}\), \(\mathcal{ALE}\), or extensions thereof with role hierarchies \(\mathcal{H}\). All of the previous results are then still valid, if the expressivity is not higher than that of \(\mathcal{MH}\). Figure 5 gives an overview on description logics that have a lower expressivity than \(\mathcal{MH}\), and can thus also be used for knowledge acquisition.
As a future step, it would be interesting to investigate methods that also take into account complex role inclusions, e.g., consider the description logic \(\mathcal{MR}\). A complex role inclusion is an expression r 1 ∘ … ∘ r n ⊑ s where r 1, …, r n, s ∈ N R are role names. Its semantics is defined by
where ∘ denotes composition of binary relations, i.e.,

13 Conclusion
We have provided an extension of the results of Baader and Distel [2, 3, 16] for the deduction of knowledge bases from interpretations in the more expressive description logic \(\mathcal{MH}\) w.r.t. descriptive semantics and role-depth bounds, and furthermore explained how this technique can be applied to social graphs. Since role-depth-bounded model-based most specific concept descriptions always exist, this technique can always be applied. Furthermore, the construction of knowledge bases has been reduced to the computation of implication bases of formal contexts, which is a well-understood problem that has several available algorithms—for example the standard NextClosure algorithm by Ganter [21, 23], or the parallel algorithm NextClosures that was introduced in [28, 30–32] and implemented in [27]. The presented methods in this document are also prototypically implemented in Concept Explorer FX [27].
Notes
- 1.
For a subset X ⊆ P of a quasi-ordered set (P, ≤ ), we use the expression Min(X) to denote the set of all those elements in X which are minimal with respect to ≤, i.e., x ∈ Min(X) if, and only if, x ∈ X and there is no other element y ∈ X such that y ≤ x and y ≢ x.
- 2.
Please note that
 .
.
References
Baader, F.: Least common subsumers and most specific concepts in a description logic with existential restrictions and terminological cycles. In: Gottlob, G., Walsh, T. (eds.) IJCAI-03, Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence, pp. 319–324, Acapulco, 9–15 August 2003. Morgan Kaufmann, San Francisco (2003). http://dblp.uni-trier.de/rec/bib/conf/ijcai/Baader03
Baader, F., Distel, F.: A finite basis for the set of \(\mathcal{E\!L}\)-implications holding in a finite model. In: Medina, R., Obiedkov, S.A. (eds.) Formal Concept Analysis, Proceedings of the 6th International Conference, ICFCA 2008, Montreal, 25–28 February 2008. Lecture Notes in Computer Science, vol. 4933, pp. 46–61. Springer, Heidelberg (2008). DOI 10.1007/978-3-540-78137-0∖_4. http://dblp.uni-trier.de/rec/bib/conf/icfca/BaaderD08
Baader, F., Distel, F.: Exploring finite models in the description logic \(\mathcal{E\!L}_{\mathrm{gfp}}\). In: Ferré, S., Rudolph, S. (eds.) Formal Concept Analysis, Proceedings of the 7th International Conference, ICFCA 2009, Darmstadt, 21–24 May 2009. Lecture Notes in Computer Science, vol. 5548, pp. 146–161. Springer, Heidelberg (2009). DOI 10.1007/978-3-642-01815-2∖_12. http://dblp.uni-trier.de/rec/bib/conf/icfca/BaaderD09
Baader, F., Küsters, R., Molitor, R.: Computing least common subsumers in description logics with existential restrictions. In: Dean, T. (ed.) Proceedings of the Sixteenth International Joint Conference on Artificial Intelligence, IJCAI 99, pp. 96–103, Stockholm, 31 July–6 August 1999. 2 Volumes, 1450 pages. Morgan Kaufmann, San Francisco (1999). http://dblp.uni-trier.de/rec/bib/conf/ijcai/BaaderKM99
Baader, F., Horrocks, I., Sattler, U.: Description logics. In: van Harmelen, F., Lifschitz, V., Porter, B.W. (eds.) Handbook of Knowledge Representation. Foundations of Artificial Intelligence, vol. 3, pp. 135–179. Elsevier, Amsterdam (2008). DOI 10.1016/S1574-6526(07)03003-9. http://dblp.uni-trier.de/rec/bib/reference/fai/3
Babin, M.A., Kuznetsov, S.O.: Recognizing pseudo-intents is coNP-complete. In: Kryszkiewicz, M., Obiedkov, S.A. (eds.) Proceedings of the 7th International Conference on Concept Lattices and Their Applications, Sevilla, 19–21 October 2010. CEUR Workshop Proceedings, vol. 672, pp. 294–301. CEUR-WS.org (2010). http://dblp.uni-trier.de/rec/bib/conf/cla/BabinK10
Babin, M.A., Kuznetsov, S.O.: Computing premises of a minimal cover of functional dependencies is intractable. Discrete Appl. Math. 161(6), 742–749 (2013). DOI 10.1016/j.dam.2012.10.026. http://dblp.uni-trier.de/rec/bib/journals/dam/BabinK13
Bazhanov, K., Obiedkov, S.A.: Optimizations in computing the Duquenne-Guigues basis of implications. Ann. Math. Artif. Intell. 70(1–2), 5–24 (2014). DOI 10.1007/s10472-013-9353-y. http://dblp.uni-trier.de/rec/bib/journals/amai/BazhanovO14
Beeri, C., Bernstein, P.A.: Computational problems related to the design of normal form relational schemas. ACM Trans. Database Syst. 4(1), 30–59 (1979). DOI 10.1145/320064.320066. http://doi.acm.org/10.1145/320064.320066. http://dblp.uni-trier.de/rec/bib/journals/tods/BeeriB79
Borchmann, D.: Towards an error-tolerant construction of \(\mathcal{EL}^{\!\perp }\)-ontologies from data using formal concept analysis. In: Cellier, P., Distel, F., Ganter, B. (eds.) Formal Concept Analysis, Proceedings of the 11th International Conference, ICFCA 2013, Dresden, 21–24 May 2013. Lecture Notes in Computer Science, vol. 7880, pp. 60–75. Springer, Heidelberg (2013). DOI 10.1007/978-3-642-38317-5∖_4. http://dblp.uni-trier.de/rec/bib/conf/icfca/Borchmann13
Borchmann, D.: Learning terminological knowledge with high confidence from erroneous data. Ph.D. thesis, Dresden University of Technology (2014). http://dblp.uni-trier.de/rec/bib/phd/dnb/Borchmann14
Borchmann, D., Distel, F., Kriegel, F.: Axiomatisation of general concept inclusions from finite interpretations. J. Appl. Non-Classical Log. 26(1), 1–46 (2016). DOI 10.1080/11663081.2016.1168230. http://dblp.uni-trier.de/rec/bib/journals/jancl/BorchmannDK16
Davey, B.A., Priestley, H.A.: Introduction to Lattices and Order, 2nd edn. Cambridge University Press, Cambridge (2002). http://dblp.uni-trier.de/rec/bib/books/daglib/0023601
Distel, F.: Model-based most specific concepts in description logics with value restrictions. Tech. Rep. 08-04, Institute for theoretical computer science, TU Dresden, Dresden (2008). http://lat.inf.tu-dresden.de/research/reports.html
Distel, F.: Hardness of enumerating pseudo-intents in the lectic order. In: Kwuida, L., Sertkaya, B. (eds.) Formal Concept Analysis, Proceedings of the 8th International Conference, ICFCA 2010, Agadir, 15–18 March 2010. Lecture Notes in Computer Science, vol. 5986, pp. 124–137. Springer, Heidelberg (2010). DOI 10.1007/978-3-642-11928-6∖_9. http://dblp.uni-trier.de/rec/bib/conf/icfca/Distel10
Distel, F.: Learning description logic knowledge bases from data using methods from formal concept analysis. Ph.D. thesis, Dresden University of Technology (2011). http://dblp.uni-trier.de/rec/bib/phd/de/Distel2011
Distel, F., Sertkaya, B.: On the complexity of enumerating pseudo-intents. Discrete Appl. Math. 159(6), 450–466 (2011). DOI 10.1016/j.dam.2010.12.004. http://dblp.uni-trier.de/rec/bib/journals/dam/DistelS11
Donini, F.M., Colucci, S., Noia, T.D., Sciascio, E.D.: A tableaux-based method for computing least common subsumers for expressive description logics. In: Boutilier, C. (ed.) IJCAI 2009, Proceedings of the 21st International Joint Conference on Artificial Intelligence, pp. 739–745, Pasadena, CA, 11–17 July 2009 (2009). http://dblp.uni-trier.de/rec/bib/conf/ijcai/DoniniCNS09
Facebook: Facebook (2016). https://www.facebook.com
Facebook for Developers: The Graph API (2016). https://developers.facebook.com/docs/graph-api
Ganter, B.: Two Basic Algorithms in Concept Analysis. FB4-Preprint 831, Technische Hochschule Darmstadt, Darmstadt (1984)
Ganter, B.: Attribute exploration with background knowledge. Theor. Comput. Sci. 217(2), 215–233 (1999). DOI 10.1016/S0304-3975(98)00271-0. http://dblp.uni-trier.de/rec/bib/journals/tcs/Ganter99
Ganter, B.: Two basic algorithms in concept analysis. In: Kwuida, L., Sertkaya, B. (eds.) Formal Concept Analysis, Proceedings of the 8th International Conference, ICFCA 2010, Agadir, 15–18 March 2010. Lecture Notes in Computer Science, vol. 5986, pp. 312–340. Springer, Heidelberg (2010). DOI 10.1007/978-3-642-11928-6∖_22. http://dblp2.uni-trier.de/rec/bib/conf/icfca/Ganter10
Ganter, B., Wille, R.: Formal Concept Analysis - Mathematical Foundations. Springer, Heidelberg (1999). http://dblp.uni-trier.de/rec/bib/books/daglib/0095956
Guigues, J.L., Duquenne, V.: Famille minimale d’implications informatives résultant d’un tableau de données binaires. Math. Sci. Hum. 95, 5–18 (1986)
Hitzler, P., Krötzsch, M., Rudolph, S.: Foundations of Semantic Web Technologies. Chapman and Hall/CRC Press, Boca Raton (2010). http://dblp.uni-trier.de/rec/bib/books/crc/Hitzler2010
Kriegel, F.: Concept Explorer FX (2010–2017). Software for Formal Concept Analysis with Description Logic Extensions. https://github.com/francesco-kriegel/conexp-fx
Kriegel, F.: NextClosures – parallel exploration of constrained closure operators. LTCS-Report 15–01, Chair for Automata Theory, Technische Universität Dresden (2015). http://lat.inf.tu-dresden.de/research/reports.html
Kriegel, F.: Axiomatization of general concept inclusions from streams of interpretations with optional error tolerance. In: Kuznetsov, S.O., Napoli, A., Rudolph, S. (eds.) Proceedings of the 5th International Workshop “What can FCA do for Artificial Intelligence”? Co-located with the European Conference on Artificial Intelligence, FCA4AI@ECAI 2016, The Hague, 30 August 2016. CEUR Workshop Proceedings, vol. 1703, pp. 9–16. CEUR-WS.org (2016). http://dblp.uni-trier.de/rec/bib/conf/ecai/Kriegel16
Kriegel, F.: NextClosures with constraints. In: Huchard, M., Kuznetsov, S.O. (eds.) Proceedings of the Thirteenth International Conference on Concept Lattices and Their Applications, Moscow, 18–22 July 2016. CEUR Workshop Proceedings, vol. 1624, pp. 231–243. CEUR-WS.org (2016). http://dblp2.uni-trier.de/rec/bib/conf/cla/Kriegel16
Kriegel, F.: Parallel attribute exploration. In: Haemmerlé, O., Stapleton, G., Faron-Zucker, C. (eds.) Graph-Based Representation and Reasoning - Proceedings of the 22nd International Conference on Conceptual Structures, ICCS 2016, Annecy, 5–7 July 2016. Lecture Notes in Computer Science, vol. 9717, pp. 91–106. Springer, Heidelberg (2016). DOI 10.1007/978-3-319-40985-6∖_8. http://dblp2.uni-trier.de/rec/bib/conf/iccs/Kriegel16
Kriegel, F., Borchmann, D.: NextClosures: parallel computation of the canonical base. In: Ben Yahia, S., Konecny, J. (eds.) Proceedings of the Twelfth International Conference on Concept Lattices and Their Applications, Clermont-Ferrand, 13–16 October 2015. CEUR Workshop Proceedings, vol. 1466, pp. 181–192. CEUR-WS.org (2015). http://dblp.uni-trier.de/rec/bib/conf/cla/KriegelB15
Küsters, R., Molitor, R.: Computing least common subsumers in ALEN. In: Nebel, B. (ed.) Proceedings of the Seventeenth International Joint Conference on Artificial Intelligence, IJCAI 2001, pp. 219–224, Seattle, WA, 4–10 August 2001. Morgan Kaufmann, San Francisco (2001). http://dblp.uni-trier.de/rec/bib/conf/ijcai/KustersM01
Kuznetsov, S.O.: On computing the size of a lattice and related decision problems. Order 18(4), 313–321 (2001). DOI 10.1023/A:1013970520933. http://dblp.uni-trier.de/rec/bib/journals/order/Kuznetsov01
Kuznetsov, S.O.: On the intractability of computing the Duquenne-Guigues base. J. UCS 10(8), 927–933 (2004). DOI 10.3217/jucs-010-08-0927. http://dblp.uni-trier.de/rec/bib/journals/jucs/Kuznetsov04
Kuznetsov, S.O., Obiedkov, S.A.: Counting pseudo-intents and #p-completeness. In: Missaoui, R., Schmid, J. (eds.) Formal Concept Analysis, Proceedings of the 4th International Conference, ICFCA 2006, Dresden, 13–17 February 2006. Lecture Notes in Computer Science, vol. 3874, pp. 306–308. Springer, Heidelberg (2006). DOI 10.1007/11671404∖_21. http://dblp.uni-trier.de/rec/bib/conf/icfca/KuznetsovO06
Kuznetsov, S.O., Obiedkov, S.A.: Some decision and counting problems of the Duquenne-Guigues basis of implications. Discrete Appl. Math. 156(11), 1994–2003 (2008). DOI 10.1016/j.dam.2007.04.014. http://dblp.uni-trier.de/rec/bib/journals/dam/KuznetsovO08
Mac Lane, S.: Categories for the Working Mathematician. Graduate Texts in Mathematics, vol. 5, 2nd edn. Springer, New York (1978). DOI 10.1007/978-1-4757-4721-8∖_1. http://dx.doi.org/10.1007/978-1-4757-4721-8_1
Maier, D.: The Theory of Relational Databases. Computer Science Press, Rockville (1983). http://dblp.uni-trier.de/rec/bib/books/cs/Maier83
Mantay, T.: Computing least common subsumers in expressive description logics. In: Foo, N.Y. (ed.) Advanced Topics in Artificial Intelligence, Proceedings of the 12th Australian Joint Conference on Artificial Intelligence, AI ’99, Sydney, 6–10 December 1999. Lecture Notes in Computer Science, vol. 1747, pp. 218–230. Springer, Heidelberg (1999). DOI 10.1007/3-540-46695-9∖_19. http://dblp.uni-trier.de/rec/bib/conf/ausai/Mantay99
Mantay, T.: A least common subsumer operation for an expressive description logic. In: Loganantharaj, R., Palm, G. (eds.) Intelligent Problem Solving, Methodologies and Approaches, Proceedings of the 13th International Conference on Industrial and Engineering Applications of Artificial Intelligence and Expert Systems, IEA/AIE 2000, New Orleans, LA, 19–22 June 2000. Lecture Notes in Computer Science, vol. 1821, pp. 474–481. Springer, Heidelberg (2000). DOI 10.1007/3-540-45049-1∖_57. http://dblp.uni-trier.de/rec/bib/conf/ieaaie/Mantay00
Obiedkov, S.A., Duquenne, V.: Attribute-incremental construction of the canonical implication basis. Ann. Math. Artif. Intell. 49(1–4), 77–99 (2007). DOI 10.1007/s10472-007-9057-2. http://dblp.uni-trier.de/rec/bib/journals/amai/ObiedkovD07
Sertkaya, B.: Some computational problems related to pseudo-intents. In: Ferré, S., Rudolph, S. (eds.) Formal Concept Analysis, Proceedings of the 7th International Conference, ICFCA 2009, Darmstadt, 21–24 May 2009. Lecture Notes in Computer Science, vol. 5548, pp. 130–145. Springer, Heidelberg (2009). DOI 10.1007/978-3-642-01815-2∖_11. http://dblp.uni-trier.de/rec/bib/conf/icfca/Sertkaya09
Sertkaya, B.: Towards the complexity of recognizing pseudo-intents. In: Rudolph, S., Dau, F., Kuznetsov, S.O. (eds.) Conceptual Structures: Leveraging Semantic Technologies, Proceedings of the 17th International Conference on Conceptual Structures, ICCS 2009, Moscow, 26–31 July 2009. Lecture Notes in Computer Science, vol. 5662, pp. 284–292. Springer, Heidelberg (2009). DOI 10.1007/978-3-642-03079-6∖_22. http://dblp.uni-trier.de/rec/bib/conf/iccs/Sertkaya09
Stumme, G.: Attribute exploration with background implications and exceptions. In: Studies in Classification, Data Analysis, and Knowledge Organization, pp. 457–469. Springer, Berlin/Heidelberg (1996). DOI 10.1016/S0304-3975(98)00271-0. http://dblp.uni-trier.de/rec/bib/journals/tcs/Ganter99
(W3C), W.W.W.C.: Owl 2 web ontology language document overview, 2nd edn. (2012). https://www.w3.org/TR/owl2-overview/
Wild, M.: Computations with finite closure systems and implications. In: Du, D., Li, M. (eds.) Computing and Combinatorics, Proceedings of the First Annual International Conference, COCOON ’95, Xi’an, 24–26 August 1995. Lecture Notes in Computer Science, vol. 959, pp. 111–120. Springer, Heidelberg (1995). DOI 10.1007/BFb0030825. http://dx.doi.org/10.1007/BFb0030825. http://dblp.uni-trier.de/rec/bib/conf/cocoon/Wild95
Wille, R.: Restructuring Lattice Theory: An Approach Based on Hierarchies of Concepts, pp. 445–470. Springer, Dordrecht (1982). DOI 10.1007/978-94-009-7798-3∖_15. http://dx.doi.org/10.1007/978-94-009-7798-3_15
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Kriegel, F. (2017). Acquisition of Terminological Knowledge from Social Networks in Description Logic. In: Missaoui, R., Kuznetsov, S., Obiedkov, S. (eds) Formal Concept Analysis of Social Networks. Lecture Notes in Social Networks. Springer, Cham. https://doi.org/10.1007/978-3-319-64167-6_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-64167-6_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-64166-9
Online ISBN: 978-3-319-64167-6
eBook Packages: Computer ScienceComputer Science (R0)





 is a vertex labeling function, and
is a vertex labeling function, and is an edge labeling function.
is an edge labeling function.
 ?
?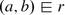 ?
? is a vertex labelling, and
is a vertex labelling, and is an edge labelling.
is an edge labelling. implies ∅⊧E ⊑ F.
implies ∅⊧E ⊑ F.

 .
. is a model of X → Y.
is a model of X → Y. is a model of X → Y.
is a model of X → Y. , there is a subset
, there is a subset  such that
such that 

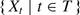 be a family of subsets
be a family of subsets  is indeed a role-depth-bounded model-based most specific concept description of
is indeed a role-depth-bounded model-based most specific concept description of  . (It would also be possible to dually prove that
. (It would also be possible to dually prove that  is a least common subsumer of the concept descriptions
is a least common subsumer of the concept descriptions  is a subset of the extension
is a subset of the extension  . By definition, it holds that
. By definition, it holds that  . It then immediately follows that each X
t must be a subset of the extension
. It then immediately follows that each X
t must be a subset of the extension  .
. , then C subsumes
, then C subsumes  with respect to the empty TBox ∅. By definition of RMMSCs then we infer that each
with respect to the empty TBox ∅. By definition of RMMSCs then we infer that each  must be subsumed by C, too.
must be subsumed by C, too. it holds true that
it holds true that  .
. it holds true that
it holds true that  .
. for δ > 0. By induction hypothesis,
for δ > 0. By induction hypothesis,  occurring in
occurring in  . By induction hypothesis, Y is a subset of
. By induction hypothesis, Y is a subset of  .
.  :
: .
. :
: .
. :
: , we infer that each r-successor of each element in X is in the extension
, we infer that each r-successor of each element in X is in the extension 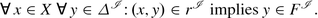

 ):
): , i.e., every element x ∈ X has n or more r-successors which are in the extension of F. Thus,
, i.e., every element x ∈ X has n or more r-successors which are in the extension of F. Thus,  for all x ∈ X, and consequently there is a set
for all x ∈ X, and consequently there is a set  such that
such that 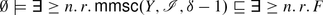 where the subsumee is a top-level conjunct in
where the subsumee is a top-level conjunct in  ):
): yields that for every element x ∈ X, the number of r-successors of x does not exceed n. It is readily verified that then n(X, r) ≤ n, and thus
yields that for every element x ∈ X, the number of r-successors of x does not exceed n. It is readily verified that then n(X, r) ≤ n, and thus  . Of course,
. Of course,  is contained as a top-level conjunct in
is contained as a top-level conjunct in  ):
): it follows that each element x ∈ X is an r-successor of itself, i.e.,
it follows that each element x ∈ X is an r-successor of itself, i.e.,  . By definition,
. By definition,  as a top-level conjunct. □
as a top-level conjunct. □


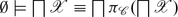





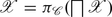





 we deduce that
we deduce that  .
.





 , then
, then  is a model-based most specific concept description of
is a model-based most specific concept description of  .
. holds, cf. Statement 4 of Theorem
holds, cf. Statement 4 of Theorem  . Furthermore, from Lemma
. Furthermore, from Lemma  is expressible in terms of
is expressible in terms of  .
. , and Lemma
, and Lemma  , i.e.,
, i.e.,  is a RMMSC.
is a RMMSC. . Furthermore, it follows that
. Furthermore, it follows that  . In particular then
. In particular then  holds, and according to Lemma
holds, and according to Lemma 

 :
:
 :
: . We can infer the following.
. We can infer the following.

 the incidence relation of which we denote as J.
the incidence relation of which we denote as J. , too.
, too. .
.
 .
.