Mathematical Model for Determining the Contour of a New Type of Profiled Rotor

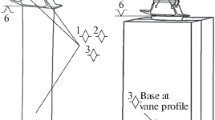
Abstract

The first part of the paper presents the constructive solution for a new type of volumetric meter for liquid flow rate measurement.

The meter consists of two special profiled rotors, which ensure a high accuracy in measuring the liquid flow rate.

Mathematical computing relations for the rotor contour in (x_i y_i) coordinates are presented; a computer program has been used afterwards to obtain these coordinates necessary to build the rotors using a numerical controlled center (N.C.C.).

1 Introduction

The profiled rotor architecture established in this paper leads to several uses in thermal and hydraulic rotating machines field.

The constructive solution presented in this paper can be used in several ways.

It can be considered: p_a - the fluid suction pressure and p_r – the discharge pressure, then there are distinguished:

• 1. If p_a > p_r, then the solution can be used as:

  • Steam engine;

  • Hydrostatic motor;

  • Volumetric meter.

• 2. If p_a < p_r, the solution can be used as:

  • Pump for liquid circulation;

  • Fan;

  • Low-pressure compressor (blower).

In both cases the torque received by the shaft or the motor torque generated by the fluid will be maximized: M = Fbsinα (Nm); α = 90°; M – received torque; F – the force provided by the liquid flow or the engine; b – the lever arm.

In [1] a comparison between the constructive solution presented here and the Roots compressor is carried out highlighting the advantages of this solution. For a certain constructive solution, original equations are set that will generate the rotor profile contour.

A complex computation program that specifies the coordinates (x_i y_i) of the piston contour was developed. With these coordinates, a computer program can be developed through which the rotors will be built on a numerical controlled center (N.C.C.), which provides an execution accuracy of 0.01 mm [3].

2 The Constructive Solution Description

The fluid is transported to the discharge and after a 90° rotation of both rotors, the situation in Fig. 1b and thereafter in Fig. 1c is reached.

Fig. 1.

The operating principle of the volumetric meter 1, 2, 3′, 4′-rotating pistons; 1′, 2′, 3, 4-cavities in which the rotating pistons enters; 5-upper rotor; 6-lower rotor; 7-upper case; 8-lower case; 9-upper shaft; 10-lower shaft

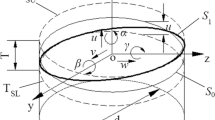
From Fig. 1a one observes that the case radius (R _c ) is the sum of the rotor radius (R _r ) and the piston height (z).

During the rotational movement, the pistons (1) and (2) of the upper rotor (5) enter into the cavities (1′) and (2′) of the lower rotor (6). Similarly, the pistons (3) and (4) of the lower rotor (6) enter into the cavities (3′) and (4′) of the upper rotor (5). The two rotors are identical; during each rotation, two liquid volumes, equal with V _u (Fig. 1b) are transported to discharge.

3 The Equations that Specifies the Curvilinear Contour of the Rotating Piston

It is considered that the two rotors have equal rotor and case radiuses (R _r and R _c ).

Their difference provides the height of the rotating piston (z) R_c − R_r = z.

The two rotors are tangent and rotate in the direction indicated in Fig. 2.

Fig. 2.

Computing notations: 1 - lower rotor; 2 - upper rotor

If the upper rotor (O2) is fixed, the point E, located on the lower rotor (O1), which is mobile, will reach the point A.

What path will the point E describe on the annular surface R _r ÷ R _c when the two rotors are movable?

To solve this problem, a rotating axes system xO2y is chosen to determining the A point coordinates (X _A , Y _A ).

The A point coordinates will be:

$$ X_{A} \,\, = \,\, - O_{2} B\,\, = \,\, - CD\,\, = \,\, - AC\cos \alpha $$

(1)

From the O1EC triangle, one obtains:

$$ \cos \,\theta \,\, = \,\,\frac{{O_{1} E}}{{O_{1} C}}\,\, = \,\,\frac{{R_{r} }}{{R_{r} + AC}} $$

(2)

From (2) one obtains:

$$ AC\,\, = \,\,\frac{{R_{r} (1 - \cos \,\theta )}}{\cos \,\theta } $$

(3)

Because in the O1EC triangle:

$$ \theta + 90^{ \circ } + \theta + \alpha \,\, = \,\,180^{ \circ } $$

(4)

Results:

$$ \alpha \,\, = \,\,90^{ \circ } - 2\theta $$

(5)

Introducing relationships (3) and (5) in (1) results:

$$ X_{A} \,\, = \,\, - \frac{{R_{r} (1 - \cos \,\theta )}}{\cos \,\theta } \cdot \cos \,(90^{ \circ } - 2\theta ) $$

(6)

Or

$$ X_{A} \,\, = - \,\,\frac{{R_{r} (1 - \cos \,\theta )}}{\cos \,\theta } \cdot \sin \,2\theta $$

(7)

$$ Y_{A} \,\, = \,\, - AB\,\, = \,\, - (BD + DA)\,\, = \,\, - \left( {O_{2} C\, + DA} \right) $$

(8)

From the O2EC triangle, one obtains:

$$ \cos \,\theta \,\, = \,\,\frac{{O_{2} E}}{{O_{2} C}}\,\, = \,\,\frac{{R_{r} }}{{O_{2} C}} $$

(9)

$$ Y_{A} = - \left( {\frac{{R_{r} }}{\cos \theta } + AC\sin \alpha } \right) = - \left[ {\frac{{R_{r} }}{\cos \theta } + \frac{{R_{r} (1 - \cos \theta )}}{\cos \theta }\sin (90^{ \circ } - 2\theta )} \right] $$

(10)

$$ Y_{A} \,\, = \,\, - \left[ {\frac{{R_{r} }}{\cos \,\theta } + \frac{{R_{r} (1 - \cos \,\theta )}}{\cos \,\theta }\cos \,2\theta } \right] $$

(11)

Hence, the coordinates of point A will be:

$$ \left\{ {\begin{array}{*{20}l} {X_{A} = - \frac{{R_{r} (1 - \cos {\mkern 1mu} \theta )}}{{\cos {\mkern 1mu} \theta }} \cdot \sin 2\theta } \hfill \\ {Y_{A} = - \left[ {\frac{{R_{r} }}{{\cos {\mkern 1mu} \theta }} + \frac{{R_{r} (1 - \cos {\mkern 1mu} \theta )}}{{\cos {\mkern 1mu} \theta }}\cos 2\theta } \right]} \hfill \\ \end{array} } \right. $$

(12)

If in Eq. (12) the rotor radius: R _r  = 0.025 m and ϑ ₁ = 0°…22.7° are inserted, the coordinates of the points located on one side (AB) of the curvilinear piston, are obtained. For the point A, the value YA = 0.04 m, i.e. the case radius (R _c ) must be specified.

If the axis system xOy rotates [6, 7] the situation in Fig. 5 is reached.

The values of the angles involved in the calculation are:

• For the AB arc, the coordinates of point B are XB = 0.009567 m, YB = 0.023097 m

  $$ \tan \,\theta_{1} = \frac{{X_{B} }}{{Y_{B} }}{ = }\frac{0.009567}{0.023097} = 0.4142\;[{\text{rad}}];\quad \theta_{1} = 22.7^{ \circ } $$

• For the BC arc, the value of ϑ ₂ is determined as follows:

  The value of ϑ ₁ is 22.7°; ϑ ₃ has the same value. As a result:

  $$ \theta_{2} = 90^{ \circ } - \left( {\theta_{1} + \theta_{3} } \right) = 90^{ \circ } - (22.7^{ \circ } + 22.7^{ \circ } ) = 44.6^{ \circ } $$

  ϑ ₁, ϑ ₂, ϑ ₃ are considered to be on upper rotor as the center angles.

• For the CD arc, which specifies the cavity profile, the calculation of ϑ ₃ can be performed on the lower rotor, establishing its value, calculated in paragraph 5:

  $$ \theta_{3} \,\, = \,\,\theta_{f} $$

4 The Equations that Specifies the Circle Arc that Forms Part of the Rotor Contour

The curve BC is a circle arc with a radius equal to the rotor radius.

The arc has a central angle equal to ϑ ₂ = 44.6°.

So, the value of ϑ ₂ is between ϑ ₁ = 22.7° and 22.7° + 44.6° = 67.3°.

The coordinates of the points on the BC circle arc can be obtained in two ways:

• (1) The rotor radius intersects with the circle of R _r radius, in other words, the following system is solved:

  $$ \left\{ \begin{aligned} y = mx \hfill \\ x^{2} + y^{2} = R_{r}^{2} \hfill \\ \end{aligned} \right. $$

  (13)

• (2) It is calculated:

  $$ \left\{ \begin{aligned} x = R_{r} \cos \,\theta_{2} \hfill \\ y\, = \, - R_{r} \sin \theta_{2} \hfill \\ \end{aligned} \right. $$

  (14)

5 The Equations that Specifies the Cavity Contour

Theoretically, if the upper rotor (2) would be fixed, the piston tip of the lower rotor (1), i.e. the point A, describes a circle arc of O1A radius; in fact, the rotor (2) is mobile and the path of point A will not be a circle arc, but a curve whose path determines the cavity profile.

To draw the cavity profile, the radius O1A = R _r  + z moves from position (ϑ ₁ = 0°) to the final one (ϑ = ϑ _f ), the point A leaves the upper rotor surface (the rotating piston exits the cavity).

It is aimed to establish the motion parametric equations of the piston tip of the lower rotor (1) inside the upper rotor (2).

From Fig. 3 is observed that R _c  = R _r  + z = O1A.

Fig. 3.

Computing notations for the cavity profile: 1 - lower rotor; 2 - upper rotor

The coordinates of point A are:

$$ X_{A} \,\, = \,\,PA\sin \,2\theta $$

(15)

$$ Y_{A} \,\, = \,\, - O_{2} P + A\cos \,2\theta $$

(16)

$$ X_{A} = AO{}_{1} - PO_{1} = R_{c} - \left( {\frac{{R_{r} }}{\cos \theta }} \right) \cdot \sin \,2\theta $$

(17)

$$ Y_{A} \,\, = \,\, - \frac{{R_{r} }}{\cos \theta } + \left( {R_{c} - \frac{{R_{r} }}{\cos \theta }} \right)\cos \,2\theta $$

(18)

But: $\sin 2\theta = 2\sin \theta \cos \theta = 2\cos \theta \sqrt {1 - \cos^{2} }$

Or: $X_{A} = R_{c} - \left( {\frac{{R_{r} }}{\cos \theta }} \right) \cdot 2\cos \theta \sqrt {1 - \cos^{2} \theta }$

$$ Y_{A} \,\, = \,\, - \frac{{R_{r} \cos \,2\theta }}{\cos \theta } + R_{c} \cos \,2\theta $$

(19)

But: cos 2θ = 2 cos²θ – 1

$$ Y_{A} \,\, = \,\,2R_{c} \cos^{2} \theta - 2R_{r} \cos \theta - R_{c} $$

(20)

$$ X_{A} = 2\left( {R_{c} \cos \theta - R_{r} } \right)\sqrt {1 - \cos^{2} \theta } $$

(21)

$$ Y_{A} \,\, = \,\,2\cos \theta \left( {R_{c} \cos \theta - R_{r} } \right) - R_{c} $$

(22)

The relations (21) and (22) represent the motion parameters equations of the piston of the lower rotor (1) inside the upper rotor (2).

One can observe that:

$$ X_{A} = f\left( {R_{c} ,\;R_{r} ,\;\vartheta } \right)\;{\text{and}}\;Y_{A} = f\left( {R_{c} ,\;R_{r} ,\;\vartheta } \right) $$

To determine the value of ϑ _f , from Fig. 4 one observes that: O1A = R _c ; O2A = R _r ; O1O2 = 2R _r .

Fig. 4.

Computing notations for ϑ _f = ϑ ₃ determination

The triangle O1O2A is considered in which the law of cosines applies:

$$ \left( {O_{2} A} \right)^{2} = \left( {O_{1} A} \right)^{2} + \left( {O_{1} O_{2} } \right)^{2} - 2\left( {O_{1} O_{2} } \right)\left( {O_{1} A} \right)\cos \theta_{f} $$

(23)

$$ \cos \theta_{f} = \frac{{R_{c}^{2} + (2R_{r} )^{2} - R_{r}^{2} }}{{2R_{r} 2R_{c} }} $$

(24)

$$ \cos \theta_{f} = \frac{{R_{c}^{2} + 3R_{r}^{2} }}{{4R_{r} R_{c} }} $$

(25)

If R _c  = 40 mm, R _r  = 25 mm it follows:

$$ \cos \theta_{f} = \frac{{40^{2} + 3 \cdot 25^{2} }}{4 \cdot 40 \cdot 25} = 0.868 $$

which corresponds to an angle of 29.7°.

6 The Location of (X _i , Y _i ) on the Contour of the First Rotor Profile Quarter

In the previous paragraphs, the point coordinates specifying the rotor profile contour were calculated, in a coordinate system rotated relative to the known one xOy (Ox - horizontal axis, Oy - vertical axis).

Computing relations giving the point coordinates for the rotor profile contours were established, coordinates that can be represented directly at scale. A computer program to establish the coordinates (x_i, y_i) of the profile contour with very high accuracy (six decimals) was developed; this because both rotors and the case will be built on a N.C.C.

Three computing areas (I, II, III) of the rotor profile contour can be observed in Fig. 5.

Fig. 5.

Computing areas for one quarter of the rotor profile contour

R _r  = 25 mm; R _c  = 40 mm; z = R _c  − R _r  = 15 mm.

A-B - the point coordinates located on a side of the curvilinear piston (Fig. 4) which is determined by the relations (12).

Point A is identical to point 1 (Fig. 5) and point B with point 105.

B′-C – the point coordinates located on the circular portion (Fig. 5). Point B′ is identical to B, i.e., has the same coordinates, but from it to point C the computing relations are (13).

Point B′ is thus the same as B, and point C coincides with point 150.

C′-D - the point coordinates located on the rotor profile convexity (Fig. 5). Point C′ is identical to C but from it to the point D the computing relations are (21) and (22). Point C′ is identical to 150 (Fig. 2) and point D with point 179 (Fig. 6).

Fig. 6.

The construction in symmetry of the entire the rotor contour profile: (a) quarter profile; (b) half profile; (c) the entire rotor profile

7 Conclusions

The mathematical model developed to calculate the coordinates of the rotor profile contour is general; it may be modified for other rotor dimensions being necessary only to specify the values of the rotor radius (Rr) and the case radius (Rc).

The computing step for the angle θ can be 0.5° or 1°, a value that provides better computing accuracy.

After obtaining these coordinates, a computer program for the rotor construction in a machining center (N.C.C.) will be developed.

In order to ensure a better sealing between the rotor and the case, the piston profile should not be triangular but curvilinear.