Recent Progress in Linear Response Eigenvalue Problems

Abstract

Linear response eigenvalue problems arise from the calculation of excitation states of many-particle systems in computational materials science. In this paper, from the point of view of numerical linear algebra and matrix computations, we review the progress of linear response eigenvalue problems in theory and algorithms since 2012.

1 Introduction

The standard Linear Response Eigenvalue Problem (LREP) is the following eigenvalue problem

$$\displaystyle{ \left [\begin{array}{*{10}c} A& B\\ -B & -A \end{array} \right ]\left [\begin{array}{*{10}c} u\\ v \end{array} \right ] =\lambda \left [\begin{array}{*{10}c} u\\ v \end{array} \right ], }$$

(1)

where A and B are n × n real symmetric matrices such that the symmetric matrix $\left [\begin{array}{*{10}c} A&B\\ B & A \end{array} \right ]$ is positive definite. Such an eigenvalue problem arises from computing excitation states (energies) of physical systems in the study of collective motion of many particle systems, ranging from silicon nanoparticles and nanoscale materials to the analysis of interstellar clouds (see, for example, [12, 27, 33, 34, 38, 50] and references therein). In computational quantum chemistry and physics, the excitation states and absorption spectra for molecules or surface of solids are described by the Random Phase Approximation (RPA) or the Bethe-Salpeter (BS) equation. For this reason, the LREP (1) is also called the RPA eigenvalue problem [17], or the BS eigenvalue problem [5, 6, 42]. There are immense recent interest in developing new theory, efficient numerical algorithms of the LREP (1) and the associated excitation response calculations of molecules for materials design in energy science [16, 28, 40, 41].

In this article, we survey recent progress in the LREP research from numerical linear algebra and matrix computations perspective. We focus on recent work since 2012. A survey of previous algorithmic work prior to 2012 can be found in [2, 51] and references therein. The rest of this paper is organized as follows. In Sect. 2, we survey the recent theoretical studies on the properties of the LREP and minimization principles. In Sect. 3, we briefly describe algorithmic advances for solving the LREP. In Sect. 4, we state recent results on perturbation and backward error analysis of the LREP. In Sect. 5, we remark on several related researches spawn from the LREP (1), including a generalized LREP.

2 Theory

Define the symmetric orthogonal matrix

$$\displaystyle{ J = \frac{1} {\sqrt{2}}\left [\begin{array}{*{10}c} I_{n}& I_{n} \\ I_{n}&-I_{n}\\ \end{array} \right ]. }$$

(2)

It can be verified that $J^{\mathop{\mathrm{T}}\nolimits }J = J^{2} = I_{2n}$ and

$$\displaystyle{ J^{\mathop{\mathrm{T}}\nolimits }\left [\begin{array}{*{10}c} A& B \\ -B &-A \end{array} \right ]J = \left [\begin{array}{*{10}c} 0 &A - B \\ A + B & 0 \end{array} \right ]. }$$

(3)

This means that the LREP (1) is orthogonally similar to

$$\displaystyle{ Hz:= \left [\begin{array}{*{10}c} 0 &K\\ M & 0 \end{array} \right ]\left [\begin{array}{*{10}c} y\\ x \end{array} \right ] =\lambda \left [\begin{array}{*{10}c} y\\ x \end{array} \right ] =:\lambda z, }$$

(4)

where K = A − B and M = A + B. Both eigenvalue problems (1) and (4) have the same eigenvalues with corresponding eigenvectors related by

$$\displaystyle{ \left [\begin{array}{*{10}c} y\\ x \end{array} \right ] = J^{\mathop{\mathrm{T}}\nolimits }\left [\begin{array}{*{10}c} u\\ v \end{array} \right ]\quad \mbox{ and}\quad \left [\begin{array}{*{10}c} u\\ v \end{array} \right ] = J\left [\begin{array}{*{10}c} y\\ x \end{array} \right ]. }$$

(5)

Furthermore, the positive definiteness of the matrix $\left [\begin{array}{*{10}c} A&B\\ B & A \end{array} \right ]$ is translated into that both K and M are positive definite since

$$\displaystyle{ J^{\mathop{\mathrm{T}}\nolimits }\left [\begin{array}{*{10}c} A&B \\ B &A \end{array} \right ]J = \left [\begin{array}{*{10}c} A + B & 0 \\ 0 &A - B \end{array} \right ] = \left [\begin{array}{*{10}c} M & 0\\ 0 &K \end{array} \right ]. }$$

(6)

Because of the equivalence of the eigenvalue problems (1) and (4), we still refer to (4) as an LREP which will be one to be studied from now on, unless otherwise explicitly stated differently.

2.1 Basic Eigen-Properties

It is straightforward to verify that

$$\displaystyle{ H\left [\begin{array}{*{10}c} y\\ x \end{array} \right ] =\lambda \left [\begin{array}{*{10}c} y\\ x \end{array} \right ]\quad \Rightarrow \quad H\left [\begin{array}{*{10}c} y\\ -x \end{array} \right ] = -\lambda \left [\begin{array}{*{10}c} y\\ -x \end{array} \right ]. }$$

(7)

This implies that the eigenvalues of H come in pair {λ, −λ} and their associated eigenvectors enjoy a simple relationship. In fact, as shown in [1], there exists a nonsingular $\varPhi \in \mathbb{R}^{n\times n}$ such that

$$\displaystyle{ K =\varPsi \varLambda ^{2}\varPsi ^{\mathop{\mathrm{T}}\nolimits }\quad \mbox{ and}\quad M =\varPhi \varPhi ^{\mathop{\mathrm{T}}\nolimits }, }$$

(8a)

where $\varLambda =\mathop{ \mathrm{diag}}\nolimits (\lambda _{1},\lambda _{2},\ldots,\lambda _{n})$ and $\varPsi =\varPhi ^{-\mathop{\mathrm{T}}\nolimits }$. In particular

$$\displaystyle{ H\left [\begin{array}{*{10}c} \varPsi \varLambda & \varPsi \varLambda \\ \varPhi &-\varPhi \end{array} \right ] = \left [\begin{array}{*{10}c} \varPsi \varLambda & \varPsi \varLambda \\ \varPhi &-\varPhi \end{array} \right ]\left [\begin{array}{*{10}c} \varLambda & 0 \\ 0&-\varLambda \end{array} \right ]. }$$

(8b)

Thus H is diagonalizable and has the eigen-decomposition (8b).

The notion of invariant subspace (aka eigenspace) is an important concept for the standard matrix eigenvalue problem not only in theory but also in numerical computation. In the context of LREP (4), with consideration of its eigen-properties as revealed by (7) and (8b), in [1, 2] we introduced a pair of deflating subspaces of {K, M}, by which we mean a pair $\{\mathscr{U},\mathscr{V }\}$ of two k-dimensional subspaces $\mathscr{U} \subseteq \mathbb{R}^{n}$ and $\mathscr{V } \subseteq \mathbb{R}^{n}$ such that

$$\displaystyle{ K\mathscr{U} \subseteq \mathscr{V }\quad \mbox{ and}\quad M\mathscr{V } \subseteq \mathscr{U}. }$$

(9)

Let $U \in \mathbb{R}^{n\times k}$ and $V \in \mathbb{R}^{n\times k}$ be the basis matrices of $\mathscr{U}$ and $\mathscr{V }$, respectively. Then (9) can be restated as that there exist $K_{\text{R}} \in \mathbb{R}^{k\times k}$ and $M_{\text{R}} \in \mathbb{R}^{k\times k}$ such that

$$\displaystyle{ KU = V K_{\text{R}}\quad \mbox{ and}\quad MV = UM_{\text{R}}, }$$

(10)

and vice versa, or equivalently,

$$\displaystyle{H\left [\begin{array}{*{10}c} V & 0\\ 0 &U \end{array} \right ] = \left [\begin{array}{*{10}c} V & 0\\ 0 &U \end{array} \right ]H_{\text{R}}\quad \mbox{ with}\quad H_{\text{R}}:= \left [\begin{array}{*{10}c} 0 &K_{\text{R}} \\ M_{\text{R}} & 0 \end{array} \right ],}$$

i.e., $\mathscr{V } \oplus \mathscr{U}$ is an invariant subspace of H [1, Theorem 2.4]. We call {U, V, K _R , M _R } an eigen-quaternary of {K, M} [57].

Given a pair of deflating subspaces $\{\mathscr{U},\mathscr{V }\} =\{ \mathscr{R}(U),\mathscr{R}(V )\}$, a part of the eigenpairs of H can be obtained via solving the smaller eigenvalue problem [1, Theorem 2.5]. Specifically, if

$$\displaystyle{ H_{\text{R}}\hat{z}:= \left [\begin{array}{*{10}c} 0 &K_{\text{R}} \\ M_{\text{R}} & 0 \end{array} \right ]\left [\begin{array}{*{10}c} \hat{y}\\ \hat{x} \end{array} \right ] =\lambda \left [\begin{array}{*{10}c} \hat{y}\\ \hat{x} \end{array} \right ] =:\lambda \hat{ z}, }$$

(11)

then $(\lambda,\left [\begin{array}{*{10}c} V \hat{y}\\ U\hat{x} \end{array} \right ])$ is an eigenpair of H. The matrix H _R is the restriction of H onto $\mathscr{V } \oplus \mathscr{U}$ with respect to the basis matrices V ⊕ U. Moreover, the eigenvalues of H _R are uniquely determined by the pair of deflating subspaces $\{\mathscr{U},\mathscr{V }\}$ [2].

There are infinitely many choices of {K _R , M _R } in (10). The most important one introduced in [57] is the Rayleigh quotient pair, denoted by {K _RQ , M _RQ }, of the LREP (4) associated with $\{\mathscr{R}(U),\mathscr{R}(V )\}$:

$$\displaystyle{ K_{\text{RQ}}:= (U^{\mathop{\mathrm{T}}\nolimits }V )^{-1}U^{\mathop{\mathrm{T}}\nolimits }KU\quad \mbox{ and}\quad M_{\text{ RQ}}:= (V ^{\mathop{\mathrm{T}}\nolimits }U)^{-1}V ^{\mathop{\mathrm{T}}\nolimits }MV, }$$

(12)

and accordingly,

$$\displaystyle{H_{\text{RQ}} = \left [\begin{array}{*{10}c} 0 &K_{\text{RQ}} \\ M_{\text{RQ}} & 0 \end{array} \right ].}$$

Note that H _RQ so defined is not of the LREP type because K _RQ and M _RQ are not symmetric unless $U^{\mathop{\mathrm{T}}\nolimits }V = I_{k}$. To circumvent this, we factorize $W:= U^{\mathop{\mathrm{T}}\nolimits }V$ as $W = W_{1}^{\mathop{\mathrm{T}}\nolimits }W_{2}$, where $W_{i} \in \mathbb{R}^{k\times k}$ are nonsingular, and define

$$\displaystyle{ H_{\text{SR}}:= \left [\begin{array}{*{10}c} 0 &W_{1}^{-\mathop{\mathrm{T}}\nolimits }U^{\mathop{\mathrm{T}}\nolimits }KUW_{1}^{-1} \\ W_{2}^{-\mathop{\mathrm{T}}\nolimits }V ^{\mathop{\mathrm{T}}\nolimits }MV W_{2}^{-1} & 0 \end{array} \right ] = [W_{2}\oplus W_{1}]H_{\text{RQ}}[W_{2}\oplus W_{1}]^{-1}. }$$

(13)

Thus H _RQ is similar to H _SR . The latter is of the LREP type and has played an important role in [1, 2] for the LREP, much the same role as played by the Rayleigh quotient matrix in the symmetric eigenvalue problem [36].

Up to this point, our discussion is under the assumption that $\{\mathscr{R}(U),\mathscr{R}(V )\}$ is a pair of deflating subspaces. But as far as the construction of H _RQ is concerned, this is not necessary, so long as $U^{\mathop{\mathrm{T}}\nolimits }V$ is nonsingular. The same statement also goes for H _SR . In fact, a key component in [2, 58] on eigenvalue approximations for the LREP is the use of the eigenvalues of H _SR to approximate part of the eigenvalues of H.

2.2 Thouless’ Minimization Principle

Back to 1961, Thouless [49] showed that the smallest positive eigenvalue λ ₁ of the LREP (1) admits the following minimization principle:

$$\displaystyle{ \lambda _{1} =\min _{u,v}\rho _{t}(u,v), }$$

(14)

where ρ _t (u, v) is defined by

$$\displaystyle{ \rho _{t}(u,v) = \frac{\left [\begin{array}{*{10}c} u\\ v \end{array} \right ]^{\mathop{\mathrm{T}}\nolimits }\left [\begin{array}{*{10}c} A&B\\ B & A \end{array} \right ]\left [\begin{array}{*{10}c} u\\ v \end{array} \right ]} {\vert u^{\mathop{\mathrm{T}}\nolimits }u - v^{\mathop{\mathrm{T}}\nolimits }v\vert }. }$$

(15)

The minimization in (14) is taken among all vectors u, v such that $u^{\mathop{\mathrm{T}}\nolimits }u - v^{\mathop{\mathrm{T}}\nolimits }v\neq 0$.

By the similarity transformation (3) and using the relationships in (5), we have

$$\displaystyle{ \rho _{t}(u,v) \equiv \rho (x,y):= \frac{x^{\mathop{\mathrm{T}}\nolimits }Kx + y^{\mathop{\mathrm{T}}\nolimits }My} {2\vert x^{\mathop{\mathrm{T}}\nolimits }y\vert }, }$$

(16)

and thus equivalently

$$\displaystyle{ \lambda _{1} =\min _{x,y}\rho (x,y). }$$

(17)

The minimization here is taken among all vectors x, y such that $x^{\mathop{\mathrm{T}}\nolimits }y\neq 0$ [53].

We will refer to both ρ _t (u, v) and ρ(x, y) as the Thouless functionals but in different forms. Although ρ _t (u, v) ≡ ρ(x, y) under (5), in this paper we primarily work with ρ(x, y) to state extensions of (17) and efficient numerical methods.

2.3 New Minimization Principles and Cauchy Interlacing Inequalities

In [1], we have systematically studied eigenvalue minimization principles for the LREP to mirror those for the standard symmetric eigenvalue problems [7, 36]. We proved the following subspace version of the minimization principle (14):

$$\displaystyle{ \sum _{i=1}^{k}\lambda _{ i} = \frac{1} {2}\min _{U^{\mathop{\mathrm{T}}\nolimits }V =I_{k}}\mathop{ \mathrm{trace}}\nolimits (U^{\mathop{\mathrm{T}}\nolimits }KU + V ^{\mathop{\mathrm{T}}\nolimits }MV ), }$$

(18)

among all $U,V \in \mathbb{R}^{n\times k}$. Moreover if λ _k < λ _k+1, then for any U and V that attain the minimum, $\{\mathscr{R}(U),\mathscr{R}(V )\}$ is a pair of deflating subspaces of {K, M} and the corresponding H _RQ has eigenvalues ±λ _i (1 ≤ i ≤ k).

Equation (18) suggests that

$$\displaystyle{ \frac{1} {2}\mathop{\mathrm{trace}}\nolimits (U^{\mathop{\mathrm{T}}\nolimits }KU + V ^{\mathop{\mathrm{T}}\nolimits }MV )\quad \mbox{ subject to }U^{\mathop{\mathrm{T}}\nolimits }V = I_{ k} }$$

(19)

is a proper subspace version of the Thouless functional in the form of ρ(⋅ , ⋅ ). Exploiting the close relation through (5) between the two different forms of the Thouless functionals ρ _t (⋅ , ⋅ ) and ρ(⋅ , ⋅ ), we see that

$$\displaystyle{ \frac{1} {2}\mathop{\mathrm{trace}}\nolimits (\left [\begin{array}{*{10}c} U\\ V \end{array} \right ]^{\mathop{\mathrm{T}}\nolimits }\left [\begin{array}{*{10}c} A&B \\ B &A \end{array} \right ]\left [\begin{array}{*{10}c} U\\ V \end{array} \right ])\quad \mbox{ subject to }U^{\mathop{\mathrm{T}}\nolimits }U-V ^{\mathop{\mathrm{T}}\nolimits }V = 2I_{k},\ U^{\mathop{\mathrm{T}}\nolimits }V = V ^{\mathop{\mathrm{T}}\nolimits }U }$$

(20)

is a proper subspace version of the Thouless functional in the form of ρ _t (⋅ , ⋅ ). Also as a consequence of (18), we have

$$\displaystyle{ \sum _{i=1}^{k}\lambda _{ i} = \frac{1} {2}\,\min _{{ U^{\mathop{\mathrm{T}}\nolimits }U-V^{\mathop{\mathrm{T}}\nolimits }V =2I_{k} \atop U^{\mathop{\mathrm{T}}\nolimits }V =V^{\mathop{\mathrm{T}}\nolimits }U} }\mathop{ \mathrm{trace}}\nolimits (\left [\begin{array}{*{10}c} U\\ V \end{array} \right ]^{\mathop{\mathrm{T}}\nolimits }\left [\begin{array}{*{10}c} A&B \\ B &A \end{array} \right ]\left [\begin{array}{*{10}c} U\\ V \end{array} \right ]) }$$

(21)

among all $U,V \in \mathbb{R}^{n\times k}$.

In [1], we also derived the Cauchy-type interlacing inequalities. Specifically, let $U,V \in \mathbb{R}^{n\times k}$ such that $U^{\mathop{\mathrm{T}}\nolimits }V$ is nonsingular, and denote by ±μ _i (1 ≤ i ≤ k) the eigenvalues of¹ H _RQ , where 0 ≤ μ ₁ ≤ ⋯ ≤ μ _k . Then

$$\displaystyle{ \lambda _{i} \leq \mu _{i} \leq \gamma \,\lambda _{i+n-k}\quad \mbox{ for }1 \leq i \leq k, }$$

(22)

where $\gamma = \sqrt{\min \{\kappa (K),\kappa (M)\}}/\cos \angle (\mathscr{U},\mathscr{V })$, $\mathscr{U} = \mathscr{R}(U)$ and $\mathscr{V } = \mathscr{R}(V )$. Furthermore, if λ _k < λ _k+1 and λ _i = μ _i for 1 ≤ i ≤ k, then $\{\mathscr{U},\mathscr{V }\}$ is a pair of deflating subspaces of {K, M} corresponding to the eigenvalues ±λ _i (1 ≤ i ≤ k) of H when both K and M are definite.

2.4 Bounds on Eigenvalue Approximations

Let $U,\,V \in \mathbb{R}^{n\times k}$ and $U^{\mathop{\mathrm{T}}\nolimits }V = I_{k}$. $\{\mathscr{R}(U),\mathscr{R}(V )\}$ is a pair of approximate deflating subspaces intended to approximate $\{\mathscr{R}(\varPhi _{1}),\mathscr{R}(\varPsi _{1})\}$, where Φ ₁ = Φ _{(: ,1: k)} and Ψ ₁ = Ψ _{(: ,1: k)}. Construct H _SR as in (13). We see H _SR = H _RQ since $U^{\mathop{\mathrm{T}}\nolimits }V = I_{k}$. Denote the eigenvalues of H _SR by

$$\displaystyle{ -\mu _{k} \leq \ldots \leq -\mu _{1} \leq \mu _{1} \leq \ldots \leq \mu _{k}. }$$

We are interested in bounding

• 1. the errors in μ _i as approximations to λ _i in terms of the error in $\{\mathscr{R}(U),\mathscr{R}(V )\}$ as an approximation to $\{\mathscr{R}(\varPhi _{1}),\mathscr{R}(\varPsi _{1})\}$, and conversely

• 2. the error in $\{\mathscr{R}(U),\mathscr{R}(V )\}$ as an approximation to $\{\mathscr{R}(\varPhi _{1}),\mathscr{R}(\varPsi _{1})\}$ in terms of the errors in μ _i as approximations to λ _i .

To these goals, define

$$\displaystyle{ \delta _{k}:=\sum _{ i=1}^{k}(\mu _{ i}^{2} -\lambda _{ i}^{2}). }$$

(23)

We know 0 < λ _i ≤ μ _i by (22); so δ _k defines an error measurement in all μ _i as approximations to λ _i for 1 ≤ i ≤ k. Suppose λ _k < λ _k+1. It is proved in [58] that

$$\displaystyle\begin{array}{rcl} (\lambda _{k+1}^{2} -\lambda _{ k}^{2})\|\sin \varTheta _{ M^{-1}}(U,\varPhi _{1})\|_{\mathop{\mathrm{F}}\nolimits }^{2}\,\leq \,\delta _{ k}& \,\leq \,&\sum _{i=1}^{k}\lambda _{ i}^{2} \cdot \tan ^{2}\theta _{ M^{-1}}(U,MV ) \\ & & + \frac{\lambda _{n}^{2} -\lambda _{1}^{2}} {\cos ^{2}\theta _{M^{-1}}(U,MV )}\|\sin \varTheta _{M^{-1}}(U,\varPhi _{1})\|_{\mathop{\mathrm{F}}\nolimits }^{2},{}\end{array}$$

(24a)

$$\displaystyle\begin{array}{rcl} (\lambda _{k+1}^{2} -\lambda _{ k}^{2})\|\sin \varTheta _{ K^{-1}}(V,\varPsi _{1})\|_{\mathop{\mathrm{F}}\nolimits }^{2}\,\leq \,\delta _{ k}& \,\leq \,&\sum _{i=1}^{k}\lambda _{ i}^{2} \cdot \tan ^{2}\theta _{ K^{-1}}(V,KU) \\ & & + \frac{\lambda _{n}^{2} -\lambda _{1}^{2}} {\cos ^{2}\theta _{K^{-1}}(V,KU)}\|\sin \varTheta _{K^{-1}}(V,\varPsi _{1})\|_{\mathop{\mathrm{F}}\nolimits }^{2},{}\end{array}$$

(24b)

where $\varTheta _{M^{-1}}(U,\varPhi _{1})$ is the diagonal matrix of the canonical angles between subspaces $\mathscr{R}(U)$ and $\mathscr{R}(\varPhi )$ in the M ⁻¹-inner product, the largest of which is denoted by $\theta _{M^{-1}}(U,\varPhi _{1})$, and similarly for $\theta _{M^{-1}}(U,MV )$, $\varTheta _{K^{-1}}(V,\varPsi _{1})$, and $\theta _{K^{-1}}(V,KU)$ (see, e.g., [58] for precise definitions). As a result,

$$\displaystyle{ \|\sin \varTheta _{M^{-1}}(U,\varPhi _{1})\|_{\mathop{\mathrm{F}}\nolimits } \leq \sqrt{ \frac{\delta _{k } } {\lambda _{k+1}^{2} -\lambda _{k}^{2}}}, }$$

(25a)

$$\displaystyle{ \|\sin \varTheta _{K^{-1}}(V,\varPsi _{1})\|_{\mathop{\mathrm{F}}\nolimits } \leq \sqrt{ \frac{\delta _{k } } {\lambda _{k+1}^{2} -\lambda _{k}^{2}}}. }$$

(25b)

The inequalities in (24) address item 1 above, while item 2 is answered by these in (25).

3 Numerical Algorithms

In [2], we reviewed a list of algorithms for solving the small dense and large sparse LREPs up to 2012. In the recent work [42] for solving dense complex and real LREP, authors established the equivalence between the eigenvalue problem and real Hamiltonian eigenvalue problem. Consequently, a structure preserving algorithm is proposed and implemented using ScaLAPACK [10] on distributed memory computer systems. In this section, we will review recently proposed algorithms for solving large sparse LREPs.

3.1 Deflation

Whether already known or computed eigenpairs can be effectively deflated away to avoid being recomputed is crucial to numerical efficiency in the process of computing more eigenpairs while avoiding the known ones. In [4], we developed a shifting deflation technique by a low-rank update to either K or M and thus the resulting K or M performs at about comparable cost as the original K or M when it comes to do matrix-vector multiplication operations. This deflation strategy is made possible by the following result.

Let $\mathbb{J} =\{ i_{j}\,:\, 1 \leq j \leq k\} \subset \{ 1,2,\ldots,n\}$, and let $V \in \mathbb{R}^{n\times k}$ with $\mathop{\mathrm{rank}}\nolimits (V ) = k$ satisfying $\mathscr{R}(V ) = \mathscr{R}(\varPsi _{(:,\mathbb{J})})$, or equivalently $V =\varPsi _{(:,\mathbb{J})}Q$ for some nonsingular $Q \in \mathbb{R}^{k\times k}$. Let ξ > 0, and define

$$\displaystyle{ \underline{H} = \left [\begin{array}{*{10}c} 0 &\underline{K}\\ M & 0 \end{array} \right ]:= \left [\begin{array}{*{10}c} 0 &K +\xi V V ^{\mathop{\mathrm{T}}\nolimits } \\ M & 0 \end{array} \right ]. }$$

(26)

Then H and $\underline{H}$ share the same eigenvalues ±λ _i for $i\not\in \mathbb{J}$ and the corresponding eigenvectors, and the rest of eigenvalues of $\underline{H}$ are the square roots of the eigenvalues of $\varLambda _{1}^{2} +\xi QQ^{\mathop{\mathrm{T}}\nolimits }$, where $\varLambda _{1} =\mathop{ \mathrm{diag}}\nolimits (\lambda _{i_{1}},\ldots,\lambda _{i_{k}})$. There is a version of this result for updating M only, too.

3.2 CG Type Algorithms

One of the most important numerical implications of the eigenvalue minimization principles such as the ones presented in Sect. 2.2 is the possibility of using optimization approaches such as the steepest descent (SD) method, conjugate gradient (CG) type methods, and their improvements. A key component in these approaches is the line search. But in our case, it turns out that the 4D search is a more natural approach to take. Consider the Thouless functional ρ(x, y). Given a search direction $\left [\begin{array}{*{10}c} q\\ \,p \end{array} \right ]$ from the current position $\left [\begin{array}{*{10}c} y\\ x \end{array} \right ]$, the basic idea of the line search [27, 29] is to look for the best possible scalar argument t to minimize ρ:

$$\displaystyle{ \min _{t}\rho (x + tp,y + tq) }$$

(27)

on the line $\left \{\left [\begin{array}{*{10}c} y\\ x \end{array} \right ] + t\left [\begin{array}{*{10}c} \,q\\ \,p \end{array} \right ]\,:\, t \in \mathbb{R}\right \}.$ While (27) does have an explicit solution through calculus, it is cumbersome. Another related search idea is the so-called dual-channel search [13] through solving the minimization problem

$$\displaystyle{ \min _{s,t}\rho (x + sp,y + tq), }$$

(28)

where the search directions p and q are selected as the partial gradients ∇ _x ρ and ∇ _y ρ to be given in (31). The minimization problem (28) is then solved iteratively by freezing one of s and t and minimizing the functional ρ over the other in an alternative manner.

In [2] we proposed to look for four scalars α, β, s, and t for the minimization problem

$$\displaystyle{ \inf _{\alpha,\beta,s,t}\rho (\alpha x + sp,\beta y + tq) =\min _{u\in \mathscr{R}(U),\,\,v\in \mathscr{R}(V )}\rho (u,v), }$$

(29)

where U = [x, p] and V = [y, q]. This no longer performs a line search (27) but a 4-dimensional subspace search (4D search for short) within the 4-dimensional subspace:

$$\displaystyle{ \left \{\left [\begin{array}{*{10}c} \beta y + tq\\ \alpha x + sp \end{array} \right ]\quad \mbox{ for all scalars }\alpha,\ \beta,\ s,\text{ and }t\right \}. }$$

(30)

There are several advantages of this 4D search over the line search (27) and dual-channel search (28): (1) the right-hand side of (29) can be solved by the LREP for the 4 × 4 H _SR constructed with U = [x, p] and V = [y, q], provided $U^{\mathop{\mathrm{T}}\nolimits }V$ is nonsingular; (2) the 4D search yields a better approximation because of the larger search subspace; (3) most importantly, it paves the way for a block version to simultaneously approximate several interested eigenpairs.

The partial gradients of the Thouless functional ρ(x, y) with respect to x and y will be needed for various minimization approaches. Let x and y be perturbed to x + p and y + q, respectively, where p and q are assumed to be small in magnitude. Assuming $x^{\mathop{\mathrm{T}}\nolimits }y\neq 0$, up to the first order in p and q, we have [2]

$$\displaystyle{ \rho (x + p,y + q) =\rho (x,y) + \frac{1} {x^{\mathop{\mathrm{T}}\nolimits }y}\,p^{\mathop{\mathrm{T}}\nolimits }\left [Kx -\rho (x,y)\,y\right ] + \frac{1} {x^{\mathop{\mathrm{T}}\nolimits }y}\,q^{\mathop{\mathrm{T}}\nolimits }\left [My -\rho (x,y)\,x\right ] }$$

to give the partial gradients of ρ(x, y) with respect to x and y

$$\displaystyle{ \nabla _{x}\rho = \frac{1} {x^{\mathop{\mathrm{T}}\nolimits }y}\left [Kx -\rho (x,y)\,y\right ],\quad \nabla _{y}\rho = \frac{1} {x^{\mathop{\mathrm{T}}\nolimits }y}\left [My -\rho (x,y)\,x\right ]. }$$

(31)

With the partial gradients (31) and the 4D-search, extensions of the SD method and nonlinear CG method for the LREP are straightforward. But more efficient approaches lie in their block versions. In [39], a block 4D SD algorithm is presented and validated for excitation energies calculations of simple molecules in time-dependent density functional theory. Most recently, borrowing many proven techniques in the symmetric eigenvalue problem such as LOBPCG [19] and augmented projection subspace approaches [15, 18, 23, 37, 55], we developed an extended locally optimal block preconditioned 4-D CG algorithm (ELOBP4dCG) in [4]. The key idea for its iterative step is as follows. Consider the eigenvalue problem for

$$\displaystyle{ \underline{\boldsymbol{A}}-\lambda \boldsymbol{B} \equiv \left [\begin{array}{*{10}c} M & 0\\ 0 &\underline{K} \end{array} \right ]-\lambda \left [\begin{array}{*{10}c} 0&I\\ I & 0 \end{array} \right ] }$$

(32)

which is equivalent to the LREP for $\underline{H}$ in (26). This is a positive semidefinite pencil in the sense that $\boldsymbol{A} -\lambda _{0}\boldsymbol{B}\succeq 0$ for λ ₀ = 0 [25, 26]. Now at the beginning of the (i + 1)st iterative step, we have approximate eigenvectors

$$\displaystyle{z_{j}^{(i)}:= \left [\begin{array}{*{10}c} y_{j}^{(i)} \\ x_{j}^{(i)} \end{array} \right ],\quad z_{j}^{(i-1)}:= \left [\begin{array}{*{10}c} y_{j}^{(i-1)} \\ x_{j}^{(i-1)} \end{array} \right ]\quad \mbox{ for }1 \leq j \leq n_{b},}$$

where n _b is the block size, the superscripts (i−1) and (i) indicate that they are for the (i − 1)st and ith iterative steps, respectively. We then compute a basis matrix $\left [\begin{array}{*{10}c} V _{1} \\ U_{1} \end{array} \right ]$ of

$$\displaystyle{ \bigcup _{j=1}^{n_{b} }\mathscr{K}_{m}(\varPi [\underline{\boldsymbol{A}} -\rho (x_{j}^{(i)},y_{ j}^{(i)})\boldsymbol{B}],z_{ j}^{(i)}), }$$

(33)

where Π is some preconditioner such as $\underline{\boldsymbol{A}}^{-1}$ and $\mathscr{K}_{m}(\varPi [\underline{\boldsymbol{A}} -\rho (x_{j}^{(i)},y_{j}^{(i)})\boldsymbol{B}],z_{j}^{(i)})$ is the mth Krylov subspace, and then compute two basis matrices V and U for the subspaces

$$\displaystyle{ \mathscr{V } = \mathscr{R}(V _{1}) +\mathop{ \mathrm{span}}\nolimits \big\{y_{j}^{(i-1)},\,\,\mbox{ for }1 \leq j \leq n_{ b}\big\}, }$$

(34a)

$$\displaystyle{ \mathscr{U} = \mathscr{R}(U_{1}) +\mathop{ \mathrm{span}}\nolimits \big\{x_{j}^{(i-1)},\,\,\mbox{ for }1 \leq j \leq n_{ b}\big\}, }$$

(34b)

respectively, and finally solve the projected eigenvalue problem for

$$\displaystyle{ \left [\begin{array}{*{10}c} U & 0\\ 0 &V \end{array} \right ]^{\mathop{\mathrm{T}}\nolimits }(H-\lambda I)\left [\begin{array}{*{10}c} V & 0 \\ 0 &U \end{array} \right ] = \left [\begin{array}{*{10}c} 0 &U^{\mathop{\mathrm{T}}\nolimits }KU \\ V ^{\mathop{\mathrm{T}}\nolimits }MV & 0 \end{array} \right ]-\lambda \left [\begin{array}{*{10}c} U^{\mathop{\mathrm{T}}\nolimits }V & \\ &V ^{\mathop{\mathrm{T}}\nolimits }U \end{array} \right ] }$$

(35)

to construct new approximations z _j ⁽ⁱ⁺¹⁾ for 1 ≤ j ≤ n _b . When m = 2 in (33), it gives the LOBP4dCG of [1].

Fig. 1

Top row: convergence of LOB4dCG (i.e., m = 2) without preconditioning (left) and with deflation (right). Bottom row: convergence of extended LOB4dCG (ELOB4dCG) with m = 3 without preconditioning (left) and with deflation (right)

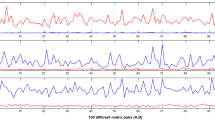
As an illustrative example to display the convergence behavior of ELOBP4dCG, Fig. 1, first presented in [4], shows iterative history plots of LOBP4dCG and ELOBP4dCG on an LREP arising from a time-dependent density-functional theory simulation of a Na₂ sodium in QUANTUM EXPRESSO [39]. At each iteration i, there are 4 normalized residuals $\|\underline{H}z -\mu z\|_{1}/((\|\underline{H}\|_{1}+\mu )\|z\|_{1})$ which move down as i goes. As soon as one reaches 10⁻⁸, the corresponding eigenpair (μ, z) is deflated and locked away, and a new residual shows up at the top. We see dramatic reductions in the numbers of iterations required in going from from m = 2 to m = 3, and in going from “without preconditioning” to “with preconditioning”. The powers of using a preconditioner and extending the searching subspace are in display prominently. More detail can be found in [4].

3.3 Other Methods

There is a natural extension of Lanczos method based on the following decompositions. Given $0\neq v_{0} \in \mathbb{R}^{n}$ and $0\neq u_{0} \in \mathbb{R}^{n}$ such that Mv ₀ = u ₀, there exist nonsingular $U,\,V \in \mathbb{R}^{n\times n}$ such that V e ₁ = αv ₀ and Ue ₁ = βu ₀ for some $\alpha,\beta \in \mathbb{R}$, and

$$\displaystyle{ U^{\mathop{\mathrm{T}}\nolimits }KU = T,\quad V ^{\mathop{\mathrm{T}}\nolimits }MV = D, }$$

(36)

where T is tridiagonal, D is diagonal and $U^{\mathop{\mathrm{T}}\nolimits }V = I_{n}$. Partially realizing (36) leads to the first Lanczos process in [46]. A similar Lanczos process is also studied in [11] for estimating absorption spectrum with the linear response time-dependent density functional theory. There is an early work by Tsiper [52, 53] on a Lanczos-type process to reduce both K and M to tridiagonal. Generically, Tsiper’s Lanczos process converges at only half the speed of the Lanczos process based on (36).

Recently, Xu and Zhong [56] proposed a Golub-Kahan-Lanczos type process that partially realize the factorizations:

$$\displaystyle{KX = Y G,\quad MY = XG^{\mathop{\mathrm{T}}\nolimits },}$$

where G is bidiagonal, $X^{\mathop{\mathrm{T}}\nolimits }KX = I_{n}$ and $Y ^{\mathop{\mathrm{T}}\nolimits }MY = I_{n}$. The basic idea is to use the singular values of the partially realized G to approximate some positive eigenvalues of H. Numerical results there suggest that the Golub-Kahan-Lanczos process performs slightly better than the Lanczos process based on (36).

The equations in (8a) implies KM = ΦΛ ² Φ ⁻¹. Noticing λ _i ² for 1 ≤ i ≤ k lie in low end of the spectrum of KM, in [48] the authors devised a block Chebyshev-Davidson approach to build subspaces through suppress components of vectors in the direction of eigenvectors associated with λ _i ² for i > k + 1. Numerical results there show that the approach can work quite well.

Most recently, structurally inverse-based iterative solvers for very large scale BS eigenvalue problem using the reduced basis approach via low-rank tensor factorizations are presented in [5, 6]. In [21], an indefinite variant of LOBPCG is also proposed.

4 Perturbation and Error Analysis

First we consider the perturbation of the LREP (4). Recall the eigen-decompositions in (8), and let

$$\displaystyle{ Z = \left [\begin{array}{*{10}c} \varPsi \varLambda ^{1/2} & \varPsi \varLambda ^{1/2} \\ -\varPhi \varLambda ^{-1/2} & \varPhi \varLambda ^{-1/2} \end{array} \right ]. }$$

(37)

Suppose H is perturbed to $\widetilde{H}$ with correspondingly positive definite $\widetilde{K}$ and $\widetilde{M}$. The same decompositions as in (8) for $\widetilde{H}$ exist. Adopt the same notations for the perturbed LREP for $\widetilde{H}$ as those for H except with a tilde on each symbol. It was proved in [57] that

$$\displaystyle{ \max _{1\leq i\leq n}\vert \widetilde{\lambda }_{i} -\lambda _{i}\vert \leq \| Z\|_{2}\|\widetilde{Z}\|_{2}\max \{\|\widetilde{M} - M\|_{2},\|\widetilde{K} - K\|_{2}\}, }$$

(38a)

$$\displaystyle{ \sqrt{\sum _{i=1 }^{n }\vert \widetilde{\lambda }_{i } -\lambda _{i } \vert ^{2}} \leq \frac{1} {\sqrt{2}}\|Z\|_{2}\|\widetilde{Z}\|_{2}\sqrt{\|\widetilde{M} - M\|_{\mathop{\mathrm{F} }\nolimits }^{2 } +\|\widetilde{ K} - K\|_{\mathop{\mathrm{F} }\nolimits }^{2}}. }$$

(38b)

These inequalities involve the norms ∥Z∥₂ and $\|\widetilde{Z}\|_{2}$ which are not known a priori. But they can be bounded in terms of the norms of K, M, their inverses, and bounds on λ ₁ and λ _n .

Previously in Sect. 2.1, we note that for an exact pair $\{\mathscr{U},\mathscr{V }\}$ of deflating subspaces we have (10). In particular, KU = V K _RQ and MV = UM _RQ , where $U \in \mathbb{R}^{n\times k}$ and $V \in \mathbb{R}^{n\times k}$ are the basis matrices for $\mathscr{U}$ and $\mathscr{V }$, respectively. When $\{\mathscr{U},\mathscr{V }\}$ is only an approximate pair, it would be interesting to seek backward perturbations ΔK and ΔM to K and M, respectively, such that

$$\displaystyle{ (K +\varDelta K)U = V K_{\text{RQ}}\quad \mbox{ and}\quad (M +\varDelta M)V = UM_{\text{RQ}}. }$$

(39)

In the other word, $\{\mathscr{U},\mathscr{V }\}$ is an exact pair for {K + ΔK, M + ΔM}. Since K and M are symmetric, we further restrict ΔK and ΔM to be symmetric, too. The first and foremost question is, naturally, if such perturbations ΔK and ΔM exist, i.e., if the set

$$\displaystyle{ \mathbb{B}:=\big\{ (\varDelta K,\varDelta M)\,:\,\varDelta K^{\mathop{\mathrm{T}}\nolimits } =\varDelta K,\,\varDelta M^{\mathop{\mathrm{T}}\nolimits } =\varDelta M \in \mathbb{R}^{n\times n}\,\,\mbox{ satisfying (39)}\big\}, }$$

(40)

is not empty. Indeed $\mathbb{B}\neq \varnothing$ [57]. Next we are interested in knowing

$$\displaystyle{ \eta (U,V ):=\min _{(\varDelta K,\varDelta M)\in \mathbb{B}}(\|\varDelta K\| +\|\varDelta M\|), }$$

(41)

where ∥⋅ ∥ is some matrix norm. Without loss of generality, we assume $U^{\mathop{\mathrm{T}}\nolimits }U = V ^{\mathop{\mathrm{T}}\nolimits }V = I_{k}$. It is obtained in [57] that

$$\displaystyle\begin{array}{rcl} \eta _{\mathop{\mathrm{F}}\nolimits }(U,V )& =& \sqrt{2\|\mathscr{R}_{K } (K_{\text{RQ} } )\|_{\mathop{\mathrm{F} }\nolimits }^{2 } -\| U^{\mathop{\mathrm{T} }\nolimits } \mathscr{R}_{K } (K_{\text{RQ} } )\|_{\mathop{\mathrm{F} }\nolimits }^{2}} \\ & & \quad + \sqrt{2\|\mathscr{R}_{M } (M_{\text{RQ} } )\|_{\mathop{\mathrm{F} }\nolimits }^{2 } -\| V ^{\mathop{\mathrm{T} }\nolimits } \mathscr{R}_{M } (M_{\text{RQ} } )\|_{\mathop{\mathrm{F} }\nolimits }^{2}},{}\end{array}$$

(42)

$$\displaystyle\begin{array}{rcl} \eta _{2}(U,V ) =\|\mathscr{ R}_{K}(K_{\text{RQ}})\|_{2} +\|\mathscr{ R}_{M}(M_{\text{RQ}})\|_{2},& &{}\end{array}$$

(43)

where $\eta _{\mathop{\mathrm{F}}\nolimits }$ and η ₂ are the ones of (41) with the Frobenius and spectral norms, respectively, and $\mathscr{R}_{K}(K_{\text{RQ}}):= KU - V K_{\text{RQ}}$ and $\mathscr{R}_{M}(M_{\text{RQ}}):= MV - UM_{\text{RQ}}$. An immediate consequence of such backward error analysis is bounds on approximation errors by the eigenvalues of H _RQ to some of those of H.

There are a couple of recent work [47, 54] on the perturbation of partitioned LREP. Let K and M be partitioned as

(44)

If K ₂₁ = M ₂₁ = 0, then $\{\mathscr{U}_{0},\mathscr{V }_{0}\}$ is a pair of deflating subspaces, where $\mathscr{U}_{0} = \mathscr{V }_{0} = \mathscr{R}(\left [\begin{array}{*{10}c} I_{k}\\ 0\end{array} \right ])$. But what if K ₂₁ ≠ 0 and/or M ₂₁ ≠ 0 but tiny in magnitude? Then $\{\mathscr{U}_{0},\mathscr{V }_{0}\}$ can only be regarded as a pair of approximate deflating subspaces, and likely there would exist an exact pair $\{\widetilde{\mathscr{U}},\widetilde{\mathscr{V }}\}$ of deflating subspaces nearby. Specifically, we may seek

$$\displaystyle{\widetilde{\mathscr{U}} = \mathscr{R}(\widetilde{U}),\,\,\widetilde{\mathscr{V }} = \mathscr{R}(\widetilde{V })\quad \mbox{ with}\quad \widetilde{U} = \left [\begin{array}{*{10}c} I_{k}\\ P\end{array} \right ],\quad \widetilde{V } = \left [\begin{array}{*{10}c} I_{k} \\ Q\end{array} \right ]}$$

for some P and Q. It resembles the well-known Stewart’s perturbation analysis for the standard and generalized eigenvalue problems [43–45]. The study along this line for the LREP has been recently conducted in [54].

Alternatively, if K ₂₁ = M ₂₁ = 0 in (44), then $\mathop{\mathrm{eig}}\nolimits (H) =\mathop{ \mathrm{eig}}\nolimits (H_{1}) \cup \mathop{\mathrm{eig}}\nolimits (H_{2})$, where $H_{i} = \left [\begin{array}{*{10}c} 0 &K_{i} \\ M_{i}& 0 \end{array} \right ]$ for i = 1, 2, and $\mathop{\mathrm{eig}}\nolimits (H)$ is the set of eigenvalues of H and similarly for $\mathop{\mathrm{eig}}\nolimits (H_{i})$. Again what if K ₂₁ ≠ 0 and/or M ₂₁ ≠ 0 but tiny in magnitude? They may be treated as tiny perturbations. It would be interesting to know the effect on the eigenvalues from resetting them to 0, as conceivably to decouple H into two smaller LREPs. It is shown that such an action brings changes to the eigenvalues of H at most proportional to ∥K ₂₁∥₂ ² + ∥M ₂₁∥₂ ² and reciprocally proportional to the gaps between $\mathop{\mathrm{eig}}\nolimits (H_{1})$ and $\mathop{\mathrm{eig}}\nolimits (H_{2})$ [47].

5 Concluding Remarks

Throughout, we have focused on recent studies of the standard LREP (4) with the assumption that K and M are real and symmetric as deduced from the original LREP (1). There are several directions to expand these studies by relaxing the assumption on K and M and, for that matter, accordingly on A and B.

An immediate expansion is to allow K and M to be complex but Hermitian and still positive definite. All surveyed results with a minor modification (by changing all transposes to conjugate transposes) hold. Most of the theoretical results in Sects. 2.2 and 2.3 are still valid when only one of K and M is positive and the other is semidefinite, after changing “min” in (17) and (14) to “inf”.

Although often K and M are definite, there are cases that one of them is indefinite while the other is still definite [35]. In such cases, all theoretical results in Sects. 2.2–2.4 no longer hold. But some of the numerical methods mentioned in Sect. 3.3, namely, the Lanczos type methods in [46] and the Chebyshev-Davidson approach [48], still work. Recently in [24], a symmetric structure-preserving ΓQR algorithm is developed for LREPs in the form of (1) without any definiteness assumption.

The following generalized linear response eigenvalue problem (GLREP) [14, 32, 33]

$$\displaystyle{ \left [\begin{array}{*{10}c} A& B\\ -B & -A \end{array} \right ]\left [\begin{array}{*{10}c} u\\ v \end{array} \right ] =\lambda \left [\begin{array}{*{10}c} \varSigma &\varDelta \\ \varDelta &\varSigma \end{array} \right ]\left [\begin{array}{*{10}c} u\\ v \end{array} \right ] }$$

(45)

was studied in [3], where A and B are the same as the ones in (1), and and Σ and Δ are also n × n with Σ being symmetric while Δ skew-symmetric (i.e., $\varDelta ^{\mathop{\mathrm{T}}\nolimits } = -\varDelta$) such that $\left [\begin{array}{*{10}c} \varSigma &\varDelta \\ \varDelta &\varSigma \end{array} \right ]$ is nonsingular. Performing the same orthogonal similarity transformation, we can transform GLREP (45) equivalently to

$$\displaystyle{ \left [\begin{array}{*{10}c} 0 &K\\ M & 0 \end{array} \right ]\left [\begin{array}{*{10}c} y\\ x \end{array} \right ] =\lambda \left [\begin{array}{*{10}c} E_{+} & 0 \\ 0 &E_{-} \end{array} \right ]\left [\begin{array}{*{10}c} y\\ x \end{array} \right ], }$$

(46)

where $E_{+}^{\mathop{\mathrm{T}}\nolimits } = E_{-}$ is nonsingular. Many results parallel to what we surveyed so far for the LREP (4) are obtained in [3].

Both (4) and (46) are equivalent to the generalized eigenvalue problem for

$$\displaystyle{\boldsymbol{A}-\lambda \boldsymbol{B}\,\,\mbox{ with}\quad \boldsymbol{A} = \left [\begin{array}{*{10}c} M & 0\\ 0 &K \end{array} \right ],\,\,\boldsymbol{B} = \left [\begin{array}{*{10}c} 0 &I_{n} \\ I_{n}& 0 \end{array} \right ]\,\,\mbox{ or}\,\,\left [\begin{array}{*{10}c} 0 &E_{-} \\ E_{+} & 0 \end{array} \right ].}$$

Since $\boldsymbol{A} - 0 \cdot \boldsymbol{ B} =\boldsymbol{ A}$ is positive definite, $\boldsymbol{A} -\lambda \boldsymbol{ B}$ falls into the category of the so-called positive semi-definite matrix pencils (positive definite if both K and M are positive definite). Numerous eigenvalue min-max principles, as generalizations of the classical ones, are obtained in [8, 9, 20, 22, 30, 31] and, more recently, [25, 26].