A Posteriori Error Estimation for the Non-associated Plasticity Drucker-Prager Model with Hardening

Abstract

The numerical solution of non-associated elastoplasticity is still a key aspect of research and development in computational plasticity. Approximate solution procedures are based, in the context of a displacement method, on a weak form of the equilibrium and reply upon two main ingredients: the numerical integration of the rate constitutive relations over a generic time step (local stage) and the iterative algorithm exploited to solve the nonlinear equilibrium equations (global stage). The fully discrete problem is the obtained by performing a spatial discretization of the field equations and a time-integration of the evolution rule. The interest is here given to the discretization errors, which are caused by the numerical discretization of the continuous mathematical model in order to define an adaptive strategy.

The aim of this paper is to extend the concept of error in the constitutive equations to non-associated plasticity Drucker-Prager model to handle non-associative rate-independent plasticity problems solved by employing the incremental displacement conforming finite element method.

Numerical examples by PLSAER2D (a Matlab program) for both the associated and the non-associated cases for Drucker-Prager model with hardening are also presented.

1 Introduction

The numerical solution of nonlinear boundary value problems arising in rate-independent elastoplasticity with prescribed accuracy is still a key aspect of research and development in computational plasticity. Approximate solution procedures are based, in the context of a displacement method, on a weak form of the equilibrium and rely upon two main ingredients: the numerical integration of the rate constitutive relations over a generic time step (local stage) and the iterative algorithm exploited to solve the nonlinear equilibrium equations (global stage). The fully discrete problem is the obtained by performing a spatial discretization of the field equations and a time-integration of the evolution rules. The interest is here given to the discretization errors, which are caused by the numerical discretization of the continuous mathematical model. Both time and space discretization produce errors which need to be estimated in order to devise an adaptive strategy. Since a priori error estimates are not available for nonlinear time-dependent problems, useful error estimation must employ a posteriori technique to predict the overall discretization error. A posteriori error estimates are computed locally and contain significant information about the distribution of error among individual elements referred to as error indicators, which can form the basis of adaptive procedures. Today, the procedures available for error estimation can be essentially reduced to two kinds. In the first class, error measures are constructed based on local residuals of the numerical solution as introduced originally by Babuska and Rheinbolt [3]. In the second approach, a more accurate representation of the unknowns is sought prior estimating the error. This stage is known as the recovery process where emphasis has been put on self-equilibrating patches [19].

For nonlinear time-dependent problems, techniques devised for linear problems or time-independent nonlinear problems have been used at each time instant [1, 8] then suggested a posteriori error estimates for the primal variational formulation of elasto-plasticity with linear hardening [5, 9, 13, 18].

A family of error measures with a clear physical meaning and capable to account for effects of time and space discretization is given by the error in the constitutive equations. The concept, introduced by Ladevèze in 1975 for linear problems, was then extended to history-dependent materials modeled with functional constitutive relations [13] and to constitutive models with internal variables and described by a standard evolution rule. For the latter formulation, the potential structure and the convexity property of the state laws and evolution laws is exploited by adopting equivalent scalar formulations of the tensorial constitutive equations. More precisely both state and evolution equations are formulated using a scalar equation which involves two convex scalar “pseudo” potentials. The key property is the positiveness of the residual. The concept of dissipation error, introduced by Ladevèze and Moës [12], exploits this scalar nature of the constitutive relations. The error is quantified by the residual in the evolution law produced by time continuous admissible solutions that satisfy the compatibility relations, the equilibrium equations, the state law and the initial conditions. It was shown that the proposed error measure is able to account for effects of time and space discretization.

The dissipation error was then extended in [11] and [5, 8] by removing the state laws from the admissibility conditions. Applications of this error measure were given for a coupled elastoplastic- damage model [11] where the non-incremental LATIN method was used to solve the discrete problem [14]. The extended dissipation error was successfully applied by Orlando [17] to the finite element solution of elastoplastic problems discretized in time with the classical incremental finite element method with change of finite element mesh from one-time step to the other, which introduces a discontinuity jump in the time linear interpolation of the discrete values of the solution.

In this paper, we propose a natural extension of the concept of error in the constitutive equations to non-standard plasticity Drucker-Prager models [4,5,6, 8, 9] whose evolution is also described by a scalar equation which involve a unique scalar-valued function of both the velocity vector and the generalized stresses. This function is called bi-potential developed by de Saxcé et al. [7, 9], standard models are particular cases where the bi-potential can be represented as the sum of two scalar functions. Both the generalized evolution rule as well as its inverse are derived from this function using normality. Within this framework, the positiveness of the residual is kept which permit the extension of the generalized dissipation error to non-standard models described by a bi-potential.

2 Pseudo-Potentials and Bi-Potentials

The notation used here will be one in which symmetric second-order tensors, denoted by double underlined bold letters $(\varvec{\pi ,\kappa })$, are represented as six-dimensional vectors. The vectors are bolded and more complex operators are double capitalized (e.g. ${\mathbb{C}}$ for Hooke’s tensor).

In research investigating the structure of mechanical law, Moreau proposed to relax the differentiability condition by allowing potential to be non-differentiable as an appropriate way to take into account some multivalued laws within the same formalism then the concept of pseudo-potential, which is merely a scalar-valued non-differentiable function and made use of non-smooth analysis tools to set up his formulation, since classical tools of differential calculus are no longer applicable [16]. However, the pseudo-potential can be derived only for a standard plastic model.

The function is said to be a bi-potential if the following inequality holds:

$$ b_{p} (\dot{\varvec{\kappa }}'\varvec{,\pi }') \ge \,\varvec{\pi}' \cdot \dot{\varvec{\kappa }}'\,\varvec{,}\,\,\,\,\,\,\forall (\dot{\varvec{\kappa }}',\varvec{\pi}') \in {\mathbf{F}} \times {\mathbf{V}} $$

(1)

A pair $(\dot{\varvec{\kappa }},\varvec{\pi})$ is said to be extremal if the equality is achieved for this pair:

$$ b_{p} (\dot{\varvec{\kappa }},\varvec{\pi})=\varvec{\pi}\cdot \dot{\varvec{\kappa }} $$

(2)

Then, any extremal pair is characterized by the following relations:

$$ \forall \dot{\varvec{\kappa }}^{{\prime }} \in {\mathbf{V}}\quad :\quad b_{p} (\dot{\varvec{\kappa }}^{{\prime }} \varvec{,\pi }) - b_{p} (\varvec{\dot{\kappa },\pi }) \ge\varvec{\pi}\cdot (\dot{\varvec{\kappa }}^{{\prime }} - \dot{\varvec{\kappa }}) $$

(3)

$$ \forall\varvec{\pi}^{{\prime }} \in {\mathbf{F}}\quad :\quad b_{p} (\varvec{\dot{\kappa },\pi }^{{\prime }} ) - b_{p} (\varvec{\dot{\kappa },\pi }) \ge \,\dot{\varvec{\kappa }} \cdot (\varvec{\pi}^{{\prime }} -\varvec{\pi}) $$

(4)

Let us remark that the extremal pairs satisfy

$$ b_{p} (\varvec{\dot{\kappa },\pi }) -\varvec{\pi}\cdot \dot{\varvec{\kappa }} = \mathop {\inf }\limits_{{\dot{\varvec{\kappa }}'}} \left[ {b_{p} (\dot{\varvec{\kappa }}^{{\prime }} \varvec{,\pi }) - \dot{\varvec{\kappa }}^{{\prime }} \cdot\varvec{\pi}} \right] = \mathop {\inf }\limits_{{\varvec{\pi}'}} \left[ {b_{p} (\varvec{\dot{\kappa },\pi }^{{\prime }} ) - \dot{\varvec{\kappa }} \cdot\varvec{\pi}^{{\prime }} } \right] $$

(5)

These relations represent a multivalued constitutive relationship which is now implicit in the sense of the implicit function theorem. This explains the name of Implicit Standard Materials proposed by de Saxcé [7] for this class of materials. Of course, explicit standard materials are particular cases of implicit standard ones with separable bi-potentials [9]:

$$ b_{p} (\dot{\varvec{\kappa }},\varvec{\pi})= \varphi (\dot{\varvec{\kappa }}) + \varphi^{ * } (\varvec{\pi}) $$

(6)

3 Non-associated Drucker-Prager Model with Hardening

It is well known that the soil materials have a very complicated behavior. Idealizations are, therefore, often necessary in order to develop simple mathematical constitutive laws for practical applications. Several models can be found in the literature, most of them are complex and require many parameters, where some can be physically meaningless. The relative simplicity of the Drucker-Prager model [4,5,6, 8, 9], which can reflect some characteristics of soils behavior with only three parameters, explains why this model is widely used. Hence, the model is described by the dual variables $(\varvec{\varepsilon}^{p} ,p),\,\,(\sigma ,R)$ where

$$ \begin{aligned} & \text{stress}\,\,{\varvec{\upsigma}} = \left( {{\mathbf{s}}\text{,}s_{m} } \right)\,\,\text{with}\,\,s_{m} = \frac{\text{1}}{\text{3}}\text{Tr}({\varvec{\upsigma}})\,\,\text{deviator}\,\,{\mathbf{s}} = {\varvec{\upsigma}} - s_{m} {\mathbf{1}} \\ & \text{strain}\,\,{\dot{\mathbf{\varepsilon }}}^{p} = \text{(}{\dot{\mathbf{e}}}^{p} ,\dot{e}_{m}^{p} \text{)}\,\,\text{with}\,\,\dot{e}_{m}^{p} = \text{Tr}({\dot{\mathbf{\varepsilon }}}^{p} )\,\,\text{deviator}\,\,{\dot{\mathbf{e}}}^{p} = {\dot{\mathbf{\varepsilon }}}^{p} - \frac{{\dot{e}_{m}^{p} }}{\text{3}}{\mathbf{1}} \\ & {\mathbf{1}} = \left\{ {\begin{array}{*{20}c} \text{1} & \text{1} & \text{1} & \text{0} & \text{0} & \text{0} \\ \end{array} } \right\}^{\text{T}} \\ \end{aligned} $$

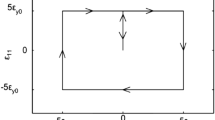
At each time the stress must belong to the set convex $K_{\phi }$ of the plastically admissible stresses defined by (Fig. 1)

Fig. 1.

Drucker-Prager with hardening criterion

$$ \text{K}_{\phi } = \left\{ {\pi \in {\mathbb{R}}^{m} \left| {\tfrac{\text{1}}{{\text{k}_{d} }}\left\| {\mathbf{s}} \right\|} \right. + \text{s}_{m} \text{tan}\phi - ({\text{c + }}R) \le 0} \right\} $$

(7)

where c is the cohesion, $\phi$ the friction angle and ${\text{k}}_{d}$ a constant. Its boundary defines the yield function. Assuming an isotropic hardening law, the evolution of the elastic domain is governed by the relation R = h.p with p is the cumulated plastic deformation and h is the hardening modulus.

The flow rule restricts the plastic strain rate to belong to the cone defined by

$$ {\text{K}}_{\theta }^{*} = \left\{ {\left( {{\dot{\mathbf{e}}}^{p} ,{\dot{e}}_{m}^{p} } \right) \, \left| {{\dot{e}}_{m}^{p} } \right. \ge \text{k}_{d} \,\text{tan}\theta \text{ }\left\| {{\dot{\mathbf{e}}}^{p} } \right\|} \right\} $$

(8)

in which $\uptheta$ is the dilatancy angle; $\text{K}_{\phi }$ and ${\text{K}}_{\theta }^{*}$ are dual cones.

For any stress state situated on the regular part of the yield surface, the plastic strain rate vector inclination with respect to the vertical axis, is constant and less than the frictional angle $\phi$. At the apex, this vector belongs to a cone of vectors defined by inclinations equal or greater than $\tan \theta$. Simple geometrical considerations allow us to write the flow rule in the following compact form:

$$ \left( {{\dot{e}}_{m}^{p} + \text{k}_{d} \left( {\text{tan}\phi - \text{tan}\theta } \right)\left\| {{\dot{\mathbf{e}}}^{p} } \right\|,{\dot{\mathbf{e}}}^{p} } \right) \in {\partial }_{\varvec{\sigma}} {\mathbf{I}}_{{K_{\phi } }} ({\varvec{\uppi}}) $$

(9)

where ${\rm I}_{K} \left( \pi \right)$ is the indicator function of the closed convex set $K$.

Although the preceding considerations seem quite obvious, it has the advantage to rule out definitively the question of existence of a convex pseudo-potential in the present situation. When the pseudo-potential exists, the cyclic monotony condition gives a means to construct its expression. Then, this law does not admit a convex pseudo-potential. Nevertheless, it admits a bi-potential defined by

$$ b_{p} (\varvec{\dot{\kappa },\pi } )= \frac{c}{{\text{t} an\phi }}\dot{e}_{m}^{p} + k_{d} \left( {\text{t} \text{an}\phi - \text{t} \text{an}\theta } \right)\left[ {\frac{c + R}{\tan \phi } - \text{s}_{m} } \right]\left\| {{\dot{\mathbf{e}}}^{p} } \right\| + {\rm I}_{{{\text{K}}_{\phi } }} \left(\varvec{\pi}\right) + {\rm I}_{{{\text{K}}_{\theta }^{*} }} \left( {\dot{\varvec{\kappa }}} \right) + {\rm I}_{\text{C}} \left( {\dot{\varvec{\kappa }}} \right) $$

(10)

When $\uptheta = \phi$, the mixed term disappears and the bi-potential reduces to the sum of two dual pseudo-potentials:

$$ b_{p} (\varvec{\dot{\kappa },\pi } )= \underbrace {{\frac{c}{{\text{tan}\phi }}\dot{e}_{m}^{p} + {\rm I}_{{{\text{K}}_{\phi }^{*} }} \left( {\dot{\varvec{\kappa }}} \right) + {\rm I}_{\text{C}} \left( {\dot{\varvec{\kappa }}} \right)}}_{{\varphi \left( {\dot{\varvec{\kappa }}} \right)}} + \underbrace {{{\rm I}_{{{\text{K}}_{\phi } }} \left(\varvec{\pi}\right)}}_{{\varphi^{*} \left(\varvec{\pi}\right)}} $$

(11)

4 A Posteriori Error Estimation

The first error measure for nonlinear evolution problems is based on the Drucker inequality. It applies to dissipative problems where the functional formalism is adopted for the constitutive modeling and the conditions of Drucker stability [4] are fulfilled by the material. The definition of this error is due to Ladevèze in 1985 and has be used to control the accuracy of F.E. calculations in path/time dependent problems [13, 14].

In the constitutive formulation with internal variables, the potential structure and the convexity property of the state laws and evolution laws is exploited by adopting equivalent scalar formulations of the tensorial constitutive equations. The first use of the error in the constitutive equations to standard constitutive models described in terms of internal variables is due to Ladevèze [13], the state equations have been added to the first group of equations. The admissibility conditions then combine the kinematic compatibility relations, the equilibrium equations, the state equation and the initial conditions. Accordingly, the only equation which is left out is the evolution law that governs the dissipative process. By exploiting the convexity structure of this equation, Ladevèze introduced the concept of dissipation error given by the residual in the evolution law, which is appropriately reformulated in terms of the dissipation pseudo-potential and its Legendre-Fenchel transform. The dissipation error has been applied by Ladevèze and Moës [11, 12] to assess the accuracy of incremental finite element solutions of evolution problems of standard materials. Furthermore, error indicators which separate the sources of the different discretization errors have been defined and used to drive the adaptive process in time and space.

By removing the state laws from the admissibility conditions, new measure of the error in the constitutive equations, called extended dissipation error, has been introduced in Ladevèze [14] and Hjiaj [8]. This new error measure is a natural extension of the dissipation error. Applications of this error measure were given for an elastic-damage coupled model [14] solved with the non-incremental LATIN method and to the Prandtl-Reuss plasticity model in Orlando and Peric [17] solved with the classical incremental finite element method. The extension of this error measure to non-standard behaviour has been given by Hjiaj and Dao [6, 8]. This extension is based on a generalization of the Fenchel inequality, proposed by de Saxcé, to cover a broader range of behaviour including non-standard models.

For this new measure of error, the admissibility conditions include the kinematic compatibility relations, the equilibrium equations and the initial conditions. As a result, the only equations left apart are the complete constitutive equations, i.e. the state laws and the evolution law. The residual produced in the state equations and the evolution law is used as a direct measure of the discretization error.

Definition of Error

The equations that are not satisfied by an admissible solution are the state law and the evolution rule. The residual in the evolution law and the residual in the state equation are considered to assess the quality of the approximation associated with the given admissible solution. A natural measure of this residual is provided by the equivalent formulation of the state equations which exploits the convexity properties of the law. Furthermore, given the nature of the state laws that relate the current value of the kinematic variables to the corresponding static ones, a global measure of the error is obtained by integrating the pointwise residual over the domain and over the time interval. Therefore, the relative error associated with an element is given by:

$$ {\mathbf{e}}^{2}_{ext} (T) = \mathop {\sup }\limits_{t \le T} \left\{ {\int_{\Omega } {{}^{s}\zeta_{{\varvec{x},t}}^{2} \left( {\varvec{\eta}_{ad} \varvec{ - \kappa }_{ad} ,\varvec{\pi}_{ad} } \right){\text{d}}\Omega } + \int_{\Omega } {\int_{0}^{t} {{}^{d}\zeta_{{\varvec{x},t}}^{2} \left( {\dot{\varvec{\kappa }}_{ad} ,\varvec{\pi}_{ad} } \right)} \,{\text{d}}\tau \,{\text{d}}\Omega } } \right\} $$

(12)

The extended dissipation error ${\mathbf{e}}_{ext}^{2} (T)$ has a finite value if and only if

$$ \begin{array}{*{20}l} {\left( {\dot{\varvec{\kappa }}_{ad} ,\varvec{\pi}_{ad} } \right) \in dom\,b_{p} } \hfill & {{\text{non - standard}}\,{\text{model}}} \hfill \\ {(\varvec{\sigma}_{ad} ,R_{ad} )\in dom\,\varvec{\varphi }^{\text{ * }} \,\,{\text{et}}\,\,(\dot{\varvec{\varepsilon }}_{ad}^{p} ,\dot{p}_{ad} ) \in dom\,\varvec{\varphi }} \hfill & {{\text{standard}}\,{\text{model}}} \hfill \\ \end{array} $$

(13)

Given an admissible solution $s_{ad} = s_{ad} (\varvec{x},t)$ we have the following fundamental property of the extended dissipation error:

$$ \begin{array}{*{20}l} {{\mathbf{e}}_{ext}^{2} (T) \ge 0} \hfill \\ {\text{and}} \hfill \\ {{\mathbf{e}}_{ext}^{2} (T) = 0 \Leftrightarrow s_{ad} (\varvec{x},t) = s_{ex} (\varvec{x},t)\quad \forall \varvec{x} \in\Omega \,\,{\text{et}}\,\,\forall t \in [0,{\text{T}}]} \hfill \\ \end{array} $$

(14)

Since most a posteriori error estimates are computed locally, they contain significant information about the distribution of error among individual elements providing useful error indicators than can used to devise adaptive strategies. The extended dissipation error measure defines a global error measure that account of both time and space discretization. The relative extended dissipation error is defined as follow:

$$ \varepsilon^{2} = \frac{{\text{e}^{2}_{ext} (T)}}{{\mathop {\sup }\limits_{{t \in \left[ {0,T} \right]}} \text{D}^{\text{2}} \left( t \right)}} $$

(15)

In which

$$ \text{D}^{2} (t) = \int_{\Omega } {^{s} \text{D}_{{\varvec{x},t}}^{2} \left( {\varvec{\eta}_{ad} \varvec{ - \kappa }_{ad} ,\varvec{\pi}_{ad} } \right){\text{d}}\Omega } + \int_{\Omega } {\int_{0}^{t} {^{d} \text{D}_{{\varvec{x},t}}^{2} \left( {\dot{\varvec{\kappa }}_{ad} ,\varvec{\pi}_{ad} } \right)} \,{\text{d}}\tau \,{\text{d}}\Omega } $$

(16)

With

$$ {}^{s}\text{D}^{2}_{x,t} \left( {\varvec{\eta}_{ad} \varvec{ - \kappa }_{ad} ,\varvec{\pi}_{ad} } \right) = \psi \,\varvec{\eta}_{ad} (\varvec{x},t)\varvec{ - \kappa }_{ad} (\varvec{x},t) + \psi^{ * }\varvec{\pi}_{ad} (\varvec{x},t) $$

(17)

And

$$ ^{d} \text{D}_{{\varvec{x},t}}^{2} \left( {\dot{\varvec{\kappa }}_{ad} ,\varvec{\pi}_{ad} } \right) = b_{p} \left( {\dot{\varvec{\kappa }}_{ad} (\varvec{x},t),\varvec{\pi}_{ad} (\varvec{x},t)} \right) $$

(18)

The contribution of an element E to the extended dissipation error is obtained by integrating the pointwise residual over the considered element. The relative error associated with an element is given by:

$$ \varepsilon^{2}_{E} = \frac{{\text{e}^{2}_{ext,E} (T)}}{{\mathop {\sup }\limits_{t \in [0,T]} \text{D}_{E}^{2} (t)}} $$

(19)

With

$$ \text{e}^{2}_{ext,E} (T) = \underbrace { \sup }_{0 \le t \le T}\left\{ {^{s} \zeta_{{\Omega _{E} }}^{2} (t) +^{d} \zeta_{{\Omega _{E} }}^{2} (t)} \right\} $$

(20)

In the definition of an admissible solution for the computation of the extended dissipation error, the statically admissible variables are not constrained to their conjugate variables by means of the state laws as it happens in the dissipation error. This allows more information from the finite element solution to be included in building the corresponding admissible solution and strengthen the link between the two solutions. Likewise, conforming finite element displacements can be used as part of the admissible solution and do not need to be modified, unlike for the definition of the admissible solution to compute the dissipation error [5, 8, 10, 15].

5 Numerical Application

The numerical application investigates the load-displacement of two rigid strip footings resting on a homogenous cohesive-frictional soil of great depth using PLSAER2D - a Matlab [20] program proposed by Dao [5]. Each footing is having a width B and the space between the footings is denoted S. Each footing is subjected to a vertical load at its centerline. It is assumed that the footings are smooth and the soil is weightless. The length of each footing, denoted B, is supposed large enough such that a condition of plane strain will exist in the soil mass supporting the foundations. The cohesive frictional soil is assumed to be a linear elastic-plastic material obeying the Drucker-Prager yield criterion with a non-associated flow rule and linear hardening. This model requires the specification of the Young Modulus E, the Poisson ratio ν, a cohesion c, a friction angle φ, a dilatancy angle θ and a hardening modulus H. All calculations are based on values of B = 2 m, S = 6 m, E = 2.5x10⁵ kN/m², ν = 1/3, c = 2kN/m² and φ = 35^o. The constant k_d is obtained by imposing that the Drucker-Prager yield surface is inscribed in the Coulomb one. The load-displacement curve is computed for the following value of the angle of dilatation θ: 35^o, 30^o, 25^o and 20^o. Any restriction on the soil to flow freely in the vicinity of failure may have a significant influence on the computed load- displacement curve. Hence, the boundaries of the domain should be far away from the footings in order to be able to accommodate the plastic zone without any restriction on the soil displacement (Fig. 2).

Fig. 2.

a. Finite element model for four strips footings (Mesh N1: 339 elements), b. Mesh N2 (1332 elements) and Mesh N3 (1332 elements)

Load-displacement curves. For each dilation angle, three hardening modulus are considered: h = 100, h = 1 and h = 0.01. The last value of h has been considered in order to simulate the perfectly plastic case and therefore estimate the bearing capacity of the footing. In Fig. 3, the load-displacement curves predicted by the Drucker-Prager model with isotropic hardening for the considered values of the dilatancy angle θ are shown for the coarse mesh. The load represents the force applied to a single footing and is calculated as the sum of nodal forces at the footing nodes. As can be seen from Fig. 3, the structure is less stiff for a non-associated flow rule, i.e. the displacements are larger for the same values of the vertical load. It is worth noting that calculations have converged for all values of θ greater than 20^o, for smaller values convergence problems may occur as mentioned elsewhere in the literature [2, 4, 16].

Fig. 3.

Load-displacement curves

Plastic zones. A study of the plastic zone developed below the footing, the contour plots of the norm of the plastic strain at the end of the loading process are shown in the Fig. 4 for the coarse mesh. It shows that for smooth footings, all the soil immediately below the footing becomes plastic. For the non-associated flow rule case, the plastic zones are somewhat different from those for the associated flow rule case. They are not contiguous. As the dilatancy angle decreases, the shape of the failure surface for the non-associated model becomes significantly different from a log-spiral curve.

Fig. 4.

Plastic zones (Mesh N1)

Error estimation. The evolution of the relative error with loading is depicted in Fig. 5a for the coarse mesh and for each value of the dilatancy angle (h = 100). It appear clearly that the relative error increases significantly with decreasing dilatancy angle. For instance, the relative error for θ = 20^o is equal to 34.23% compared to 16.31% for θ = φ = 35^o. Let us define the degree of non-associativity (tan φ – tan θ), this degree is always positive and is equal to zero if the flow rule is associated, we can say that the relative error increases with the degree of non-associativity even though the size of the plastic zone decreases with increasing values of degree of non-associativity. Refinement strategies aims to highlight the effect of the space discretization error. For the problem under consideration, refinement is need it around the footing. Further the mesh pattern near the singularity at the edges of the footings must be kept. This mesh pattern permits the stress field to change rapidly and yield to accurate solution. The domain size and the associated finite element mesh are kept the same for all values of θ and it was found to be acceptable for all cases. The evolution of the relative global error with loading is depicted in Fig. 5b for the second mesh (Mesh N2) and Fig. 6 for the finest mesh (Mesh N3) and for each value of the dilatancy angle. The relative global error seems to evolve with the load in a similar manner for each mesh, only the magnitude of the relative error change with the mesh density. The relative global error at the end of the loading process for all meshes and all dilatancy is reported Table 1. For the associate case, the most refined mesh yield to a global relative error equal to 9.45%.

Fig. 5.

Relative global error -displacement curves (Mesh N1 & N2, h = 100)

Fig. 6.

Relative global error -displacement curves (Mesh N3, h = 100)

Table 1. Relative error with different value of θ

To this end numerical simulations have been carried out on given finite element mesh whereas the time step size Δt was changed (with h = 100). In general a reduction of the extended dissipation error is observed as the time step size Δt is reduced, though the reduction is not as pronounced as the one obtained by enrichment of the mesh. Dividing the size of step by four doesn’t reduce significantly the error (see Table 2), it means that 8 steps is more than enough. We observe a decrease of the relative global error with decreasing values of the hardening modulus h.

Table 2. Relative error with different numbers of steps (Mesh N1)

6 Conclusions

In this paper, the assessment of the global quality of displacement finite element solutions for Drucker-Prager plasticity model, non-standard elastoplastic problems discretized in time has been presented.

On the introduction of a unique potential, function of the rates and the associated force, which is used by Ladevèze et al. [10,11,12] to extend the notion of dissipation error also to this class of material models, whereas applications of the new measure of error have been given in Hjiaj and Dao [6, 8]. This is a measure of the error in the constitutive equations, the extended dissipation error capability to capture the effects of time and space discretization has been shown in the assessment of the quality of finite element solutions of elastoplastic problems using Drucker-Prager plasticity model with linear hardening and illustrated with a numerical example. This has shown that all trends on the state law and dissipation contribution to the error were meaningful.