Quantifying and Optimizing Robustness of Bipedal Walking Gaits on Rough Terrain

Abstract

Legged robots need “good” disturbance rejection to operate reliably in real-world environments, and achieving this goal arguably requires quantifying robustness. In this work, we consider a point-foot biped on variable-height terrain and measure robustness by the expected number of steps before failure. Unlike our previous work, in which we always assumed a fixed set of low-level gait controllers exist and focused on high-level control design, in this work we finally use quantification of robustness to benchmark and optimize a given (low-level) controller itself. Specifically, we study two particular control strategies as case demonstrations. One scheme is the now-familiar hybrid zero dynamics approach and the other is a method using piece-wise reference trajectories with a sliding mode control. This work provides a methodology for optimization of a broad variety of parameterizable gait control strategies and illustrates dramatic increases in robustness due to both gait optimization and choice of control strategy.

1 Introduction

Quantifying robustness of legged locomotion is essential toward developing more capable robots with legs. In this work, we study underactuated biped walking models. For such systems, various sources of disturbance can be introduced for robustness analysis. While keeping the methods generic, this paper focuses on two-legged locomotion and studies stability on rough terrain, or equivalently, robustness to terrain disturbance.

An intuitive and capacious approach is to use two levels for controlling bipedal locomotion. Fixed low-level controllers are blind to environmental information, such as the terrain estimation. Given environment and state information, the high-level control problem defines a policy to choose the right low-level controller at each step. Our previous work has always assumed a fixed set of low-level gait controllers exist and focused on the high-level control design [1]; in this work, we finally address the more fundamental issue of tuning a particular gait (low-level controller) itself.

For optimization of low-level control for stability, quantification is a critical step. In many approaches to biped walking control, stability is conservatively defined as a binary metric based on maintaining the zero-moment point (ZMP) strictly within a support polygon, to avoid rotation of the stance foot and ensure not falling [2]. However, robust, dynamic, fast, agile, and energy efficient human walking exploits underactuation by foot rolling. For such robots, including point-feet walkers, local stability of a particular limit cycle is studied by investigating deviations from the trajectories (gait sensitivity norm [3], $H_{\infty }$ cost [4], and L2 gain [5]), or the speed of convergence back after such deviations (using Floquet theory [6, 7]). The L2 gain calculation in [5] was successfully extended and implemented on a real robot in [8]. Alternatively, the largest single-event terrain disturbance was maximized in [9] and trajectories were optimized to replicate human-walking data in [10].

Another approach to robustness quantification begins by stochastic modeling of the disturbances and (conservatively) defining what a failure is, e.g., slippage, scuffing, stance foot rotation, or a combination of such events. After discretizing the disturbance and state sets by meshing, step-to-step dynamics are studied to treat the system as a Markov Chain. Then, the likelihood of failure can be easily quantified by calculating the expected number of steps before falling, or mean first-passage time (MFPT) [11]. Optimizing a low-level controller for MFPT was previously impractical due to high computation time of MFPT for a given controller. However, our work over the years now allows us to estimate this number very quickly, and in turn, various low-level controllers can be optimized and benchmarked.

The rest of this paper is organized as follows. The walker model we study and the terrain model we employ are presented in Sect. 2. We then present two low-level control schemes in Sect. 3: (1) A hybrid zero dynamics strategy, with trajectories based on Bézier polynomials and joint-tracking via PD control as suggested in [12], and (2) sliding mode control with time-invariant piece-wise constant joint references adopted in [1]. Section 4 shows the discretization of the dynamics. Tools for generating and working on a Markov chain are presented in Sect. 5. Section 6 gives results, including both performance benchmarks, using the MFPT metric, and also tables documenting the optimal control parameters found using our algorithm. The latter is of particular use to anyone wishing to repeat and build upon our methods. Finally, Sect. 7 gives conclusions and discusses future work.

2 Model

2.1 The Biped

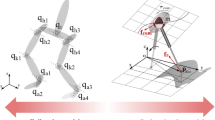
The planar 5-link biped with point feet and rigid links illustrated in Fig. 1 is adopted as the walker model in this paper. The ankles have no torque, so the model is underactuated. The ten dimensional state of the robot is given by $x:=[q \ ; \ \dot{q}]$, where ${q:=[q_1 \ \ q_2 \ \ q_3 \ \ q_4 \ \ q_5]^T}$ is the vector of angles shown in the figure.

Fig. 1

Illustration of the five-link robot with symmetric legs. As will be explained, $\theta$ is called the phase variable

When only one of the legs is in contact with the ground, the robot is in the single support phase, which has continuous dynamics. Using the Lagrangian approach, the dynamics can be derived as

$$\begin{aligned} D(q)\ddot{q}+C(q,\dot{q})\dot{q}+G(q)=Bu, \end{aligned}$$

(1)

where u is the input. Equation (1) can be equivalently expressed as

$$\begin{aligned} \dot{x}=\begin{bmatrix} \dot{q}\\ -D^{-1}(C\dot{q}+G) \end{bmatrix}+\begin{bmatrix} 0\\ D^{-1}B \end{bmatrix}u=:f(x)+g(x)u. \end{aligned}$$

(2)

On the other hand, if both legs are contacting the ground, then the robot is in its double support phase, which can be approximated as an impact map given by

$$\begin{aligned} x^+=\varDelta (x^-), \end{aligned}$$

(3)

where $x^-$ and $x^+$ are the states just before and after the impact respectively. Conservation of energy and the principle of virtual work give the mapping $\varDelta$ [13, 14].

A step consists of a single support phase and an impact event. Since walking consists of steps in sequence, it has hybrid dynamics. For a step to be successful, certain “validity conditions” must be satisfied, which are listed next. After impact, the former stance leg must lift from ground with no further interaction with the ground until the next impact. Also, the swing foot must have progressed past the stance foot before the impact of the next step. Only the feet should contact the ground. Furthermore, the force on stance tip during the swing phase and the force on the swing tip at impact should satisfy the no-slip constraint given by

$$\begin{aligned} F_{friction}=F_{normal} \ \mu _s>|F_{transversal}|. \end{aligned}$$

(4)

If validity conditions are not met, the step is labeled as unsuccessful and the system is modeled as transitioning to an absorbing failure state. This is a conservative model because in reality violating these conditions does not necessarily mean failure.

2.2 The Terrain

In this paper we assume the terrain ahead of the robot is a constant slope until an impact. So each step experiences a slope and the terrain is angular. As shown in Fig. 1, we denote the slope by $\gamma$. This terrain assumption captures the fact that to calculate the pre-impact state, the terrain for each step can simply be interpreted as a ramp with the appropriate slope.

An alternative and perhaps more common choice is modeling the rough terrain with varying heights like stairs. Both models of rough terrain are equally complex, valid, and important for this paper’s purpose and combining the two is a topic of future work. What they both do not consider is the possibility of various intermediate “bumps” that might cause tripping.

3 Control Scheme

This section summarizes two low-level controller strategies that are used to demonstrate the applicability of our method.

1. Hybrid Zero Dynamics Using Proportional-Derivative Control and Bézier Polynomials

The hybrid zero dynamics (HZD) controller framework provides stable walking motions on flat ground. We summarize some key points here and refer interested reader to [12] for details.

While forming trajectories, instead of time, the HZD framework uses a phase variable denoted by $\theta$. Since it is an internal-clock, phase needs to be monotonic through the step. As the phase variable, we use $\theta$ drawn in Fig. 1, which corresponds to $\theta =cq$ with $c=\left[ -1 \ 0 \ -1/2\ 0\ -1\right]$. Second, since there are only four actuators, four angles to be controlled need to be chosen, which are denoted by $h_0$. Controlling the relative (internal) angles means $h_0:=\left[ q_1 \ q_2 \ q_3 \ q_4 \right] ^T$. Then $h_0$ is in the form of $h_0=H_0q$, where $H_0=\left[ I_4 \ 0 \right]$.

Let $h_d(\theta )$ be the references for $h_0$. Then the tracking error is given by

$$\begin{aligned} h(q):=h_0(q)-h_d(\theta )=H_0q-h_d(cq). \end{aligned}$$

(5)

Taking the first derivative with respect to time reveals

$$\begin{aligned} \dot{h}=\frac{\partial h}{\partial x}\dot{x}=\frac{\partial h}{\partial x}f(x)=:\mathcal {L}_fh, \end{aligned}$$

(6)

where we used the fact that $\frac{\partial h}{\partial x}g(x)=0$. Then, the second derivative of tracking error with respect to time is given by

$$\begin{aligned} \ddot{h}=\mathcal {L}_f^2h+\mathcal {L}_g\mathcal {L}_fh \ u. \end{aligned}$$

(7)

Substituting the linearizing controller structure

$$\begin{aligned} u(x)=(\mathcal {L}_g\mathcal {L}_fh)^{-1}(-\mathcal {L}_f^2h+v) \end{aligned}$$

(8)

to (7) yields

$$\begin{aligned} \ddot{h}=v. \end{aligned}$$

(9)

To force h (and $\dot{h}$) to zero, a simple PD controller given by

$$\begin{aligned} v=-K_Py-K_D\dot{y} \end{aligned}$$

(10)

can be employed, where $K_P$ and $K_D$ are the proportional and derivative gains, respectively.

As suggested in [12], we use Bézier polynomials to form the reference ($h_d$). Let $\theta ^+$ and $\theta ^-$ be the phase at the beginning and end of limit cycle walking on flat terrain respectively. An internal clock which ticks from 0 to 1 during this limit cycle can be defined by

$$\begin{aligned} \tau (q):=\frac{\theta (q)-\theta ^+}{\theta ^--\theta ^+}. \end{aligned}$$

(11)

Then, the Bézier curves are in the form of

$$\begin{aligned} b_i(\tau )=\sum _{k=0}^{M}\alpha _k^i \frac{M!}{k!(M-k)!}\tau ^k(1-\tau )^{M-k}, \end{aligned}$$

(12)

where M is the degree and $\alpha _k^i$ are the coefficients. Then, the reference trajectory is determined as

$$\begin{aligned} h_d(\theta ):=\begin{bmatrix} b_1(\tau )\\ b_2(\tau )\\ b_3(\tau )\\ b_4(\tau ) \end{bmatrix}. \end{aligned}$$

(13)

Choosing $M=6$ yields $(6+1)\times 4=28$ $\alpha _k^i$ parameters to optimize. However, for hybrid invariance, $h=\dot{h}=0$ just before an impact on flat terrain should imply $h=\dot{h}=0$ after the impact. This constraint eliminates $2\times 4 =8$ of the parameters as explained in [12]. In total, $20+2=22$ parameters must be chosen, including the PD controller gains.

2. Sliding Mode Control with Time-Invariant Piece-Wise Constant References

The second controller strategy of this paper is adopting sliding mode control (SMC) to track piece-wise constant references [1, 15].

As in the HZD control, let $h_0$ denote the four variables to control. As a result of our experience in previous work [16], we proceed with

$$\begin{aligned} h_0:=[\theta _2 \ \ q_3 \ \ q_4 \ \ q_5]^T, \end{aligned}$$

(14)

where $\theta _2:=q_2+q_5$ is an absolute angle. Equivalently we can write $h_0=H_0q$, where

$$\begin{aligned} \ H_0=\begin{bmatrix} 0&1&0&0&1\\ 0&0&1&0&0\\ 0&0&0&1&0\\ 0&0&0&0&1 \end{bmatrix}. \end{aligned}$$

(15)

Substituting the control input

$$\begin{aligned} u=(H_0 D^{-1}B)^{-1}(v+H_0 D^{-1}(C\dot{q}+G)), \end{aligned}$$

(16)

into (1) yields

$$\begin{aligned} \ddot{h}_0=v. \end{aligned}$$

(17)

We then design v such that $h_0$ acts as desired ($h_d$). The tracking error is again given by $h=h_0-h_d$ and the generalized error is defined as

$$\begin{aligned} \sigma _i=\dot{h_i}+h_i/\tau _i \ \ \ i=\{1,2,3,4\}, \end{aligned}$$

(18)

where $\tau _i$s are time constants for each dimension of h. Note that when the generalized error is driven to zero, i.e. $\sigma _i=0$, we have

$$\begin{aligned} 0=\dot{h_i}+h_i/\tau _i. \end{aligned}$$

(19)

The solution to this equation is given by

$$\begin{aligned} h_i(t)=h_i(t_0) \ exp(-(t-t_0)/\tau _i), \end{aligned}$$

(20)

which drives $h_i$ to 0 exponentially fast. Next, v in (17) is chosen to be

$$\begin{aligned} v_i=-k_i|\sigma _i|^{2\alpha _i-1}sign(\sigma _i), \ \ \ i=\{1,2,3,4\}, \end{aligned}$$

(21)

where $k_i>0$ and $0.5<\alpha _i<1$ are called the convergence coefficient and convergence exponent respectively. Note that if we had $\alpha _i=1$, this would simply be a standard PD controller. Then, $\tau _i$ and $k_i$ are analogous to the proportional gain and derivative time of a PD controller. However, $0.5<\alpha _i<1$ ensures finite time convergence. For further reading on SMC please refer to [17]. Note that SMC has $4\times 3=12$ parameters to be optimized.

For faster optimization, it is preferable to have fewer parameters to optimize. Motivated by simplicity, we use references in the form of

$$\begin{aligned} h_d={\left\{ \begin{array}{ll} [\theta _2^{ref1} \, \, q_3^{ref} \, \, q_4^{ref1} \, \, q_5^{ref}]^T, &{} \theta _1:=q_1+q_5>\pi ,\\ {[}\theta _2^{ref2} \, \, q_3^{ref} \, \, q_4^{ref2} \, \, q_5^{ref}]^T, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(22)

Note that the references are piecewise constant and time-invariant. What makes this reference structure appealing is the fact that there are only 6 parameters to optimize. So, in total, $12+6=18$ parameters are optimized.

4 Discretization

4.1 Discretization of the Dynamics

The impacts when a foot comes into contact with the ground provide a natural discretization of the robot motion. For the terrain profile described in Sect. 2.2, using (2) and (3) the step-to-step dynamics can be written as

$$\begin{aligned} x[n+1]=\rho (x[n],\gamma [n],\zeta [n]), \end{aligned}$$

(23)

where x[n] is the state of the robot and $\gamma [n]$ is the slope ahead at step n.

4.2 Discretization of the Slope Set

Our method requires a finite slope set $\varGamma$, which we typically set as

$$\begin{aligned} \varGamma =\left\{ \gamma ^\circ \ : \ \ \frac{\gamma }{d_{\gamma }}\in \mathbb {Z}, \ -20\le \gamma \le 20\right\} , \end{aligned}$$

(24)

where $d_\gamma$ is a parameter determining the slope set density. The range needs to be wide enough so that the robot is not able to walk at the boundaries of the randomness set.

4.3 Meshing Reachable State Space

There are two key goals in meshing. First, while the actual state x might be any value in the 10 dimensional state space, the reachable state space for system is a lower dimensional manifold once we implement particular low-level control options and allow only terrain height variation as a perturbation source. The meshed set of states, X, needs to well cover the (reachable) part of state space the robot can visit. This set should be dense enough for accuracy while not having “too many” elements for computational efficiency. Second, we want to learn what the step-to-step transition mapping, $\rho (x,\gamma ,\zeta )$, is for all $x\in X$ and $\gamma \in \varGamma$. Next, an initial mesh, $X_i$, should be chosen. In this study, we use an initial mesh consisting of only two points. One of these points ($x_1$) represents all (conservatively defined) failure states, no matter how the robot failed, e.g. a foot slipped, or the torso touched the ground. The other point ($x_2$) should be in the controllable subspace. In other words, it should be in the basin of attraction for controller $\zeta$.

Then, our algorithm explores the reachable state space deterministically. We initially start by a queue of “unexplored” states, $\overline{X}=\{x\in X_i \ : \ x\ne x_1\}$, which corresponds to all the states that are not simulated yet for all possible terrains. Then we start the following iteration: As long as there is a state $x\in \overline{X}$, simulate to find all possible $\rho (x,\gamma ,\zeta )$ and remove x from $\overline{X}$. For the points newly found, check their distance to other states in X. If the minimum such distance exceeds some threshold, a new point is then added to X and $\overline{X}$.

A crucial question is how to set the (threshold) distance metric so that the resulting X has a small number of states while accurately covering the reachable state space? The standardized (normalized) Euclidean distance turns out to be extremely useful, because it dynamically adjusts the weights for each dimension. The distance of a vector $\bar{x}$ from X is calculated as

$$\begin{aligned} d(\bar{x},X):=\underset{x \in X}{{\text {min}}} \left\{ \sum \limits _{i} \left( \frac{\bar{x}_i-x_i}{r_i}\right) ^2\right\} , \end{aligned}$$

(25)

where $r_i$ is the standard deviation of $i^{th}$ dimension of all existing points in set X. In addition, the closest point in X to $\bar{x}$ is given by

$$\begin{aligned} c(\bar{x},X):=\underset{x \in X}{{\text {argmin}}} \left\{ \sum \limits _{i} \left( \frac{\bar{x}_i-x_i}{r_i}\right) ^2\right\} . \end{aligned}$$

(26)

We are now ready to present the pseudocode in Algorithm 1. Two important tricks to make the algorithm run faster are as follows. First, the slope set allows a natural cluster analysis. We can classify states using the inter-leg angle they possess. So, the distance comparison for a new point can be made only with the points that are associated with the same (preceding) slope. This might result in more points in the final mesh, but it speeds up the meshing and later calculations significantly. Secondly, consider a state x. We can simulate $\rho (x,-20^{\circ },\zeta )$ just once and then extract $\rho (x,\gamma ,\zeta )$ for all $\gamma \in \varGamma$. The reason is, for example, in order robot to experience an impact at $-20^{\circ }$, it has to pass through all possible (less steep) impact points in the slope set.

While meshing the whole 10D state space is infeasible, this algorithm is able to avoid the curse of dimensionality because the reachable state space is actually a quasi-2D manifold [18]. As a result, the meshing can be done with a relatively small number of iteration steps.

5 Metastable Markov Chains

5.1 Obtaining a Markov Chain

To obtain a finite state machine representation of the system, we need to approximate the dynamics for points $\rho (x,\gamma ,\zeta )\not \in X$. The most elementary approach is 0’th order approximation given by

$$\begin{aligned} x[n+1]\approx c(\rho (x[n],\gamma [n],\zeta [n]),X), \end{aligned}$$

(27)

where $c(\bar{x},X)$ is the closest point $x\in X$ to $\bar{x}$ for the employed distance metric. Then the deterministic state transition matrix can be written as

$$\begin{aligned} T^d_{ij}(\gamma , \zeta )={\left\{ \begin{array}{ll} 1,&{} \text {if } x_j=c(\rho (x_i,\gamma ,\zeta ),X) \\ 0,&{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(28)

The nearest-neighbor approximation in (27) appears to work well in practice. More sophisticated approximations result in transition matrices not just having one or zero elements, but also fractional values in between [19], and it does not provide much increase in accuracy to the authors’ experience.

A Markov Chain can be represented by a stochastic state-transition matrix T defined as

$$\begin{aligned} T_{ij}:=Pr(x[n+1]=x_j \ | \ x[n]=x_i). \end{aligned}$$

(29)

To calculate this matrix, the first thing we need to do is assume a distribution over slope set, noted by

$$\begin{aligned} P_\varGamma (\gamma )=Pr(\gamma [n]=\gamma ). \end{aligned}$$

(30)

In this paper, we assume a normal distribution for $P_\varGamma$, with mean $\mu _\gamma$, and standard deviation $\sigma _\gamma$. After distributing $\gamma$ values, T can be calculated as

$$\begin{aligned} T(\zeta )=\sum \limits _{\gamma \in \varGamma } P_\varGamma (\gamma ) \ T^d(\gamma , \zeta ). \end{aligned}$$

(31)

As we make $d_{thr}$ and $d_\gamma$ smaller, we have more accurate representations of the full dynamics at the expense of higher numbers of states in the final mesh.

5.2 Expected Number of Steps Before Failure

This section serves as a summary on how we estimate the expected number of steps before failure, or mean first-passage time (MFPT). For details, we invite interested reader to [20].

The eigenvalues of T cannot have magnitude larger than one. However, the largest eigenvalue is equal to 1 because we model failure as absorbing. Also, the second largest eigenvalue, denoted by $\lambda _2$, is non-negative and real.

No matter what the initial condition is, if the robot does not fall within several steps, then the probability density function for the system converges to its metastable distribution. Starting with this distribution, with $1-\lambda _2$ probability the walker is going to fall on the next step, otherwise the probability distribution does not change. Then, the probability of taking n steps only, equivalently falling at the nth step is simply

$$\begin{aligned} Pr(x[n]=x_1, \ x[n-1]\ne x_1)=\lambda _2^{n-1}(1-\lambda _2). \end{aligned}$$

(32)

For $\lambda _2<1$, realize that as $n\rightarrow \infty$, the right hand side goes to zero, i.e., the system will eventually fail. Note that we also count the step which ended up in failure as a step. An intuitive check is to consider failing at the first step (taking 1 step only). When $n=1$ is substituted, we get $1-\lambda _2$ as expected. Then, the average number of steps can be then calculated as

$$\begin{aligned} \begin{aligned} MFPT&= E[FPT] \\&= \sum \limits _{n=1}^{\infty } n \ Pr(x[n]=x_1,\ x[n-1]\ne x_1) \\&= \sum \limits _{n=1}^{\infty }n \lambda _2^{n-1} (1-\lambda _2) = \frac{1}{1-\lambda _2}, \end{aligned} \end{aligned}$$

(33)

where we used the fact that $\lambda _2<1$. As a result, MFPT can then be calculated using

$$\begin{aligned} M={\left\{ \begin{array}{ll} \infty &{} \lambda _2=1 \\ \frac{1}{1-\lambda _2} &{} \lambda _2<1. \end{array}\right. } \end{aligned}$$

(34)

Note that being stable corresponds to $\lambda _2=1$, but we will introduce enough roughness so that we always have $\lambda _2<1$. This is achieved with a wide-enough slope set and high enough $\sigma _\gamma$.

We would like to mention that instead of steps, expected distance before failure can alternatively be calculated as explained in [21]. However, as listed later in the following section, we did not observe high variances in step width values. So, number of steps is a good indicator of how much the robot travels.

6 Results

Unless stated otherwise, we use the “minimize” function from [22], which is based on fminsearch function, in MATLAB to optimize. At every iteration the reachable state space for given controller parameters is meshed and the corresponding Markov chain is obtained to calculate the expected number of steps as explained in the previous sections. In this paper we optimize for $\mu _\gamma =0^\circ$, i.e., zero average slope. However, we optimize control for each of a range of particular values of $\sigma _\gamma$. If it is too small, then the MFPT turns out to be very large, which may not be calculated due to numeric software capabilities. Using MATLAB, we can calculate MFPT values up to around $10^{14}$ reliably. On the other hand, $\sigma _\gamma$ should not be too large, otherwise it may not be as easy to differentiate different controllers’ performance with all controllers performing “badly” as $\sigma _\gamma$ gets large enough. Appropriate range for $\sigma _\gamma$ can be easily decided by calculating MFPT for different values with a single mesh. Once we decide on $\sigma _\gamma$, we pick $d_\gamma$. $d_\gamma =\sigma _\gamma /2$ is the rule of thumb we apply in this paper. Just like $d_\gamma$, $d_{thr}$ can be made smaller for higher accuracy in the expense of higher computation time. Whether $d_\gamma$ and $d_{thr}$ are small enough can be checked after the optimization by using smaller values and confirming MFPT estimation does not change much. For the $d_\gamma$ and $d_{thr}$ values listed later in this section, each cost computation (iteration) took around a minute. Typically, a couple of hours are enough to optimize controller parameters.

1. Hybrid Zero Dynamics Using Proportional-Derivative Control and Bézier Polynomials

For the HZD scheme, the base controller, $\zeta ^{1}_{\text {Base}}$, is obtained by assuming flat terrain, fixing speed to be 0.8 m/s and minimizing energy usage as in [12]. To obtain $\zeta ^{1}_{\text {COT}}$, we remove the speed constraint and optimize for cost of transport (COT) given by

$$\begin{aligned} COT=\frac{W}{mgd}, \end{aligned}$$

(35)

where m is the mass, g is the gravitational constant, and d is the distance traveled. In this paper we use a conservative definition of “energy spent” by regarding negative work is also done by the robot, i.e., $W=|W_{positive}|+|W_{negative}|$.

Table 1 Parameters for the first controller scheme in radians

Both of these controllers assume flat terrain, i.e., $\sigma _\gamma =0^\circ$, in optimization. In addition, the HZD framework shows how to obtain the trajectories only, but not the controller gains. So, we just picked $K_P=100$ and $K_D=10$, which works on flat terrain. To obtain $\zeta ^{1}_{\text {MFPT}}$, we used the “patternsearch” algorithm in MATLAB to optimize for MFPT with $\sigma _\gamma =1^\circ$, $d_\gamma =0.5$ and $d_{thr}=0.3$. Table 1 lists the parameters for each controller.

We compare the stability of each controller versus the roughness of the terrain in Fig. 2. Noting the logarithmic y-axis, we immediately notice the huge improvement in stability by optimizing with the suggested method.

Fig. 2

Average number of steps before falling calculated using (33) versus $\sigma _\gamma$ for the first controller scheme. Slopes ahead of the robot are assumed to be normally distributed with $\mu _\gamma =0^\circ$

We note that Monte Carlo simulations are not a computationally practical means of verifying MFPT when it is very high, which has motivated our methodology throughout. However, we present a Monte Carlo study in Table 2 for $\sigma _\gamma =2^\circ$, where MFPT is small. To obtain the second row in this table, we simulated 10 thousand times. To allow the robot to “forget” the initial condition, we omit the first step, i.e., we only consider cases where it took more than a single step and do not count that first step.

Table 2 Estimation of MFPT for First Controller Scheme with $\mu _\gamma =0^\circ$ and $\sigma _\gamma =2^\circ$

2. Sliding Mode Control with Time-Invariant Piece-Wise Constant References

We start optimizing the second controller scheme with the hand-tuned parameters taken from [16], which we refer to with $\zeta ^{2}_{\text {Base}}$. We first optimize for Cost of Transport (COT) of the limit cycle gait on flat terrain to obtain $\zeta ^{2}_{\text {COT}}$. We then optimize for MFPT with $\sigma _\gamma =2^\circ$, $d_\gamma =1$ and $d_{thr}=1$. This results with controller $\zeta ^{2}_{\text {MFPT}}$. The parameters for each controller are given in Table 3.

Table 3 Parameters for the second controller scheme

Figure 3 compares the stability of each controller versus the roughness of the terrain. Again noting the logarithmic y-axis, the suggested method provides a dramatic increase in the stability, just like in Fig. 2.

Fig. 3

Average number of steps before falling calculated using (33) versus $\sigma _\gamma$ for the second controller scheme. Slopes ahead of the robot are assumed to be normally distributed with $\mu _\gamma =0^\circ$. Note that both the range of $\sigma _\gamma$ and the y-axis scaling are different from Fig. 2

Table 4 presents the Monte Carlo study obtained assuming $\sigma _\gamma =5^\circ$. Just like in Table 2, we omit the first step to allow the simulation to “forget” the initial condition.

Table 4 Estimation of MFPT for Second Controller Scheme with $\mu _\gamma =0^\circ$ and $\sigma _\gamma =5^\circ$

3. Comparison

We first note that all six controllers are stable on flat ground ($\sigma _\gamma =0^\circ$), because they all exhibit stable limit cycles. However, as Table 5 shows, there is a huge difference between $\zeta ^{2}_{\text {MFPT}}$ and any of the HZD controllers. Comparing the results in Figs. 2 and 3 also emphasizes this dramatic difference. So, we conclude that the second controller scheme is much more capable in terms of stability. One of the main goals of this paper is to illustrate this benchmarking capability.

We note that many parameters of $\zeta ^{2}_{\text {Base}}$ and $\zeta ^{2}_{\text {MFPT}}$ in Table 3 are very close. We suspect that we only find local minimums. Indeed, starting with different initial conditions yields different final gaits.

Table 5 Comparison of controller schemes for $\mu _\gamma =0^\circ$

A major problem in the first controller scheme, we believe, is the fact that reference is designed only for flat terrain. For example, the controller does not really know what to do when $\theta >\theta ^+$ (or $\tau >1$). This is because Bézier polynomials are designed for $0\le \tau (q)\le 1$, and they quickly deviate outside this range. As a result, $\zeta ^{1}_{\text {Base}}$ cannot take more than several steps on inclined terrain with a slope of $-1^{\circ }$. We discovered an easy fix to the problem by adopting the following policy: If $\tau (q)>0.95$, then do not apply any torque. With this update, the controller can still walk on flat terrain. In addition, it seems to be stable on $-9^{\circ }$ degree sloped terrain! However, we did not present the result with this policy because it ends up with a low MFPT for $\mu _\gamma =0^\circ$. The reason is, it works very badly on uphill slopes. The fact that turning the controller off greatly helps when going downhill shows the need for a better reference parametrization to keep controller on at all times. Reference [21] presents an attempt to achieve this goal.

7 Conclusions and Future Work

In this work, we present a methodology for optimizing a low-level control scheme and of benchmarking final performance on rough terrain using the MFPT metric for reliability. We apply the approach to two particular control schemes as a motivating example; however, the approach is designed to provide a systematic means of optimizing and benchmarking any of a wide variety of control strategies, not only for walking systems but also for other dynamic systems subject to stochastic environments, more generally.

As mentioned in the previous section, we end up with a local minimum for the second controller scheme. We aim to find the global solution in a future study. The sensitivity of our stability metric to model mismatch is another important future work topic.

Reference [21] is a work that builds on this paper. It presents a controller scheme that is more capable than the two studied in this paper. It also shows that we can also optimize under constraints, e.g., for desired speed, step width, or ground clearance. Furthermore, by designing multiple controllers for different mean slopes, it demonstrates how to increase stability dramatically. Finally, we may use cost functions that incorporate other performance metrics also, similar to [23]. For example, a practical goal is to increase stability while decreasing energy consumption, balancing the two aims as desired.