Slip Detection and Recovery for Quadruped Robots

Abstract

What should a legged robot do when it slips? When traction is lost, the locomotion can be irreversibly hampered. Being able to detect slippage at the very beginning and promptly recover the traction is crucial for body stability and can make the difference in a situation where falling is not an option. Indeed, the majority of locomotion controllers and state estimation algorithms rely on the assumption that the stance feet are not slipping. The following work presents a methodology for slip detection and estimation of the friction parameters, plus a recovery strategy which exploits the capabilities of a whole body controller, implemented for locomotion, which optimizes for the ground reaction forces (GRFs). The estimation makes use only of proprioceptive sensors (no vision). Even though the essence of the approach is quite general, the implementation is specialized for the quadruped robot HyQ. Simulation results demonstrate the effectiveness of the proposed approach while walking on challenging terrains (a slippery ramp or an ice slab).

1 Introduction

Being able to deal with slippage is of great importance for legged robots which are meant to traverse unstructured terrains. In particular, a strategy for detecting slippage and recover from it, becomes crucial when whole body inverse dynamics approaches are implemented for robot control [1, 14, 18]. Actually, they rely on the assumption that the stance feet constraints are not violated (e.g. they are not moving or are supposed to move very little [8]). Indeed, a violation of the stance constraints makes the inverse dynamics compute joint torques which are not physically meaningful anymore. This would result in: (i) errors in the realization of the desired body wrench (because the slip limits the amount of tangential force that the ground is able to deliver) (ii) degeneration of the support triangle. These two facts would eventually lead to a loss of stability even in case of very slow motions. On the same line, kinematic-based state estimation or odometry techniques [3, 6], which rely on the assumption that none of the stance feet is slipping, are prone to drift if the amount of slip is relevant (or if there is a compliance between the base and the ground which is not modelled). Even if the controller incorporates the optimization of the ground reaction forces, there are two types of uncertainties which can cause slippage during locomotion:

• 1. Uncertainty on the estimate of the surface normal ${\mathbf {n}}$. This is commonly estimated by vision [17] or by fitting a plane (gradient-based terrain detection) through the feet that are on the ground (stance feet) [26]. The fitting plane can be a very crude approximation of the terrain surface inclination which can have local discontinuities (e.g. like the ramp illustrated in Fig. 4). Any deviation from a planar shape results in errors in the estimation of the inclination of the surface which is under the foot at the moment of the touch-down.

• 2. Uncertainty on the friction coefficient $\mu$. Most of the times $\mu$ cannot be known in advance and is commonly inferred according to semantic information (e.g. ice) coming from vision [22].

An earlier work on slip recovery is from Takemura [26], who presented both a long term and a short term strategy for slip recovery. The former aims to change gait frequency and stride length when approaching slippery surfaces. However, changing locomotion parameters to address slippage can be successful only on terrain with limited roughness and moderate slipperiness. Conversely, if very challenging environment is considered (e.g. crossing a river or walking on ice), the occurrence of slippage might result in unrecoverable loss of stability because any other footstep can be infeasible. A short term strategy is needed in these cases. At this extent, Takemura proposes to instantaneously add a force (at the occurrence of slippage) to have the ground reaction forces (GRFs) back in the friction cone. This approach has several shortcomings: (1) it is based on the idea that the normal is properly estimated; (2) the required force might not be necessarily realizable at the foot, since the ground reaction force is the result of the robot motion in interaction with the environment. More precisely, the GRFs can only be controlled to a limited extent (e.g. creating internal forces) in the null-space of the contact constraints. In addition to this (in static conditions) the maximum applicable total normal force is constrained by the robot weight.

To address the above limitations we propose a short term slip recovery strategy, which is built on top of a whole body controller [9, 10]. In essence the controller we use, is formulated as a QP problem where the goal is to realize a certain body wrench while optimizing for ground reaction forces (decision variables). We added inequality constraints to the problem to obtain forces that obey friction cones limits, additionally accounting for the fact that the ground can only push and not pull (unilateral constraints). The body wrench is the 6D vector of forces/moments coming from the body motion task that aims to track a specified trajectory for the CoM and the trunk orientation.

In this context, assuming a reliable low level tracking of the joint torques and no external disturbances, a slippage can only occur if the controller uses a wrong estimate of the surface normal or of the friction coefficient. In fact, this results in GRFs which are out of the real friction cones (cf. Sect. 4.1). Therefore, differently from Takemura, instead of striving to apply the correct GRFs (which might not be feasible), we propose to correct the estimate of the surface inclination and of the friction coefficient in order to allow the robot to apply forces which satisfy the friction limits.

More recently, in one of the online videos,¹ the BigDog robot demonstrated to successfully recover from slipping on ice. However, to date, no experimental results have been published and no details have been reported on the repeatability of the used approach.

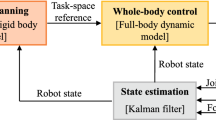
Within the context of legged robots, the main contribution of this paper is a methodology to: (1) detect slippage, (2) on-line estimate the friction coefficient $\mu$ and the normal n of the surface making use of only proprioceptive information (torque measurement and encoder readings) (3) on-line recovery from slippage by smoothly accommodating (but in a short time interval) the value of the normal used in the optimization to the estimated one. The whole slip recovery pipeline is graphically summarized in Fig. 1. We have implemented the slip detection/estimation/recovery strategy for a model of HyQ [24], a 80 kg quadruped robot with point feet. HyQ is shown to perform a (statically stable) walk on a highly slippery (flat) surface and on a moderately slippery ramp.

Fig. 1

Slip recovery pipeline (blue blocks): detection, estimation and correction. The yellow blocks are: the body, feet trajectory generation and the high level control (whole body) and the low level one (torque)

The applicability of this approach is limited to torque controlled robots equipped with a high-level controller which optimizes for ground reaction forces. We will show simulations where the slip is detected only in one leg and when there are at least three legs in contact with the ground. A possible solution for the detection in the case of more than two legs slipping is only drafted.

This paper is structured as follows: Sect. 2 presents a robust way to detect slippage, followed by Sect. 3 that illustrates the on-line estimation of the friction parameters. Section 4 describes the implemented strategy to recover traction during slippage. Sections 5 and 6 contain the results of simulations with HyQ and the conclusions, respectively.

2 Slip Detection

The approaches to address the problem of slip detection can be divided into two big groups: force based and kinematic based approaches. The force based, require the availability of a 6-axis force sensor which is usually located at the contact point (e.g. the foot-tip). If the friction coefficient is known in advance, the slippage could simply be detected by checking if the ratio of the tangential/normal component of the contact forces [20] is within the limit of static friction. When the friction coefficient $\mu$ is unknown, a possible strategy is to check the frequency content of the tangential contact force signal. As a matter of facts, in presence of slippage, a high frequency ripple in the force signal appears, due to the local stick-slip phenomena that occurs between the contacting surfaces. First Holweg [15] and more recently Palli [21], claimed that, after performing a Fourier analisis (FFT) of the higher harmonics of the force signal, it was possible to recognize the deformations which precedes the real slip. These approaches are of limited applicability to legged robots, because they need a high cost force/torque sensor to be attached to the foot tip. However, due to the repetitive impacts with the ground, in the long run, this can result in a damage of the sensor. Furthermore, during locomotion, the touchdown event can create discontinuities in the force signals and jeopardize the detection. As a matter of facts, it is not easy to measure the instant when the force oscillation, due to the touch-down, has settled down, in order to have a detection without false positives. Conversely, a detection strategy based on kinematics, it preferable in the context of legged robots where ground impacts are the order of the day.

A kinematic strategy can be implemented at the acceleration, velocity or position level. In [26] Takemura considered slippage as an impulse-like leg acceleration, and attached accelerometers to the lower-leg links to detect slippage. A drawback of this approach is that accelerometers are usually affected by noise.

Alternatively, slippage could be estimated at the position level, by checking the inter-distances between the stance feet. Indeed slippage of one (or more) feet can be detected if the mutual distance of the stance feet (which is set at the moment a new touchdown event occurs) changes within the duration of a single stance configuration. However, when traction is lost the resulting acceleration will create also a velocity difference among the stance feet. Being the position the integral of velocity this difference can be detected more promptly in velocity than in position. Thus, we propose to check the slippage at the velocity level. It is important to underline that the choice of the frame in which the feet velocities are compared, directly affects the robustness of the approach. The most intuitive way is to check if the Cartesian velocities of the stance feet are all zero in an inertial (world $\mathcal {W}$) frame. However, expressing the foot velocity in the world frame (${}_w\dot{{\mathbf {x}}}_f$), requires an estimation of the robot base linear velocity ${}_{w}\dot{{\mathbf {x}}}_{b}$:

$$\begin{aligned} 0 \approxeq {}_{w}\dot{{\mathbf {x}}}_f = {}_{w}\dot{{\mathbf {x}}}_{b} + {}_w{\mathbf {R}}_b \underbrace{({}_{b}\dot{{\mathbf {x}}}_f + {}_b{\varvec{\omega }}_b \times {}_{b}{\mathbf {x}}_f)}_{ {}_{b}\dot{\tilde{{\mathbf {x}}}}_f } \end{aligned}$$

(1)

where ${}_w{\mathbf {R}}_b \in \mathbb {R}^{3\times 3}$ is the rotation matrix representing the orientation of the robot base, while ${}_b{\varvec{\omega }}_b$ is its angular velocity. ${}_{b}{\mathbf {x}}_f$, ${}_{b}\dot{{\mathbf {x}}}_f$ are, respectively, the position and velocity of the foot expressed in the base frame ($\mathcal {B}$). The angular velocity ${}_b\omega _b$ can be measured with reasonable accuracy by an on-board IMU sensor, while the base linear velocity, as common practice in robotics, can be inferred through leg odometry or state estimation techniques [3]. Therefore, if we compare the feet velocities in the world frame, they are influenced by errors in the state estimation, which can result into false positives in the slip detection. A more robust approach would be to compare the feet velocities in the base frame (term ${}_{b}\dot{\tilde{{\mathbf {x}}}}_f$ in (1) which accounts also for the influence of the moving frame). The advantage of this, is that the kinematics is always accurate because it directly depends on direct sensor measurements (e.g. encoders, gyro). Differently from the world frame case, the stance feet velocities ${}_{b}\dot{\tilde{{\mathbf {x}}}}_f$ have to be equal in norm and direction (and opposite to the base linear velocity ${}_{b}\dot{{\mathbf {x}}}_{b}$). Thus, in a manner similar to what a car ABS braking system is doing [2], a fruitful strategy for slip detection is to compare the values of the norm $v_i=\Vert {}_{b}\dot{\tilde{{\mathbf {x}}}}_{f_i} \Vert$ of the velocities of the stance feet and discriminate the outlier with appropriate statistical tools. Henceforth, for the sake of brevity, we denote the norm with v and the associated Cartesian vector with ${\mathbf {v}}$.

One leg slip detection: Following, we present a pseudo-code implementation of the slip detection for one leg of a legged robot:

At each control loop the median of the norms of the stance feet velocities is computed. The median will have a value in between the velocities of the non slipping legs and the slipping one. The slipping leg will be the one with a velocity far from the median beyond a certain margin th, that can be tuned experimentally. During locomotion the detection algorithm is continuously checking, within the set of active stance legs, if there is any slippage. Whenever a slip is detected, if the leg was a stance leg, this should be removed from the set of stance legs accounted in the state estimation/odometry, while it can be incorporated back at the end of the slip (see Fig. 1). This is crucial to prevent the corruption of the state estimate.

Multiple leg slip detection: A more subtle situation is when two legs are slipping at the same time. In this case, it is hard to detect with the median approach, who are the slipping legs and who are the stance legs (we just know that they have pair-wise different velocities). In this case, checking which of the feet velocities ${\mathbf {v}}_i$ are kinematically consistent with the base velocity ${}_{b}{\dot{{\mathbf {x}}}}_{b}$, could help us to discriminate the slipping legs. At this extent a short-time integration of the base linear acceleration (IMU) can be the only resort. It is known that integrating accelerometers is prone to drift but, for a limited time interval, the estimate should be accurate enough.

3 Surface Normal and Friction Coefficient Estimation

Once that the slip is in act, it is crucial to estimate the friction coefficient $\mu$ and the surface normal n in the early milliseconds of slippage, in order to be able to apply a corrective action as described in Sect. 4.

Remark: Along the paper, we will not make a distinction between static and dynamic friction.

Firstly, we make the following assumptions:

Assumption 1: The frictional properties of the surface around the foot are isotropic (coefficient of friction equal in all directions).

Assumption 2: when the leg starts to slip (it will start slow), it will cover a surface where the normal is uniformly constant.

Assumption 3: we assume no soft contact. Since the robot has point feet we can neglect the influence of the rotational friction about the normal direction (more complex than the linear one because it depends on the size of the contact area).

We can get useful insights for the estimation considering the following facts:

• 1. if unilateral constraints are always satisfied (e.g. the legs are always pushing on the ground and the feet are not detaching), the direction of the foot slip velocity ${\mathbf {v}}$ will always be tangent to the surface. This means the surface normal ${\mathbf {n}}$ forms a right angle with the velocity vector ${\mathbf {v}}$. Furthermore, physics tells us that the normal should lie in the plane $\varPi$ passing through the direction of the ground force ${\mathbf {F}}$ and of the velocity ${\mathbf {v}}$ (see Fig. 2(left)). These two facts allow us to easily determine the surface normal ${\mathbf {n}}$ by simple geometric computations:

  $$\begin{aligned}&{\varvec{\pi }} = \frac{{\mathbf {v}}\times {\mathbf {F}}}{ \Vert {\mathbf {v}} \times {\mathbf {F}} \Vert } \quad \quad&{\mathbf {n}} = \frac{{\varvec{\pi }} \times {\mathbf {v}}}{\Vert {\varvec{\pi }} \times {\mathbf {v}} \Vert } \end{aligned}$$

  (2)

  where ${\varvec{\pi }}$ is the normal to the plane $\varPi$.

• 2. during the slipping motion, the ground force ${\mathbf {F}}$ is always lying on one edge of the friction cone. Therefore, while the foot is slipping, the angular distance $\phi$ between ${\mathbf {F}}$ and ${\mathbf {n}}$ (see Fig. 2), can be an estimate of the real friction coefficient ($\mu = tan(\phi )$):

  $$\begin{aligned} \mu = tan(\phi ) = \dfrac{sin(\phi )}{cos(\phi )} = \dfrac{\Vert {\mathbf {F}}\times {\mathbf {n}} \Vert }{{\mathbf {F}} \cdot {\mathbf {n}}} \end{aligned}$$

  (3)

Fig. 2

Left vector definitions for slip detection (for a generic foot on a slope). The red dot is the foot location, $\varPi$ is the plane where the ground reaction force ${\mathbf {F}}$ and the foot velocity vector ${\mathbf {v}}$ lie while ${\mathbf {n}}$ is the estimated surface normal. Right slip recovery definitions: ${\hat{{\mathbf {n}}}}$ is the actual normal used in the controller. ${\hat{{\mathbf {e}}}}$ is the axis of rotation to move ${\hat{{\mathbf {n}}}}$ towards ${\mathbf {n}}$ while $\varDelta \theta$ is the correction angle

To obtain a noise-free estimation of the normal ${\mathbf {n}}$, we compute a moving average on N samples, by using a parametric representation of the geodesic [12], while for the friction coefficient $\mu$ we perform a moving average with linear weighting (last sample is weighted most).

Observation: the value of $\mu$ found with this approach, represents a “sample” of the friction coefficient in a certain direction. Depending on the way the friction constraints are implemented in the optimization (e.g. if the friction cone is approximated with an inscribed polyhedron to have linear constraints [25]) an appropriate scaling should be considered. For instance, in the case we approximate the cone with the inscribed pyramid, the estimated $\mu$ should be scaled by $1/\sqrt{2}$ which is the ratio between the edge of the inscribed pyramid and the diameter of the cone.

4 Slip Recovery

4.1 Dynamics of Slippage

To obtain insights to draft a strategy for slip recovery it is useful to understand the dynamics of slippage.

1D case: Let us consider the simple case of a mass standing on a plane with friction under the effect of a vertical force (Fig. 3(top)). We can model the contact as a set of tiny bristles [13]. If an external force is applied to the mass which has a tangential component $F_{{ext}_t}$ the “bristles” at the contact interface start to deform (b) and the friction force with the plane $F_f$ builds up until the breaking point $\vert \tilde{F}_f \vert = \mu \vert F_{{ext}_n}\vert$ is achieved, where the bristles start to slide over each other. From then onward they will apply a constant resistance force $\tilde{F}_f$ which is opposing the motion direction (c). The subsequent motion will depend on the mass dynamics ($mdv^{}/dt =F_{{ext}_t}-\tilde{F}_f$) and any tangential component of $F_{ext}$ will increase the kinetic energy of the body, increasing the slippage. If $F_{{ext}_t}$ is removed (d), the accumulated momentum will keep the mass in motion but $\tilde{F}_f$ will decelerate it until $v=0$.

3D case: Consider now the case of a point foot on a frictional plane (Fig. 3(bottom)). In the situation (a), the ground reaction force ${\mathbf {F}}$ is able to balance the external force ${\mathbf {F}}_{ext}$ and the body is in equilibrium (${\mathbf {v}}=0$). If an external load is applied which would require a force which is out of the friction cone to be balanced (b), the ground will be able to balance only with a ${\mathbf {F}}$ which is constrained to lie on the boundary of the cone (satisfying the relationship $\Vert {\tilde{{\mathbf {F}}}}_t \Vert = \mu \Vert {\mathbf {F}}_n \Vert$). The foot will then start moving because there is a net force (black) accelerating it.

Now, as long as $v\ne 0$, ${\mathbf {F}}$ will stay on the cone boundary and be opposing the motion. However, if the external force is applied inside the friction cone (c), by the composition of vectors, the net force will have a decelerating component that will slow down the slipping motion until $v=0$ and the grip will be recovered (d). In this situation ${\mathbf {F}}_{ext}$ will balance again ${\mathbf {F}}$ and the contact will be stable.

Fig. 3

Slip dynamics: (top) 1D case (bottom) 3D case

4.2 Smooth Correction of Friction Parameters

When slippage occurs some action should be undertaken. The detection phase, illustrated in Sect. 2, has provided the estimated values of ${\mathbf {n}}$ and $\mu$. The goal of our short term slip recovery strategy is to make the actual surface inclination $\hat{{\mathbf {n}}}$ (e.g. coming from a terrain estimation algorithm) and the friction coefficient $\hat{\mu }$, which are used in the optimization, converge to the estimated ones. Once that $\hat{{\mathbf {n}}}$ is set to the appropriate direction (inside the cone), the slippage will naturally end-up after a short transient, because the tangential component of the GRF (see Sect. 4.1) will “make work” against the slipping motion and eventually stop it. To prevent step-wise torque discontinuities, we choose to perform the correction in a smooth fashion. The following recursive equations result in a smooth ($1^{st}$ order) convergence of $\hat{{\mathbf {n}}}$ toward ${\mathbf {n}}$ and of $\hat{\mu }$ toward $\mu$:

$$\begin{aligned}&\varDelta \theta (k) = atan\left( \Vert {\hat{{\mathbf {n}}}}\times {\mathbf {n}} \Vert / ({\hat{{\mathbf {n}}}} \cdot {\mathbf {n}}\right) ) \\ \nonumber&{\varvec{\omega _{\theta }}}(k) = {\hat{{\mathbf {e}}}}(k) K_n \varDelta \theta (k) \\ \nonumber&{\hat{{\mathbf {n}}}}(k+1) = {\mathbf {R}}( {\varvec{\omega _{\theta }}}(k) dt) {\hat{{\mathbf {n}}}}(k) \\ \nonumber&\hat{\mu }(k+1) = K_{\mu }\mu + (1- K_{\mu }) \hat{\mu } \end{aligned}$$

(4)

where $\varDelta \theta$ $\in \mathbb {R}$ is the angular error between $\hat{{\mathbf {n}}}$ and ${\mathbf {n}}$ at time k (see Fig. 2 (right)). ${\hat{{\mathbf {e}}}}$ $\in \mathbb {R}^3$ is the instantaneous rotation axis perpendicular to both ${\hat{{\mathbf {n}}}}$ and ${\mathbf {n}}$, and ${\mathbf {R}}(.) \in \mathbb {R}^{3\times 3}$ is the rotation matrix associated to the rotation vector ${\varvec{\omega _{\theta }}}dt$, which is obtained by the Rodrigues’ formula. $K_n$ and $K_w$ are scalar gains to set the convergence rates of ${\hat{{\mathbf {n}}}}$ and $\hat{\mu }$, respectively. dt is the control loop duration.

Comment: It is well known that for a legged robot static/dynamic stability is dependent on the relationship between the CoM/ZMP and the support polygon [27]. In the case the feet are standing on non-coplanar surfaces more elaborated computations should be carried out [4, 5]. In our work we assume that a stabilizing controller is available for the robot. The main goal of our approach is to eliminate slippage in a very short time interval (tens of ms) such that the support polygon does not suffer significant changes and hence the robot stability is not affected. An analysis of the maximum amount of slippage which is tolerable in the context of locomotion in order to preserve stability is out of the scope of this paper and will be part of future works.

4.3 Freezing Mode

If, during the slip recovery, the ground frictional force is not sufficient to reduce the slip velocity in a reasonable time (tens of ms) the slipping foot accumulates a significant position error (with respect to the desired set-point). This can likely result in significant degradation of the support polygon shape and possible loss of stability. In this case, the last resort is to stiffen all the joints in the actual configuration and make the robot behave like a “wooden chair” (freezing mode in Fig. 1). In such a way, a stable situation can be achieved even if all legs are slipping at the same time. Such a strategy is often successfully adopted by humans when slipping on ice.

5 Simulation Results

In this section we show the effectiveness of the proposed slip detecion/estimation/ recovery strategies simulating a walking of the dynamic model of the quadruped HyQ [24] on very slippery surfaces. Namely, an ice slab with locally different frictional properties and a ramp. HyQ is 1 m long and weights 80 kg. Our simulation environment is composed of two software packages. The first, called SL [23], is a multi-process application that provides a low level joint controller, a customizable trajectory generator, and a simulator. The robot-specific software, namely the kinematics and dynamics engine, is implemented with RobCoGen which provides an optimized C++ implementation of kinematics and dynamics [11] based on spatial-vectors algebra and state-of-the-art numerical algorithms [7]. As far as contact forces are concerned, the SL simulator implements a simple spring damper contact model, together with a Coulomb model for friction. The simulation is based purely on rigid body dynamics, and as such it assumes ideal force sources at the actuated joints. To be consistent with a real implementation on the real robot, we estimate the ground reaction forces at the feet from torque measurements (HyQ is not currently equipped with foot sensors). Both the loop for the optimization and the rigid body simulation run at 1 kHz, which is the frequency of the low level controller in the real platform. The state (position/orientation) of the robot base is estimated through leg odometry. The terrain inclination (roll and pitch) is computed by fitting a plane through the stance feet in a least-square fashion. The evaluation is carried out after each touch-down event and this provides an initial estimate of the surface normal ${\hat{{\mathbf {n}}}}_0$ (see Fig. 1).

Fig. 4

Simulation screen-shots of the robot walking on ice patches (left) and on a ramp (right). In the left plot, olive green lines represent the cone boundaries while the ground reaction forces are depicted in light green. In the right plot $\hat{n}$ is converging toward n while the LF foot is slipping after the touch-down

5.1 Ice Patches

Figure 4(left) shows a simulation of the robot walking on a slippery set of patches located on flat ground. The patches have friction coefficients ($\mu = 0.15-0.3$) comparable to the one of an ice-shoe contact [16]. Refer to [19], for different pairs of materials. The robot has point feet and, thus, the friction forces are lower compared a robot which has flat feet. Indeed foot-ground contact in humanoids is usually modeled with 4 contact points located at the foot edges and slippage occurs when all of them break the contact. For a point foot morphology, walking on ice is challenging and slip recovery becomes crucial for the success of the task.

With the ice patches simulation we want to show the robustness of our algorithm in estimating the friction coefficients of the different surfaces for all the 4 feets. The blue/green patches have $\mu = 0.25, 0.2$ while the white/red $\mu = 0.3, 0.15$. They are all 75 cm long. Our online video² shows that, without any slip recovery strategy, the robot falls at the very beginning after a few steps. Conversely, with the slip recovery enabled, is able to traverse effectively all the patches, including the last ones which have lower friction coefficients. In Fig. 5 we show the plots of the friction coefficient estimates for the 4 legs starting from $\mu =0.6$ which is the default value set at the beginning of the simulation, in the controller. LF, RF, LH and RH stand for Left-Front, Right-Front, Left-Hind and Right-Hind leg, respectively. For the estimate we used a moving average window of 4 samples. The percent error in the estimation is always below 13%.

Fig. 5

Friction coefficients estimation for the 4 legs in the ice patches simulation. Upper plot solid lines are the estimated $\mu$, dashed lines are the ground truth. Lower plot are the percent estimation errors

The slip recovery is beneficial also to avoid the accumulation of big estimation errors in the leg odometry. From the same simulation data, the upper plot of Fig. 6, shows that slippage created an estimation errors in the X direction (before falling) of 18 cm out of 50 cm walked, while using the slip recovery (lower plot) the maximum error is below 1 cm for the same time window.

Fig. 6

Plot of the Cartesian components of the odometry error, without (upper plot) and with (lower plot) slip recovery. The black line is the covered distance (right ordinate)

Observation: In the enclosed video, a little slip is always present at the touch-down, that in principle should not occur, because the friction coefficient has been properly identified after stepping on the surface. This is due to the actual implementation of the stance detection. When the swing foot touches the ground it must apply a force beyond a certain threshold, to trigger the stance and to start optimizing the force. This little force (before the trigger) is not optimized and it causes a little slippage, which however is immediately recovered.

5.2 Slippery Ramp

A transition from walking on flat terrain to a ramp (inclination 0.25 rad) is a good template to demonstrate the effectiveness of the algorithm in estimating the surface normal. Indeed, in the moment in which the robot is standing with only the front feet on the ramp, there is a big error (see Fig. 4 (right)) on the terrain inclination estimate. This results in a wrong estimation of the surface normal ${\hat{{\mathbf {n}}}}$ which is set perpendicular to the estimated plane. If the surface is slippery enough (we set $\mu = 0.5$) the front legs will slip and the slip recovery intervention is necessary to climb the ramp. In Fig. 7 we magnify one slip event for the LF leg after the swing phase. The slip is detected at time $t=28$ ms, the estimation phase is shaded in red, while the correction phase is in blue. The slip transient ends at $t=80$ ms. In the upper plots, we show the convergence of ${\hat{{\mathbf {n}}}}$ to the estimated value ${\mathbf {n}}$ while ${\mathbf {n}}_{gt}$ is the ground truth. The lower plot shows that the friction cone constraint is violated (in a strict sense) for the whole slippage situation (time interval $t=$ 28–80 ms). We underline that the torques of the stance legs (e.g. cf. the knee of RH in Fig. 7(bottom)), do not suffer from step-wise discontinuity, because of the smooth correction implemented for $\hat{n}$ and $\hat{\mu }$.

Fig. 7

Slip event for the LF foot at the touch-down (ramp simulation). (First 3 upper plots) Cartesian components of the surface normal where: ${\hat{{\mathbf {n}}}}$ is the actual value, ${\mathbf {n}}$ is the estimated value and ${\mathbf {n}}_{gt}$ is the ground truth (from simulation). Lower plot the blue line depicts the friction cone violation (in a [0–1] range) while the red line is the torque in the knee joint of the RH leg (stance). The estimation phase is shaded in red, while the correction phase is in blue

Differently from Fig. 7 which shows the LF foot slipping after a swing phase, Fig. 8 shows a slip occurring during the body motion where the LF leg is in stance. The upper plot shows the velocities (norm) v of the feet while the lower one plots boolean variables that tell which leg is slipping. Around $t=170$ ms the LF foot starts to slip and this is visible looking at its velocity which significantly differs from the ones of the other feet. The picture also shows that from the point of detection, thanks to the recovery action the slip terminates (the norm of the velocity goes back to the values of the other feet velocities) in less than 40 ms.

Fig. 8

Slip event for the LF leg during the body motion. Upper plot of the velocity (norm) v of the feet. Lower boolean flags which monitor which leg is slipping

6 Conclusions and Future Works

We presented a methodology to detect slippage and estimate the relevant friction parameters together with a short term strategy to recover from slippage during locomotion. The detection is based on kinematic measurement (plus the trunk angular velocity) and, in the context of legged robots, is more suitable than a force-based approach which involves the use of 6 axis force/torque sensors at the foot-tips. Having an idea of the friction properties of the terrain during locomotion can be also useful to set different level of “cautiousness”, selecting more or less conservative gaits according to the situation at hand. On the other hand, the recovery strategy (which was able to reduce slippage in less than 40 ms), was implemented at the force level. The idea behind the strategy was to correct the surface normal toward the estimated one resulting in GRFs which were back inside the real friction cone. The slip recovery strategy has been demonstrated to be essential for locomotion on very slippery surfaces, or in situations (ramp) where the terrain inclination was wrongly estimated.

In future works we plan to speed-up the recovery action by setting (in the optimization) constraints on the tangential component on the GRF in order to “help” the frictional force in decelerating the slipping foot. We are aware that with the actual implementation, the estimated friction coefficient can only decrease. Indeed, if the robot enters in a less slippery terrain after coming from a slippery one, it will keep the previous friction coefficient which will be too conservative.

In the future, we are planning to fuse the actual approach with semantic information coming from vision. according to the terrain the robot is traversing the purpose of vision is to provide a default value for the friction coefficient together with an estimate of its “difficulty”.

Finally, we plan to perform extensive experimental validation of the proposed approach on the real robot platform (HyQ). In particular we are planning to make it walk on slippery slopes and Teflon patches.