Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

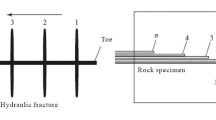
Fracture advancement in saturated porous media is generally a discontinuous process both for fluid pressure induced fracture and for fracture induced by mechanical action. This is certainly true for mode I fracturing and for many situations in mixed mode fracturing. This has been observed in the field for geophysics, in hydraulic fracturing operations, and laboratory tests. As far as field observations from geophysics are concerned, see [4, 5, 11, 12, 16, 18, 47,48,−50, 53, 62, 65]. This list contains both cases of fluid pressure induced fracture and fracture due to changes of mechanical boundary conditions. Intermittent fracture advancement is the most plausible mechanism to explain the existence of volcanic and subduction tremor. Field observations in case of non-conventional hydrocarbon extraction through hydraulic fracturing are reported by Okland et al. [51], Soliman et al. [68], and de Pater [19]. Laboratory tests evidencing the stepwise advancement have been carried out for hydraulic fracturing by Black et al. [6], Lhomme et al. [39] and Lhomme [38]. See for instance Fig. 1 from Lhomme et al. [39]. There are also tests which do not evidence the phenomenon, apart from the tests with a high viscosity fluid and low flow rate of [39], not deemed representative for hydraulic fracturing in the field. There are different reasons for this: sometimes test design criteria are introduced in order to obtain results that are directly comparable with the modeling [10, 35]; in other experiments the rate of fluid flow into the fracture is not constant and therefore cannot be described in terms of a single value of imposed flux [9] or time does not appear explicitly in the solution, which takes the form of a classical traveling wave-type solution and the sampling time is sometimes too large if compared to the experiment referred to [33]. On the other hand, some irregularity of the phenomenon can be seen also in these experiments, even though when modeling this is ignored.

Fig. 1
figure 1

Experimental pressure record and fracture inlet opening for low viscosity/high flow rate configuration. Redrawn with permission from Lhomme et al. [39]

Full size image

For the case of mechanical load [54] clearly showed the stepwise behavior. Despite of the overwhelming evidence only very few numerical models and no analytical model capture the phenomenon as will be shown in the extensive literature survey of the next section.

We have investigated recently the fracturing behavior of geomaterials with both deterministic methods (Cao et al. [13]) and methods from statistical physics [43] and have found that already in dry geomaterials under mechanical loading the fracturing process is time discontinuous. In a two-phase fracture context and under mechanical loading, not only the fluid follows the fate of the solid phase and gives rise to pressure peaks at the fracturing event, but it also influences this event to a certain extent. These pressure peaks are shown in Fig. 2. In case of pressure induced fracture, pressure peaks appear too but are of opposite sign: we observe pressure drops at the fracturing event, see Fig. 3.

Fig. 2
figure 2

Pressure rise at fracturing in case of a mechanical load. Redrawn with permission from Milanese et al. [43]

Full size image
Fig. 3
figure 3

Pressure drops at fracturing in case of pressure driven fracture. Redrawn with permission from Milanese et al. [43]

Full size image

The following explanation has been given for this behavior, based on Biot’s theory [43]: if a load, pressure, or displacement boundary condition is applied suddenly (all acting on the equilibrium of the solid–liquid mixture), then the fluid takes initially almost all the induced solicitation because its immediate response is undrained and it is much less compressible than the solid skeleton. It discharges hence the solid. Then through the coupling with the fluid through the volumetric strain, the overpressures dissipate and the solid is reloaded. Hence, we have a pressure rise upon rupture. Pressures and stresses evolve out of phase. On the contrary if flow is specified (acting on the continuity of the fluid) its effect is transmitted to the solid through the pressure coupling term in the effective stress. The solid is loaded and upon rupture produces a sudden increase of the volumetric strain. This in turn produces a drop in pressure. In this case stresses and pressures evolve in phase. In both cases the intervals between two crack tip advancements are found to be irregularly distributed. This is true even for homogeneous media.

In mode II fracturing the behavior is brittle while in mixed mode there appears a combination of pressure rises and drops [45]. After an extensive literature survey addressing both analytical and numerical solutions the behavior under mode I fracture will be evidenced first for heterogeneous media using a lattice model and statistical analysis and then for homogeneous media by examples obtained with a lattice model, XFEM, and a model based on Standard Galerkin Finite Elements in conjunction with remeshing and cohesive fracture. Some conclusions will then be drawn.

2 Detailed Literature Review

2.1 Analytical Solutions

Contributions to the mathematical modeling of fluid-driven fractures have been made continuously since the 1960s, beginning with [17, 20, 29, 30, 52, 59]. Other papers deal with solid and fluid behavior near the crack tip (e.g. [2, 24]).

Traditional analytical solutions of hydraulic fracture problems rely on typical simplifying assumptions of asymptotic analyses that influence the real local pattern of time dependent parameters such as the tip velocity and pressure distribution near the tip. The most common ones concern fluid flow, fracture shape and velocity, leakage from the fracture, the presence of fluid lag and linear fracture mechanics for the solid. Further, uncoupled solutions are frequent, e.g. the solid/fluid interactions are analyzed in two-step procedures in which only one field evolves in time. In more recent papers, (e.g. [1, 34]) a mixed approach is presented in which an asymptotic formulation is partially solved with numerical tools to reduce the above-mentioned simplifying assumptions, especially using finite differences in time.

Problems may arise with the assumption of linear fracture mechanics in a coupled environment. In fact, this implies a stress singularity in the tip region, hence a singularity in pressure, because of the effective stress principle. The fluid pressure consistent with the crack aperture asymptote of LEFM is weaker than x(−1/2) and reflects the finiteness of rate of energy dissipated by crack propagation. Consideration from lubrication theory, combined with LEFM results, implies that the fluid pressure has a logarithmic singularity. Any fluid pressure singularity is, however, precluded if the rock is permeable and diffusion of pore fluid is taking place. Indeed, a fluid pressure singularity would cause an infinite rate of energy dissipation by diffusion of fluid in the porous rock [22]. Further, LEFM is not the best model to investigate hydraulic fracturing. De Pater [19] states in fact that “carefully scaled laboratory studies have revealed that conventional models for fracture propagation which are based on LEFM cannot adequately describe propagation. Instead, propagation should at least be based on tensile failure over a cohesive zone”.

However, these analytical approaches certainly delineate the limits of the propagation regimes [25] and other important features such as the length scales. In fact, hydraulic fracturing represents a special class of cracking, due to the coupling between different processes (solid deformation, rock fracturing, fluid flow in the fracture, leak-off) taking place near the tip. As already mentioned each of these processes can be associated with a characteristic length-scale [21, 25]. Predominance amongst these length-scales determines the fracture response (the propagation regime), characterized by the order of the stress (or pressure) singularity. This yields a complex multi-scale solution for the propagation of the fracture. Even though these solutions are obtained at the scale of the near-tip region, the propagation regime of the whole fracture is determined by the tip [1]. Further, these authors remark that there is always a region immediately adjacent to the fluid front where the solution is dominated by fluid loss and most of the pressure drop occurs near the fracture tip, hence special care needs to be taken to obtain accurate results in this area.

For simple fracture geometries (radial, KGD, and PKN), the time scales can be expressed explicitly in terms of the problem parameters (fluid viscosity, rock properties, and injection rates). Recognition of the existence of multiple time scales led to the identification of particular solutions that correspond to a regime of fracture propagation dominated by one process only. For example, under conditions where the in situ stress is large enough (as is usually the case for deep stimulation treatments), two time scales characterize the evolution of a radial fracture: the first tracks the transition between a regime of propagation where most of the energy essentially is dissipated in viscous flow of the fracturing fluid, and another regime where most of the energy is used to fracture the rock; and a second time scale that characterizes the evolution from situations where the injected fluid essentially is stored in the fracture to situations where most of the fluid has leaked into the rock. Analytical solutions are always smooth hence they do not reproduce the stepwise behavior of the tip advancement previously discussed and experimentally recorded. Further they do not represent an evolutionary problem in a domain with a real complexity, continuously changing with the evolution of the phenomenon and do not account for a material behavior more realistic than linear. Only numerical methods give the continuous alternation of the different regimes, depending on forcing functions, boundary conditions and intrinsic time scales. This fact stresses also the need of a careful time discretization of the governing equations combined with a careful choice of the crack advancement algorithm.

2.2 Numerical Simulations

From the preceding remarks, it follows clearly that a numerical solution, including coupling of fracture propagation and fluid exchange between the fracture and the formation, is the most appropriate way to simulate fracturing in fluid saturated media. We analyze briefly whether the solutions found in literature were able to evidence and model the stepwise crack advancement and pressure fluctuations experimentally observed. Given that this behavior can be properly explained by means of the generalized Biot’s theory, numerical models base on fluid–solid interaction of the Biot’s type should be capable of simulating the steps and pressure jumps provided that a proper crack advancement/time stepping algorithm is used. If this is not the case the respective models perturb the interactions.

The first numerical model for hydraulic fracture has been presented by Boone and Ingraffea [7]. It uses a Biot’s approach coupled with linear fracture mechanics, accounts for fluid leakage in the medium surrounding the fracture and assumes a moving crack depending on the applied loads and material properties. A finite element solution for solid and finite differences for flow equation is adopted. It is assumed however that the path of the fracture is known a priori and contact elements are placed along this path. Crack length, mouth opening displacement together with mouth and fracture pressure versus time show a regular pattern.

Carter et al. [15] extended the application to a fully 3-D hydraulic fracture frame. Their model relies on hypotheses similar to [7], in particular assuming the positions where fractures initiate, but neglects the fluid continuity equation in the medium surrounding the fracture. The quasi-static solution consists of a series of snapshots in time, where the fracture geometry is fixed and the corresponding time is determined. In both cases, no care is devoted to the tip region velocity and to its regular/irregular distribution in time.

Starting from these pioneering works different numerical approaches have been presented, which are discussed next. Biot’s theory in conjunction with a discrete fracture approach making use of remeshing in an unstructured mesh and automatic mesh refinement has been used by Schrefler et al. [60, 61], in a 2D setting. An element threshold number (i.e. number of elements over the cohesive zone) was identified to obtain mesh-independent results. This approach has been extended to 3D situations by Secchi and Schrefler [63]. The last two cited papers show clearly the stepwise fracture advancement and oscillations of the crack mouth pressure. The advancement steps are irregularly distributed in time which is conjectured to be a signature that the steps are of physical nature and not numerical artifacts.

Réthoré et al. [57] proposed a two-scale model for fluid flow in a deforming, unsaturated and progressively fracturing porous medium within the realm of Biot’s theory. At the microscale, the flow in the cohesive crack is modeled using Darcy’s relation for fluid flow in a porous medium, considering changes in the permeability due to the progressive damage evolution inside the cohesive zone. By exploiting the partition-of-unity property of the finite element shape functions, the position and direction of the fractures are independent from the underlying discretization. A pre-notched plate is solved but the authors do not show crack advancement nor mention any fluctuations whatsoever. In our opinion two scales procedures interfere with the interacting velocities and hence affect adversely the solution.

Extended Finite Elements (XFEM) have been applied to hydraulic fracturing in a partially saturated porous medium by Réthoré et al. [58] in a 2D setting. In this case, again a two scale-model has been developed for the fluid flow. As example, rupture of a saturated square plate in plane strain conditions is investigated under a prescribed fixed vertical velocity in opposite direction at the top and bottom of the plate (tensile loading). No stepwise advancement nor pressure fluctuations are evidenced, probably because the two-step solution influences the velocity fields.

Partition of unity finite elements (PUFEM) are used for 2D mode I crack propagation in saturated ionized porous media by Kraaijeveld and Huyghe [31] and Kraaijeveld et al. [32]. A pull test, a delamination test and an osmolarity test are simulated with rather fine regular meshes. Stepwise advancement and flow jumps were found by Kraaijeveld and Huyghe [31] with a strong and a weak discontinuity model for flow while in [30] the stepwise advancement in mode I crack propagation is difficult to see because a continuous pressure profile across the crack is used which only works for sufficiently fine meshes. In that case, the advantage of PUFEM, which allows keeping the mesh pretty rough all over the continuum, would be lost. In mode II as shown in Kraaijeveld et al. [32] a discontinuous pressure across the crack is accounted for. It is not attempted to resolve the steep pressure gradient but this gradient is reconstructed afterwards, using the Terzaghi analytical solution for pressure diffusion. This two-step procedure allows for using a rough mesh, and still handling a realistic pressure gradient. However, the resulting steps show a regular pattern and are thought to be of numerical origin, see Remij et al. [56].

Carier and Granet [14] developed a zero-thickness finite element to model hydraulic fracture in a permeable medium within the framework of Biot’s theory. The fracture propagation is governed by a cohesive zone model and the flow within the fracture by the lubrication equation. The solutions are smooth. Mohammadnejad and Kohei [47] show a fully coupled numerical model for hydraulic fracture propagation in porous media using the extended finite element method in conjunction with the cohesive crack model. The governing equations are derived within the framework of the generalized Biot’s theory. The fluid flow within the fracture is modeled using Darcy’s law, in which the fracture permeability follows the cubic law. Among the two examples the one related to hydraulic fracturing shows very small regular steps in the fracture advancement which according to the authors are of numerical origin and are bound to disappear with more refined meshes. The pressures are smooth.

Mohammadnejad and Kohei [46] solve the same problem as in Réthoré et al. [58], also with XFEM, using full two-phase flow throughout the region. Cavitation is found in both papers, also due to the impervious boundary conditions chosen. Here all solutions are smooth.

A two scale model is used Remij et al. [55] where the pressure approximation in the fracture is enhanced by including an additional degree of freedom. The pressure gradient due to fluid leakage near the fracture surface is reconstructed based on Terzaghi’s consolidation solution. This is supposed to ensure that all fluid flow goes exclusively in the fracture and it is not necessary to use a dense mesh near the fracture to capture the pressure gradient. The spatial discretization of the balance equations is based on the partition-of-unity property of finite element shape functions. The two-step procedure, the large time step size and coarse mesh influence the resulting fluid velocities and neither fluctuation nor stepwise advancement is reported. Use of the same method but with very small elements however clearly evidences the stepwise advancement and the pressure oscillations, see Milanese et al. [44].

Phase field models for propagating fluid-filled fractures coupled to a surrounding porous medium were applied in [28, 36, 40−42, 69, 71]. The published numerical results are smooth, in line with what expected from a diffuse representation of the fracture. Only Heider and Markert [28] report some pressure oscillation.

Grassl et al. [27] use a lattice approach but fail to evidence the intermittent behavior while the lattice model of [43], discussed below, clearly evidences the phenomenon.

Numerical models not relying on Biot’s theory have also been published. These usually start from the same hypotheses as the analytical approaches. For instance, Lecampion and Detournay [34] presented an implicit moving mesh algorithm for the study of the propagation of plane-strain hydraulic fracture, with the fluid front distinct from the fracture tip. In our opinion, beyond the usual restrictions of the analytic approaches, further limits of this method are evident: the problem is assumed as 1D channel (integration is performed along the linear fracture) based on a relationship between fracture opening and internal pressure valid in a very unrealistic infinite elastic medium. In addition, an impermeable surrounding medium is assumed, which hides important phenomena such as the leaching from the fracture and certainly results in a smooth solution.

From this survey, it appears that while a large majority of authors uses Biot’s theory, only the Standard Galerkin Finite Element Method (SGFEM) with or without a continuous updating of the mesh [60, 61, 23], XFEM with very small elements [13, 44] and the lattice model of [43] have captured the physics of fracturing in saturated porous media.

3 Governing Equations

According to Biot’s theory of porous media the mathematical model here used is composed of an equilibrium of the overall mixture and a mass balance equation for the fluid (Lewis and Schrefler [36]). We just indicate the governing equations for sake of completeness. Considering the symbols of Fig. 4, the linear momentum balance of the mixture, discretized in space, is written as

Fig. 4
figure 4

Definition of cohesive crack geometry and hydraulic fracture domain. Redrawn with permission from Schrefler et al. [61]

Full size image
$${\mathbf{M}}{\mathbf{v}} + \int\limits_{\Omega } {{\mathbf{B}}^{{\mathbf{T}}} } {\varvec{\upsigma}}^{{\prime \prime }} d\Omega - {\mathbf{Qp}} - {\mathbf{f}}^{(1)} - \int\limits_{{\Gamma ^{{\prime }} }} {({\mathbf{N}}^{u} )^{{\mathbf{T}}} } {\mathbf{c}}d\Gamma ^{{\prime }} = 0$$
(1)
$${\mathbf{f}}^{\left( 1 \right)} = \int\limits_{\Omega } {\left( {{\mathbf{N}}^{u} } \right)}^{{\mathbf{T}}} \rho {\mathbf{b}}d\Omega + \int\limits_{{\Gamma _{t} }} {\left( {{\mathbf{N}}^{u} } \right)}^{{\mathbf{T}}} \overline{{\text{t}^{g} }} d\Gamma$$
(2)

where \(\Gamma ^{{\prime }}\) is the boundary of the fracture and process zone and c the cohesive traction acting in the process zone as defined e.g. in Simoni and Schrefler [67]. The cohesive traction c is different from zero only if the element has a side on the lips of the fracture \(\Gamma ^{{\prime }}\) within the process zone. The submatrices of this and the following equations are the usual ones of soil consolidation [37], except for those specified in the sequel.

The fully saturated porous medium surrounding the fracture has constant absolute permeability and the discretized mass balance equation reads as

$${\mathbf{Qu}} + {\mathbf{Hp}} + {\mathbf{Sp}} - {\mathbf{f}}^{(2)} + \int\limits_{{\Gamma^{{\prime }} }} {({\mathbf{N}}^{p} )^{{\mathbf{T}}} \overline{q}^{w} } d\Gamma^{{\prime }} = 0$$
(3)

where \(\overline{q}^{w}\) represents the water leakage flux along the fracture toward the surrounding medium; this term is defined along the entire fracture, i.e. the open part and the process zone. f (2) contains the assigned flow terms. Given that the liquid phase is continuous over the whole domain, leakage flux along the opened fracture lips is accounted for through the H matrix. In the present formulation, non-linear terms arise through cohesive forces in the process zone. Discretization in time is then performed with time Discontinuous Galerkin approximation following Simoni et al. [66].

We present here briefly the numerical methods used in the applications for multi-phase crack propagation.

4 Numerical Methods

4.1 Lattice Model for Homogeneous and Heterogeneous Porous Media

Statistical models are used to consider material disorder without the need of using averaged values of material properties, nor phenomenological models, such as cohesive ones, nor of locating geometrical singularities to trigger cracks. In Milanese et al. [43] a lattice model is used to analyse fracture propagation in a multiphase system. The interested reader is referred to this paper for major details.

To account for material disorder, the mechanical properties of each element of the lattice are picked randomly from a statistical distribution. Because of this assumption, the exact crack path cannot be predicted and several cracks may appear at the same time within the domain. The solution of the crack problem requires several simulations run with the same boundary conditions but randomly varying material properties: a statistical analysis is then carried on the gathered data. This analysis focuses on the so-called “avalanche behaviour” of the specimen, i.e. the number of failing elements per step. It is known that in dry samples the probability distribution function of the recorded avalanches size displays power-law behaviour (see e.g. [71]). We will investigate whether adding a fluid phase changes this behaviour.

In a 2D context, the studied continuous solid domain is replaced by a lattice squared specimen with vertical, horizontal and diagonal bonds while the coupling matrix and the flow matrices are obtained by the finite element method (Fig. 5) as explained below. Random assumption of the properties of the bonds results in an isotropic macroscopic material behaviour. A central force model is locally adopted: the elements have only the axial degree of stress and strain, i.e. behave as truss elements. Linear measure of strain and constitutive equation are used.

Fig. 5
figure 5

Representation of the overlapping three-layer unitary element of the model. From the bottom to the top: the fluid pressure 4-node plane element (blue), the coupling 9-node plane element (orange) and the solid skeleton made of 20 trusses (green)

Full size image

Each bar of the lattice is provided with a stress threshold at which the bond fails. The vector of the stress thresholds of the overall bars is defined by a uniform distribution in the interval [0,1] MPa. In this way, the disorder of the medium is represented. Each time the stress in a bond exceeds its threshold, this is updated from a new uniform distribution in the same interval.

Moreover, at the beginning of the simulation the Young’s modulus is set to the same value for all the bars. During the simulation, when the stress in an element exceeds the local threshold, its elastic modulus is reduced, as E new  = (1 − D)E old : where D = 0 means no damage and D = 1 means that the truss is completely broken and does not contribute anymore to the global stiffness. D is set equal to 0.1 and each truss can be damaged up to thirty times before the final failure, thus conveying an asymptotically decreasing damage rule. The model displays a clear and broad plastic phase.

Referring to the mechanical problem of Sect. 5.2.1 and to a generic load step, a uniform displacement distribution is imposed on boundary nodes. The governing equations are iteratively solved, updating the properties (elastic modulus and stress threshold) of any damaged truss, to reach an equilibrium state in which no stress threshold is exceeded in any bond. Then the successive load step is applied.

The avalanche size s is defined as the number of trusses damaged between two subsequent displacement increments.

In a two-phase plane problem, the solid field, the fluid and the coupling terms are overlapping and must be approximated: a 20-bar system, which mimics a 9-node continuous element, is assumed for the solid, a continuous 2D 4-node element is used for the fluid (matrices H and S in Eq. 3) and 9-node element for the coupling terms Q in Eqs. 2 and 3 (Fig. 5). This results in a unitary element that builds up the lattice and can be viewed as a three-layer element with size L u  = 2. In this way, the Babuska-Brezzi condition is satisfied [3, 8].

According to the statistical approach, two time scales are used: one for the increments of the external loading Δt and another for the fracturing process within Biot’s theory. The external loading is increased once the rearrangements are over, while a time interval for Biot’s theory is fixed (in the application the value of 3000 s is assumed). The size of this interval allows to study the interaction between the two phases. If a much smaller value is chosen, no consolidation type behavior is allowed between subsequent loading steps and damage localizes on the elements close to the border; if a much larger time increment value is chosen, consolidation type behaviour runs out before the load is increased in the following step and no interaction with the fluid phase appears. At any step n two scenarios can take place:

  1. (a)

    t = tn: specified displacements are increased, Biot’s coupled problem is solved and equilibrium is reached without any rearrangement (avalanche). Thus, time at step n + 1 equals to \(\text{t}_{{\text{n} + 1}} = \text{t}_{\text{n}} + {\Delta}\text{t}\);

  2. (b)

    t = tn: specified displacements are increased, Biot’s coupled problem is solved and equilibrium is not reached without rearrangements and m more sub-steps where Biot’s coupled problem is solved are needed. Once the equilibrium is reached, the time for the external loading is updated. Thus, time at step n + 1 equals to \(\text{t}_{{\text{n} + 1}} = \text{t}_{\text{n}} + \text{m}*\Delta{\text{t}}\).

4.2 SGFEM with Remeshing

In this approach, governing equations within the domain are supplemented by the fluid mass balance within the crack and a phenomenological equation for the solid behavior, i.e. the cohesive law. Two non-overlapping fluid domains are hence present (Fig. 4) and, because of their continuity, interactions such as leaching due to pressure gradients are easily accounted for. Fluid flow equation within the crack takes the following form, which highlights the different contributions and the transport law [65],

$${\mathbf{Hp}} + {\mathbf{Sp}} + {\mathbf{p}}\int\limits_{{\Gamma ^{'} }} {({\mathbf{N}}^{p} )^{{\mathbf{T}}} } \overline{q}^{w} d\Gamma ^{'} = 0$$
(4)

with

$${\mathbf{H}} = \int\limits_{{\overline{\Omega } }} {\left( {{\nabla }{\mathbf{N}}^{p} } \right)}^{{\mathbf{T}}} \frac{{w^{2} }}{{12\mu_{w} }}{\nabla }{\mathbf{N}}^{p} d\overline{\Omega }$$
(5)
$${\mathbf{S}} = \int\limits_{{\overline{\Omega } }} {\left( {{\mathbf{N}}^{p} } \right)^{{\mathbf{T}}} } \frac{1}{{Q^{*} }}{\mathbf{N}}^{p} d\overline{\Omega }$$
(6)

In Eq. 5, w represents the fracture aperture. The last term of Eq. 4 embodies the leakage flux toward the surrounding porous medium across the fracture borders. In this formulation, this coupling term does not require special assumptions, as, e.g. in Remij et al. [55], or oversimplified assumptions that hide important phenomena taking place in the fracture domain, as e.g. in Réthoré et al. [57]. It can be represented by means of Darcy’s law using the permeability of the surrounding medium and pressure gradient generated by the application of water pressure on the fracture lips.

Because of the continuous variation of the domain due to the propagation of the cracks the domain \({\overline{\Omega }}\), its boundary \(\Gamma ^{{\prime }}\) and the related mechanical conditions change. Along the formed crack edges and in the process zone, boundary conditions are the direct result of the field equations while the mechanical parameters must be updated. The fracture path, the position of the process zone and the cohesive forces are unknown and must be regarded as products of the mechanical analysis.

The substantial improvements of SGFEM capabilities in solving hydro-mechanically coupled problems originate from the remeshing procedure. This has been discussed in detail in Schrefler et al. [61], to which the interested reader is referred. It is a common opinion that remeshing is a cumbersome, time consuming and difficult task. This is not true, if efficient mesh generators are available. For instance, to build a triangular unstructured mesh in 2D possessing optimal characteristics (i.e. all elements are almost equilateral triangles) in a very complex domain (Venice Lagoon, 550 km2 with a hundred islands) using our mesh generator [63] 4.55 s are needed producing about 37,000 nodes and 67,500 elements. The advantage of this approach is to dynamically refine the mesh in areas presenting high gradients of the field variables and coarsening in others, to account for time changes of the spatial domain, with boundaries moving and singularity positions propagating in a not predictable way. Further, all equations of the mathematical model are naturally solved, without the necessity of scale length (as for instance the length of the process zone or the dimension of the area interested by the leaching from the fracture). Obviously limits exist for this approach, as in the case of micro-cracks and their coalescence, whereas nucleation and branching of macro-cracks are easily handled.

At each tip movement, the fracture domain is recognized during meshing operations, which accounts also for the process zone and fluid lag, then Eq. 4 is associated as mass balance, whereas the equilibrium equation is weakened by strongly reducing the material Young’s modulus (see [65], for more details).

5 Numerical Applications

5.1 Heterogeneous Media, Lattice Model, Statistical Analysis

First, we show the results of a statistical analysis for heterogeneous dry and saturated media by means of the lattice model. In particular, the power law behavior and avalanche distribution versus time is addressed. With this model the cases of assigned biaxial boundary tractions, assigned pressures and assigned flow have been investigated. A square lattice of side 60 mm (mesoscopic level) is meshed according to L = 16, where L is the number of three layer unitary elements (Fig. 5) aligned on the side direction. It has been shown in Milanese et al. [43] that, in the case of disordered media, lattices meshed with L = 16; 32; 64 elements per side display the same power law behavior i.e. the cut off of the avalanche size probability distribution scales with the system size and the solution is hence scale-free. This observation is confirmed in Girard et al. [26] for a mesh made of triangular elements and in Zapperi et al. [71] for a fuse model; it allows considering a sample with a smaller number of elements.

Figure 6 presents the statistical distribution of the avalanches and power law behavior obtained for a dry material. The addition of fluid to a dry sample does not change the statistical distribution of the avalanches nor the power law behavior, see Figs. 7 and 8. Imposing a pressure increase at the center of the saturated sample, changes the statistical behavior (bigger events are seen), not the power-law, see Fig. 8. Note that an imposed pressure is a boundary condition acting on the first of the Biot equations (equilibrium equation which is elliptic). On the contrary, by imposing fluid flow at the centre (hydraulic fracturing), the power-law does not hold anymore (see Fig. 9) except for very low flux values which are outside practical importance. Note that assigned flow acts on the second of the Biot equation, i.e. on the continuity equation which is parabolic. The results have been obtained by Monte Carlo analyses with per case some 55,000 avalanches collected on about 70 runs.

Fig. 6
figure 6

Dry material square sample under boundary tractions: probability density function P(s) versus avalanche size (left) and damaged bonds number (avalanches) versus time (right)

Full size image
Fig. 7
figure 7

Fully saturated square sample under boundary tractions: probability density function P(s) versus avalanche size (left) and damaged bonds number (avalanches) versus time (right)

Full size image
Fig. 8
figure 8

Fully saturated square sample under boundary tractions and pressure increase assigned at the centre: probability density function P(s) versus avalanche size (left) and damaged bonds number (avalanches) versus time (right)

Full size image
Fig. 9
figure 9

Fully saturated square sample under imposed flow at the centre: probability density function P(s) versus avalanche size (left) and damaged bonds number (avalanches) versus time (right)

Full size image

5.2 Homogeneous Media, Single Runs

Since the case of hydraulic fracturing had been extensively addressed in Milanese et al. [44], we focus here our attention on the case of fracturing under mechanical load and compare the behavior under dry and saturated conditions. For the lattice model the results of only single runs are shown.

5.2.1 Forced Displacement in a Pre-notched Plate

The first test case analyses the fracture of a square plate 0.25 m sided with an edge notch of length 0.05 m lying along its horizontal symmetry axis in plane strain conditions. The test case is the same as in Réthoré et al. [58]. The plate is loaded in tension by two uniform vertical velocities with magnitude 2.35 × 10−2 μm/s applied in opposite directions to the top and bottom edges. The Young’s modulus is E = 25.85 GPa, fracture energy G = 95 N/m and the cohesive strength σc = 2.7 MPa.

As far as the fluid field is concerned, two opposite conditions are assumed:

  • The plate has permeable boundaries i.e. a drained boundary condition is enforced at all faces of the plate. The intrinsic permeability is k = 2.78 × 10−10 m2 and the dynamic viscosity of the fluid (water) μ = 5×10−4 Pa s. In these conditions the fluid does not influence the solid behavior and the problem is referred to as “dry”.

  • The intrinsic permeability is k = 2.78 × 10−21 m2 and the dynamic viscosity of the fluid (water) μ = 5×10−4 Pa s. The permeability assumed is very low, lower than a high strength concrete. Therefore, no significant flow will develop. However, the impervious boundary condition imposes an isochoric constraint on the fluid which influences the process. This situation is referred to as “saturated”.

Comparison will be presented between two solution approaches discussed above, i.e. the lattice model at the mesoscale and the traditional SGFEM with remeshing (Cao et al. [13]). In the first case, a square domain of side 64 mm (mesoscopic level) is analyzed (Fig. 10): the lattice model is meshed according to L = 30, where L is the number of unitary overlapping elements aligned on the side direction. Recall that in case of disordered media lattices meshed with different number of elements per side display the same power law behavior, i.e. the cut off-of the avalanche size probability distribution scales with the system size. The solution is hence scale-free. Note that because of the scale-free behavior of the lattice models, the following results hold also for macroscopic scale. Time step for loading application and overall time domain discretization is 1 s.

Fig. 10
figure 10

Lattice model for the pre-notched plate at the beginning of the analysis: the first bars near the notch tip are breaking

Full size image

In the SGFEM, for comparison purposes, a fixed mesh composed of 0.0025 m square elements is used, hence without accounting for the mesh refinement capabilities. Time step for overall time domain discretization is 0.125 s. The results of Fig. 13 show several advancement steps.

The obtained results suggest some interesting remarks:

  • The two approaches, very different from the theoretical point of view, give rise to consistent results;

  • Breakdown is always sudden (unstable fracture propagation) and occurs first for the dry case;

  • For the “dry” case (Fig. 11), the time at which the fracture is triggered is the same (nearly 560 s) in both solutions, but the complete rupture is faster in the SGFM (575 s vs. 700 s), see Fig. 13;

    Fig. 11
    figure 11

    Pre-notched plate test: lattice model solution for “dry” case (intrinsic permeability 2.78 × 10−10 m2 and drained boundary conditions)

    Full size image

  • Slightly higher differences arise in the “saturated” case (Fig. 12): the lattice method presents a brittle fracture at time 700 s, versus the time 575 s for the SGFM. This is because in the lattice model the external loading is increased once the rearrangements are over, i.e. overpressures completely dissipate, whereas in the SGFM there is only one time scale (the one of the external loading);

    Fig. 12
    figure 12

    Pre-notched plate test: lattice model solution for “saturated” case (intrinsic permeability 2.78 × 10−21 m2 and undrained boundary conditions)

    Full size image

  • The “dry” case shows softening behaviour, starting from the strain value 1×10−4, corresponding to the cohesive strength. Whereas in the “saturated” case the behaviour is brittle, with maximum strain nearly the same as the previous case.

  • The same problem has been solved using XFEM (see Cao et al. [13]) and results are shown in Fig. 14: in all the analysed cases (dry and saturated drained/undrained conditions), intermittent movements of the fracture tip are not obtained, the cohesive zone extends over the whole sample length and the breakdown is sudden as in the “saturated” application of the lattice model (Fig. 12).

    Fig. 13
    figure 13

    Pre-notched plate test: SGFEM solutions for “saturated” undrained case (red line, intrinsic permeability k = 2.78 × 10−21 m2) and “dry” drained case (blue line, intrinsic permeability k = 2.78 × 10−10 m2)

    Full size image
    Fig. 14
    figure 14

    Pre-notched plate test: XFEM solutions for “saturated” drained/undrained case and “dry” material. Redrawn with permission from Cao et al. [13]

    Full size image

5.2.2 Peel Test of a Hydrogel Material

The second application originates from the lab experiment results shown in Pizzocolo et al. [54], where the propagation of a crack in a saturated hydrogel is studied and stepwise fracture propagation is obtained. Hydrogels are incompressible materials, hence require special care in the numerical analysis. The geometrical squared domain used in case Sect. 5.2.1 is now scaled to be representative of the loaded part of the lab test sample and the Young’s modulus of each bar is selected equal to 1.924 MPa corresponding to a global modulus for the model of 0.8 MPa; the threshold of the trusses is 0.076 MPa and once exceeded the trusses are immediately removed from the lattice. Symmetry of the domain is not accounted for in the analysis, to avoid that other fracture modes could be hidden. A constant relative vertical displacement increment is applied to the left top/bottom nodes with a rate of 0.00064 mm/s.

The two limiting sets of hydraulic materials and boundary conditions, as illustrated in the previous case, are here assumed, in order to represent a “dry” and a “saturated” material.

The results are displayed in Figs. 15 and 16. The number of breaking events can be seen from the stress-strain diagram. The avalanche distribution is not regular also for this homogeneous material.

Fig. 15
figure 15

Peel test: lattice model solution for “dry” case (intrinsic permeability is k = 2.78 × 10−10 m2, and drained boundary conditions)

Full size image
Fig. 16
figure 16

Peel test: lattice model solution for “saturated” case (intrinsic permeability k = 2.78 × 10−21 m2 and drained boundary conditions)

Full size image

Some comments can be made to the obtained results:

  • in dry conditions fracture events and breakdown take place prior to those in saturated conditions; stepwise crack advancement is evident, as observed in the laboratory experiment, and, before the collapse, avalanches are of small dimensions and quite regular except for a large event near the beginning;

  • maximum stress values are in accordance in the two different material cases, whereas strains are higher in saturated conditions;

  • the overall behavior is plastic in dry conditions and brittle in the other.

6 Conclusions

We have analyzed fracturing in dry and saturated heterogeneous and homogeneous porous media. For the heterogeneous case a lattice model in conjunction with the Monte Carlo method has been used while for the homogeneous case the lattice model and the standard Galerkin Finite Element method have been adopted. In one case of homogeneous material also a comparison with XFEM has been shown. The results of all methods appear consistent.

From the statistical analysis for heterogeneous porous media by means of the central force (lattice) model the following conclusions can be drawn: under mechanical loading (acting on the equilibrium equations) there is no difference between dry and saturated samples: the same power law is always obtained. In the case of imposed flux (through the flow continuity equation), the picture changes: no more a power law is obtained and statistical distribution of the avalanches is different.

For homogeneous media in the case of mechanical boundary conditions, also for two very different materials, the dry sample breaks earlier. The saturated sample breaks later and the rupture is rather brittle probably due to the isochoric condition exerted by the fluid. This is somewhat similar to what happens in strain localization analysis. For the homogeneous case this conclusion has been obtained with three numerical methods, namely the Standard Galerkin FEM, the central force lattice method and a XFEM method with rather small elements. From the comparisons carried out it appears that the different methods yield qualitatively similar results but the quantitative behavior differs from method to method.