Error Modelling and Sensitivity Analysis of a Planar 3-PRP Parallel Manipulator

Abstract

This paper presents an analytical error prediction model of a 3PRP planar parallel manipulator using the screw theory. This analytical approach is used to find the effect of mechanical inaccuracies contributing to the end-effector pose errors and their sensitivity coefficients. Finally, parameter sensitivity analysis of non-compensable errors of two different configurations based on their fixed base shape namely Δ-shape and U-shape fixed bases are analysed and compared.

1 Introduction

Planar parallel manipulators (PPMs) are having higher attention in the recent years due to their simplicity in design and other potential advantages over serial manipulators [6]. In specific, manipulators having first joint as active prismatic joint in each leg has several advantages than others [5]. In this respect, one of the commercially available manipulators namely Hephaist [3] is a 3PRP U-shape PPM and the manipulator proposed by Damien Chablat et al. is a Δ-shape 3-PRP PPM [1], both of them are promising in terms of their kinematic and dynamic performances. This 3PRP configuration has shown potential advantage in industrial usage but which of these two base configurations is better in terms of accuracy in presence of mechanical inaccuracies are yet to be explored. Accuracy analysis of these configurations due to the actuator inaccuracies using the geometric approach is presented by Yu et al. [8], but in this work, effect of other non-compensable errors and kinematic parameter errors are not included. It is significant to quantify the sources of errors which are contributing the end-effector pose errors in order to find the quality of task performed by the manipulator, which directly affects the positional accuracy of the manipulator. These pose errors can be of three kinds: kinematic errors, encoder errors and the errors due to joint clearances. The kinematic errors are due to the misalignments and the manufacturing imperfections and tolerances. These kinematic errors for manipulators can be estimated and many researches has found methods to quantify and compensate them [3, 4]. Encoder errors can be of two types, the first one is due to least count of the encoders and other one is due to incorrect index of the encoder reading. Index errors can be corrected by zero point confirmation, but least count errors are non-compensable. Similarly, error due to joint clearances and backlashes are also non-compensable in nature.

Therefore, in this paper, a complete error prediction model considering all possible errors i.e., due to mechanical inaccuracies (including the kinematic parameter errors and error due to joint clearances in the rotary and prismatic joints which are non-compensable in nature) based on screw theory [2] is derived and presented. This technique is already been utilized and verified by G. Wu et al. [7] for modelling the error prediction model for 3-PPR configuration. This configuration has a simple model due to its forward kinematics relationship, which is independent of its end-effector orientation. But, in case of 3-PRP configuration, the kinematic relationship is dependent on the end effector orientation. The proposed mathematical error model has incorporated all these changes and used it for the error sensitivity analysis. This errors estimation is done for the xy-plane only, the error z-axis is not derived in this model as manipulator functioning is restricted to xy-plane only. Further, the effects of the non-compensable errors are compared to identify the best configuration among U-shape and Δ-shape fixed base configurations (which one is less susceptible to the non-compensable errors).

2 Kinematic Model of the Manipulator

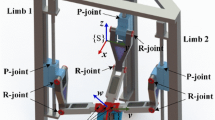
Here in this section, a generalized kinematic solution for the 3PRP configuration is presented. This kinematic model is established on the basis of screw theory. The kinematic arrangement of the 3PRP configuration is presented in Fig. 1. In Fig. 1, the point $T$ is the position of the end-effector and $\varphi$ is its orientation angle, the point $O$ represents the origin of the frame of reference, points $G_{i}$, $P_{i}$, $R_{i}$ and $F_{i}$ represent the beginning limit of the linear actuators, the current position of the linear actuators, the point where the passive prismatic joint starts and the point at which the prismatic link connects to the end effector of the $i^{th}$ link, respectively. The vectors i $_{i}$, j $_{i}$, k $_{i}$, l $_{i}$ and m $_{i}$ are the vectors leading from the fixed reference frame (origin) to the end-effector (moving reference frame). Representation of the each vector for the first kinematic chain (leg) is shown in Fig. 1, and it is similar to the other kinematic chains with corresponding index number. These vectors are characterized by the angles $\alpha_{i}$, $\beta_{i}$, $\gamma_{i}$, $\theta_{i}$, $\varphi$ and $\psi_{i}$, where angles $\alpha_{i}$, $\beta_{i}$, $\gamma_{i}$, $\theta_{i}$ and $\varphi$ are with respect to the origin reference frame while $\psi_{i}$ is with respect to end-effector’s reference frame and $i$ = 1,2,3, which is the index of the kinematic link chain.

Fig. 1.

Generalized kinematic parameter diagram for 3PRP manipulator

From the closed looped kinematic chain $O - G_{i} - P_{i} - R_{i} - F_{i} - T - O$

Forward kinematics equation for the position vector of the end-effector, ${\mathbf{T}}$, is given as:

$$ {\mathbf{T}} = a_{i} {\mathbf{i}}_{i} + b_{i} {\mathbf{j}}_{i} + c_{i} {\mathbf{k}}_{i} + d_{i} {\mathbf{l}}_{i} + e_{i} {\mathbf{m}}_{i} ,i = 1,2,3 $$

(1)

$$ {\text{With}},{\mathbf{i}}_{i} = \left[ {\cos \,\alpha_{i} \,\sin \alpha_{i} } \right]^{T} ,{\mathbf{j}}_{i} = \left[ {\cos \,\beta_{i}^{\text{'}} \,\sin \beta_{i}^{\text{'}} } \right]^{T} ,{\mathbf{k}}_{i} = \left[ {\cos \gamma_{i}^{\text{'}} \,\sin \gamma_{i}^{\text{'}} } \right]^{T} , $$

$$ {\mathbf{l}}_{i} = \left[ {\cos \theta_{i}^{\text{'}} \,\sin \theta_{i}^{\text{'}} } \right]^{T} ,\,{\mathbf{m}}_{i} = \left[ {\cos \left( {\phi + \psi_{i} } \right)\,\sin \left( {\phi + \psi_{i} } \right)} \right]^{T} \,\text{and} $$

$$ \beta_{i}^{\text{'}} = \alpha_{i} + \beta_{i} ,\,\gamma_{i}^{\text{'}} = \alpha_{i} + \beta_{i} + \gamma_{i} + \phi ,\,\theta_{i}^{\text{'}} = \alpha_{i} + \beta_{i} + \gamma_{i} + \phi + \theta_{i} $$

The inverse kinematics solution for the manipulator can be derived from Eq. (1)

$$ \begin{aligned} b_{i} = \left( {{\mathbf{l}}_{i}^{T} {\mathbf{Ej}}_{i} } \right)^{ - 1} {\mathbf{l}}_{i}^{T} {\mathbf{E}}\left( {{\mathbf{T}} - a_{i} {\mathbf{i}}_{i} - c_{i} {\mathbf{k}}_{i} - e_{i} {\mathbf{m}}_{i} } \right) \hfill \\ d_{i} = \left( {{\mathbf{j}}_{i}^{T} {\mathbf{El}}_{i} } \right)^{ - 1} {\mathbf{j}}_{i}^{T} {\mathbf{E}}\left( {{\mathbf{T}} - a_{i} {\mathbf{i}}_{i} - c_{i} {\mathbf{k}}_{i} - e_{i} {\mathbf{m}}_{i} } \right) \hfill \\ \end{aligned} $$

(2)

where, E is the right angle rotation matrix and defined as: ${\mathbf{E}} = \left[ {\begin{array}{*{20}c} 0 & { - 1} \\ 1 & 0 \\ \end{array} } \right]$

Geometric parameters for the U-shape and Δ-shape fixed base 3-PRP manipulators are given in Tables 1 and 2. The CAD models are presented in Fig. 2.

Table 1. Geometric parameters for the U-shape fixed base 3PRP manipulator

Table 2. Geometric parameters for the Δ-shape fixed base 3PRP manipulator

Fig. 2.

CAD models of the U-shape and Δ-shape fixed base 3-PRP manipulators

3 Jacobian and Singularities of the Manipulator

Velocity expression can be derived from the Eq. (1) by taking time derivative and eliminating the coefficient of l $_{i}$, as below:

$$ {\mathbf{A}}\left[ {\begin{array}{*{20}c} {{\dot{\mathbf{T}}}} & {\dot{\phi }} \\ \end{array} } \right]^{T} = {\mathbf{B\dot{b}}} $$

(3)

where, ${\mathbf{A}}$ and ${\mathbf{B}}$ are the forward and inverse Jacobian of the manipulators, respectively. These matrices are analytically given as follows:

$$ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{\text{l}}_{1}^{T} {\text{E}}^{T} } & { - d_{1} - c_{1} {\text{l}}_{1}^{T} {\text{k}}_{1} - e_{1} {\text{l}}_{1}^{T} {\text{m}}_{1} } \\ {{\text{l}}_{2}^{T} {\text{E}}^{T} } & { - d_{2} - c_{2} {\text{l}}_{2}^{T} {\text{k}}_{2} - e_{2} {\text{l}}_{2}^{T} {\text{m}}_{2} } \\ {{\text{l}}_{3}^{T} {\text{E}}^{T} } & { - d_{3} - c_{1} {\text{l}}_{1}^{T} {\text{k}}_{1} - e_{1} {\text{l}}_{2}^{T} {\text{m}}_{2} } \\ \end{array} } \right],{\mathbf{B}} = \left[ {\begin{array}{*{20}c} {{\text{l}}_{1}^{T} {\text{E}}^{T} {\text{j}}_{1} } & 0 & 0 \\ 0 & {{\text{l}}_{2}^{T} {\text{E}}^{T} {\text{j}}_{2} } & 0 \\ 0 & 0 & {{\text{l}}_{3}^{T} {\text{E}}^{T} {\text{j}}_{3} } \\ \end{array} } \right] $$

The kinematic Jacobain of the manipulator is given as:

$$ {\mathbf{J}} = {\mathbf{A}}^{ - 1} {\mathbf{B}} $$

(4)

where, Matrix ${\mathbf{A}}$ is never singular while matrix ${\mathbf{B}}$ is singular only when the angle $\phi = \pm \, 90^\circ$, which is not possible for the manipulator within workspace, so neither serial nor parallel singularity is present in the manipulator. So this configuration is a singularity-free within its given workspace.

4 Error Modelling

In order to include the effect of joint clearances, the rotary joint the clearance is characterized by using a small distance $\delta \rho_{i}$ between the points ${\mathbf{P}}_{i}$ and ${\mathbf{P}}_{i} '$ in the $i^{th}$ link as shown in Fig. 3. To obtain the error for the end effector at point ${\mathbf{T}}$ Eq. (1) is differentiated to obtain Eq. (5).

Fig. 3.

Error variables in the joint parameters of 3PRP manipulator

$$ \begin{aligned} \delta {\mathbf{T}} = & \delta a_{i} {\text{i}}_{i} + a_{i} \delta \alpha_{i} {\mathbf{Ei}}_{i} + \delta b_{i} {\mathbf{j}}_{i} + b_{i} \delta \beta_{i} '{\mathbf{Ej}}_{i} + \delta \rho_{i} {\mathbf{n}}_{i} + \delta c_{i} {\mathbf{k}}_{i} + c_{i} \delta \gamma_{i} '{\mathbf{Ek}}_{i} + \delta d_{i} {\mathbf{l}}_{i} \\ & + d_{i} \delta \theta_{i} '{\mathbf{El}}_{i} + e_{i} (\delta \phi + \delta \psi_{i} ){\mathbf{Em}}_{i} ,\begin{array}{*{20}c} {} & {i = 1,2,3} \\ \end{array} \\ \end{aligned} $$

(5)

$$ \begin{aligned} & \delta \beta_{i} ' = \delta \alpha_{i} + \delta \beta_{i} \\ & \delta \gamma_{i} ' = \delta \alpha_{i} + \delta \beta_{i} + \delta \gamma_{i} + \delta \phi \\ & \delta \theta_{i} ' = \delta \alpha_{i} + \delta \beta_{i} + \delta \gamma_{i} + \delta \phi + \delta \theta_{i} \\ \end{aligned} $$

(6)

where, $\delta {\mathbf{T}}$ and $\delta \phi$ are the positioning and orientation error at the end effector.

Other variables namely, $\delta a_{i}$, $\delta \alpha_{i}$, $\delta b_{i}$, $\delta \beta_{i}$, $\delta c_{i}$, $\delta \gamma_{i}$, $\delta d_{i}$, $\delta \theta_{i}$, $\delta e_{i}$ and $\delta \psi_{i}$ show the variations in the geometric parameters of the link arrangement. Other than these effects, it is also introduced a joint distance which represents the joint clearance of a rotary joint and denoted as $\delta \rho_{i}$. The associated vector with this distance variable is n $_{i}$ = $\left[ {\begin{array}{*{20}c} {\cos \zeta_{i} } & {\sin \zeta_{i} } \\ \end{array} } \right]^{T}$, by substituting the values of Eq. (6) in Eq. (5) and eliminating the variable $\delta d_{i}$, it gives

$$ \begin{aligned} & {\mathbf{l}}_{i}^{T} {\mathbf{E}}^{{\mathbf{T}}} \delta {\text{T}} = \delta a_{i} {\mathbf{l}}_{i}^{T} {\mathbf{E}}^{{\mathbf{T}}} {\mathbf{i}}_{i} + \delta \alpha_{i} \left[ {{\mathbf{l}}_{i}^{T} \left( {a_{i} {\mathbf{i}}_{i} + b_{i} {\mathbf{j}}_{i} + c_{i} {\mathbf{k}}_{i} } \right) + d_{i} } \right] + \delta b_{i} {\mathbf{l}}_{i}^{T} {\mathbf{E}}^{{\mathbf{T}}} {\mathbf{j}}_{i} \\ & \quad + \delta \beta_{i} \left[ {{\mathbf{l}}_{i}^{T} \left( {b_{i} {\mathbf{j}}_{i} + c_{i} {\mathbf{k}}_{i} } \right) + d_{i} } \right] + \delta \rho_{i} {\mathbf{l}}_{i}^{T} {\mathbf{E}}^{{\mathbf{T}}} {\mathbf{n}}_{i} + \delta c_{i} {\mathbf{l}}_{i}^{T} {\mathbf{E}}^{{\mathbf{T}}} {\mathbf{k}}_{i} + \delta \gamma_{i} \left( {c_{i} {\mathbf{l}}_{i}^{T} {\mathbf{k}}_{i} + d_{i} } \right) \\ & \quad + d_{i} \delta \theta_{i} + \delta \phi \left( {c_{i} {\mathbf{l}}_{i}^{T} {\mathbf{k}}_{i} + d_{i} + e_{i} {\mathbf{l}}_{i}^{T} {\mathbf{m}}_{i} } \right) + \delta e_{i} {\mathbf{l}}_{i}^{T} {\mathbf{E}}^{{\mathbf{T}}} {\mathbf{m}}_{i} + \delta \psi_{i} e_{i} {\mathbf{l}}_{i}^{T} {\mathbf{m}}_{i} \\ \end{aligned} $$

(7)

If substituting the values of $i = 1, \, 2, \, 3$ in Eq. (7) and arrange it in vector form as:

$$ \begin{aligned} {\mathbf{A}}\left[ {\begin{array}{*{20}c} {\delta x} \\ {\delta y} \\ {\delta \phi } \\ \end{array} } \right] = {\mathbf{H}}_{a} \left[ {\begin{array}{*{20}c} {\delta a_{1} } \\ {\delta a_{2} } \\ {\delta a_{3} } \\ \end{array} } \right] + {\mathbf{H}}_{\alpha } \left[ {\begin{array}{*{20}c} {\delta \alpha_{1} } \\ {\delta \alpha_{2} } \\ {\delta \alpha_{3} } \\ \end{array} } \right] + {\mathbf{B}}\left[ {\begin{array}{*{20}c} {\delta b_{1} } \\ {\delta b_{2} } \\ {\delta b_{3} } \\ \end{array} } \right] + {\mathbf{H}}_{\beta } \left[ {\begin{array}{*{20}c} {\delta \beta_{1} } \\ {\delta \beta_{2} } \\ {\delta \beta_{3} } \\ \end{array} } \right] + {\mathbf{H}}_{\rho } \left[ {\begin{array}{*{20}c} {\delta \rho_{1} } \\ {\delta \rho_{2} } \\ {\delta \rho_{3} } \\ \end{array} } \right] \hfill \\ \quad \quad + {\mathbf{H}}_{c} \left[ {\begin{array}{*{20}c} {\delta c_{1} } \\ {\delta c_{2} } \\ {\delta c_{3} } \\ \end{array} } \right] + {\mathbf{H}}_{\gamma } \left[ {\begin{array}{*{20}c} {\delta \gamma_{1} } \\ {\delta \gamma_{2} } \\ {\delta \gamma_{3} } \\ \end{array} } \right] + {\mathbf{H}}_{\theta } \left[ {\begin{array}{*{20}c} {\delta \theta_{1} } \\ {\delta \theta_{2} } \\ {\delta \theta_{3} } \\ \end{array} } \right] + {\mathbf{H}}_{e} \left[ {\begin{array}{*{20}c} {\delta e_{1} } \\ {\delta e_{2} } \\ {\delta e_{3} } \\ \end{array} } \right] + {\mathbf{H}}_{\psi } \left[ {\begin{array}{*{20}c} {\delta \psi_{1} } \\ {\delta \psi_{2} } \\ {\delta \psi_{3} } \\ \end{array} } \right] \hfill \\ \end{aligned} $$

(8)

By multiplying ${\mathbf{A}}^{ - 1}$ on both sides, using Eq. (4) and replacing ${\mathbf{J}}_{q}$ with ${\mathbf{A}}^{ - 1} {\mathbf{H}}_{q}$, where $q \in \left\{ {a,\alpha ,\beta ,\rho ,c,\gamma ,d,\theta ,e,\psi } \right\}$. The error sensitivity equation for the manipulator is given as:

$$ \begin{aligned} \left[ {\begin{array}{*{20}c} {\delta x} \\ {\delta y} \\ {\delta \phi } \\ \end{array} } \right] = {\mathbf{J}}_{a} \left[ {\begin{array}{*{20}c} {\delta a_{1} } \\ {\delta a_{2} } \\ {\delta a_{3} } \\ \end{array} } \right] + {\mathbf{J}}_{\alpha } \left[ {\begin{array}{*{20}c} {\delta \alpha_{1} } \\ {\delta \alpha_{2} } \\ {\delta \alpha_{3} } \\ \end{array} } \right] + {\mathbf{J}}\left[ {\begin{array}{*{20}c} {\delta b_{1} } \\ {\delta b_{2} } \\ {\delta b_{3} } \\ \end{array} } \right] + {\mathbf{J}}_{\beta } \left[ {\begin{array}{*{20}c} {\delta \beta_{1} } \\ {\delta \beta_{2} } \\ {\delta \beta_{3} } \\ \end{array} } \right] + {\mathbf{J}}_{\rho } \left[ {\begin{array}{*{20}c} {\delta \rho_{1} } \\ {\delta \rho_{2} } \\ {\delta \rho_{3} } \\ \end{array} } \right] \hfill \\ \begin{array}{*{20}c} {} & {^{{}} } \\ \end{array} + {\mathbf{J}}_{c} \left[ {\begin{array}{*{20}c} {\delta c_{1} } \\ {\delta c_{2} } \\ {\delta c_{3} } \\ \end{array} } \right] + {\mathbf{J}}_{\gamma } \left[ {\begin{array}{*{20}c} {\delta \gamma_{1} } \\ {\delta \gamma_{2} } \\ {\delta \gamma_{3} } \\ \end{array} } \right] + {\mathbf{J}}_{\theta } \left[ {\begin{array}{*{20}c} {\delta \theta_{1} } \\ {\delta \theta_{2} } \\ {\delta \theta_{3} } \\ \end{array} } \right] + {\mathbf{J}}_{e} \left[ {\begin{array}{*{20}c} {\delta e_{1} } \\ {\delta e_{2} } \\ {\delta e_{3} } \\ \end{array} } \right] + {\mathbf{J}}_{\psi } \left[ {\begin{array}{*{20}c} {\delta \psi_{1} } \\ {\delta \psi_{2} } \\ {\delta \psi_{3} } \\ \end{array} } \right] \hfill \\ \end{aligned} $$

(9)

The coefficients of the error vectors in the above relation are the corresponding sensitivity matrices related to each error variables. These analytical expressions are validated using the virtual prototype with the help of MSC ADAMS software. Further, these relations are used for accuracy and sensitivity analyses in the following section.

5 Error Sensitivity Analysis

Errors due to joint (bearing) clearances and the actuator inaccuracies (least count errors) may cause alteration in the end-effector’s pose which cannot be compensated. Other structural parameter errors related to the link lengths and actuator indexing errors can be compensated by the help of the calibration techniques or parameter identification methods suggested for parallel manipulators. But the error caused due to the presence of clearances, actuator inaccuracies and encoder least count errors are non-compensable by such calibration techniques. Therefore, pose errors are estimated due to the joint clearances, actuator inaccuracies and encoder least count errors using commercially available data for rotary and prismatic joints and, encoder resolution. For the rotary joint, joint clearances are assumed as:

$0\,\text{mm}\, \le \,\delta \rho_{i} \, \le \,0.016\,\text{mm}$ and the contact angle $\zeta_{i}$ can vary from 0 to $2\pi$ radians, where $\delta \rho_{i}$ is the center to center distance of the mating bodies of the rotary joints. The error variable $\delta \theta_{i}$ depends on the joint clearance of the prismatic joint and angular deviation because of that which is $- 0.0 4^\circ \le \delta \theta_{i} \le 0.0 4^\circ$ and the least count error is taken as half of the least count which cannot be detected by the encoders here taken as $0\,\text{mm}\, \le \delta b_{i} \le 0.025\,\text{mm}$. The analytical error prediction model is solved simultaneously as an optimization problem using the genetic algorithms. For numerical computation, the Matlab function namely, “ga” an in-build genetic algorithms optimization solver is used. The test region for the error sensitivity analysis is considered as a square area of 80 mm × 80 mm for the given actuator span of 200 mm in all three legs. To compare the effect of the non-compensable errors in U-shape and Δ-shape fixed base parallel configurations the data for joint clearances and encoder resolutions are taken from the industrial product catalogues [7]. Local maximum possible pose errors of the end-effector are obtained through the optimization code for the given workspace region for the constant end-effector orientation. Error contour plots are presented in Figs. 4 and 5.

Fig. 4.

Non-compensable error contour plots of the U-shape fixed base 3-PRP PPM

Fig. 5.

Non-compensable error contour plots of the Δ-shape fixed base 3-PRP PPM

The local maximum position errors due to the non-compensable errors in U-shape and Δ-shape fixed base parallel configurations are presented in Figs. 4 and 5, respectively. The result shows that the pose errors due the non-compensable errors for the selected workspace region are varying from 110 μm to 150 μm for U-shape 3-PRP PPM and 70 μm to 95 μm for Δ-shape 3-PRP PPM. From the results, it is observed that Δ-shape (symmetric shape) fixed base configuration performs better than U-shape fixed base configurations in presence of non-compensable errors for 3-PRP kinematic arrangement.

6 Conclusions

In this paper, an analytical error prediction model for the planar 3PRP parallel configuration is derived by considering all possible mechanical inaccuracies. Solution for the joint parameter’s dependency on the orientation angle of the end-effector is solved and demonstrated. From the results, it is found that the Δ-shape fixed base configuration is less sensitive to the non-compensable errors. These non-compensable errors cannot be compensated by the offline calibration method. But, it can be minimized or compensated by using a task-space motion control strategy in trajectory tracking, which would be considered as a future work.