Development of Data-Driven Turbulence Models in OpenFOAM${^{\textregistered }}$: Application to Liquid Fuel Nuclear Reactors

Abstract

The following chapter presents a new approach for the development of turbulent models, with potential application to the design of liquid fuel nuclear reactors. To begin the chapter, the work being carried out at LPSC (Grenoble) for validating the modeling of molten salt coolants is presented, alongside a Backward-Facing Step (BFS) geometry, which will be studied throughout this work. In the subsequent section, various turbulence models are evaluated in the BFS and their advantages and limitations are analyzed, with the conclusion that some improvements in the turbulence modeling are necessary. Therefore, the next section introduces a methodology for developing a nonlinear closure for turbulence models by means of Symbolic Regression via Genetic Evolutionary Programming (GEATFOAM). Then, this new methodology is implemented for direct numerical simulation data of the BFS, obtaining a new nonlinear closure for the standard k–$\varepsilon$ model. Finally, the new model is compared against classical turbulence models for the BFS, and, then, the extrapolability of this model is analyzed for available experimental data of an axial expansion in a pipe. Encouraging results are obtained in both cases.

This project has received funding from the Euratom research and training program 2014–2018 under grant agreement No. 661891.

The content of this article does not reflect the official opinion of the European Union. Responsibility for the information and/or views expressed in the article lies entirely with the authors.

1 Introduction

Molten salt nuclear reactors are an auspicious new concept in the nuclear industry, because of the innovative design and safety possibilities opened up by the use of a liquid nuclear fuel [1]. In particular, among these reactors, the Molten Salt Fast Reactor (MSFR) is a type of fourth-generation liquid fuel nuclear reactor, which is presently being studied in the framework of the H2020 European project SAMOFAR (2015–2019) [2]. Among the undertakings of this project, the SWATH (Salt at Walls: Thermal excHanges) experiment is being carried out at LPSC in Grenoble. This experiment intends to improve the understanding and predictions of the thermal-hydraulic behavior of high-temperature molten salt internal flows over diverse geometries. The foreseen outcomes of the experiment are validated mathematical models for describing the heat exchange phenomena in such flows.

Fig. 1

The SWATH experiment

The experimental layout of SWATH (shown in Fig. 1) includes two tanks filled with a molten salt (FLiNaK), a test section hosted inside a glovebox and instrumentation for performing the measurements. A pressure difference between the two tanks generates a molten salt flow through the test section. No pump is therefore present in the system, reducing the risks of component failure.

The high complexity of molten salt flows demands a parsimonious validation of the proposed mathematical models. Therefore, the substantiation process for the models is executed in two steps: first, the fluid mechanics models are validated without thermal exchanges in the SWATH-W facility (using water), and, second, the thermal exchange models are tested in the SWATH-S facility (using molten FLiNaK). The SWATH-W experiment is a one-to-one scale mockup operating with water, for the purpose of validating the fluid mechanics models. The water flow in the mockup can be generated either by the pressure difference between two tanks or by a centrifugal pump. Precise Particle Image Velocimetry [3] measurements are performed on the test sections (SWATH-W), allowing us to validate the proposed fluid mechanics models (without heat transfer). Afterward, the validated models are completed with the modeling of the thermal exchange phenomena. Finally, by preserving the dynamic similarity, the complete fluid mechanics and thermal exchange models are compared against the data obtained in the main molten salt experiment (SWATH-S).

Computational Fluid Dynamics (CFD) is the name given to the simulation of fluid dynamics phenomena by means of a computer. Different CFD techniques have been proposed for resolving the mean and fluctuating components of the velocity in a turbulent flow. The Direct Numerical Simulation (DNS) technique aims for a complete resolution of both mean and fluctuating components at an expensive computational cost [4]. For the purpose of reducing the computational cost while resolving turbulence fields, Reynolds Average Navier Stokes (RANS) and Large Eddy Simulations (LES) techniques apply integral filters to the velocity and model the extra term appearing in the Navier–Stokes as a result of this filtering process [5]. In the RANS method, the velocity is time-filtered, whereas in the LES method, the filters are spatiotemporal, allowing us to control the size of the resolved scales [6].

In order to perform the required multiphysics studies in the MSFR, thermal-hydraulic models should be coupled to neutronics and thermal-mechanics models. Given the reactor geometry and the complexity of the phenomena, only RANS models present a good compromise between computational cost and accuracy [7].

A Backward-Facing Step (BFS) geometry has been selected as one of the sections to be studied in the SWATH experiment, since the flow phenomena in this geometry are representative of the entrance region of the MSFR. This section is interesting, since standard RANS models cannot fully predict the richness of the turbulent structures generated past the BFS [8]. The ultimate modeling objective is to produce an accurate RANS turbulence model, able to predict the bulk velocities in the BFS with an error of less than $5\%$. Accurate predictions of the molten salt bulk velocities in the MSFR are needed for similarly accurate predictions of the coupled phenomena of the reactor. Currently, Particle Image Velocimetry (PIV) measurements are being carried out for a BFS in the SWATH-W experiment. As the results are not yet available, the methodological approach of the current work is developed according to the precise DNS simulation performed by [9, 10] on a BFS, referred to from now on as DNS data.

2 Application of State-of-the-Art Turbulence Models for the BFS

The studied BFS section is shown in Fig. 2. It consists of a 2D section, with an expansion rate of 2. The mean inlet velocity U is fixed so that the Reynolds number in the inlet throat is $Re=\frac{Uh}{\nu }=9000$, where $\nu =10^{-6} \,\frac{\hbox {m}^2}{\hbox {s}}$ is the kinematic viscosity (of water at $20\,^{\circ }\hbox {C}$).

The BFS geometry was discretized in two dimensions (assuming plane symmetry) with a regular structured quadrilateral mesh, having a maximum aspect ratio of 5 and a maximum skewness ratio of $10^{-6}$. The mesh was refined until the predictions in the bulk velocities were unchanged by further refinements for each turbulence model tested in the section. This standard mesh convergence procedure [11] allows us to obtain results that are independent of the mesh employed, depending only on the applied turbulence model. As expected, the mesh in the region next to the expansion of the BFS (see Fig.  2) was found to be key for an accurate description of the turbulence phenomena in the bulk region of the BFS. This is a consequence of the tripping of the boundary layer arising in this zone. In addition, the predictions in the tripping of the boundary layer were found to be very sensitive to the adopted wall functions. Therefore, since the goal is to make the results only dependent on the turbulence model used, an enhanced wall treatment procedure was imposed in the simulations, i.e., no wall functions were implemented. In this regard, the centers of the mesh cells along the walls of the BFS were adjusted, using a uniform inflation ratio boundary layer, obtaining a dimensionless wall distance ($y^+$) that varied between 0.5 and 1.5 in these cells. The meshes were generated using the snappyHexMesh utility in OpenFOAM${^{\textregistered }}$ [12].

Fig. 2

Top: Dimensions of the BFS section in mm; the stream-wise velocity profile is completely developed before the sudden expansion and in the exit of the domain. Bottom: Three flow zones in the BFS section are distinguished: a main shear layer, a recirculation zone, and a mainstream zone. Also, the vertical lines over which the stream-wise component of the velocity will be studied during the present study are displayed

An incompressible and isothermal flow in a backward-facing step can be mathematically described by the incompressible Navier–Stokes equations, asserting the conservation of mass and linear momentum. Assuming a description in an Eulerian inertial reference frame, without exterior surface or body forces applied to the fluid, these equations can be read as

$$\begin{aligned} \nabla \cdot \mathbf {u} = 0,\end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial }{\partial t}\mathbf {u}+\mathbf {u}\cdot \nabla \mathbf {u}=-\nabla \frac{p}{\rho }+\nu \nabla ^2 \mathbf {u}, \end{aligned}$$

(2)

where $\mathbf {u}(\mathbf {x},t)$ is the velocity, $p(\mathbf {x},t)$ is the pressure, $\rho$ is the density, and $\nu$ is the kinematic viscosity. When measuring the velocities at a point in a turbulent flow, it is found that the velocity field can be decomposed into a mean and fluctuating component $\mathbf {u}(\mathbf {x},t)=\overline{\mathbf {u}(\mathbf {x},t)}+\mathbf {u}(\mathbf {x},t)'$ [13].

By applying these filtering techniques to the Navier–Stokes equations (2), the following set of filtered equations is obtained:

$$\begin{aligned} \nabla \cdot \overline{\mathbf {u}} = 0,\end{aligned}$$

(3)

$$\begin{aligned} \frac{\partial }{\partial t}\overline{\mathbf {u}}+\bar{\mathbf {u}} \cdot \nabla \bar{\mathbf {u}} =-\nabla \frac{\overline{p}}{\rho }+\nu \nabla \cdot (\nabla \overline{\mathbf {u}} - \mathbf {\tau ^f}). \end{aligned}$$

(4)

Comparing Eqs. 2 and 4, besides the overbar in the variables indicating its mean component, the difference arrives in a newly introduced term $\mathbf {\tau ^f}$ that results from the filtering process. For RANS models, $\mathbf {\tau ^f}=\overline{\mathbf {u}'\mathbf {u}'}$, and this is called the Reynolds Shears Stress (RSS) Tensor. For LES models, $\mathbf {\tau ^f}=\mathbf {\tau ^r}$, and this is usually called the residual stress tensor or Sub-Grid Scale (SGS) stress tensor.

For RANS models, the RSS tensor is symmetric and has six independent components. The simpler models for the RSS tensor are the linear eddy viscosity models, wherein it is assumed that $\overline{\mathbf {u}'\mathbf {u}'} \approx \nu _t \mathbf {S}$, where $\mathbf {S}=\frac{1}{2}(\nabla \mathbf {\overline{u}}+{\nabla \mathbf {\overline{u}}}^T)$ is the strain rate tensor and $\nu _t$ is the turbulent viscosity (assumed to be a function of the solved turbulence variables k and $\varepsilon$). One of the models studied in the present work is the k–$\varepsilon$ model [14] in which $\nu _t=C_\mu \frac{k^2}{\varepsilon }f_{\mu }\mathbf {S}$, where $k=\frac{1}{2}tr(\overline{\mathbf {u}'\mathbf {u}'})$ is the turbulent kinetic energy, $\varepsilon$ is the specific dissipation rate of turbulent kinetic energy $\varepsilon =\nu \overline{\nabla \mathbf {u}'\cdot \nabla \mathbf {u}'}$, and $f_{\mu }$ is a Van Driest-like damping function that reduces the turbulent viscosity value close to the walls [15]. Specific transport equations are derived for k and for $\varepsilon$, introducing closure coefficients when approximations are done (for specific details, see [16]). The introduction of $f_{\mu }$ into the model, as well as the corrections in the modeling of k and $\varepsilon$ close to solid surfaces, is known as standard wall functions. However, when performing enhanced wall treatment, wall corrections are not introduced, since the turbulent phenomena next to the walls is considered to be readily resolved by the fine mesh next to the walls (i.e., $f_{\mu }=1$). The k–$\varepsilon$ model is not unique, since several other linear eddy viscosity models exist. In particular, the Wilcox k–$\omega$ model [17], available in OpenFOAM${^{\textregistered }}$, was also considered during the present analysis.

An important limitation of the linear eddy viscosity models is that the tensorial character of the RSS is solely dependent on the instantaneous strain rate and, therefore, the history of the development of turbulent stresses in the fluid field is not resolved. Consequently, the assumption of linear viscosity is misled in the BFS case, wherein the richness of turbulent structures in the flow is generated by a vortex rolling mechanism in the shear layer soon after the tripping of the boundary layer [18]. Therefore, the turbulence field (and hence the RSS tensor) at a given point will be strongly dependent on the upstream flow or fluid history.

An immediate improvement is proposed by the nonlinear eddy viscosity models. First, the RSS tensor is divided into its isotropic and non-isotropic components $\overline{\mathbf {u}'\mathbf {u}'}=\frac{2}{3}k\mathbf {I}+k\mathbf {a}$, where the tensor describing the non-isotropic component $\mathbf {a}$ is known as the anisotropy tensor. Following the previous definition, the anisotropy tensor is traceless $tr(\mathbf {a})=0$ and symmetrical $\mathbf {a}=\mathbf {a}^T$. Based on these arguments, and introducing the vorticity tensor as $\mathbf {W}=\frac{1}{2}(\nabla \mathbf {\overline{u}}-{\nabla \mathbf {\overline{u}}}^T)$, the modeling of the anisotropy tensor based on the k–$\varepsilon$ model can be constructed to third orders as follows:

$$\begin{aligned} \mathbf {a} = \sum _{i_1}^n C_i\mathbf {T_i},\end{aligned}$$

(5)

$$\begin{aligned} \texttt {First-order terms:}\mathbf {T_1} = C_1\frac{\nu _t}{k}\mathbf {S},\end{aligned}$$

(6)

$$\begin{aligned} \texttt {Second-order terms:} \mathbf {T_2} = C_2\frac{\nu _t}{\varepsilon }(\mathbf {S}\mathbf {W}-\mathbf {W}\mathbf {S})\end{aligned}$$

(7)

$$\begin{aligned} \mathbf {T_3} = C_3\frac{\nu _t}{\varepsilon }(\mathbf {S}\cdot \mathbf {S}-\frac{1}{3}\mathbf {S}:\mathbf {S})\mathbf {I} \mathbf {T_4} = C_4\frac{\nu _t}{\varepsilon }(\mathbf {W}\cdot \mathbf {W}-\frac{1}{3}\mathbf {W}:\mathbf {W}\mathbf {I}), \nonumber \\ \texttt {Third-order closure:} \mathbf {T_5} = C_5\frac{\nu _tk}{\varepsilon ^2}(\mathbf {S}\cdot \mathbf {S}\mathbf {W}-\mathbf {W}\mathbf {S}\cdot \mathbf {S}) \nonumber \\ \mathbf {T_6} = C_6\frac{\nu _tk}{\varepsilon ^2}(\mathbf {W}\cdot \mathbf {W}\mathbf {S}+\mathbf {S}\mathbf {W}\cdot \mathbf {w}-\frac{2}{3}\mathbf {S}:\mathbf {W}\cdot \mathbf {W}) \nonumber \\ \mathbf {T_7} = C_7\frac{\nu _tk}{\varepsilon ^2}(\mathbf {S}\mathbf {S}:\mathbf {S}) , \mathbf {T_8} = C_8\frac{\nu _tk}{\varepsilon ^2}(\mathbf {S}\mathbf {W}:\mathbf {W}). \end{aligned}$$

(8)

Since the model for the anisotropic tensor includes terms up to the third order, it is said to be a cubic order closure. During the solution process, the k–$\varepsilon$ equations are solved at each iteration and, subsequently, $\nu _t$ and $\mathbf {a}$ are computed. The near wall treatment in the simulations could be done identically to that of the k–$\varepsilon$ model. However, for the reasons explained earlier in the text, no special wall treatment is introduced when doing enhanced wall treatment. For closing the set of equations, this model requires the empirical fitting of 13 coefficients. The nonlinear cubic model proposed by Craft et al. [19] was implemented in OpenFOAM${^{\textregistered }}$, along with the proposed fitting coefficients.

The Reynolds Shear Stress (RSS) modeling technique consists in solving a set of seven transport equations, derived from the six independent components of the RSS tensor and the turbulent kinetic energy k. This set of equations is known as the RSS transport equations. In these equations, the pressure–strain correlation, the pressure and turbulence diffusion, and the specific turbulent kinetic energy dissipation terms require specific modeling. In the present work, the RSS model of [20], already implemented in OpenFOAM${^{\textregistered }}$, was tested in the BFS.

In the LES technique, for the accurately modeling of the wide range of anisotropic turbulent structures of the BFS, the multi-gradient model for the Sub-Grid Scale (SGS) stress tensor developed by [21] was implemented in OpenFOAM${^{\textregistered }}$. The multi-gradient equations for the SGS stress tensor are

$$\begin{aligned} \mathbf {\tau ^r} = \frac{8\bar{\varDelta }^2}{C_\varepsilon ^2}(-\frac{\mathbf {G}}{tr(\mathbf {G})}\mathbf {S})^2(\frac{\mathbf {G}}{tr(\mathbf {G})})H(P),\nonumber \\ \mathbf {G} = \frac{1}{12}[(\mathbf {D} \cdot (\nabla \mathbf {u}))(\mathbf {D} \cdot (\nabla \mathbf {u})^T)], \end{aligned}$$

(9)

where $\mathbf {D} = (\varDelta _x,\varDelta _y,\varDelta _z)$ is the grid filter vector, $\bar{\varDelta } = (\varDelta _x\varDelta _y\varDelta _z)^{1/3}$ is the grid filter length, and $C_\varepsilon$ is a coefficient that depends on whether the local equilibrium or global equilibrium hypothesis is used [22]. This last coefficient was taken as equal to 1 in the present case. Furthermore, H(P) is a Heaviside function that turns off the model whenever the turbulent production term $P=-\mathbf {\tau ^r}\cdot \mathbf {S}$ becomes negative. The filter length was taken as twice the mesh size ($\bar{\varDelta }=2\varDelta$) in the simulations.

Fig. 3

Top-left: Results for the normalized steady-state stream-wise component of the velocity for the lines $\frac{x}{H}=0.5$. Top-right: $\frac{x}{H}=4.0$. Bottom-left: $\frac{x}{H}=8.0$. Bottom-right: $\frac{x}{H}=20.0$. In the above results, the LES model corresponds to a multi-gradient SGS model [21] implemented in OpenFOAM${^{\textregistered }}$ with no near wall treatment, the k–$\varepsilon$ [14], and k–$\omega$ [17] models are the standard models used in OpenFOAM${^{\textregistered }}$, the nonlinear cubic model corresponds to the one developed by Craft [19] and implemented in OpenFOAM${^{\textregistered }}$ and the RSS model is the SSG model available in OpenFOAM${^{\textregistered }}$ developed by Speziale [20]

The results for the steady-state stream-wise component of the velocity, for the y-lines displayed in Fig. 2, are shown in Fig. 3. Simulations were performed for each of the above turbulence models (k–$\varepsilon$, k–$\omega$, RSS, cubic nonlinear and multi-gradient LES). As previously discussed, all simulations were performed in a converged mesh.

The results of these models are compared against the DNS data, which is taken as the reference. The general performance of the k–$\varepsilon$ model for the BFS is judged to be poor. This is a result of the overestimation of the turbulent dissipation $\varepsilon$, as well as the turbulent kinetic energy k. Thereupon, the k–$\varepsilon$ model predicts an early development of the velocity profile past the BFS expansion. The results predicted by the k–$\omega$ model are, however, in much better agreement with the DNS data. This is because, when calculating $\omega =\frac{\varepsilon }{k}$, both overpredictions compensate remarkably well. The nonlinear viscosity model has a good agreement with the DNS data close to the middle stream, but it performs badly next to the walls. Since the closure coefficients of this model were fitted by Craft [19] for the development of a boundary layer over a flat plate, it is not surprising that they are misled for the highly anisotropic internal flow of the BFS (in which the flow velocity perpendicular to the walls may be important). The RSS transport model shows good results in the region immediately after the detachment of the boundary layer. However, it underestimates the dissipation of the turbulent kinetic energy in the stream-wise direction, causing an over diffusion of the shear layer and significant errors in the predicted velocities downstream. Finally, the multi-gradient LES model shows an almost perfect agreement with the DNS data.

To quantitatively analyze the error of the turbulence models, the mis-prediction in the axial velocity on the y-lines displayed in Fig. 2 is weighted by the importance of this mis-prediction. Therefore, the average weighted quadratic error is computed for each y-line l ($\frac{x}{H}=0.5,4,8,20$) with $n_l$ data points as

$$\begin{aligned} L_w = \frac{1}{4}\sum _{l=1}^{4}\frac{1}{n_l}\sum _{i=1}^{n_l}w(y_{il})(\frac{u_{DNS_{il}}-u_{MODEL_{il}}}{u_{DNS_{il}}})^2, \nonumber \\ w(y) = 1-(1-\frac{y}{h})^2, \end{aligned}$$

(10)

where $u_{DNS_{il}}$ is the velocity stream-wise component of the DNS data for the line l at point $y_i$ and $u_{MODEL_{il}}$ is the predicted stream-wise velocity for the turbulence model under consideration. The function w(y) is a Poiseuille-like weighting function that maximizes the importance of the errors in the middle stream of the section. This function is introduced regarding the expansion of the MSFR reactor, in which the middle stream region in the flow has a larger importance than the region close to the walls, due to neutronic considerations. The errors obtained and the CPU time to convergence to steady state in the simulations are shown in Table 1. The only model that allows to obtain an error smaller than $5\%$ is the multi-gradient LES model, but its computational cost is prohibitively expensive when considering its application to the scale of the MSFR. In addition, the nonlinear stress model is close to the targeted error. A good attempt might have been made to improve the closure coefficients for this model, but due to its complexity, further improvements are difficult to develop. Therefore, a new nonlinear eddy viscosity model based on the k–$\varepsilon$ model, developed by means of symbolic regression using the GEATFOAM tool, is discussed in the following section.

Table 1 Relative errors and computational cost for the different turbulence models

3 Optimization of a k–$\varepsilon$ Model with GEATFOAM

The Genetic Evolutionary Algorithms for Turbulence modeling tool (GEATFOAM) is a library developed in C++ that can be compiled with the OpenFOAM${^{\textregistered }}$ libraries. The library implements symbolic regression and gradients optimization techniques for constructing a mathematical expression for the anisotropy tensor.

Symbolic regression techniques are a subset of regression techniques, which allow you to search the space of mathematical expressions for a model that best fits the data [23, 24] , which, in the present case, is the stream-wise velocity over the y-lines displayed in Fig. 2. In symbolic regression analysis, new expressions are generated by randomly combining mathematical building blocks (such as constants or tensor, or some of their more complicated functions). The expressions are then tested against the data and catalogued according to an error, determined by some previously defined measure [25]. Subsequently, new expressions are constructed by recombining (more or less randomly in genetic algorithms) the previously obtained ones. The core concept beneath the recombination process is to prioritize the recombination of the better-fitting expressions, decreasing the mean error of the newly obtained expressions, and obtaining better-fitting ones for each subsequent iteration. Several techniques can be applied for performing the recombination process, namely, genetic programming [26], neural networks [25], and support vector machines [25]. However, genetic programming techniques have been demonstrated to outperform the others on problems in which simple and interpretable expressions should be obtained [27]. For the recombination process, GEATFOAM implements a symbolic tensorial version of the NSGA-II evolutionary algorithm proposed in [28].

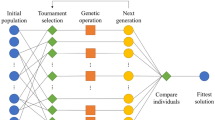
The flowchart of the library is presented in Appendix. The initial step consists in the generation of the mathematical blocks (constants and tensors) on which the expressions for the anisotropy tensor are built on. In mathematical terms, these building blocks belong to two different sets: a variable set and an operation set.

$$\begin{aligned} \varphi = \{ \mathbf {T_i}, C_i, I_2(\mathbf {S}),I_3(\mathbf {S}),I_4(\mathbf {S}), I_2(\mathbf {W}),I_3(\mathbf {W}),I_4(\mathbf {W}) \}, \nonumber \\ \vartheta = \{ *_{\mathfrak {R}^2,\mathfrak {R}^0},*_{\mathfrak {R}^0,\mathfrak {R}^0},/_{\mathfrak {R}^0,\mathfrak {R}^0},+_{\mathfrak {R}^2,\mathfrak {R}^2},+_{\mathfrak {R}^0,\mathfrak {R}^0},-_{\mathfrak {R}^2,\mathfrak {R}^2},-_{\mathfrak {R}^0,\mathfrak {R}^0}\}. \end{aligned}$$

(11)

The functional set $\varphi$ contains the variables for describing the nonlinear anisotropy tensor. In the present case, due to the rank of the anisotropy tensor and the geometric considerations explained in Sect. 2, the variables are the $\mathbf T _i$ tensors in Eqs. 6–8, the fitting constants and the second, third, and fourth invariants [29] of the shear rate and the vorticity tensors. The operator set $\vartheta$ contains the set of operations allowed over the set. For the present case, they are scalar-matrix multiplication ($*_{\mathfrak {R}^2,\mathfrak {R}^0}$), scalar multiplication ($*_{\mathfrak {R}^0,\mathfrak {R}^0}$) and division ($/_{\mathfrak {R}^0,\mathfrak {R}^0}$), matrix addition ($+_{\mathfrak {R}^2,\mathfrak {R}^2}$) and subtraction ($-_{\mathfrak {R}^2,\mathfrak {R}^2}$), and scalar addition ($+_{\mathfrak {R}^0,\mathfrak {R}^0}$) and subtraction ($-_{\mathfrak {R}^0,\mathfrak {R}^0}$).

Then, an initial number of ten expressions for the anisotropy tensor (referred to as individuals in genetic programming) are randomly generated, combining the variables from the allowed operations (e.g., $\mathbf {a}=C_1\mathbf {T_1}+C_3I_2(\mathbf {S})\mathbf {T_2}+C_3\mathbf {T_3}$). In GEATFOAM, each individual is represented by an open reading frame (ORF) [30]. Each expression may contain a set of fitting constants $C_i$, which are not necessarily optimally fitted to the data. Therefore, the next step is to optimize the fitting constants in each expression so as to minimize the value of the fitness function defined by Eq. 10. In proper mathematical terms, this is an unconstrained optimization problem for a fitness function $L_w:R^n \rightarrow R$, where n is the number of $C_i$ coefficients in the optimization model, a number that may vary between individuals. Defining $\mathbf {C}$ as the vector of coefficients to be optimized for the fitness problem, $\mathbf {g}=g_i=\frac{\partial L_w}{\partial C_i} \approx \frac{\varDelta L_w}{\varDelta C_i}$ as the finite difference approximated gradient of the fitness function at certain values of $C_i$, and $\mathbf {H}=H_{ij}=\frac{\partial ^2 L_w}{\partial C_i \partial C_j} \approx \frac{\varDelta L_w/\varDelta C_i}{\varDelta C_j}$ as the finite difference approximated Hessian, the iterative quasi-Newton optimization problem is implemented as follows:

$$\begin{aligned} \mathbf {H}^{(n)} \mathbf {p}^{(n)}= -\mathbf {g}^{(n)}, \nonumber \\ \mathbf {C}^{(n+1)} = \mathbf {C}^{(n)} + \mathbf {p}^{(n)}. \end{aligned}$$

(12)

At this point, a limitation is discovered, the optimization problem is not necessarily convex or, equivalently, the Hessian matrix is not necessarily positive-defined. This implies that the previous system may not converge to a minimum. To solve this issue, the method proposed by Forsgren et al. [31] is applied, in which the Hessian is factorized by a Cholesky algorithm with row pivoting. The Hessian factorization becomes $\mathbf {H}=\mathbf {L}\mathbf {D}\mathbf {L}^T$, replacing the negative values in the matrix diagonal with small positive values during the factorization process. Therefore, a descendent direction toward a minimum can be found independently of the convexity of the problem. This technique is usually referred to as the active set method.

Once the coefficients for each model have been optimized, the obtained expressions are arranged in a stack list that confers its fitting error to the data. Additionally, an extra error proportional to the size of the individual ORF is added for to prioritize simple expressions for the anisotropy models. Then, the recombination process takes place, in which a set of random genetic operations is applied to the ORFs prioritizing the reproduction of the better-fitting individuals. The genetic operations supported by GEATFOAM consist in changing terms in the tail of the ORF by introducing terms of other ORF (recombination), by introducing terms of the head of the same ORF (transposition) or changing it through random fragments of operators and/or variables (mutation). Once the genetic operations have taken place, a new set of averagely more fit expressions is introduced back into the loop. When an expression arrives to satisfy the error criteria imposed on the fitness function (less than $5\%$ of error in the stream-wise velocity over the y-lines), the iteration process finishes and the individual is extracted.

4 A Nonlinear Quadratic Closure for the Anisotropy Tensor Developed with the GEATFOAM Tool

The model obtained for the anisotropy tensor, resulting from the iteration process of the GEATFOAM process with a randomly generated initial population, is

$$\begin{aligned} \mathbf {a} = 0.074\mathbf {T_1}+0.521\mathbf {T_2}+0.071\frac{I_2(\mathbf {S})I_3(\mathbf {S})}{I_2(\mathbf {W})I_3(\mathbf {W})}\mathbf {T_3}-0.180\mathbf {T_4}. \end{aligned}$$

(13)

The output of GEATFOAM for the anisotropy tensor is a nonlinear quadratic model, since large extra weights have been assigned to big expressions during the optimization process. In order to assess the repeatability of the evolutionary process, different sets of random initial populations have been tested, obtaining a success ratio [32] for the model proposed in Eq. 13 of $85\%$, meaning that the model was obtained in $85\%$ of the evolutionary lines studied. None of the other models resulting from offsprings in the evolutionary process had a smaller error than Eq. 13, according to the definition of error by Eq. 10.

The results obtained for the optimized nonlinear quadratic model (Eq. 13) are compared against the DNS data, the standard k–$\varepsilon$ [14] and the nonlinear cubic model (Eqs. 5–8 [19]) in Fig. 4, for the stream-wise velocity over the y-lines shown in Fig. 2. Both nonlinear models outperform the standard k–$\varepsilon$ model. The model that best fits the DNS data is the optimized nonlinear quadratic model (13), which presents a uniform accuracy over all y-lines. The nonlinear cubic model (5–8) performs well on the first three lines, where the turbulence production is important, but have important errors downstream, where the turbulent dissipation should compensate the production.

The values for the fitness function $L_w$ of these models are compared in Table 2; it is observed that the optimized nonlinear quadratic model (13) satisfies the originally imposed error criteria. In terms of the turbulent kinetic energy and specific turbulent dissipation, the nonlinear modeling of the viscosity allows us to account for the turbulent structures produced by the shear stress history in the flow. This, in turn, allows to avoid the overprediction of k and $\varepsilon$ after the step expansion, accurately modeling the production and dissipation in the main recirculation bubble (graphical results are presented in the Appendix).

Fig. 4

Top-left: Results for the normalized stream-wise steady-state velocity for the lines $\frac{x}{H}=0.5$. Top-right: $\frac{x}{H}=4.0$. Bottom-left: $\frac{x}{H}=8.0$. Bottom-right: $\frac{x}{H}=20.0$. The DNS data points are taken as reference values. The results were obtained using the standard k–$\varepsilon$ model [14], the optimized nonlinear model (13), and Craft’s cubic nonlinear model [19]

Table 2 Assessment of the optimized nonlinear model against the standard k–$\varepsilon$ model and Craft’s nonlinear cubic model

In order to evaluate the extrapolability of the constructed anisotropic model, the results are applied to an axisymmetrical pipe expansion with a different Reynolds number. In principle, since the underlying physics of the axisymmetric expansion should be similar to that of the BFS, the developed nonlinear quadratic model (13) should perform well on this new geometry. Measured data for the axial velocities is provided in the work done by [33] at $x=0.05D$ and $x=0.25D$ after the expansion, and is taken as reference in the present case. The section has an expansion rate of 1.94 and the mean inlet velocity is fixed so that $Re=\frac{UD}{\nu }=2 \times 10^5$, taking the value of the kinematic viscosity as $\nu =10^{-5}\,\frac{\hbox {m}^2}{\hbox {s}}$. The standard k–$\varepsilon$ model [14] and the optimized nonlinear quadratic model (13) were tested on this geometry. Steady-state and 2D axisymmetrical simulations were performed, converging the mesh in each case. The results are shown in Fig. 5. A good agreement is observed between the nonlinear quadratic model (13) and the experimental results [33].

Fig. 5

Results for the normalized axial steady-state velocity for the lines Left: $\frac{x}{D}=0.05$ and Right: $\frac{x}{D}=0.025$. The results were obtained using the standard k–$\varepsilon$ [14] model and the evolved nonlinear quadratic model (13) model by means of nonlinear modeling of the anisotropy. The measured velocities are taken as reference values. For the k–$\varepsilon$ turbulent model, $L_w=11.51\%$, and for the modified model, $L_w=4.05\%$

5 Conclusions

In the present work, different turbulence models have been evaluated for a BFS geometry, with the objective of validating a model to be applied in the design of a molten salt fast reactor. On the RANS models side, the Wilcox k–$\omega$ model [17], the implemented cubic nonlinear viscosity model [19] and the SSG Reynolds Shear Stress transport model [20] mispredict the stream-wise components of the bulk velocities by 5–10%. In addition, the standard k–$\varepsilon$ model [14] presents an error of $15\%$ in the prediction of these velocities. As a consequence, they all fail to attain the required error of less than $5\%$ of mis-prediction in the stream-wise velocities. An LES multi-gradient [21] model was also tested in the BFS, having less than $1\%$ of error in the prediction of the stream-wise velocities. However, it consumes excessive computational resources and its convergence is complicated for complex geometries, making it inadequate to use for design purposes and for its application to the MSFR. Therefore, the development of an adapted turbulent model was necessary for the BFS section. A new nonlinear quadratic model for the anisotropy tensor, based on the k–$\varepsilon$ equations, was developed by means of symbolic regression through genetic evolutionary programming (the GEATFOAM tool).

To the current extent, the tool still presents the limitation that the results found are sensible to the initial population proposed in the evolutionary process, and different results for the anisotropy tensor are obtained between successive runs of the tool. However, by increasing the cost of high-order nonlinear models, an efficient quadratic model for the anisotropy tensor was found, having an error of less than $5\%$ for the analyzed BFS. Furthermore, the extrapolability of this new model was successfully evaluated for a pipe expansion case.

Appendix

See Figs. 6 and 7

Fig. 6

Flowchart of the GEATFOAM tool. First, an initial population is proposed and its chromosomes are expressed in ORFs. A first internal loop optimizes the free scalar coefficients of the ORF through a conjugate gradient method. Then, a set of genetic operations is introduced, changing the population for one with a better fit and the iterations are repeated. The process ends when one individual attains the error criteria

Fig. 7

Results obtained for the normalized turbulent kinetic energy $k^*=\frac{k}{U_{mean}^2}$ and the normalized specific turbulent dissipation $\varepsilon ^*=\frac{\varepsilon \nu }{U_{mean}^4}$. The standard k–$\varepsilon$ model overpredicts k and $\varepsilon$ after the expansion, causing an overprediction in the turbulent viscosity $nu_T$ and a rapid development of the velocity profile after the step. The optimized nonlinear k–$\varepsilon$ model correctly models the turbulent viscosity as a function of the history of the stresses in the fluid, allowing us to avoid the initial burst of the standard k–$\varepsilon$ turbulent model and being able to resolve the evolution of k and $\varepsilon$ in the main recirculation bubble of the BFS