Cavitating Flow in a 3D Globe Valve

Abstract

The efficiency of control valves operating with liquids is highly conditioned by the occurrence of cavitation when they undergo large pressure drops. For severe service control valves, the subsequent modification of their performance can be crucial for the safety of an installation. In this work, the solver interPhaseChangeFoam, implemented in OF v2.3, is used to characterize the flow in a globe valve, with the objective to evaluate its capability in solving cavitating flows in complex 3D geometries. An Homogeneous Equilibrium approach is adopted, and phase change is modeled using the Schnerr and Sauer cavitation model. Confrontation with experimental data is carried out in order to validate the numerical results. It is found that the solver predicts correctly the location of vapor cavities, but tends to underestimate their extension. The flow rate is correctly calculated, but in strong cavitating regimes, it is affected by the underprediction of vapor cavities. The force acting on the stem is found to be more sensitive to the computation parameters.

1 Introduction

In nuclear power plants and petrochemical installations, certain specific control valves play a critical role in the functioning of the plants. Therefore, these severe service valves have to be responsive, precise and perfectly reliable. The efficiency of control valves operating with liquids is highly conditioned by the occurrence of cavitation when they undergo large pressure drops. In the vena contracta that develops in the restriction region, the fluid is accelerated such that the local pressure may decrease below the vapor pressure and generate cavitation. When cavitation is fully developed, it can modify the performance of the valve and even limit the flow rate close to chocked flow conditions. In practice, the occurrence of cavitation is difficult to detect, because of the harsh and noisy conditions under which the valves operate. This is why CFD has become an important tool for the design and characterization of severe service control valves. However, it has scarcely been used up to now for cavitating flows, due to the important computational times involved and the sensitivity of the solvers to empirical parameters. Chen and Stoffel [4] investigate the transient effects of cavitation in a poppet valve during closure, but their computational domain is axisymmetric and limited to the vicinity of the restriction region. Bernad et al. [1] extend the analysis of cavitation to a 3D poppet valve. Beune et al. [2] were the first to publish a validated CFD study with a safety relief valve. They show that taking into account phase change in CFX allows for reducing the overestimation of the mass flow rate in the valve and the force exerted by the fluid on the stem in a spectacular way. Couzinet et al. [5] also use a mixture model in CFX to predict the flow capacity of a safety relief valve in cavitating regimes, and they propose a correction of the liquid vapor pressure to take into account the effect of turbulence. The topology of the flow field is very well validated with experimental data obtained through Particle Image Velocimetry. Ferrari and Leutwyler [6] also propose a single phase numerical study of the flow in a globe valve with Fluent. But more importantly, they perform an extensive experimental study, gathering unsteady measurements of flow forces on the stem and flow visualizations on a transparent mock-up.

Up to now, all the numerical studies were conducted with commercial codes. In this paper, we propose evaluating the capabilities of the open source CFD code OpenFoam$^{\textregistered }$ (OF) in predicting the unsteady cavitating flow in a 3D globe valve geometry. For that, we validate the performances of the solver interPhaseChangeFoam using the experimental data of Ferrari and Leutwyler [6] to validate the results.

2 Numerical Approach

2.1 Governing Equations

To simulate cavitating flows, the two phases, liquid (l) and vapor (v), have to be taken into account in the governing equations, and the phase transition mechanism due to evaporation-condensation has to be modeled. In the interPhaseChangeFoam solver, implemented in OpenFoam$^{\textregistered }$ v2.3, the two phases are assumed to be homogeneously mixed and in mechanical equilibrium, following the Homogeneous Equilibrium approach. Hence, only one set of momentum and continuity equations is solved for the mixture. It is assumed that there is no interaction and no slip between vapor bubbles. The VOF (Volume of Fluid) technique is used to track the interface between liquid and vapor.

Since liquid and vapor are assumed to be perfectly mixed within each cell of the mesh, the density and viscosity of the mixture are expressed as a function of the liquid and vapor volume fractions, $\alpha _l$ and $\alpha _v$, respectively

$$\begin{aligned} \rho= & {} \alpha _{l} \rho _{l}+\alpha _{v} \rho _{v} \end{aligned}$$

(1)

$$\begin{aligned} \mu= & {} \alpha _{l} \mu _{l}+\alpha _{v} \mu _{v} \end{aligned}$$

(2)

The subscripts l and v stand for the properties of pure liquid and pure vapor, respectively. The constraint condition to fullfill is

$$\begin{aligned} \alpha _{l}+\alpha _{v} = 1. \end{aligned}$$

(3)

To close the system, a transport equation for $\alpha _l$ is needed. Using Eq. (1) in the continuity equation, and considering the mass transfer between phases due to cavitation, the transport equation for $\alpha _l$ can be derived as [11]

$$\begin{aligned} \frac{\partial \alpha _{l}}{\partial t}+\nabla \cdot {}(\alpha _{l} \mathbf U ) + \nabla \cdot {}(\alpha _l(1-\alpha _l)\mathbf U _r) = \frac{\dot{m}^- -\dot{m}^+}{\rho _l} \end{aligned}$$

(4)

where $\mathbf U$ is the velocity vector, $\mathbf U _r$ is the relative velocity vector at the interface between the two phases, $\dot{m}^+$ is the mass transfer rate by vaporization and $\dot{m}^-$ the one by condensation.

2.2 Cavitation Model

The source term of mass transfer (RHS of Eq. 4) requires an appropriate cavitation model. Different cavitation models can be found in the literature. In this work, the cavitation model of Sauer and Schnerr [11] is chosen. This model considers an initial amount of micro-spherical vapor bubbles with a radius R, which constitute nucleation sites for cavitation. They grow and collapse according to the bubble pressure dynamics governed by the first-order Rayleigh Plesset equation.

In the model of Sauer and Schneer [11], the vapor fraction is calculated based on the volume of the spherical nuclei with radius R, and their number per cubic meter of liquid, $n_0$, as

$$\begin{aligned} \alpha _{v}=\alpha _{l} \cdot n_0 \frac{4}{3} \pi R^3 \end{aligned}$$

(5)

The combination of Reyleigh Plesset equation and Eqs. (4) and  (5) gives the final expression for the mass transfer source terms

$$\begin{aligned} \dot{m}^+=C_v (1-\alpha _v) \frac{3\alpha _v}{R} \frac{\rho _v \rho _l}{\rho }\sqrt{\frac{2}{3}\frac{\vert max(0, p_v -p) \vert }{\rho _l}} \end{aligned}$$

(6)

$$\begin{aligned} \dot{m}^-=C_c (1-\alpha _v) \frac{3\alpha _v}{R} \frac{\rho _v \rho _l}{\rho } \sqrt{\frac{2}{3}\frac{\vert max(0, p -p_v) \vert }{\rho _l}} \end{aligned}$$

(7)

where R is derived from Eq. (5).

As inputs, the model therefore requires the volumetric concentration of nuclei $n_{0}$, their initial radius R, and the empirical coefficients $C_v$ and $C_c$. The latter depend on the state of deaeration of the liquid and the mean flow. To quantify the influence of those parameters in the OpenFoam$^{\textregistered }$ solver, a sensitivity study was conducted for a sharp orifice by Gosset et al. [7], who concluded that there was no significant difference between results for $n_0 \le 10^{10}$ m$^{-3}$ and $10^{-7} \le R \le 10^{-5}$ m. In this work, the value of the parameters are set at $R=5 \times 10^{-6}$ m, $n_0=10^{14}$ m$^{-3}$, $C_v=1$ and $C_c=2$ ($C_c=2$ because condensation is considered faster than vaporization). Note that $C_v$ and $C_c$ are set empirically, and the latter values are known as being valid for a wide range of flows.

Originally, in the model by Sauer and Schneer, the phase change threshold pressure ($p_v$) is assumed to be equal to the saturation pressure ($p_{vap}$) in the absence of dissolved gases. In this study, the value of $p_{vap}$ is set at 3540 Pa, which is estimated with the Rankine formula for water at 26 $^\circ$C. Nevertheless, several investigations have shown significant effects of turbulence on cavitating flows e.g., [9]. Several authors, including Singhal et al. [12] and Bouziad [3], have suggested taking it into account by integrating in time the contributions of $\dot{m}_{v}^+$ and $\dot{m}_{c}^-$ assuming a probability density function of the pressure fluctuations due to turbulence. Bouziad [3] proposes a simple approach based on a correction of $p_v$ using the shear strain to modify the bubble pressure. The corrected value of $p_v$ becomes

$$\begin{aligned} p_v=p_{vap}+(\mu +\mu _t)S \end{aligned}$$

(8)

where S is the shear strain and $\mu _t$ is the turbulent viscosity.

Couzinet et al. [5] and Rodriguez Calvete et al. [10] evaluate the effect of using this approach in a safety relief valve and globe valve flows, respectively. They show that turbulence effects contribute to an increase of up to 500% of the vapor threshold pressure ($p_v$), which directly influences the location and extension of cavitation. It must be noted that this kind of approach is highly dependent on the quality of turbulence prediction, therefore an appropriate turbulence model should be chosen.

2.3 Turbulence Model

For this 3D pressure-driven flow, a URANS model for turbulence is adopted instead of Large Eddy Simulation, disregarded in this study due to its time cost. In this study, the $k-\omega -SST$ has been chosen for all the computations. Default parameters of the turbulence model were used. The Reynolds number varies between 1.81 and $3.3 \times 10^5$ for all of the cases in this study.

On the other hand, the strong pressure gradients expected in the flow make it necessary to solve the boundary layer accurately up to the viscous sublayer, especially close to the stagnation zone. This means that a high resolution mesh at the wall is needed, so that the use of standard wall functions is avoided. $k-\omega -SST$ adapts to the local mesh density in the boundary layer region using the Spalding wall function (nutSpaldingWallFunction). The $y^+$ values range from 0.1 to 15 on the piston, with an average of 5.

2.4 Computational Domain

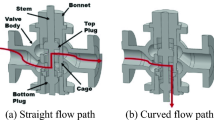
The computational domain is defined from the geometrical model sketched in Fig. 1 which matches the geometry of a 2$^{\prime \prime }$ commercial globe valve. It corresponds exactly to the mock-up built by Ferrari and Leutwyler [6] to visualize the flow inside the valve. Under cavitating conditions, Couzinet et al. [5] find that the flow is substantially asymmetric in a safety relief valve, which is why the whole domain is simulated here.

Fig. 1

Valve model and computational domain

The mesh is designed with the meshing software Ansys-ICEM, using a fully structured topology and only hexahedral cells. In order to preserve low $y^+$ at the wall, a special refinement in the restriction is made, as shown in Fig. 2. A focus on the 6 mm lift of the stem is proposed in this study. A mesh independence study is performed using three different grid sizes. Since cavitation develops not only in the restriction region, but also downstream of the valve body, in the outlet duct, special attention is given to the refinement of this region (Fig. 2). The results in terms of volumetric flow rate (Q), transversal and axial force acting on the stem ($F_{\textit{trans}}$ and $F_{\textit{axial}}$) are presented in Table 1 for the different meshes. Slight differences are found between the coarse and the medium mesh, which become negligible between the medium and the fine mesh. In addition, the extension of vapor cavities is very similar for the two finest grids. Therefore, the medium mesh of 1.65 million cells is chosen as the base mesh.

Fig. 2

Mesh restriction detail

For the boundary conditions, a total absolute pressure is fixed at the inlet ($p_{t,in}$) and a static pressure is fixed at the outlet ($p_{out}$) (Fig. 1). For velocity, corresponding Neuman conditions are set (i.e., pressureVelocityInlet at the inlet and zeroGradient at the outlet).

2.5 Numerical Methodology

The algorithm PIMPLE, which combines both SIMPLE and PISO for unsteady simulations, is used in order to keep the computational time within reasonable limits. It should be underlined that even if the time step can be set to guarantee the stability of the solution, the phase change process due to cavitation is very fast, and the time step must be sufficiently small so as to capture the relevant phenomena and control the non linearities generated by the mass transfer term.

Table 1 Results of the mesh sensitivity study

Regarding time schemes, the second-order backward and Crank Nicholson schemes both result in numerical instabilities and divergence of the solution, even with $C_{o,max} < 1$. Therefore, a first order Euler implicit scheme is adopted. An adaptive time step based on a maximum Courant number, $C_{o,max}=3$, is set. For the spatial discretization, second-order bounded schemes (limitedLinear 1.0) are used for the divergence terms related to U, k and $\omega$ . For divergence of alpha div(phi,alpha) and for the compression of the interface div(phirb,alpha), the vanLeer and interfaceCompression schemes are respectively chosen. Regarding gradient schemes, cellMDLimited Gauss linear 0.777 is set as default. To avoid unboundedness issues in k and $\omega$, the edgeCellsLeastSquares 1.0 scheme is set. For Laplacian schemes, Gauss linear limited 0.333 is used to overcome non-orthogonal features, which are difficult to avoid in such a complex 3D geometry.

3 Results

3.1 Operating Conditions

The numerical study is based on the experimental conditions described in [6]. The authors run experiments for a set of cavitating conditions, varying the pressure drop across the valve $\varDelta p$ and the valve opening (lift). To relate the pressure drop with the intensity of cavitation, the cavitation number $\sigma$ is defined as

$$\begin{aligned} \sigma = \frac{p_{in}-p_{out}}{p_{in}-p_{vap}} \end{aligned}$$

(9)

The simulations are performed for valve openings of 6 and 4 mm. Table 2 reports the conditions corresponding to the different computations.

The outlet pressure $p_{out}$ is set at values of 0.4 and 0.8bar, in order to induce earlier cavitation. Cases Dp07 and Dp08, with $p_{out} = 0.8$ bar, correspond to non-cavitating conditions, in agreement with the experimental observations. In contrast, cases Dp15-18-23, with $p_{out}=0.4$ bar, correspond to fully developed cavitating conditions, as shown in Fig. 3.

Table 2 Experimental and numerical conditions

Fig. 3

Isosurface $\alpha _v =0.5$ at cases $\varDelta p = 1.5$ bar ($\sigma = 0.80$) , $\varDelta p = 1.8$ bar ($\sigma =0.83$) and $\varDelta p = 2.3$ bar ($\sigma = 0.86$)

3.2 Influence of Turbulence on $p_v$

As mentioned above, the correction of $p_v$ (8) accounts for the influence of turbulence on cavitation. Figure 4 shows the ratio of the corrected pressure threshold ($P_v$) and the saturation pressure ($P_{vap}$), which confirms how the correction affects the areas where cavitation is developed. Therefore, this correction is implemented into the interPhaseChangeFoam solver to account for turbulence effects on the prediction of cavitation.

Fig. 4

Vapor phase iso-surface ($\alpha _v$ = 0.5) with and without $p_v$ correction in OpenFoam$^{\textregistered }$

3.3 Flow Topology

Figure 3 shows the extension of vapor cavities at 3 different pressure drops. It can be seen how an increase of $\sigma$ from 0.80 ($\varDelta p = 0.71$ bar) to 0.86 ($\varDelta p = 2.22$ bar) leads to an increase of the vapor extension towards the valve outlet.

Finally, Fig. 5 illustrates the unsteady behavior of cavitation by comparing the experimental observations with the predictions of OpenFoam$^{\textregistered }$, both at $\varDelta p=1.54$ bar (lift 4 mm). Two isosurfaces, at $\alpha _v =0.5$ and $\alpha _v = 0.1$, are superimposed to illustrate the extent of vapor–liquid mixing. Experimentally, the sequence of images is captured by a high-speed camera at a frequency of 13 KHz, while the vapor fraction fields are sampled at 2 KHz. The sequences are synchronized in time to compare the behavior of vapor cavities qualitatively. In this close-up, it can be clearly seen how the vapor cavities grow in the restriction region around the stem, and extend downstream the valve body in both cases. The location of vapor cavities is well predicted, and a certain synchronization of the bubble growth and collapse can be seen as well.

Fig. 5

Left: Experimental high-speed camera visualization (Lift 4 mm, $\varDelta p$ = 1.54 bar, Q = 23 m$^3$/h); Right: Numerical cavitation sequences of isosurfaces $\alpha _v = 0.5$ (Blue), $\alpha _v = 0.1$ (Yellow), with OpenFoam$^{\textregistered }$ (Lift 4 mm, $\varDelta p$ = 1.54 bar, Q = 26.4 m$^3$/h)

3.4 Flow Curve

For single phase turbulent flows through control valves, the flow rate Q in m$^3$/h is a linear function of the square root of the pressure drop ${\varDelta p}$ in bar across the valve [8]. This relation is expressed as

$$\begin{aligned} Q = K_v \sqrt{\varDelta p} \end{aligned}$$

(10)

where $K_v$ is the flow coefficient, and the slope of the characteristic curve of the valve. In fact, $K_v$ represents the volumetric flow rate of water circulating in a valve under a 1 bar pressure drop, at a given valve aperture. Under cavitating conditions, the characteristic flow curve deviates from this linear behavior, until it reaches the chocked flow condition. The latter occurs when Q no longer varies with $\varDelta p$ due to a vapor blockage at the valve outlet.

The volumetric flow rates obtained numerically are compared to the experimental data [6] in Fig. 6. The prediction by OpenFoam$^{\textregistered }$ presents a good agreement with the experiments, with an error of 1.5% on the prediction of $K_v$. However, it can be noticed that at the highest pressure drops, the flow rates predicted numerically remain on a linear curve, while the experimental values deviate slightly from their linear evolution. This indicates that the solver tends to underestimate the influence of vapor cavities on the head loss across the valve.

Fig. 6

Characteristic flow curve for a valve opening of 6 mm

3.5 Forces on the Stem

The experimental study [6] focuses on the components of the force acting on the stem. Figure 7a, b compare the axial and transversal force components found experimentally and numerically, at 4 and 6 mm lift, respectively. It can be seen that the code strongly underestimates the transversal forces and overestimates the axial forces at 6 mm lift (error up to 350%), while at 4 mm lift the error on the axial forces is less than 20%. Unfortunately, the experimental data of transversal forces at 4 mm are not available. This behavior, where the axial force is dominant, normally corresponds to small valve apertures [6]. It is at larger apertures that the force ratio is inversed, possibly due to the acceleration of the fluid under the disk, which generates lower pressures. According to experimental results [6], transversal forces are already dominant at a valve opening of 6 mm. Probably, the transition between the two behaviors (axial/transversal dominant force) is located within this range of lift (4–6 mm). Axial force measurements are also known to be affected by the friction of the stem in its seating, which may cause a bias in the measurement of the hydrodynamic force.

Fig. 7

Forces on the stem

4 Conclusions

In this work, the interPhaseChangeFoam solver is assessed for the simulation of a 3D cavitating flow in a globe valve that was characterized experimentally. The code succeeds reasonably well in predicting the flow rate through the valve, but it tends to underestimate the mass transfer by cavitation, which explains why the quality of the predictions decreases slightly under conditions of fully developed cavitation. Qualitatively, OpenFoam$^{\textregistered }$ correctly calculates the location of cavitation, and the highly unsteady behavior of cavities is well reproduced. Regarding the force exerted by the fluid on the stem, at 6 mm lift, it predicts an axial force larger than the transversal one, in contrast with the experiments, possibly due to measurement errors. A similar behavior was found with a coupled solver in Ansys-CFX [10]. The simulations at 4mm lift are in much better agreement with the experiments in terms of axial force prediction. Probably, the transition between the two behaviors (axial/transversal dominant force) is located within this range of lift (4–6 mm). The influence of the treatment of the vapor phase is also under investigation, to try to improve the prediction of vapor extension.