1 The Interfacial Flow Equations

We start by writing the equations of motion governing the flow of two incompressible, immiscible fluids. To keep things simple, we will ignore viscous effects and surface tension. What remains are the passive advection equation,

$$\begin{aligned} \frac{\partial \rho }{\partial t} + \nabla \cdot (\rho \mathbf u) = 0, \end{aligned}$$
(1)

the incompressibility equation,

$$\begin{aligned} \nabla \cdot \mathbf u = 0, \end{aligned}$$
(2)

and the Euler equations,

$$\begin{aligned} \frac{\partial \rho \mathbf u}{\partial t} + \nabla \cdot (\rho \mathbf u\mathbf u) = -\nabla p +\rho \mathbf g. \end{aligned}$$
(3)

Here, \(\rho \) is the fluid density field taking the constant value, \(\rho _1\), in the reference fluid and the constant value, \(\rho _2\), in the other fluid, \(\mathbf u\) is the velocity field, p is the fluid pressure and \(\mathbf g\) is the constant downward pointing gravity vector. In the interFoam solver of OpenFOAM\(^{\textregistered }\), these equations are discretized in the finite volume framework and advanced in time in a segregated manner. Within a time step, Eq. 1 is used to update the density field in time, followed by a procedure for solving Eqs. 2 and 3 to update the pressure and velocity field in time. The details of the implementation are well-described in the paper [3], which also gives an overview of the challenge faced by the interfacial CFD community in keeping the density field sharp and bounded, with spurious velocities at the interface, and with handling of large density ratios. The development of the isoAdvector interface advection method is a first step in our efforts to solve these problems and increase the general performance and accuracy of interfacial flow simulations. In the following, we will briefly explain how isoAdvector works.

2 IsoAdvector for Interface Advection

The basic equation that we will solve is Eq. 1, recast in the volume-of-fluid formulation. For this recasting, we need a number of definitions: First, we divide the computational domain into cells, \(\mathscr {C}_1, \mathscr {C}_2, \ldots \), and define the notation for the cell-averaged value of a field, \(f(\mathbf x,t)\), at time t,

$$\begin{aligned} \langle f \rangle _i(t) \equiv \frac{1}{V_i}\int _{\mathscr {C}_i} f(\mathbf x,t) dV, \end{aligned}$$
(4)

where \(V_i\) is the volume of cell i. Defining the indicator field

$$\begin{aligned} H(\mathbf x,t) \equiv \frac{\rho (\mathbf x,t)-\rho _2}{\rho _1-\rho _2}, \end{aligned}$$
(5)

the volume fraction (of fluid 1) in cell i is then defined as

$$\begin{aligned} \alpha _i(t) \equiv \langle H \rangle _i. \end{aligned}$$
(6)

We will denote the mesh faces, \(\mathscr {F}_1,\mathscr {F}_2,\ldots \), and the list of labels of faces on the boundary of cell i will be denoted \(B_i\). On the time axis, the times, \(t_1< t_2 < \cdots \) define the time intervals (or steps), \([t_n,t_{n+1}]\), over which the governing equations are integrated. We will use superscripts to denote a function evaluated at one of these times, \(f^n = f(t_n)\).

With these definitions in place, we can now rewrite Eq. 1 in terms of H and integrate it over the volume of cell i and over the time interval \(\left[ t_n,t_{n+1}\right] \). This converts the equation into an evolution equation for the volume fraction in cell i. Unfortunately, space does not allow a full derivation here (the reader is referred to [1] for more details), but the form of the equation is

$$\begin{aligned} \alpha _i^{n+1} = \alpha _i^n -\frac{1}{V_i}\sum _{j\in B_i} \varDelta V_{ij}^n, \end{aligned}$$
(7)

where the quantity \(\varDelta V_{ij}^n\) is the total volume of fluid 1 flowing from cell i during the time interval \([t_n,t_{n+1}]\) into the neighbour cell with which it shares face j. This important quantity is defined by

$$\begin{aligned} \varDelta V_{ij}^n \equiv \int _{t_n}^{t_{n+1}}\int _{\mathscr {F}_j}H(\mathbf x,\tau )\mathbf u(\mathbf x,\tau )\cdot d\mathbf S_{ij}d\tau . \end{aligned}$$
(8)

Here, \(d\mathbf S_{ij}\) is the infinitesimal surface element of face j, oriented out of cell i, so if cell k is the other cell of face j, then \(d\mathbf S_{kj} = -d\mathbf S_{ij}\) and \(\varDelta V_{kj}^n = -\varDelta V_{ij}^n\).

The art of constructing a volume-of-fluid algorithm is all about coming up with the best possible approximation of \(\varDelta V_{ij}^n\) given the incomplete available data. In our collocated finite volume framework, the available data consists of the volume fractions \(\alpha _i^n\), the cell- averaged velocities, \(\langle \mathbf u\rangle _i^n\), and the volumetric face fluxes,

$$\begin{aligned} \phi _{ij}^n \equiv \int _{\mathscr {F}_j}\mathbf u(\mathbf x,t_n)\cdot d\mathbf S_{ij}. \end{aligned}$$
(9)

In the following, we show how isoAdvector uses these data and a number of geometric considerations to come up with an approximation for \(\varDelta V_{ij}^n\).

Fig. 1
figure 1

Interpolation of volume fraction to a vertex from all surrounding cells

Full size image

2.1 Interface Reconstruction

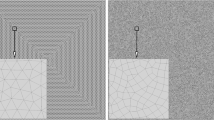
We start by noting that most cells will normally be fully immersed in either fluid 1 or fluid 2 during the time interval, and for such a cell, the advection problem is trivial, since there is only one fluid fluxed through all its faces. The surface cells requiring special treatment are those containing both fluid 1 and fluid 2. We will define a surface cell as one with \(\varepsilon< \alpha _i^n<1-\varepsilon \), where we typically set \(\varepsilon = 10^{-8}\) in our calculations. The first step in finding \(\alpha _i^{n+1}\) for such cells is to reconstruct the fluid interface inside the cell from the available data, \(\alpha _i^n\) at time \(t_n\). In the isoAdvector method, this is done by calculating an isosurface inside the cell. For this purpose, we need to first interpolate the volume fractions from the cell centres to the vertices. This process is illustrated in Fig. 1. This interpolation can be done in various ways. For convenience, we have chosen the inverse distance weighting provided by the volPointInterpolation class.

With volume fractions interpolated to all vertices of cell i, we can choose an isovalue, \(\alpha _0\), and construct the \(\alpha _0\)-isosurface inside the cell. This we do by going through all the cell’s edges and determining whether they are cut by the isosurface. An edge is cut, if the interpolated volume fraction at one end is larger than \(\alpha _0\) and the value at the other end is smaller than \(\alpha _0\). If that is the case, we calculate the intersection point along the edge by linear interpolation. Connecting these intersection points across the cell faces, we construct the cell–isosurface intersection, as illustrated in Fig. 2. The representation of this intersection will be called an isoface, because it is really just an internal face cutting the cell into two subcells. We can calculate the face centre, \(\mathbf x_S\), and face unit normal vector, \(\hat{\mathbf n}_S\), for this isoface as for any other mesh face (black dot and vector in Fig. 2).

If we imagine sweeping the isovalue, \(\alpha _0\), from the lowest to the highest cell vertex \(\alpha \) value, the isoface will pass through the cell. Which isovalue in this interval should we choose for a particular surface cell? Our answer is the isovalue that makes the isoface cut the cell into subcells of subvolumes in accordance with the cell’s volume fraction, \(\alpha _i^n\). To find this isovalue (different in each surface cell), we have implemented an efficient root-finding algorithm that exploits the fact that the volume fraction is a piecewise cubic polynomial in \(\alpha _0\). The details of this algorithm are further described in [1]. This concludes our description of the interface reconstruction at time \(t_n\).

Fig. 2
figure 2

Construction of the isoface inside a surface cell

Full size image

2.2 Interface Advection

The next step is to exploit our new knowledge about the interface position inside surface cells at time \(t_n\) to estimate how much of the total fluid volume transported across a face during a time step, \([t_n,t_{n+1}]\), is fluid 1 and how much is fluid 2. We will first make the assumption that \(\mathbf u(\mathbf x,\tau )\) in Eq. 8 can be replaced by an appropriately chosen constant vector \(\tilde{\mathbf u}_j^n\), which is representative of the velocity on the face during the whole time interval. We also assume that we can write

$$\begin{aligned} d\mathbf S_{ij} = \hat{\mathbf n}_{ij}(\mathbf x)dA \approx \frac{\mathbf S_{ij}}{|\mathbf S_{ij}|} dA, \end{aligned}$$
(10)

where \(\hat{\mathbf n}_{ij}\) is the (for a non-planar face spatially varying) unit normal vector and \(\mathbf S_{ij}\) is the mean normal vector of face j pointing out of cell i. Then, the volumetric face flux can be defined as \(\tilde{\phi }_{ij}^n \equiv \tilde{\mathbf u}_j^n\cdot \mathbf S_{ij}\), and \(\varDelta V_{ij}^n\) in Eq. 8 can be approximated by

$$\begin{aligned} \varDelta V_{ij}^n \approx \frac{\tilde{\phi }_{ij}^n}{|\mathbf S_{ij}|}\int _{t_n}^{t_{n+1}}\int _{\mathscr {F}_j}H(\mathbf x,\tau )dA d\tau . \end{aligned}$$
(11)

In the current implementation, we simply use the volumetric face fluxes, \(\phi _{ij}^n\), at the beginning of the time step for \(\tilde{\phi }_{ij}^n\).Footnote 1 The remaining area integral in Eq. 11 is just the area of face j that is submerged in the reference fluid. This area we will denote by

$$\begin{aligned} A_j(\tau ) \equiv \int _{\mathscr {F}_j}H(\mathbf x,\tau )dA. \end{aligned}$$
(12)

If we want to be able to take time steps in which the interface moves a substantial fraction of a cell size, we should come up with an estimate of how \(A_j\) varies with time within a time step. The topmost face of the polygonal prism cell in Fig. 2 is reproduced in Fig. 3 with the initial face–interface intersection line at \(t_n\) shown in blue.

Fig. 3
figure 3

Face–interface intersection line sweeping the face

Full size image

To estimate how this line sweeps over the face as the isoface moves in the velocity field, we first interpolate the velocity field to the initial isoface centre, \(\mathbf x_s\), shown with a black dot in Fig. 2. We can then take the dot product of the interpolated velocity with the isoface unit normal, \(\hat{\mathbf n}_S\), to obtain the speed of the isoface motion perpendicular to itself, \(U_S\). For a vertex, \(\mathbf x_v\), in Fig. 3, we can also estimate the perpendicular distance to the isoface by \(d_v = (\mathbf x_v-\mathbf x_S)\cdot \hat{ \mathbf {n}}_S\). With the calculated isoface normal speed and vertex-to-isoface distance, we can then estimate the time of arrival at vertex \(\mathbf x_v\) to be \(\tau _v = d_v/U_S\). In this way, we obtain the “vertex arrival times”, \(\tau _1,\tau _2,\ldots \), shown in Fig. 3. As illustrated, some of these will generally be outside the integration interval, \([t_n,t_{n+1}]\) and some will be inside. The crucial point is now, that between two such times, say, \(\tau _2\) and \(\tau _3\) in Fig. 3, the face–interface intersection line sweeps a quadrilateral. If we assume the line sweeps this quadrilateral steadily, we can come up with an analytical expression for the way in which \(A_j\) depends on \(\tau \) on this sub-interval. This expression is a quadratic polynomial in \(\tau \) and its coefficients depend only on the shape of the quadrilateral. The resulting time variation of \(A_j(\tau )\) as the line sweeps the face is illustrated in Fig. 4.

With a piecewise quadratic polynomial for \(A_j(\tau )\) in Eq. 12, its time integral in Eq. 11 is a piecewise cubic polynomial, and \(\varDelta V_{ij}^n\) is finally obtained as the sum of the contributions from these sub-intervals. We note that a face of a surface cell may initially be fully immersed in fluid 1 or 2, and then become intersected during the time interval \([t_n,t_{n+1}]\). With the calculated vertex arrival times, this situation corresponds to \(\tau _1 > t_n\) (the \(t_n\) line in Fig. 4 would then be further to the left), and it is treated by fluxing pure fluid 1 or 2 through the face in the sub-interval \([t_n,\tau _1]\). Similarly, if the interface leaves the face during \([t_n,t_{n+1}]\), we will have \(\tau _5 < t_{n+1}\) for a pentagonal face (the \(t_{n+1}\) line would then be further to the right in Fig. 4), and we must flux pure fluid 1 or 2 through the face during the last sub time interval \([\tau _5,t_{n+1}]\).

There is one final decision we must make before our advection routine is complete: for a face j, both its owner and neighbour cell may be surface cells with their isofaces not coinciding exactly on face j due to the different isovalues used in the two cells and not moving with exactly the same velocity due to the spatial variations in the velocity field. Which cell should be used to calculate \(\varDelta V_{ij}^n\) for this face? In our current implementation, we have chosen to let \(\varDelta V_{ij}^n\) be determined by the upwind cell, i.e., the owner if \(\phi _j^n > 0\) and the neighbour if \(\phi _j^n < 0\).

Fig. 4
figure 4

Submerged face are, \(A_j(\tau )\), as a piecewise quadratic polynomial

Full size image

2.3 Bounding

The test cases provided with the released isoAdvector code [2] show that the method outlined above generally gives very good estimates of \(\varDelta V_{ij}^n\) and leads to accurate interface advection, as long as the interface is well resolved by the mesh and time step size is limited to CFL \(< 1\). In some situations, there may, however, arise small inaccuracies, which can build up over time and lead to intolerable levels of unboundedness. To prevent the gradual build up of unboundedness, we have introduced a bounding step that detects unboundedness and tries to adjust the \(\varDelta V_{ij}^n\)’s of unbounded cells with a procedure that is described in detail in [1]. If this pure redistribution step fails, the provided code also gives the option of brute-force non-volume preserving chopping \(\alpha _i^{n+1}\) after each advection step to guarantee boundedness. Activating this will ruin the machine precision volume conservation, but our experience so far indicates that, in many situations, the resulting volume conservation error is very small.

In the current isoAdvector implementation, we assume that there is only a single isoface inside a cell. There are several occasions when one would expect more isofaces inside a cell. One such situation is when a planar interface passes a non-planar mesh face with which it is close to parallel. During the passage, the face and interface will intersect at more than two points and the face–interface intersection cannot be represented by a single straight line. Proper treatment of such an event can be implemented by on-the-fly decomposition of the non-planar face into triangular subfaces sharing the face centre as their common apex. A face–interface intersection line can then be calculated for each triangle separately (a triangular face can, at most, have two intersection points with the interface).

Another situation with more than one isoface inside a cell is when two separate volumes of fluid approach each other and collide inside a cell. Then, there will be a time interval just before the collision during which each volume has its own separate piece of interface within the cell. In this event, the solution could be to decompose the whole cell into tetrahedra sharing the cell centre as their common apex and separately reconstruct the interface in each subcell. This solution has not yet been implemented.

We have experienced that, due to these shortcomings of the current implementation, the bounding errors can be substantial, e.g., on polyhedral meshes with many highly non-planar faces of the type obtained by generating the dual mesh of a random tetrahedral mesh. The method still works on such meshes if switching on the brute-force chopping described above, but one may then experience substantial loss of volume conservation. We plan to implement the fixes described above in a future release of the code.

3 Pure Advection Tests

In this section, we compare the performance of isoAdvector and MULES with two standard pure advection test cases with a predefined velocity field.

3.1 Notched Disc in Solid Body Rotation

Our first test case is the notched disc in solid body rotation, which has become a standard test case since its introduction in [4]. The domain is the unit square, the velocity field is the solid body rotation around the point (0.5, 0.5):

$$\begin{aligned} u = -2\pi (y-0.5), \quad v = 2\pi (x-0.5). \end{aligned}$$
(13)
Fig. 5
figure 5

Notched disc advection test. Volume fraction field shown after one full rotation. 0.5-contour shown with a black curve

Full size image

The initial volume fraction field is 1 within the disc of radius 0.15 centred at (0.5, 0.75), except in a slit of width 0.06 going up to y=0.85. The disc rotates around (0.5, 0.5) and returns to its original position at time t = 1. The resulting interface shape after such a rotation with isoAdvector and MULES is shown in Fig. 5 for three different mesh types with square, triangular and polygonal cells. All simulations have been performed with CFL = 0.1 and 0.5, but since the isoAdvector simulations with CFL = 0.1 and 0.5 are almost indistinguishable, we only show the latter. Tables 1 and 2 show the error compared to the exact solution and the calculation time for the 9 simulations. From the figure and Tables 1 and 2, we remark that:

  • IsoAdvector with CFL = 0.5 performs better than MULES with both CFL = 0.5 and 0.1 on square, triangular and polygonal meshes.

  • MULES severly distorts the shape on all mesh types with CFL = 0.5.

  • On square and polygonal meshes, MULES improves dramatically when going from CFL = 0.5 to 0.1, but not on the triangular mesh.

  • isoAdvector is \(\sim \)3 times faster than MULES with CFL = 0.5.

Table 1 Error for the notched disc: \(E_1 \equiv \sum _i |\alpha _i - \alpha _i^{\text {exact}}|V_i /\sum _i \alpha _i^{\text {exact}}V_i \) (sums are over all cells)
Full size table
Table 2 Calculation times in seconds for notched disc simulations on a single processor
Full size table

3.2 Sphere in Shear Flow

Our second pure advection case is from [5]. The domain is the unit box and the initial volume fraction field is 1 within the sphere of radius 0.15 centred at (0.5, 0.75, 0.25) and 0 elsewhere. The velocity field in which the interface is advected is

$$\begin{aligned} \mathbf u(\mathbf x,t) =\cos \left( \frac{2\pi t}{T}\right) \left[ \sin (2\pi y)\sin ^2(\pi x),-\sin (2\pi x)\sin ^2(\pi y), \left( 1-2r\right) ^2\right] , \end{aligned}$$
(14)

where \(T = 6\) and \(r = \sqrt{(x-0.5)^2+(y-0.5)^2}\). In this flow, the initial spherical interface is sheared into a thin spiralling sheet until, at \(t = 1.5\), it has reached its maximum deformation and flows back to its initial shape and position at time \(t = 3\). We run the case on a polyhedral mesh of the type generated with the pMesh tool of cfMesh [6]. In Fig. 6, we show the results obtained with isoAdevector and MULES using CFL = 0.5 and 0.1.

Fig. 6
figure 6

Sphere deformed in a 3D shear flow with isoAdvector and MULES for CFL = 0.5 and 0.1. The initial sphere is shown in red. The interface shape at maximum deformation (\(t = 1.5\)) and at the time of return to the spherical shape (\(t = 3\)) is shown in grey

Full size image
Table 3 \(E_1\) error (left) and calculation times (right) for a sphere in a reversed 3D shear flow on a polyhedral mesh
Full size table

From Fig. 6 and Tables 3, we see that with this test case, isoAdvector is more accurate and approximately three times faster than MULES, but also note that MULES does a decent job, even with CFL = 0.5. We also observe that the \(E_1\) error with isoAdvector actually increases slightly with smaller time steps.

4 Using isoAdvector in interFoam

In interFoam, the MULES explicit solver code does not only provide the updated volume fractions, \(\alpha _i^{n+1}\), but also provides the quantity rhoPhi, which is used in the convective term, fvm::div(rhoPhi, U), in the momentum matrix equation, UEqn. To understand the way in which we should construct rhoPhi from \(\varDelta V_{ij}^n\), let us start by looking at the convective term in the Euler equations in Eq. 3, formally integrated over a small time interval and over a cell:

$$\begin{aligned} \langle \rho \mathbf u\rangle _i^{n+1} = \langle \rho \mathbf u\rangle _i^n - \frac{1}{V_i}\int _{t_n}^{t_{n+1}}\int _{\mathscr {C}_i} \nabla \cdot \left[ \rho (\mathbf x,\tau )\mathbf u(\mathbf x,\tau )\mathbf u(\mathbf x,\tau )\right] dVd\tau + \cdots \end{aligned}$$
(15)

We will denote this integrated convective term by \(C_i^n\) and use Gauss’s theorem to write it as

$$\begin{aligned} C_i^n = \frac{1}{V_i} \sum _{j\in B_i}\int _{t_n}^{t_{n+1}}\int _{\mathscr {F}_j} \rho (\mathbf x,\tau )\mathbf u(\mathbf x,\tau )\mathbf u(\mathbf x,\tau ) \cdot d\mathbf S d\tau . \end{aligned}$$
(16)

We now approximate \(\mathbf u(\mathbf x,\tau )\) with a constant representative velocity vector, \(\tilde{\mathbf u}_j^n\) and use \(\mathbf u\cdot d\mathbf S \approx \tilde{\phi }_{ij}^n/|\mathbf S_j|dA\) as described at the beginning of Sect. 2. This allows us to write

$$\begin{aligned} C_i^n \approx \frac{1}{V_i} \sum _{j\in B_i}\tilde{\mathbf u}_j^n \frac{\tilde{\phi }_{ij}^n}{|\mathbf S_{ij}|} \int _{t_n}^{t_{n+1}}\int _{\mathscr {F}_j} \rho (\mathbf x,\tau )d A d\tau . \end{aligned}$$
(17)

Now, using the definition of \(H(\mathbf x,t)\) in terms of \(\rho (\mathbf x,t)\) in Eq. 5 and the definition of the submerged face area, \(A_j\), in terms of H in Eq. 12, we can write Eq. 17 as

$$\begin{aligned} C_i^n \approx \frac{1}{V_i} \sum _{j\in B_i}\tilde{\mathbf u}_j^n \frac{\tilde{\phi }_{ij}^n}{|\mathbf S_{ij}|} \int _{t_n}^{t_{n+1}}\left[ \rho _2 + (\rho _1 -\rho _2)A_j(\tau ) \right] d\tau . \end{aligned}$$
(18)

With the definition of \(\varDelta V_{ij}^n\) in Eq. 8, we can finally write the convective term as

$$\begin{aligned} C_i^n \approx \frac{1}{V_i} \sum _{j\in B_i}\tilde{\mathbf u}_j^n\left[ \rho _2 \tilde{\phi }_{ij}^n \varDelta t_n + (\rho _1-\rho _2)\varDelta V_{ij}^n\right] . \end{aligned}$$
(19)

Here, the content of the square brackets is exactly the desired expression for rhoPhi. The specific expression for \(\tilde{\mathbf u}_j^n\) in terms of the cell-averaged velocities is determined by the settings in fvSchemes for the convective term.

5 The damBreak Case

For an initial investigation of the behaviour of our new interFoam solver using isoAdvector instead of MULES, we run a refined version of the standard dam break tutorial shipped with OpenFOAM\(^{\textregistered }\)-4.0. The domain is a box of width and height 0.584 m, with a small rectangular obstacle on the bottom and the water initially placed in a rectangular column on the left side of the domain. The case is run with an adaptive time step using maxAlphaCo = maxCo = 0.5 . In Fig. 7, we show snapshots of the volume fraction field at two times. In the top panels, just after impact with the obstacle on the floor, we clearly see how isoAdvector—in contrast to MULES—is capable of keeping the interface sharp, even for droplets of only a few cells’ width. In the bottom panels, the water is starting to settle, and we see how the interface produced with isoAdvector is only one cell wide, whereas the interface produced with MULES covers many cells. Calculation times are similar for the two runs.

Fig. 7
figure 7

Dam break at times \(t = 0.32\) s (top) and 1.1 s (bottom), run with isoAdvector (left) and MULES (right). Cells with \(0.001< \alpha _i^n < 0.999\) at \(t = 1.1\) s are coloured yellow in the lower panels

Full size image

This is to be thought of as a kind of “Hello World!” case for our new solver, and caution should be taken in drawing quantitative conclusions from this setup. In future work, we will conduct more quantitative investigations based, e.g. on the experimental data provided in [7].

We remark that a razor-sharp interface is not always the best representation of the physical water distribution on the given mesh. If the encounter with the obstacle in a real physical damBreak experiment causes the interface to explode into a cloud of subcell-sized droplets, then a smeared representation, together with an appropriate dispersed flow model, may be a better representation of the physical reality. To prevent nonphysical sharpening of the interface in regions with clouds of subcell droplets and bubbles, one could introduce a quantitative criterion for detecting such regions and replace the isoAdvector interface treatment for surface cells in these regions with a dispersed treatment.

Fig. 8
figure 8

Stream function wave with H = 10 m, D = 20 m and T = 14 s at time t = 10 s. From top: MULES-Euler, MULES-Crank–Nicolson, isoAdvector-Euler, isoAdvector-Crank–Nicolson

Full size image

6 Steady Stream Function Wave

The purpose of our final test case is to investigate the effect of replacing MULES with isoAdvector on the propagation of a steady stream function wave. The initial surface elevation, velocity and pressure fields are calculated using a Fourier approximation method, which is well described in [8]. The derivation is based on potential flow theory with vacuum above the wave. This corresponds to \(\rho _2 = 0\), which is not practically possible with the interFoam solver, because it involves division by \(\rho \) in the PISO loop. We, therefore, use \(\rho _2 = 0.1\) kg/m\(^3\) and \(\rho _1 = 1000\) kg/m\(^3\). As in [9], we use a wave with height \(H = 10\) m and period \(T = 14\) s on depth \(D = 20\) m. This gives rise to a wavelength of \(L = 193.23\) m, which we choose as the length of our rectangular domain with, cyclic boundary conditions on the sides. The cells in the interface region are squares of side length 0.5 m corresponding to 20 cells per wave height and \(\sim \)386 cells per wavelength. Above and below the interface region, the mesh is coarser, with cell size up to 2 m. For div(rho*phi,U), we use Gauss limitedLinearV 1, as opposed to the upwind scheme used in [9]. Another difference is that in our setup, we initialise the wave in a co-moving frame, and so the surface elevation and velocity field should ideally not change throughout the transient simulation. Also, we use a fixed time step of 0.002 s, which based on the theoretical crest particle velocity of 5.95 m/s, gives a CFL number of 0.0238. We run the setup with MULES and isoAdvector, using both Euler and crankNicolson 0.5 for time integration. The resulting wave shape and velocity magnitudes for the four combinations a short time after the simulations have been started (\(t = 10\) s) are shown in Fig. 8. The interface thickness is shown by plotting the 0.5 and 0.0001 contours of the volume fraction data. We see that the interface is sharper and smoother in the isoAdvector simulations than in the MULES simulations. But we also observe that the air speed in a narrow band just above the surface takes values almost twice as high in the isoAdvector simulations (note the different colour scales in the different panels). These larger air velocities do not seem to affect the interface significantly, as illustrated in Fig. 9, where we show the surface elevations from the four runs after 105 s corresponding to 7.5 wave periods.

Fig. 9
figure 9

Stream function wave with H = 10 m, D = 20 m and T = 14 s at time 105 s. The x-axis has been compressed by a factor of 4. Black: exact surface elevation (0.5 contour). Orange: MULES-Euler. Blue: MULES-Crank–Nicolson. Red: isoAdvector-Euler. Green: isoAdvector-Crank–Nicolson

Full size image

All simulations have a celerity that is slightly too high, causing all waves to have drifted almost a quarter of a wavelength to the right compared to the theoretical steady profile crest centred in the middle of the domain. The MULES-Euler wave (orange) has broken, giving rise to a jerky profile. The MULES-Crank–Nicolson wave crest (blue) has grown significantly and the trough is wrinkled. The isoAdvector waves with Euler (red) and Crank–Nicolson (green) also have slight overshoots in wave height, but these are much smaller and with much smoother profiles. This is a preliminary test and since many things can change if the case setup is adjusted, one should not jump to conclusions before a more thorough study has been conducted. It is, however, safe to conclude that using isoAdvector instead of MULES in surface wave propagation simulations does have a clear effect on the solution. It is also safe to conclude, that the spurious tangential velocities observed at the interface for large density ratios are not caused by MULES alone. More likely, the problem is also associated with the PISO loop implementation in interFoam not taking the large density jump properly into account, e.g., when interpolating density-dependent quantities between cell centres and face centres. We expect that an improved density jump treatment in this part of the code can be achieved by using the information provided by isoAdvector about the interface position inside surface cells.

7 Summary

We have given a brief description of the isoAdvector algorithm for advection of a sharp interface across general meshes. We added two pure advection cases to the suite of test cases already presented in [1], demonstrating the superior behaviour of isoAdvector compared to MULES with respect to accuracy and efficiency. We derive an expression for the convective term in the momentum equation so that isoAdvector can be used in interFoam instead of MULES. The resulting solver is tested using the damBreak case and a steady stream function wave in a periodic domain. From these tests, we conclude that using isoAdvector in interFoam is feasible and leads to a sharper interface. Using isoAdvector for the tested wave propagation case leads to significantly higher spurious tangential velocities in the lighter phase, but nevertheless, the quality of the solution is improved. In future work, we will exploit the isoface data to impose consistent physical boundary conditions at the interface in the PISO loop.