Computerized Simulation of Manufacturing Errors in Cylindrical Spur Gears and Their Compensation Through Flank Modifications

Abstract

AGMA and ISO standards consider different types of deviation of gear geometry caused during manufacturing processes of cylindrical gears through a system of accuracy grades, in which each grade corresponds to deviations within a certain range. The gear drive behavior is affected by the level and type of deviation, causing transmission errors, shifts in the bearing contact, increase of contact and bending stresses, and vibration and noise. The main goal of this paper is the investigation of the influence of manufacturing errors on transmission errors and contact and bending stresses, and the determination of the corresponding flank modifications required for their compensation. The contact pattern and the unloaded function of transmission errors are obtained through application of tooth contact analysis (TCA) . Application of finite element analysis (FEA) allows for contact and bending stresses to be determined along one or two cycles of meshing. Surface deformations are used for determination of the loaded function of transmission errors in which its peak-to-peak value is related to the vibration and noise response in operating conditions. Several numerical examples considering different levels and types of manufacturing error and their compensation through predefined flank modifications are presented.

1 Introduction

Manufacturing errors play a fundamental role in gear drive performance. Manufacturing errors cause transmission errors and influence the appearance of dynamic loads, noise and vibration, not only in the gear drive, but in all elements along the power transmission path. In order to ensure the quality of the gears and to limit the maximum magnitudes of manufacturing errors along with it, the AGMA (American Gear Manufacturers Association) and the ISO (International Organization for Standardization) have proposed a system of accuracy grades. The ISO system of gear accuracy comprises 13 accuracy grades (Q = 0, 1, 2 … 12) of which grade 0 is the highest and grade 12 the lowest degree of accuracy [1]. The AGMA system [2] comprises 10 accuracy grades numbered A2 through A11, of which A2 is the highest and A11 is the lowest degree of accuracy. The achievement of higher quality gears implies a higher cost of production, so that a trade-off has to be found between the required performance in terms of noise, vibration, and strength and the cost of production by selecting the required accuracy grade.

Application of manufacturing errors such as time-varying mesh stiffness and tooth separations have been considered in dynamic models to predict a vibrational response in cylindrical and planetary gear sets [3]. However, a static model in which predefined deviations are provided within the gear geometry would be very useful for predicting transmission errors and contact and bending stresses, and judging the appropriateness of flank modifications for compensation of manufacturing errors as well. In this regard, the effect of a number of manufacturing and assembly-related carrier and gear errors on the load sharing among the planets was presented in [4]. In [5], the results of an experimental study to describe the impact of certain types of manufacturing errors on gear stresses and the individual planet loads in planetary gear sets were presented.

Using purely analytical methods, in [6], the results of a study on how accuracy grades affect the calculation of stresses were presented. The design of experiments and Monte Carlo simulation techniques were used to quantify the effects of different manufacturing and assembly errors on root and contact stresses. In that study, it was shown that the increment in stresses due to profile and lead deviations are certainly significant, being as high as 26% for the root stresses of an example with accuracy grade 8. In [7], a comparative investigation of the effect of helix slope and form deviation tolerances as specified by grades 5 and 7 of the ISO 1328-1 was presented. In that work, the consequences of longitudinal flank crowning and radial tip relief modifications were investigated. It was concluded that reducing or increasing the quality class of a gear pair will proportionally influence the gear’s performance as well as its life [7]. In this paper, the influence of manufacturing errors on transmission errors and contact and bending stresses, and the determination of flank modifications required for their compensation, will be investigated. The influence of pitch deviation, profile deviation, and helix deviation errors on the contact and bending stresses of cylindrical gears are studied. The direction of profile deviation is also considered in this study, because, apparently, it may have an important effect on contact stresses. Micro-geometry modifications comprising the required tip relief, and longitudinal and profile crowning are proposed to reduce the effect of those mentioned manufacturing errors on the mechanical behavior of the gear drive.

2 Geometry Deviations Due to Manufacturing Errors

The ISO and AGMA classify geometry deviations due to manufacturing errors into three main categories. These categories are pitch deviations, profile deviations, and helix deviations [1, 2]. Each of these categories contains multiple parameters which determine the grade of the gear. The equations relating these parameters to ISO grade are outlined in the ISO’s “Cylindrical Gears—ISO System of Flank Tolerance Classification—Part 1” [1]. Also worthy of note, the factor between each consecutive ISO grade is $\sqrt 2$, meaning that moving up two ISO grades equates to tolerance levels twice as large.

2.1 Pitch Deviations

The single pitch deviation is the algebraic difference between the actual pitch and the corresponding theoretical pitch in the transverse plane, defined on a circle concentric with the gear axis at approximately the mid-depth of the tooth [1]. The cumulative pitch deviation is the algebraic difference over a sector of several pitches between the actual length and the theoretical length of the relevant arc [1]. It is equal to the algebraic sum of the single pitch deviations of the same considered pitches. In this work, pitch deviations are modeled through superimposition of two sinusoidal functions that takes into account the total cumulative pitch deviation $F_{p}$ and the single pitch deviation $f_{pt}$.

The cumulative pitch deviation $F_{pk}^{(1)}$ of the first function is defined as

$$ F_{pk}^{(1)} = A_{1} \sin \left( {k\frac{2\pi }{{N_{g} }}} \right)\quad \quad k = (0,1,2, \ldots ,N_{g - 1} ). $$

(1)

Here, $A_{1}$ is the amplitude of the sinusoidal function and $N_{g}$ is the gear tooth number.

The cumulative pitch deviation $F_{pk}^{(2)}$ of the second function is defined as

$$ F_{pk}^{(2)} = A_{2} \sin \left( {k\frac{\pi }{2}} \right)\quad \quad k = (0,1,2, \ldots ,N_{g - 1} ), $$

(2)

where $A_{2}$ is the amplitude of the sinusoidal function.

The maximum increment of the single pitch deviation occurs at $k = 0$, and can be obtained as

$$ \Delta f_{pt,max} = (F_{p1}^{(1)} + F_{p1}^{(2)} ) - (F_{p0}^{(1)} + F_{p0}^{(2)} ) = A_{1} \sin \frac{2\pi }{{N_{g} }} + A_{2} . $$

(3)

Amplitudes $A_{1}$ and $A_{2}$ can be derived as a function of $f_{pt}$ and $F_{p}$ by imposing the conditions

$$ F_{p} = 2(A_{1} + A_{2} ) $$

(4)

$$ (F_{p1}^{(1)} + F_{p1}^{(2)} ) - (F_{p0}^{(1)} + F_{p0}^{(2)} ) = f_{pt} - 0. $$

(5)

The necessity of the two sinusoidal functions is due to the two values, $f_{pt}$ and $F_{p}$, that each accuracy grade provides. The sinusoidal functions are used for the location of each single tooth on the reference circle, and this means that each tooth has to be generated individually for the modelling of the pitch deviation. Since the maximum increment of the single pitch deviation occurs from $k = 0$ to $k = 1$ (or from $k = N_{g} - 1$ to $\left. {k = 0} \right)$, the finite element model will consider those teeth with indexes $k = (N_{g} - 2,N_{g} - 1,0,1,2)$ (see Sect. 4).

2.2 Profile Deviations

Profile deviation is the amount by which a measured profile deviates from the design profile [2]. As shown in Fig. 1, the total profile deviation $F_{\alpha }$ is the superposition of the profile form deviation $f_{f\alpha }$ and the profile slope deviation $f_{H\alpha }$. The profile evaluation range, $L_{\alpha }$, according to [1], is considered equal to 92% of the active length, which is defined as the difference between two base tangents, one corresponding to the tip tooth limit T, and the other one corresponding to the endpoint E of the effective contact with the mating gear

$$ L_{\alpha } = 0.92\left( {\sqrt {r_{T}^{2} - r_{b}^{2} } - \sqrt {r_{E}^{2} - r_{b}^{2} } } \right). $$

(6)

Here, $r_{b}$ is the base radius of the gear.

Fig. 1

Schematic representation of the components of the total profile deviation: a profile deviation $F_{\alpha }$, b profile form deviation $f_{f\alpha }$, and c profile slope deviation $f_{H\alpha }$

In this work, profile deviations are modelled by variation of the pressure angle of the gear. We will assume here that the profile form deviation $f_{f\alpha }$, mainly caused by the roughness or small undulations along the profile direction, is zero, and therefore the profile slope deviation $f_{H\alpha }$ is the only deviation affecting the considered value of the profile deviation. In relation to profile deviation, the influence of positive or negative profile slope deviations will be considered. The profile slope deviation direction is positive when the profile line shows an increase in the material towards the tooth tip, relative to the design profile, corresponding to a negative pressure angle deviation.

The total profile deviation for an accuracy grade of 5 is obtained by considering the following equation [1]:

$$ F_{\alpha } = 3.2\sqrt m + 0.22\sqrt d + 0.7, $$

(7)

where m is the module and d the pitch radius of the gear. Once the profile deviation and the profile evaluation distance are known, the variation of the pressure angle to simulate the profile deviation $\Delta \alpha$ is determined as

$$ \Delta \alpha = \arctan \left( {\frac{{F_{\alpha } }}{{L_{\alpha } \tan \alpha }}} \right), $$

(8)

where α is the pressure angle.

2.3 Helix Deviations

Helix deviation is the amount by which a measured helix deviates from the design helix [2]. As shown in Fig. 2, the total helix deviation $F_{\beta }$ is the superposition of the helix form deviation $f_{f\beta }$ and the helix slope deviation $f_{H\beta }$. In Fig. 2, $L_{\beta }$ is the helix evaluation range, which is given by the face width shortened at both sides by the smaller value of the 5% of the face width or a length equal to one module.

Fig. 2

Schematic representation of the components of the total helix deviation: a total helix deviation $F_{\beta }$, b helix form deviation $f_{f\beta }$, and c helix slope deviation $f_{H\beta }$

In this work, helix deviations are modeled by variation of the helix angle of the gear. For that, we assume that the helix form deviation $f_{f\beta }$, mainly caused by the roughness of the surface, is zero, so that the helix slope deviation $f_{H\beta }$ is the only deviation affecting the helix deviation. In order to consider the most unfavorable scenario for simulations, the value of the total helix deviation $F_{\beta }$ according to the ISO will be considered for determination of the effective variation of the helix angle $\Delta \beta$, and therefore,

$$ \Delta \beta = \arctan \left( {\frac{{F_{\beta } }}{{L_{\beta } }}} \right). $$

(9)

The total helix deviation for an accuracy grade of 5 is obtained by considering the following equation [1]:

$$ F_{\beta } = 0.1\sqrt d + 0.63\sqrt b + 4.2. $$

(10)

Here, d is the pitch radius of the gear and b is the face width.

3 Geometry Modifications

The application of intended micro-geometry modifications is investigated to determine if they are effective in absorbing the effect of manufacturing errors on transmission errors, and contact and bending stresses for different accuracy grades. The following typologies of gear tooth surface micro-geometry modifications are considered.

3.1 Tip Relief

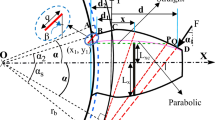
AGMA [8] defines tip relief as “a modification of a tooth profile whereby a small amount of material is removed near the tip of the gear tooth.” It is used to avoid premature contact between contacting teeth due to the elastic deformation of gear tooth surfaces and pitch or profile errors. Tip relief can be defined for cylindrical gears with involute profiles by defining the amount of tip relief at the addendum radius, δ, the shape of the tip relief (linear or parabolic) and the starting point on the involute profile. For definition of the starting point, the following three definition methods can be considered: (i) the datum length for tip relief, L, (ii) the rolling length, r _L , or (iii) the rolling angle, ε. As shown in Fig. 3, the relation between the rolling length and the corresponding rolling angle is

Fig. 3

Towards definition of rolling length and rolling angle

$$ r_{L} = r_{b} \varepsilon , $$

(11)

where $r_{b}$ is the base radius of the gear. Given one of the following tip relief definition factors, the radius $r_{P}$ of the starting point for tip relief can be obtained as follows:

• Datum length, L:

$$ r_{P} = r_{a} - L; $$

(12)

• Rolling length, $r_{L}$:

$$ r_{P} = \sqrt {r_{b}^{2} + r_{L}^{2} } ; $$

(13)

• Rolling angle, $\epsilon$:

$$ r_{P} = \sqrt {r_{b}^{2} + (r_{b} \varepsilon )^{2} } = r_{b} \sqrt {1 + \varepsilon^{2} } . $$

(14)

The starting point for tip relief, $r_{P}$, being known, the profile of the gear tooth surfaces will be modified from this radius to the addendum radius, $r_{a}$, according to the shape of the tip relief (linear or parabolic) in order to reach the maximum modification at the addendum radius. Figure 4 shows the tip relief with parabolic shape on a spur gear drive as a function of the datum length L and the amount of tip relief at the addendum radius δ.

Fig. 4

Representation of tip relief with parabolic shape in a spur gear drive

3.2 Longitudinal Crowning

AGMA [8] defines longitudinal crowning as “teeth which have surfaces modified in the length-wise direction to produce localized contact or to prevent contact at their ends.” It is known that at high torques, crowning can benefit gear performance by localizing contact stresses in the center of the gear tooth, away from the edges [9]. In that study, it was also shown that there exist optimal crowning parameters. Longitudinal crowning has also been analytically demonstrated to contribute to reduction of the stress distribution factor [10]. A visual representation of longitudinal crowning with a parabolic shape applied to the tooth surfaces of a spur gear is shown in Fig. 5.

Fig. 5

Longitudinal crowning of 20 μm applied to the active tooth surfaces of a spur gear

3.3 Profile Crowning

Profile crowning is considered in which a constantly increasing amount of material is removed from the transverse section of the gear tooth in the direction of the tip and root circle, starting at the middle of the calculated tooth flank length. It can be achieved through the selection of a generating profile that deviates from a straight profile. It can be considered parabolic or circular, and therefore the parabola coefficient of the profile for the first case, or the radius of the circular profile for the second one, are design parameters to be determined. For spur cylindrical gears, the profile crowning is responsible for the predesign of a parabolic function of transmission errors that will absorb the linear or quasi-linear functions of transmission errors caused by errors of alignment or manufacturing errors [11].

4 Methodology

The geometry of spur gears with manufacturing errors is generated and simulated by a custom-made software. This software allows for gear geometry to be modified to reflect manufacturing errors and intentional profile modifications. Manufacturing errors will only be applied to the pinion of the gear drive. The gear will always be considered to be free of any manufacturing error, and therefore it will always have the expected targeted geometry.

The finite element method is used to determine the contact and bending stresses for gears under different limits of manufacturing errors . Figure 6 shows an example of the sort of finite element model with five pairs of contacting teeth that has been considered in this work. It is assumed that all nodes at the cutoff rim surface remained perfectly rigid. Considering five pairs of teeth keeps the cutoff rim surface away from the teeth in contact and avoids influence on the contact and bending stresses to be obtained. The model size consists of 106,000 elements and 131,922 nodes. The contacting surfaces are made of 1200 elements corresponding to 20 elements in the longitudinal direction and 60 elements in the profile direction. Gear active tooth surfaces have been defined as master surfaces, while pinion active tooth surfaces have been defined as slave surfaces. Three-dimensional solid elements of type C3D8I [12] have been used, being hexahedral first order elements enhanced by incompatible deformation modes in order to improve their bending behavior. Pinion and gear material is steel defined with an elastic modulus of 210 GPa and a Poisson ratio of 0.3.

Fig. 6

Finite element mesh applied for determination of contact and bending stresses

An advanced freeform design tool is used to modify the active part of the gear tooth surface according to the typology of the intentional geometry modifications to be applied. Three possible geometry modifications will be investigated in this paper. Firstly, a parabolic tip relief will be considered to smooth the transition between the active part of the gear tooth surface and the tip relief area. This type of parabolic relief does not increase the Hertzian contact stresses in the way that linear relief does [13]. No bottom relief will be considered for the pinion and gear tooth surfaces, because the tip relief applied to both members of the gear drive plays the same role. Secondly, a longitudinal parabolic crowning will be considered, and finally, a parabolic profile crowning will be applied.

The design of experiments (DOE) methodology is used to evaluate the influence of the different types of manufacturing error on contact and bending stresses, using a two-level full factorial numerical experiment. Design of experiments (DOE) is a well-known technique extensively applied in many fields of engineering to evaluate which design variables or process inputs have the largest impact on different outputs. The tested cases will be organized according to the selected full factorial design, and in this way, with a limited series of tested cases, a general analysis of the different factors and their combined effects on the selected output will be performed.

5 Numerical Examples

Table 1 shows the macro-geometry design parameters of two spur gear drives with pressure angles of 20° and 25° applied for investigation of the compensation of manufacturing errors by the application of flank modifications. Table 2 shows the derived geometrical data of the tested gears.

Table 1 Macro-geometry parameters of tested gears

Table 2 Derived data of tested gears

Firstly, the influence of the magnitude of pitch deviations, profile deviations, helix deviations, and direction of the profile slope deviation (positive or negative) on contact and bending stresses is investigated for gears with and without profile modifications. The considered parameters for the designed experiment can be seen in Table 3. The limits of the considered deviations or input parameters will be the same for both geometries 1 and 2 described in Table 1. The selected minimum and maximum values represent the maximum tolerances expected for gears having an ISO accuracy grade of 2 and 6, with the additional parameter of profile slope deviation direction as positive or negative. For the pitch deviation, the values provided correspond to the cumulative pitch deviation and the single pitch deviation in parentheses.

Table 3 Parameters of designed experiment

A full factorial experiment set up with the parameters shown in Table 3 yields sixteen runs, with the details of each run shown in Table 4.

Table 4 Details of the configuration of each run for the experiment

The minimum principal stress at the integration points of the finite element mesh forming the contacting surfaces is considered to be contact stress and the values will be represented in MPa. The maximum principal stress at the integration points of the elements forming the fillets of the contacting sides of pinion and gear tooth surfaces is considered to be the bending stress and will also be represented in MPa.

Results of the influence of manufacturing errors on contact and bending stresses have been obtained for the two considered geometries depicted in Table 1. Results will be presented in separate sections for Geometry 1 having a pressure angle of 20° and Geometry 2 having a pressure angle of 25°.

5.1 Geometry 1 with Pressure Angle of 20°

Figure 7 shows the Pareto chart of the standardized effect of manufacturing errors on the pinion contact and bending stresses for a spur gear drive with macro-geometry represented as Geometry 1 in Table 1 and no micro-geometry modifications. A Pareto chart is a bar diagram in which the length of each of the bars represents the influence of the factors represented on the left on the considered objective variable. Here, the Pareto chart is arranged with bars distributed horizontally, with the longest bars (high influence) at the top and the shortest bars (lower influence) at the bottom of the diagram. In this way, the Pareto chart gives visual information on the most important factors of influence on the considered objective variable, ranking those factors after the analysis of the considered factorial design (as shown in Table 4). The represented dashed line is shown for all analyses as a reference. Any effect which extends beyond that mentioned dashed reference line is considered significant for the investigated objective. Therefore, according to the results shown in Fig. 7-left, the main factors affecting the maximum contact stresses on the pinion tooth surfaces are the profile slope deviation direction and the helix deviation. The pitch deviation and the combined effect of profile deviation with the profile slope deviation direction are also of relevant influence on contact stresses on the pinion tooth surfaces. Regarding the maximum bending stress (Fig. 7-right), the main factor of influence is the helix deviation. The profile deviation direction, although its influence is not as relevant as the helix deviation, is also considered to be an influence factor on bending stresses for the pinion.

Fig. 7

Pareto chart of the standardized effect of manufacturing errors on pinion tooth contact stress (left) and bending stress (right) for Geometry 1 without micro-geometry modifications

Figure 8 shows the Pareto chart of the standardized effect of manufacturing errors on gear contact and bending stresses for the gear drive with Geometry 1. For contact stresses (Fig. 8-left), the two main factors of influence are, similarly as for the pinion, the profile slope deviation direction and the helix deviation applied as manufacturing errors to the pinion. Regarding the bending stresses (Fig. 8-right), the main factors of influence are the helix deviation and the profile slope deviation direction.

Fig. 8

Pareto chart of the standardized effect of manufacturing errors on gear tooth contact stress (left) and bending stress (right) for Geometry 1 without micro-geometry modifications

The results show that, in general, for a spur gear drive without any flank modifications, the most sensitive factor for the maximum contact stress is the profile deviation direction. The profile deviation direction dictates whether the gear or the pinion receives increased loading due to this deviation. For positive profile deviations, representing an increase of material towards the tooth tip, and corresponding to a negative variation of the pressure angle, the contact stresses will increase considerably. The second most significant manufacturing error affecting the maximum contact stress is the helix deviation, followed by pitch deviations. For bending stresses, the most sensitive tolerance is the helix deviation.

In order to reduce the increase of contact and bending stresses due to manufacturing errors , the application of a tip-relief for the pinion and gear tooth surfaces is first investigated. The same sixteen runs listed in Table 4 will be performed for a gear drive with pinion and gear designed with tip relief, as defined in Table 5. No lead or profile crowning is applied at this time. The selected tip relief geometric parameters were chosen based on values which were previously calculated to provide a smooth evolution of contact stresses all over the cycle of meshing without the appearance of edge contacts when a torque of 1000 Nm is applied to the pinion. This process of determination of the best design of tip relief is performed without the consideration of manufacturing errors.

Table 5 Micro-geometry parameters of tested gears

Figure 9 shows the Pareto chart of standardized effect of manufacturing errors on pinion tooth contact stress (left) and bending stress (right) for Geometry 1 with pinion and gear geometry modified with tip relief. Now, after application of tip relief as a micro-geometry modification, the only relevant factor that affects the contact and bending stresses on the pinion is the helix deviation. The designed tip relief helps significantly to reduce the sensitivity of the maximum contact stresses and the maximum bending stresses with respect to all manufacturing errors except the helix deviation.

Fig. 9

Pareto chart of the standardized effect of manufacturing errors on pinion tooth contact stress (left) and bending stress (right) for Geometry 1 with pinion and gear geometry modified with tip relief

Figure 10 shows the Pareto chart of the standardized effect of manufacturing errors on the gear tooth contact stress (left) and bending stress (right) for Geometry 1 with pinion and gear geometry modified with tip relief. Helix deviation is again the most relevant effect on contact and bending stresses.

Fig. 10

Pareto chart of the standardized effect of manufacturing errors on gear tooth contact stress (left) and bending stress (right) for Geometry 1 with pinion and gear geometry modified with the optimum tip relief

In an effort to reduce this sensitivity of contact and bending stresses with the helix deviation error, the same tip relief that was previously applied will be considered now, together with a parabolic longitudinal crowning (or lead crowning) of six microns of maximum deviation at the front and back sections of the pinion.

Figure 11 shows the Pareto chart of the standardized effect of manufacturing errors on pinion tooth contact stress (left) and bending stress (right) for Geometry 1 with pinion and gear geometry modified with tip relief and longitudinal crowning according to the data shown in Table 5 applied to the pinion member of the gear set. The sensitivity of contact and bending stresses on the pinion tooth surfaces with respect to the helix deviation after consideration of longitudinal crowning is reduced by a factor of almost four, showing that the application of a longitudinal crowning is an effective way to absorb the helix deviation and minimize its effect on contact and bending stresses. The same results are obtained for the gear (see Fig. 12).

Fig. 11

Pareto chart of the standardized effect of manufacturing errors on pinion tooth contact stress (left) and bending stress (right) for Geometry 1 with pinion and gear geometry modified with the optimum tip relief and longitudinal parabolic crowning

Fig. 12

Pareto chart of the standardized effect of manufacturing errors on gear tooth contact stress (left) and bending stress (right) for Geometry 1 with pinion and gear geometry modified with the optimum tip relief and longitudinal parabolic crowning

Figure 13 shows the Pareto chart of the standardized effect of manufacturing errors on the peak-to-peak level of loaded transmission errors for Geometry 1 with pinion and gear geometry without flank modifications (left) and with tip relief (right). The peak-to-peak level of loaded transmission errors when the geometry has no intentional modifications (Fig. 13-left) strongly depends on the profile deviation, followed, in order of importance, by the profile slope deviation direction, the interaction between the pitch deviation and the profile slope deviation direction, and finally, the pitch deviation.

Fig. 13

Pareto chart of the standardized effect of manufacturing errors on the peak-to-peak level of transmission errors for Geometry 1 with pinion and gear geometry without flank modification (left) and with tip relief (right)

The application of tip relief (Fig. 13-right) for the modification of the pinion and gear contacting surfaces allows us to reduce the sensitivity of the peak-to-peak level of transmission errors with the pitch deviation and its interaction with the profile slope deviation direction. However, the dependency with the magnitude of the profile deviation and the profile deviation direction still remains. Application of a longitudinal crowning showed no improvement on the effect of manufacturing errors on the peak-to-peak level of loaded transmission errors with respect to that shown in Fig. 13-right corresponding to the consideration of tip relief.

The next step in this investigation has been the consideration of a 16 μm profile crowning of parabolic shape applied to the pinion tooth surfaces. The application of a profile parabolic crowning yielded the same results regarding the effect of manufacturing errors on the contact and bending stresses as those shown for the application of tip relief and longitudinal crowning. However, in terms of the peak-to-peak level of loaded transmission errors, the application of profile crowning effectively absorb the profile deviation error, as shown in Fig. 14. The effect of the profile slope deviation direction and its interaction with the profile deviation are the factors of influence on the peak-to-peak level of loaded transmission errors after all intended modification has been applied.

Fig. 14

Pareto chart of the standardized effect of manufacturing errors on the peak-to-peak level of transmission errors for Geometry 1 with pinion and gear geometry with tip relief and pinion modified with profile and lead crowning

Figure 15 shows the evolution of contact stresses on the pinion tooth surfaces of the gear set with Geometry 1 and no flank modifications for the 16 runs of the first experiment. The effect of the negative profile slope deviation direction on the increment of the maximum contact stresses (runs 9–16) when no flank modifications are applied is clearly seen in Fig. 15-right. In this case, a negative profile slope deviation direction increases the effect of edge contacts on contact stresses. Application of tip relief is directed mainly towards removing those peaks on contact stresses. Figure 16 shows how the application of the right-chosen tip relief indeed removes any increment on contact stresses due to edge contacts and leaves naked the effect of the different manufacturing errors on contact stresses. It is also observed how Cases 1–4 (with a helix deviation of 3.0 μm) yield lower maximum contact stresses than Cases 5–8 (with a helix deviation of 12.0 μm). The same behavior is found for Cases 9–12 with respect to Cases 13–16. Finally, Fig. 17 shows how the application of tip relief and longitudinal crowning reduce the difference in the maximum contact stresses with respect to the different manufacturing errors .

Fig. 15

Evolution of contact stresses for Geometry 1 with manufacturing errors and no flank modifications

Fig. 16

Evolution of contact stresses for Geometry 1 with manufacturing errors and tip relief as surface modification

Fig. 17

Evolution of contact stresses for Geometry 1 with manufacturing errors , and tip relief and longitudinal crowning as surface modifications

5.2 Geometry 2 with Pressure Angle of 25°

For the sake of brevity, the content of this section will only show the results of the effect of manufacturing errors on contact and bending stresses for the pinion member of the gear set with Geometry 2, having a pressure angle of 25°. The goal here is to observe whether there is any influence of the pressure angle on the individual effect of the different manufacturing errors on contact and bending stresses or if the intended geometry modifications are effectively absorbing the effect of manufacturing errors. Although the results for the gear member of the gear set are not shown here, it was observed that the effect of the manufacturing errors are similar to that shown for the pinion, following a similar pattern as that for Geometry 1.

Figure 18 shows the Pareto chart of the standardized effect of manufacturing errors on pinion tooth contact stress (left) and bending stress (right) for Geometry 2, wherein no micro-geometry modifications are applied to the pinion member of the gear drive. Similarly as for the pinion of Geometry 1, the main factors affecting the maximum contact stresses on the pinion tooth surfaces of Geometry 2 (Fig. 18-left) are the profile slope deviation direction and the helix deviation. The combined effect of profile deviation with the profile slope deviation direction and the pitch deviation also shows a relevant influence on contact stresses for the pinion tooth surfaces. The maximum bending stress (Fig. 18-right), depends mainly on the helix deviation.

Fig. 18

Pareto chart of the standardized effect of manufacturing errors on pinion tooth contact stress (left) and bending stress (right) for Geometry 2

A higher value of tip relief was needed for the pinion of Geometry 2 in order to avoid the influence of edge contacts on contact stresses (see Table 5). The sensitivity of contact stresses to errors of manufacturing was reduced with application of tip relief to the pinion and gear to the helix deviation alone (Fig. 19-left). For bending stresses, Geometry 2 has better behaviour, and the design of experiment technique shows that there is no influence of manufacturing errors, although the most relevant factor affecting the maximum value of bending stresses remains the helix deviation (Fig. 19-right).

Fig. 19

Pareto chart of the standardized effect of manufacturing errors on pinion tooth contact stress (left) and bending stress (right) for Geometry 2 with pinion and gear modified with tip relief

Figure 20 shows the Pareto chart of the standardized effect of manufacturing errors on pinion tooth contact stress (left) and bending stress (right) for Geometry 2 with pinion and gear modified with tip relief and pinion modified with longitudinal crowning. As expected, the application of a longitudinal crowning reduces the effect of the helix deviation on contact and bending stresses.

Fig. 20

Pareto chart of the standardized effect of manufacturing errors on pinion tooth contact stress (left) and bending stress (right) for Geometry 2 with pinion and gear modified with tip relief and pinion modified with longitudinal crowning

5.3 Optimal Longitudinal Crowning Versus Magnitude of Helix Deviation

With the knowledge that tip relief can compensate for manufacturing defects other than helix deviation, and that longitudinal crowning contributes effectively to reducing the effect of helix deviation, the next step is to find, if it exists, an optimal longitudinal crowning for different values of helix deviations. The criterion for optimization is the minimization of the absolute value of the minimum principal stress (largest compression stress) on the pinion tooth flanks. Simulations were run for gears of varying helix deviations and magnitudes of longitudinal crowning. Helix deviation was varied to reflect the maximum magnitudes of different ISO grades, whereas crowning magnitudes were incremented by 0.5 μm until an optimal was found. The results obtained are shown in Fig. 21 for both Geometries 1 and 2. As seen in the plot, optimal longitudinal crowning and helix deviation are linearly related. A regression analysis yielded the trend lines shown in Fig. 21, which are described by Eqs. (15) and (16) for Geometries 1 and 2, respectively. Both trend lines feature an $R^{2}$ value higher than $0.99$.

Fig. 21

Optimal longitudinal crowning for different values of helix deviation

$$ {\text{Optimal}}\,{\text{longitudinal}}\,{\text{crowning}} = 2.7244 + 0.3744\,F_{\beta } $$

(15)

$$ {\text{Optimal}}\,{\text{longitudinal}}\,{\text{crowning}} = 3.1434 + 0.3502\,F_{\beta } $$

(16)

6 Conclusions

Based on the performed research, the following general conclusions can be drawn:

• Gear drives with no flank modifications applied to any of the gear members show a very sensitive tolerance for contact stresses with the profile slope deviation direction and the magnitude of the helix deviation. The effect of the profile slope deviation direction on contact stresses is amplified for higher values of profile deviation due to the effect of an interaction between those two factors.

• Maximum bending stress is mainly affected by the value of the helix deviation.

• Consideration of the optimal tip relief micro-geometry modification to the pinion and the gear causes sensitivity of contact stresses with respect to all parameters to decrease substantially. After application of tip relief, the only parameter which has a significant effect on contact stresses is the helix deviation. The application of tip relief does not improve the sensitivity of maximum bending stresses to helix deviation.

• Application of longitudinal crowning reduces the sensitivity of contact stresses with respect to the helix deviation to very low levels. The sensitivity of bending stresses to helix deviation is also reduced with the application of a longitudinal crowning.

• Application of profile crowning has no effect on contact or bending stresses, but it is able to reduce the sensitivity of the peak-to-peak level of loaded transmission errors with respect to pitch, profile, and helix deviations. The main effect that remains in regard to the maximum peak-to-peak level of the function of transmission errors after intended flank modifications is the profile slope deviation direction and its interaction with the profile deviation.

• The optimal longitudinal crowning and the value of maximum helix deviation are linearly related. Equations that give the optimal longitudinal crowning as a function of the helix deviation have been proposed.