Capacitive-Based Adiabatic Logic

Abstract

This paper introduces a new paradigm to implement logic gates based on variable capacitance components instead of transistor elements. Using variable capacitors and Bennett clocking, this new logic family is able to discriminate logic states and cascade combinational logic operations. In order to demonstrate this, we use the capacitive voltage divider circuit with the variable capacitor modulated by an input bias state to the set output state. We propose the design of a four-terminal capacitive element which is the building block of this new logic family. Finally, we build a Verilog-A model of an electrically-actuated MEMS capacitive element and analyze the energy transfer and losses within this device during adiabatic actuation. The proposed model will be used for capacitive-based adiabatic logic circuit design and analysis, including construction of reversible gates.

1 Introduction

Field-effect transistor (FET) scaling is probably not a long-term answer to dramatically increase the energy-efficiency of logical computation. Therefore, a trade-off between the leakage and conduction losses still exists at each CMOS technology node: the energy per operation can be minimized using an appropriate supply voltage and operating frequency. However, despite the nanoscale transistor size, the lowest dissipation per operation is nowadays a few decades higher than the theoretical limit introduced by Landauer [1, 2]. Even though Landauer’s theory is still being discussed, it is possible to decrease the energy required to implement the logical operation at the hardware level. Adiabatic logic based on FET has been introduced to alleviate this inherent trade-off and reduce the conduction loss [3]. By smoothing transitions between logic states, the charge and discharge of the FET gate capacitance C through the FET channel resistance R of the previous stage is lowered by a factor of $\frac{2RC}{T}$, where T is the ramp duration. But there is still a reduction limit factor due to the FET threshold voltage $V_{TH}$. This non-adiabatic part of the conduction limit remains equal to $\frac{CV_{TH}^2}{2}$. On the other hand, adiabatic operation reduces the operation frequency and magnifies the FET leakage loss. Even if the energy per operation is slightly reduced, by only a factor of ten, there is still a trade-off between the non-adiabatic conduction and leakage loss. This therefore limits the interest of FET-based adiabatic logic.

To suppress the leakage, electromechanical relays have been used in the literature [4]. As they are based on metal-metal contact instead of a semiconductor junction, the leakage becomes almost negligible [5]. The Shockley law, which basically links the on-state resistance and leakage in the off-region, is not valid in relay devices as it is based on electrical contact between two plates [6]. Moreover, the main bottleneck of the relay-based adiabatic logic is the mechanical reliability of devices [7, 8]. To overcome these limitations, we propose a new logic family called Capacitive-based Adiabatic Logic (CAL) [9]. By substituting relays with variable capacitors, this approach avoids electrical contact. Mechanical contact between the electrodes is then no longer required. For this reason, CAL could be more reliable compared to electromechanical relays.

The first section of this paper presents an overview of the new logic family, at the gate-level. We focus on buffer, inverter, and AND and OR gates, operated using Bennett clocking. These gates (excluding the NOT gate) are irreversible, but we also suppose that CAL could be used for reversible gates construction. Next, we address the question of the cascadability of CAL gates, and a solution to implement the elementary CAL device based on MEMS technology is proposed. Finally, we analyze the energy transfer and losses within this device.

2 Buffer and Inverter Functions in CAL

CMOS-based adiabatic logic circuits basically operate with two types of architecture: the quasi adiabatic pipeline and Bennett clocking. Power supplies called power clocks (PC’s) are quite different for these two architectures. In a pipeline architecture, a four-phase power supply is used. The logic state is received from the previous gate during the evaluate interval, then transmitted to the next gate during the hold interval. In the recovery stage, the electrical energy stored in the capacitor of the next gate is recovered. The symmetrical idle phase is added for reasons of cascadability. In order to guarantee constant output signal from the previous gate during the evaluation stage, a 90$^{\circ }$ phase shift between subsequent PC’s is needed.

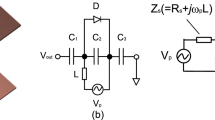
The second type of PC is called Bennett clocking. Here, the power supply voltage of the current gate increases and decreases only when the inputs are stable, as presented in Fig. 1(a). In this work, we use Bennett clocking in order to avoid problems with maintaining the signal during the hold interval in the pipeline architecture [2]. The CAL can also be operated in 4-phase PC’s, but it is out the scope of this paper.

Fig. 1.

Schematics depicting (a) the Bennett clocking principle, and (b) the capacitive voltage divider circuit.

As the PC provides an AC signal, the resistive elements (transistors) in a voltage divider circuit can be replaced by capacitive ones. In CAL, we keep the FET transistor notations, i.e. the input voltage is applied between the gate (G) and the ground. These two terminals are isolated from the drain (D) and source (S) terminals, which form output with a capacitance $C_{DS}$. Let us consider the capacitive divider circuit presented in Fig. 1(b). In the first assumption, $C_{DS}(V_{in})$ is a variable capacitor which depends only on the input voltage $V_{in}$. The fixed capacitor $C_0$ is the equivalent load of the next gate(s) and the interconnections. The output voltage is defined by the capacitance ratio and the PC voltage $V_{PC}(t)$ such that:

$$\begin{aligned} V_{out}(t)=\frac{C_{DS}(V_{in})}{C_0+C_{DS}(V_{in})}V_{PC}(t). \end{aligned}$$

(1)

In this and the next section, the voltages are normalized to the maximum voltage reached by the PC, $V_{PCmax}$, i.e. voltages range from 0 to 1. Two limiting cases emerge which are:

• when $C_{DS} \gg C_0$, the output voltage value is close to one;

• when $C_{DS} \ll C_0$, the output voltage value is close to zero.

Thus, with an appropriate $C_{DS}(V_{in})$ characteristic, the output voltage can be triggered by $V_{in}$. A particular electromechanical implementation of this variable capacitor will be discussed later.

There are two possible behaviors of capacitance as a function of the input voltage. The curve $C_{DS}(V_{in})$ can have a positive or negative slope, as presented in Fig. 2(a). The former case is called positive variation capacitance (PVC) and the latter, negative variation capacitance (NVC). The low and high-capacitance values are denoted $C_L$ and $C_H$, respectively. PVC and NVC voltage-controlled capacitors could play the same role in CAL as NMOS and PMOS in FET-based logic. According to (1), the load capacitance $C_0$ is a critical parameter in the design of cascadable gates. In order to minimize the low logic state and maximize the high logic state, the load capacitance must satisfy the following condition:

$$\begin{aligned} C_0=\sqrt{C_LC_H}. \end{aligned}$$

(2)

Fig. 2.

(a) C(V) characteristics and symbols for PVC (solid line) and NVC (dash-dot line) capacitors. (b) Electrical schematics of simple CAL buffer (left) and inverter (right) circuits. (c-d) Spice-simulated input and output signals (first graph), $C_{DS}$ and $C_0$ (second graph) of the buffer (c) and inverter (d) gates over time. For (a), (c) and (d), we used the following parameters: $C_L = 0.2$ pF, $C_H = 5$ pF, $C_0 = 1$ pF, $V_{PCmax} = 1$ V, $V_T$ = 0.5 V, $a=10$ V$^{-1}$, $V_{inmax} = 0.83$ V, $R = 1$ k$\Omega$, $T = 100$ ns.

For electrical modeling purposes, we assume that the capacitances of PVC and NVC blocks are given by (3) and (4), respectively.

$$\begin{aligned} C_{DS}(V_{in})=\frac{C_H+C_L}{2} + \left( \frac{C_H-C_L}{2}\right) \tanh \left( a(V_{in}-V_T)\right) \end{aligned}$$

(3)

$$\begin{aligned} C_{DS}(V_{in})=\frac{C_H+C_L}{2} - \left( \frac{C_H-C_L}{2}\right) \tanh \left( a(V_{in}-V_T)\right) \end{aligned}$$

(4)

In (3) and (4), $V_T$ is the threshold voltage and a is a positive parameter that defines the slope of the $C_{DS}(V_{in})$ curve.

Buffer and inverter logic gates can be implemented using a capacitive voltage divider containing a variable capacitor. CAL buffer and inverter circuits are shown in Fig. 2(b). Relation (1) is true for buffer and inverter circuits only if the voltage drop in the series resistance is small, and generally this is the case in adiabatic logic. The results of electrical simulation of a buffer and an inverter are presented in Fig. 2(c) and (d), respectively. With the set of parameters arbitrarily chosen here, the logic states can easily be identified in the output. In order to imitate the cascade of elements, the high and low values of the input voltage are set equal to the high and low values of the output voltage.

The ratio $\frac{C_H}{C_L}$ needs to be maximized in order to clearly identify the logic states. For example, for a buffer gate with a capacitance ratio of about 25, the minimal output voltage is equal to 0.17 and the maximal output voltage is equal to 0.83 (cf. Fig. 2(c)). With a capacitance ratio of about 4, these voltages become 0.33 and 0.66, respectively.

Fig. 3.

(a) The cascade of 4 inverters. (b) Spice-simulated: input voltage $V_{in}$, $V_{PC1}$, output of the first inverter $V_{G1}$ (first graph), $V_{PC2}$, output of the second inverter $V_{G2}$ (second graph), $V_{PC3}$, output of the third inverter $V_{G3}$ (third graph), input voltage $V_{in}$, $V_{PC4}$, output voltage of the fourth inverter $V_{out}$ (fourth graph) over time. The model parameters are the same as in Fig. 2.

To prove the ability of CAL to process and transfer logic states through N logic gates, we investigated the cascading of the 4 inverters presented in Fig. 3(a). Here, we use Bennett clocking and assume that the input capacitance of the next gate $C_0$ is constant. It should be noted that from an energy point of view, this hypothesis is inaccurate as it does not take into account the work of electrical force (see later). The binary input logic word is “0 1”. The input voltage levels are the same as in the previous simulation. The results of electrical simulation of the 4 cascaded inverters are shown in Fig. 3(b). We compare the PC signal and the output voltage of each gate. As expected, the input logic word has been transmitted through the 4 inverters. In addition, the amplitude of the output signal is the same as the amplitude of the input signal.

3 Implementation of AND and OR Gates in CAL

The possible realizations of AND and OR gates based on PVC elements are shown in Fig. 4(a). The parameters of the circuits are the same as in the previous calculations. The simulated evolution of the output voltage of an AND gate is given in Fig. 4(b) as a function of the input voltage over time. As expected, the output reaches a high level only if both AND gate inputs are high. However, the third graph of Fig. 4(b) shows that the output voltage for low-low and high-high inputs decreases compared to the case of the buffer examined above. For example, the high level output voltage drops from 0.83 to 0.7. This is due to the decrease of the equivalent capacitance, caused by the series connection of the two variable capacitors $C_{DS1}$ and $C_{DS2}$.

Fig. 4.

(a) AND and OR gate circuits. (b) Evolution of the input voltages (first graph), capacitances (second graph), PC and output voltage for AND (third graph) and OR (fourth graph) gates over time.

We now examine the case of an OR gate. The corresponding output voltage is reported in the fourth graph of Fig. 4(b). A high output is reached when one or both inputs are high. In contrast with the case of the AND gate, the output voltage for low-low and high-high inputs is now higher than for the case of the buffer. The low level output voltage for low-low inputs rises from 0.17 to 0.3. This is due to the increase of the equivalent capacitance, caused by the connection in parallel of the two variable capacitors $C_{DS1}$ and $C_{DS2}$.

Serial and parallel connection of variable capacitors reduces the difference between low and high logic states. This could be an issue for CAL operation. The same limitation applies to the quantity of gates, N, connected to the output, i.e. for fan-out operation. Total value of the load capacitance should be in the range of the variation of the variable capacitor $C_{DS}$, i.e.:

$$\begin{aligned} C_L<NC_0<C_H. \end{aligned}$$

(5)

4 Electromechanical Model of a Four-Terminal Variable Capacitor Element

The key challenge of CAL development is being able to define the scalable hardware necessary to implement the elementary PVC and NVC devices. The capacitor value can be modulated by the variation of relative permittivity, plate surface and gap thickness. In principle, there are a wide range of available actuators to realize this modulation: magnetic, piezoelectric, electrostatic, etc. For further analysis, we selected electrostatic actuators as electrostatic MEMS relays for scaling with sub-1-volt operation [6], as a possibility for the integration of the MEMS relays in VSLI circuits has already been demonstrated [4]. The basic electromechanical device of CAL consists of the two electrically-isolated and mechanically-coupled capacitors.

4.1 Two-Terminal Parallel Plate Transducer

Let us consider a 1D parallel-plate transducer model of a gap-variable capacitor with an initial air-filled gap $g_0$, equivalent mass m and equivalent spring constant k. The electromechanical transducer model in up-state position is shown in the left part of Fig. 5(a). The up-state capacitance equals:

$$\begin{aligned} C_{G\_U}=\frac{\epsilon _0A_G}{g_{eff}}, \end{aligned}$$

(6)

where $\epsilon _0$ is the permittivity constant of a vacuum, $g_{eff}=g_0+t_d/\epsilon _d$ is the effective electrostatic gap, $A_G$ is the electrode area of the gate capacitance, and $t_d$, $\epsilon _d$ are the thickness and relative permittivity of the dielectric layer, respectively.

When $V_G$ is applied to the electrodes, the electrostatic attractive force (7) acting on the piston causes its static displacement z. This displacement is defined by the equilibrium equation related to the restoring force of the spring (8).

$$\begin{aligned} F_{elG}(z)=\frac{\epsilon _0A_GV_G^2}{2(g_{eff}-z)^2} \end{aligned}$$

(7)

$$\begin{aligned} \frac{\epsilon _0A_GV_G^2}{2(g_{eff}-z)^2}=kz \end{aligned}$$

(8)

It can be shown that there is a critical displacement from which the electrostatic force is no longer balanced by the restoring force and the piston falls down to the bottom electrode as presented in the right-hand part of Fig. 5(a). The static pull-in point displacement equals one third of the effective gap and the pull-in voltage is given by:

$$\begin{aligned} V_{PI}=\sqrt{\frac{8}{27}\frac{kg_{eff}^3}{\epsilon _0A_G}}. \end{aligned}$$

(9)

The down-state capacitance is defined by the dielectric layer thickness and equals:

$$\begin{aligned} C_{G\_D}=\frac{\epsilon _0\epsilon _dA_G}{t_d}. \end{aligned}$$

(10)

In this configuration, the high down-state to up-state capacitance ratio is achievable. However, there is a problem induced by a non-adiabatic pull-down motion. According to [10], the impact kinetic energy loss is one of the dominant loss mechanisms in a MEMS relay. The kinetic energy loss cannot be suppressed by the increasing ramping time, as after the pull-in point, we lose control under the motion of the piston. In order to avoid this issue, a solution with a controlled dynamic should be proposed.

Fig. 5.

(a) Electromechanical capacitance in up (left) and down (right) states. (b) Electrostatically-controlled variable capacitor $C_{DS}$. (c) $C_G$ and $C_{DS}$ capacitances according to $V_G$ ($V_{DS}$ = 0 V). (d) Test circuit.

As we discussed above, the static pull-in point displacement equals one third of the effective gap. We can thus avoid collapse if we add a stopper with a thickness greater than $2g_{eff}$/3 to stop the mechanical motion before the pull-in. This solution allows us to reduce the impact energy loss and eliminate the uncontrolled dynamic caused by the voltage $V_G$.

4.2 Four-Terminal Parallel Plate Transducer with Stopper

Figure 5(b) shows a viable candidate for PCV implementation, where the gap between the electrodes can be modulated by the electrostatic force caused by the gate voltage, $V_G$, and the drain-source voltage, $V_{DS}$. The right part (input) is electrically isolated from the left which has the drain and source terminals (output). The output capacitance $C_{DS}$ should be insensitive to $V_{DS}$ when $V_G$ = 0 V. In order to guarantee this, we add two couples of symmetrical electrodes, which form two capacitors $C_{DS\_T}$ and $C_{DS\_D}$. The $C_{DS}$ capacitance is the sum of the latter. When the input voltage $V_G$ and the displacements are small, the electrostatic attractive force $F_{elDS}(z)$ in the output is almost balanced:

$$\begin{aligned} F_{elDS}(z)=\frac{\epsilon _0A_{DS}V_{DS}^2}{2(g_0/3+t_d/\epsilon _d-z)^2}-\frac{\epsilon _0A_{DS}V_{DS}^2}{2(g_0/3+t_d/\epsilon _d+z)^2}, \end{aligned}$$

(11)

where $A_{DS}$ is the symmetrical output electrode area of the $C_{DS}$ capacitance and the initial output gap thickness equals $g_0/3$. For the selected gap value, the piston contacts the bottom electrode when $V_G$ equals the contact voltage, $V_{con}$ (12).

$$\begin{aligned} V_{con}=\sqrt{\frac{2kg_0(2g_0/3+t_d/\epsilon _d)^2}{3\epsilon _0A_G}}. \end{aligned}$$

(12)

In the beginning of this paper, we assumed that $C_{DS}$ depends only on the input voltage $V_G$. The proposed structure provides us with the same behavior as with the Bennett clocking PC. The symmetric output capacitance $C_{DS}$ allows pull-in to be avoided by applying non-zero $V_{DS}$ when the input $V_G$ = 0 V. When the input voltage $V_G$ is ramped higher than the contact voltage, the piston comes into contact with the dielectric layer in the stopper area. After this contact, the value of $V_{DS}$ no longer affects the position of the piston, and consequently, neither the input nor the output capacitances. The capacitances $C_{G}$ and $C_{DS}$ as a function of input voltage $V_G$ are presented in Fig. 5(c) ($V_{DS}$ = 0 V). The ratio $\frac{C_H}{C_L}$ for $C_{DS}$ is about 9, whereas the variation of $C_G$ capacitance is not as high and does not exceed 50%.

The dynamic behavior of the parallel plate transducer with an air-filled cavity is described by the following differential equation of motion:

$$\begin{aligned} m{\ddot{z}}=F_{elG}(z)+F_{elDS}(z)+F_{con}(z)-b{\dot{z}}-kz, \end{aligned}$$

(13)

where we assume that the viscous damping coefficient b does not depend on the piston displacement. The limit of piston displacement due to the stopper is modelled by injecting an additional restoring force $F_{con}$ as in work [11]. The adhesion force is neglected. The mechanical resonant frequency f and Q–factor of the system can be defined from (14) and (15).

$$\begin{aligned} f=\frac{1}{2\pi }\sqrt{\frac{k}{m}} \end{aligned}$$

(14)

$$\begin{aligned} Q=\frac{\sqrt{mk}}{b} \end{aligned}$$

(15)

4.3 Energy Conversion and Losses

In order to study the dynamic behavior of the 4-terminal variable capacitor, we performed transient electromechanical simulation of the circuit depicted in Fig. 5(d). However in this paper, only the case of maximal displacement and large capacitance variation is discussed ($V_G \ge V_{con}$). The equivalent parameters of the model are extracted from a fixed-fixed gold plate: length 103 $\upmu$m, width 30 $\upmu$m and thickness 0.5 $\upmu$m, according to [11]. The residual stresses in the plate equal zero and only the linear component of stiffness is used in the model. The energy components in this system are:

$$\begin{aligned}&E_{S1}=\int _0^{t_0} V_{PC1}(t)i_G(t)\mathrm {d}t&~~~ \text {Energy delivered by the first voltage source} \\&E_{S2}=\int _0^{t_0} V_{PC2}(t)i_{DS}(t)\mathrm {d}t&~~~ \text {Energy delivered by the second voltage source} \\&E_{C_G}=\frac{1}{2}C_GV_G^2&~~~ \text {Electrical energy stored in }C_G \\&E_{C_{DS}}=\frac{1}{2}C_{DS}V_{DS}^2&~~~ \text {Electrical energy stored in }C_{DS} \\&E_{R_G}=R_G\int _0^{t_0} i_G(t)^2\mathrm {d}t&~~~ \text {Energy dissipated in the resistor } R_G \\&E_{R_{DS}}=R_{DS}\int _0^{t_0} i_{DS}(t)^2\mathrm {d}t&~~~ \text {Energy dissipated in the resistor } R_{DS} \end{aligned}$$

$$\begin{aligned}&E_{M}=\frac{1}{2}kz^2&~~~ \text {Mechanical spring energy} \\&E_{KIN}=\frac{1}{2}mv^2&~~~ \text {Kinetic energy} \\&E_{D}=b\int _0^{t_0} v(t)^2\mathrm {d}t&~~~ \text {Energy loss in damping} \\&\varDelta E=E_{S1}-E_{C_G}-E_{R_G}-E_{M}-E_{KIN}-E_{D}&~~~ \text {Energy balance} \end{aligned}$$

where $V_{PC1}$, $V_{PC2}$ are the output voltages of the two PC’s, and $i_G$, and $i_{DS}$ the currents through the resistors $R_G$ and $R_{DS}$, respectively.

Fig. 6.

Evolution of voltages applied to the four-terminal transducer model (first graph), currents (second graph), equivalent mass displacement (third graph), capacitances (fourth graph), energy components of electrical part (fifth graph), mechanical spring energy and damping loss (sixth graph), resistive losses (seventh graph), kinetic energy and energy balance (eighth graph) over time. We used the following parameters: $g_0 = 1$ $\upmu$m, $t_d = 0.1$ $\upmu$m, $\epsilon _d =$ 7.6, $m = 1.19\cdot 10^{-11}$ kg, k = 4.72 N/m, $b = 7.48\cdot 10^{-6}$ Ns/m, $A_G = 8.53\cdot 10^{-10}$ m$^2$, $A_{DS} = 0.47\cdot 10^{-10}$ m$^2$, $V_{con} =$ 13.8 V, $f =$ 100 kHz, $Q =$ 0.5, $T = 50\, \upmu$s, $R_G = R_{DS} =1$ $k\Omega$.

The smooth transition needed in any adiabatic logic family reduces the frequency. In CMOS-based digital circuits, logic states are encoded through two distinct voltage values, e.g. 0 and $V_{DD}$. Switching of a bit requires capacitance C to be charged or discharged. This represents the input capacitance of the following gate. In standard CMOS circuitry, switches are operated sharply over a time period $T<<RC$, where R is the resistance in the charging part of the circuit. This leads to a power dissipation of about $\frac{1}{2}CV_0^2$ per operation [12]. In adiabatic computing, energy saving is achieved by operating the circuit in the $T>>RC$ range. This allows the energy of the logic states to be recycled and reused, instead of conversion into heat [13]. In an electromechanical system such as CAL, the total dissipation is the sum of the losses in the electrical and mechanical domains [14]. To reduce power dissipation, the ramping time should be much more than both the electrical RC and mechanical $\propto$ 1/f time constants. The time constants of the model follow 1/f = 10 $\upmu$s, so that $R_{DS}C_{DSmax}=32.5$ ps. The time required for the variable capacitance to mechanically change up-state to down-state is significantly longer than the RC electrical constant. This means that mechanical motion is adiabatic in the electrical domain. However, a smooth transition is needed for the maximal time constant.

For the first simulation and model verification, we selected a Bennett clocking PC with $T = 5$/$f = 50\,\upmu$s and $V_{PC1max} = V_{PC2max} =$ 20 V. The results are shown in Fig. 6. During the charging process of $C_G$, part of the electrical energy is converted into mechanical energy. Charging or discharging the $C_{DS}$ capacitor does not lead to energy conversion as the capacitance remains constant. When discharging $C_G$, part of the mechanical spring energy stored in the system is recovered in the first voltage source. The difference between transferred and received energy is determined by damping, kinetic and resistive losses. However, mechanical loss dominates, and the resistive loss is 5 orders of magnitude lower than the mechanical one. The kinetic energy loss is only 6% of the damping loss for this particular case. The total dissipated energy during one cycle is 172 fJ. The ratio of the total dissipated energy to the energy delivered by the first voltage source is 0.067. Consequently, most of the energy provided is recovered. We also checked the difference between the energy provided by the voltage sources and all the other energy components (eighth graph of Fig. 6). The energy saving law is satisfied, i.e. the step in the $\varDelta$E graph is caused by kinetic energy loss during impact. This step is related to the work by the contact force $F_{con}$ which limits the piston motion. This simulation therefore allows us to verify that the proposed model is energy consistent and can be used for further variable capacitance development.

In Fig. 7(a), we present the effect of ramping time T on the maximum energy components during one cycle. All other parameters are the same as in the previous calculation. The resistive loss is very small and is thus not given in Fig. 7. As discussed above, increasing the ramping time decreases the mechanical and total loss values. The latter decreases proportionally: $T^{-0.8}$. This demonstrates the absence of any non-adiabatic losses for the proposed design. However, the main drawback of this approach is the decrease in the operating frequency.

Fig. 7.

Simulated maximal energy components: (a) according to ramping time (Q = 0.5); (b) according to Q–factor (Tf = 5).

The results for the maximum energy components during one cycle in relation to Q–factor are shown in Fig. 7(b). The ramping time is fixed and equals 50 $\upmu$s (5/f). The increase in Q–factor decreases the total mechanical loss value. For example the Q–factor increases from 0.5 to 10 which reduces the total loss from 172 fJ to 45 fJ per cycle. The loss reduction is monotonous for this case. Therefore, we can say that an increase in Q–factor allows a decrease in loss without dramatically decreasing the operating frequency. The maximal value of the Q–factor is limited by the idle phase between the ramping-down and ramping-up stages. This time should be sufficient to decay the vibration after input voltage decrease.

The developed electromechanical model of the variable MEMS capacitance has been successfully verified. In addition, the main loss mechanisms have been established, and the adiabatic loss decreases also demonstrated for an electromechanical device with Bennett clocking actuation. The energy dissipated during one cycle is in the order hundreds of fF and still far from the energy dissipated by a nano-scale FET transistor which is in the order a fraction of fF. However, scalability is possible for the proposed electromechanical devices and with appropriate ramping time and Q–factor selection it could overcome this level and try to confirm or go lower than the Landauer limit. The proposed model will be used for further CAL circuit design and analysis, including reversible gate circuits.

5 Conclusion

The present work focused on the analysis and hardware implementation of CAL at the gate level. First, we demonstrated that basic logic functions can be implemented using a capacitive voltage divider with variable capacitors. It was then shown that the load capacitance of the next logic gates is a critical parameter in the design of CAL-based circuits. A possible design of a four-terminal variable capacitors has been proposed and discussed.

In order to analyze all loss mechanisms, an analytical compact model of the electrostatically-actuated variable capacitor has been developed. In electromechanical adiabatic systems, total loss is a sum of the losses in all electrical and mechanical domains, where mechanical loss dominates due to a relatively high mechanical time constant. To decrease these losses, the ramping time T and Q–factor should be appropriately chosen. The main drawback of an increase in ramping time is the decrease in operating frequency. The absence of non-adiabatic losses and leakages allows us to construct reversible gates with ultra-low power consumption.

The developed electromechanical model of the variable MEMS capacitance will be used for further CAL circuits design and analysis.