1 Introduction

The high level of variable loading, that most civil and mechanical engineering structures or structural components are subjected to, force them to develop irreversible strains that may lead them to asymptotic limit states related to global excessive deformations (ratcheting) or local ones (low cycle fatigue). For civil engineering structures, like bridges, pavements, buildings, and offshore structures, such typical loadings are heavy traffic, earthquakes or waves. On the other hand, the coexistence of thermal and mechanical loadings on mechanical engineering structures, like, for example, nuclear reactors aircraft propulsion engines, lead them also to stress regimes well beyond their elastic limit. Below a certain level of the applied loading, a favorable asymptotic state exists that, after some initial plastic straining the structure behaves elastically. This safe state is known as shakedown which has an effect to extend the life cycle of a structure.

When the exact loading history is known, one may estimate the long term behavior of a structure and determine whether shakedown has occurred, using cumbersome time stepping calculations. A much better alternative, that requires much less computing time, is offered by the direct methods. Moreover, it very often happens that the complete time history of loading is not known, but only its variation intervals. In these cases, direct methods are the only way to establish safety margins.

Based on the fact that for structures made of stable materials [1] an asymptotic state always exists [2], direct methods try to estimate this state right from the start of the calculations. Most direct methods for shakedown analysis are based on the lower bound [3] or the upper bound [4] theorems and they are formulated within the framework of mathematical programming.

The present work refers to a recently appeared in the literature numerical approach, which may be used for the evaluation of the shakedown load of elastoplastic structures under cyclic loading. The approach has been called RSDM-S and has its roots to the Residual Stress Decomposition Method (RSDM) [5, 6] which may estimate any asymptotic state under a given cyclic loading history. According to RSDM the residual stresses are decomposed into Fourier series whose terms are evaluated iteratively by satisfying equilibrium and compatibility at several time points inside the cycle. When looking for shakedown limits the exact history is not known but only the variation intervals of the loads and thus any curve varying between these intervals may convert the problem to an equivalent prescribed loading one. Then the RSDM-S generates a sequence of descending loading cyclic solutions through the use of the RSDM. The limit of this sequence is the shakedown load when the only remaining term in the Fourier series of the residual stresses is the constant term [7,8,9]. The procedure was originally proposed in [7] and may be implemented in any standard finite element program. In this work the efficiency of the approach to predict shakedown boundaries for complex loading domains is demonstrated by its application to two-dimensional structures under mechanical or thermomechanical loads.

2 Description of the RSDM-S

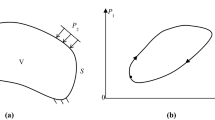
Let us suppose that a structure made of elastic-perfectly plastic von Mises type of material is subjected to a mechanical and a thermal load that vary independent to each other. These loads may have a cyclic variation between a specified maximum and a minimum value, just like the cyclic program shown in (Fig. 1a) \((0\, \to \,P^{*} \, \to \,(P^{*} ,\theta^{*} )\, \to \,\theta^{*} \, \to \,0)\). Without loss of generality we assume that the minimum values of the two loads are zero with the starred quantities corresponding to the maximum values of the loads. Two-dimensional loading domains are considered herein. In the case the structure is subjected to only mechanical loadings the corresponding cyclic program is \((0\, \to \,P_{1}^{*} \, \to \,(P_{1}^{*} ,P_{2}^{*} )\, \to \,P_{2}^{*} \, \to \,0)\).

Fig. 1
figure 1

Independent cyclic loading variation over one time period a in load space, b in time domain

Full size image

In the time domain this cyclic loading may be expressed as:

$${\mathbf{P}}(\tau ) = \left\{ {\begin{array}{*{20}c} {P(\tau )} \\ {\theta (\tau )} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {P^{*} \alpha_{1} (\tau )} \\ {\theta^{*} \alpha_{2} (\tau )} \\ \end{array} } \right\}\;{\text{or }}{\mathbf{P}}(\tau ) = \left\{ {\begin{array}{*{20}c} {P_{1} (\tau )} \\ {P_{2} (\tau )} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {P_{1}^{*} \alpha_{1} (\tau )} \\ {P_{2}^{*} \alpha_{2} (\tau )} \\ \end{array} } \right\}$$
(1)

where \(\tau\) denotes a cycle time point (\(0 \le \tau \le 1\)) and \(\alpha_{1} (\tau ),\alpha_{2} (\tau )\) are time functions.

Indicative variations of the two loads may be seen in Fig. 1b. For loads, varying proportionally, different time functions should be used [10].

Due to the convexity of the yield surface it has been stated [11] that if a given structure shakes down over the path of Fig. 1a that defines the domain \(\Omega\), then it shakes down over any load path contained within \(\Omega\).

Equation (1) converts the problem of a prescribed loading domain to an equivalent prescribed cyclic loading in the time domain. The loading domain may be varied isotropically by multiplying the variation of the loads with a factor \(\gamma\).

The stresses in the structure at a cycle point τ are decomposed into an elastic part \({\varvec{\upsigma}}^{el} (\tau )\), in equilibrium with the applied external cyclic loading and a residual stress part \({\varvec{\uprho}}(\tau )\). In the search for shakedown the elastic stresses are themselves multiplied by this factor \(\gamma\). Thus the total stress vector can now be written:

$${\varvec{\upsigma}}(\tau ) = \gamma {\varvec{\upsigma}}^{el} (\tau ) + {\varvec{\uprho}}(\tau )$$
(2)

where \({\varvec{\upsigma}}^{el} (\tau )\) are calculated from the vector of nodal displacements \({\mathbf{r}}^{el} (\tau )\):

$${\varvec{\upsigma}}^{el} (\tau ) = {\mathbf{D}} \cdot ({\mathbf{B}} \cdot {\mathbf{r}}^{el} (\tau ) - {\mathbf{e}}^{\theta } (\tau ))$$
(3)

where D and B are the material and compatibility matrices of a continuum which has been discretized with the aid of the finite element (FE) method. \({\mathbf{e}}^{\theta } (\tau )\) are the thermal strains and may be determined using the coefficient of the thermal expansion.

On the other hand \({\mathbf{r}}^{el} (\tau )\) is determined by solving the equation:

$${\mathbf{K}} \cdot {\mathbf{r}}^{el} (\tau ) = \int\limits_{V} {{\mathbf{B}}^{T} } \cdot {\mathbf{D}} \cdot {\mathbf{e}}^{\theta } (\tau )dV + {\mathbf{R}}_{\text{P}} (\tau )$$
(4)

where \({\mathbf{K}} = \int_{V} {{\mathbf{D}}^{T} \cdot {\mathbf{B}} \cdot {\mathbf{D}}dV}\) is the stiffness matrix of the structure, and \({\mathbf{R}}_{\text{P}} (\tau )\) the nodal forces due to the mechanical load.

Also, in relation to (1), \({\mathbf{e}}^{\theta } (\tau ) = \alpha_{2} (\tau ) \cdot {\mathbf{e}}^{{\theta^{*} }}\) and \({\mathbf{R}}_{\text{P}} (\tau ) = \alpha_{1} (\tau ) \cdot {\mathbf{R}}_{{P^{*} }}\).

In the case where a mechanical load is applied in the place of the thermal load the equations are changed appropriately [7, 9].

Having established the elastic part the residual stress part may be estimated based on the expected cyclic nature of the residual stresses at the asymptotic cycle. Thus one may decompose them into Fourier series:

$${\varvec{\uprho}}(\tau ) = \frac{1}{2}{\mathbf{a}}_{0} + \sum\limits_{k = 1}^{\infty } {\left\{ {\cos (2k\pi \tau ) \cdot {\mathbf{a}}_{k} + \sin (2k\pi \tau ) \cdot {\mathbf{b}}_{k} } \right\}}$$
(5)

The RSDM method may be used to find iteratively the coefficients \({\mathbf{a}}_{0}^{{}} ,{\mathbf{a}}_{k}^{{}}\) and \({\mathbf{b}}_{k}^{{}}\) [5].

According to Melan’s theorem [3] the conditions for shakedown consist of the two following statements [12]:

  1. (a)

    The structure will shake down under a cyclic loading if there exists a time-independent distribution of residual stresses \({\bar{\mathbf{\rho }}}\) such that, under any combination of loads inside prescribed limits, its superposition with the ‘elastic’ stresses \({\varvec{\upsigma}}^{el}\), i.e. \({\varvec{\upsigma}}^{el} + {\bar{\mathbf{\rho }}}\), results in a total safe stress state at any point of the structure.

  2. (b)

    Shakedown never takes place unless a time-independent distribution of residual stresses can be found such that, under all the possible load combinations, the sum of the residual and ‘elastic’ stresses constitutes an allowable stress state.

For a structure subjected to a prescribed cyclic loading program, these statements define the limit cycle which is a transition cycle between one with plastic straining and one without plastic straining. It may be proved [12] that the residual stress distribution of this cycle is unique, being independent of the preceding deformation history.

The numerical procedure RSDM-S is a transition process to this cycle [7, 8]. It starts from a high load factor, which is sequentially lowered by shrinking the loading domain in a continuous way up to the point that the conditions of the limit cycle are reached.

Decomposition of the residual stresses in Fourier series provides a natural way to implement this transition. Thus the procedure stops the first time the only remaining term of the Fourier series is the constant term \({\mathbf{a}}_{0}^{{}}\). When this is achieved, we have the parameters of the limit cycle for the applied loading (1) together with the shakedown factor \(\gamma_{sh}\) of the loading domain [7].

To briefly describe the numerical implementation one could underline that first there is an initialization phase, where the starting loading factor is definitely higher than the shakedown factor as it is calculated so that the whole structure has become plastic [7].

Then we enter an iterative phase of two iteration loops, one inside the other. Let us denote with μ a typical iteration of the outer loop of the descending load factor. The outer loop includes the following steps:

  1. (1)

    Enter the inner loop, which consists of the steps of the RSDM [5, 6]. For the current load factor \(\gamma^{(\mu )}\), the iterations of RSDM start using, as a first estimate, the Fourier coefficients and the residual stresses of the cyclic solution, of the previous loading factor \(\gamma^{(\mu - 1)}\).

  2. (2)

    On exit from the inner loop, a cyclic stress state has been reached and the cyclic solution values

    \({\mathbf{a}}_{0}^{(\mu )} ,{\mathbf{a}}_{k}^{(\mu )} ,{\mathbf{b}}_{k}^{(\mu )} \, \Rightarrow \,{\varvec{\uprho}}^{(\mu )} (\tau )\), for the current load factor, have been obtained.

  3. (3)

    Calculation of the sum of the norms of the vectors of the updated coefficients of the trigonometric part of the Fourier series

    $$\varphi \left( {\gamma^{\left( \mu \right)} } \right) = \sum\limits_{k = 1}^{\infty } {{\mathbf{a}}_{k}^{(\mu )} } + \sum\limits_{k = 1}^{\infty } {{\mathbf{b}}_{k}^{(\mu )} }$$
    (6)
  4. (4)

    Obtain an update of the loading factor through the function \(\varphi\)

    $$\gamma_{{}}^{{\left( {\mu + 1} \right)}} \cdot P_{{}}^{*} = \gamma_{{}}^{\left( \mu \right)} \cdot P_{{}}^{*} - \omega \cdot \varphi \left( {\gamma_{{}}^{\left( \mu \right)} } \right)$$
    (7)

    where the mechanical load is expressed as pressure load.

  5. (5)

    Check the convergence of the load factor between two successive iterations within some tolerance.

If they equal each other the procedure stops, as only constant terms remain in the Fourier series.

Due to the positive sign of φ in Eq. (7), a descending sequence of cyclic solutions is produced which ends up with the parameters of the limit cycle for elastic shakedown. To avoid cases of overshooting below shakedown a convergence parameter \(\omega\) is used. Analytical convergence considerations and a detailed description of the procedure are represented in [7].

3 Application Examples

The versatility of the proposed numerical method, to establish shakedown boundaries, is demonstrated in four examples, a thick cylinder, a holed plate, a frame and a continuous beam. The examples address loading domains of different complexity. Quadrilateral finite elements were used to model all the structures.

3.1 Bree Problem

The first example is a Bree problem where either a plate or a tube wall thickness is subjected to axial stress \(P(\tau )\) and a fluctuation of temperature difference \(\Delta \theta (\tau )\), assumed to be linearly distributed along the width of the plate (Fig. 2). The plate is assumed homogeneous, isotropic, elastic-perfectly plastic with the material data of Table 1. The plate is constrained from in-plane bending, thus making the problem essentially one dimensional. The finite element mesh consists of one hundred and twenty, eight-noded, iso-parametric elements with 3 × 3 Gauss integration points (Fig. 2). Plane stress conditions are assumed.

Fig. 2
figure 2

Geometry, loading and finite element mesh for the Bree problem

Full size image
Table 1 Material properties of the plate
Full size table

Two different load cases of thermo-mechanical loading were considered. In the first one, a constant in time axial load and a variable temperature difference \(\Delta \theta (\tau )\) (Fig. 3a), whereas for the second one, a proportional variation between the axial load and the temperature difference (Fig. 3b) is assumed.

Fig. 3
figure 3

Different cyclic loading cases

Full size image

3.1.1 Constant Axial Load \(P\), Variable Temperature \(\Delta \theta (\tau )\)

A prescribed loading in the time domain for the varying temperature may be established using a polynomial time function. One may thus write for both loads:

$$P(\tau ) = \left\{ {\begin{array}{*{20}c} {P^{*} \alpha_{1} (\tau )} \\ {\Delta \theta^{*} \alpha_{2} (\tau )} \\ \end{array} } \right\}\;{\text{where}}\,{\text{the}}\,{\text{time}}\,{\text{functions}}\;\alpha_{1} (\tau ),\alpha_{2} (\tau )\,{\text{are:}}$$
$$\begin{aligned} \alpha_{1} \left( \tau \right) & = const \\ \alpha_{2} (\tau ) & = 3.3334\tau^{4} - 6.6667\tau^{3} + 0.1667\tau^{2} + 3.1667\tau \\ \end{aligned}$$

In Fig. 4 one may see the constructed shakedown domain by the RSDM-S and its comparison with the analytical solution of Bree [13]. The two domains are almost identical.

Fig. 4
figure 4

Shakedown domain produced by the RSDM-S and its comparison with the analytical solution of Bree [13] (load case 1)

Full size image

3.1.2 Proportional Variation of Axial Load \(P(\tau )\) and Temperature \(\Delta \theta (\tau )\)

The proportional variation of the cyclic loading in the load domain may be described by the path \((0\, \to \,(P^{*} ,\Delta \theta^{*} )\, \to \,0)\) (Fig. 3b).

Let us now consider a prescribed loading in the time domain using the equation:

$$P(\tau ) = \left\{ {\begin{array}{*{20}c} {P^{*} \alpha (\tau )} \\ {\Delta \theta^{*} \alpha (\tau )} \\ \end{array} } \right\}\;{\text{where}}\;\alpha (\tau ) = 3.3334\tau^{4} - 6.6667\tau^{3} + 0.1667\tau^{2} + 3.1667\tau$$

Bree’s findings have been analytically extended by Bradford [14] for a case of proportional loading. The results of the RSDM-S as well as its good agreement with Bradford’s results [14] may be seen in Fig. 5.

Fig. 5
figure 5

Shakedown domain produced by the RSDM-S and its comparison with Bradford’s solution [14] (load case 2)

Full size image

3.2 Square Plate with a Central Hole

The second example of application is a holed square plate under a combination of mechanical and thermal loads (Fig. 6). The plate is assumed homogeneous, isotropic, elastic-perfectly plastic with the material data of Table 1. The boundary conditions as well as its finite element mesh discretization are shown in Fig. 6. The ratio between the diameter \(D\) of the hole and the length \(L\) of the plate is equal to \(0.2\). Also the ratio of the thickness \(d\) of the plate to its length is equal to \(0.05\). Due to the symmetry of the structure and the loading, only one quarter of the plate is analyzed. The finite element mesh discretization of the plate consists of ninety-eight, eight-noded, iso-parametric elements with 3 × 3 Gauss integration points (Fig. 6).

Fig. 6
figure 6

The geometry, loading and the finite element mesh of a quarter of the plate

Full size image

The plate is subjected to a temperature difference \(\Delta \theta (\tau )\) between the edge of the hole and the edge of the plate, and a uniaxial tension \(P(\tau )\) along the one side of the plate (Fig. 6). The variation of the temperature with radius \(r\) has the same logarithmic form as in [8, 15]:

$$\theta (r,\tau ) = \theta_{0} + \frac{{\Delta \theta (\tau )\,*\,\ln \left( {\frac{5D/2}{r}} \right)}}{\ln 5}$$

The above relation defines a temperature distribution inside the plate giving a value of \(\theta_{1} (\tau ) = \theta_{0} + \Delta \theta (\tau )\) around the edge of the hole \(\left( {r = {D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}} \right)\) and \(\theta_{1} = \theta_{0}\) at the outer edges of the plate \(\left( {r = {{5D} \mathord{\left/ {\vphantom {{5D} 2}} \right. \kern-0pt} 2}} \right)\). The temperature \(\theta_{0}\) is assumed to be equal to zero. It should be noted that in the results \(\sigma_{t}\) denotes the maximum effective thermal elastic stress due to the fluctuating temperature.

The shakedown domains were calculated by the RSDM-S assuming two different load cases (Fig. 3). The polynomial time functions that were used to describe the two load paths are the same ones used in the Bree example.

In Fig. 7 one may see the comparison between the results of the RSDM-S with the ones obtained in [15] for the case of constant mechanical load. On the other hand, assuming simultaneous variation of both the thermal and mechanical load, the results of the RSDM-S and its comparison with [16] are plotted in Fig. 8. The results match quite well.

Fig. 7
figure 7

The elastic shakedown domain for the holed plate (load case 1)

Full size image
Fig. 8
figure 8

The elastic shakedown domain for the holed plate (load case 2)

Full size image

3.3 Frame in a General Loading Domain

In the third example, a simple frame, shown in Fig. 9 is considered. This example has been investigated by Tran et al. [18] using an edge-based smoothed finite element method (ES-FEM) and a primal-dual shakedown algorithm, and by Garcea et al. [17] using a strain driven strategy.

Fig. 9
figure 9

Geometry, loading and finite element mesh of the frame

Full size image

The frame is assumed homogeneous, isotropic, elastic-perfectly plastic, having the material data shown in Table 2. The finite element mesh discretization of the frame, shown also in Fig. 9, consists of 400 eight-noded, iso-parametric elements with 3 × 3 Gauss integration points.

Table 2 Material properties of the frame
Full size table

The frame is subjected to two uniform distributed loads \(P_{1} \left( \tau \right)\) and \(P_{2} \left( \tau \right)\), applied on the external faces of AB and BC respectively. A general rectangular loading domain is considered herein (Fig. 10) with the two loads \(P_{1} \left( \tau \right)\) and \(P_{2} \left( \tau \right)\) varying independently, between the values \(\left[ {1.2,3} \right]\) and \(\left[ {0.4,1} \right]\) respectively. A case of a regular loading domain having its origin at zero was studied in [7].

Fig. 10
figure 10

Loading domain of frame example

Full size image

A prescribed loading in time domain that passes through the four vertices of the rectangle may be defined by using the following equations:

$${\text{where}}\;P(\tau ) = \left\{ {\begin{array}{*{20}c} {P_{1}^{*} \alpha_{1} (\tau )} \\ {P_{2}^{*} \alpha_{2} (\tau )} \\ \end{array} } \right\}\;{\text{and}}\,{\text{the}}\,{\text{time}}\,{\text{functions}}\;\alpha_{1} \left( \tau \right), \, \alpha_{2} \left( \tau \right)\,{\text{are:}}$$
$$\begin{aligned} \alpha_{1} \left( \tau \right) & = - 9.6\tau^{2} + 4.8\tau + 0.4,\alpha_{2} \left( \tau \right) = 0.4 ,\quad \tau \, \in \,[0,1/4] \\ \alpha_{1} \left( \tau \right) & = 1,\alpha_{2} \left( \tau \right) = - 9.6\tau^{2} + 9.6\tau - 1.4 ,\quad \tau \, \in \,(1/4,1/2] \\ \alpha_{1} \left( \tau \right) & = - 9.6\tau^{2} + 9.6\tau - 1.4,\alpha_{2} \left( \tau \right) = 1 ,\quad \tau \, \in \,(1/2,3/4 ] { } \\ \alpha_{1} \left( \tau \right) & = 0.4,\alpha_{2} \left( \tau \right) = - 9.6\tau^{2} + 14.4\tau - 4.4 ,\quad \tau \, \in \,(3/4,1] \\ \end{aligned}$$

In this case \(P_{1}^{*} = 3\), \(P_{2}^{*} = 1\) and \(0.4\, \le \,\alpha_{1} (\tau ),\alpha_{2} (\tau )\, \le \,1\).

For this example the initial convergence parameter \(\omega\), in the process of the iterations, had to be halved twice, for the RSDM-S to converge to the final shakedown limit which was found equal to 3.91.

The present results of the RSDM-S, compared to those of different analysis methods in the literature, are shown in Table 3. It may be seen that they match quite well.

Table 3 Comparison of the numerical results
Full size table

3.4 Symmetric Continuous Beam in a General Loading Domain

Let us now consider the symmetric continuous beam of Fig. 11. The beam is subjected to two uniform distributed loads \(P_{1} \left( \tau \right)\) and \(P_{2} \left( \tau \right)\), applied on each span. The beam is assumed homogeneous, isotropic, elastic-perfectly plastic, having the material data shown in Table 4. The finite element mesh discretization of the beam, shown also in Fig. 11, consists of 800 eight-noded, iso-parametric elements with 3 × 3 Gauss integration points.

Fig. 11
figure 11

Geometry, loading and finite element mesh for the continuous beam

Full size image
Table 4 Material properties of the continuous beam
Full size table

A general rectangular loading domain is considered (Fig. 12) with the two loads \(P_{1} \left( \tau \right)\) and \(P_{2} \left( \tau \right)\) varying independently, between the values \(\left[ {1.2,2} \right]\) and \(\left[ {0,1} \right]\) respectively. A case of a regular loading domain having its origin at zero was studied in [7].

Fig. 12
figure 12

Loading domain of beam example

Full size image

A prescribed loading in time domain that passes through the four vertices of the rectangular may be defined by using the following time functions \(\alpha_{1} (\tau ),\alpha_{2} (\tau )\):

$$\begin{aligned} \alpha_{1} \left( \tau \right) & = - 6.4\tau^{2} + 3.2\tau + 0.6,\alpha_{2} \left( \tau \right) = 0 ,\quad \tau \, \in \,[0,1/4] \\ \alpha_{1} \left( \tau \right) & = 1,\alpha_{2} \left( \tau \right) = - 16\tau^{2} + 16\tau - 3 ,\quad \tau \, \in \,(1/4,1/2] \\ \alpha_{1} \left( \tau \right) & = - 6.4\tau^{2} + 6.4\tau - 0.6,\alpha_{2} \left( \tau \right) = 1 ,\quad \tau \, \in \,(1/2,3/4 ] { } \\ \alpha_{1} \left( \tau \right) & = 0.6,\alpha_{2} \left( \tau \right) = - 16\tau^{2} + 24\tau - 8 ,\quad \tau \, \in \,(3/4,1] \\ \end{aligned}$$

It is assumed that \(P_{1}^{*} = 2\), \(P_{2}^{*} = 1\) and \(0.6\, \le \,\alpha_{1} (\tau )\, \le \,1,0\, \le \,\alpha_{2} (\tau )\, \le \,1\).

For this example, the initial convergence parameter \(\omega\), in the process of the iterations, had to be halved three times, for the RSDM-S to converge to the final shakedown limit which is equal to 3.177. The shakedown factor obtained by the RSDM-S, and its comparison with the results of different analysis methods [17,18,19], is shown in Table 5. It may be seen that there is a good agreement.

Table 5 Comparison of numerical results of the symmetric continuous beam
Full size table

Briefing from the present numerical applications, as well as all the ones that have been reported so far, in the literature, one has to note the good and quick convergence characteristics of the RSDM-S approach, as the stiffness matrix must be formed and decomposed only once and only the first three terms of the Fourier series were enough to get accurate results, with the cycle time points being around forty.

4 Concluding Remarks

The direct method, RSDM-S, has been used in the present work to evaluate the shakedown load and provide shakedown boundaries for cyclically loaded elasto-plastic structures under mechanical or thermo-mechanical loading. The loading domain is first converted into a prescribed loading using time functions. In the present work it was shown that the procedure may be easily applied to more general domains, than the already published ones, whose origin is different than zero, by just modifying the time functions. The prescribed loading is then multiplied by a load factor. Starting from a factor high above shakedown, a descending sequence of loading factors is formed which converges to the parameters of the limit cycle, where the residual stresses are constant in time. The approach turns out to be simple, numerically stable and efficient and may be implemented in any existing FE code as opposed to mathematical programming methods where a special optimization algorithm must be supplied.