Convergence of Even Simpler Robots without Position Information

Abstract

The design of distributed gathering and convergence algorithms for tiny robots has recently received much attention. In particular, it has been shown that the convergence problem, that is, the problem of moving robots close to each other (i.e., inside an area of some maximum size, where the position of the area is not fixed beforehand), can even be solved for very weak, oblivious robots: robots which cannot maintain state from one round to the next. The oblivious robot model is hence attractive from a self-stabilization perspective, where the state is subject to adversarial manipulation. However, to the best of our knowledge, all existing robot convergence protocols rely on the assumption that robots, despite being “weak”, can measure distances.

We in this paper initiate the study of convergence protocols for even simpler robots, called monoculus robots: robots which cannot measure distances. In particular, we introduce two natural models which relax the assumptions on the robots’ cognitive capabilities: (1) a Locality Detection ($\mathscr {LD}$) model in which a robot can only detect whether another robot is closer than a given constant distance or not, (2) an Orthogonal Line Agreement ($\mathscr {OLA}$) model in which robots only agree on a pair of orthogonal lines (say North-South and West-East, but without knowing which is which).

The problem turns out to be non-trivial, as simple strategies like median and angle bisection can easily increase the distances among robots (e.g., the area of the enclosing convex hull) over time. Our main contribution is deterministic self-stabilizing convergence algorithms for these two models. We also show that in some sense, the assumptions made in our models are minimal: by relaxing the assumptions on the monoculus robots further, we run into impossibility results.

S. Schmid—Trip to IIT Guwahati and research funded by the Global Initiative of Academic Networks (GIAN), an initiative by the Govt. of India for Higher Education.

1 Introduction

1.1 The Context: Tiny Robots

In the recent years, there has been a wide interest in the cooperative behavior of tiny robots. In particular, many distributed coordination protocols have been devised for a wide range of models and a wide range of problems, like convergence, gathering, pattern formation, flocking, etc. At the same time, researchers have also started characterizing the scenarios in which such problems cannot be solved, deriving impossibility results.

1.2 Our Motivation: Even Simpler Robots

An interesting question regards the minimal cognitive capabilities that such tiny robots need to have for completing a particular task. In particular, researchers have initiated the study of “weak robots” [6]. Weak robots are anonymous (they do not have any identifier), autonomous (they work independently), homogeneous (they behave the same in the same situation), and silent (they also do not communicate with each other). Weak robots are usually assumed to have their own local view, represented as a Cartesian coordinate system with origin and unit length and axes. The orientation of axes, or the chirality (relative order of the orientation of axes or handedness), is not common among the robots. The robots move in a sequence of three consecutive actions, Look-Compute-Move: they observe the positions of other robots in their local coordinate system and the observation step returns a set of points to the observing robot. The robots cannot distinguish if there are multiple robots at the same position, i.e., they do not have the capability of multiplicity detection. Importantly, the robots are oblivious and cannot maintain state between rounds (essentially moving steps). The computation they perform are always based on the data they have collected in the current observation step; in the next round they again collect the data. Such weak robots are therefore interesting from a self-stabilizing perspective: as robots do not rely on memory, an adversary cannot manipulate the memory either. Indeed, researchers have demonstrated that weak robots are sufficient to solve a wide range of problems.

We in this paper aim to relax the assumptions on the tiny robots further. In particular, to the best of our knowledge, all prior literature assumes that robots can observe the positions of other robots in their local view. This enables them to calculate the distance between any pair of robots. This seems to be a very strong assumption, and accordingly, we in this paper initiate the study of even weaker robots which cannot locate other robots positions in their local view, preventing them from measuring distances. We define these kinds of robots as monoculus robots.

In particular, we explore two natural, weaker models for monoculus robots with less cognitive capabilities, those are Locality Detection and Orthogonal Line Agreement. The locality detection model is motivated by, e.g., capacitive sensing or sensing differences in temperature or vibration. The orthogonal line model is practically motivated by robots having a simple compass align for orthogonal line agreement.

1.3 The Challenge: Convergence

We focus on the fundamental convergence problem for monoculus robots and show that the problem is already non-trivial in this setting.

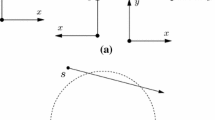
In particular, many naive strategies lead to non-monotonic behaviors. For example, strategies where boundary robots (robots located on the convex hull) move toward the “median” robot (i.e., the median in the local ordering of the robots) they see, may actually increase the area of the convex hull in the next round, counteracting convergence as shown in Fig. 1(a). A similar counterexample exists for a strategy where robots move in the direction of the angle bisector as shown in Fig. 1(b).

Fig. 1.

The 4 boundary robots are moving (a) towards the median robot (b) along the angle bisector. The discs are the old positions and circles are the new positions. The old convex hull is drawn in solid line, the new convex hull is dashed. The arrows denote the direction of moving.

But not only enforcing convex hull invariants is challenging, also the fact that visibility is restricted and we cannot detect multiplicity: We in this paper assume that robots are not transparent, and accordingly, a robot does not see whether and how many robots may be hidden behind a visible robot. As robots are also not able to perform multiplicity detection (i.e., determine how many robots are collocated at a certain point), strategies such as “move toward the center of gravity” (the direction in which most robots are located), are not possible.

1.4 Our Contributions

This paper studies distributed convergence problems for anonymous, autonomous, oblivious, non-transparent, monoculus, point robots under a most general asynchronous scheduling model and makes the following contributions.

• 1. We initiate the study of a new kind of robot, the monoculus robot which cannot measure distances. The robot comes in two natural flavors, and we introduce the Locality Detection ($\mathscr {LD}$) and the Orthogonal Line Agreement ($\mathscr {OLA}$) model accordingly.

• 2. We present and formally analyze deterministic and self-stabilizing distributed convergence algorithms for both $\mathscr {LD}$ and $\mathscr {OLA}$.

• 3. We show our assumptions in $\mathscr {LD}$ and $\mathscr {OLA}$ are minimal in the sense that robot convergence is not possible for monoculus robots.

• 4. We report on the performance of our algorithms through simulation.

• 5. We show that our approach can be generalized to higher dimensions and, with a small extension, supports termination.

1.5 Related Work

The problems of gathering [13], where all the robots gather at a single point, convergence [2], where robots come very close to each other and pattern formation [5, 13] have been studied intensively in the literature.

Flocchini et al. [6] introduced the CORDA or Asynchronous (ASYNC) scheduling model for weak robots. Suzuki et al. [12] have introduced the ATOM or Semi-synchronous (SSYNC) model. In [13], the impossibility of gathering for $n=2$ without assumptions on local coordinate system agreement for SSYNC and ASYNC is proved. Also, for $n>2$ it is impossible to solve gathering without assumptions on either coordinate system agreement or multiplicity detection [10]. Cohen and Peleg [1] have proposed a center of gravity algorithm for convergence of two robots in ASYNC and any number of robots in SSYNC. Flocchini et al. [7] propose algorithm to gather robots with limited visibility and agreement in coordinate system in ASYNC model. Souissi et al. have proposed an algorithm to gather robots with limited visibility if the compass achieves stability eventually in SSYNC in [11]. For two robots with unreliable compass Izumi et al. [9] investigate the necessary conditions required to gather them under SSYNC and ASYNC setting.

In many of the previous works, the mathematical models assume that the robots can find out the location of other robots in their local coordinate system in the Look step. This in turn implies that the robots can measure the distance between any pair of robots albeit in their local coordinates. All the algorithms exploit this location information to create an invariant point or a robot where all the other robots gather. But in this paper, we deprive the robots of the capability to determine the location of other robots. This leads to robots incapable of finding any kind of distance or angles. Note that any kind of pattern formation requires these robots to move to a particular point of the pattern. Since the monoculus robots cannot figure out locations, they cannot stop at a particular point. Hence any kind of pattern formation algorithm described in the previous works which require location information as input are obsolete. Gathering problem is nothing but the point formation problem [13]. Hence gathering is also not possible for the monoculus robots.

1.6 Paper Organization

The rest of this paper is organized as follows. Section 2 introduces the necessary background and preliminaries. Section 3 introduces two algorithms for convergence. Section 4 presents an impossibility result which shows the minimality of our assumptions. We report on simulation results in Sect. 5 and discuss extensions in Sect. 6. We finally conclude in Sect. 7.

2 Preliminaries

2.1 Model

We are given a system of n robots, $R = \{r_1,r_2,\cdots ,r_n\}$, which are located in the Euclidean plane. We consider anonymous, autonomous, homogeneous, oblivious point robots with unlimited visibility. The robots are non-transparent, so any robot can see at most one robot in any direction. The robots have their local coordinate system, which may not be the same for all the robots. The robots in each round execute a sequence of Look-Compute-Move steps: First, each robot $r\in R$ observes other robots and obtains a set of directions $LC =\{\theta _1,\theta _2,\cdots ,\theta _k\}$ where $k\le n-1$ (Look step). Each $\theta \in LC$ is the angle of a robot in the local coordinate system of robot r with respect to the positive direction of the x-axis with the robot itself as the origin. Second, on the basis of the observed information, it executes an algorithm which computes a direction (Compute step); the robot then moves in this direction (Move step), for a fixed distance b (the step size). The robots are silent, cannot detect multiplicity points, and can pass over each other. We ignore the collisions during movement. We name this kind of robots as monoculus robots. We also consider the following two additional capability of the monoculus robots.

Locality Detection $(\mathscr {LD})$ : Locality detection is the ability of a robot to determine whether its distance from any visible robot is greater than a predefined value c or not.

A robot with locality detection capability can divide the visible robots into two sets based on the distance from itself. So a monoculus robot with locality detection can partition the set LC to two disjoint sets $LC_{local}$ and $LC_{non-local}$, where $LC_{local}$ and $LC_{non-local}$ are the set of directions of robots with distances less than equal to c and more than c respectively.

Orthogonal Line Agreement $(\mathscr {OLA})$ : The robots agree on a pair of orthogonal lines, but can neither distinguish the two lines in a consistent way nor have a common sense of direction.

Robots with orthogonal line agreement capability agree on the direction of two perpendicular lines, but the lines themselves are indistinguishable: the robots neither agree on a direction (e.g., North) nor can they mark a line as, e.g., the North-South or East-West line. In other words, any two robots agreeing on the pair of orthogonal lines, either have their x-axis parallel or perpendicular to the other. In case of parallel orientation, the plus/minus direction of the x-axis may point to the same or the opposite direction, and in the case of a perpendicular orientation, the rotation of the axis can be clockwise or counter-clockwise.

We consider the most general CORDA or ASYNC scheduling model known from weak robots [6] as well as the ATOM or Semi-Synchronous (SSYNC) model [12]. These models define the activation schedule of the robots: the SSYNC model considers instantaneous computation and movement, i.e., the robots cannot observe other robots in motion, while in the ASYNC model any robot can look at any time. In SSYNC the time is divided into global rounds and a subset of the robots are activated in each round which finish their Look-Compute-Move within that round. In case of ASYNC, there is no global notion of time. The Fully-synchronous (FSYNC) model is a special case of SSYNC, in which all the robots are activated in each round. The algorithms presented in this paper, work in both the ASYNC and the SSYNC setting. For the sake of generality, we present our proofs in terms of the ASYNC model.

2.2 Notation and Terminology

A Configuration (C) is a set containing all the robot positions in 2D. At any time t the configuration (the mapping of robots in the plane) is denoted by $C_t$. The convex hull of configuration $C_t$ is denoted as $CH_t$. We define Augmented Configuration at time t ($AC_t$) as $C_t$ augmented with the destinations of each robot from the most recent look state on or before t. If all the robots are idle at time t, then $AC_t$ is the same as $C_t$. The convex hull of $AC_t$ is denoted as $ACH_t$ as shown in Fig. 2. Convergence is achieved when the distance between any pair of robots is less than a predefined value $\zeta$ (and subsequently does not violate this). Our multi-robot system is vulnerable to adversarial manipulation, however, the algorithms presented in this paper are self-stabilizing [4] and robust to state manipulations. Since the robots are oblivious, they only depend on the current state: if the state is perturbed, the algorithms are still able to converge in a self-stabilizing manner [8].

Fig. 2.

$r_4'$ is the destination of robot $r_4$ from the most recent look state on or before time t, and analogously for $r_5$. At t, is both the $CH_t$ and $ACH_t$. At $t'$ ($>t$), is $CH_{t'}$, while . $ACH_t$ contains both $r_4$ and $r_4'$ because $r_4$ has not moved. $ACH_{t'}$ contains $r_4'$ as a corner which is outside $CH_{t'}$, because $r_5$ moved to $r_5'$.

3 Convergence Algorithms

The robot convergence is the problem of moving all the robots inside a sufficiently small non-predefined area. In this section, we present distributed robot convergence algorithms for both our models, $\mathscr {LD}$ and $\mathscr {OLA}$. We converge the robots inside a disc and a square, respectively, for the two models.

3.1 Convergence for $\mathscr {LD}$

In this section, we consider the convergence problem for the monoculus robots in the $\mathscr {LD}$ model. Our claims hold for any $c\ge 2b$, where c is the predefined distance of locality detection and b is the step size a robot moves each time it is activated. The step size b and locality detection distance c is common for all the robots. Algorithm 1 distinguishes between two cases: (1) If the robot only sees one other robot, it infers that the current configuration must be a line (of 2 or more robots), and that this robot must be on the border of this line; in this case, the boundary robots always move inside (usual step size b). (2) Otherwise, a robot moves towards any visible, non-local robot (distance at least c), for a b distance (the step size). The algorithm works independent of n, the number of robots present, but depends on D, the diameter of smallest enclosing circle in the initial configuration.

Our proof unfolds in a number of lemmas followed by a theorem. First, Lemma 1 shows that it is impossible to have a pair of robots with distance larger than 2c in the converged situation. Lemma 2 shows that our algorithm ensures a monotonically decreasing convex hull size. Lemma 3 then proves that the decrement in perimeter for each movement is greater than a constant (the convex hull decrement is strictly monotonic). Combining all the three lemmas, we obtain the correctness proof of the algorithm. In the following, we call two robots neighboring if they see each other (line of sight is not obstructed by another robot).

Lemma 1

If there exists a pair of robots at distance more than 2c in a non-linear configuration, then there exists a pair of neighboring robots at distance more than c.

Proof

Proof by contradiction. If there is a pair of robots with distance more than 2c, then they themselves are the neighboring pair with more than c distance. To prevent them from being a neighboring pair with more than c distance, there should be at least two robots on the line joining them positioned such that each neighboring pair has a distance less than c. Since the robots are non-transparent, the end robots cannot look beyond their neighbors to find another robot at a distance more than c. In Fig. 3, $r_1$ and $r_4$ are 2c apart. So $r_2$ and $r_3$ block the view such that $\overline{r_{1}r_{2}}<c$, $\overline{r_{2}r_{3}}<c$ and $\overline{r_{3}r_{4}}<c$. Since it is a non-linear configuration, say robot $r_5$ is not on the line joining $r_1$ and $r_4$. l is the perpendicular bisector of $\overline{r_{1}r_{4}}$. If $r_5$ is on the left side of l, then it is more than c distance away from $r_4$ and if it is on the right side of l then it is more than c distance away from $r_1$. If there is another robot on $\overline{r_{4}r_{5}}$, then consider that as the new robot in a non-linear position, and we can argue similarly considering that robot to be $r_5$. If $r_5$ is on l, then $\overline{r_{1}r_{5}} = \overline{r_{4}r_{5}} > c$. Hence there would at least be a single robot similar to $r_5$ in a non-linear configuration for which the distance is more than c.    $\square$

Fig. 3.

A non-linear configuration with a pair of robots at a distance 2c

Lemma 2

For any time $t' > t$ before convergence, $ACH_{t'}\subseteq ACH_{t}$.

Proof

The proof follows from a simple observation. Consider any robot $r_i$. If $r_i$ decides to move towards some robot, say $r_j$, then it moves on the line joining two robots. There are two cases.

• Case 1: If all the robots are on a straight line, then the boundary robots move monotonically closer in each step. The distance between the end robots is a monotonically decreasing sequence until it reaches c.

• Case 2: For a non-linear configuration the robot moves when the distance between $r_i$ and $r_j$ is more than c and it moves only a distance b, where $c\ge 2b$. The movement path at the time when it looks, is always contained inside the $CH_t$, and $CH_t \subseteq ACH_t$. So the $ACH_t$ contains its entire movement path and it continues to do so until the robot has reached its destination. For any $t' > t$, parts of the path traversed by the robot and outside $CH_{t'}$ are removed from $ACH_t$.

Hence $ACH_{t'}\subseteq ACH_{t}$.    $\square$

Fig. 4.

On activation, $r_i$ and $r_j$ will move outside the solid circle inside the convex hull. The radius of the solid circle is b/2. The robot $r_k$ moves a distance b towards $r_i$ because the distance between them is more than 2b and stops at D. In the second figure the shadowed area is the decrement considered for each corner and the central convex hull inside solid lines is the new convex hull after every robot moves.

Lemma 3

After each robot is activated at least once, the decrement in the perimeter of the convex hull is at least $b \left( 1- \sqrt{\frac{1}{2}\left( 1+\cos \left( \frac{2\pi }{n}\right) \right) }\right)$, where b is the step size and n is the total number of robots.

Proof

Suppose the n robots form a k ($k\le n$) sided convex hull. The sum of internal angles of a k-sided convex polygon is $(k-2)\pi$. So there exists a robot r at a corner A (ref. Fig. 4) of the convex hull such that the internal angle is less than $\left( 1-\frac{2}{n}\right) \pi$, where n is the total number of robots. Let B and C be the points where the circle centered at A with radius b/2 intersects the convex hull. Any robot lying outside the circle will not move inside the circle according to Algorithm 1, because the maximum distance between any two points in the circle is b and all the robots move towards a robot which is more than c distance apart, and $c\geqslant 2b$. All the robots inside the circle will eventually move out once they are activated, because the robot which is activated will have to move at least b distance, and since the distance between any two points in the b/2 radius circle is less than or equal to b, the robot will find itself outside the b/2 radius circle inside the convex hull. After all the robots are activated at least once, the decrement in the perimeter is at least $AB + AC - BC$. From cosine rule,

$$\begin{aligned} AB + AC - BC&=\frac{b}{2}+\frac{b}{2} -\sqrt{\left( \frac{b}{2}\right) ^2+\left( \frac{b}{2}\right) ^2- 2\frac{b}{2}\frac{b}{2}\cos \left( \pi -\frac{2\pi }{n}\right) } \\&= b \left( 1- \sqrt{\frac{1}{2}\left( 1+\cos \left( \frac{2\pi }{n}\right) \right) }\right) \end{aligned}$$

   $\square$

Remark 1

Let us consider a special case of the execution of the algorithm. Here all n robots are on the boundary of the convex hull with side length more than c and move only on the boundary of the convex hull. Then the n-sided polygon will again become an n-sided polygon, but the perimeter will decrease overall as a consequence of Lemma 3 as shown in Fig. 5.

Fig. 5.

Robots on the boundary of a square moving along the boundary (a) all in the clockwise direction, (b) not all in the same direction. The dotted line represent the configuration before movement and the solid line represents the configuration after movement.

Theorem 1

(Correctness). Algorithm 1 always terminates after at most $\Theta \left( \frac{D}{b}\right)$ fair scheduling rounds and for any arbitrary but fixed n, where D is the diameter of smallest enclosing circle in initial configuration and b is the step size. After termination all the robots converge within a c radius disc.

Proof

If a corner robot on the boundary of convex hull is activated, then the perimeter of the convex hull decreases from Lemma 3. If non-corner robots are activated, then the perimeter of the convex hull remains the same. If we have a fair scheduler, the idle time for robots are unpredictable but finite. Consequently, the time between successive activations is also finite. So we can always assume a time step which is large enough for each robot to activate at least once. The total number of robots n is finite and invariant throughout the execution, so $1- \sqrt{\frac{1}{2}\left( 1+\cos \left( \frac{2\pi }{n}\right) \right) }=\delta$ is constant. Hence the decrement of perimeter is at least $b\delta$ according to Lemma 3. Notice that the perimeter of convex hull is always smaller than the perimeter of the smallest enclosing circle. According to Lemma 1, eventually there will not be a pair of robots with more than 2c distance. Note that the distance between any two points in a disc of radius c is less than or equal to 2c. In other words, $\zeta = 2c$. Hence the robots will converge within a disc of radius c. So the perimeter of the circle at termination is $2\pi c$. Now the decrement in the perimeter is $\pi D - 2\pi c$. Total time required is $\frac{\pi (D - 2c)}{\delta b} = \Theta \left( \frac{D}{b}\right)$.

   $\square$

3.2 Convergence for $\mathscr {OLA}$

In this section, we consider monoculus robots in the $\mathscr {OLA}$ model. Our algorithm will distinguish between boundary-, corner- and inner-robots, defined in the canonical way. We note that robots can determine their type: From the Fig. 6, we can observe that for $r_2$, all the robots lie below the horizontal line. That means, one side of the horizontal line is empty and therefore $r_2$ can figure out that it is a boundary robot. Similarly all $r_i$, $i\in \{3,4,5,6,7,8\}$ are boundary robots. Whereas, for $r_1$, both horizontal and vertical lines have one of the sides empty, hence $r_1$ is a corner robot. Other robots are all inner robots. Consequently, we define boundary robots to be those, which have exactly one side of one of the orthogonal lines empty.

Fig. 6.

Movement direction of the boundary robots

Algorithm 2 (ConvergeQuadrant) can be described as follows. A rectangle can be constructed with lines parallel to the orthogonal lines passing through boundary robots such that, all the robots are inside this rectangle. In Fig. 6, each boundary robot always moves inside the rectangle perpendicular to the boundary and the inside robots do not move. Note that the corner robot $r_1$ has two possible directions to move. So it moves toward any robot in that common quadrant. Gradually the distance between opposite boundaries becomes smaller and smaller and the robots converge. In case all the robots are on a line which is parallel to either of the orthogonal lines, then the robots will find that both sides of the line are empty. In that case, they should not move. But the robots on either end of the line would only see one robot. So they would move along the line towards that robot.

Theorem 2

(Correctness). Algorithm 2 moves all the robots inside some 2b-sided square in finite time, where b is the step size.

Proof

Consider the distance between the robots on the left and right boundary. The horizontal distance between them decreases each time either of them gets activated. The rightmost robot will move towards the left and the leftmost will move towards the right. The internal robots do not move. So in at most n activation rounds of the boundary robot, the distance between two of the boundary nodes will decrease by at least b. Hence the distance is monotonically decreasing until 2b. Afterward, the total distance will never exceed 2b anymore.

If there is a corner robot present in the configuration, that robot will move towards any robot in the non-empty quadrant. So, the movement of the corner robot contributes to the decrement in distance in both directions. If an inside robot is very close to one of the boundaries and the corner robot moves towards that robot, then the decrement in one of the dimensions can be small (an $\epsilon > 0$). Consider for example the configuration of a strip of width b, then the corner robot becomes the adjacent corner in the next round; this can happen only finitely many times. Each dimension converges within a distance 2b, so in the converged state the shape of the converged area would be 2b-sided square, i.e., $\zeta = 2\sqrt{2}b$.    $\square$

Remark 2

If the robots have some sense of angular knowledge, the corner robots can always move in a $\pi /4$ angle, so the decrement in both dimension is significant, hence convergence time is less on average.

4 Impossibility and Optimality

Given these positive results, we now show that the assumptions we made on the capability of monoculus robots are minimal for achieving convergeability: the following theorem shows that monoculus robots by themselves cannot converge deterministically.

Theorem 3

There is no deterministic convergence algorithm for monoculus robots.

Proof

We prove the theorem using a symmetry argument. Consider the two configurations $C_1$ and $C_2$ in Fig. 7. In $C_1$, all the robots are equidistant from robot r, while in $C_2$, the robots are at different distances, however, the relative angle of the robots is the same at r. Now considering the local view of robot r, it cannot distinguish between $C_1$ and $C_2$. Say a deterministic algorithm $\phi$ decides a direction of movement for robot r in configuration $C_1$. Since both $C_1$ and $C_2$ are the same from robot r’s perspective, the deterministic algorithm outputs the same direction of movement for both cases.

Now consider the convex hull $CH_1$ and $CH_2$ of $C_1$ and $C_2$ respectively. The robot r moves a distance b in one round. The distance from any point inside $CH_1$ is more than b but we can skew the convex hull in the direction of movement, so to make it like $CH_2$, where if the robot r moves a distance b it exits $CH_2$. Therefore there exists a situation for any algorithm $\phi$ such that the area of the convex hull increases. Hence it is impossible for the robots to converge.    $\square$

Fig. 7.

Locally indistinguishable configurations with respect to r

5 Simulation

We now complement our formal analysis with simulations, studying the average case. We assume that robots are distributed uniformly at random in a square initially, that $b=1$ and $c=2$, and we consider fully synchronous (FSYNC) scheduling [13]. As a baseline to evaluate performance, we consider the optimal convergence distance and time if the robots had the capability to observe positions, i.e., they are not monoculus. Moreover, as a lower bound, we compare to an algorithm which converges all robots to the centroid, defined as follows: $\{\bar{x}, \bar{y}\} = \left\{ \frac{\sum _{i=1}^nx_i}{n},\frac{\sum _{i=1}^ny_i}{n}\right\}$ where $\{x_i,y_i\} \forall i \in \{1,2,\cdots ,n\}$ are the robots’ coordinates. We calculate the distance $d_i$ from each robot to the centroid in the initial configuration. The optimal distance we have use as convergence distance is the sum of distances from each robot to the unit disc centered at the centroid. So the sum of the optimal convergence distances $d_{opt}$ is given by $d_{opt} = \sum _{i=1}^n (d_i -1),$ if $d_i>1$.

In the simulation of Algorithm 1, we define $d_{CL}$ as the cumulative number of steps taken by all the robots to converge (sometimes also known as the work). Now we define the performance ratio, $\rho _{CL}$ as $\rho _{CL} = \frac{d_{CL}}{d_{opt}}$. Similarly for Algorithm 2 we define $d_{CQ}$ and $\rho _{CQ}$.

We have used BoxWhiskerChart [3] to plot the distributions. The BoxWhiskerChart in the Figs. 8 and 9 show four quartiles of the distribution notched at the median taken from 100 executions of the algorithms. Figures 8, and 9 show the comparison between the performance ratio (PR) for distance. We can observe that the distance traveled compared to optimal distance increases for same size region as the number of robots increase for Algorithm 1 but it remains almost the same for Algorithm 2. We can observe that Algorithm 2 performs better. This is due to the fact that, in Algorithm 2 only boundary robots move.

Fig. 8.

$\rho _{CL}$ vs $\rho _{CQ}$ for the same size of region

Fig. 9.

$\rho _{CL}$ vs $\rho _{CQ}$ for the same number of robots

Fig. 10.

$\tau _{CL}$ vs $\tau _{CQ}$ for the same number of robots

Fig. 11.

$\tau _{CL}$ vs $\tau _{CQ}$ for the same size of region

Let $d_{max}$ be the distance of farthest robot from the centroid and $t_{CL}$ be the number of synchronous rounds taken by Algorithm 1 for convergence. We define $\tau _{CL}$ as follows $\tau _{CL} =\frac{t_{CL}}{d_{max}}$. Similarly for Algorithm 2, we define $t_{CQ}$ and $\tau _{CQ}$. $\tau _{CL}$ and $\tau _{CQ}$ show performance ratio for convergence time of Algorithms 1 and 2 respectively. In Figs. 10 and 11, we can observe that $\tau _{CL}$ is very close to 1, so Algorithm 1 converges in almost the same number of synchronous rounds (proportional to distance covered, since step size $b=1$) as the maximum distance from the centroid of the initial configuration. We can observe that Algorithm 2 takes more time as the number of robots and the side length of square region increases. Since Algorithm 2 only boundary robots move, the internal robots wait to move until they are on the boundary. As expected, this creates a chain of dependence which in turn increases the convergence time.

6 Discussion

This section shows that our approach supports some interesting extensions.

6.1 Termination for $\mathscr {OLA}$ Model

While we only focused on convergence and not termination so far, we can show that with a small amount of memory, termination is also possible in the $\mathscr {OLA}$ model.

To see this, assume that each robot has a 2-bit persistent memory in the $\mathscr {OLA}$ model for each dimension, total 4-bits for two dimensions. Algorithm 2 has been modified to Algorithm 3 such that it can accommodate termination. All the bits are initially set to 0. Each robot has its local coordinate system, which remains consistent over the execution of the algorithm. The four bits correspond to four boundaries in two dimensions, i.e., left, right, top and bottom. If a robot finds itself on one of the boundaries according to its local coordinate system, then it sets the corresponding bit of that boundary to 1. Once both bits corresponding to a dimension become 1, the robot stops moving in that dimension. Consider a robot r. Initially, it was on the left boundary in its local coordinate system. Then it sets the first bit of the pair of bits corresponding to x-axis. It moves towards right. Once it reaches the right boundary, then it sets the second bit corresponding to x-axis to 1. Once both the bits are set to 1, it stops moving along the x-axis. Similar movement termination happens on the y-axis also. Once all the 4-bits are set to 1, the robot stops moving.

6.2 Extension to d-Dimensions

Both our algorithms can easily be extended to d-dimensions. For the $\mathscr {LD}$ model, the algorithm remains exactly the same. For the proof of convergence, similar arguments as Lemma 3 can be used in d dimensions. We can consider the convex hull in d-dimensions and the boundary robots of the convex hull always move inside. The size of convex hull reduces gradually and the robots converge.

Analogously for the $\mathscr {OLA}$ model, the distance between two robots in the boundary of any dimension gradually decreases and the corner robots always move inside the d-dimensional cuboid. Hence it converges. Here the robot would require 2d number of bits for termination.

7 Conclusion

This paper introduced the notion of monoculus robots which cannot measure distance: a practically relevant generalization of existing robot models. We have proved that the two basic models still allow for convergence (and with a small memory, even termination), but with less capabilities, this becomes impossible.

The $\mathscr {LD}$ model converges in an almost optimal number of rounds, while the $\mathscr {OLA}$ model takes more time. But the cumulative number of steps is less for the $\mathscr {OLA}$ model compared to the $\mathscr {LD}$ model since only boundary robots move. Although we found in our simulations that the median and angle bisector strategies successfully converge, finding a proof accordingly remains an open question. We see our work as a first step, and believe that the study of weaker robots opens an interesting field for future research.