A Very Compact Masked S-Box for High-Performance Implementation of SM4 Based on Composite Field

Abstract

Implementations of the SM4 algorithm, including different hardware applications with limited resources, are vulnerable to Side-Channel Attacks. This paper presents a countermeasure against such attacks by adding a random “mask” to the input plaintext and protect all variables through the whole encryption process. As is known to all, the unique nonlinear step in each round of SM4 algorithm is the “S-Box” and the previous works using lookup-table method to implement the S-Box always incur large area and high power. Here we give the compact design of masked S-Box using the normal basis in the composite field (consisting of a Galois inversion and several affine transformations). Then we compute the different masks diffused to all the steps in the SM4 algorithm process. The proposed design results in ultra-low cost of hardware and capability to resist first-order differential power analysis (DPA), which is suitable for the resource constrained devices. The synthesis result of masked S-Box shows that the area under the SMIC 0.13 $\upmu$m is only about 978-gates, 46.8% fewer than the other works. Further, we apply the pipeline technique to our proposed “masked S-Box”, thereby to the whole masked SM4 algorithm. The results of FPGA implementation present that our works have achieved an ultra-high speed with frequency nearly 551 MHz and the throughput over 70 Gbps.

1 Introduction

With the rapid development of the computer science and internet technology in the modern world, the information and data security have become more and more important. Thus, preventing the significant information from attacking by any other unauthorized parts is a challenging and essential task. There is no doubt that the security of hardware is the basis for data transmission, especially in the Wireless Local Area Network (WLAN). For this reason, plenty of methods about hardware cryptography (e.g. hiding, masking, etc.) have been come up with to protect the sensitive data and applied in different domains, such as embedded systems, wireless handsets and smart cards. In January 2006, the Office of State Commercial Cipher Administration of China (OSCCA) announced a specific encryption standard named SM4 block cipher, the purpose of which is to form the Wireless LAN Authentication and Privacy Infrastructure (WAPI) standard for our country [1]. Since then, there have been a large variety of researches focusing on improving the performance and security of SM4. On the other hand, some researchers try to seek the weakness of SM4 algorithm and do attacks on the specific hardware implementations. For example, smart cards may be vulnerable to first order side-channel attacks such as differential power analysis, which takes advantages of the leakage of information to do the physical analysis such as power consumption, electromagnetic radiation and so on, then to deduce the real secret key of the algorithm.

Due to the potential attacks above, this paper proposes a countermeasure against the first order side-channel attacks, applying the masking strategy to the nonlinear S-Box as well as the data path in the SM4 algorithm based on the composite field introduced by the previous work [2]. Compared to the other method to achieve the masking, this protection saves 46.8% area for the whole circuit. However, it incurs some other parts which slow down the encryption process. Thus we make use of the pipeline technique to accelerate the calculation, resulting in an ultra-high clock frequency up to 551 MHz and throughput over 70 Gbps for the masked SM4 algorithm.

The organization of this paper is as follows. In Sect. 2, we describe the SM4 block cipher and the algebraic description of S-Box very briefly. Section 3 shows the detailed masking strategy for S-Box, including masking the inversion and the affine transformation, and the reutilization of the masks. Section 4 presents the implementation of the SM4 algorithm using the masked S-Box. Also, the architecture of pipelined masked SM4 is designed and implemented in this part. Then we state the low-cost results of area using masking strategy and the high speed in pipeline scheme for SM4 in Sect. 5. At last, Sect. 6 concludes the paper.

2 Algebraic Description for S-Box

SM4 block cipher is a 32-round iterative algorithm with 128-bit input plaintext, secret key and output ciphertext. The input plaintext is first divided into four words and each word consists of 32 bits. Before encryption, the key for each round ($rk_{i}$) will be generated through the key expansion arithmetic, which is nearly identical with the encryption process, and the only difference between them is the linear part—round shifting left. With the $rk_{i}$, a new word, i.e. $X_{i+4}$ will be produced in the i-th round of the encryption process by doing XOR, nonlinear substitution and round shifting left operations ($X_{i+4}=X_{i}\oplus T(X_{i+1}\oplus X_{i+2}\oplus X_{i+3}\oplus rk_{i})(i=0,...,31$)), shown in Fig. 1. Finally, the order of the last four words will be reversed to form the output ciphertext. The XOR and round shifting left operations are linear with respect to the data block, so it provides “diffusion”; While the S-Box is the only nonlinear step that provides “confusion”.

Fig. 1.

SM4 round arithmetic

The S-Box can be implemented using the lookup tables, which occupies the majority of the cost in devices. In 2007, Liu et al. [3] gave the algebraic structure for SM4 algorithm, comprising two substeps: (i) regarding the byte as an element in the Galois Field $GF(2^{8})$, get its inversion in this field (Note that the zero byte has no inversion, so it keeps unchanged); (ii) regarding the result of the inversion as a vector of bits in $GF(2^{8})$, then multiply it by a given bit matrix and add a constant row vector, that is the procedure of an affine transformation. The inversion and affine transformation are shown below in Eq. (1):

$$\begin{aligned} S(\mathbf X )=I(\mathbf X \cdot A+\mathbf C ) \cdot A+\mathbf C , \end{aligned}$$

(1)

where the input of S-Box (S) is a 8-bit row vector $\mathbf X =\mathbf X _{7-0}$, and the cyclic matrix A in the algebraic expression is

$$\begin{aligned} A= \begin{pmatrix} 1 &{} 1 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 1 &{} 1 &{} 1 &{} 1 &{} 0 &{} 0 &{} 1\\ 1 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1\\ 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1\\ 1 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 1\\ \end{pmatrix}, \end{aligned}$$

and the row vector C is

$$\mathbf C =\mathbf C _{7-0}=[1, 1, 0, 1, 0, 0, 1, 1].$$

For SM4 in the specific Galois Field, a byte represents a polynomial where the bits are coefficients of corresponding powers of x, and multiplication is modulo the irreducible primitive polynomial:

$$f(x)=x^{8}+x^{7}+x^{6}+x^{5}+x^{4}+x^{2}+1.$$

We could consider the root of this polynomial as $\theta$, then $f(\theta )=0$ in $GF(2^{8})$. Thus the bits of a byte could be related to the coefficients of powers of $\theta$, e.g., $3=\theta , 4=\theta \,+\,1, 9=\theta ^{2}$, etc. Therefore the bits make up a vector with respect to what is known as polynomial basis. However, we can change the representation of the polynomial basis in $GF(2^{8})$ to a different one, named normal basis in composite field [4]. Instead of a vector of dimension 8 in GF(2), we regard a byte as a vector of dimension 2 in $GF(2^{4})$, where each 4-bit element is in turn a vector of dimension 2 in $GF(2^{2})$, and each 2-bit element is a vector of dimension 2 in GF(2). For each of these subfields, it has been introduced in details, referring to [5].

3 Masking Strategy

To convert the standard polynomial representation to the composite field representation, we need to choose the appropriate basis and build an isomorphic matrix. For more detailed information, please refer to [4]. In this paper, we try to add an additive mask to all the steps during the inversion, which will described below.

3.1 Inversion Without Masking

Now we apply the following convention: upper-case bold symbols stand for elements in the main field (e.g. $\mathbf A \in GF(2^{8})$); upper-case italic symbols represent elements in the subfield (e.g. ${A} \in GF(2^{4})$); lower-case bold symbols are for the sub-subfield (e.g. $\mathbf a \in GF(2^{2})$); and lower-case italic symbols are used for single bits (e.g. ${a} \in GF(2)$).

To begin with, we don’t concern about the mask. So the inversion in $GF(2^{8})/GF(2^{4})$ (this expresses the representation of $GF(2^{8})$ as vectors in $GF(2^{4})$ using a normal basis $[\mathbf Y ^{16}, \mathbf Y ]$), where $\mathbf Y ^{16}$ and $\mathbf Y$ are the roots of $\mathbf Y ^{2}+\mathbf Y +{N}$ and ${N} \in GF(2^{4})$ is the norm (${N} = Y^{16} \cdot Y$), is given as [4]:

$$\begin{aligned} \mathbf A&={A}_{h}{} \mathbf Y ^{16}+{A}_{l}{} \mathbf Y (\texttt {known}),\end{aligned}$$

(2)

$$\begin{aligned} {B}&={N} \otimes ({A}_{h}\oplus {A}_{l})^{2} \oplus {A}_{h}\otimes {A}_{l},\end{aligned}$$

(3)

$$\begin{aligned} \mathbf A ^{-1}&=({A}_{l} \otimes {B}^{-1})\mathbf Y ^{16} + ({A}_{h} \otimes {B}^{-1})\mathbf Y (\texttt {result}). \end{aligned}$$

(4)

Here we make a agreement on the meaning of the operators above: $\oplus$ and $\otimes$ denote addition and multiplication in Galois Field, respectively. The expression ${A}_{h}{} \mathbf Y ^{16}+{A}_{l}{} \mathbf Y$ is an algebraic method using the normal basis to denote the vector $[{A}_{h}, {A}_{l}]$ (i.e. $[A_{h}, A_{l}]=[\mathbf A _{7-4}, \mathbf A _{3-0}]$). To achieve the inversion in $GF(2^{8})$, it requires the inversion, addition, multiplication and the combined square-scaling operation (${N} \otimes {A}^{2}$) in the subfield $GF(2^{4})$. In the same way, the inversion in $GF(2^{4})/GF(2^{2})$ which uses a normal basis $[X^{4}, X]$, where the ${X}^{4}$ and X are the roots of ${X}^{2}\,+\,{X}\,+\,\mathbf n$ (and $\mathbf n \in GF(2^{2})$ is the norm ($\mathbf n =X^{4} \cdot X$)), is given as:

$$\begin{aligned} {B}&=\mathbf b _{h}X^{4}+\mathbf b _{l}X (\texttt {known}), \end{aligned}$$

(5)

$$\begin{aligned} \mathbf c&=\mathbf n \otimes (\mathbf b _{h}\oplus \mathbf b _{l})^{2} \oplus \mathbf b _{h}\otimes \mathbf b _{l},\end{aligned}$$

(6)

$$\begin{aligned} {B}^{-1}&=(\mathbf b _{l} \otimes \mathbf c ^{-1})X^{4} + (\mathbf b _{h} \otimes \mathbf c ^{-1})X (\texttt {result}). \end{aligned}$$

(7)

However, finding the inversion in the sub-subfield $GF(2^{2})$, using the normal basis $[\mathbf w ^{2}, \mathbf w ]$, where $\mathbf w ^{2}$ and $\mathbf w$ are the roots of $\mathbf w ^{2}+\mathbf w +1$ (and here we define the norm as 1), is very easy. It is equivalent to the squaring operation, shown as a bit swap:

$$\begin{aligned} \mathbf c&= {c}_{h}{} \mathbf w ^{2}+{c}_{l}{} \mathbf w (\texttt {known}),\end{aligned}$$

(8)

$$\begin{aligned} \mathbf c ^{-1}&= {c}_{l}{} \mathbf w ^{2}+{c}_{h}{} \mathbf w (\texttt {result}). \end{aligned}$$

(9)

All the steps above are used to obtain the inversion in $GF(2^{8})$ without masking. In the following, we will detail the steps about how to mask the inversion.

3.2 Masking the Inversion

As is mentioned above, additive mask becomes our preference due to its resistance to zero-value attacks. It has been analyzed in [2] that the statistical distribution of masks is uniform over the field by adding a random mask. Therefore the operands appear randomly, uncorrelated to either the input plaintext or the secret key. Thus the data leaked from the side channel is independent of the chosen input plaintext, might regarded as noise, and the key in this way will be protected against first-order differential power attacks. To ensure the correct process from the input mask to the output mask, we apply the masking strategy as follows.

In $GF(2^{8})$, we express the masked byte with a tilde (i.e. ${\tilde{\mathbf{A}}}$), and similarly for the other masked variables. Now we use the mask (M) to mask the input plaintext.

$$\begin{aligned} \mathbf{M }&= {{M}}_{h} \mathbf Y ^{16} + {{M}}_{l}{} \mathbf Y ;\end{aligned}$$

(10)

$$\begin{aligned} {\tilde{\mathbf{A}}}&= \mathbf A \oplus \mathbf{M } = {\tilde{\mathbf{A}}}_{h} \mathbf Y ^{16} + {\tilde{\mathbf{A}}}_{l}{} \mathbf Y \end{aligned}$$

(11)

Then let

$$\begin{aligned} {\tilde{B}}&= {N} \otimes ({\tilde{A}}_{h} \oplus {\tilde{A}}_{l})^{2} \oplus {\tilde{A}}_{h} \otimes {\tilde{A}}_{l} \oplus {\tilde{A}}_{h} \otimes {M}_{l} \oplus {\tilde{A}}_{l} \otimes {M}_{h} \oplus {M}_{h} \otimes {M}_{l}, \end{aligned}$$

(12)

$$\begin{aligned} {M}_{2}&= {N} \otimes ({M}_{h} \oplus {M}_{l})^{2}, \end{aligned}$$

(13)

Here the result ${\tilde{B}}$ is B above in Eq. (3) masked by ${M}_{2}$ (i.e. ${\tilde{B}}={B} \oplus {M}_{2}$). Note that the products in Eq. (12) must be added in turn to make all the intermediate results uniformly distributed and masked, so that the information about the original data will not be leaked out.

For the inversion in $GF(2^{4})$, say ${\tilde{B}}={\tilde{\mathbf{b }}}_{h}X^{4}+{\tilde{\mathbf{b }}}_{l}X$ and ${M}_{2}=\mathbf{m }_{h}X^{4}+\mathbf m _{l}X$, then let

$$\begin{aligned} {\tilde{\mathbf{c }}}&= \mathbf n \otimes ({\tilde{\mathbf{b }}}_{h} \oplus {\tilde{\mathbf{b }}}_{l})^{2} \oplus {\tilde{\mathbf{b }}}_{h} \otimes {\tilde{\mathbf{b }}}_{l} \oplus {\tilde{\mathbf{b }}}_{h} \otimes \mathbf{m }_{l} \oplus {\tilde{\mathbf{b }}}_{l} \otimes \mathbf{m }_{h} \oplus \mathbf{m }_{h} \otimes \mathbf{m }_{l},\end{aligned}$$

(14)

$$\begin{aligned} \mathbf p&= \mathbf n \otimes (\mathbf{m }_{h}\oplus \mathbf m _{l})^{2}, \end{aligned}$$

(15)

and ${\tilde{\mathbf{c }}}$ is $\mathbf c$ above in Eq. (6), masked by $\mathbf p$ (say $\mathbf p = {p}_{h}{} \mathbf w ^{2}+{p}_{l}{} \mathbf w$, and let $\mathbf q =\mathbf p ^{2}=\mathbf n ^{2} \otimes (\mathbf{m }_{h}\oplus \mathbf m _{l})= {p}_{l}{} \mathbf w ^{2}+{p}_{h}{} \mathbf w$). Above we employ the convention of the inversion as squaring in the sub-subfield $GF(2^{2})$, so

$$\begin{aligned} {\tilde{\mathbf{c }}}^{-1}=(\mathbf c \oplus \mathbf p )^{-1}=(\mathbf c \oplus \mathbf p )^{2}=\mathbf c ^{2}\oplus \mathbf p ^{2}=\mathbf c ^{-1}\oplus \mathbf q , \end{aligned}$$

(16)

Therefore ${\tilde{\mathbf{c }}}^{-1}$ (say ${\tilde{\mathbf{c }}}^{-1}={\tilde{c}}_{l}W^{2}+{\tilde{c}}_{h}W$) is $\mathbf c ^{-1}$ above in Eq. (9) masked by another mask $\mathbf q$.

Now we introduce a new 4-bit mask $S=\mathbf s _{h}X^{4}+\mathbf s _{l}X$, and let

$$\begin{aligned} {\tilde{\mathbf{b }}}^{-1}_{h}&=\mathbf s _{h}\oplus \mathbf b _{h}^{-1}=\mathbf s _{h}\oplus (\mathbf b _{l} \otimes \mathbf c ^{-1}),\nonumber \\&=\mathbf s _{h}\oplus [({\tilde{\mathbf{b }}}_{l}\oplus \mathbf{m }_{l}) \otimes ({\tilde{\mathbf{c }}}^{-1} \oplus \mathbf q )],\nonumber \\&=\mathbf s _{h} \oplus {\tilde{\mathbf{b }}}_{l} \otimes {\tilde{\mathbf{c }}}^{-1} \oplus {\tilde{\mathbf{b }}}_{l} \otimes \mathbf q \oplus \mathbf{m }_{l} \otimes {\tilde{\mathbf{c }}}^{-1} \oplus \mathbf{m }_{l} \otimes \mathbf q ,\end{aligned}$$

(17)

$$\begin{aligned} {\tilde{\mathbf{b }}}^{-1}_{l}&=\mathbf s _{l}\oplus \mathbf b _{l}^{-1}=\mathbf s _{l}\oplus (\mathbf b _{h} \otimes \mathbf c ^{-1})\nonumber \\&=\mathbf s _{l}\oplus [({\tilde{\mathbf{b }}}_{h}\oplus \mathbf{m }_{h}) \otimes ({\tilde{\mathbf{c }}}^{-1} \oplus \mathbf q )]\nonumber \\&= \mathbf s _{l} \oplus {\tilde{\mathbf{b }}}_{h} \otimes {\tilde{\mathbf{c }}}^{-1} \oplus {\tilde{\mathbf{b }}}_{h} \otimes \mathbf q \oplus \mathbf{m }_{h} \otimes {\tilde{\mathbf{c }}}^{-1} \oplus \mathbf{m }_{h} \otimes \mathbf q , \end{aligned}$$

(18)

thus the result ${\tilde{\textit{B}}}^{-1}={\tilde{\mathbf{b }}}_{h}^{-1}{X}^{4}+{\tilde{\mathbf{b }}}_{l}^{-1}{X}$ is ${B}^{-1}$ above in Eq. (7) masked by S.

Similarly, apply the output 8-bit mask $\mathbf T ={T}_{h}{} \mathbf Y ^{16}+{T}_{l}{} \mathbf Y$ to the output $\mathbf A ^{-1}$, and let:

$$\begin{aligned} {\tilde{\textit{A}}}^{-1}_{h} = {T}_{h}&\oplus {\tilde{A}}_{l} \otimes {\tilde{\textit{B}}}^{-1} \oplus {\tilde{A}}_{l} \otimes {S} \oplus {M}_{l} \otimes {\tilde{\textit{B}}}^{-1} \oplus {M}_{l} \otimes {S},\end{aligned}$$

(19)

$$\begin{aligned} {\tilde{\textit{A}}}^{-1}_{l} = {T}_{l}&\oplus \;{\tilde{A}}_{h} \otimes {\tilde{\textit{B}}}^{-1} \oplus {\tilde{A}}_{h} \otimes {S} \oplus {M}_{h} \otimes {\tilde{\textit{B}}}^{-1} \oplus {M}_{h} \otimes {S} \end{aligned}$$

(20)

So the result ${\tilde{\mathbf{A }}}^{-1}={\tilde{\textit{A}}}_{h}^{-1}{} \mathbf Y ^{16}+{\tilde{\textit{A}}}_{l}^{-1}{} \mathbf Y$ is the original inversion $\mathbf A ^{-1}$ above in Eq. (4) masked by the output mask T:

$$\begin{aligned} {\tilde{\mathbf{A }}}^{-1}=\mathbf{A }^{-1} \oplus \mathbf T . \end{aligned}$$

(21)

3.3 Reutilization of Masks

Canright and Batina [2] shows the re-using of the masks to make the implementation more vulnerable to the higher-order differential side channel attacks and save the cost of the same operations. Firstly, by replacing the mask $\mathbf q$ by $\mathbf{m }_{l}$ or $\mathbf m _{h}$, we can modify the expression as follows:

$$\begin{aligned} {\tilde{\mathbf{c }}}^{-1}&=({\tilde{\mathbf{c }}}_{l}{} \mathbf w ^{2}+{\tilde{\mathbf{c }}}_{h}{} \mathbf w )\oplus \mathbf{m }_{h}\oplus \mathbf q \quad (\texttt {masked} \; \texttt {by} \; \mathbf{m }_{h}),\end{aligned}$$

(22)

$$\begin{aligned} {\tilde{\mathbf{b }}}^{-1}_{h}&=\mathbf{m }_{1h} \oplus {\tilde{\mathbf{b }}}_{l} \otimes {\tilde{\mathbf{c }}}^{-1} \oplus \underline{{\tilde{\mathbf{b }}}_{l} \otimes \mathbf{m }_{h}} \oplus \mathbf{m }_{l} \otimes {\tilde{\mathbf{c }}}^{-1} \oplus \underline{\mathbf{m }_{l} \otimes \mathbf{m }_{h}},\end{aligned}$$

(23)

$$\begin{aligned} {\tilde{\mathbf{c }}}^{-1}_{2}&={\tilde{\mathbf{c }}}^{-1}\oplus (\mathbf{m }_{l}\oplus \mathbf m _{h})\quad (\texttt {masked} \; \texttt {by} \; \mathbf{m }_{l}),\end{aligned}$$

(24)

$$\begin{aligned} {\tilde{\mathbf{b }}}^{-1}_{l}&=\mathbf{m }_{1l} \oplus {\tilde{\mathbf{b }}}_{h} \otimes {\tilde{\mathbf{c }}}^{-1}_{2} \oplus \underline{{\tilde{\mathbf{b }}}_{h} \otimes \mathbf{m }_{l}} \oplus \mathbf{m }_{h} \otimes {\tilde{\mathbf{c }}}^{-1}_{2} \oplus \underline{\mathbf{m }_{h} \otimes \mathbf{m }_{l}}, \end{aligned}$$

(25)

where the underlined products had already been calculated in Eq. (14), so here we can re-use these results. Now the result ${\tilde{\textit{B}}}^{-1}={\tilde{\mathbf{b }}}^{-1}_{h}X^{4}+{\tilde{\mathbf{b }}}^{-1}_{l}X$ is ${B}^{-1}$ above, but here masked by ${M}_{h}=\mathbf{m }_{1h}X^4+\mathbf m _{1l}X$, which is the upper nibble of the input mask $\mathbf{M }$. In the same way, we get the updated masked $\mathbf A ^{-1}$ in the following:

$$\begin{aligned} {\tilde{A}}_{h}^{-1}&= {T}_{h} \oplus {\tilde{A}}_{l} \otimes {\tilde{B}}^{-1} \oplus \underline{{\tilde{A}}_{l} \otimes {M}_{h}} \oplus {M}_{l} \otimes {\tilde{B}}^{-1} \oplus \underline{{M}_{l} \otimes {M}_{h}},\end{aligned}$$

(26)

$$\begin{aligned} {\tilde{B}}^{-1}_{2}&={\tilde{B}}^{-1}\oplus {M}_{l}\oplus {M}_{h} \quad (\texttt {masked} \; \texttt {by} \; {M}_{l}),\end{aligned}$$

(27)

$$\begin{aligned} {\tilde{A}}_{l}^{-1}&= {T}_{l} \oplus {\tilde{A}}_{h} \otimes {\tilde{B}}^{-1}_{2} \oplus \underline{{\tilde{A}}_{h} \otimes {M}_{l}} \oplus {M}_{h} \otimes {\tilde{B}}^{-1}_{2} \oplus \underline{{M}_{h} \otimes {M}_{l}}, \end{aligned}$$

(28)

the underlined products are re-used and the output ${\tilde{\mathbf{A }}}^{-1}$ is still $\mathbf A ^{-1}$ above masked by output mask $\mathbf T$ (which might be same with the input mask $\mathbf{M }$ or not):

$$\begin{aligned} {\tilde{\mathbf{A}}}^{-1}=\mathbf A ^{-1} \oplus \mathbf T . \end{aligned}$$

(29)

Fig. 2.

Architecture of masked S-Box: (a) Single cycle (without the red dash line); (b) Pipeline (the red dash line is the pipeline registers) (Color figure online)

3.4 Mask Transformation

Equation (1) shows the algebraic expression of unmasked S-Box. Here we make some changes to the mathematical relationship and deduce the correct mask transformation from input to output, where the function I stands for inversion process in $GF(2^{8})$ and the function Inv represents inversion process in the “tower field”, i.e. $GF(((2^{2})^{2})^{2})$. Note the matrix $\delta$ is the isomorphic mapping from the normal basis in composite field to the standard polynomial basis (and $\delta ^{-1}$ is the reversed mapping).

$$\begin{aligned} S(\mathbf X +\mathbf{M })&=I[(\mathbf X +\mathbf{M }) \cdot A+\mathbf C ] \cdot A+\mathbf C \end{aligned}$$

(30)

$$\begin{aligned}&=A^{T} \cdot I[A^{T} \cdot (\mathbf X +\mathbf{M }) + \mathbf C ^{T}]+\mathbf C ^{T} \nonumber \\&=A^{T} \cdot I[(A^{T}{} \mathbf X + C^{T}) + A^{T}\mathbf{M }]+\mathbf C ^{T} \nonumber \\&=A^{T}\delta \cdot Inv[\delta ^{-1}(A^{T}{} \mathbf X + \mathbf C ^{T}) + \delta ^{-1}A^{T}\mathbf{M }]+\mathbf C ^{T} \end{aligned}$$

(31)

where $A^{T}$ is the transposition of A (also similar with $\mathbf C ^{T}$). Here we can learn from Eq. (29) that $Inv(\hat{\mathbf{A }}+{\hat{\mathbf{M }}})=Inv({\hat{\mathbf{A }}})+{\hat{\mathbf{M }}}$ only if the output mask is equal to the input mask: $\mathbf S = \mathbf{M }$ (this is the conclusion in $GF(((2^{2})^{2})^2)$. With this assumption, Eq. (31) in $GF(2^{8})$ could be modified as follows:

$$\begin{aligned} S(\mathbf X +\mathbf{M })&= (31)\nonumber \\&=A^{T} \cdot I(A^{T}{} \mathbf X +\mathbf C ^{T}) + \mathbf C ^{T} + A^{T}A^{T}\mathbf{M } \nonumber \\&=S(\mathbf X )+ A^{T}A^{T}\mathbf{M } \end{aligned}$$

(32)

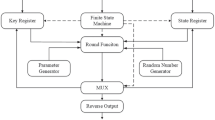
If the input mask of S-Box is $\mathbf{M }$, the Eq. (32) shows the correct output mask of S-Box in $GF(2^{8})$, i.e. $A^{T}A^{T}\mathbf{M }$, which is the “confusion” of the mask. Until now, we have achieved the masking process using the normal basis in composite field. Figure 2 gives the complete hardware implementation of the masked S-Box, depending on all the mathematical computing above.

4 Implementation of Masked SM4

In this section, we apply our “masked S-Box” to the encryption process and illustrate the architecture of the SM4 round arithmetic in two different directions: (i) use the iterative architecture and make all the steps of SM4 secure, the purpose of which is to decrease the cost of the area; (ii) insert some registers inside the S-Box appropriately to increase the clock frequency and improve the throughput, which will be very useful in high-speed applications.

Fig. 3.

Architecture of masked SM4 round arithmetic using the single cycle “Masked S-Box” (the underlined elements in this picture are masked variables and ($\cdot$) in the architecture shows the transient mask at that step. The red dash rectangle is the round shifting left function) (Coloe figure online)

4.1 Iterative Architecture of Masked SM4

In Fig. 3. The $rk_{i}$ is well prepared in RAM or it can be produced by the iterative architecture presented in [4] before each round. Here the latter is our preference and we just concentrate on the masked encryption. For instance, we choose a 32-bit mask $\mathbf{M }$ for our design. Before the first round of encryption, the mask is produced and extended to 128 bits (e.g. {4{$\mathbf{M }$}}), which is XORed to the input 128-bit plaintext to obtain the masked input $\underline{\mathbf{X }}=(\underline{X}_{0},\underline{X}_{1},\underline{X}_{2},\underline{X}_{3})$ for the first round. It is obvious that all the variables before the function “Masked S-Box” are masked by $\mathbf{M }$. As is shown above, the outputs of the “Masked S-Box” are masked by $A^{T}A^{T}\mathbf{M }$. So we do the same round shifting left to $A^{T}A^{T}\mathbf{M }$, then add the outputs together and XOR the $\underline{X}_{0}$ simultaneously. Thus the mask $A^{T}A^{T}\mathbf{M }$ is eliminated and the output $\underline{X}_{4}$ has been already masked by $\mathbf{M }$, which is diffused from $\underline{X}_{0}$. In this way, we redo the arithmetic for 32 rounds, then reverse the last four words and finally XOR the output with {4{$\mathbf{M }$}}, we can certainly get the right result of ciphertext.

4.2 Pipelined Architecture of Masked SM4

For the pipeline scheme, we use the synchronous technique to adjust the structure of the round arithmetic of SM4. However, one key problem is to balance the pipeline stages. So we divide the round arithmetic into several periods to achieve one round encryption in order to ensure the approximate executing time for each part, which means to decrease the time of the critical-path. The registers being inserted into the S-Box are shown as red dash line in Fig. 2. Although the pipelined S-Box is well designed, the SM4 round arithmetic needs to be seriously considered according to the linear parts execution. Here we present the optimized architecture for pipelined masked SM4, given as Fig. 4. To keep the variables of each period secure, we add the random mask to all the input elements and transfer them to their corresponding buffers in each pipeline stage (shown as the yellow registers in Fig. 4). In this way, all the elements in the round encryption are securely masked and can be parallel implemented.

Figure 4 is just one round encryption for the SM4 algorithm, which contains five levels for the pipeline. As we expect, we implement 32 same structures and finally do the reversion function. The right results are realized and it will be shown in next section.

Fig. 4.

Pipelined round arithmetic of masked SM4 (the red dash rectangle is pipelined masked S-Box described above in Fig. 2, similarly with the modules P1, P2 and P3) (Color figure online)

5 Results

The proposed SM4 algorithm implemented in two different ways based on “Masked S-Box” in composite field has been realized by Verilog HDL and simulated in Modelsim software. All the input plaintexts have achieved correct output ciphertexts.

Besides, the area reports of the masked S-Box under the SMIC 0.13 $\upmu$m in the Synopsys Design Compiler indicate that the equivalent amount of gates is 978, at least 46.8% fewer than 1,840 in [6] (where the area has been divided by 9.79, which is the area of one NAND2X1 cell under the SMIC 0.18 $\upmu$m). We firmly believe that our compact masked S-Box has occupied the lowest area and it certainly contributes to the low-cost iterative masked SM4 algorithm very much.

In addition, comparing to the other designs, we implement it in different FPGA boards and show the results in Table 1. Because of the large cost for masking, our design has reached a very suitable and satisfying resource usage and it is still much lower than some other works without anti-attack methods (Table 2).

Table 1. Resources comparison

Table 2. Performance comparison

Furthermore, by employing the pipelined masked S-Box to the SM4 algorithm, the pipeline SM4 round arithmetic shown in Fig. 4 achieve the ultra-high clock frequency up to 551 MHz under Xilinx FPGAs, resulting in the ultra-high throughput over 70 Gbps. To our knowledge, this is the highest speed and throughput to date.

6 Conclusion

In this paper, the process to design a very compact “Masked S-Box” has been described clearly using normal basis in composite field at first. Second, we analyze the “diffusion” and “confusion” of the mask through the whole SM4 algorithm, and make sure every variable during encryption has been securely masked. Third, we implement the masked S-Box in two architecture: iteration and pipeline. Then we simulate all the designs and get the correctly inspiring results. The synthesis results in different devices have been compared with other works. As far as we know, our proposed work has reached the lowest area of masked S-Box, which leads to the lowest cost for masked SM4 implementation. What’s more, the proposed pipelined S-Box has been implemented to construct a pipelined masked SM4 architecture, which achieves the highest speed to date. We believe this work has developed a good countermeasure to the side-channel attacks and will be widely used in resource constrained devices and speed demanded area in the future.