Keywords

1 Introduction

In the control field, saturation nonlinearity of the actuators is universal phenomenon. So optimizing control of systems in which actuators have problem of saturating nonlinearity, is a major and increasing concern [1, 2]. However, these traditional methods were proposed without considering the optimal control problem. In order to overcome this shortcoming, Lewis et al. [3] used adaptive dynamic programming (ADP) algorithm. The ADP algorithm [4,5,6], an effective brain-like method, which can give the solution to Hamilton-Jacobi-Bellman (HJB) equation forward-in-time, provides an important way of obtaining policy of optimizing control. The value and policy iteration algorithms [7, 8] are key of the ADP algorithms. Considering the superiority of ADP algorithm, growing researchers chose ADP algorithm in terms of optimal control. Zhang et al. [9] used greedy ADP algorithm to design the infinite-time optimal tracking controller. Qiao et al. [10] applied ADP algorithm to a large wind farm and a STATCOM, with focusing on Coordinated reactive power control. Liu et al. [11] developed an optimizing controller for some systems which were discrete-time nonlinear and had control constraints by DHP. As mentioned in [12], ADP algorithm is also suitable for time-delay systems with the same saturation challenge as above. However, in order to realize constrained optimal control, there is still no research using the generalized policy iteration ADP algorithm.

This paper focuses on the generalized policy iteration ADP algorithm. The present algorithm has i-iteration and j-iteration. When j is equal to zero, the proposed algorithm will be a value iteration algorithm, while becoming a policy iteration algorithm when j approaches the infinity. Firstly, the nonquadratic performance function is introduced to overcome the saturation nonlinearity. Then, the process of the generalized policy iteration algorithm is given. Lastly, the simulation results verify the efficiency of the developed method.

2 Problem Statement

We will study the following discrete-time nonlinear systems:

$$\begin{aligned} x_{k+1}&=F(x_k,u_k)\nonumber \\&=f(x_k)+g(x_k)u_k \end{aligned}$$
(1)

where \(u_k\in {\mathbb {R}}^m\) is control vector, \(x_k\in {{\mathbb {R}}^{n}}\) is the state vector, \(f(x_k)\in ~{\mathbb {R}}^n\) and \(g(x_k)\in {\mathbb {R}}^{n\times m}\) are system functions. We denote \({{\varOmega }_{u}}=\{ u_k|u_k={{[ {{u}_{1k}},{{u}_{2k}},\ldots ,{{u}_{mk}} ]}^{\mathsf {T}}}\in {{\mathbb {R}}^{m}},| {{u}_{ik}} |\le {{{\overline{u}}}_{i}},i=1,2,\ldots ,m \}\), where \({{\overline{u}}_{i}}\) can be regarded as the saturating bound. Let \(\overline{U}=diag[{{\overline{u}}_{1}},{{\overline{u}}_{2}},\ldots ,{{\overline{u}}_{m}}]\).

The generalized nonquadratic performance index function is \(J(x_k,{\underline{u}}_k)=\sum \limits _{i=k}^{\infty }{\left\{ x{_{i}^{\mathsf {T}}}Qx_i+W(u_i) \right\} }\), where \({\underline{u}}_k=\left\{ u_k,u_{k+1},u_{k+2},\ldots \right\} \), the weight matrix Q and \(W(u_i)\in \mathbb {R}\) are positive definite.

Inspired by the paper [3], we can introduced \( W(u_i)=2\int _{0}^{u_i}{{{\varLambda }^{-{\mathsf {T}}}}({{{\overline{U}}}^{-1}}s)\overline{U}Rds}\), where R is positive definite, \(s\in {{\mathbb {R}}^{m}}\), \(\varLambda \in {{\mathbb {R}}^{m}}\), \({{\varLambda }^{-{\mathsf {T}}}}\) denotes \({{({{\varLambda }^{-1}})}^{\mathsf {T}}}\), and \(\varLambda (\cdot )\) can choose \(\tanh (\cdot )\).

Then we can use \({{J}^{*}}(x_k)=\underset{{\underline{u}}_k}{\mathop {\min }}\,J(x_k,{\underline{u}}_k)\) to stand for the optimal performance index function and use \(u_{k}^{*}\) to be the optimal control vector. So from the principle of discrete-time Bellman’s optimality, we can obtain the optimal performance index function as

$$\begin{aligned} {{J}^{*}}(x_k)=\underset{u_k}{\mathop {\min }}\,\left\{ x{_{k}^{\mathsf {T}}}Qx_k+2\int _{0}^{u_k}{{{\varLambda }^{-{\mathsf {T}}}}({{{\overline{U}}}^{-1}}s)\overline{U}Rds}+{{J}^{*}}(x_{k+1})) \right\} . \end{aligned}$$
(2)

And we can use the following equation to stand for the optimal control vector:

$$\begin{aligned} {u_{k}^{*}}=\arg \underset{u_k}{\mathop {\min }}\,\left\{ x{_{k}^{\mathsf {T}}}Qx_k+2\int _{0}^{u_k}{{{\varLambda }^{-{\mathsf {T}}}}({{{\overline{U}}}^{-1}}s)\overline{U}Rds}+{{J}^{*}}(x_{k+1}) \right\} . \end{aligned}$$
(3)

The goal of this paper is to get the optimal control vector \({u_{k}^{*}}\) and the optimal performance index function \({{J}^{*}}(x_k)\).

3 Derivation of the Generalized Policy Iteration ADP Algorithm

From [16], it’s known that the traditional ADP algorithm just have one iteration procedure. However, the generalized policy iteration ADP algorithm has i-iteration and j-iteration. Specially, for i-iteration, the generalized policy iteration ADP algorithm doesn’t need to solve the HJB equation, which speed the convergence rate of the developed ADP algorithm.

According to [17], if a control vector can stabilize the system (1) and make the performance index function finite at the same time, it can be concluded that the control vector is admissible.

Next, we will get that the control vector and cost function of the developed generalized policy iteration ADP algorithm are updated in each iteration. First, the cost function \({{V}_{0}}(x_k)\) can be initialed as follows:

$$\begin{aligned} {{V}_{0}}(x_k)=x{_{k}^{\mathsf {T}}}Qx_k+2\int _{0}^{{v}_{0}(x_k)}{{{\varLambda }^{-{\mathsf {T}}}}({{\overline{U}}^{-1}}s)\overline{U}Rds}+{{V}_{0}}(F(x_k,{{{v}}_{0}}(x_k)), \end{aligned}$$
(4)

where the \({{{v}}_{0}(x_k)}\) is an initial admissible control vector. Then, for \(i=1\), the control vector \({{{v}}_{1}}(x_k)\) can be gained by:

$$\begin{aligned} {{{v}}_{1}}(x_k)=\arg \underset{u_k}{\mathop {\min }}\,\left\{ x{_{k}^{\mathsf {T}}}Qx_k+2\int _{0}^{u_k}{{{\varLambda }^{-{\mathsf {T}}}}({{\overline{U}}^{-1}}s)\overline{U}Rds}+{{V}_{0}}(F(x_k,u_k))\right\} . \end{aligned}$$
(5)

Then, we will introduced the second iteration procedure. Define an arbitrary non-negative integer sequence, that is \(\{ {{L}_{1}},{{L}_{2}},{{L}_{3}},\ldots \}\). \({{L}_{1}}\) is the upper boundary of \({{j}_{1}}\). When \({{j}_{1}}\) increases from 0 to \({{L}_{1}}\), we can have the iterative cost function by

$$\begin{aligned} {{V}_{1,{{j}_{1}}+1}}(x_k)=x{_{k}^{\mathsf {T}}}Qx_k+2\int _{0}^{{v}_{1}(x_k)}{{{\varLambda }^{-{\mathsf {T}}}}({{\overline{U}}^{-1}}s)\overline{U}Rds}+{{V}_{1,{{j}_{1}}}}(F(x_k,{{{v}}_{1}}(x_k))), \end{aligned}$$
(6)

where

$$\begin{aligned} {{V}_{1,0}}(x_k)=x{_{k}^{\mathsf {T}}}Qx_k+2\int _{0}^{{v}_{1}(x_k)}{{{\varLambda }^{-{\mathsf {T}}}}({{\overline{U}}^{-1}}s)\overline{U}Rds}+{{V}_{0}}(F(x_k,{{{v}}_{1}}(x_k))). \end{aligned}$$
(7)

In the second iteration, the cost function changes to be \({{V}_{1}}(x_k)={{V}_{1,{{L}_{1}}}}(x_k)\). For \(i=2,3,4,\ldots \), the control vector and cost function of the developed ADP algorithm are updated by:

  1. (1)

    i-iteration

    $$\begin{aligned} {{{v}}_{i}}(x_k)=\arg \underset{u_k}{\mathop {\min }}\,\left\{ x{_{k}^{\mathsf {T}}}Qx_k+2\int _{0}^{u_k}{{{\varLambda }^{-{\mathsf {T}}}}({{\overline{U}}^{-1}}s)\overline{U}Rds}+{{V}_{i-1}}(F(x_k,u_k))\right\} , \end{aligned}$$
    (8)
  2. (2)

    j-iteration

    $$\begin{aligned} {{V}_{i,{{j}_{i}}+1}}(x_k)=x{_{k}^{\mathsf {T}}}Qx_k+2\int _{0}^{{v}_{i}(x_k)}{{{\varLambda }^{-{\mathsf {T}}}}({{\overline{U}}^{-1}}s)\overline{U}Rds}+{{V}_{i,{{j}_{i}}}}(F(x_k,{{{v}}_{i}}(x_k))), \end{aligned}$$
    (9)

    where \({{j}_{i}}=0,1,2,\ldots , L_i\),

    $$\begin{aligned} {{V}_{i,0}}(x_k)=x{_{k}^{\mathsf {T}}}Qx_k+2\int _{0}^{{v}_{i}(k)}{{{\varLambda }^{-{\mathsf {T}}}}({{\overline{U}}^{-1}}s)\overline{U}Rds}+{{V}_{i-1}}(F(x_k,{{{v}}_{i}}(x_k))) \end{aligned}$$
    (10)

    and we can get the iterative cost function by

    $$\begin{aligned} {{V}_{i}}(x_k)={{V}_{i,{{L}_{i}}}}(x_k). \end{aligned}$$
    (11)

From (4)–(11), we make use of \({{V}_{i,{{j}_{i}}}}(x_k)\) to approximate \({{J}^{*}(x_k)}\) and \({{{v}}_{i}}(x_k)\) to approximate \(u_{k}^{*}\). In the following, an example is applied to illustrate the convergence and feasibility of the presented ADP algorithm.

4 Simulation Example

The following nonlinear system is mass-spring system:

$$\begin{aligned} x(k+1)=f(x_k)+g(x_k)u(k), \end{aligned}$$
(12)

where

$$\begin{aligned}&x_k=\left[ \begin{matrix} {{x}_{1k}} \\ {{x}_{2k}} \\ \end{matrix} \right] \!\!, \nonumber \\&f(x_k)=\left[ \begin{matrix} {{x}_{1k}}+0.05{{x}_{2k}} \\ -0.0005{{x}_{1k}}-0.0335x_{1k}^{3}+{{x}_{2k}} \\ \end{matrix} \right] \!\!, \nonumber \\&g(x_k)=\left[ \begin{matrix} 0 \\ 0.05 \\ \end{matrix} \right] \!, \end{aligned}$$

and the system is controlled with control constraint of \(\left| u \right| \le 0.6\). The cost function is defined by

$$\begin{aligned} J(x_k)=\sum \limits _{i=k}^{\infty }{\left\{ x{_i^{\mathsf {T}}}Qx_i+2\int _{0}^{u_i}{{{\tanh }^\mathsf {-T}}({{\overline{U}}^{-1}}s)\overline{U}Rds} \right\} }, \end{aligned}$$

where \(Q=\left[ \begin{array}{ll} 1 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] \), \(R=0.5\), \(\overline{U}=0.6\).

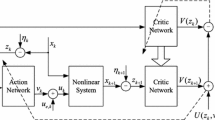
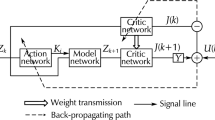
The developed iteration ADP algorithm is implemented by NNs. The hidden layers of the critic network and action network both are 10 neurons. For each iteration step, we train the networks for 4000 training steps so as to make the training error become minimum. The learning rate of the above two networks both are 0.01.

From Fig. 1(a) and (b), we can get the convergent process of the cost function \({{V}_{i,{{j}_{i}}}}(x_k)\) and the subsequence \({{V}_{i}}(x_k)\). Next, we use the optimal control vectors to control the system (12) with the initial state \(x(0)={{\left[ 1,-1 \right] }^{\mathsf {T}}}\) for 200 time steps. Figure 1(c) and (d) display the changing curves of the state x and the control u. The effective of the presented ADP algorithm in handling optimal control problem for discrete-time nonlinear systems with actuator saturation is verified through the simulation results.

Fig. 1.
figure 1

Simulation results (a) Convergence of \({{V}_{i,{{j}_{i}}}}\) (b) Convergence of \({{V}_{i}}\) (c) State trajectories (d) Control vectors

Full size image

5 Conclusion

In this paper, a novel ADP algorithm is chosen to treat the optimal control problem for discrete-time nonlinear systems with control constraint. One example demonstrates the convergence and feasibility of the presented iteration ADP algorithm. Since the time-delay problem is another hot topic in the control field, it’s significant to use the developed ADP algorithm to handle the time-delay systems in the future.