Keywords

1 Introduction

Underwater vehicles play an supporting role in the undersea exploration by human beings. Usually three kinds of underwater vehicle are available in performing underwater missions, which refer to as HOVs (human occupied vehicles), ROVs (remotely operated vehicles) and AUVs (autonomous underwater vehicles). A underwater vehicle-manipulator system (UVMS) is formed when a n-link manipulator is attached to an underwater vehicle such as ROV and AUV. By means of UVMS, complicated underwater missions can be fulfilled for instance undersea sampling, fixing or repairing. In the meantime, the safety and operability of an UVMS become more important, comparing an UVMS with an AUV or ROV. A control system with high performance can guarantee the safety and operability requirements.

One of the difficulties in obtaining a high-performance controller for an UVMS is how to deal with the uncertainties in the plant. Such uncertainties result from the disturbance by environment (e.g., current, oceanic internal wave), variation of payload and tether force, noises in the mechanical equipments, parametric perturbation, etc. Consequently, the robustness of the control system of an UVMS is of great importance. During the past years, developing an adaptive robust controller for an UVMS is of interest for many researchers. For example, Mohan and Kim presented a coordinated motion control scheme using a disturbance observer for an autonomous UVMS [1]. Xu et al. proposed a neuro-fuzzy approach to the control of UVMS in the presence of payload variation and hydrodynamic disturbance [2]. Han and Chung presented the use of restoring moments to the motion control of an UVMS with uncertainties caused by external disturbances [3]. Korkmaz et al. proposed the inverse dynamics control algorithm for the trajectory tracking of an underactuated UVMS in the presence of parameter uncertainty and disturbance [4]. Antonelli and Cataldi addressed the low level control of an UVMS affected by external disturbance using a recursive adaptive control scheme [5] and a virtual decomposition approach [6]. Barbalata et al. proposed a proportional-integral limited controller for a lightweight UVMS affected by disturbance [7]. Ji et al. presented the motion control of an UVMS affected by uncertainties and disturbances using zero moment point equation [8]. Woolfrey et al. studied the kinematic control of an UVMS affected by wave disturbance using model predictive control [9].

This paper presents a neural network approach to the tracking control of the manipulator of a UVMS. A three-link manipulator is considered to be attached to an AUV. In the study, it is assumed that the AUV is hovering when the manipulation is being performed. The interaction between the AUV and the manipulator is viewed as an external disturbance to the control of manipulator. An on-line forward neural network is applied to identify the nonlinearity that involves the disturbance. The overall control system is obtained using Lyapunov design to guarantee the stability of controller.

2 Problem Formulations

For an underwater vehicle with a n-link manipulator, a general model can be described as

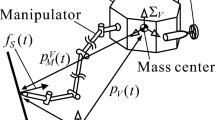
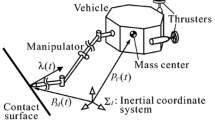
$$\begin{aligned} M(q)\dot{\zeta }+C(q,\zeta )\zeta +D(q,\zeta )\zeta +g(q,R_{B}^{I})=\tau . \end{aligned}$$
(1)

where \(q \in {{\mathbb {R}}^{n}}\) is the vector of joint position, \(\zeta \in {{\mathbb {R}}^{(6+n)}}\) is the vector of generalized velocity, \(R_{B}^{I}\) is the transformation from the body-fixed frame to the inertia frame, \(M(q)\in {{\mathbb {R}}^{(6+n)\times (6+n)}}\) is the inertia matrix, \(C(q,\zeta )\zeta \in {{\mathbb {R}}^{(6+n)}}\) is the vector of Coriolis and centripetal terms, \(D(q,\zeta )\zeta \in {{\mathbb {R}}^{(6+n)}}\) is the vector of dissipative effects, \(g(q,R_{B}^{I})\in {{\mathbb {R}}^{(6+n)}}\) is the vector of gravity and buoyancy effects, \(\tau \in {{\mathbb {R}}^{(6+n)}}\) is the vector of generalized forces [10]. An UVMS with a 3-link manipulator and the coordinate system can be depicted as Fig. 1, where \(o-xyz\) denotes the inertia (or earth-fixed) reference frame while \(o_i-x_iy_iz_i\) denote the body-fixed reference frames.

Fig. 1.
figure 1

An UVMS with 3-link manipulator

Full size image

When the vehicle is kept hovering while the manipulator is working, the body-fixed frame \(o_0-x_0y_0z_0\) can be viewed as an inertia frame. The dynamics of the manipulator can be described as

$$\begin{aligned} M(q)\ddot{q}+C(q,\dot{q})\dot{q}+D(q,\dot{q})\dot{q}+g(q)+w={{\tau }_{m}}. \end{aligned}$$
(2)

where w represents the interaction between the vehicle and the manipulator. Since it is difficult to express such an interaction in precise mathematical equation, w is taken as an external disturbance to the plant. In the study, it is assumed that the first link of the manipulator rotates around axis \(o_0z_0\) (as shown in Fig. 1) with the angle \(q_1\); the second and the third links rotate in the plane \(o_0z_0x_1\) with \(q_2\) and \(q_3\) respectively. Such a motion allocation guarantees the end effector can reach the object through the rotation of the three links.

Suppose the three links are driven by DC motors, the force vector \(\tau _m\) in (2) can be calculated by

$$\begin{aligned} \tau _m = K_mI. \end{aligned}$$
(3)

where \(K_m\) is the conversion coefficient matrix from electrical current to torque, I is the vector of electrical current.

The dynamics of the electrical circuit can be described as

$$\begin{aligned} L\dot{I}+RI+K\dot{q}={{u}_{e}}. \end{aligned}$$
(4)

where L is the matrix of armature inductance, R is the matrix of armature resistance, K is the voltage constant matrix, \(u_e\) is the vector of armature voltage.

Equations (2) and (4) constitute a cascaded system involving a mechanical subsystem and an electrical one. As can be recognized, the output of the cascaded system is the vector \(q=[q_1,q_2,q_3]^T\) while the controller input is \(u_e\).

3 Control Design

3.1 NN Based Controller

To obtain the torque in the mechanical subsystem, a desired signal is designed as

$$\begin{aligned} {{I}_{d}}=K_{m}^{-1}(M(q){{\ddot{q}}_{d}}+C(q,\dot{q}){{\dot{q}}_{d}}+D(q,\dot{q})\dot{q}+g(q)+{{u}_{1}}) . \end{aligned}$$
(5)

where \(q_d\) is the desired trajectory, \(u_1\) is introduced as an auxiliary controller. Similarly, another auxiliary controller can be introduced in the electrical subsystem:

$$\begin{aligned} u_e=RI_d+K\dot{q_d}+u_2. \end{aligned}$$
(6)

Define \(e=q_d-q\), \(\eta ={{I}_{d}}-I\), \(\xi =\dot{e}+\alpha e(\alpha >0)\), one has

$$\begin{aligned} M(q)\dot{\xi }=(\alpha M(q)-C(q,\dot{q}))\dot{e}+w+{{K}_{m}}\eta -{{u}_{1}}, \end{aligned}$$
(7)

and

$$\begin{aligned} L\dot{\eta }=-R\eta -K(\xi -\alpha e)+L{{\dot{I}}_{d}}-{{u}_{2}}. \end{aligned}$$
(8)

Lyapunov design is applied to the error systems (7) and (8). A positive definite Lyapunov function can be defined as

$$\begin{aligned} {{V}_{1}}=\frac{1}{2}({{e}^{T}}e+{{\xi }^{T}}M\xi +{{\eta }^{T}}L\eta ). \end{aligned}$$
(9)

Its derivative is

$$\begin{aligned} {{\dot{V}}_{1}}=- & {} \alpha {{e}^{T}}e+{{\xi }^{T}}({{K}_{m}}\eta +\alpha M(q)\dot{e}+\alpha C(q,\dot{q})e+e+w-{{u}_{1}})\nonumber \\+ & {} {{\eta }^{T}}(-R\eta -K(\xi -\alpha e)+L{{\dot{I}}_{d}}-{{u}_{2}}). \end{aligned}$$
(10)

On-line forward neural networks are applied to identify the nonlinearities in the above equation. In detail, let:

$$\begin{aligned} {{f}_{1}}=\alpha M(q)\dot{e}+\alpha C(q,\dot{q})e+e+w=W_{1}^{T}\phi (X_1)+{{\varepsilon }_{1}}, \end{aligned}$$
(11)
$$\begin{aligned} {{f}_{2}}={{K}_{m}}\xi -R\eta -K(\xi -\alpha e)+L{{\dot{I}}_{d}}=W_{2}^{T}\phi ({{X}_{2}})+{{\varepsilon }_{2}}. \end{aligned}$$
(12)

where \(W_i\) are weight matrices, \(X_i\) are net inputs, \(\varepsilon _i\) are approximation errors [11].

The two auxiliary controllers \(u_1\) and \(u_2\) can be designed as:

$$\begin{aligned} {{u}_{1}}=W_{1e}^{T}\phi ({{X}_{1}})+{{\alpha }_{1}}M(q)\xi , \end{aligned}$$
(13)

and

$$\begin{aligned} {{u}_{2}}=W_{1e}^{T}\phi ({{X}_{2}})+{{\alpha }_{2}}L\eta . \end{aligned}$$
(14)

where \(W_{ie}\) are updated weight matrices, \(\alpha _i\) are control gains.

3.2 Stability Analysis

Substituting Eqs. (13) and (14) into (10) yields:

$$\begin{aligned} {{\dot{V}}_{1}}=- & {} \alpha {{e}^{T}}e+({{\xi }^{T}}{{\varepsilon }_{1}}+{{\eta }^{T}}{{\varepsilon }_{2}})\nonumber \\+ & {} {{\xi }^{T}}\tilde{W}_{1}^{T}\phi ({{X}_{1}})+{{\eta }^{T}}\tilde{W}_{2}^{T}\phi ({{X}_{2}})-{{\alpha }_{1}}{{\xi }^{T}}M(q)\xi -{{\alpha }_{2}}{{\eta }^{T}}L\eta . \end{aligned}$$
(15)

where \(\tilde{W}_i = W_i-W_{ie}\) are weight error matrices. To guarantee the robustness of the net weight, the algorithms of updated weight matrices are designed as:

$$\begin{aligned} {{\dot{W}}_{1e}}={{k}_{1}}\phi ({{X}_{1}}){{\xi }^{T}}-{{k}_{2}}\left\| \xi \right\| {{W}_{1e}}, \end{aligned}$$
(16)
$$\begin{aligned} {{\dot{W}}_{2e}}={{k}_{1}}\phi ({{X}_{2}}){{\eta }^{T}}-{{k}_{2}}\left\| \zeta \right\| {{W}_{2e}}. \end{aligned}$$
(17)

where \(\zeta = [\xi , ~\eta ]^T\) is an augmented error vector. A stepping Lyapunov function is defined as

$$\begin{aligned} {{V}_{2}}=V_1+\frac{1}{2k_1}(\left\| {{{\tilde{W}}}_{1}} \right\| _{F}^{2}+\left\| {{{\tilde{W}}}_{2}} \right\| _{F}^{2}). \end{aligned}$$
(18)

Its derivative is

$$\begin{aligned} {{\dot{V}}_{2}}\le- & {} 2{{\alpha }_{0}}{{V}_{2}}+({{\xi }^{T}}{{\varepsilon }_{1}}+{{\eta }^{T}}{{\varepsilon }_{2}})-a({{\alpha }_{1}}{{\xi }^{T}}M(q)\xi +{{\alpha }_{2}}{{\eta }^{T}}L\eta )\nonumber \\+ & {} \frac{{{k}_{2}}}{{{k}_{1}}}\left\| \zeta \right\| ({{({{\tilde{W}}_{1}},{{W}_{1}})}_{F}}+{{({{\tilde{W}}_{2}},{{W}_{2}})}_{F}}-a\left\| {{{\tilde{W}}}_{1}} \right\| _{F}^{2}-a\left\| {{{\tilde{W}}}_{2}} \right\| _{F}^{2}), \end{aligned}$$
(19)

where \(a\in [0,~1]\), \({{\alpha }_{0}}=\min \{(1-a){{\alpha }_{1}},(1-a){{\alpha }_{2}},(1-a){{k}_{2}}\left\| \xi \right\| ,(1-a){{k}_{2}}\left\| \zeta \right\| \}\). Define a compact set \(U(\zeta )=\{\left. \zeta \right| \left\| \zeta \right\| \le b,b>0\}\), the following inequality can be obtained:

$$\begin{aligned} {{\dot{V}}_{2}}\le -2{{\alpha }_{0}}{{V}_{2}}+\lambda , (\lambda >0) \end{aligned}$$
(20)

when \(\zeta \) is within the set \(U(\zeta )\). Otherwise, if \(\left\| \zeta \right\| >b\), the following inequality can be derived

$$\begin{aligned} {{\dot{V}}_{2}}\le -2{{\alpha }_{0}}{{V}_{2}}, \end{aligned}$$
(21)

by selecting appropriate controller parameters.

It can be concluded from inequalities (20) and (21) that the tracking system is stable. Moreover, it should be noted that UUB (uniformly ultimately bounded) stability rather than asymptotic stability can be guaranteed.

4 Numerical Simulation

To demonstrate the validity of the proposed controller, an example is studied with respect to an AUV-manipulator system. The particulars of the manipulator are: \(l_1=l_2=l_3=1\)m, \(m_1=m_2=1\)kg, \(m_3=2m_1\), \(L=diag(0.1, ~0.1, ~0.1)\)H, \(R=diag(1, ~1, ~1)\varOmega \), \(K=diag(0.5, ~0.5, ~0.5)\)V\(\cdot \)s/rad, \(K_m=diag(1,~1,~1)\)N\(\cdot \)m/A. The interaction between the vehicle and the manipulator is assumed as a disturbance acted on the first link of the manipulator. In the study, it is selected as an uniformly distributed pseudorandom signals in the interval [0, 200N]. Moreover, a disturbance is assumed to act on the end effector at the time t = 1.5–1.7 s with the amplitude 200N.

The controller parameters are selected as: \(\alpha _1=\alpha _2=200\), \(k_1=50, k_2=0.8\). Sigmoid function is employed as the activation function of hidden layers. The initial weights are set as zeros. To confirm the advantage of the proposed controller over conventional controllers, a PD controller is taken as:

$$\begin{aligned} {{u}_{e}}={{\lambda }_{1}}\dot{e}+{{\lambda }_{2}}e, \end{aligned}$$
(22)

by selecting \(\lambda _1=\lambda _2=300\).

Figure 2 presents the tracking results of the joint positions. Figures 3 and 4 show the results of the trajectory tracking of the end effector. As can be recognized from the comparison results, better performance of the NN controller proposed in the study is achieved.

Fig. 2.
figure 2

Tracking results of the joint positions

Full size image
Fig. 3.
figure 3

Tracking results of the trajectory of the end effector

Full size image
Fig. 4.
figure 4

Space tracking results of the trajectory of the end effector

Full size image

5 Conclusions

Neural networks are applied to the control of the manipulator of an UVMS. To guarantee the robustness of the controller, Lyapunov design is incorporated. Simulation results show the validity of the proposed control scheme. It should be noted however that a specific case is studied in the paper. The vehicle is assumed to be hovering while the manipulation is being performed, which means that the manipulator can be dealt with as a ground robot. The validity of the proposed control scheme should be verified in a more complicated case, e.g., both the vehicle and the manipulator are under controlled.