Abstract
These are lecture notes from author’s mini-course on W-algebras during Session 1: “Vertex algebras, W-algebras, and application” of INdAM Intensive research period “Perspectives in Lie Theory”, at the Centro di Ricerca Matematica Ennio De Giorgi, Pisa, Italy. December 9, 2014–February 28, 2015.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
This note is based on lectures given at the Centro di Ricerca Matematica Ennio De Giorgi, Pisa, in Winter of 2014–2015. They are aimed as an introduction to W-algebras and their representation theory. Since W-algebras appear in many areas of mathematics and physics there are certainly many other important topics untouched in the note, partly due to the limitation of the space and partly due to the author’s incapability.
The W-algebras can be regarded as generalizations of affine Kac-Moody algebras and the Virasoro algebra. They appeared [34, 70, 78] in the study of the classification of two-dimensional rational conformal field theories. There are several ways to define W-algebras, but it was Feigin and Frenkel [36] who found the most conceptual definition of principal W-algebras that uses the quantized Drinfeld-Sokolov reduction, which is a version of Hamiltonian reduction. There are a lot of works on W-algebras (see [26] and references therein) mostly by physicists in 1980s and 1990s, but they were mostly on principal W-algebras, that is, the W-algebras associated with principal nilpotent elements. It was quite recent that Kac et al. [60] defined the W-algebra \(\mathcal{W}^{k}(\mathfrak{g},f)\) associated with a simple Lie algebra and its arbitrary nilpotent element f by generalizing the method of quantized Drinfeld-Sokolov reduction.
The advantage of the method of quantized Drinfeld-Sokolov reduction is its functoriality, in the sense that it gives rise to a functor from the category of representations of affine Kac-Moody algebras and to the category of representations of W-algebras. Since it is difficult to study W-algebras directly (as no presentation by generators and relations (OPE’s) is known for a general W-algebra), in this note we spend the most of our efforts in understanding this functor.
Although our methods apply to much more general settings [4, 6, 9, 10, 12] we focus on the W-algebras associated with Lie algebras \(\mathfrak{g}\) of type A and its principal nilpotent element that were originally defined by Fateev and Lykyanov [34]. They can be regarded as affinization of the center of the universal enveloping algebra of \(\mathfrak{g}\) via Konstant’s Whittaker model [65] and Kostant-Sternberg’s description [66] of Hamiltonian reduction via BRST cohomolgy, as explained in [36]. For this reason we start with a review of Kostant’s results and proceed to the construction of BRST complex in the finite-dimensional setting in Sect. 2. W-algebras are not Lie algebras, not even associated algebras in general, but vertex algebras. In many cases a vertex algebra can be considered as a quantization of arc spaces of an affine Poisson scheme. In Sect. 3 we study this view point that is useful in understanding W-algebras and their representation theory. In Sect. 4 we study Zhu’s algebras of vertex algebras that connects W-algebras with finite W-algebras [27, 75]. In Sect. 5 we introduce W-algebras and study their basic properties. In Sect. 6 we start studying representation theory of W-algebras. In Sect. 7 we quickly review some fundamental results on irreducible representations of W-algebras obtained in [5]. One of the fundamental problems (at least mathematically) on W-algebras was the conjecture of Frenkel et al. [44] on the existence and construction of so called the minimal models of W-algebras, which give rive to rational conformal field theories as in the case of the integrable representations of affine Kac-Moody algebras and the minimal models of the Virasoro algebra. In Sect. 8 we give an outline of the proof [10] of this conjecture.
2 Review of Kostant’s Results
2.1 Companion Matrices and Invariant Polynomials
Let \(G = GL_{n}(\mathbb{C})\) be the general linear group, and let \(\mathfrak{g} = \mathfrak{g}\mathfrak{l}_{n}(\mathbb{C})\) be the general linear Lie algebra consisting of n × n matrices. The group G acts on \(\mathfrak{g}\) by the adjoint action: x ↦ Ad(g)x = gxg −1, g ∈ G. Let \(\mathbb{C}[\mathfrak{g}]^{G}\) be the subring of the ring \(\mathbb{C}[\mathfrak{g}]\) of polynomial functions on \(\mathfrak{g}\) consisting of G-invariant polynomials.
Recall that a matrix
is called the companion matrix of the polynomial \(a_{1} + a_{2}t + a_{3}t^{2} +\ldots +a_{n}t^{n-1} + t^{n} \in \mathbb{C}[t]\) since
Let  be the affine subspace of \(\mathfrak{g}\) consisting of companion matrices of the form (1).
be the affine subspace of \(\mathfrak{g}\) consisting of companion matrices of the form (1).
Lemma 1
For \(A \in \mathfrak{g}\) the following conditions are equivalent.
-
1.
 .
. -
2.
There exists a vector \(v \in \mathbb{C}^{n}\) such that v, Av, A 2 v, …, A n−1 v are linearly independent.
Theorem 1
The restriction map gives the isomorphism

Proof
Let \(f \in \mathbb{C}[\mathfrak{g}]\) be a G-invariant polynomial such that  . Then clearly
. Then clearly  . On the other hand it follows from Lemma 1 that
. On the other hand it follows from Lemma 1 that  is a Zariski open subset in \(\mathfrak{g}\). Therefore f = 0. To see the surjectiveness define \(p_{1},\ldots,p_{n} \in \mathbb{C}[\mathfrak{g}]^{G}\) by
is a Zariski open subset in \(\mathfrak{g}\). Therefore f = 0. To see the surjectiveness define \(p_{1},\ldots,p_{n} \in \mathbb{C}[\mathfrak{g}]^{G}\) by
By (2), we have  . This completes the proof.
. This completes the proof.
Put

Note that f is a nilpotent element of \(\mathfrak{g}\), that is, (adf)r = 0 for a sufficiently large r. We have

where
Let \(\mathfrak{b}\), \(\mathfrak{n}\) be the subalgebras of \(\mathfrak{g}\) defined by
and let N be the unipotent subgroup of G corresponding to \(\mathfrak{n}\), i.e.,
Let ( | ) be the invariant inner product of \(\mathfrak{g}\) defined by \((x\vert y) =\mathop{ \mathrm{tr}}\nolimits (xy)\). This gives a G-equivariant isomorphism \(\mathfrak{g}\;\stackrel{_{\sim }}{\rightarrow }\;\mathfrak{g}^{{\ast}}\).
Define \(\chi \in \mathfrak{n}^{{\ast}}\) by
Note that χ is a character of \(\mathfrak{n}\), that is, \(\chi ([\mathfrak{n},\mathfrak{n}]) = 0\). Hence χ defines a one-dimensional representation of N.
Consider the restriction map
Then
Here \(\mathfrak{g}\) is identified with \(\mathfrak{g}^{{\ast}}\) via ( | ). Since μ is N-equivariant and χ is a one-point orbit of N, it follows that \(f + \mathfrak{b}\) is stable under the action of N.
Theorem 2 (Kostant [65])
The adjoint action gives the isomorphism

of affine varieties.
Proof
It is not difficult to see that the adjoint action gives the bijection  . Since it is a morphism of irreducible varieties and \(f + \mathfrak{b}\) is normal, the assertion follows from Zariski’s Main Theorem (see e.g., [76, Corollary 17.4.8]).
. Since it is a morphism of irreducible varieties and \(f + \mathfrak{b}\) is normal, the assertion follows from Zariski’s Main Theorem (see e.g., [76, Corollary 17.4.8]).
Corollary 1
The restriction map gives the isomorphisms

Proof
By Theorem 2, we have
 Hence the assertion follows from Theorem 1.
Hence the assertion follows from Theorem 1.
2.2 Transversality of to G-Orbits
to G-Orbits
Lemma 2
The affine spaces
 and
\(f + \mathfrak{b}\)
intersect transversely at f to AdG ⋅ f.
and
\(f + \mathfrak{b}\)
intersect transversely at f to AdG ⋅ f.
Proof
We need to show that

But \(T_{f}\mathfrak{g}\cong \mathfrak{g}\),  , \(T_{f}(\mathrm{Ad}G \cdot f)\cong [\mathfrak{g},f]\). The assertion follows since \(\mathfrak{g} = \mathfrak{a} + [\mathfrak{g},f]\).
, \(T_{f}(\mathrm{Ad}G \cdot f)\cong [\mathfrak{g},f]\). The assertion follows since \(\mathfrak{g} = \mathfrak{a} + [\mathfrak{g},f]\).
Using the Jacobson-Morozov theorem, we can embed f into an \(\mathfrak{s}\mathfrak{l}_{2}\)-triple {e, f, h} in \(\mathfrak{g}\). Explicitly, we can choose the following elements for e and h:
where e i, j denotes the standard basis element of \(\mathfrak{g} =\mathop{ \mathrm{Mat}}\nolimits _{n}(\mathbb{C})\).
The embedding \(\mathfrak{s}\mathfrak{l}_{2} =\mathop{ \mathrm{span}}\nolimits _{\mathbb{C}}\{e,h,f\} \rightarrow \mathfrak{g}\) exponents to a homomorphism SL 2 → G. Restricting it to the torus \(\mathbb{C}^{{\ast}}\) consisting of diagonal matrices we obtain a one-parameter subgroup \(\gamma: \mathbb{C}^{{\ast}}\rightarrow G\). Set
Then
Thus it define a \(\mathbb{C}^{{\ast}}\)-action on \(\mathfrak{g}\) that preserves \(f + \mathfrak{b}\) and  . This action on \(f + \mathfrak{b}\) and
. This action on \(f + \mathfrak{b}\) and  contracts to f, that is, ρ(t)x → f when t → 0.
contracts to f, that is, ρ(t)x → f when t → 0.
Proposition 1
The affine space
\(f + \mathfrak{b}\)
(resp.
 ) intersects AdG ⋅ x transversely at any point
\(x \in f + \mathfrak{b}\)
(resp.
) intersects AdG ⋅ x transversely at any point
\(x \in f + \mathfrak{b}\)
(resp.
 ).
).
Proof
By Lemma 2 the intersection of \(f + \mathfrak{b}\) with AdG-orbits is transversal at each point in some open neighborhood of f in \(f + \mathfrak{b}\). By the contracting \(\mathbb{C}^{{\ast}}\)-action ρ, it follows that the same is true for all points of \(f + \mathfrak{b}\).
2.3 The Transversal Slice as a Reduced Poisson Variety
as a Reduced Poisson Variety
The affine variety \(\mathfrak{g}^{{\ast}}\) is equipped with the Kirillov-Kostant Poisson structure: the Poisson algebra structure of \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\) is given by
Consider the restriction map \(\mu: \mathfrak{g}^{{\ast}}\rightarrow \mathfrak{n}^{{\ast}}\), which is a moment map for the N-action on \(\mathfrak{g}^{{\ast}}\). That is, μ is a regular N-equivariant morphism that gives the following commutative diagram of Lie algebras:

Here \(\mu ^{{\ast}}: \mathfrak{n} \rightarrow \mathfrak{g} \subset \mathbb{C}[\mathfrak{g}^{{\ast}}]\) is the pullback map, the map \(\mathbb{C}[\mathfrak{g}^{{\ast}}] \rightarrow \mathop{\mathrm{Der}}\nolimits \mathbb{C}[\mathfrak{g}^{{\ast}}]\) is given by ϕ ↦ {ϕ, ?}, and \(\mathfrak{n} \rightarrow \mathop{\mathrm{Der}}\nolimits \mathbb{C}[\mathfrak{g}^{{\ast}}]\) is the Lie algebra homomorphism induced by the coadjoint action of G on \(\mathfrak{g}^{{\ast}}\).
The transversality statement of Proposition 1 for \(f + \mathfrak{b}\) is equivalent to that χ is a regular value of μ. By Theorem 2, the action of N on \(\mu ^{-1}(\chi ) =\chi +\mathfrak{n}^{\perp }\) is free and

Therefore  has the structure of the reduced Poisson variety, obtained from \(\mathfrak{g}^{{\ast}}\) by the Hamiltonian reduction.
has the structure of the reduced Poisson variety, obtained from \(\mathfrak{g}^{{\ast}}\) by the Hamiltonian reduction.
The Poisson structure of  is described as follows. Let
is described as follows. Let
so that
Then  can be identified as the subspace of \(\mathbb{C}[\mathfrak{g}^{{\ast}}]/I_{\chi }\) consisting of all cosets \(\phi +\mathbb{C}[\mathfrak{g}^{{\ast}}]I_{\chi }\) such that \(\{x,\phi \}\in \mathbb{C}[\mathfrak{g}^{{\ast}}]I_{\chi }\) for all \(x \in \mathfrak{n}\). In this realization, the Poisson structure on
can be identified as the subspace of \(\mathbb{C}[\mathfrak{g}^{{\ast}}]/I_{\chi }\) consisting of all cosets \(\phi +\mathbb{C}[\mathfrak{g}^{{\ast}}]I_{\chi }\) such that \(\{x,\phi \}\in \mathbb{C}[\mathfrak{g}^{{\ast}}]I_{\chi }\) for all \(x \in \mathfrak{n}\). In this realization, the Poisson structure on  is defined by the formula
is defined by the formula
for ϕ, ϕ′ such that \(\{x,\phi \},\{x,\phi '\} \in \mathbb{C}[\mathfrak{g}^{{\ast}}]I_{\chi }\) for all \(x \in \mathfrak{n}\).
Proposition 2
We have the isomorphism
 as Poisson algebras. In particular the Poisson structure of
as Poisson algebras. In particular the Poisson structure of
 is trivial.
is trivial.
Proof
The restriction map  (see Corollary 1) is obviously a homomorphism of Poisson algebras.
(see Corollary 1) is obviously a homomorphism of Poisson algebras.
In the next subsection we shall describe the above Hamiltonian reduction in more factorial way, in terms of the BRST cohomology (where BRST refers to the physicists Becchi, Rouet, Stora and Tyutin) for later purpose.
2.4 BRST Reduction
Let Cl be the Clifford algebra associated with the vector space \(\mathfrak{n} \oplus \mathfrak{n}^{{\ast}}\) and its non-degenerate bilinear form (⋅ | ⋅ ) defined by ( f + x | g + y) = f( y) + g(x) for \(f,g \in \mathfrak{n}^{{\ast}},x,y \in \mathfrak{n}\). Namely, Cl is the unital \(\mathbb{C}\)-superalgebra that is isomorphic to \(\varLambda (\mathfrak{n}) \otimes \varLambda (\mathfrak{n}^{{\ast}})\) as \(\mathbb{C}\)-vector spaces, the natural embeddings \(\varLambda (\mathfrak{n})\hookrightarrow Cl\), \(\varLambda (\mathfrak{n}^{{\ast}})\hookrightarrow Cl\) are homogeneous homomorphism of superalgebras, and
(Note that [x, f] = xf + fx since x, f are odd.)
Let \(\{x_{\alpha }\}_{\alpha \in \varDelta _{+}}\) be a basis of \(\mathfrak{n}\), \(\{x_{\alpha }^{{\ast}}\}_{\alpha \in \varDelta _{+}}\) the dual basis of \(\mathfrak{n}^{{\ast}}\), and c α, β γ the structure constants of \(\mathfrak{n}\), that is, [x α , x β ] = ∑ α, β γ c αβ γ x γ .
Lemma 3
The following map gives a Lie algebra homomorphism.
We have
Define an increasing filtration on Cl by setting \(Cl_{p}:=\varLambda ^{\leqslant p}(\mathfrak{n}) \otimes \varLambda (\mathfrak{n}^{{\ast}})\). We have
where \(N = \mathrm{dim}\mathfrak{n} = \frac{n(n-1)} {2}\), and
Let \(\overline{Cl}\) be its associated graded algebra:
By (8), \(\overline{Cl}\) is naturally a graded Poisson superalgebra, called the classical Clifford algebra.
We have \(\overline{Cl} =\varLambda (\mathfrak{n}) \otimes \varLambda (\mathfrak{n}^{{\ast}})\) as a commutative superalgebra. Its Poisson (super)bracket is given by
Lemma 4
We have \(\overline{Cl}^{\mathfrak{n}} =\varLambda (\mathfrak{n})\) , where \(\overline{Cl}^{\mathfrak{n}}:=\{ w \in \overline{Cl}\mid \{x,w\} = 0,\forall x \in \mathfrak{n}\}\).
The Lie algebra homomorphism \(\rho: \mathfrak{n}\longrightarrow Cl_{1} \subset Cl\) induces a Lie algebra homomorphism
where σ 1 is the projection \(Cl_{1} \rightarrow Cl_{1}/Cl_{0} \subset \mathop{\mathrm{gr}}\nolimits Cl\). We have
Set
Since it is a tensor product of Poisson superalgebras, \(\bar{C}(\mathfrak{g})\) is naturally a Poisson superalgebra.
Lemma 5
The following map gives a Lie algebra homomorphism:
that is, \(\{\bar{\theta }_{\chi }(x),\bar{\theta }_{\chi }(\,y)\} =\bar{\theta } _{\chi }([x,y])\) for \(x,y \in \mathfrak{n}\).
Let \(\bar{C}(\mathfrak{g}) =\bigoplus _{n\in \mathbb{Z}}\bar{C}^{n}(\mathfrak{g})\) be the \(\mathbb{Z}\)-grading defined by degϕ ⊗ 1 = 0 (\(\phi \in \mathbb{C}[\mathfrak{g}^{{\ast}}]\)), deg1 ⊗ f = 1 (\(f \in \mathfrak{n}^{{\ast}}\)), deg1 ⊗ x = −1 (\(x \in \mathfrak{n}\)). We have
Lemma 6 ([20, Lemma 7.13.3])
There exists a unique element \(\bar{Q} \in \bar{ C}^{1}(\mathfrak{g})\) such that
We have \(\{\bar{Q},\bar{Q}\} = 0\).
Proof
Existence. It is straightforward to see that the element
satisfies the condition.
Uniqueness. Suppose that \(\bar{Q}_{1},\bar{Q}_{2} \in \bar{ C}^{1}(\mathfrak{g})\) satisfy the condition. Set \(R = Q_{1} - Q_{2} \in \bar{ C}^{1}(\mathfrak{g})\). Then {R, 1 ⊗ x} = 0, and so, \(R \in \mathbb{C}[\mathfrak{g}^{{\ast}}] \otimes \overline{Cl}^{\mathfrak{n}}\). But by Lemma 4, \(\overline{Cl}^{\mathfrak{n}} \cap \overline{Cl}^{1} = 0\). Thus R = 0 as required.
To show that \(\{\bar{Q},\bar{Q}\} = 0\), observe that
(note that \(\bar{Q}\) is odd). Applying Lemma 4 twice, we get that \(\{\bar{Q},\bar{Q}\} = 0\).
Since \(\bar{Q}\) is odd, Lemma 6 implies that
for any \(a \in \bar{ C}(\mathfrak{g})\). That is, \(\mathrm{ad}\bar{Q}:=\{\bar{ Q},\cdot \}\) satisfies that
Thus, \((\bar{C}(\mathfrak{g}),\mathrm{ad}\bar{Q})\) is a differential graded Poisson superalgebra. Its cohomology \(H^{\bullet }(\bar{C}(\mathfrak{g}),\mathrm{ad}\bar{Q}) =\bigoplus \limits _{i\in \mathbb{Z}}H^{i}(\bar{C}(\mathfrak{g}),\mathrm{ad}\bar{Q})\) inherits a graded Poisson superalgebra structure from \(\bar{C}(\mathfrak{g})\).
According to Kostant and Sternberg [66] the Poisson structure of  may be described through the following isomorphism:
may be described through the following isomorphism:
Theorem 3 ([66])
We have \(H^{i}(\bar{C}(\mathfrak{g}),\mathrm{ad}\bar{Q}) = 0\) for i ≠ 0 and

as Poisson algebras.
Proof
Give a bigrading on \(\bar{C}:=\bar{ C}(\mathfrak{g})\) by setting
so that \(\bar{C} =\bigoplus \limits _{i\geqslant 0,j\leqslant 0}\bar{C}^{i,j}\).
Observe that \(\mathrm{ad}\bar{Q}\) decomposes as \(\mathrm{ad}\bar{Q} = d_{+} + d_{-}\) such that
Explicitly, we have
Since \(\mathrm{ad}\bar{Q}^{2} = 0\), (10) implies that
It follows that there exists a spectral sequence
such that
Observe that \((\bar{C}(\mathfrak{g}),d_{-})\) is identical to the Koszul complex \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\) associated with the sequence x 1 −χ(x 1), x 2 −χ(x 2. )…, x N −χ(x N ) tensorized with \(\varLambda (\mathfrak{n}^{{\ast}})\). Since \(\mathbb{C}[\mu ^{-1}(\chi )] = \mathbb{C}[\mathfrak{g}^{{\ast}}]/\sum _{i}\mathbb{C}[\mathfrak{g}^{{\ast}}](x_{i} -\chi (x_{i}))\), we get that
Next, notice that \((H^{0}(C(\mathfrak{g}),d_{-}),d_{+})\) is identical to the Chevalley complex for the Lie algebra cohomology \(H^{\bullet }(\mathfrak{n}, \mathbb{C}[\mu ^{-1}(\chi )])\). Therefore Theorem 2 gives that

Hence the spectral sequence collapses at E 2 = E ∞ and we get that \(H^{i}(\bar{C}(\mathfrak{g}),\mathrm{ad}\bar{Q}) = 0\) for i ≠ 0. Moreover, there is an isomorphism

This completes the proof.
Theorem 4
The natural map \(\mathbb{C}[\mathfrak{g}^{{\ast}}]^{G}\longrightarrow H^{0}(\bar{C}(\mathfrak{g}),\mathrm{ad}\bar{Q})\) defined by sending p to p ⊗ 1 is an isomorphism of Poisson algebras.
Proof
It is clear that the map is a well-defined homomorphism of Poisson algebras since \(\mathbb{C}[\mathfrak{g}^{{\ast}}]^{G}\) is the Poisson center of \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\). The assertion follows from the commutativity of the following diagram.

2.5 Quantized Hamiltonian Reduction
We shall now quantize the above construction following [66].
Let \(\{U_{i}(\mathfrak{g})\}\) be the PBW filtration of the universal enveloping algebra \(U(\mathfrak{g})\) of \(\mathfrak{g}\), that is, \(U_{i}(\mathfrak{g})\) is the subspace of \(U(\mathfrak{g})\) spanned by the products of at most i elements of \(\mathfrak{g}\). Then
The associated graded space \(\mathop{\mathrm{gr}}\nolimits U(\mathfrak{g}) =\bigoplus _{i\geqslant 0}U_{i}(\mathfrak{g})/U_{i-1}(\mathfrak{g})\) is naturally a Poisson algebra, and the PBW Theorem states that
as Poisson algebras. Thus, \(U(\mathfrak{g})\) is a quantization of \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\).
Define
It is naturally a \(\mathbb{C}\)-superalgebra, where \(U(\mathfrak{g})\) is considered as a purely even subsuperalgebra. The filtration of \(U(\mathfrak{g})\) and Cl induces the filtration of \(C(\mathfrak{g})\): \(C_{p}(\mathfrak{g}) =\sum _{i+j\leqslant p}U_{i}(\mathfrak{g}) \otimes Cl_{j}\), and we have
as Poisson superalgebras. Therefore, \(C(\mathfrak{g})\) is a quantization of \(\bar{C}(\mathfrak{g})\).
Define the \(\mathbb{Z}\)-grading \(C(\mathfrak{g}) =\bigoplus \limits _{n\in \mathbb{Z}}C^{n}(\mathfrak{g})\) by setting deg(u ⊗ 1) = 0 (\(u \in U(\mathfrak{g})\)), deg(1 ⊗ f) = 1 (\(f \in \mathfrak{n}^{{\ast}}\)), deg(1 ⊗ x) = −1 (\(x \in \mathfrak{n}\)). Then
Lemma 7
The following map defines a Lie algebra homomorphism.
Lemma 8 ([20, Lemma 7.13.7])
There exists a unique element \(Q \in C^{1}(\mathfrak{g})\) such that
We have Q 2 = 0.
Proof
The proof is similar to that of Lemma 6. In fact the element Q is explicitly given by the same formula as \(\bar{Q}\):
Since Q is odd, Lemma 8 implies that
Thus, \((C(\mathfrak{g}),\mathrm{ad}Q)\) is a differential graded algebra, and its cohomology \(H^{\bullet }(C(\mathfrak{g}),\mathrm{ad}Q)\) is a graded superalgebra.
However the operator on \(\mathop{\mathrm{gr}}\nolimits C(\mathfrak{g}) =\bar{ C}(\mathfrak{g})\) induced by adQ does not coincide with \(\mathrm{ad}\bar{Q}\). To remedy this, we introduce the Kazhdan filtration \(K_{\bullet }C(\mathfrak{g})\) of \(C(\mathfrak{g})\) as follows: Defined a \(\mathbb{Z}\)-grading on \(\mathfrak{g}\) by
where h is defined in (6). Then \(\mathfrak{n} =\bigoplus _{j>0}\mathfrak{g}_{j} \subset \mathfrak{b} =\bigoplus _{j\geqslant 0}\mathfrak{g}_{j}\), and
is the Cartan subalgebra of \(\mathfrak{g}\) consisting of diagonal matrices. Extend the basis \(\{x_{\alpha }\}_{\alpha \in \varDelta _{+}}\) of \(\mathfrak{n}\) to the basis \(\{x_{a}\}_{a\in \varDelta _{+}\sqcup I}\) of \(\mathfrak{b}\) by adding a basis {x i } i ∈ I of \(\mathfrak{h}\). Let c a, b d denote the structure constant of \(\mathfrak{b}\) with respect to this basis.
Lemma 9
The map \(\rho: \mathfrak{n} \rightarrow Cl\) extends to the Lie algebra homomorphism
Define the Lie algebra homomorphism
and define a \(\mathbb{Z}\)-grading on \(C(\mathfrak{g})\) by
Set
Then \(K_{\bullet }C(\mathfrak{g})\) defines an increasing, exhaustive, separated filtration of \(C(\mathfrak{g})\) such that \(K_{p}C(\mathfrak{g}) \cdot K_{q}C(\mathfrak{g}) \subset K_{p+q}C(\mathfrak{g})\), \([K_{p}C(\mathfrak{g}),K_{q}C(\mathfrak{g})] \subset K_{p+q-1}C(\mathfrak{g})\), and \(\mathop{\mathrm{gr}}\nolimits _{K}C(\mathfrak{g}) =\bigoplus _{p}K_{p}C(\mathfrak{g})/K_{p-1}C(\mathfrak{g})\) is isomorphic to \(\bar{C}(\mathfrak{g})\) as Poisson superalgebras. Moreover, the complex \((\mathop{\mathrm{gr}}\nolimits _{K}C(\mathfrak{g}),\mathrm{ad}Q)\) is identical to \((\bar{C}(\mathfrak{g}),\mathrm{ad}\bar{Q})\).
Let  be the center of \(U(\mathfrak{g})\).
be the center of \(U(\mathfrak{g})\).
Theorem 5 ([65])
We have
\(H^{i}(C(\mathfrak{g}),\mathrm{ad}Q) = 0\)
for i ≠ 0 and the map
 defined by sending z to [z ⊗ 1] is an isomorphism of algebras. Here [z ⊗ 1] denotes the cohomology class of z ⊗ 1.
defined by sending z to [z ⊗ 1] is an isomorphism of algebras. Here [z ⊗ 1] denotes the cohomology class of z ⊗ 1.
Proof
We have the spectral sequence
such that
Therefore the spectral sequence collapses at E 1 = E ∞ , so we get
Since the homomorphism  , z ↦ [z ⊗ 1], respects the filtration
, z ↦ [z ⊗ 1], respects the filtration  and \(K_{\bullet }H^{0}(C(\mathfrak{g}),\mathrm{ad}Q)\), where
and \(K_{\bullet }H^{0}(C(\mathfrak{g}),\mathrm{ad}Q)\), where  , \(K_{p}H^{\bullet }(C(\mathfrak{g}),\mathrm{ad}Q) =\mathop{ \mathrm{Im}}\nolimits (H^{0}(K_{p}C(\mathfrak{g}),\mathrm{ad}Q) \rightarrow H^{0}(C(\mathfrak{g}),\mathrm{ad}Q))\), we get the desired isomorphism.
, \(K_{p}H^{\bullet }(C(\mathfrak{g}),\mathrm{ad}Q) =\mathop{ \mathrm{Im}}\nolimits (H^{0}(K_{p}C(\mathfrak{g}),\mathrm{ad}Q) \rightarrow H^{0}(C(\mathfrak{g}),\mathrm{ad}Q))\), we get the desired isomorphism.
Remark 1 (See [5, § 2] for the Details)
As in the case of \(\bar{C}(\mathfrak{g})\), \(C(\mathfrak{g})\) is also bigraded, we can also write adQ = d + + d − such that d +(C i, j) ⊂ C i+1, j, d −(C i, j) ⊂ C i, j+1 and get a spectral sequence
such that
Where \(\mathbb{C}_{\chi }\) is the one-dimensional representation of \(\mathfrak{n}\) defined by the character χ. Thus we get the Whittaker model isomorphism [65]

2.6 Classical Miura Map
Let \(\mathfrak{n}_{-} =\bigoplus \limits _{j<0}\mathfrak{g}_{j}\) be the subalgebra of \(\mathfrak{g}\) consisting of lower triangular matrices, and set \(\mathfrak{b}_{-} =\bigoplus \limits _{j\leqslant 0}\mathfrak{g}_{j} = \mathfrak{n}_{-}\mathop{\oplus }\mathfrak{h}\). We have
Extend the basis \(\{x_{a}\}_{a\in \varDelta _{+}\sqcup I}\) to the basis \(\{x_{a}\}_{a\in \varDelta _{+}\sqcup I\sqcup \varDelta _{-}}\) by adding a basis \(\{x_{\alpha }\}_{\alpha \in \varDelta _{-}}\) of \(\mathfrak{n}_{-}\). Let c a, b d be the structure constant with respect to this basis. Extend \(\theta _{0}: \mathfrak{b} \rightarrow C(\mathfrak{g})\) to the linear map \(\theta _{0}: \mathfrak{g} \rightarrow C(\mathfrak{g})\) by setting
We already know that the restriction of θ 0 to \(\mathfrak{n}\) is a Lie algebra homomorphism and
Although θ 0 is not a Lie algebra homomorphism, we have the following.
Lemma 10
The restriction of θ 0 to \(\mathfrak{b}_{-}\) is a Lie algebra homomorphism. We have [θ 0(x), 1 ⊗ y] = 1 ⊗ ad∗(x)( y) for \(x \in \mathfrak{b}_{-}\) , \(y \in \mathfrak{n}^{{\ast}}\) , where ad∗ denote the coadjoint action and \(\mathfrak{n}^{{\ast}}\) is identified with \((\mathfrak{g}/\mathfrak{b}_{-})^{{\ast}}\).
Let \(C(\mathfrak{g})_{+}\) denote the subalgebra of \(C(\mathfrak{g})\) generated by \(\theta _{0}(\mathfrak{n})\) and \(\varLambda (\mathfrak{n}) \subset Cl\), and let \(C(\mathfrak{g})_{-}\) denote the subalgebra generated by \(\theta _{0}(\mathfrak{b}_{-})\) and \(\varLambda (\mathfrak{n}^{{\ast}}) \subset Cl\).
Lemma 11
The multiplication map gives a linear isomorphism
Lemma 12
The subspaces \(C(\mathfrak{g})_{-}\) and \(C(\mathfrak{g})_{+}\) are subcomplexes of \((C(\mathfrak{g}),\mathrm{ad}Q)\) . Hence \(C(\mathfrak{g})\cong C(\mathfrak{g})_{-}\otimes C(\mathfrak{g})_{+}\) as complexes.
Proof
The fact that \(C(\mathfrak{g})_{+}\) is subcomplex is obvious (see Lemma 8). The fact that \(C(\mathfrak{g})_{-}\) is a subcomplex follows from the following formula.
(a ∈ Δ −⊔ I, α ∈ Δ +).
Proposition 3
\(H^{\bullet }(C(\mathfrak{g})_{-},\mathrm{ad}Q)\cong H^{\bullet }(C(\mathfrak{g}),\mathrm{ad}Q)\).
Proof
By Lemma 12 and Kunneth’s Theorem,
On the other hand we have ad(Q)(1 ⊗ x α ) = θ χ (x α ) = θ 0(x α ) −χ(x α ) for α ∈ Δ −. Hence \(C(\mathfrak{g})_{-}\) is isomorphic to the tensor product of complexes of the form \(\mathbb{C}[\theta _{\chi }(x_{\alpha })] \otimes \varLambda (x_{\alpha })\) with the differential θ χ (x α ) ⊗ x α ∗, where x α ∗ denotes the odd derivation of the exterior algebra Λ(x α ) with one variable x α such that x α ∗(x α ) = 1. Each of these complexes has one-dimensional zeroth cohomology and zero first cohomology. Therefore \(H^{i}(C(\mathfrak{g})_{+},\mathrm{ad}Q) =\delta _{i,0}\mathbb{C}\). This completes the proof.
Note that the cohomological gradation takes only non-negative values on \(C(\mathfrak{g})_{-}\). Hence by Proposition 3 we may identify  with the subalgebra \(H^{0}(C(\mathfrak{g})_{-},\mathrm{ad}Q) =\{ c \in C(\mathfrak{g})_{-}^{0}\mid \mathrm{ad}Q(c) = 0\}\) of \(C(\mathfrak{g})_{-}\).
with the subalgebra \(H^{0}(C(\mathfrak{g})_{-},\mathrm{ad}Q) =\{ c \in C(\mathfrak{g})_{-}^{0}\mid \mathrm{ad}Q(c) = 0\}\) of \(C(\mathfrak{g})_{-}\).
Consider the decomposition
Note that \(C(\mathfrak{g})_{-,0}^{0}\) is generated by \(\theta _{0}(\mathfrak{h})\) and is isomorphic to \(U(\mathfrak{h})\). The projection
is an algebra homomorphism, and hence, its restriction

is also an algebra homomorphism.
Proposition 4
The map Υ is an embedding.
Let \(K_{\bullet }C(\mathfrak{g})_{\pm }\) be the filtration of \(C(\mathfrak{g})_{\pm }\) induced by the Kazhdan filtration of \(C(\mathfrak{g})\). We have the isomorphism
as complexes. Similarly as above, we have \(H^{i}(\mathop{\mathrm{gr}}\nolimits _{K}C(\mathfrak{g})_{+},\mathrm{ad}\bar{Q}) =\delta _{i,0}\mathbb{C}\), and
Proof (Proof of Proposition 4 )
The filtration \(K_{\bullet }U(\mathfrak{h})\) of \(U(\mathfrak{h})\cong C(\mathfrak{g})_{-,0}^{0}\) induced by the Kazhdan filtration coincides with the usual PBW filtration. By (12) and Theorem 3, the induced map
can be identified with the restriction map

It is sufficient to show that \(\bar{\varUpsilon }\) is injective.
If \(\varphi \in \mathbb{C}[\,f + \mathfrak{b}]^{N}\) is in the kernel, φ(g. x) = 0 for all g ∈ N and \(x \in f + \mathfrak{h}\). Hence it is enough to show that the image of the the action map
is Zariski dense in \(f + \mathfrak{b}\).
The differential of this morphism at \((1,x) \in N \times (\,f + \mathfrak{h})\) is given by
This is an isomorphism if \(x \in f + \mathfrak{h}_{\mathop{\mathrm{reg}}\nolimits }\), where \(\mathfrak{h}_{\mathop{\mathrm{reg}}\nolimits } =\{ x \in \mathfrak{h}\mid \mathfrak{n}^{x} = 0\}\). Hence (14) is a dominant morphism as required, see e.g. [76, Theorem 16.5.7].
Remark 2
The fact that \(\bar{\varUpsilon }\) is injective is in fact well-known. Indeed, under the identifications  , \(\mathbb{C}[\,f + \mathfrak{h}]\cong \mathbb{C}[\mathfrak{h}]\), \(\bar{\varUpsilon }\) is identified with the Chevalley restriction map \(\mathbb{C}[\mathfrak{g}]^{G}\;\stackrel{_{\sim }}{\rightarrow }\;\mathbb{C}[\mathfrak{h}]^{W}\), where \(W = \mathfrak{S}_{n}\).
, \(\mathbb{C}[\,f + \mathfrak{h}]\cong \mathbb{C}[\mathfrak{h}]\), \(\bar{\varUpsilon }\) is identified with the Chevalley restriction map \(\mathbb{C}[\mathfrak{g}]^{G}\;\stackrel{_{\sim }}{\rightarrow }\;\mathbb{C}[\mathfrak{h}]^{W}\), where \(W = \mathfrak{S}_{n}\).
The advantage of the above proof is that it applies to a general finite W-algebra [71], and also, it generalizes to the affine setting, see Sect. 5.9.
The map Υ is called the classical Miura map.
2.7 Generalization to an Arbitrary Simple Lie Algebra
It is clear that the above argument works if we replace \(\mathfrak{g}\mathfrak{l}_{n}\) by \(\mathfrak{s}\mathfrak{l}_{n}\), and \(\mathfrak{a}\) by \(\mathfrak{a} \cap \mathfrak{s}\mathfrak{l}_{n}\).
More generally, let \(\mathfrak{g}\) be an arbitrary simple Lie algebra. Let f be a principal (regular) nilpotent element of \(\mathfrak{g}\), {e, f, h} an associated \(\mathfrak{s}\mathfrak{l}_{2}\)-triple. One may assume that
where f
i
is a root vector of roots α
i
and {α
i
}
i ∈ I
is the set of simple roots of \(\mathfrak{g}\). Define the Kostant slice
 by
by

where \(\mathfrak{g}^{e}\) is the centralizer of e in \(\mathfrak{g}\).
Then all the statements in previous subsections that make sense hold by replacing the set of companion matrices by the Kostant slice [65].
2.8 Generalization to Finite W-Algebras
In fact, the above argument works in more general setting of Hamiltonian reduction. In particular for Slodowy slices. Namely, for a non-zero nilpotent element f of a finite-dimensional semisimple Lie algebra \(\mathfrak{g}\), we can use Jacobson-Morozov’s theorem to embed f into an sl 2-triple {e, f, h}. The Slodowy slice at f is defined to be the affine subslace

of \(\mathfrak{g}\).
The Slodowy slice  has the following properties.
has the following properties.
-
 intersects the G-orbits at any point of
intersects the G-orbits at any point of  , where G is the adjoint group of \(\mathfrak{g}\).
, where G is the adjoint group of \(\mathfrak{g}\). -
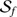 admits a \(\mathbb{C}^{{\ast}}\)-action which is contracting to f.
admits a \(\mathbb{C}^{{\ast}}\)-action which is contracting to f.
As in the case of the set of companion matrices  can be realized by Hamiltonian reduction. Let \(\mathfrak{g}_{j} =\{ x \in \mathfrak{g}\mid [h,x] = 2jx\}\), so that
can be realized by Hamiltonian reduction. Let \(\mathfrak{g}_{j} =\{ x \in \mathfrak{g}\mid [h,x] = 2jx\}\), so that
Then the subspace \(\mathfrak{g}_{1/2}\) admits a symplectic form defined by 〈x | y〉 = ( f | [x, y]). Choose a Lagrangian subspace l of \(\mathfrak{g}_{1/2}\) with respect to this form, and set \(\mathfrak{m} = l +\sum _{j\geqslant 1}\mathfrak{g}_{j}\). Then \(\mathfrak{m}\) is a nilpotent subalgebra of \(\mathfrak{g}\) and \(\chi: \mathfrak{m} \rightarrow \mathbb{C}\), x ↦ ( f | x), defines a character. Let M be the unipotent subgroup of G corresponding to \(\mathfrak{m}\), that is, \(\mathop{\mathrm{Lie}}\nolimits M = \mathfrak{m}\). The adjoint action of M on \(\mathfrak{g}\) is Hamiltonian, so we can consider the moment map of this action
which is just a restriction map. Then we have the following realization of the Slodowy slice.

To obtain the BRST realization of this Hamiltonian reduction we simply replace the Clifford algebra Cl by \(Cl_{\mathfrak{m}}\), i.e., the Clifford algebra associated to \(\mathfrak{m} \oplus \mathfrak{m}^{{\ast}}\). Then we can define the operator \(\mathrm{ad}\bar{Q}\) similarly and get a differential cochain complex \((\mathbb{C}[\mathfrak{g}^{{\ast}}] \otimes \overline{Cl}_{\mathfrak{m}},\mathrm{ad}\bar{Q})\). We have

as Poisson algebras.
As above, this construction has a natural quantization and the quantization \(U(\mathfrak{g},f)\) of  thus defined is called the finite W-algebra associated to the pair
\((\mathfrak{g},f)\) [75]:
thus defined is called the finite W-algebra associated to the pair
\((\mathfrak{g},f)\) [75]:
where \(\mathbb{C}_{\chi }\) is the one-dimensional representation of \(\mathfrak{m}\) defined by χ (cf. [5, 29]).
3 Arc Spaces, Poisson Vertex Algebras, and Associated Varieties of Vertex Algebras
3.1 Vertex Algebras
A vertex algebra is a vector space V equipped with | 0〉 ∈ V (the vacuum vector), \(T \in \mathop{\mathrm{End}}\nolimits V\) (the translation operator), and a bilinear product
where \(a(z) =\sum _{n\in \mathbb{Z}}a_{(n)}z^{-n-1}\), \(a_{(n)} \in \mathop{\mathrm{End}}\nolimits V\), such that
-
1.
( | 0〉)(z) = id V ,
-
2.
a(z) | 0〉 ∈ V [[z]] and \(\lim \limits _{z\rightarrow 0}a(z)\vert 0\rangle = a\) for all a ∈ V,
-
3.
(Ta)(z) = ∂ z a(z) for all a ∈ V, where ∂ z = d∕dz,
-
4.
for any a, b ∈ V, \((z - w)^{N_{a,b}}[a(z),b(w)] = 0\) for some \(N_{a,b} \in \mathbb{Z}_{+} =\{ 0,1,2,\ldots \}\).
The last condition is called the locality, which is equivalent to the fact that
where \(\delta (z - w) =\sum _{n\in \mathbb{Z}}w^{n}z^{-n-1} \in \mathbb{C}[[z,w,z^{-1},w^{-1}]]\).
A consequence of the definition is the following Borcherds identities:
We write (15) as
and call it the λ-bracket of a and b. (We have a (n) b = 0 if (z − w)n[a(z), b(w)] = 0.)
Here are some properties of λ-brackets.
The normally ordered product on V is defied as: ab: = a (−1) b. We also write: ab: (z) =: a(z)b(z): . We have
where a(z)+ = ∑ n < 0 a (n) z −n−1, \(a(z)_{-} =\sum _{n\geqslant 0}a_{(n)}z^{-n-1}\). We have the following non-commutative Wick formula.
3.2 Commutative Vertex Algebras and Differential Algebras
A vertex algebra V is called commutative if
or equivalently, a (n) = 0 for \(n\geqslant 0\) in \(\mathop{\mathrm{End}}\nolimits V\) for all a ∈ V. This condition is equivalent to that
by (16).
A commutative vertex algebra has the structure of a unital commutative algebra by the product
where the unite is given by the vacuum vector | 0〉. The translation operator T of V acts on V as a derivation with respect to this product:
Therefore a commutative vertex algebra has the structure of a differential algebra, that is, a unital commutative algebra equipped with a derivation. Conversely, there is a unique vertex algebra structure on a differential algebra R with a derivation T such that
for a ∈ R. This correspondence gives the following.
Theorem 6 ([24])
The category of commutative vertex algebras is the same as that of differential algebras.
3.3 Arc Spaces
Define the (formal) disc as
For a scheme X, a homomorphism α: D → X is called an arc of X.
Theorem 7 ([25, 33, 52])
Let X be a scheme of finite type over \(\mathbb{C}\) , Sch the category of schemes of finite type over \(\mathbb{C}\) , Set the category of sets. The contravariant functor
is represented by a scheme JX, that is,
for any Y ∈ Sch. Here \(Y \widehat{ \times } D\) is the completion of Y ×D with respect to the subscheme \(Y \widehat{ \times }\{ 0\}\).
By definition, the \(\mathbb{C}\)-points of JX are
that is, the set of arcs of X. The reason we need the completion \(Y \widehat{ \times } D\) in the definition is that \(A \otimes \mathbb{C}[[t]] \subsetneq A[[t]] = A\widehat{ \otimes } \mathbb{C}[[t]]\) in general.
The scheme JX is called the arc space, or the infinite jet scheme, of X.
It is easy to describe JX when X is affine:
First, consider the case \(X = \mathbb{C}^{N} =\mathop{ \mathrm{Spec}}\nolimits \mathbb{C}[x_{1},x_{2},\cdots \,,x_{N}]\). The \(\mathbb{C}\)-points of JX are the arcs \(\mathop{\mathrm{Hom}}\nolimits _{Sch}(D,JX)\), that is, the ring homomorphisms
Such a map is determined by the image
of each x i , and conversely, the coefficients {γ i, (−n−1)} determines a \(\mathbb{C}\)-point of JX. If we choose coordinates x i, (−n−1) of JX as x i, (−n−1)(γ) = γ i, (−n−1), we have
Next, let \(X =\mathop{ \mathrm{Spec}}\nolimits R\), with \(R = \mathbb{C}[x_{1},x_{2},\cdots \,,x_{N}]/\langle f_{1},f_{2},\cdots \,,f_{r}\rangle\). The arcs of X are
An element \(\gamma \in \mathop{\mathrm{Hom}}\nolimits _{\mathop{\mathrm{ring}}\nolimits }(\mathbb{C}[x_{1},x_{2},\cdots \,,x_{n}], \mathbb{C}[[t]])\) is an element of this subset if and only if γ( f i ) = 0 for i = 1, 2, ⋯ , r. By writing
with \(f_{i,m} \in \mathbb{C}[x_{i,(-n-1)}]\), where \(x_{i}(t):=\sum _{m\geqslant 0}x_{i,(-m-1)}t^{m}\), we get that
Lemma 13
Define the derivation T of \(\mathbb{C}[x_{i(n)}\vert i = 1,2,\cdots \,,N;n = -1,-2,\cdots \,]\) by
Then f i, m = T n f i for \(n\geqslant 0\) . Here we identify x i with x i(−1).
With the above lemma, we conclude that for the affine scheme \(X =\mathop{ \mathrm{Spec}}\nolimits R\), \(R = \mathbb{C}[x_{1},x_{2},\cdots \,,x_{n}]/\langle f_{1},f_{2},\cdots \,,f_{r}\rangle\), its arc space JX is the affine scheme \(\mathop{\mathrm{Spec}}\nolimits (JR)\), where
and T is as defined in the lemma.
The derivation T acts on the above quotient ring JR. Hence for an affine scheme \(X =\mathop{ \mathrm{Spec}}\nolimits R\), the coordinate ring \(JR = \mathbb{C}[JX]\) of its arc space JX is a differential algebra, hence is a commutative vertex algebra.
Remark 3
The differential algebra JR has the universal property that
for any differential algebra A, where \(\mathop{\mathrm{Hom}}\nolimits _{\text{diff. alg.}}(JR,A)\) is the set of homomorphisms JR → A of differential algebras.
For a general scheme Y of finite type with an affine open covering {U
i
}
i ∈ I
, its arc space JY is obtained by glueing JU
i
(see [33, 52]). In particular, the structure sheaf  is a sheaf of commutative vertex algebras.
is a sheaf of commutative vertex algebras.
There is a natural projection π ∞ : JX → X that corresponds to the embedding R ↪ JR, x i → x i, (−1), in the case X is affine. In terms of arcs, π ∞ (α) = α(0) for \(\alpha \in \mathop{\mathrm{Hom}}\nolimits _{Sch}(D,X)\), where 0 is the unique closed point of the disc D.
The map from a scheme to its arc space is functorial. i.e., a scheme homomorphism f: X → Y induces a scheme homomorphism Jf: JX → JY that makes the following diagram commutative:

In terms of arcs, Jf(α) = f ∘α for \(\alpha \in \mathop{\mathrm{Hom}}\nolimits _{Sch}(D,X)\).
We also have
Indeed, for any scheme Z,
Lemma 14
The natural morphism \(X_{\mathop{\mathrm{red}}\nolimits } \rightarrow X\) induces an isomorphism \(JX_{\mathop{\mathrm{red}}\nolimits } \rightarrow JX\) of topological spaces, where \(X_{\mathop{\mathrm{red}}\nolimits }\) denotes the reduced scheme of X.
Proof
We may assume that \(X =\mathop{ \mathrm{Spec}}\nolimits R\). An arc α of X corresponds to a ring homomorphism \(\alpha ^{{\ast}}: R \rightarrow \mathbb{C}[[t]]\). Since \(\mathbb{C}[[t]]\) is an integral domain it decomposes as \(\alpha ^{{\ast}}: R \rightarrow R/\sqrt{0} \rightarrow \mathbb{C}[[t]]\). Thus, α is an arc of \(X_{\mathop{\mathrm{red}}\nolimits }\).
If X is a point, then JX is also a point, since \(\mathop{\mathrm{Hom}}\nolimits (D,X) =\mathop{ \mathrm{Hom}}\nolimits (\mathbb{C}, \mathbb{C}[[t]])\) consists of only one element. Thus, Lemma 14 implies the following.
Corollary 2
If X is zero-dimensional then JX is also zero-dimensional.
Theorem 8 ([64])
JX is irreducible if X is irreducible.
Lemma 15
Let Y be irreducible, and let f: X → Y be a morphism that restricts to a bijection between some open subsets U ⊂ X and V ⊂ Y. Then Jf: JX → JY is dominant.
Proof
Jf restricts to the isomorphism \(JU\;\stackrel{_{\sim }}{\rightarrow }\;JV\), and the open subset JV is dense in JY since JY is irreducible.
3.4 Arc Space of Poisson Varieties and Poisson Vertex Algebras
Let V be a commutative vertex algebra, or equivalently, a differential algebra. V is called a Poisson vertex algebras if it is equipped with a bilinear map
also called the λ-bracket, satisfying the following axioms:
where the arrow means that λ + T should be moved to the right, that is, \(\{a_{\lambda +T}c\}_{\rightarrow }b =\sum _{n\geqslant 0}(a_{(n)}c)\frac{(\lambda +T)^{n}} {n!} b\).
The first equation in (28) says that a (n), \(n\geqslant 0\), is a derivation of the ring V. (Do not confuse \(a_{(n)} \in \mathop{\mathrm{Der}}\nolimits (V )\), \(n\geqslant 0\), with the multiplication a (n) as a vertex algebra, which should be zero for a commutative vertex algebra.)
Note that (25), (26), (27) are the same as (18), (19), (20), and (28) is the same with (21) and (22) without the third terms. In particular, by (27), we have
Theorem 9 ([7, Proposition 2.3.1])
Let X be an affine Poisson scheme, that is, \(X =\mathop{ \mathrm{Spec}}\nolimits R\) for some Poisson algebra R. Then there is a unique Poisson vertex algebra structure on \(JR = \mathbb{C}[JX]\) such that
where {a, b} is the Poisson bracket in R.
Proof
The uniqueness is clear by (18) since JR is generated by R as a differential algebra. We leave it to the reader to check the well-definedness.
Remark 4
More generally, let X be a Poisson scheme which is not necessarily affine. Then the structure sheaf  carries a unique vertex Poisson algebra structure such that {f
λ
g} = {f, g} for
carries a unique vertex Poisson algebra structure such that {f
λ
g} = {f, g} for  , see [16, Lemma 2.1.3.1].
, see [16, Lemma 2.1.3.1].
Example 1
Let G be an affine algebraic group, \(\mathfrak{g} =\mathop{ \mathrm{Lie}}\nolimits G\). The arc space JG is naturally a proalgebraic group. Regarding JG as the \(\mathbb{C}[[t]]\)-points of G, we have JG = G[[t]]. Similarly, \(J\mathfrak{g} = \mathfrak{g}[[t]] =\mathop{ \mathrm{Lie}}\nolimits (JG)\).
The affine space \(\mathfrak{g}^{{\ast}}\) is a Poisson variety by the Kirillov-Kostant Poisson structure, see Sect. 2.3. If {x i }is a basis of \(\mathfrak{g}\), then
Thus
So we may identify \(\mathbb{C}[J\mathfrak{g}^{{\ast}}]\) with the symmetric algebra \(S(\mathfrak{g}[t^{-1}]t^{-1})\).
Let x = x (−1) | 0〉 = (xt −1) | 0〉, where we denote by | 0〉 the unite element in \(S(\mathfrak{g}[t^{-1}]t^{-1})\). Then (29) gives that
So the Lie algebra \(J\mathfrak{g} = \mathfrak{g}[[t]]\) acts on \(\mathbb{C}[J\mathfrak{g}^{{\ast}}]\). This action coincides with that obtained by differentiating the action of JG = G[[t]] on \(J\mathfrak{g}^{{\ast}}\) induced by the coadjoint action of G. In other words, the vertex Poisson algebra structure of \(\mathbb{C}[J\mathfrak{g}^{{\ast}}]\) comes from the JG-action on \(J\mathfrak{g}^{{\ast}}\).
3.5 Canonical Filtration of Vertex Algebras
Haisheng Li [68] has shown that every vertex algebra is canonically filtered: For a vertex algebra V, let F p V be the subspace of V spanned by the elements
with a 1, a 2, ⋯ , a r ∈ V, \(n_{i}\geqslant 0\), \(n_{1} + n_{2} + \cdots + n_{r}\geqslant p\). Then
It is clear that TF p V ⊂ F p+1 V.
Set \((F^{p}V )_{(n)}F^{q}V:=\mathop{ \mathrm{span}}\nolimits _{\mathbb{C}}\{a_{(n)}b\vert a \in F^{p}V,b \in F^{q}V \}\).
Lemma 16
We have
Proposition 5
-
(1)
(F p V )(n)(F q V ) ⊂ F p+q−n−1 V. Moreover, if \(n\geqslant 0\) , we have (F p V )(n)(F q V ) ⊂ F p+q−n V.
-
(2)
The filtration F • V is separated, that is, \(\bigcap _{p\geqslant 0}F^{p}V =\{ 0\}\) , if V is a positive energy representation over itself.
Proof
It is straightforward to check. [(2) also follows from Lemma 17 below.]
In this note we assume that the filtration F • V is separated.
Set
We denote by σ p : F p V ↦ F p V∕F p+1 V for \(p\geqslant 0\), the canonical quotient map.
Proposition 5 gives the following.
Proposition 6 ([68])
The space \(\mathop{\mathrm{gr}}\nolimits V\) is a Poisson vertex algebra by
for a ∈ F p V, b ∈ F q V, \(n\geqslant 0\).
Set
Note that \(F^{1}V =\mathop{ \mathrm{span}}\nolimits _{\mathbb{C}}\{a_{(-2)}b\mid a,b \in V \}\).
Proposition 7 ([68, 79])
The restriction of the Poisson structure gives R V a Poisson algebra structure, that is, R V is a Poisson algebra by
where \(\bar{a} =\sigma _{0}(a)\).
Proof
It is straightforward from Proposition 6.
In the literature F 1 V is often denoted by C 2(V ) and the Poisson algebra R V is called Zhu’s C 2 -algebra.
A vertex algebra V is called finitely strongly generated if R V is finitely generated as a ring. If the images of vectors a 1, …, a N ∈ V generate R V , we say that V is strongly generated by a 1, …, a N .
Below we always assume that a vertex algebra V is finitely strongly generated.
Note that if ϕ: V → W is a homomorphism of vertex algebras, ϕ respects the canonical filtration, that is, ϕ(F p V ) ⊂ F p W. Hence it induces the homomorphism \(\mathop{\mathrm{gr}}\nolimits V \rightarrow \mathop{\mathrm{gr}}\nolimits W\) of Poisson vertex algebra homomorphism which we denote by \(\mathop{\mathrm{gr}}\nolimits \phi\).
3.6 Associated Variety and Singular Support of Vertex Algebras
Definition 1
Define the associated scheme \(\tilde{X}_{V }\) and the associated variety X V of a vertex algebra V as
It was shown in [68, Lemma4.2] that \(\mathop{\mathrm{gr}}\nolimits V\) is generated by the subring R V as a differential algebra. Thus, we have a surjection \(JR_{V } \rightarrow \mathop{\mathrm{gr}}\nolimits V\) of differential algebras by Remark 3. This is in fact a homomorphism of Poisson vertex algebras:
Theorem 10 ([68, Lemma4.2], [7, Proposition 2.5.1])
The identity map R V → R V induces a surjective Poisson vertex algebra homomorphism
Let a 1, …, a n be a set of strong generators of V. Since \(\mathop{\mathrm{gr}}\nolimits V \cong V\) as \(\mathbb{C}\)-vector spaces by the assumption that F • V is separated, it follows from Theorem 10 that V is spanned by elements
Definition 2
Define the singular support of a vertex algebra V as
Theorem 11
We have dimSS(V ) = 0 if and only if dimX V = 0.
Proof
The “only if” part is obvious sine \(\pi _{\infty }(SS(V )) =\tilde{ X}_{V }\), where \(\pi _{\infty }: J\tilde{X}_{V } \rightarrow \tilde{ X}_{V }\) is the projection. The “if” part follows from Corollary 2.
Definition 3
We call V lisse (or C 2 -cofinite) if dimX V = 0.
Remark 5
Suppose that V is \(\mathbb{Z}_{+}\)-graded, so that \(V =\bigoplus _{i\geqslant 0}V _{i}\), and that \(V _{0} = \mathbb{C}\vert 0\rangle\). Then \(\mathop{\mathrm{gr}}\nolimits V\) and R V are equipped with the induced grading:
So the following conditions are equivalent:
-
1.
V is lisse.
-
2.
X V = {0}.
-
3.
The image of any vector a ∈ V i for \(i\geqslant 1\) in \(\mathop{\mathrm{gr}}\nolimits V\) is nilpotent.
-
4.
The image of any vector a ∈ V i for \(i\geqslant 1\) in R V is nilpotent.
Thus, lisse vertex algebras can be regarded as a generalization of finite-dimensional algebras.
Remark 6
Suppose that the Poisson structure of R V is trivial. Then the Poisson vertex algebra structure of JR V is trivial, and so is that of \(\mathop{\mathrm{gr}}\nolimits V\) by Theorem 10. This happens if and only if
If this is the case, one can give \(\mathop{\mathrm{gr}}\nolimits V\) yet another Poisson vertex algebra structure by setting
(We can repeat this procedure if this Poisson vertex algebra structure is again trivial.)
3.7 Comparison with Weight-Depending Filtration
Let V be a vertex algebra that is \(\mathbb{Z}\)-graded by some Hamiltonian H:
Then there is [67] another natural filtration of V defined as follows.
For a homogeneous vector a ∈ V Δ , Δ is called the conformal weight of a and is denote by Δ a . Let G p V be the subspace of V spanned by the vectors
with \(\varDelta _{a^{1}} +\ldots +\varDelta _{a^{r}}\leqslant p\). Then G • V defines an increasing filtration of V:
Moreover we have
It follows that \(\mathop{\mathrm{gr}}\nolimits _{G}V =\bigoplus G_{p}V/G_{p-1}V\) is naturally a Poisson vertex algebra.
It is not too difficult to see the following.
Lemma 17 ([7, Proposition 2.6.1])
We have
where F p V Δ = V Δ ∩ F p V, G p V Δ = V Δ ∩ G p V. Therefore
as Poisson vertex algebras.
3.8 Example: Universal Affine Vertex Algebras
Let \(\mathfrak{a}\) be a Lie algebra with a symmetric invariant bilinear form κ. Let
be the Kac-Moody affinization of \(\mathfrak{a}\). It is a Lie algebra with commutation relations
Let
where \(\mathbb{C}\) is one-dimensional representation of \(\mathfrak{a}[t] \oplus \mathbb{C}\mathbf{1}\) on which \(\mathfrak{a}[t]\) acts trivially and 1 acts as the identity. The space \(V ^{\kappa }(\mathfrak{a})\) is naturally graded: \(V ^{\kappa }(\mathfrak{a}) =\bigoplus _{\varDelta \in \mathbb{Z}_{\geqslant 0}}V ^{\kappa }(\mathfrak{a})_{\varDelta }\), where the grading is defined by setting degxt n = −n, deg | 0〉 = 0. Here | 0〉 = 1 ⊗ 1. We have \(V ^{\kappa }(\mathfrak{a})_{0} = \mathbb{C}\vert 0\rangle\). We identify \(\mathfrak{a}\) with \(V ^{\kappa }(\mathfrak{a})_{1}\) via the linear isomorphism defined by x ↦ xt −1 | 0〉.
There is a unique vertex algebra structure on \(V ^{\kappa }(\mathfrak{a})\) such that | 0〉 is the vacuum vector and
(So x (n) = xt n for \(x \in \mathfrak{a} = V ^{\kappa }(\mathfrak{a})_{1}\), \(n \in \mathbb{Z}\)).
The vertex algebra \(V ^{\kappa }(\mathfrak{a})\) is called the universal affine vertex algebra associated with (\(\mathfrak{a}\), κ).
We have \(F^{1}V ^{\kappa }(\mathfrak{a}) = \mathfrak{a}[t^{-1}]t^{-2}V ^{\kappa }(\mathfrak{a})\), and the Poisson algebra isomorphism
Thus
We have the isomorphism
because the graded dimensions of both sides coincide. Therefore
The isomorphism (34) follows also from the fact that
where \(\{U_{p}(\mathfrak{a}[t^{-1}]t^{-1})\}\) is the PBW filtration of \(U(\mathfrak{a}[t^{-1}]t^{-1})\).
3.9 Example: Simple Affine Vertex Algebras
For a finite-dimensional simple Lie algebra \(\mathfrak{g}\) and \(k \in \mathbb{C}\), we denote by \(V ^{k}(\mathfrak{g})\) the universal affine vertex algebra \(V ^{k\kappa _{0}}(\mathfrak{g})\), where κ 0 is the normalized invariant inner product of \(\mathfrak{g}\), that is,
where θ is the highest root of \(\mathfrak{g}\). Denote by \(V _{k}(\mathfrak{g})\) the unique simple graded quotient of \(V ^{k}(\mathfrak{g})\). As a \(\hat{\mathfrak{g}}\)-module, \(V _{k}(\mathfrak{g})\) is isomorphic to the irreducible highest weight representation L(kΛ 0) of \(\widehat{\mathfrak{g}}\) with highest weight kΛ 0, where Λ 0 is the weight of the basic representation of \(\widehat{\mathfrak{g}}\).
Theorem 12
The vertex algebra \(V _{k}(\mathfrak{g})\) is lisse if and only if \(V _{k}(\mathfrak{g})\) is integrable as a \(\hat{\mathfrak{g}}\) -module, which is true if and only if \(k \in \mathbb{Z}_{+}\).
Lemma 18
Let (R, ∂) be a differential algebra over \(\mathbb{Q}\) , I a differential ideal of R, i.e., I is an ideal of R such that ∂I ⊂ I. Then \(\partial \sqrt{I} \subset \sqrt{I}\).
Proof
Let \(a \in \sqrt{I}\), so that a m ∈ I for some \(m \in \mathbb{N} =\{ 1,2,\ldots \}\). Since I is ∂-invariant, we have ∂ m a m ∈ I. But
Hence \((\partial a)^{m} \in \sqrt{I}\), and therefore, \(\partial a \in \sqrt{I}\).
Proof (Proof of the “if” Part of Theorem 12)
Suppose that \(V _{k}(\mathfrak{g})\) is integrable. This condition is equivalent to that \(k \in \mathbb{Z}_{+}\) and the maximal submodule N k of \(V ^{k}(\mathfrak{g})\) is generated by the singular vector (e θ t −1)k+1 | 0〉 [54]. The exact sequence \(0 \rightarrow N_{k} \rightarrow V ^{k}(\mathfrak{g}) \rightarrow V _{k}(\mathfrak{g}) \rightarrow 0\) induces the exact sequence
where I k is the image of N k in \(R_{V ^{k}(\mathfrak{g})} = \mathbb{C}[\mathfrak{g}^{{\ast}}]\), and so, \(R_{V _{k}(\mathfrak{g})} = \mathbb{C}[\mathfrak{g}^{{\ast}}]/I_{k}\). The image of the singular vector in I k is given by e θ k+1. Therefore, \(e_{\theta } \in \sqrt{I}\). On the other hand, by Lemma 18, \(\sqrt{I_{k}}\) is preserved by the adjoint action of \(\mathfrak{g}\). Since \(\mathfrak{g}\) is simple, \(\mathfrak{g} \subset \sqrt{I}\). This proves that \(X_{V _{k}(\mathfrak{g})} =\{ 0\}\) as required.
The proof of “only if” part follows from [30]. We will give a different proof using W-algebras in Remark 13.
In view of Theorem 12, one may regard the lisse condition as a generalization of the integrability condition to an arbitrary vertex algebra.
4 Zhu’s Algebra
In this section we will introduce and study the Zhu’s algebra of a vertex algebra, which plays an important role in the representation theory.
See [55] in this volume for the definition of modules over vertex algebras.
4.1 Zhu’s C 2-Algebra and Zhu’s Algebra of a Vertex Algebra
Let V be a \(\mathbb{Z}\)-graded vertex algebra. Zhu’s algebra ZhuV [43, 79] is defined as
where \(V \circ V:=\mathop{ \mathrm{span}}\nolimits \{a \circ b\vert a,b \in V \}\) and
for homogeneous elements a, b and extended linearly. It is an associative algebra with multiplication defined as
for homogeneous elements a, b ∈ V.
For a simple positive energy representation \(M =\bigoplus _{n\in \mathbb{Z}_{+}}M_{\lambda +n}\), M λ ≠ 0, \(\lambda \in \mathbb{C}\), of V, let M top be the top degree component M λ of M. Also, for a homogeneous vector a ∈ V, let \(o(a) = a_{(\varDelta _{a}-1)}\), so that o(a) preserves the homogeneous components of any graded representation of V.
The importance of Zhu’s algebra in vertex algebra theory is the following fact that was established by Yonchang Zhu.
Theorem 13 ([79])
For any positive energy representation M of V, \(\overline{a}\mapsto o(a)\) defines a well-defined representation of Zhu(V ) on M top . Moreover, the correspondence M ↦ M top gives a bijection between the set of isomorphism classes of irreducible positive energy representations of V and that of simple Zhu(V )-modules.
A vertex algebra V is called a chiralization of an algebra A if \(\mathrm{Zhu}(V )\cong A\).
Now we define an increasing filtration of Zhu’s algebra. For this, we assume that V is \(\mathbb{Z}_{+}\)-graded: \(V =\bigoplus _{\varDelta \geqslant 0}V _{\varDelta }\). Then \(V _{\leqslant p} =\bigoplus _{ \varDelta =0}^{p}V _{\varDelta }\) gives an increasing filtration of V. Define
Obviously, we have
Also, since \(a_{(n)}b \in V _{\varDelta _{a}+\varDelta _{b}-n-1}\) for \(a \in V _{\varDelta _{a}}\), \(b \in V _{\varDelta _{b}}\), we have
The following assertion follows from the skew symmetry.
Lemma 19
We have
and hence,
By Lemma 19, we have
By (35) and (36), the associated graded \(\mathop{\mathrm{gr}}\nolimits \mathrm{Zhu}(V ) =\bigoplus _{p}\mathrm{Zhu}_{p}(V )/\mathrm{Zhu}_{p-2}(V )\) is naturally a graded Poisson algebra.
Note that \(a \circ b \equiv a_{(-2)}b\pmod \bigoplus _{\varDelta \leqslant \varDelta _{a}+\varDelta _{b}}V _{\varDelta }\) for homogeneous elements a, b ∈ V.
Lemma 20 (Zhu, See [29, Proposition 2.17(c)], [17, Proposition 3.3])
The following map defines a well-defined surjective homomorphism of Poisson algebras.
Remark 7
The map η V is not an isomorphism in general. For an example, let \(\mathfrak{g}\) be the simple Lie algebra of type E 8 and \(V = V _{1}(\mathfrak{g})\). Then dimR V > dimZhu(V ) = 1.
Corollary 3
If V is lisse then Zhu(V ) is finite dimensional. Hence the number of isomorphic classes of simple positive energy representations of V is finite.
In fact the following stronger facts are known.
Theorem 14 ([1])
Let V be lisse. Then any simple V -module is a positive energy representation. Therefore the number of isomorphic classes of simple V -modules is finite.
Theorem 15 ([31, 73])
Le V be lisse. Then the abelian category of V -modules is equivalent to the module category of a finite-dimensional associative algebra.
4.2 Computation of Zhu’s Algebras
We say that a vertex algebra V admits a PBW basis if R V is a polynomial algebra and the map \(\mathbb{C}[JX_{V }] \twoheadrightarrow \mathop{\mathrm{gr}}\nolimits V\) is an isomorphism.
Theorem 16
If V admits a PBW basis, then \(\eta _{V }: R_{V } \twoheadrightarrow \mathop{\mathrm{gr}}\nolimits \mathrm{Zhu}V\) is an isomorphism.
Proof
We have \(\mathop{\mathrm{gr}}\nolimits \mathrm{Zhu}(V ) = V/\mathop{\mathrm{gr}}\nolimits (V \circ V )\), where \(\mathop{\mathrm{gr}}\nolimits (V \circ V )\) is the associated graded space of V ∘ V with respect to the filtration induced by the filtration \(V _{\leqslant p}\). We wish to show that \(\mathop{\mathrm{gr}}\nolimits (V \circ V ) = F^{1}V\). Since \(a \circ b \equiv a_{(-2)}b\pmod F_{\leqslant \varDelta _{a}+\varDelta _{b}}V\), it is sufficient to show that a ∘ b ≠ 0 implies that a (−2) b ≠ 0.
Suppose that a (−2) b = (Ta)(−1) b = 0. Since V admits a PBW basis, \(\mathop{\mathrm{gr}}\nolimits V\) has no zero divisors. That fact that V admits a PBW basis also shows that Ta = 0 implies that a = c | 0〉 for some constant \(c \in \mathbb{C}\). Thus, a is a constant multiple of | 0〉, in which case a ∘ b = 0.
Example 2 (Universal Affine Vertex Algebras)
The universal affine vertex algebra \(V ^{\kappa }(\mathfrak{a})\) (see Sect. 3.8) admits a PBW basis. Therefore
On the other hand, from Lemma 19 one finds that
gives a well-defined algebra homomorphism. This map respects the filtration on both sides, where the filtration in the left-hand-side is the PBW filtration. Hence it induces a map between their associated graded algebras, which is identical to \(\eta _{V ^{\kappa }(\mathfrak{a})}\). Therefore (37) is an isomorphism, that is to say, \(V ^{\kappa }(\mathfrak{a})\) is a chiralization of \(U(\mathfrak{a})\).
Exercise 1
Extend Theorem 16 to the case that \(\mathfrak{a}\) is a Lie superalgebra.
Example 3 (Free Fermions)
Let \(\mathfrak{n}\) be a finite-dimensional vector space. The Clifford affinization \(\hat{Cl}\) of \(\mathfrak{n}\) is the Clifford algebra associated with \(\mathfrak{n}[t,t^{-1}] \oplus \mathfrak{n}^{{\ast}}[t,t^{-1}]\) and its symmetric bilinear form defined by
for \(x,y \in \mathfrak{n}\), \(f,g \in \mathfrak{n}^{{\ast}}\), \(m,n \in \mathbb{Z}\).
Let \(\{x_{\alpha }\}_{\alpha \in \varDelta _{+}}\) be a basis of \(\mathfrak{n}\), {x α ∗} its dual basis. We write ψ α, m for \(x_{\alpha }t^{m} \in \hat{ Cl}\) and ψ α, m ∗ for \(x_{\alpha }^{{\ast}}t^{m} \in \hat{ Cl}\), so that \(\hat{Cl}\) is the associative superalgebra with
-
odd generators: \(\psi _{\alpha,m},\psi _{\alpha,m}^{{\ast}},m \in \mathbb{Z},\alpha \in \varDelta _{+}\).
-
relations: [ψ α, m , ψ β, n ] = [ψ α, m ∗, ψ β, n ∗] = 0, [ψ α, m , ψ β, n ∗] = δ α, β δ m+n, 0.
Define the charged fermion Fock space associated with \(\mathfrak{n}\) as

It is an irreducible \(\hat{Cl}\)-module, and as \(\mathbb{C}\)-vector spaces we have

There is a unique vertex (super)algebra structure on  such that the image of 1 is the vacuum | 0〉 and
such that the image of 1 is the vacuum | 0〉 and
We have  , and it follows that there is an isomorphism
, and it follows that there is an isomorphism

as Poisson superalgebras. Thus,

where \(\varPi \mathfrak{n}\) is the space \(\mathfrak{n}\) considered as a purely odd affine space. The arc space \(JT^{{\ast}}\varPi \mathfrak{n}\) is also regarded as a purely odd affine space, such that \(\mathbb{C}[JT^{{\ast}}\varPi \mathfrak{n}] =\varLambda (\mathfrak{n}^{{\ast}}[t^{-1}]) \otimes \varLambda (\mathfrak{n}[t^{-1}]t^{-1})\). The map  is an isomorphism and
is an isomorphism and  admits a PBW basis. Therefore we have the isomorphism
admits a PBW basis. Therefore we have the isomorphism

by Exercise 1. On the other hand the map

gives an algebra homomorphism that respects the filtration. Hence we have

That is,  is a chiralization of Cl.
is a chiralization of Cl.
5 W-Algebras
We are now in a position to define W-algebras. We will construct a differential graded vertex algebra, so that its cohomology algebra is a vertex algebra and that will be our main object to study.
For simplicity, we let \(\mathfrak{g} = \mathfrak{g}\mathfrak{l}_{n}\) and we only consider the principal nilpotent case. However the definition works for any simple Lie algebra. The general definition for an arbitrary nilpotent element will be similar but one does need a new idea (see [60] for the most general definition).
5.1 The BRST Complex
Let \(\mathfrak{g},\mathfrak{n}\) be as in Sect. 2.1. Denote by \(\kappa _{\mathfrak{g}}\) the Killing form on \(\mathfrak{g}\) and \(\kappa _{0} = \frac{1} {2n}\kappa _{\mathfrak{g}}\), so that κ 0(θ, θ) = 2.
Choose any symmetric invariant bilinear form κ on \(\mathfrak{g}\) and let \(V ^{\kappa }(\mathfrak{g})\) be the universal affine vertex algebra associated with \((\mathfrak{g},\kappa )\) (see Sect. 3.8) and let  be the fermion Fock space as in Example 3.
be the fermion Fock space as in Example 3.
We have the following commutative diagrams:

Define

Since it is a tensor product of two vertex algebras, \(C^{\kappa }(\mathfrak{g})\) is a vertex algebra. We have

and

Thus, \(C^{\kappa }(\mathfrak{g})\) is a chiralization of \(C(\mathfrak{g})\) considered in Sect. 2.5. Further we have

So we have the following commutative diagram:

Define a gradation

by setting \(\mathrm{deg}\psi _{\alpha,m} = -1,\mathrm{deg}\psi _{\alpha,k}^{{\ast}} = 1,\forall i,j \in I,m,k \in \mathbb{Z}\), deg | 0〉 = 0. This induces a \(\mathbb{Z}\)-grading (that is different from the conformal grading) on \(C^{\kappa }(\mathfrak{g})\):

Let \(V (\mathfrak{n})\) be the the universal affine vertex algebra associated with \(\mathfrak{n}\) and the zero bilinear form, which is identified with the vertex subalgebra of \(V ^{\kappa }(\mathfrak{g})\) generated by x α (z) with α ∈ Δ +.
Lemma 21
The following defines a vertex algebra homomorphism.

Remark 8
In the above formula the normally ordered product is not needed because \(\mathfrak{n}\) is nilpotent.
The map \(\hat{\rho }\) induces an algebra homomorphism

and a Poisson algebra homomorphism

that are identical to ρ and \(\bar{\rho }\) (see Lemma 3 and 9), respectively.
Recall the character \(\chi: \mathfrak{n} \rightarrow \mathbb{C}\), x ↦ ( f | x).
Lemma 22
The following defines a vertex algebra homomorphism.
The map \(\hat{\theta }_{\chi }\) induces an algebra homomorphism
and a Poisson algebra homomorphism

that are identical to θ χ and \(\bar{\theta }\), respectively (see Lemmas 5 and 7).
The proof of the following assertion is similar to that of Lemma 6.
Proposition 8
There exists a unique element \(\hat{Q} \in C^{k,1}(g)\) such that
We have \([\hat{Q}_{\lambda }\hat{Q}] = 0\).
The field \(\hat{Q}(z)\) is given explicitly as
Since \(\hat{Q}\) is odd and \([\hat{Q}_{\lambda }\hat{Q}] = 0\), we have
(Recall that we write \(\hat{Q}(z) =\sum _{n\in \mathbb{Z}}\hat{Q}_{(n)}z^{-n-1}\).) So \((C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\) is a cochain complex.
Lemma 23
If it is nonzero, the cohomology \(H^{\bullet }(C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\) inherits the vertex algebra structure from \(C^{\kappa }(\mathfrak{g})\).
Proof
Set \(Z:=\{ v \in C^{\kappa }(\mathfrak{g})\mid \hat{Q}_{(0)}v = 0\}\), \(B =\hat{ Q}_{(0)}C^{\kappa }(\mathfrak{g}) \subset Z\), so that \(H^{\bullet }(C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)}) = Z/B\). From the commutator formula (16), we know that
Thus, if a, b ∈ Z, then \(\hat{Q}_{(0)}(a_{(m)}b) = 0\), that is, a (m) b ∈ Z. It follows that Z a vertex subalgebra of \(C^{\kappa }(\mathfrak{g})\). Further, if a ∈ Z and \(b =\hat{ Q}_{(0)}b' \in B\), then \(a_{(m)}b = a_{(m)}\hat{Q}_{(0)}b' =\hat{ Q}_{(0)}(a_{(m)}b) \in B\). Hence B is an ideal of Z. This completes the proof.
Definition 4
The W-algebra \(\mathcal{W}^{\kappa }(\mathfrak{g}) =\mathcal{ W}^{\kappa }(\mathfrak{g},f)\) associated to \((\mathfrak{g},f,\kappa )\) is defined to be the zero-th cohomology of the cochain complex \((C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\), that is,
This definition of \(\mathcal{W}^{\kappa }(\mathfrak{g})\) is due to Feigin and Frenkel [36]. In Sect. 5.9 we show that the above \(\mathcal{W}^{\kappa }(\mathfrak{g})\) is identical to the original W-algebra defined by Fateev and Lukyanov [34].
5.2 Cohomology of Associated Graded
We have \(\hat{Q}_{(0)}F^{p}C^{\kappa }(\mathfrak{g}) \subset F^{p}C^{\kappa }(\mathfrak{g})\), so \((\mathop{\mathrm{gr}}\nolimits ^{F}C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\) is also a cochain complex. The cohomology \(H^{\bullet }(\mathop{\mathrm{gr}}\nolimits ^{F}C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\) inherits a Poisson vertex algebra structure from \(\mathop{\mathrm{gr}}\nolimits ^{F}C^{\kappa }(\mathfrak{g})\).
Theorem 17
We have \(H^{i}(\mathop{\mathrm{gr}}\nolimits ^{F}C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)}) = 0\) for i ≠ 0 and

as Poisson vertex algebras, where
 is the slice defined in Sect.
2
.
is the slice defined in Sect.
2
.
Proof
The proof is an arc space analogue of that of Theorem 3.
The moment map \(\mu: \mathfrak{g}^{{\ast}}\longrightarrow \mathfrak{n}^{{\ast}}\) for the N-action on \(\mathfrak{g}\) induces a JN-equivariant morphism
The pullback \((J\mu )^{{\ast}}: \mathbb{C}[J\mathfrak{n}^{{\ast}}] \rightarrow \mathbb{C}[J\mathfrak{g}^{{\ast}}]\) is an embedding of vertex Poisson algebras.
The point χ = Jχ of \(J\mathfrak{n}^{{\ast}}\) corresponds to the arc \(\alpha \in \mathop{\mathrm{Hom}}\nolimits (D,\mathfrak{n}^{{\ast}}) =\mathop{ \mathrm{Hom}}\nolimits (\mathbb{C}[\mathfrak{n}^{{\ast}}], \mathbb{C}[[t]])\) such that α( f) = χ(x) for \(x \in \mathfrak{n} \subset \mathbb{C}[\mathfrak{n}^{{\ast}}]\).
We have
and the adjoint action gives the isomorphism

Now put
and define a bigrading on C by
As before, we can decompose the operator \(\hat{Q}_{(0)}\) as the sum of two suboperators such that each of them preserves one grading but increase the other grading by 1. Namely, we have
This shows that
Thus we can get a spectral sequence \(E_{r}\Longrightarrow H^{\bullet }(C,\hat{Q}_{(0)})\) such that
This is a converging spectral sequence since C is a direct sum of subcomplexes \(F^{p}C^{\kappa }(\mathfrak{g})/F^{p+1}C^{\kappa }(\mathfrak{g})\), and the associated filtration is regular on each subcomplex.
The complex \((C,\hat{d}_{-})\) is the Koszul complex with respect to the sequence
where \(N = \mathrm{dim}\mathfrak{n}\). Hence we have
Next, by (43), the complex \((H^{0}(C,\hat{d}_{-}),\hat{d}_{+})\) is identical to the Chevalley complex for the Lie algebra cohomology \(H^{\bullet }(\mathfrak{n}[t], \mathbb{C}[J\mu ^{-1}(\chi )])\). By (40),

We conclude that

Thus, the spectral sequence E r collapses at E 2 = E ∞ , and we get the desired isomorphisms.
Theorem 18 ([36, 40])
We have \(H^{0}(C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)}) = 0\) for i ≠ 0 and

In particular,
 , so
, so
 ,
,
 .
.
The proof of Theorem 18 will be given in Sect. 5.6.
Note that there is a spectral sequence for \(H^{\bullet }(C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\) such that \(E_{1}^{\bullet,q} = H^{q}(\mathop{\mathrm{gr}}\nolimits C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\). Hence Theorem 18 would immediately follow from Theorem 17 if this spectral sequence converges. However, this is not clear at this point because our algebra is not Noetherian.
Remark 9
The complex \((C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\) is identical to Feigin’s standard complex for the semi-infinite \(\mathfrak{n}[t,t^{-1}]\)-cohomology \(H^{\frac{\infty } {2} +\bullet }(\mathfrak{n}[t,t^{-1}],V ^{\kappa }(\mathfrak{g}) \otimes \mathbb{C}_{\hat{\chi }})\) with coefficient in the \(\mathfrak{g}[t,t^{-1}]\)-module \(V ^{\kappa }(\mathfrak{g}) \otimes \mathbb{C}_{\hat{\chi }}\) [35], where \(\mathbb{C}_{\hat{\chi }}\) is the one-dimensional representation of \(\mathfrak{n}[t,t^{-1}]\) defined by the character \(\hat{\chi }: \mathfrak{n}[t,t^{-1}] \rightarrow \mathbb{C}\), xt n ↦ δ n, −1 χ(x):
5.3 W-Algebra Associated with \(\mathfrak{s}\mathfrak{l}_{n}\)
It is straightforward to generalize the above definition to an arbitrary simple Lie algebra \(\mathfrak{g}\). In particular, by replacing \(V ^{\kappa }(\mathfrak{g}\mathfrak{l}_{n})\) with \(V ^{k}(\mathfrak{s}\mathfrak{l}_{n})\), \(k \in \mathbb{C}\), we define the W-algebra
associated with \((\mathfrak{s}\mathfrak{l}_{n},f)\) at level k.
We have \(V ^{\kappa }(\mathfrak{g}\mathfrak{l}_{n}) =\pi _{\kappa } \otimes V ^{\kappa }(\mathfrak{s}\mathfrak{l}_{n})\), where \(\kappa \vert _{\mathfrak{s}\mathfrak{l}_{n}\times \mathfrak{s}\mathfrak{l}_{n}} = k\kappa _{0}\) and π κ is the rank 1 Heisenberg vertex algebra generated by I(z) = ∑ i = 1 n e ii (z) with λ-bracket [I λ I] = κ(I, I)λ. It follows that \(C^{k}(\mathfrak{g}\mathfrak{l}_{n}) =\pi _{\kappa } \otimes C^{k}(\mathfrak{s}\mathfrak{l}_{n})\). As easily seen, \(\hat{Q}_{(0)}I = 0\). Hence \(H^{\bullet }(C^{\kappa }(\mathfrak{g}\mathfrak{l}_{n})) =\pi _{\kappa } \otimes H^{\bullet }(C^{k}(\mathfrak{s}\mathfrak{l}_{n}))\), so that
In particular if we choose the form κ to be kκ 0, we find that π κ belongs to the center of \(\mathcal{W}^{\kappa }(\mathfrak{g}\mathfrak{l}_{n})\) as π κ belongs to the center of \(C^{\kappa }(\mathfrak{g}\mathfrak{l}_{n})\). Thus, \(\mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\) is isomorphic to the quotient of \(\mathcal{W}^{k\kappa _{0}}(\mathfrak{g}\mathfrak{l}_{n})\) by the ideal generated by I (−1) | 0〉.
5.4 The Grading of \(\mathcal{W}^{\kappa }(\mathfrak{g})\)
The standard conformal grading of \(C^{\kappa }(\mathfrak{g})\) is given by the Hamiltonian H defined by
However H is not well-defined in \(\mathcal{W}^{\kappa }(\mathfrak{g})\) since H does not commute with the action of
Here and below we omit the tensor product sign.
To remedy this, define the linear operator \(H_{\mathcal{W}}\) by
Here ρ ∨ = 1∕2h, where h is defined in (6). Set \(C^{\kappa }(\mathfrak{g})_{\varDelta,new} =\{ v \in C^{\kappa }(\mathfrak{g})\mid H_{\mathcal{W}}c =\varDelta c\}\). Then
Since \([\hat{Q},H_{\mathcal{W}}] = 0\), \(C^{\kappa }(\mathfrak{g})_{\varDelta,new}\) is a subcomplex of \(C^{\kappa }(\mathfrak{g})\). We have
In particular \(\mathcal{W}^{\kappa }(\mathfrak{g}) =\bigoplus _{\varDelta \in \mathbb{Z}}\mathcal{W}^{\kappa }(\mathfrak{g})_{\varDelta }\). Note that the grading (46) is not bounded from below.
If k ≠ − n then the action of \(H_{\mathcal{W}}\) on the vertex subalgebra \(\mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\) of \(\mathcal{W}^{k}(\mathfrak{g})\) is inner: Set

where L sug (z) is the Sugawara field of \(V ^{k}(\mathfrak{s}\mathfrak{l}_{n})\):
and

Here {x a } is a basis of \(\mathfrak{s}\mathfrak{l}_{n}\) and {x a} is the dual basis of {x a } with respect to ( | ). Then \(\hat{Q}_{(0)}L = 0\), and so L defines an element of \(\mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\). It is a conformal vector of \(\mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\), that is to say, \(L_{0} = H_{\mathcal{W}}\) and L −1 = T and
where \(c \in \mathbb{C}\) is the central charge of L, which is in this case given by
5.5 Decomposition of BRST Complex
We extend the map in Sect. 2.6 to the linear map \(\widehat{\theta }_{0}: \mathfrak{g}[t,t^{-1}] \rightarrow C^{\kappa }(\mathfrak{g})\) by setting
Proposition 9
-
1.
The correspondence
$$\displaystyle{ x_{a}(z)\mapsto J_{a}(z):=\widehat{\theta } _{0}(x_{a}(z))\quad (x_{a} \in \mathfrak{b}_{-}) }$$defines a vertex algebra embedding \(V ^{\kappa _{\mathfrak{b}}}(\mathfrak{b})\hookrightarrow C^{\kappa }(\mathfrak{g})\) , where \(\kappa _{\mathfrak{b}}\) is the bilinear form on \(\mathfrak{b}\) defined by \(\kappa _{\mathfrak{b}}(x,y) =\kappa (x,y) + \frac{1} {2}\kappa _{\mathfrak{g}}(x,y)\) . We have
$$\displaystyle{ [J_{a}{}_{\lambda }\psi _{\alpha }^{{\ast}}] =\sum _{\beta \in \varDelta _{+}}c_{a,\beta }^{\alpha }\psi _{ \beta }^{{\ast}}. }$$ -
2.
The correspondence
$$\displaystyle{ x_{\alpha }(z)\mapsto J_{\alpha }(z):=\widehat{\theta } _{0}(x_{\alpha })\quad (x_{\alpha } \in \mathfrak{n}) }$$defines a vertex algebra embedding \(V (\mathfrak{n})\hookrightarrow C^{\kappa }(\mathfrak{g})\) . We have
$$\displaystyle{ [J_{\alpha }{}_{\lambda }\psi _{\beta }] =\sum _{\beta \in \varDelta _{+}}c_{\alpha,\beta }^{\gamma }\psi _{ \gamma }^{{\ast}}. }$$
Let \(C^{\kappa }(\mathfrak{g})_{+}\) denote the subalgebra of \(C^{\kappa }(\mathfrak{g})\) generated by J α (z) and ψ α (z) with α ∈ Δ +, and let \(C^{\kappa }(\mathfrak{g})_{-}\) denote the subalgebra generated by J a (z) and ψ α ∗(z) with a ∈ Δ −⊔ I, α ∈ Δ +.
The proof of the following assertions are parallel to that of Lemmas 11, 12 and Proposition 3.
Lemma 24
The multiplication map gives a linear isomorphism
Lemma 25
The subspaces \(C^{\kappa }(\mathfrak{g})_{-}\) and \(C^{\kappa }(\mathfrak{g})_{+}\) are subcomplexes of \((C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\) . Hence \(C^{\kappa }(\mathfrak{g})\cong C^{\kappa }(\mathfrak{g})_{-}\otimes C^{\kappa }(\mathfrak{g})_{+}\) as complexes.
Theorem 19 ([28, 40])
We have \(H^{i}(C^{\kappa }(\mathfrak{g})_{+},\hat{Q}_{(0)}) =\delta _{i,0}\mathbb{C}\) . Hence \(H^{\bullet }(C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)}) = H^{\bullet }(C^{\kappa }(\mathfrak{g})_{-},\hat{Q}_{(0)})\) . In particular \(\mathcal{W}^{\kappa }(\mathfrak{g}) = H^{0}(C^{\kappa }(\mathfrak{g})_{-},\hat{Q}_{(0)})\).
Since the complex \(C^{\kappa }(\mathfrak{g})_{-}\) has no positive cohomological degree, its zeroth cohomology \(\mathcal{W}^{k}(\mathfrak{g}) = H^{0}(C^{\kappa }(\mathfrak{g})_{-},\hat{Q}_{(0)})\) is a vertex subalgebra of \(C^{\kappa }(\mathfrak{g})_{-}\). Observe also that \(C^{\kappa }(\mathfrak{g})_{-}\) has no negative degree with respect to the Hamiltonian \(H_{\mathcal{W}}\), and each homogeneous space is finite-dimensional:
Here \(C^{\kappa }(\mathfrak{g})_{-,\varDelta,new} = C^{\kappa }(\mathfrak{g})_{-}\cap C^{\kappa }(\mathfrak{g})_{\varDelta,new}\).
5.6 Proof of Theorem 18
As \(\hat{Q}_{(0)}F^{p}C^{\kappa }(\mathfrak{g})_{-}\subset F^{p}C^{\kappa }(\mathfrak{g})_{-}\), one can consider a spectral sequence for \(H^{\bullet }(C^{\kappa }(\mathfrak{g})_{-},\hat{Q}_{(0)})\) such that the E 1-term is \(H^{\bullet }(\mathop{\mathrm{gr}}\nolimits C^{\kappa }(\mathfrak{g})_{-},\hat{Q}_{(0)})\). This spectral sequence clearly converges, since \(C^{\kappa }(\mathfrak{g})_{-}\) is a direct sum of finite-dimensional subcomplexes \(C^{\kappa }(\mathfrak{g})_{-,\varDelta,new}\).
We have \(\mathop{\mathrm{gr}}\nolimits C^{\kappa }(\mathfrak{g})_{-}\cong S(\mathfrak{b}_{-}[t^{-1}]t^{-1}) \otimes \varLambda (\mathfrak{n}[t^{-1}]t^{-1})\cong \mathbb{C}[J\mu ^{-1}(\chi )] \otimes \varLambda (\mathfrak{n}[t^{-1}]t^{-1})\), and the complex \((\mathop{\mathrm{gr}}\nolimits C^{\kappa }(\mathfrak{g})_{-},\hat{Q}_{(0)})\) is identical to the Chevalley complex for the Lie algebra cohomology \(H^{\bullet }(\mathfrak{n}[t], \mathbb{C}[J\mu ^{-1}(\chi )])\). Therefore

Thus the spectral sequence collapses at E 1 = E ∞ , and we get

Here \(\mathop{\mathrm{gr}}\nolimits ^{G}H^{i}(C^{\kappa }(\mathfrak{g})_{-},\hat{Q}_{(0)})\) is the associated graded space with respect to the filtration \(G^{\bullet }H^{i}(C^{\kappa }(\mathfrak{g})_{-},\hat{Q}_{(0)})\) induced by the filtration \(F^{\bullet }C^{\kappa }(\mathfrak{g})_{-}\), that is,
We claim that the filtration \(G^{\bullet }H^{0}(C^{\kappa }(\mathfrak{g})_{-},\hat{Q}_{(0)})\) coincides with the canonical filtration of \(H^{0}(C^{\kappa }(\mathfrak{g})_{-},\hat{Q}_{(0)}) =\mathcal{ W}^{\kappa }(\mathfrak{g})\). Indeed, from the definition of the canonical filtration we have \(F^{p}W^{k}(\mathfrak{g}) \subset G^{p}\mathcal{W}^{\kappa }(\mathfrak{g})\) for all p, and hence, there is a Poisson vertex algebra homomorphism

that restricts to a surjective homomorphism

Since  is generated by
is generated by  as differential algebras it follows that (49) is surjective. On the other hand the cohomology vanishing and the Euler-Poincaré principle imply that the graded character of \(\mathcal{W}^{\kappa }(\mathfrak{g})\) and
as differential algebras it follows that (49) is surjective. On the other hand the cohomology vanishing and the Euler-Poincaré principle imply that the graded character of \(\mathcal{W}^{\kappa }(\mathfrak{g})\) and  are the same. Therefore (49) is an isomorphism, and thus, \(G^{p}\mathcal{W}^{\kappa }(\mathfrak{g}) = F^{p}\mathcal{W}^{\kappa }(\mathfrak{g})\) for all p.
are the same. Therefore (49) is an isomorphism, and thus, \(G^{p}\mathcal{W}^{\kappa }(\mathfrak{g}) = F^{p}\mathcal{W}^{\kappa }(\mathfrak{g})\) for all p.
Finally the embedding \(\mathop{\mathrm{gr}}\nolimits C^{\kappa }(\mathfrak{g})_{-}\rightarrow \mathop{\mathrm{gr}}\nolimits C^{\kappa }(\mathfrak{g})\) induces an isomorphism
by Theorem 17 and (48). This completes the proof. □
5.7 Zhu’s Algebra of W-Algebra
Let \(\mathrm{Zhu}_{new}(C^{\kappa }(\mathfrak{g}))\) be Zhu’s algebra of \(C^{\kappa }(\mathfrak{g})\) with respect to the Hamiltonian H W , \(\mathrm{Zhu}_{old}(C^{\kappa }(\mathfrak{g}))\) Zhu’s algebra of \(C^{\kappa }(\mathfrak{g})\) with respect to the standard Hamiltonian H. We have
see [10, Proposition 5.1] for the details. Then it is legitimate to write \(\mathrm{Zhu}(C^{\kappa }(\mathfrak{g}))\) for \(\mathrm{Zhu}_{new}(C^{\kappa }(\mathfrak{g}))\) or \(\mathrm{Zhu}_{old}(C^{\kappa }(\mathfrak{g}))\).
By the commutation formula, we have
Here the circle ∘ is defined as in the definition of the Zhu algebra (with respect to the grading \(H_{\mathcal{W}}\)). So \((\mathrm{Zhu}_{new}C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\) is a differential, graded algebra, which is identical to \((C(\mathfrak{g}),\mathrm{ad}Q)\).
Theorem 20 ([5])
We have

Proof
By Theorem 18, it follows that \(\mathcal{W}^{\kappa }(\mathfrak{g})\) admits a PBW basis. Hence \(\eta _{\mathcal{W}^{\kappa }(\mathfrak{g})}:\mathop{ \mathrm{gr}}\nolimits \mathrm{Zhu}\mathcal{W}^{\kappa }(\mathfrak{g}) \rightarrow R_{\mathcal{W}_{k}(\mathfrak{g})}\) is an isomorphism by Theorem 16. On the other hand we have a natural algebra homomorphism \(\mathrm{Zhu}\mathcal{W}^{\kappa }(\mathfrak{g})\longrightarrow H^{0}(\mathrm{Zhu}C^{\kappa }(\mathfrak{g}),\hat{Q}_{(0)})\) which makes the following diagram commute.

Note that we have the isomorphisms  and
and  in the diagram. Now the other three isomorphisms will give the desired isomorphism.
in the diagram. Now the other three isomorphisms will give the desired isomorphism.
We conclude that we have the following commutative diagram:

Remark 10
The same proof applies for an arbitrary simple Lie algebra \(\mathfrak{g}\). In particular, we have  . In fact the same proof applies for the W-algebra associated with a simple Lie algebra \(\mathfrak{g}\) and an arbitrary nilpotent element f of \(\mathfrak{g}\) to show its Zhu’s algebra is isomorphic to the finite W-algebra \(U(\mathfrak{g},f)\) [29].
. In fact the same proof applies for the W-algebra associated with a simple Lie algebra \(\mathfrak{g}\) and an arbitrary nilpotent element f of \(\mathfrak{g}\) to show its Zhu’s algebra is isomorphic to the finite W-algebra \(U(\mathfrak{g},f)\) [29].
5.8 Explicit Generators
It is possible to write down the explicit generators of \(\mathcal{W}^{\kappa }(\mathfrak{g}) \subset C^{\kappa }(\mathfrak{g})_{-}\).
Recall that the column-determinant of a matrix A = (a ij ) over an associative algebra is defined by
Introduce an extended Lie algebra \(\mathfrak{b}[t^{-1}]t^{-1} \oplus \mathbb{C}\tau\), where the element τ commutes with 1, and
where x (−n) = xt −n. This induces an associative algebra structure on the tensor product space \(U\big(\mathfrak{b}[t^{-1}]t^{-1}\big)\mathop{\oplus }\mathbb{C}[\tau ]\).
Consider the matrix
with entries in \(U(\mathfrak{b}[t^{-1}]t^{-1}]) \otimes \mathbb{C}[\tau ] \otimes \mathbb{C}[\alpha ]\), where α is a parameter.
For its column-determinantFootnote 1 we can write
for certain coefficients W α (r) which are elements of \(U(\mathfrak{b}[t^{-1}]t^{-1}]) \otimes \mathbb{C}[\alpha ]\). Set
This is an element of \(U(\mathfrak{b}[t^{-1}]t^{-1})\), which we identify with \(V ^{\kappa _{\mathfrak{b}}}(\mathfrak{b}) \subset C^{\kappa }(\mathfrak{g})_{ -}\).
Theorem 21 ([14])
\(\mathcal{W}^{k}(\mathfrak{g})\) is strongly generated by W (1), …, W (n).
5.9 Miura Map
The Cartan subalgebra \(\mathfrak{h}\) of \(\mathfrak{g}\) acts on \(C^{\kappa }(\mathfrak{g})_{+}\) by x i ↦ (J i )(0), i ∈ I, see Proposition 9. Let \(C^{\kappa }(\mathfrak{g})_{+}^{\lambda }\) be the weight space of weight \(\lambda \in \mathfrak{h}^{{\ast}}\) with respect to this action. Then
The vertex algebra \(V ^{\kappa _{\mathfrak{h}}}(\mathfrak{h})\) is the Heisenberg vertex algebra associated with \(\mathfrak{h}\) and the bilinear form \(\kappa _{\mathfrak{h}}:=\kappa _{\mathfrak{b}}\vert _{\mathfrak{h}\times \mathfrak{h}}\).
The projection \(C^{\kappa }(\mathfrak{g})_{+} \rightarrow C^{\kappa }(\mathfrak{g})_{+}^{0} = V ^{\kappa _{\mathfrak{h}}}(\mathfrak{h})\) with respect to this decomposition is a vertex algebra homomorphism. Therefore it restriction
is also a vertex algebra homomorphism that is called the Miura map.
Theorem 22
The Miura map is injective for all \(k \in \mathbb{C}\).
Proof
The induced Poisson vertex algebra homomorphism

is just a restriction map and coincides with \(J\bar{\varUpsilon }\), where \(\bar{\varUpsilon }\) is defined in (13). Clearly, it is sufficient to show that \(J\bar{\varUpsilon }\) is injective.
Recall that the action map gives an isomorphism
where U is some open subset of \(f + \mathfrak{b}\), see the proof of Proposition 4. Therefore, by Lemma 15, the action map \(JN \times J(\,f + \mathfrak{h}) \rightarrow J(\,f + \mathfrak{b})\) is dominant. Thus, the induced map \(\mathbb{C}[J(\,f + \mathfrak{b})] \rightarrow \mathbb{C}[JN \times J(\,f + \mathfrak{h})]\) is injective, and so is \(J\bar{\varUpsilon }: C[J(\,f + \mathfrak{b})]^{JN} \rightarrow \mathbb{C}[JN \times J(\,f + \mathfrak{h})]^{JN} = \mathbb{C}[J(\,f + \mathfrak{h})]\).
Remark 11
It is straightforward to generalize Theorem 22 for the W-algebra \(\mathcal{W}^{k}(\mathfrak{g})\) associated with a general simple Lie algebra \(\mathfrak{g}\).
Theorem 23
Let \(x_{i} = E_{ii} \in \mathfrak{h} \subset \mathfrak{g} = \mathfrak{g}\mathfrak{l}_{n}\) , and J i (z) the corresponding field of \(V ^{\kappa _{k}}(\mathfrak{h})\) . The image Υ(W (i)(z)) of W (i)(z) by the Miura map is described by
where α = k + n − 1, W (0)(z) = 1, \([\partial _{z},J_{i}(z)] = \frac{d} {dz}J_{i}(z)\).
Proof
It is straightforward from Theorem 21.
Note that if we choose κ to be kκ 0 and set ∑ i = 1 N J i (z) = 0, we obtain the image of the generators of \(\mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\) by the Miura map \(\hat{\varUpsilon }\). For k + n ≠ 0, this expression can be written in more symmetric manner: Set \(b_{i}(z) = \frac{1} {\sqrt{k+n}}J_{i}(z)\), so that ∑ i = 1 n b i (z) = 0, and
Then we obtain the following original description of the \(\mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\) due to Fateev and Lukyanov [34].
Corollary 4
Suppose that k + n ≠ 0. Then the image of \(\mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\) by the Miura map is the vertex subalgebra generated by fields \(\tilde{W}_{2}(z)\ldots,\tilde{W}_{n}(z)\) defined by
where α 0 = α + + α − , \(\alpha _{+} = \sqrt{k + n}\) , \(\alpha _{-} = -1/\sqrt{k + n}\) , \(\tilde{W}_{0}(z) = 1\) , \(\tilde{W}_{1}(z) = 0\).
Corollary 5
Suppose that k + n ≠ 0. We have
where L k is defined by (k + n)(L k + n) = 1.
Example 4
Let \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{2}\), k ≠ − 2. Set \(b(z) = \sqrt{2}b_{1}(z) = -\sqrt{2}b_{2}(z)\), so that [b λ b] = λ. Then the right-hand-side of the formula in Corollary 5 becomes
where
It is well-known and is straightforward to check that the field generates the Virasoro algebra of central charge 1 − 6(k + 1)2∕(k + 2). Thus \(\mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{2})\), k ≠ − 2, is isomorphic to the universal Virasoro vertex algebra of central charge 1 − 6(k + 1)2∕(k + 2).
In the case that \(\kappa =\kappa _{c}:= -\frac{1} {2}\kappa _{\mathfrak{g}}\), then it follows from Theorem 22 that \(\mathcal{W}^{\kappa _{c}}(\mathfrak{g}\mathfrak{l}_{n})\) is commutative since \(V ^{(\kappa _{c})_{\mathfrak{h}}}(\mathfrak{h})\) is commutative. In fact the following fact is known: Let \(Z(V ^{\kappa }(\mathfrak{g})) =\{ z \in V ^{\kappa }(\mathfrak{g})\mid [z_{(n)},a_{(n)}] = 0\}\), the center of \(V ^{\kappa }(\mathfrak{g})\).
Theorem 24 ([37])
We have the isomorphism
This is a chiralization of Kostant’s Theorem 5 in the sense that we recover Theorem 5 from Theorem 24 by considering the induced map between Zhu’s algebras of both sides. The statement of Theorem 24 holds for any simple Lie algebra \(\mathfrak{g}\) [37].
Remark 12
For a general simple Lie algebra \(\mathfrak{g}\), the image of the Miura map for a generic k is described in terms of screening operators, see [40, 15.4]. Theorem 23 for \(\mathfrak{g} = \mathfrak{g}\mathfrak{l}_{n}\) also follows from this description (the proof reduces to the case \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{2}\)). An important application of this realization is the Feigin-Frenkel duality which states
where \(^{L}\mathfrak{g}\) is the Langlands dual Lie algebra of \(\mathfrak{g}\), r ∨(k + h ∨)(L k +L h ∨) = 1. Here r ∨ is the maximal number of the edges of the Dynking diagram of \(\mathfrak{g}\) andL h ∨ is the dual Coxeter number of \(^{L}\mathfrak{g}\). In [37, 40] this isomorphism was stated only for a generic k, but it is not too difficult to see the isomorphism remains valid for an arbitrary k using the injectivity of the Miura map.
The Miura map is defined [60] for the W-algebra \(\mathcal{W}^{k}(\mathfrak{g},f)\) associated with an arbitrary f, which is injective as well since the proof of Theorem 22 applies. Recently Naoki Genra [46] has obtained the description of the image by the Miura map in terms of screening operators for the W-algebra \(\mathcal{W}^{k}(\mathfrak{g},f)\) associated with an arbitrary nilpotent element f.
5.10 Classical W-Algebras
Since the Poisson structure of  is trivial, we can give \(\mathop{\mathrm{gr}}\nolimits \mathcal{W}^{\kappa }(\mathfrak{g})\) a Poisson vertex algebra structure by the formula (32). The Poisson structure of \(R_{V ^{k+n}(\mathfrak{h})} = \mathbb{C}[\mathfrak{h}]\) is also trivial, hence \(\mathop{\mathrm{gr}}\nolimits V ^{\kappa _{\mathfrak{h}}}(\mathfrak{h}) = \mathbb{C}[J\mathfrak{h}^{{\ast}}]\) is equipped with the Poisson vertex algebra structure by the formula (32) as well. Then the map \(\mathop{\mathrm{gr}}\nolimits \hat{\varUpsilon }:\mathop{ \mathrm{gr}}\nolimits \mathcal{W}^{\kappa }(\mathfrak{g})\hookrightarrow \mathop{\mathrm{gr}}\nolimits V ^{\kappa _{\mathfrak{h}}}(\mathfrak{h})\) is a homomorphism of Poisson vertex algebras with respect to these structures. Set κ = kκ
0, \(k \in \mathbb{C}\), and consider its restriction \(\mathop{\mathrm{gr}}\nolimits \hat{\varUpsilon }:\mathop{ \mathrm{gr}}\nolimits \mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\hookrightarrow \mathop{\mathrm{gr}}\nolimits V ^{\kappa _{\mathfrak{h}}}(\mathfrak{h}')\), where \(\mathfrak{h}'\) is the Cartan subalgebra of \(\mathfrak{s}\mathfrak{l}_{n}\).
is trivial, we can give \(\mathop{\mathrm{gr}}\nolimits \mathcal{W}^{\kappa }(\mathfrak{g})\) a Poisson vertex algebra structure by the formula (32). The Poisson structure of \(R_{V ^{k+n}(\mathfrak{h})} = \mathbb{C}[\mathfrak{h}]\) is also trivial, hence \(\mathop{\mathrm{gr}}\nolimits V ^{\kappa _{\mathfrak{h}}}(\mathfrak{h}) = \mathbb{C}[J\mathfrak{h}^{{\ast}}]\) is equipped with the Poisson vertex algebra structure by the formula (32) as well. Then the map \(\mathop{\mathrm{gr}}\nolimits \hat{\varUpsilon }:\mathop{ \mathrm{gr}}\nolimits \mathcal{W}^{\kappa }(\mathfrak{g})\hookrightarrow \mathop{\mathrm{gr}}\nolimits V ^{\kappa _{\mathfrak{h}}}(\mathfrak{h})\) is a homomorphism of Poisson vertex algebras with respect to these structures. Set κ = kκ
0, \(k \in \mathbb{C}\), and consider its restriction \(\mathop{\mathrm{gr}}\nolimits \hat{\varUpsilon }:\mathop{ \mathrm{gr}}\nolimits \mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\hookrightarrow \mathop{\mathrm{gr}}\nolimits V ^{\kappa _{\mathfrak{h}}}(\mathfrak{h}')\), where \(\mathfrak{h}'\) is the Cartan subalgebra of \(\mathfrak{s}\mathfrak{l}_{n}\).
In \(\mathop{\mathrm{gr}}\nolimits V ^{\kappa _{\mathfrak{h}}}(\mathfrak{h}')\) we have
and this uniquely determines the λ-bracket of \(\mathop{\mathrm{gr}}\nolimits V ^{\kappa _{\mathfrak{h}}}(\mathfrak{h}')\). Hence it is independent of k provided that k ≠ − n. Since the image of \(\mathop{\mathrm{gr}}\nolimits \mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\) is strongly generated by elements of \(\mathbb{C}[(\mathfrak{h}')^{{\ast}}]^{W}\), it follows that the Poisson vertex algebra structure of \(\mathop{\mathrm{gr}}\nolimits \mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\), k ≠ − n, is independent of k. We denote this Poisson vertex algebra by \(\mathcal{W}^{cl}(\mathfrak{s}\mathfrak{l}_{n})\).
The Poisson vertex algebra \(\mathcal{W}^{cl}(\mathfrak{s}\mathfrak{l}_{n})\) is called the classical W-algebra associated with \(\mathfrak{s}\mathfrak{l}_{n}\), which appeared in the works of Adler [3], Gelfand-Dickey [45] and Drinfeld-Sokolov [32]. Thus, the W-algebra \(\mathcal{W}^{k}(\mathfrak{s}\mathfrak{l}_{n})\), k ≠ − n, is a deformation of \(\mathcal{W}^{cl}(\mathfrak{s}\mathfrak{l}_{n})\).
On the other hand the \(\mathcal{W}\)-algebra \(\mathcal{W}^{-n}(\mathfrak{s}\mathfrak{l}_{n})\) at the critical level can be identified with the space of the \(\mathfrak{s}\mathfrak{l}_{n}\) -opers [21] on the disk D. We refer to [39, 40] for more on this subject.
6 Representations of W-Algebras
From now on we set \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{n}\) and study the representations of \(\mathcal{W}^{k}(\mathfrak{g})\) [see (45)].
6.1 Poisson Modules
Let R be a Poisson algebra. Recall that a Poisson R-module is a R-module M in the usual associative sense equipped with a bilinear map
which makes M a Lie algebra module over R satisfying
for r 1, r 2 ∈ R, m ∈ M. Let \(R\mathop{\mathrm{-PMod}}\nolimits\) be the category of Poisson modules over R.
Lemma 26
A Poisson module over \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\) is the same as a \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\) -module M in the usual associative sense equipped with a Lie algebra module structure \(\mathfrak{g} \rightarrow \mathop{\mathrm{End}}\nolimits M\) , x ↦ ad(x), such that
for \(x \in \mathfrak{g}\) , \(f \in \mathbb{C}[\mathfrak{g}^{{\ast}}]\) , m ∈ M.
6.2 Poisson Vertex Modules
Definition 5
A Poisson vertex module over a Poisson vertex algebra V is a V -module M as a vertex algebra equipped with a linear map
satisfying
for all a, b ∈ V, \(m,n\geqslant 0\), v ∈ M.
A Poisson vertex algebra R is naturally a Poisson vertex module over itself.
Example 5
Let M be a Poisson vertex module over \(\mathbb{C}[J\mathfrak{g}^{{\ast}}]\). Then by (55), the assignment
defines a \(J\mathfrak{g} = \mathfrak{g}[[t]]\)-module structure on M. In fact, a Poisson vertex module over \(\mathbb{C}[J\mathfrak{g}^{{\ast}}]\) is the same as a \(\mathbb{C}[J\mathfrak{g}^{{\ast}}]\)-module M in the usual associative sense equipped with an action of the Lie algebra \(J\mathfrak{g}\) such that (xt n)m = 0 for n ≫ 0, \(x \in \mathfrak{g}\), m ∈ M, and
for \(x \in \mathfrak{g}\), \(n\geqslant 0\), \(a \in \mathbb{C}[J\mathfrak{g}^{{\ast}}]\), m ∈ M.
Below we often write a (n) for a (n) M.
The proofs of the following assertions are straightforward.
Lemma 27
Let R be a Poisson algebra, E a Poisson module over R. There is a unique Poisson vertex JR-module structure on JR ⊗ R E such that
for \(n\geqslant 0\) , a ∈ R ⊂ JR, b ∈ JR. m ∈ E (Recall that \(JR = \mathbb{C}[J\mathop{\mathrm{Spec}}\nolimits R]\) .)
Lemma 28
Let R be a Poisson algebra, M a Poisson vertex module over JR. Suppose that there exists a R-submodule E of M (in the usual commutative sense) such that a (n) E = 0 for n > 0, a ∈ R, and M is generated by E (in the usual commutative sense). Then there exists a surjective homomorphism
of Poisson vertex modules.
6.3 Canonical Filtration of Modules Over Vertex Algebras
Let V be a vertex algebra graded by a Hamiltonian H. A compatible filtration of a V -module M is a decreasing filtration
such that
For a compatible filtration Γ • M the associated graded space
is naturally a graded vertex Poison module over the graded vertex Poisson algebra \(\mathop{\mathrm{gr}}\nolimits ^{F}V\), and hence, it is a graded vertex Poison module over \(JR_{V } = \mathbb{C}[\tilde{X}_{V }]\) by Theorem 10.
The vertex Poisson JR V -module structure of \(\mathop{\mathrm{gr}}\nolimits ^{\varGamma }M\) restricts to the Poisson R V -module structure of M∕Γ 1 M = Γ 0 M∕Γ 1 M, and a (n)(M∕Γ 1 M) = 0 for a ∈ R V ⊂ JR V , n > 0. It follows that there is a homomorphism
of vertex Poisson modules by Lemma 28.
Suppose that V is positively graded and so is a V -module M. We denote by F • M the Li filtration [68] of M, which is defined by
It is a compatible filtration of M, and in fact is the finest compatible filtration of M, that is, F p M ⊂ Γ p M for all p for any compatible filtration Γ • M of M. The subspace F 1 M is spanned by the vectors a (−2) m with a ∈ V, m ∈ M, which is often denoted by C 2(M) in the literature. Set
which is a Poisson module over \(R_{V } =\bar{ V }\). By [68, Proposition 4.12], the vertex Poisson module homomorphism
is surjective.
Let {a i; i ∈ I} be elements of V such that their images generate R V in usual commutative sense, and let U be a subspace of M such that M = U + F 1 M. The surjectivity of the above map is equivalent to that
Lemma 29
Let V be a vertex algebra, M a V -module. The Poisson vertex algebra module structure of \(\mathop{\mathrm{gr}}\nolimits ^{F}M\) restricts to the Poisson module structure of \(\bar{M}:= M/F^{1}M\) over R V , that is, \(\bar{M}\) is a Poisson R V -module by
A V -module M is called finitely strongly generated if \(\bar{M}\) is finitely generated as a R V -module in the usual associative sense.
6.4 Associated Varieties of Modules Over Affine Vertex Algebras
A \(\widehat{\mathfrak{g}}\)-module M of level k is called smooth if x(z) is a field on M for \(x \in \mathfrak{g}\), that is, xt n m = 0 for n ≫ 0, \(x \in \mathfrak{g}\), m ∈ M. Any \(V ^{k}(\mathfrak{g})\)-module M is naturally a smooth \(\widehat{\mathfrak{g}}\)-module of level k. Conversely, any smooth \(\widehat{\mathfrak{g}}\)-module of level k can be regarded as a \(V ^{k}(\mathfrak{g})\)-module. It follows that a \(V ^{k}(\mathfrak{g})\)-module is the same as a smooth \(\widehat{\mathfrak{g}}\)-module of level k.
For a \(V = V ^{k}(\mathfrak{g})\)-module M, or equivalently, a smooth \(\widehat{\mathfrak{g}}\)-module of level k, we have
and the Poisson \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\)-module structure is given by
For a \(\mathfrak{g}\)-module E let
where E is considered as a \(\mathfrak{g}[t]\mathop{\oplus }\mathbb{C}K\)-module on which \(\mathfrak{g}[t]\) acts via the projection \(\mathfrak{g}[t] \rightarrow \mathfrak{g}\) and K acts as multiplication by k. Then
where the Poisson \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\)-module structure is given by
for \(f,g \in \mathbb{C}[\mathfrak{g}^{{\ast}}]\), v ∈ V.
Let  be the category
be the category  of \(\widehat{\mathfrak{g}}\) of level k [53], KL
k
the full subcategory of
of \(\widehat{\mathfrak{g}}\) of level k [53], KL
k
the full subcategory of  consisting of modules M which are integrable over \(\mathfrak{g}\). Note that V
E
k is a object of KL
k
for a finite-dimensional representation E of \(\mathfrak{g}\). Thus, \(V ^{k}(\mathfrak{g}) = V _{\mathbb{C}}^{k}\) and its simple quotient \(V _{k}(\mathfrak{g})\) are also objects of KL
k
.
consisting of modules M which are integrable over \(\mathfrak{g}\). Note that V
E
k is a object of KL
k
for a finite-dimensional representation E of \(\mathfrak{g}\). Thus, \(V ^{k}(\mathfrak{g}) = V _{\mathbb{C}}^{k}\) and its simple quotient \(V _{k}(\mathfrak{g})\) are also objects of KL
k
.
Both  and KL
k
can be regarded as full subcategories of the category of \(V ^{k}(\mathfrak{g})\)-modules.
and KL
k
can be regarded as full subcategories of the category of \(V ^{k}(\mathfrak{g})\)-modules.
Lemma 30
For M ∈ KL k the following conditions are equivalent.
-
1.
M is finitely strongly generated as a \(V ^{k}(\mathfrak{g})\) -module,
-
2.
M is finitely generated as a \(\mathfrak{g}[t^{-1}]t^{-1}\) -module,
-
3.
M is finitely generated as a \(\widehat{\mathfrak{g}}\) -module.
For a finitely strongly generated \(V ^{k}(\mathfrak{g})\)-module M define its associated variety X M by
equipped with a reduced scheme structure.
Example 6
\(X_{V _{E}^{k}} = \mathfrak{g}^{{\ast}}\) for a finite-dimensional representation E of \(\mathfrak{g}\).
6.5 Ginzburg’s Correspondence
Let  be the full subcategory of the category of Poisson \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\)-modules on which the Lie algebra \(\mathfrak{g}\)-action (see Lemma 26) is integrable.
be the full subcategory of the category of Poisson \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\)-modules on which the Lie algebra \(\mathfrak{g}\)-action (see Lemma 26) is integrable.
Lemma 31
For M ∈ KL
k
, the Poisson
\(\mathbb{C}[\mathfrak{g}^{{\ast}}]\)
-module
\(\bar{M}\)
belongs to
 .
.
By Lemma 31 we have a right exact functor

For  , \(M \otimes \overline{Cl}\) is naturally a Poisson module over \(\bar{C}(\mathfrak{g}) = \mathbb{C}[\mathfrak{g}^{{\ast}}] \otimes \overline{Cl}\). (The notation of Poisson modules natural extends to the Poisson supralgebras.) Thus, \((M \otimes \overline{Cl},\mathrm{ad}\bar{Q})\) is a differential graded Poisson module over the differential graded Poisson module \((\bar{C}(\mathfrak{g}),\mathrm{ad}\bar{Q})\). In particular it cohomology \(H^{\bullet }(\bar{M} \otimes \overline{Cl},\mathrm{ad}\bar{Q})\) is a Poisson module over
, \(M \otimes \overline{Cl}\) is naturally a Poisson module over \(\bar{C}(\mathfrak{g}) = \mathbb{C}[\mathfrak{g}^{{\ast}}] \otimes \overline{Cl}\). (The notation of Poisson modules natural extends to the Poisson supralgebras.) Thus, \((M \otimes \overline{Cl},\mathrm{ad}\bar{Q})\) is a differential graded Poisson module over the differential graded Poisson module \((\bar{C}(\mathfrak{g}),\mathrm{ad}\bar{Q})\). In particular it cohomology \(H^{\bullet }(\bar{M} \otimes \overline{Cl},\mathrm{ad}\bar{Q})\) is a Poisson module over  . So we get a functor
. So we get a functor

The following assertion is a restatement of a result of Ginzburg [47] (see [10, Theorem 2.3]).
Theorem 25
Let
 . Then H
i(M) = 0 for i ≠ 0, and we have an isomorphism
. Then H
i(M) = 0 for i ≠ 0, and we have an isomorphism
In particular if M is finitely generated H
0(M) is finitely generated over
 and
and

Corollary 6
The functor
 , M ↦ H
0(M), is exact.
, M ↦ H
0(M), is exact.
Denote by  the set of nilpotent elements of \(\mathfrak{g}\), which equals to the zero locus of the augmentation ideal \(\mathbb{C}[\mathfrak{g}^{{\ast}}]_{+}^{G}\) of \(\mathbb{C}[\mathfrak{g}^{{\ast}}]^{G}\) under the identification \(\mathfrak{g} = \mathfrak{g}^{{\ast}}\) via ( | ). Since the element f (defined in (3)). is regular (or principal), the orbit
the set of nilpotent elements of \(\mathfrak{g}\), which equals to the zero locus of the augmentation ideal \(\mathbb{C}[\mathfrak{g}^{{\ast}}]_{+}^{G}\) of \(\mathbb{C}[\mathfrak{g}^{{\ast}}]^{G}\) under the identification \(\mathfrak{g} = \mathfrak{g}^{{\ast}}\) via ( | ). Since the element f (defined in (3)). is regular (or principal), the orbit
is dense in  :
:

The transversality of  implies that
implies that

Theorem 26 ([47])
Let M be a finitely generated object in
 .
.
-
1.
H 0(M) ≠ 0 if and only if
 .
. -
2.
H 0(M) is nonzero and finite-dimensional if
 .
.
Proof
(1) Note that  is invariant under the \(\mathbb{C}^{{\ast}}\)-action (7) on
is invariant under the \(\mathbb{C}^{{\ast}}\)-action (7) on  , which contracts the point { f}. Hence
, which contracts the point { f}. Hence  is nonempty if and only if
is nonempty if and only if  . The assertion follows since
. The assertion follows since  is G-invariant and closed. (2) Obvious since the assumption implies that
is G-invariant and closed. (2) Obvious since the assumption implies that  .
.
6.6 Losev’s Correspondence
Let  be the category of Harish-Chandra bimodules, that is, the full subcategory of the category of \(U(\mathfrak{g})\)-bimodules on which the adjoint action of \(\mathfrak{g}\) is integrable.
be the category of Harish-Chandra bimodules, that is, the full subcategory of the category of \(U(\mathfrak{g})\)-bimodules on which the adjoint action of \(\mathfrak{g}\) is integrable.
Lemma 32
Every finitely generated object M of
 admits a good filtration, that is, an increasing filtration 0 = F
0
M ⊂ F
1
M ⊂ … such that
\(M =\bigcup F_{p}M\)
,
admits a good filtration, that is, an increasing filtration 0 = F
0
M ⊂ F
1
M ⊂ … such that
\(M =\bigcup F_{p}M\)
,
and \(\mathop{\mathrm{gr}}\nolimits ^{F}M =\bigoplus _{p}F_{p}M/F_{p-1}M\) is finitely generated over \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\).
If  and F
•
M is a good filtration, then \(\mathop{\mathrm{gr}}\nolimits ^{F}M\) is naturally a Poisson module over \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\). Therefore, it is an object of
and F
•
M is a good filtration, then \(\mathop{\mathrm{gr}}\nolimits ^{F}M\) is naturally a Poisson module over \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\). Therefore, it is an object of  .
.
Let M be a finitely generated object in  . It is known since Bernstein that
. It is known since Bernstein that
in independent of the choice of a good filtration F • M of M.
For  , M ⊗ Cl is naturally a bimodule over \(C(\mathfrak{g}) = U(\mathfrak{g}) \otimes Cl\). Thus, (M ⊗ Cl, adQ) is a differential graded bimodule over \(C(\mathfrak{g})\), and its cohomology
, M ⊗ Cl is naturally a bimodule over \(C(\mathfrak{g}) = U(\mathfrak{g}) \otimes Cl\). Thus, (M ⊗ Cl, adQ) is a differential graded bimodule over \(C(\mathfrak{g})\), and its cohomology
is naturally a module over \(H^{0}(C(\mathfrak{g}),\mathrm{ad}Q)\) that is identified with \(Z(\mathfrak{g})\) by Theorem 5. Thus, we have a functor

Let  be finitely generated, F
•
M a good filtration. Then F
p
(M ⊗ Cl): = ∑
i+j = p
F
i
M ⊗ Cl
j
defines a good filtration of M ⊗ Cl, and the associated graded space \(\mathop{\mathrm{gr}}\nolimits _{F}(M \otimes Cl) =\sum _{i}F_{p}(M \otimes Cl)/F_{p-1}(M \otimes Cl) = (\mathop{\mathrm{gr}}\nolimits _{F}M) \otimes \overline{Cl}\) is a Poisson module over \(\mathop{\mathrm{gr}}\nolimits C(\mathfrak{g}) =\bar{ C}(\mathfrak{g})\).
be finitely generated, F
•
M a good filtration. Then F
p
(M ⊗ Cl): = ∑
i+j = p
F
i
M ⊗ Cl
j
defines a good filtration of M ⊗ Cl, and the associated graded space \(\mathop{\mathrm{gr}}\nolimits _{F}(M \otimes Cl) =\sum _{i}F_{p}(M \otimes Cl)/F_{p-1}(M \otimes Cl) = (\mathop{\mathrm{gr}}\nolimits _{F}M) \otimes \overline{Cl}\) is a Poisson module over \(\mathop{\mathrm{gr}}\nolimits C(\mathfrak{g}) =\bar{ C}(\mathfrak{g})\).
The filtration F
•(M ⊗ Cl) induces a filtration F
•
H
•(M) on H
•(M), and \(\mathop{\mathrm{gr}}\nolimits _{F}H^{\bullet }(M) =\bigoplus _{p}F_{p}H^{\bullet }(M)/F_{p-1}H^{0}(M)\) is a module over  .
.
For a finitely generated  -module M, set
-module M, set  , \(\mathop{\mathrm{gr}}\nolimits M\) is the associated graded M with respect to a good filtration of M.
, \(\mathop{\mathrm{gr}}\nolimits M\) is the associated graded M with respect to a good filtration of M.
The following assertion follows from Theorems 25 and 26.
Theorem 27 ([47, 69])
-
1.
We have H i(M) = 0 for all i ≠ 0,
 . Therefore the functor (59) is exact.
. Therefore the functor (59) is exact.
-
2.
Let M be a finitely generated object of
 , F
•
M a good filtration. Then
\(\mathop{\mathrm{gr}}\nolimits _{F}H^{0}(M)\cong H^{0}(\mathop{\mathrm{gr}}\nolimits _{F}M)\)
. In particular H
0(M) is finitely generated, F
•
H
0(M) is a good filtration of H
0(M).
, F
•
M a good filtration. Then
\(\mathop{\mathrm{gr}}\nolimits _{F}H^{0}(M)\cong H^{0}(\mathop{\mathrm{gr}}\nolimits _{F}M)\)
. In particular H
0(M) is finitely generated, F
•
H
0(M) is a good filtration of H
0(M).
-
3.
For a finitely generated object M of
 ,
,
 .
.
6.7 Frenkel-Zhu’s Bimodules
Recall that for a graded vertex algebra V, Zhu’s algebra Zhu(V ) = V∕V ∘ V is defined. There is a similar construction for modules due to Frenkel and Zhu [43]. For a V -module M set
where V ∘ M is the subspace of M spanned by the vectors
for \(a \in V _{\varDelta _{a}}\), \(\varDelta _{a} \in \mathbb{Z}\), and m ∈ M.
Proposition 10 ([43])
Zhu(M) is a bimodule over Zhu(V ) by the multiplications
for \(a \in V _{\varDelta _{a}}\) , \(\varDelta _{a} \in \mathbb{Z}\) , and m ∈ M.
Thus, we have a right exact functor
Lemma 33
Let \(M =\bigoplus _{d\in h+\mathbb{Z}_{+}}M_{d}\) be a positive energy representation of a \(\mathbb{Z}_{+}\) -graded vertex algebra V. Define an increasing filtration {Zhu p (M)} on Zhu(V ) by
-
1.
We have
$$\displaystyle\begin{array}{rcl} & & \mathrm{Zhu}_{p}(V ) \cdot \mathrm{ Zhu}_{q}(M) \cdot \mathrm{ Zhu}_{r}(V ) \subset \mathrm{ Zhu}_{p+q+r}(M), {}\\ & & [\mathrm{Zhu}_{p}(V ),\mathrm{Zhu}_{q}(M)] \subset \mathrm{ Zhu}_{p+q-1}(M). {}\\ \end{array}$$Therefore \(\mathop{\mathrm{gr}}\nolimits \mathrm{Zhu}(M) =\bigoplus _{p}\mathrm{Zhu}_{p}(M)/\mathrm{Zhu}_{p-1}(M)\) is a Poisson \(\mathop{\mathrm{gr}}\nolimits \mathrm{Zhu}(V )\) -module, and hence is a Poisson R V -module through the homomorphism \(\eta _{V }: R_{V } \twoheadrightarrow \mathop{\mathrm{gr}}\nolimits \mathrm{Zhu}(V )\).
-
2.
There is a natural surjective homomorphism
$$\displaystyle{ \eta _{M}:\bar{ M}(= M/F^{1}M) \rightarrow \mathop{\mathrm{gr}}\nolimits \mathrm{Zhu}(M) }$$of Poisson R V -modules. This is an isomorphism if V admits a PBW basis and \(\mathop{\mathrm{gr}}\nolimits M\) is free over \(\mathop{\mathrm{gr}}\nolimits V\).
Example 7
Let M = V E k. Since \(\mathop{\mathrm{gr}}\nolimits V _{E}^{k}\) is free over \(\mathbb{C}[J\mathfrak{g}^{{\ast}}]\), we have the isomorphism
On the other hand, there is a \(U(\mathfrak{g})\)-bimodule homomorphism
which respects the filtration. Here the \(U(\mathfrak{g})\)-bimodule structure of \(U(\mathfrak{g}) \otimes E\) is given by
and the filtration of \(U(\mathfrak{g}) \otimes E\) is given by \(\{U_{i}(\mathfrak{g}) \otimes E\}\). Since the induced homomorphism between associated graded spaces (60) coincides with \(\eta _{V _{E}^{k}}\), (60) is an isomorphism.
Lemma 34
For M ∈ KL
k
we have
 . If M is finitely generated, then so is Zhu(M).
. If M is finitely generated, then so is Zhu(M).
6.8 Zhu’s Two Functors Commute with BRST Reduction
For a smooth \(\widehat{\mathfrak{g}}\)-module M over level k,  is naturally a module over
is naturally a module over  . Thus, (C(M), Q
(0)) is a cochain complex, and its cohomology H
•(M): = H
•(C(M), Q
(0)) is a module over \(\mathcal{W}^{k}(\mathfrak{g}) = H^{\bullet }(C^{k}(\mathfrak{g}),Q_{(0)})\). Thus we have a functor
. Thus, (C(M), Q
(0)) is a cochain complex, and its cohomology H
•(M): = H
•(C(M), Q
(0)) is a module over \(\mathcal{W}^{k}(\mathfrak{g}) = H^{\bullet }(C^{k}(\mathfrak{g}),Q_{(0)})\). Thus we have a functor
Here \(V \mathop{\mathrm{-Mod}}\nolimits\) denotes the category of modules over a vertex algebra V.
Theorem 28
-
1.
[ 9 , 41 ] We have H i(M) = 0 for i ≠ 0, M ∈ KL k . In particular the functor
$$\displaystyle{ \mathbf{KL}_{k} \rightarrow \mathcal{ W}^{k}(\mathfrak{g})\mathop{\mathrm{-Mod}}\nolimits,\quad M\mapsto H^{0}(M), }$$is exact.
-
2.
[ 9 ] For a finitely generated object M of KL ,
$$\displaystyle{ \overline{H^{0}(M)}\cong H^{0}(\bar{M}) }$$as Poisson modules over
 . In particular H
0(M) is finitely strongly generated and
. In particular H
0(M) is finitely strongly generated and

-
3.
[ 10 ] For a finitely generated object M of KL ,
$$\displaystyle{ \mathop{\mathrm{Zhu}}\nolimits (H^{0}(M))\cong H^{0}(\mathop{\mathrm{Zhu}}\nolimits (M)) }$$as bimodules over
 .
.
Let \(\mathcal{W}_{k}(\mathfrak{g})\) denote the unique simple graded quotient of \(\mathcal{W}^{k}(\mathfrak{g})\). Then \(X_{\mathcal{W}_{k}(\mathfrak{g})}\) is a \(\mathbb{C}^{{\ast}}\)-invariant subvariety of  . Therefore \(X_{\mathcal{W}^{k}(\mathfrak{g})}\) is lisse if and only if \(X_{\mathcal{W}_{k}(\mathfrak{g})} =\{\, f\}\) since the \(\mathbb{C}^{{\ast}}\)-action on
. Therefore \(X_{\mathcal{W}^{k}(\mathfrak{g})}\) is lisse if and only if \(X_{\mathcal{W}_{k}(\mathfrak{g})} =\{\, f\}\) since the \(\mathbb{C}^{{\ast}}\)-action on  contracts to the point f.
contracts to the point f.
Corollary 7
-
1.
\(H^{0}(V _{k}(\mathfrak{g}))\) is a quotient of \(\mathcal{W}^{k}(\mathfrak{g}) = H^{0}(V ^{k}(\mathfrak{g}))\) . In particular \(\mathcal{W}_{k}(\mathfrak{g})\) is a quotient of \(H^{0}(V _{k}(\mathfrak{g}))\) if \(H^{0}(V _{k}(\mathfrak{g}))\) is nonzero.
-
2.
\(H^{0}(V _{k}(\mathfrak{g}))\) is nonzero if and only if
 .
. -
3.
The simple W-algebra \(\mathcal{W}_{k}(\mathfrak{g})\) is lisse if
 .
.
Proof
-
1.
follows from the exactness statement of Theorem 28.
-
2.
\(H^{0}(V _{k}(\mathfrak{g}))\) is nonzero if and only of
 is non-empty. This happens if and only if f ∈ X
M
since \(X_{H^{0}(M)}\) is \(\mathbb{C}^{{\ast}}\)-stable. The assertion follows since X
M
is G-invariant and closed.
is non-empty. This happens if and only if f ∈ X
M
since \(X_{H^{0}(M)}\) is \(\mathbb{C}^{{\ast}}\)-stable. The assertion follows since X
M
is G-invariant and closed. -
3.
If \(X_{V _{k}(\mathfrak{g})} = \overline{G.f}\),
 , and thus, \(H^{0}(V _{k}(\mathfrak{g}))\) is lisse, and thus, so its quotient \(\mathcal{W}_{k}(\mathfrak{g})\).
, and thus, \(H^{0}(V _{k}(\mathfrak{g}))\) is lisse, and thus, so its quotient \(\mathcal{W}_{k}(\mathfrak{g})\).
Remark 13
-
1.
The above results hold for W-algebras associated with any \(\mathfrak{g}\) and any
 without any restriction on the level k [9, 10]. In particular we have the vanishing result $$\displaystyle{ H_{f}^{i}(M) = 0\quad \text{for }i\neq 0,\ M \in \mathbf{KL}_{ k}, }$$(61)
without any restriction on the level k [9, 10]. In particular we have the vanishing result $$\displaystyle{ H_{f}^{i}(M) = 0\quad \text{for }i\neq 0,\ M \in \mathbf{KL}_{ k}, }$$(61)for the BRST cohomology H f i(M) of the quantized Drinfeld-Sokolov reduction functor associated with f in the coefficient in an object M of KL k . Thus the functor
$$\displaystyle{ \mathbf{KL}_{k} \rightarrow \mathcal{ W}^{k}(\mathfrak{g},f)\mathop{\mathrm{-Mod}}\nolimits,\quad M\mapsto H_{ f}^{0}(M), }$$is exact, and moreover,

where S f is the Slodowy slice at f (see Sect. 2.8). In particular
$$\displaystyle{ H_{f}^{0}(V _{ k}(\mathfrak{g}))\neq 0\;\Longleftrightarrow\;X_{V _{k}(\mathfrak{g})} \supset \overline{G.f}. }$$(62) -
2.
In the case that f = f θ , a minimal nilpotent element of \(\mathfrak{g}\), then we also have the following result [4]:
$$\displaystyle{ H_{f_{\theta }}(V _{k}(\mathfrak{g})) = \left \{\begin{array}{@{}l@{\quad }l@{}} \mathcal{W}_{k}(\mathfrak{g},f_{\theta })\quad &\text{if }k\not\in \mathbb{Z}_{+}, \\ 0 \quad &\text{if }k \in \mathbb{Z}_{+}.\end{array} \right. }$$Here \(\mathcal{W}_{k}(\mathfrak{g},f_{\theta })\) is the simple quotient of \(\mathcal{W}^{k}(\mathfrak{g},f_{\theta })\). Together with (62), this proves the “only if” part of Theorem 12. Indeed, if \(V _{k}(\mathfrak{g})\) is lisse, then \(H_{f_{\theta }}(V _{k}(\mathfrak{g})) = 0\) by (62), and hence, \(k \in \mathbb{Z}_{+}\).
7 Irreducible Representations of W-Algebras
In this section we quickly review results obtained in [5].
Since  , by Zhu’s theorem irreducible positive energy representations of \(\mathcal{W}^{k}(\mathfrak{g})\) are parametrized by central characters of
, by Zhu’s theorem irreducible positive energy representations of \(\mathcal{W}^{k}(\mathfrak{g})\) are parametrized by central characters of  . For a central character
. For a central character  , let \(\mathbb{L}(\gamma )\) be the corresponding irreducible positive energy representations of \(\mathcal{W}^{k}(\mathfrak{g})\). This is a simple quotient of the Verma module
\(\mathbb{M}(\gamma )\) of \(\mathcal{W}^{k}(\mathfrak{g})\) with highest weight γ, which has the character
, let \(\mathbb{L}(\gamma )\) be the corresponding irreducible positive energy representations of \(\mathcal{W}^{k}(\mathfrak{g})\). This is a simple quotient of the Verma module
\(\mathbb{M}(\gamma )\) of \(\mathcal{W}^{k}(\mathfrak{g})\) with highest weight γ, which has the character
in the case that k is non-critical, where Ω is the Casimir element of \(U(\mathfrak{g})\).
In Theorem 28 we showed that the functor \(\mathbf{KL}_{k} \rightarrow \mathcal{ W}^{k}(\mathfrak{g})\mathop{\mathrm{-Mod}}\nolimits\), M ↦ H
0(M), is exact. However in order to obtain all the irreducible positive energy representation we need to extend this functor to the whole category  . However the functor
. However the functor  , M ↦ H
0(M), is not exact in general except for the case \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{2}\) [4]. Nevertheless, we can [44] modify the functor to obtain the following result.
, M ↦ H
0(M), is not exact in general except for the case \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{2}\) [4]. Nevertheless, we can [44] modify the functor to obtain the following result.
Theorem 29 ([5])
There exists an exact functor

(called the ˆˆ ˆˆ −”-reduction functor in [ 44 ]), which enjoys the following properties.
-
1.
\(H_{-}^{0}(M(\lambda ))\cong \mathbb{M}(\gamma _{\bar{\lambda }})\) , where M(λ) is the Verma module of \(\widehat{\mathfrak{g}}\) with highest weight λ, and \(\gamma _{\bar{\lambda }}\) is the evaluation of
 at the Verma module
\(M_{\mathfrak{g}}(\bar{\lambda })\)
of
\(\mathfrak{g}\)
with highest weight
\(\bar{\lambda }\).
at the Verma module
\(M_{\mathfrak{g}}(\bar{\lambda })\)
of
\(\mathfrak{g}\)
with highest weight
\(\bar{\lambda }\). -
2.
\(H_{-}^{0}(L(\lambda ))\cong \left \{\begin{array}{@{}l@{\quad }l@{}} \mathbb{L}(\gamma _{\bar{\lambda }})\quad &\mathit{\text{if }}\bar{\lambda }\mathit{\text{ is anti-dominant}}\ (\mathit{\text{that is,}}\ M_{\mathfrak{g}}(\bar{\lambda })\ \mathit{\text{is simple}}),\\ 0 \quad &\mathit{\text{otherwise.}}\end{array} \right.\)
Corollary 8
Write \(\mathop{\mathrm{ch}}\nolimits L(\lambda ) =\sum _{\mu }c_{\lambda,\mu }\mathop{ \mathrm{ch}}\nolimits M(\mu )\) with \(c_{\lambda,\mu } \in \mathbb{Z}\) . If \(\bar{\lambda }\) is anti-dominant, we have
In the case that k is non-critical, then it is known by Kashiwara and Tanisaki [62] that the coefficient c
λ, μ
is expressed in terms of Kazhdan-Lusztig polynomials. Since any central character of  can be written as \(\gamma _{\bar{\lambda }}\) with anti-dominant \(\bar{\lambda }\), Corollary 8 determines the character of all the irreducible positive energy representations of \(\mathcal{W}^{k}(\mathfrak{g})\) for all non-critical k.
can be written as \(\gamma _{\bar{\lambda }}\) with anti-dominant \(\bar{\lambda }\), Corollary 8 determines the character of all the irreducible positive energy representations of \(\mathcal{W}^{k}(\mathfrak{g})\) for all non-critical k.
On the other hand, in the case that k is critical, all \(\mathbb{L}(\gamma _{\bar{\lambda }})\) are one-dimensional since \(\mathcal{W}^{-n}(\mathfrak{g})\) is commutative. This fact with Theorem 29 can be used in the study of the critical level representations of \(\widehat{\mathfrak{g}}\), see [13].
The results in this section hold for arbitrary simple Lie algebra \(\mathfrak{g}\).
Remark 14
The condition \(\bar{\lambda }\in \mathfrak{h}^{{\ast}}\) is anti-dominant does not imply that \(\lambda \in \widehat{ \mathfrak{h}}^{{\ast}}\) is anti-dominant. In fact this condition is satisfied by all non-degenerate admissible weights λ (see below) which are regular dominant.
Remark 15
Theorem 29 has been generalized in [6]. In particular the character of all the simple ordinary representations (=simple positive energy representations with finite-dimensional homogeneous spaces) has been determined for W-algebras associated with all nilpotent elements f in type A.
8 Kac-Wakimoto Admissible Representations and Frenkel-Kac-Wakimoto Conjecture
We continue to assume that \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{n}\), but the results in this section holds for arbitrary simple Lie algebra \(\mathfrak{g}\) as well with appropriate modification unless otherwise stated.
8.1 Admissible Affine Vertex Algebras
Let \(\widehat{\mathfrak{h}}\) be the Cartan subalgebra \(\mathfrak{h}\mathop{\oplus }\mathbb{C}K\) of \(\widehat{\mathfrak{g}}\), \(\tilde{\mathfrak{h}} = \mathfrak{h}\mathop{\oplus }\mathbb{C}K\mathop{\oplus }\mathbb{C}D\) the extended Cartan subalgebra, \(\widehat{\varDelta }\) the set of roots of \(\widehat{\mathfrak{g}}\) in \(\tilde{\mathfrak{h}}^{{\ast}} = \mathfrak{h}^{{\ast}}\mathop{\oplus }\mathbb{C}\varLambda _{0}\mathop{\oplus }\mathbb{C}\delta\), where Λ 0(K) = 1 = δ(d), \(\varLambda _{0}(\mathfrak{h} + \mathbb{C}D) =\delta (\mathfrak{h}\mathop{\oplus }\mathbb{C}K) = 0\), \(\widehat{\varDelta }_{+}\) the set of positive roots. \(\widehat{\varDelta }^{re} \subset \widehat{\varDelta }\) the set of real roots, \(\widehat{\varDelta }_{+}^{re} =\widehat{\varDelta } ^{re} \cap \widehat{\varDelta }_{+}\). Let \(\widehat{W}\) be the affine Weyl group of \(\widehat{\mathfrak{g}}\).
Definition 6 ([57])
A weight \(\lambda \in \widehat{ \mathfrak{h}}^{{\ast}}\) is called admissible if
-
1.
λ is regular dominant, that is,
$$\displaystyle{ \langle \lambda +\rho,\alpha ^{\vee }\rangle \not\in - \mathbb{Z}_{ +}\quad \text{for all }\alpha \in \widehat{\varDelta }_{+}^{re}, }$$ -
2.
\(\mathbb{Q}\widehat{\varDelta }(\lambda ) = \mathbb{Q}\widehat{\varDelta }^{re}\), where \(\widehat{\varDelta }(\lambda ) =\{\alpha \in \widehat{\varDelta }^{re}\mid \langle \lambda +\rho,\alpha ^{\vee }\rangle \in \mathbb{Z}\}\).
The irreducible highest weight representation L(λ) of \(\widehat{\mathfrak{g}}\) with highest weight \(\lambda \in \widehat{ \mathfrak{h}}^{{\ast}}\) is called admissible if λ is admissible. Note that an irreducible integrable representations of \(\widehat{\mathfrak{g}}\) is admissible.
Clearly, integrable representations of \(\widehat{\mathfrak{g}}\) are admissible.
For an admissible representation L(λ) we have [56]
since λ is regular dominant, where \(\widehat{W}(\lambda )\) is the integral Weyl group [61, 74] of λ, that is, the subgroup of \(\widehat{W}\) generated by the reflections s α associated with \(\alpha \in \widehat{\varDelta }\) and w ∘λ = w(λ + ρ) −ρ. Further the condition (2) implies that \(\mathop{\mathrm{ch}}\nolimits L(\lambda )\) is written in terms of certain theta functions. Kac and Wakimoto [57] showed that admissible representations are modular invariant, that is, the characters of admissible representations form an \(SL_{2}(\mathbb{Z})\) invariant subspace.
Let λ, μ be distinct admissible weights. Then the condition (1) implies that
Further, the following fact is known by Gorelik and Kac [49].
Theorem 30 ([49])
Let λ be admissible. Then \(\mathop{\mathrm{Ext}}\nolimits _{\widehat{\mathfrak{g}}}(L(\lambda ),L(\lambda )) = 0\).
Therefore admissible representations form a semisimple fullsubcategory of the category of \(\widehat{\mathfrak{g}}\)-modules.
Recall that the simple affine vertex algebra \(V _{k}(\mathfrak{g})\) is isomorphic to L(kΛ 0) as an \(\widehat{\mathfrak{g}}\)-module.
Lemma 35
The following conditions are equivalent.
-
1.
kΛ 0 is admissible.
-
2.
kΛ 0 is regular dominant and \(k \in \mathbb{Q}\).
-
3.
k + h ∨ = p∕q, \(p,q \in \mathbb{N}\) , ( p, q) = 1, \(p\geqslant h^{\vee } = n\).
If this is the case, the level k is called admissible for \(\widehat{\mathfrak{g}}\) , and \(V _{k}(\mathfrak{g})\) is called an admissible affine vertex algebra.
For an admissible number k let Pr k be the set of admissible weights of \(\widehat{\mathfrak{g}}\) of level k. (For \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{n}\), Pr k is the same as the set of principal admissible weights of level k.)
8.2 Feigin-Frenkel Conjecture and Adamović-Milas Conjecture
The following fact was conjectured by Feigin and Frenkel and proved for the case that \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{2}\) by Feigin and Malikov [38].
Theorem 31 ([9])
The associated variety
\(X_{V _{k}(\mathfrak{g})}\)
is contained in
 if k is admissible.
if k is admissible.
In fact the following holds.
Theorem 32 ([9])
Let k be admissible, and let q ∈ N be the denominator of k, that is, k + h ∨ = p∕q, p ∈ N, ( p, q) = 1. Then
where \(\mathbb{O}_{q}\) is the nilpotent orbit corresponding to the partition
The following fact was conjectured by Adamović and Milas [2].
Theorem 33 ([11])
Let k be admissible. Then an irreducible highest weight representation L(λ) is a \(V _{k}(\mathfrak{g})\) -module if and only if k ∈ Pr k . Hence if M is a finitely generated \(V _{k}(\mathfrak{g})\) -module on which \(\widehat{\mathfrak{n}}_{+}\) acts locally nilpotently and \(\widehat{\mathfrak{h}}\) acts locally finitely then M is a direct sum of L(λ) with λ ∈ Pr k .
8.3 Outline of Proofs of Theorems 31, 32 and 33
The idea of the proofs of Theorems 31 and 33 is to reduce to the \(\widehat{\mathfrak{s}\mathfrak{l}_{2}}\)-cases.
Let \(\mathfrak{s}\mathfrak{l}_{2,i} \subset \mathfrak{g}\) be the copy of \(\mathfrak{s}\mathfrak{l}_{2}\) spanned by e i : = e i, i+1, h i : = e i, i − e i+1, i+1, f i : = e i+1, i , and let \(\mathfrak{p}_{i} = \mathfrak{s}\mathfrak{l}_{2,i} + \mathfrak{b} \subset \mathfrak{g}\), the associated minimal parabolic subalgebra. Then
where \(\mathfrak{l}_{i}\) is the Levi subalgebra \(\mathfrak{s}\mathfrak{l}_{2,i} + \mathfrak{h}\), and \(\mathfrak{m}_{i}\) is the nilradical \(\bigoplus \limits _{{ 1\leqslant p<q\leqslant n \atop (\,p,q)\neq (i,i+1)} }\mathbb{C}e_{p,q}\).
Consider the semi-infinite cohomology \(H^{\frac{\infty } {2} +0}(\mathfrak{m}_{i}[t,t^{-1}],M)\). It is defined as a cohomology of Feigin’s complex \((C(\mathfrak{m}_{i}[t,t^{-1}],M),d)\) [35]. There is a natural vertex algebra homomorphism
where k i = k + n − 2, see, e.g. [50]. Note that if k is an admissible number for \(\widehat{\mathfrak{g}}\) then k i is an admissible number for \(\widehat{\mathfrak{s}\mathfrak{l}_{2}}\).
Theorem 34 ([8])
Let k be an admissible number. The map (64) factors through the vertex algebra embedding
Proof (Outline of Proof of Theorem 31)
First, consider the case that \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{2}\). Let N k be the maximal submodule of \(V ^{k}(\mathfrak{g})\), and let I k be the image of N k in \(R_{V ^{k}(\mathfrak{g})} = \mathbb{C}[\mathfrak{g}^{{\ast}}]\), so that \(R_{V _{k}(\mathfrak{g})} = \mathbb{C}[\mathfrak{g}^{{\ast}}]/I_{k}\). It is known by Kac and Wakimoto [56] that N k is generated by a singular vector, say v k . The projection formula [72] implies that the image [v k ] of v k in I k is nonzero. Since [v k ] is a singular vector of \(\mathbb{C}[\mathfrak{g}^{{\ast}}]\) with respect to the adjoint action of \(\mathfrak{g}\), Kostant’s Separation Theorem implies that
for some \(m,n \in \mathbb{N}\) up to constant multiplication, where \(\varOmega = ef + fe + \frac{1} {2}h^{2}\). Now suppose that  and let
and let  , so that Ω(λ) ≠ 0. Then e(λ) = 0. Since \(X_{V _{k}(\mathfrak{g})}\) is G-invariant this implies that x(λ) = 0 for any nilpotent element x of \(\mathfrak{g}\). Because any element of \(\mathfrak{g}\) can be written as a sum of nilpotent elements we get that λ = 0. Contradiction.
, so that Ω(λ) ≠ 0. Then e(λ) = 0. Since \(X_{V _{k}(\mathfrak{g})}\) is G-invariant this implies that x(λ) = 0 for any nilpotent element x of \(\mathfrak{g}\). Because any element of \(\mathfrak{g}\) can be written as a sum of nilpotent elements we get that λ = 0. Contradiction.
Next, consider the case that \(\mathfrak{g}\) is general. Note that since \(X_{V _{k}(\mathfrak{g})}\) is G-invariant and closed, the condition  is equivalent to that \(X_{V _{k}(\mathfrak{g})} \cap \mathfrak{h}^{{\ast}} =\{ 0\}\). Now the complex structure of \(C(\mathfrak{m}_{i}[t,t^{-1}],V _{k}(\mathfrak{g}))\) induces the complex structure on Zhu’s C
2-algebra \(R_{C(\mathfrak{m}_{i}[t,t^{-1}],V _{k}(\mathfrak{g}))}\). The embedding in Theorem 34 induces a homomorphism
is equivalent to that \(X_{V _{k}(\mathfrak{g})} \cap \mathfrak{h}^{{\ast}} =\{ 0\}\). Now the complex structure of \(C(\mathfrak{m}_{i}[t,t^{-1}],V _{k}(\mathfrak{g}))\) induces the complex structure on Zhu’s C
2-algebra \(R_{C(\mathfrak{m}_{i}[t,t^{-1}],V _{k}(\mathfrak{g}))}\). The embedding in Theorem 34 induces a homomorphism
of Poisson algebra. Since Ω is nilpotent in \(R_{V _{k_{ i}}(\mathfrak{s}\mathfrak{l}_{2})}\), so is its image \(\varOmega _{i} = e_{i}f_{i} + f_{i}e_{i} + \frac{1} {2}h_{i}^{2}\) in \(H^{0}(R_{C(\mathfrak{m}_{i}[t,t^{-1}],V _{k}(\mathfrak{g}))},d)\). It follows that \(h_{i}^{N} \equiv 0\pmod \mathfrak{n}_{+}R_{V _{k}(\mathfrak{g})} + \mathfrak{n}_{-}R_{V _{k}(\mathfrak{g})}\) in \(R_{V _{k}(\mathfrak{g})}\) for all i = 1, …, n − q, and we get that \(X_{V _{k}(\mathfrak{g})} \cap \mathfrak{h}^{{\ast}} =\{ 0\}\) as required.
Proof (Outline of Proof of Theorem 32)
The proof is done by determining the variety \(X_{V _{k}(\mathfrak{g})}\). By Theorem 31, \(X_{V _{k}(\mathfrak{g})}\) is a finite union of nilpotent orbits. Thus it is enough to know which nilpotent element orbits is contained in \(X_{V _{k}(\mathfrak{g})}\). On the other hand, (62) says \(X_{V _{k}(\mathfrak{g})} \supset \overline{G.f}\) if and only \(H_{f}^{0}(V _{k}(\mathfrak{g}))\neq 0\). Thus, it is sufficient to compute the character of \(H_{f}^{0}(V _{k}(\mathfrak{g}))\). This is in fact possible since we know the explicit formula (63) of the character of \(V _{k}(\mathfrak{g})\), thanks to the vanishing theorem (61) and the Euler-Poincaré principle.
Proof (Outline of Proof of Theorem 33)
Let L(λ) be a \(V _{k}(\mathfrak{g})\)-module. Then, the space \(H^{\frac{\infty } {2} +i}(\mathfrak{m}_{i}[t,t^{-1}],L(\lambda ))\), \(i \in \mathbb{Z}\), is naturally a \(H^{\frac{\infty } {2} +i}(\mathfrak{m}_{i}[t,t^{-1}],V _{k}(\mathfrak{g}))\)-module. By Theorem 34, this means that \(H^{\frac{\infty } {2} +i}(\mathfrak{m}_{i}[t,t^{-1}],L(\lambda ))\) is in particular a module over the admissible affine vertex algebra \(V _{k_{i}}(\mathfrak{s}\mathfrak{l}_{2})\). Therefore Theorem 33 for \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{2}\) that was established by Adamović and Milas [2] implies that \(H^{\frac{\infty } {2} +i}(\mathfrak{m}_{i}[t,t^{-1}],L(\lambda ))\) must be a direct sum of admissible representations of \(\widehat{\mathfrak{s}\mathfrak{l}}_{2}\). This information is sufficient to conclude that L(λ) is admissible.
Conversely, suppose that L(λ) is an admissible representation of level k. If L(λ) is integrable over \(\mathfrak{g}\), then it has been already proved by Frenkel and Malikov [42] that L(λ) is a \(V _{k}(\mathfrak{g})\)-module. But then an affine analogue of Duflo-Joseph Lemma [11, Lemma 2.6] implies that this is true for a general admissible representation as well.
8.4 Lisse Property of W-Algebras
An admissible number k is called non-degenerate if  . By Theorem 32, this condition is equivalent to that
. By Theorem 32, this condition is equivalent to that
The following assertion follows immediately from Corollary 7.
Theorem 35 ([9])
Let k be a non-degenerate admissible number. Then the W-algebra \(\mathcal{W}_{k}(\mathfrak{g})\) is lisse.
8.5 Minimal Models of W-Algebras
A vertex algebra V is called rational if any V -module is completely reducible. To a lisse and rational conformal vertex algebra V one can associate rational 2d conformal field theory, and in particular, the category \(V \mathop{\mathrm{-Mod}}\nolimits\) of V -modules forms [51] a modular tensor category [19], as in the case of the category of integrable representation of \(\widehat{\mathfrak{g}}\) at a positive level and the category of minimal series representations [23] of the Virasoro algebra.
An admissible weight λ is called non-degenerate if \(\bar{\lambda }\) is anti-dominant. Let Pr k non-deg be the set of non-degenerate admissible weights of level k of \(\widehat{\mathfrak{g}}\). It is known [44] that Pr k non-deg is non-empty if and only if k is non-degenerate.
By Theorem 29, for λ ∈ Pr k, H − 0(L(λ)) is a (non-zero) simple \(\mathcal{W}^{k}(\mathfrak{g})\)-module if and only of λ ∈ Pr k non-deg, and \(H_{-}^{0}(L(\lambda ))\cong H_{-}^{0}(L(\mu ))\) if and only if μ ∈ W ∘λ for λ, μ ∈ Pr k non-deg.
Let [Pr k non-deg] = Pr k non-deg∕ ∼, where λ ∼ μ ⇔ μ ∈ W ∘λ. It is known [44] that we have a bijection
Here k + n = p∕q as before, \(\widehat{P}_{+}^{k}\) is the set of integral dominant weights of level k of \(\widehat{\mathfrak{g}}\), the cyclic group \(\mathbb{Z}_{n}\) acts diagonally on \(\widehat{P}_{+}^{p-n} \times \widehat{ P}_{+}^{q-n}\) as the Dynkin automorphism, and \(\rho = \frac{1} {2}\sum _{\alpha \in \varDelta _{+}}\alpha\).
The following assertion was conjectured by Frenkel et al. [44].
Theorem 36 ([10])
Let k be a non-degenerate admissible number. Then the simple W-algebra \(\mathcal{W}_{k}(\mathfrak{g})\) is rational, and \(\{\mathbb{L}(\gamma _{\bar{\lambda }}) = H_{-}^{0}(L(\lambda ))\mid \lambda \in [Pr_{k}^{non\mathrm{-}deg}]\}\) forms the complete set of isomorphism classes of simple \(\mathcal{W}_{k}(\mathfrak{g})\) -modules.
In the case that \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{2}\), Theorems 35 and 36 have been proved in [22, 77], and the above representations are exactly the minimal series representations of the Virasoro algebra.
The representations
are called the minimal series representations of \(\mathcal{W}^{k}(\mathfrak{g})\), and if k + n = p∕q, \(p,q \in \mathbb{N}\), ( p, q) = 1, \(p,q,\geqslant n\), then the rational W-algebra \(\mathcal{W}_{k}(\mathfrak{g})\) is called the ( p, q)-minimal model of \(\mathcal{W}^{k}(\mathfrak{g})\). Note that the ( p, q)-minimal model and the (q, p)-minimal model are isomorphic due to the duality, see Corollary 5.
Proof (Outline of the Proof of Theorem 36)
Let k be a non-degenerate admissible number. We have
by [5]. Hence by Theorem 28 (3)
From this together with Theorem 33, it is not too difficult to obtain the classification is the simple \(\mathcal{W}_{k}(\mathfrak{g})\)-modules as stated in Theorem 36. One sees that the extensions between simple modules are trivial using the linkage principle that follows from Theorem 29.
Remark 16
-
1.
We have \(\mathcal{W}_{k}(\mathfrak{g}) = \mathbb{L}(\gamma _{-(k+n)\rho })\) for a non-degenerate admissible number k. (Note that kΛ 0 ∉ Pr k non−deg.)
-
2.
Let λ ∈ Pr k . From Corollary 8 and (63), we get
$$\displaystyle{ \mathop{\mathrm{ch}}\nolimits \mathbb{L}(\gamma _{\bar{\lambda }}) =\sum _{w\in \widehat{W}(\lambda )}\epsilon (w)\mathop{\mathrm{ch}}\nolimits \mathbb{M}(\gamma _{\overline{w\circ \lambda }}). }$$(65)This was conjectured by [44].
-
3.
When it is trivial (that is, equals to \(\mathbb{C}\)), \(\mathcal{W}_{k}(\mathfrak{g})\) is obviously lisse and rational. This happens if and only if \(\mathcal{W}_{k}(\mathfrak{g})\) is the (n, n + 1)-minimal model (=the (n + 1, n)-minimal model). In this case the character formula (65) for \(\mathcal{W}_{k}(\mathfrak{g}) = \mathbb{L}(\gamma _{\bar{\lambda }})\), λ = −(k + n)ρ + kΛ 0, gives the following denominator formula:
$$\displaystyle{ \sum _{w\in \widehat{W}(\lambda )}\epsilon (w)q^{\frac{(\overline{w\circ \lambda },\overline{w\circ \lambda }+2\rho )} {2(k+n)} } =\prod _{ j=1}^{n-1}(1 - q^{j})^{n-1}. }$$In the case that \(\mathfrak{g} = \mathfrak{s}\mathfrak{l}_{2}\), we get the denominator formula for the Virasoro algebra, which is identical to Euler’s pentagonal identity.
-
4.
As a generalization of the GKO construction [48] it has been conjectured [58] that the ( p, q)-minimal model of \(\mathcal{W}^{k}(\mathfrak{g})\), with p > q, is isomorphic to the commutant of \(V _{l+1}(\mathfrak{g})\) inside \(V _{l}(\mathfrak{g}) \otimes V _{1}(\mathfrak{g})\), where l + n = q∕( p − q). (Note that \(V _{l}(\mathfrak{g})\) and \(V _{l+1}(\mathfrak{g})\) are admissible.) This conjecture has been proved in [18] for the special case that ( p, q) = (n + 1, n).
A similar conjecture exists in the case that \(\mathfrak{g}\) is simply laced.
-
5.
The existence of rational and lisse W-algebras has been conjectured for general W-algebras \(\mathcal{W}^{k}(\mathfrak{g},f)\) by Kac and Wakimoto [59]. This has been proved in [12] in part including all the cases in type A. See [15, 63] for a recent development in the classification problem of rational and lisse W-algebras.
Notes
- 1.
It is easy to verify that \(\mathop{\mathrm{cdet}}\nolimits B\) coincides with the row-determinant of B defined in a similar way.
References
T. Abe, G. Buhl, C. Dong, Rationality, regularity, and C 2-cofiniteness. Trans. Am. Math. Soc. 356(8), 3391–3402 (2004) (electronic)
D. Adamović, A. Milas, Vertex operator algebras associated to modular invariant representations for A 1 (1). Math. Res. Lett. 2(5), 563–575 (1995)
M. Adler, On a trace functional for formal pseudo differential operators and the symplectic structure of the Korteweg-de Vries type equations. Invent. Math. 50(3), 219–248 (1978/79)
T. Arakawa, Representation theory of superconformal algebras and the Kac-Roan-Wakimoto conjecture. Duke Math. J. 130(3), 435–478 (2005)
T. Arakawa, Representation theory of W-algebras. Invent. Math. 169(2), 219–320 (2007)
T. Arakawa, Representation theory of W-algebras, II, in Exploring New Structures and Natural Constructions in Mathematical Physics. Advanced Studies in Pure Mathematics, vol. 61 (Mathematical Society of Japan, Tokyo, 2011), pp. 51–90
T. Arakawa, A remark on the C 2 cofiniteness condition on vertex algebras. Math. Z. 270(1–2), 559–575 (2012)
T. Arakawa, Two-sided BGG resolution of admissible representations. Represent. Theory 19(3), 183–222 (2014)
T. Arakawa, Associated varieties of modules over Kac-Moody algebras and C 2-cofiniteness of W-algebras. Int. Math. Res. Not. 2015, 11605–11666 (2015)
T. Arakawa, Rationality of W-algebras: principal nilpotent cases. Ann. Math. 182(2), 565–694 (2015)
T. Arakawa, Rationality of admissible affine vertex algebras in the category
 . Duke Math. J. 165(1), 67–93 (2016)
. Duke Math. J. 165(1), 67–93 (2016)T. Arakawa, Rationality of W-algebras II (in preparation)
T. Arakawa, P. Fiebig, On the restricted Verma modules at the critical level. Trans. Am. Math. Soc. 364(9), 4683–4712 (2012)
T. Arakawa, A. Molev, Explicit generators in rectangular affine W-algebras of type A. Lett. Math. Phys. 107(1), 47–59 (2017)
T. Arakawa, A. Moreau, Joseph ideals and lisse minimal W-algebras. J. Inst. Math. Jussieu (published online). doi:10.1017/51474748000025
T. Arakawa, T. Kuwabara, F. Malikov, Localization of affine W-algebras. Commun. Math. Phys. 335(1), 143–182 (2015)
T. Arakawa, C.H. Lam, H. Yamada, Zhu’s algebra, C 2-algebra and C 2-cofiniteness of parafermion vertex operator algebras. Adv. Math. 264, 261–295 (2014)
T. Arakawa, C.H. Lam, H. Yamada, Parafermion vertex operator algebras and W-algebras (2017). arXiv:1701.06229 [math.RT]
B. Bakalov, A. Kirillov Jr., Lectures on Tensor Categories and Modular Functors. University Lecture Series, vol. 21 (American Mathematical Society, Providence, RI, 2001)
A.A. Beilinson, V.G. Drinfeld, Quantization of Hitchin’s fibration and Langlands’ program, in Algebraic and Geometric Methods in Mathematical Physics (Kaciveli, 1993). Mathematical Physics Studies, vol. 19 (Kluwer Academic Publishers, Dordrecht, 1996), pp. 3–7
A. Beilinson, V. Drinfeld, Opers. Preprint (2005). arXiv:math/0501398v1 [math.AG]
A. Beilinson, B. Feigin, B. Mazur, Introduction to algebraic field theory on curves. Preprint
A.A. Belavin, A.M. Polyakov, A.B. Zamolodchikov, Infinite conformal symmetry in two-dimensional quantum field theory. Nucl. Phys. B 241(2), 333–380 (1984)
R.E. Borcherds, Vertex algebras, Kac-Moody algebras, and the Monster. Proc. Natl. Acad. Sci. U. S. A. 83(10), 3068–3071 (1986)
S. Bosch, W. Lütkebohmert, M. Raynaud, Néron models. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 21 (Springer, Berlin, 1990)
P. Bouwknegt, K. Schoutens (eds.),
 -Symmetry. Advanced Series in Mathematical Physics, vol. 22 (World Scientific Publishing Co. Inc., River Edge, NJ, 1995)
-Symmetry. Advanced Series in Mathematical Physics, vol. 22 (World Scientific Publishing Co. Inc., River Edge, NJ, 1995)J. de Boer, T. Tjin, Quantization and representation theory of finite W algebras. Commun. Math. Phys. 158(3), 485–516 (1993)
J. de Boer, T. Tjin, The relation between quantum W algebras and Lie algebras. Commun. Math. Phys. 160(2), 317–332 (1994)
A. De Sole, V.G. Kac, Finite vs affine W-algebras. Jpn. J. Math. 1(1), 137–261 (2006)
C. Dong, G. Mason, Integrability of C 2-cofinite vertex operator algebras. Int. Math. Res. Not. 15 pp. (2006). Art. ID 80468
C. Dong, H. Li, G. Mason, Vertex operator algebras and associative algebras. J. Algebra 206(1), 67–96 (1998)
V.G. Drinfel′d, V.V. Sokolov, Lie algebras and equations of Korteweg-de Vries type, in Current Problems in Mathematics. Itogi Nauki i Tekhniki, vol. 24 (Akad. Nauk SSSR Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1984), pp. 81–180
L. Ein, M. Mustaṭă, Jet schemes and singularities, in Algebraic Geometry—Seattle 2005. Part 2. Proceedings of Symposia in Pure Mathematics, vol. 80 (American Mathematical Society, Providence, RI, 2009), pp. 505–546
V.A. Fateev, S.L. Lykyanov, The models of two-dimensional conformal quantum field theory with Z n symmetry. Int. J. Mod. Phys. A 3(2), 507–520 (1988)
B.L. Feigin, Semi-infinite homology of Lie, Kac-Moody and Virasoro algebras. Uspekhi Mat. Nauk 39(2(236)), 195–196 (1984)
B. Feigin, E. Frenkel, Quantization of the Drinfel′ d-Sokolov reduction. Phys. Lett. B 246(1–2), 75–81 (1990)
B. Feigin, E. Frenkel, Affine Kac-Moody algebras at the critical level and Gel′ fand-Dikii algebras, in Infinite Analysis, Part A, B (Kyoto, 1991). Advanced Series in Mathematical Physics, vol. 16 (World Sci. Publ., River Edge, NJ, 1992), pp. 197–215
B. Feigin, F. Malikov, Modular functor and representation theory of \(\widehat{\mathrm{sl}}_{2}\) at a rational level, in Operads: Proceedings of Renaissance Conferences (Hartford, CT/Luminy, 1995). Contemporary Mathematics, vol. 202 (American Mathematical Society, Providence, RI, 1997), pp. 357–405
E. Frenkel, Langlands Correspondence for Loop Groups. Cambridge Studies in Advanced Mathematics, vol. 103 (Cambridge University Press, Cambridge, 2007)
E. Frenkel, D. Ben-Zvi, Vertex Algebras and Algebraic Curves, 2nd edn. Mathematical Surveys and Monographs, vol. 88 (American Mathematical Society, Providence, RI, 2004)
E. Frenkel, D. Gaitsgory, Weyl modules and opers without monodromy, in Arithmetic and Geometry Around Quantization. Progress in Mathematics, vol. 279 (Birkhäuser Boston Inc., Boston, MA, 2010), pp. 101–121
I. Frenkel, F. Malikov, Kazhdan-Lusztig tensoring and Harish-Chandra categories. Preprint (1997) arXiv:q-alg/9703010
I.B. Frenkel, Y. Zhu, Vertex operator algebras associated to representations of affine and Virasoro algebras. Duke Math. J. 66(1), 123–168 (1992)
E. Frenkel, V. Kac, M. Wakimoto, Characters and fusion rules for W-algebras via quantized Drinfel′ d-Sokolov reduction. Commun. Math. Phys. 147(2), 295–328 (1992)
I.M. Gel′fand, L.A. Dikii, A family of Hamiltonian structures connected with integrable nonlinear differential equations. Akad. Nauk SSSR Inst. Prikl. Mat. Preprint (136), 41 (1978)
N. Genra, Screening operators for W-algebras. Sel. Math. New Ser. (2017). Published online. doi:10.1007/500029-017-0315-9, arXiv:1606.00966 [math.RT]
V. Ginzburg, Harish-Chandra bimodules for quantized Slodowy slices. Represent. Theory 13, 236–271 (2009)
P. Goddard, A. Kent, D. Olive, Virasoro algebras and coset space models. Phys. Lett. B 152(1–2), 88–92 (1985)
M. Gorelik, V. Kac, On complete reducibility for infinite-dimensional Lie algebras. Adv. Math. 226(2), 1911–1972 (2011)
S. Hosono, A. Tsuchiya, Lie algebra cohomology and N = 2 SCFT based on the GKO construction. Commun. Math. Phys. 136(3), 451–486 (1991)
Y.-Z. Huang, Rigidity and modularity of vertex tensor categories. Commun. Contemp. Math. 10(suppl. 1), 871–911 (2008)
S. Ishii, Jet schemes, arc spaces and the Nash problem. C. R. Math. Acad. Sci. Soc. R. Can. 29(1), 1–21 (2007)
V.G. Kac, Infinite-dimensional Lie algebras, and the Dedekind η-function. Funkcional. Anal. i Priložen. 8(1), 77–78 (1974)
V.G. Kac, Infinite-Dimensional Lie Algebras, 3rd edn. (Cambridge University Press, Cambridge, 1990)
V.G. Kac, Introduction to vertex algebras, Poisson vertex algebras, and integrable Hamiltonian PDE, in Perspectives in Lie Theory, vol. 19, ed. by F. Callegaro, et al. Springer INdAM Series (Springer International Publishing, 2017). doi:10.1007/978-3-319-58971-8_1
V.G. Kac, M. Wakimoto, Modular invariant representations of infinite-dimensional Lie algebras and superalgebras. Proc. Natl. Acad. Sci. U. S. A. 85(14), 4956–4960 (1988)
V.G. Kac, M. Wakimoto, Classification of modular invariant representations of affine algebras, in Infinite-Dimensional Lie Algebras and Groups (Luminy-Marseille, 1988). Advanced Series in Mathematical Physics, vol. 7 (World Scientific Publishing, Teaneck, NJ, 1989), pp. 138–177
V.G. Kac, M. Wakimoto, Branching functions for winding subalgebras and tensor products. Acta Appl. Math. 21(1–2), 3–39 (1990)
V.G. Kac, M. Wakimoto, On rationality of W-algebras. Transform. Groups 13(3–4), 671–713 (2008)
V. Kac, S.-S. Roan, M. Wakimoto, Quantum reduction for affine superalgebras. Commun. Math. Phys. 241(2–3), 307–342 (2003)
M. Kashiwara, T. Tanisaki, Kazhdan-Lusztig conjecture for symmetrizable Kac-Moody Lie algebras. III. Positive rational case. Asian J. Math. 2(4), 779–832 (1998) Mikio Sato: a great Japanese mathematician of the twentieth century
M. Kashiwara, T. Tanisaki, Characters of irreducible modules with non-critical highest weights over affine Lie algebras, in Representations and Quantizations (Shanghai, 1998) (China Higher Education Press, Beijing, 2000), pp. 275–296
K. Kawasetsu,
 -algebras with non-admissible levels and the Deligne exceptional series (2015). arXiv:1505.06985 [math.QA]
-algebras with non-admissible levels and the Deligne exceptional series (2015). arXiv:1505.06985 [math.QA]E.R. Kolchin, Differential Algebra and Algebraic Groups. Pure and Applied Mathematics, vol. 54 (Academic, New York/London, 1973)
B. Kostant, On Whittaker vectors and representation theory. Invent. Math. 48(2), 101–184 (1978)
B. Kostant, S. Sternberg, Symplectic reduction, BRS cohomology, and infinite-dimensional Clifford algebras. Ann. Phys. 176(1), 49–113 (1987)
H. Li, Vertex algebras and vertex Poisson algebras. Commun. Contemp. Math. 6(1), 61–110 (2004)
H. Li, Abelianizing vertex algebras. Commun. Math. Phys. 259(2), 391–411 (2005)
I. Losev, Finite-dimensional representations of W-algebras. Duke Math. J. 159(1), 99–143 (2011)
S.L. Luk′yanov, V.A. Fateev, Exactly soluble models of conformal quantum field theory associated with the simple Lie algebra D n . Yadernaya Fiz. 49(5), 1491–1504 (1989)
T.E. Lynch, Generalized Whittaker vectors and representation theory. PhD thesis, M.I.T., 1979
F.G. Malikov, B.L. Feigin, D.B. Fuks, Singular vectors in Verma modules over Kac-Moody algebras. Funktsional. Anal. i Prilozhen. 20(2), 25–37, 96 (1986)
A. Matsuo, K. Nagatomo, A. Tsuchiya, Quasi-finite algebras graded by Hamiltonian and vertex operator algebras, in Moonshine: The First Quarter Century and Beyond. London Mathematical Society Lecture Note Series, vol. 372 (Cambridge University Press, Cambridge, 2010), pp. 282–329
R.V. Moody, A. Pianzola, Lie Algebras with Triangular Decompositions. Canadian Mathematical Society Series of Monographs and Advanced Texts (Wiley, New York, 1995). A Wiley-Interscience Publication
A. Premet, Special transverse slices and their enveloping algebras. Adv. Math. 170(1), 1–55 (2002). With an appendix by Serge Skryabin
P. Tauvel, R.W.T. Yu, Lie Algebras and Algebraic Groups. Springer Monographs in Mathematics (Springer, Berlin, 2005)
W. Wang, Rationality of Virasoro vertex operator algebras. Int. Math. Res. Not. (7), 197–211 (1993)
A.B. Zamolodchikov, Infinite extra symmetries in two-dimensional conformal quantum field theory. Teoret. Mat. Fiz. 65(3), 347–359 (1985)
Y. Zhu, Modular invariance of characters of vertex operator algebras. J. Am. Math. Soc. 9(1), 237–302 (1996)
Acknowledgements
The author is grateful to the organizers of “Perspectives in Lie Theory”. He thanks Naoki Genra and Xiao He who wrote the first version of this note. He would also like to thank Anne Moreau and Alberto De Sole for useful comments on the preliminary version of this note. His research is supported by JSPS KAKENHI Grant Numbers 25287004 and 26610006.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Arakawa, T. (2017). Introduction to W-Algebras and Their Representation Theory. In: Callegaro, F., Carnovale, G., Caselli, F., De Concini, C., De Sole, A. (eds) Perspectives in Lie Theory. Springer INdAM Series, vol 19. Springer, Cham. https://doi.org/10.1007/978-3-319-58971-8_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-58971-8_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-58970-1
Online ISBN: 978-3-319-58971-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





 .
. to G-Orbits
to G-Orbits as a Reduced Poisson Variety
as a Reduced Poisson Variety intersects the G-orbits at any point of
intersects the G-orbits at any point of  , where G is the adjoint group of
, where G is the adjoint group of  admits a
admits a  .
.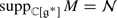 .
. . Therefore the functor (
. Therefore the functor ( , F
•
M a good filtration. Then
, F
•
M a good filtration. Then
 ,
,
 .
. . In particular H
0(M) is finitely strongly generated and
. In particular H
0(M) is finitely strongly generated and

 .
. .
. .
. is non-empty. This happens if and only if f ∈ X
M
since
is non-empty. This happens if and only if f ∈ X
M
since  , and thus,
, and thus,  without any restriction on the level k [
without any restriction on the level k [
 at the Verma module
at the Verma module
 . Duke Math. J. 165(1), 67–93 (2016)
. Duke Math. J. 165(1), 67–93 (2016) -Symmetry. Advanced Series in Mathematical Physics, vol. 22 (World Scientific Publishing Co. Inc., River Edge, NJ, 1995)
-Symmetry. Advanced Series in Mathematical Physics, vol. 22 (World Scientific Publishing Co. Inc., River Edge, NJ, 1995) -algebras with non-admissible levels and the Deligne exceptional series (2015). arXiv:1505.06985 [math.QA]
-algebras with non-admissible levels and the Deligne exceptional series (2015). arXiv:1505.06985 [math.QA]