Keywords

1 Introduction

The study of the dynamics of a quantum particle in a magnetic field is a fascinating subject of perduring interest both in physics and mathematics literature. The quantization of energy levels giving rise to the Landau levels is at the basis of our understanding of integer and fractional quantum Hall effects [11, 13, 39, 66, 77] and its higher-dimensional counterparts and generalizations, including topological insulators [14, 19, 67]. The use of vector potentials in quantum mechanics is associated in itself to very interesting consequences, such as the purely quantum mechanical interference in the Aharonov-Bohm effect [3]. On the other side, the mathematical formalism for a particle in a magnetic field has been developed and refined along the time, based on the rigorous definition of Schrödinger operators with magnetic fields [10]. An important role is played by the construction of families of observables in the presence of gauge fields relying on the progresses in gauge covariant pseudodifferential calculus [42] and the C ∗-algebraic formalism [58] (see for a review Ref. [57]). A major area of research in the field of single-particle and many-body properties in the presence of a magnetic field is provided by the study of the effects of periodic potentials. The interplay of the magnetic field and the discreteness induced by the lattice provides a paradigmatic system for the study of incommensurability effects [12, 38] and it results in an energy spectrum exhibiting a fractal structure, referred to as the Hofstadter butterfly [38]. Very interesting examples of the analysis of the so-called colored gaps can be found in [9, 68], while a discussion of the colored Hofstadter butterflies in honeycomb lattices can be found in [2].

The study of the Hofstadter Hamiltonian attracted in the years a sparkling activity, also due to its connections with the one-dimensional Harper model [36]. A concise, but very clear discussion is presented in [71], where it is shown how the Schrödinger equation for an electron in a magnetic field in the presence of a two-dimensional periodic potential can be mapped in a one-dimensional quasiperiodic equation. A derivation of Harper and Hofstadter models in the context of effective models for the conductance in magnetic fields was presented in [22], while a treatment of the Schrödinger operator in two dimensions with a periodic potential and a strong constant magnetic field perturbed by slowly varying non-periodic scalar and vector potentials has been recently discussed in [28]. A remarkable motivation for the studies of a two-dimensional electron gas in a uniform magnetic field and a periodic substrate potential is as well coming from the connection with topological invariants, as one can see from the study of the Hall conductance [72].

The theoretical studies on properties of lattice systems in a periodic potential found a experimental matching in the active research of solid-state realizations of the Hofstadter and related Hamiltonians. This effect has never been observed so far in a natural crystal due to the fact that a very large magnetic field would be required, however signatures of the Hofstadter bands has been observed in artificial superlattices [21, 27, 29, 59, 65]. This activity found recently a counterpart in the field of cold atoms, where it has been possible to load a neutral atomic gas in an optical lattice and simulate by external lasers an artificial magnetic potential [5, 60]. Given the fact that ultracold atoms, due to the high level of control and tunability of parameters [64], are an ideal physical setup in which perform quantum simulation [15], these and related experimental achievements opened the way to study a variety of lattice systems in a magnetic potential. In particular one can load on the lattice interacting bosonic and/or fermionic atoms, control the parameters of the lattice, use several components in each lattice site [54] and implement a variety of lattices of different dimensionalities (not only D = 2, but also D = 1 and D = 3).

The rationale of this Chapter is to report an introduction to the different ways to implement artificial magnetic potentials in the presence of a controllable lattice, with the goal to create a link with the many available results in theoretical and mathematical physics. From the other side we think that the variety of lattice models in magnetic fields implementable with ultracold gases may be a context in which test and apply techniques from the mathematical literature, and motivate further analytical and rigorous results, starting from the treatment of three-dimensional fermionic lattice systems. With these objectives, we then present in Sect. 2 a discussion on several different ways of realizing artificial magnetic fluxes in optical lattice systems. In Sects. 3 and 4 we present two possible applications of the results presented in Sect. 2 both to illustrate the versatility of possible uses of artificial magnetic potentials and to show results for 3D and 1D lattices. In Sect. 3 we review and study cubic lattice tight-binding models with a commensurate Abelian flux, also presenting results for the case of anisotropic fluxes. In Sect. 4 we consider 1D rings pierced by a magnetic field discussing how the latter can enhance the quantum state transfer and the entanglement entropy in the system.

We acknowledge several discussions we had along the years on the subjects treated in this chapter with several people, and special acknowledgements go to M. Aidelsburger, E. Alba, T. Apollaro, H. Buljan, A. Celi, I. C. Fulga, N. Goldman, G. Gori, M. Mannarelli, G. Mussardo, G. Panati, H. Price, M. Rizzi, P. Sodano and A. Smerzi. S. P. is supported by a Rita Levi-Montalcini fellowship of MIUR.

2 Realization of Artificial Magnetic Fluxes in Optical Lattice Systems

In the last 10 years many experiments with ultracold atoms demonstrated the possibility of realizing artificial magnetic fluxes trapped in two-dimensional optical lattices. Similar setups pave the way for a systematic study of topological phases of matter in the highly controllable environment provided by ultracold atoms [15]. Such experiments offer, on one side, the possibility of reaching regimes that are hardly achievable in solid state devices and, on the other, to verify the emergence of topological phenomena through observables typical of ultracold gases, such as the motion of the center of mass of the system, or the momentum distribution of the atoms [64]. The measurement of these quantities therefore provides useful tools to detect the appearance of topological phases of matter which are complementary to the usual transport measurements performed in solid state platforms.

The main result which enabled the experimental study of topological models in ultracold atomic systems was the realization of artificial gauge potentials. In this framework, we speak about artificial (or synthetic) gauge potentials because ultracold atoms are neutral, therefore their motion is not directly affected by the presence of a true electromagnetic field. Despite that, however, it turned out to be possible to engineer systems in which the dynamics of the slow and low-energy degrees of freedom can be described by an effective Hamiltonian in which the free, non-interacting, part is the one of a free-particle in a magnetic field. An interesting point to be observed is that the obtained Hamiltonian, featuring the presence of an artificial magnetic field, is interacting, with the interaction term tunable by e.g. Feshbach resonances or by acting on the geometry of the system. At the same time, typically, as we are going to discuss in the following, the synthetic field does not depend on the interactions or on the density of the system, being in a word a single-particle effect.

An efficient way to implement a synthetic gauge potential A giving rise to an artificial, static magnetic field B ∝ ∇×A, is to implement with ultracold atoms in optical lattice a tight-binding Hamiltonian with hopping amplitudes which are, in general, complex and whose phases depend on the position. To be more clear, we point out that the implementation of synthetic gauge potentials in lattices relies on the well-established experimental successes in the quantum simulation of tight-binding Hamiltonians for both bosons and fermions [15].

For ultracold bosons, if a condensate is loaded in an optical lattice, then one can expand the condensate wavefunctions in the basis of the Wannier functions and obtain a discrete nonlinear Schrödinger (DNLS) equation [73]. The coefficient of the nonlinear term in the DNLS equation is proportional to the s-wave scattering length a and in general the coefficients of the DNLS equation depend on integrals of the Wannier functions. For a = 0 (i.e., for an effectively non-interacting condensate) one gets the discrete linear Schrödinger, which is nothing but the tight-biding model for which one can apply consolidated numerical analyses [55] and rigorous [16] techniques for the definition and determination of the Wannier functions and their behaviour. When a ≠ 0 a rigorous theory of (nonlinear) Wannier functions does not exist, and the semiclassical equations of motion should be modified as a consequence of the existence of the nonlinearity. The development of a rigorous extension of Wannier functions in the presence of nonlinearity is a challenging mathematical problem for the future. We think this independently from the fact that an approximate determination of the Wannier functions (see e.g. for a variational approach in [18, 74, 75]) typically works very well to describe the experimental results when the laser intensity, i.e. the strength of the periodic potential, is large enough, also when the system approaches the superfluid-Mott transition and/or the gas is not longer condensate due to the presence of strong interactions [40]. Similar considerations apply for ultracold fermions: when there is in average no more than one particle per well and only the lowest band is occupied, a single-band tight-binding approximation works very well both when the dilute fermionic gas is polarized (corresponding to a = 0) and when more species or levels of fermions are present. In the following we consider tight-binding models describing ultracold atoms in optical lattices, sticking to the non-interacting limit and discussing how to simulate artificial gauge potentials in such systems. We alert anyway the reader that, albeit non-rigorous, the experimental techniques to implement synthetic magnetic field are the same also for interacting particles, even though the interacting terms may modify or generate additional coefficients in the tight-binding model and introduce corrections to the results obtained with the Peierls substitution [63].

To fix the notation, let us consider a lattice whose sites are denoted by r: for a cubic D-dimensional lattice we have \(\mathbf{r} \in \mathbb{Z}^{D}\). By using the Peierls substitution to take into account the effect of the magnetic field [45, 53, 63], the Hamiltonian we consider then reads

$$\displaystyle{ H(\{\phi \}) = -\,\sum _{\mathbf{r}\,,\,\hat{j}}w_{\hat{j}}\,c_{\mathbf{r}+\hat{j}}^{\dag }\,e^{i\phi _{j}\left (\mathbf{r}\right )}c_{\mathbf{ r}} + \text{H.c.}\,, }$$
(1)

where \(\hat{j}\) are unitary vectors characterizing the links of the lattice, \(w_{\hat{j}}\) are the hopping amplitudes (assumed isotropic in the following of the Section: \(w_{\hat{j}} \equiv w\)). The phases θ j depend in general on the position r and can be thought as the integral of an artificial and classical vector potential A(r) between neighboring sites:

$$\displaystyle{ \phi _{j}(\mathbf{r}) =\int _{ \mathbf{r}}^{\mathbf{r}+\hat{j}}\mathbf{A}(\mathbf{x}) \cdot d\mathbf{x}\,. }$$
(2)

The ladder operators c r and c r † annihilate and create an atom in the lattice site r and they may obey either fermionic or bosonic commutation relations depending on the atoms species.

It is important to emphasize that the artificial vector potential A constitutes a classical and static field; despite that, we can define U(1) gauge transformations acting on the ladder operators of the previous Hamiltonian and on the vector potentials, which leave the dynamics of the system invariant; A is thus, in this context, a properly defined gauge potential (see the reviews [20, 32] for more details). Notice as well that one can simulate gauge potentials without a periodic potential [20, 32], but that typically the implementation of magnetic potential in an optical lattice can crucially take advantage of the presence of the lattice potential itself (in other words, decreasing to zero the intensity of the laser beams amounts to make vanishing the magnetic potentials as well).

The effect of the gauge symmetry is that the main observables we must consider are gauge-invariant observables - although, due to the artificial nature of these gauge potentials, also gauge-dependent quantity may be evaluated in the experimental setups, going beyond the previous effective Hamiltonian description. The main gauge-invariant quantity determining the dynamics of the system is the magnetic flux which characterizes each plaquette in the lattice. Such flux describes an Aharonov-Bohm phase acquired by an atom hopping around a lattice plaquette and can be defined as:

$$\displaystyle{ \varPhi _{p} =\sum _{(\mathbf{r},\hat{j})\in p}\phi _{j}(\mathbf{r}) =\oint _{p}\mathbf{A}(\mathbf{x}) \cdot d\mathbf{x}\,, }$$
(3)

where \((\mathbf{r},\hat{j})\) labels the links along the plaquette p in order to consider a counterclockwise path. The lattice spacing is denoted by a, and if not differently stated is intended to be set to 1.

On the experimental side there are two broad classes of techniques which have been adopted to engineer effective Hamiltonians of the form in Eq. (1). The first corresponds to the “lattice shaking”, which consists in a fast periodic modulation of the optical lattice trapping the atoms whose effect is to reproduce, at the level of the slow motion of the atoms, the required complex hopping amplitudes. The second is the “laser-assisted tunneling” of the atoms in optical lattices in which the atom motion is suppressed along one direction and restored through the introduction of additional Raman lasers able to imprint additional space-dependent phases to the tunneling of the particles. Both these techniques allow for the generation of artificial magnetic fluxes and are based on non-trivial time-dependent Hamiltonians which determine, at the level of the slow motion of the system, a dynamics which can be described by an effective Hamiltonian of the kind in Eq. (1). In the following we will summarize first the technique developed in [31] which provides a very useful tool for the analysis of these driven time-dependent systems, and then we will describe some of the main examples of systems obtained through lattice shaking or laser-assisted tunneling.

2.1 An Effective Description for Periodically Driven Systems

The technique for the analysis of periodically driven systems proposed in [31], whose presentation we follow in this Section, is based on the distinction of two main ingredients whose combination describes the dynamics of modulated setups. The first is an effective Hamiltonian H, independent on the initial conditions of the dynamics, and capturing the long-time motion of the particles in the system. The second is a so-called kick-operator K describing the effects due to the initial and final phases of the modulation. In particular it is responsible for both the initial conditions of the system and for the so-called micro-motion, which includes the periodic dynamics of all the fast-evolving degrees of freedom. To be explicit, let us assume that the modulated system is described by a time-periodic Hamiltonian \(\tilde{H}(t) =\tilde{ H}(t + T)\). It is then possible to decompose the evolution of the system into:

$$\displaystyle{ U(t_{i} \rightarrow t_{f}) = e^{-iK(t_{f})}e^{-iH(t_{f}-t_{i})}e^{iK(t_{i})}\,. }$$
(4)

Here H is the effective, time-independent, Hamiltonian, not depending on t i and t f ; the kick operator K(t) = K(t + T) is a periodic time-dependent operator, and hereafter we set ℏ = 1. The approach in [31] consists in a series expansion of H and K in the small parameter 1∕ω = T∕(2π), where ω is the driving frequency of the system and must constitute the largest energy scale of the problem.

To study optical lattices with non-trivial artificial magnetic fluxes it is usually enough to consider the long-term dynamics of the driven system and thus the effective Hamiltonian only (the situation would be different for systems involving also spin degrees of freedom, or for the evaluation of the heating of the driven system). To this purpose, we decompose the time-dependent Hamiltonian \(\tilde{H}(t)\) into its Fourier component:

$$\displaystyle{ \tilde{H}(t) = H_{0} +\sum _{n>0}e^{in\omega t}V ^{(n)} +\sum _{ n>0}e^{-in\omega t}V ^{(-n)} }$$
(5)

with V (−n) = V (n)†. H 0 is the time-independent component of \(\tilde{H}\), whereas the operators V (−n) are associated to its harmonics. In terms of these operators it is possible to show that the effective Hamiltonian reads:

$$\displaystyle\begin{array}{rcl} H = H_{0}& +& \frac{1} {\omega } \sum _{n=1}^{\infty }\frac{1} {n}\left [V ^{(n)},V ^{(-n)}\right ] + \\ & +& \frac{1} {2\omega ^{2}}\sum _{n=1}^{\infty } \frac{1} {n^{2}}\left (\left [\left [V ^{(n)},H_{ 0}\right ],V ^{(-n)}\right ] + \text{H.c.}\right ) + O(T^{3})\,.{}\end{array}$$
(6)

This expansion allows for a determination of the effective Hamiltonian in the main examples of systems of ultracold atoms trapped in optical lattices, subject either to a modulation of the trapping lattice or two additional Raman couplings. One needs to consider carefully, though, the issue of the convergence of this series which must be evaluated specifically for each system. The readers are referred to [31] for more detail.

2.2 Artificial Gauge Potentials from Lattice Shaking

The first attempts to experimentally modify the hopping amplitudes of the effective tight-binding models for atoms trapped in optical lattices through the introduction of modulations date back to the works [25, 43, 51]. To understand how the effect of the lattice shaking can determine the tunneling amplitudes of the atoms let us first address a one-dimensional setup. Although, in this case, it is not possible to define magnetic fields and fluxes, the analysis of this simplified system will be useful to understand the appearance of artificial magnetic fluxes in higher dimensions. We consider an optical potential of the form \(V (t) = V _{0}\sin ^{2}\left (x -\xi _{0}\cos (\omega t)\right )\) where ω is the shaking frequency. The Hamiltonian with this oscillating potential can be mapped in a co-moving frame (x → x + ξ 0cos(ωt)) characterized by the following Hamiltonian:

$$\displaystyle{ \tilde{H}(t) = p^{2} + V _{ 0}\sin ^{2}\left (x\right ) -\frac{1} {2}x\xi _{0}\omega ^{2}\cos (\omega t)\,, }$$
(7)

where the last term accounts for the additional force in the non-inertial frame and we set the mass to m = 1∕2 for the sake of simplicity. Finally, by approximating with a tight-binding model we obtain:

$$\displaystyle{ \tilde{H}(t) =\sum _{x}\left [-w\,c_{x+1}^{\dag }c_{ x} - w\,c_{x}^{\dag }c_{ x+1} -\frac{1} {2}x\xi _{0}\omega ^{2}\cos (\omega t)c_{ x}^{\dag }c_{ x}\right ]. }$$
(8)

In this case it is possible to derive the full effective Hamiltonian without recurring to a series expansion to obtain [24]:

$$\displaystyle{ H = -w\mathcal{J}_{0}(\xi _{0}\omega /2)\sum _{x}c_{x+1}^{\dag }c_{ x} + c_{x}^{\dag }c_{ x+1}\, }$$
(9)

where \(\mathcal{J}_{0}\) is a Bessel function of the first kind which renormalizes the tunneling amplitude and may assume either positive or negative values depending on ξ 0 ω. Despite the fact that, in this case, the hopping amplitude remains always real, it is interesting to notice that it can change sign.

In 1D systems, such a change of sign is simply translated in a different dispersion for the single particle problem; however, it is possible to extend this naive example to higher dimensions and less trivial geometries: in this case the result of the lattice shaking provides a first tool for the engineering of non-trivial fluxes. We also observe that, applying the formalism of [31], we have that H 0 = −w∑ x c x+1 † c x + H.c., V (1) = V (−1) = −xω 2 c x † c x ∕4 and all the other harmonics are absent. The effective Hamiltonian based on Eq. (6) would then correspond to a series expansion of the Bessel function in Eq. (9) [31].

The lattice shaking techniques can be also extended to obtain complex hopping amplitudes. To this purpose, in this simple one-dimensional model, it is necessary to change the time-dependence of the modulation of the lattice in order to break the time-reversal symmetry [V (t − t 0) = V (−t − t 0)] and a shift antisymmetry [V (t) = V (t + T∕2)] [69]. This has been realized for the first time for a Rb Bose-Einstein condensate and the presence of non-trivial hopping phases has been verified through time-of-flight measurements of its momentum distribution as a function of the modulation amplitude [69]. This may be counterintuitive because, in one dimension, the observation of the hopping phase corresponds to the observation of a gauge-dependent quantity. We notice, however, that only the effective tight-binding models adopted in the description of the slow dynamics of the system, and the related observables, are indeed gauge-invariant; in the experiment, though, one can access also additional “gauge-dependent” observables through operations which do not have a physical counterpart in the effective toy model: this is the case of the time-of-flight imaging which follows from switching off the optical lattice. Such procedure maps the crystal momentum of the tight binding model (9) (which is a gauge-dependent quantity) into the velocity of the particles during the time of flight, which is an observable quantity which exists only considering the embedding of the system in the larger laboratory setting.

The effects of lattice shaking become even more remarkable in two-dimensional setups. In this case lattices may be accelerated along two different directions to cause a global periodic motion of the optical lattice around a closed orbit which yields, at the level of the effective Hamiltonian, a tight-binding model with non-trivial fluxes.

On triangular optical lattices this technique has been adopted to realize staggered flux configurations [70] and, more recently, the same method, with a circular modulation of the lattice position [61], has been used to simulate the topological Haldane model [35] on the honeycomb lattice with a gas of fermionic40 K [41]. The Haldane model represents a topological insulator of fermions hopping in a honeycomb lattice with nearest-neighbor and next-nearest-neighbor tunnelings. It is based on both the presence of a pattern of staggered fluxes Φ to break time-reversal symmetry and an onsite staggering potential to break space inversion symmetry [35]. By varying the value of either of these parameters, the model undergoes topological phase transitions, characterized by discontinuities of the Chern number of the lowest energy band. These discontinuities have been experimentally detected through measurements of the drift of the center of mass of the system in the presence of an additional magnetic gradient to add an additional constant force [41].

2.3 Artificial Gauge Potential from Laser-Assisted Tunneling

Complex hopping amplitudes in the effective Hamiltonian can be obtained also through a different technique based on the introduction of pairs of Raman lasers coupling the low-energy states of the atoms trapped in the optical lattice. In this case the phase differences and space dependence of the Raman lasers may be inherited by the dynamics of the atoms, thus allowing for complex space-dependent amplitudes.

To reach this result, however, it is necessary to first suppress the motion of the atoms in the optical lattice, at least, along one direction. This is obtained through the introduction of suitable energy offsets, depending on the positions, which shift the energy of neighboring sites by an energy Δ. These offsets can be obtained, for example, by tilting the lattice (i.e., with gravity), or by introducing suitable magnetic gradients in the system which couple with the atomic magnetic dipole moments (thus generating a position dependent Zeeman term) or through the introduction of superlattices.

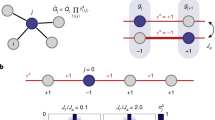
Let us start by considering one of the simplest realization of strong fluxes in optical square lattices as experimentally realized [4]. In this experiment an optical superlattice, generated by a standing wave with wavelength 2a, was used to introduce an additional staggering along the \(\hat{x}\) direction for the trapped atoms, such that the initial, time-independent setup can be modeled by the following Hamiltonian:

$$\displaystyle{ \tilde{H}_{0}^{{\prime}} = -w\,\sum _{\mathbf{ r}\,,\,\hat{j}}\left (c_{\mathbf{r}+\hat{j}}^{\dag }c_{\mathbf{ r}} + \text{H.c.}\right ) + \frac{\varDelta } {2}\sum _{\mathbf{r}}(-1)^{x}c_{\mathbf{ r}}^{\dag }c_{\mathbf{ r}}\, }$$
(10)

where r = (x, y) and Δ is the staggering related to the amplitude of the superlattice (see Fig. 1). Two running Raman lasers with wave vectors k 1,2 and frequencies ω 1,2, tuned such that ω 1 −ω 2 = Δ, are then introduced in the system. The associated electric field is E 1cos(k 1 r −ω 1 t) + E 2cos(k 2 r −ω 2 t) which, neglecting the fast oscillating terms, generates a potential:

$$\displaystyle{ V (t) =\kappa e^{i\left (\mathbf{k}_{R}\mathbf{r}-\varDelta t\right )}c_{\mathbf{ r}}^{\dag }c_{\mathbf{ r}} + \text{H.c.}\,, }$$
(11)

where κ = 2E 1 E 2 and k R = k 1 − k 2 is the recoil momentum of the Raman lasers.

Fig. 1
figure 1

Schematic illustration of the setup adopted in the experiment [4] for the realization of staggered magnetic fluxes. The tunneling along the horizontal direction is suppressed by the introduction of the staggering Δ through a superlattice. A pair of Raman lasers (red arrows) are added to the system to restore the horizontal tunneling. As a result the even horizontal links (blue dashed links) acquire a tunneling phase \(e^{-i\mathbf{k}_{R}\mathbf{r}}\), whereas the odd (red dashed links) acquire the opposite phase \(e^{i\mathbf{k}_{R}\mathbf{r}}\). k R is the recoil momentum of the pair of Raman lasers

Full size image

The time-evolution of the system is ruled by the Schrödinger equation \(i\partial _{t}\psi =\tilde{ H}'(t)\psi\), where \(\tilde{H}'(t) =\tilde{ H}_{0}^{{\prime}} + V (t)\). Since the static Hamiltonian \(\tilde{H}_{0}^{{\prime}}\) contains the staggered-potential term that explicitly diverges with the driving frequency Δ, it is convenient to apply the unitary transformation [33, 56]

$$\displaystyle{ \psi = R(t)\tilde{\psi } =\exp \left (\!-iWt\right )\tilde{\psi }, }$$
(12)

with W being the staggering term:

$$\displaystyle{ W = \frac{\varDelta } {2}\sum _{\mathbf{r}}(-1)^{x}c_{\mathbf{ r}}^{\dag }c_{\mathbf{ r}}\,. }$$
(13)

Such transformation removes the diverging term and maps \(\tilde{H}'\) into:

$$\displaystyle{ \tilde{H}(t) = R^{\dag }(t)\left [\tilde{H}'_{ 0} + V (t)\right ]R(t) - W = }$$
(14)
$$\displaystyle{ = H_{0} + V ^{(1)}e^{i\varDelta t} + V ^{(-1)}e^{-i\varDelta t}, }$$
(15)

where

$$\displaystyle\begin{array}{rcl} H_{0}& =& -w\sum _{x,y}\left (c_{x,y+1}^{\dag }c_{ x,y} + c_{x,y}^{\dag }c_{ x,y+1}\right ),{}\end{array}$$
(16)
$$\displaystyle\begin{array}{rcl} \hat{V }^{(1)}& =& \kappa \sum _{\mathbf{ r}}e^{-i\mathbf{k}_{R}\mathbf{r}}c_{\mathbf{ r}}^{\dag }c_{\mathbf{ r}} - w\sum _{x\,\mathrm{odd},y}\left (c_{x+1,y}^{\dag }c_{ x,y} + c_{x-1,y}^{\dag }c_{ x,y}\right ),{}\end{array}$$
(17)
$$\displaystyle\begin{array}{rcl} \hat{V }^{(-1)}& =& \kappa \sum _{\mathbf{ r}}e^{i\mathbf{k}_{R}\mathbf{r}}c_{\mathbf{ r}}^{\dag }c_{\mathbf{ r}} - w\sum _{x\,\mathrm{even},y}\left (c_{x+1,y}^{\dag }c_{ x,y} + c_{x-1,y}^{\dag }c_{ x,y}\right ).{}\end{array}$$
(18)

From these terms it is easy to derive the effective Hamiltonian in Eq. (6) at first order:

$$\displaystyle\begin{array}{rcl} & H& = -w\sum _{x,y}\left (c_{x,y+1}^{\dag }c_{ x,y} + c_{x,y}^{\dag }c_{ x,y+1}\right ) - \\ & -& \frac{w\,\kappa } {\varDelta } \sum _{x\,\mathrm{even},y}\left [\left (e^{-i\mathbf{k}_{R}\hat{x}} - 1\right )\left (e^{-i\mathbf{k}_{R}\mathbf{r}}c_{ x+1,y}^{\dag }c_{ x,y} + e^{i\mathbf{k}_{R}\mathbf{r}}c_{ x,y}^{\dag }c_{ x-1,y}\right ) + \text{H.c.}\right ] + O(1/\varDelta ^{2})\,,{}\end{array}$$
(19)

This effective Hamiltonian describes in general a two-dimensional model with staggered magnetic fluxes where the sign of the fluxes alternate in the plaquettes belonging to even and odd columns. In the experiment [4], the recoil momentum was chosen as \(\mathbf{k}_{R} = (\hat{x} +\hat{ y})\varPhi\). In this case the \(\hat{x}\) component has no relevance in the definition of the fluxes and the previous Hamiltonian becomes, after a suitable gauge transformation:

$$\displaystyle\begin{array}{rcl} & H& = -w_{y}\sum _{x,y}\left (c_{x,y+1}^{\dag }c_{ x,y} + c_{x,y}^{\dag }c_{ x,y+1}\right ) - \\ & \phantom{H}& w_{x}\sum _{x\,\mathrm{even},y}\left [\left (e^{-i\varPhi y}c_{ x+1,y}^{\dag }c_{ x,y} + e^{i\varPhi y}c_{ x,y}^{\dag }c_{ x-1,y}\right ) + \text{H.c.}\right ] + O(1/\varDelta ^{2}){}\end{array}$$
(20)

with w y = w and w x = 2wκsin(Φ∕2)∕Δ (this value is the one obtained at the first order in the perturbative expansion, and it must be considered only an approximation). From the Hamiltonian in Eq. (20) it is evident the alternation of fluxes ±Φ on the plaquettes along the horizontal direction.

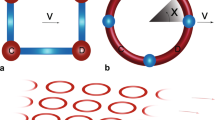
The introduction of the staggering term, however, allows also for more refined setups in which the even and odd links may be separately addressed [33]. This requires the introduction of two different pairs of Raman lasers with opposite frequency shifts ±Δ and it permits to obtain systems with a uniform magnetic flux Φ in each plaquette [33]. In this way the Hofstadter model on the square lattice has been realized for87 Rb [6] and it was possible to measure the Chern number of the different energy bands through the motion of the mass center of the system.

The staggered potential, however, it is not the only possible choice to suppress the motion along one direction. The first quantum simulations with ultracold atoms of the Hofstadter model [5, 60] were instead based on an external potential of the kind W = ∑ r Δxc r † c r . In this case the introduction of two Raman lasers yields indeed to an effective Hamiltonian with rectified fluxes, and this result can be obtained with calculations analogous to the previous one where the distinction between even and odd links is no longer required, and all the horizontal links acquire a tunneling phase of the form \(e^{i\mathbf{k}_{R}\mathbf{r}}\) consistent with a constant flux.

The laser-assisted techniques to design artificial gauge potentials are extremely versatile, and the previous approach can be generalized to different geometries and to multi-component species. The introduction of additional potential through superlattices, for example, enabled the realization of ladder models pierced by uniform fluxes which are characterized by chiral currents and a Meissner-like effect [8]. Furthermore the introduction of spin-dependent potentials, as in [5], permits to mix different spin-species subject to opposite magnetic fluxes and some theoretical proposals generalized these systems to engineer an artificial spin-orbit couplings for two-component atoms [31, 56].

3 Cubic Lattice Tight-Binding Models with Commensurate Flux

In this Section we consider cubic lattices in a magnetic field, focusing on the case of Abelian fluxes. This is a very interesting mathematical problem in itself and it has a counterpart in the experimental implementations we discussed in the previous Section.

3.1 Isotropic Flux

We start our study with a single-species tight-binding model on a cubic lattice with N = L 3 sites, in the presence of an Abelian uniform and static magnetic field B = Φ (1, 1, 1) isotropic on the three directions. This field gives rise on each plaquette of the lattice (with area a 2, a being the lattice spacing) to a magnetic flux Φ = B ⋅ a 2. The presence of this flux amounts to a phase e iΦ gathered by a particle hopping around a single plaquette, because of the Stokes theorem. The generalization of this model to many species is straightforward, since an Abelian gauge field does not mix the different species. The magnetic flux is chosen commensurate:

$$\displaystyle{ \varPhi = 2\pi \frac{m} {n} \,. }$$
(21)

The commensurate condition allows us to solve the model analytically, imposing periodic boundary condition on the lattice. At variance, in the incommensurate case the determination of spectrum requires a numerical solution of the real space tight-binding matrix, see e.g. [17, 52] - for a discussion of the Hofstadter butterfly in three dimensions see [46], while a study in higher dimensions is reported in [44].

By exploiting the gauge redundancy, the static magnetic field B can be associated to various physically equivalent gauge potentials A μ (x). For the sake of simplicity, we choose here a time-independent gauge configuration, adopting the (static) Coulomb gauge A 0(x) = 0.

Because of the magnetic phases in Eq. (2), the sites of the lattice, all equivalent each other at B = 0, get inequivalent, the inequivalence lying in the phases gathered after each hopping along the bonds starting from a certain site. In this way, the lattice gets divided, in a gauge-dependent way, in a certain number of sublattices. Exploiting this freedom, in order to perform calculations in the easiest way as possible, it is useful to look for the (set of) gauge(s) characterized, for a given commensurate magnetic flux \(\varPhi = 2\pi \frac{m} {n}\), by the smallest number of sublattices.

A simple (and still not unique) gauge fulfilling this requirement is [37]:

$$\displaystyle{ \mathbf{A} = \frac{2\pi } {a^{2}} \frac{m} {n} \,(0,x - y,y - x)\,, }$$
(22)

with permutations in x, y, z also equally acceptable. This gauge is a three-dimensional generalization of the Landau gauge in two dimensions [47], reducing indeed to the Landau gauge in this limit (\(w_{\hat{z}} \rightarrow 0\)), up to a gauge redefinition to absorb the term − y in A y .

Assuming the choice in Eq. (22), the Hamiltonian in Eq. (1) can be recast in the form

$$\displaystyle{ H = -\sum _{\mathbf{r}}\left [w_{\hat{x}}\,c_{\mathbf{r}+\hat{x}}^{\dag }\,c_{\mathbf{ r}} + w_{\hat{y}}\,U_{\hat{y}}(x,y)\,c_{\mathbf{r}+\hat{y}}^{\dag }c_{\mathbf{ r}} + w_{\hat{z}}\,U_{\hat{z}}(x,y)\,c_{\mathbf{r}+\hat{z}}^{\dag }c_{\mathbf{ r}}\right ] +\, \text{H.c.}\,, }$$
(23)

where the tunneling magnetic phases \(U_{\hat{j}}(x,y) = e^{i\,\phi _{\,\hat{j}}(x,y)}\) are defined as:

$$\displaystyle{ U_{x} = 1\,, }$$
(24)
$$\displaystyle{ U_{\hat{y}}(x,y) =\exp \left (i\,\int _{x,y,z}^{x,y+a,z}A_{ y}\,\mathrm{d}y\right ) =\exp \left (i\,2\pi \,\Big(\frac{x - y} {a} -\frac{1} {2}\Big)\,\frac{m} {n} \right )\,, }$$
(25)
$$\displaystyle{ U_{\hat{z}}(x,y) =\exp \left (i\,\int _{x,y,z}^{x,y,z+a}A_{ z}\,\mathrm{d}z\right ) =\exp \left (-i\,2\pi \,\Big(\frac{x - y} {a} \Big)\,\frac{m} {n} \right )\,. }$$
(26)

The hopping phases in Eqs. (25) and (26) explicitly depend on the positions labelled modulo n. Since the z coordinate is not present in Eq. (22), every wave-function of the Hamiltonian in Eq. (23) can be written as [50]:

$$\displaystyle{ \psi (x,y,z) = e^{ik_{z}z}\,u(x,y)\,, }$$
(27)

allowing for a dimensional reduction of the eigenvalues problem as for the corresponding problem in two dimensions where the Harper equation is found [38, 71].

The Hamiltonian in Eq. (23) with the hopping phases in Eqs. (24)–(26) is translational invariant. For gauge invariant systems, translational invariance implies that a translation of the coordinates by a vector w transforms the Hamiltonian of the system to a gauge-equivalent one [50], and one may find [49]:

$$\displaystyle{ H(\mathbf{r} + \mathbf{w}) =\mathcal{ T}_{\mathbf{w}}^{\dag }(\mathbf{r})H(\mathbf{r})\mathcal{T}_{\mathbf{ w}}(\mathbf{r})\,, }$$
(28)

with \(\mathcal{T}_{\mathbf{w}}(\mathbf{r}) \in U(1)\) being a suitably chosen local gauge transformation which depends on w.

The Hamiltonian in Eq. (23) with the gauge potential in Eq. (22) is translationally invariant because it fulfills Eq. (28). We stress that the potentials of the form in Eq. (22) are not the only ones satisfying the condition in Eq. (28), but instead all the potentials obtained from Eq. (22) through local gauge transformation are characterized by the same physical translational invariance. The property in Eq. (28) is indeed a physical property of the system which is reflected on all the gauge-invariant observables, as for example, the Wilson loops \(W(\mathcal{C}) = \mathbf{P}e^{i\oint _{\mathcal{C}}\mathbf{A}(\mathbf{r})\cdot d\mathbf{r}}\) evaluated on closed paths along the lattice.

The Hamiltonian in Eq. (23) is also periodic with period n along \(\hat{x}\ \hat{y}\), due to the presence of the nontrivial magnetic hopping phases \(U_{\hat{y}}(x,y)\,,U_{\hat{z}}(x,y)\), thus the reduced wavefunctions u(x, y) have the same periodicity. In this way the magnetic unitary cell, defined by the elementary translations leading from a site to equivalent ones in the three lattice directions, can be defined now as enlarged n times along two directions (say \(\hat{x},\hat{y}\)).

The problem to find the eigenvalues of the Hamiltonian in Eq. (23) on a lattice with N number of sites would naïvely require in general the diagonalization of a N × N adjacency matrix in real space. However, assuming translational invariance, the calculation can be remarkably simplified by exploiting the division in sublattices seen above. Indeed, in the presence of a magnetic flux \(\varPhi = 2\pi \frac{m} {n}\) and working in the gauge in Eq. (22), the cubic lattice divides in n sublattices, labelled by the quantity (x − y) mod(n). In this way the Hamiltonian in Eq. (23) becomes:

$$\displaystyle{ H = -\sum _{\hat{j}}w_{\hat{j}}\sum _{s}e^{i\phi _{s,\hat{j}} }\sum _{\mathbf{r}_{s}}\,c_{\mathbf{r}_{s}+\hat{j}}^{\dag }\,c_{\mathbf{ r}_{s}}\, + \text{H.c.}\,, }$$
(29)

where s labels the sublattices and r s labels the sites of the s-th sublattice.

Since the magnetic unitary cell is defined now as enlarged n times along two directions, the corresponding magnetic Brillouin zone (MBZ) in momentum space becomes \(\{\frac{2\pi } {a}, \frac{2\pi } {an}, \frac{2\pi } {na}\}\) [or other permutations of the factors \(\frac{1} {n}\) between the space directions, consisting in a mere redefinition of A(r)]. Correspondingly, the allowed momenta k are \(\frac{N} {n^{2}}\), of the form \(\mathbf{k} =\{ \frac{2\pi } {aL_{x}}\,p_{x}, \frac{2\pi } {aL_{y}}\,p_{y}, \frac{2\pi } {aL_{z}}\,p_{z}\}\), with \(p_{\hat{x}} = 0,\ldots,L - 1\) and \(p_{\hat{y},\hat{z}} = 0,\ldots, \frac{L} {n} - 1\). In this way, all the physical quantities display a momentum periodicity \(\mathbf{k} \rightarrow \mathbf{k} + \frac{2\pi } {na}(l_{x},l_{y},l_{z})\), with l i being again integer numbers.

The counting of the \(\frac{N} {n^{2}}\) allowed momenta proceeds as follows: each sublattice differs from another one by \(\pm \hat{x}\) or \(\pm \hat{y}\) translations that are not primary, then we correspondingly expect n sets of \(\frac{N} {n}\) inequivalent energy eigenstates [50]. These sets form n subbands in the MBZ. However, any sublattice is further divided in n sub-sublattices differing by a primary translation \(\pm (\hat{x} +\hat{ y})\), leaving invariant the potential in Eq. (22). In this way, any \(\frac{N} {n}\)-fold set of eigenstates is again partitioned in n equivalent and degenerate sub-sets, each one having \(\frac{N} {n^{2}}\) element. These elements are parametrized by the \(\frac{N} {n^{2}}\) momenta in the MBZ described above. Moreover the second partition translates in n-fold degeneracy of each subband. In the particular case Φ = π, two sub-bands are obtained, touching in Weyl cones as discussed in [23, 48, 49]; in this case the system in Eq. (23) is the direct three-dimensional generalization of the square lattice model with π-fluxes in [1].

The Hamiltonian in Eq. (29) can be expressed in momentum space using the formulas \(c_{\mathbf{r}_{s}} = \frac{1} {\sqrt{N/n^{2}}} \,\sum _{\mathbf{k}}\,c(\mathbf{k})\,e^{i\mathbf{k}\cdot \mathbf{r}_{s}}\) and \(\sum _{\mathbf{r}_{ s}}^{{\prime}}\,e^{i\mathbf{k}\cdot \mathbf{r}_{s}} = \frac{N} {n^{2}}\). The vectorial label r s runs here on the \(\frac{N} {n^{2}}\) sites of one sub-sublattice of the sublattice s, the upper index in the sum of the second formula meaning this restriction. We obtain:

$$\displaystyle{ H = -\sum _{\mathbf{k}}\sum _{\hat{j}}w_{\hat{j}}\sum _{s}e^{i\phi _{s,\hat{j}} }\,e^{-i\mathbf{k}\cdot \mathbf{j}}\,c_{ s^{{\prime}}=s+\hat{j}}^{\dag }(\mathbf{k})\,c_{ s}(\mathbf{k})\, + \text{H.c.}\,, }$$
(30)

where we have also taken into account that, starting from the s-th sublattices and moving in the \(\hat{j}\) direction, a new sublattice (denoted as s ′) is univocally found, as consequences of Eq. (22). This is the reason oh the notation \(s^{{\prime}} = s +\hat{ j}\).

The Hamiltonian in Eq. (30) can be recast in the sublattices basis as:

$$\displaystyle{ H = -\,\sum _{\mathbf{k}}\sum _{\hat{j}}w_{\hat{j}}\sum _{s}\,c_{s^{{\prime}}=s+\hat{j}}^{\dag }(\mathbf{k})\Big(T_{\hat{ j}}^{\mathrm{AB}}\Big)_{ s^{{\prime}},s}\,e^{-i\mathbf{k}\cdot \mathbf{j}}\,c_{ s}(\mathbf{k})\, +\, \text{H. c.}\,, }$$
(31)

where \(T_{\hat{j}}^{\mathrm{AB}}\) are n × n hopping matrices in the sublattice basis, reading, up to ciclic permutations Z n :

$$\displaystyle{ \begin{array}{ccccc} T_{\hat{x}}^{\mathrm{AB}} = \left (\begin{array}{cccc} 0&1& \ldots &0\\ 0 &0 & \ddots &0 \\ 0&0& \ldots &1\\ 1 &0 &0 &0\\ \end{array} \right )T_{\hat{y}}^{\mathrm{AB}} = e^{-i\pi \frac{m} {n} }\,\left (\begin{array}{cccc} 0& \ldots & 0 &\varphi _{0} \\ \varphi _{1}&0& \ldots &0 \\ 0& \ddots & 0 &0\\ 0 & \ldots &\varphi _{ n-1}&0\\ \end{array} \right )\,T_{\hat{z}}^{\mathrm{AB}} = \left (\begin{array}{cccc} \varphi _{0}& 0 & \ldots &0 \\ 0&\varphi _{n-1}&0&0 \\ 0& 0 & \ddots &0\\ 0 & 0 & \ldots &\varphi _{ 1}\\ \end{array} \right ) \end{array} \,, }$$
(32)

with \(\varphi _{l} = e^{i2\pi \frac{m} {n} l}\,,\,l = 0,\ldots,n - 1\).

The matrices \(T_{\hat{x,y,z}}^{\mathrm{AB}}\) do not commute each other, implying that the unitary cell of the lattice does not coincides with its geometric smallest cell (with area a 2), as seen above. However, the n-power of these matrices yields the identity: \(\left (T_{\{\hat{x},\hat{y},\hat{z}\}}^{\mathrm{AB}}\right )^{n} = \mathbf{1}_{n\times n}\), recovering the MBZ \(\{\frac{2\pi } {a}, \frac{2\pi } {an}, \frac{2\pi } {an}\}\). Moreover, if \(\frac{m} {n} \neq \frac{1} {2}\) the unitary matrices \(T_{\hat{x,y,z}}^{\mathrm{AB}}\) are not invariant (even possibly up to a global phase) by the conjugate operation, reflecting the breaking of the time-reversal symmetry, due to the magnetic field B itself. A notable result of the discussion above is that the diagonalization of a N × N matrix is reduced to the diagonalization of a n × n one.

We conclude this Section by observing that in the presence of more species (labelled by the index α = 1, …, m) hopping on the lattice and subject to the Abelian gauge potential in Eq. (22), the Hamiltonian in Eq. (31) generalizes to

$$\displaystyle{ H = -\sum _{\mathbf{k}}\sum _{\hat{j}}w_{\hat{j}}\sum _{s}\,c_{s^{{\prime}}=s+\hat{j},\alpha ^{{\prime}}}^{\dag }(\mathbf{k})\left (T_{\hat{ j}}^{\mathrm{AB}} \otimes \mathbf{1}_{ m\times m}\right )_{s^{{\prime}},\alpha ^{{\prime}},s,\alpha }\,e^{-i\mathbf{k}\cdot \mathbf{j}}\,c_{ s,\alpha }(\mathbf{k})\, +\, \text{H. c.}\,, }$$
(33)

where no mixing of the different species involved occurs.

3.2 Generalization: Anisotropic Abelian Lattice Fluxes

In the previous analysis we assumed that the value of the fluxes was the same for the three orientations of the plaquettes. Now we discuss some extension in which we relax this hypothesis. We analyze first the case in which the magnetic field \(\hat{z}\) is perturbed, such that we introduce an anisotropy in the previous system:

$$\displaystyle{ \mathbf{B} = \frac{2\,\pi } {a^{2}}\,\Big(\frac{m} {n}, \frac{m} {n}, \frac{m_{z}} {n_{z}} \Big)\,. }$$
(34)

Again we may assume, without any loss of generality, m z and n z prime with each other as well as m and n. In the case of Eq. (34), a gauge similar to the one in Eq. (22) can be used:

$$\displaystyle{ \mathbf{A} = \frac{2\pi } {a^{2}}\,\Big(0, \frac{m_{z}} {n_{z}} \,(x - y), \frac{m} {n} \,(y - x)\Big)\,. }$$
(35)

This choice still depends on one parameter only, thus ensuring the appearance of minimal gauge-dependent sublattices. More in detail, the lattice divides again in n 2 = l. c. m. (n, n z ) inequivalent sublattices, defined by the periodicity of the phases in the \(\hat{x}\) and \(\hat{y}\) directions and labelled by the set (x − y)mod(n 2). Indeed the hopping phases from Eq. (35) are:

$$\displaystyle{ \phi _{\mathbf{r}+\hat{j},\mathbf{r}} = \frac{2\pi } {a}\,\Big(0, \frac{m_{z}} {n_{z}} \,\Big(x - y -\frac{a} {2}\Big), \frac{m} {n} \,(y - x)\Big)\,. }$$
(36)

Similarly to the previous case, each sublattice is again divided in n 2 equivalent sub-sublattices, each one having \(\frac{N} {n_{2}^{2}}\) sites. For this reason, similarly to the Sect. 3.1, n 2 subbands appear, each of them with a n 2 degeneracy. Correspondingly the BZ divides by n 2 in two directions, so that \(\mathbf{k} =\{ \frac{2\pi } {aL_{x}}\,p_{x}, \frac{2\pi } {aL_{y}}\,p_{y}, \frac{2\pi } {aL_{z}}\,p_{z}\}\), \(p_{\hat{x}} = 0,\ldots,L - 1\), \(p_{\hat{y},\hat{z}} = 0,\ldots, \frac{L} {n_{2}} - 1\), or permutations in the pairs of the restricted momentum directions. The Hamiltonian in Eq. (1) can then be rewritten, in terms of these quasi-momenta, as in Eq. (31), by means of three m 2 × m 2 matrices in the basis of the m 2 sublattices, derived similarly to the ones in Eq. (32).

In the completely asymmetric case the magnetic potential reads

$$\displaystyle{ \mathbf{B} = \frac{2\,\pi } {a^{2}}\,\Big(\frac{m_{x}} {n_{x}}, \frac{m_{y}} {n_{y}}, \frac{m_{z}} {n_{z}} \Big)\,, }$$
(37)

a convenient gauge choice, inducing the magnetic field in Eq. (37), reads:

$$\displaystyle{ \mathbf{A}_{\mathbf{AB}} = \frac{2\pi } {a^{2}}\,\Bigg(\Big(\frac{m_{y}} {n_{y}} -\frac{m_{x}} {n_{x}} \Big)\,(z - x), \frac{m_{z}} {n_{z}} \,(x - y), \frac{m_{x}} {n_{x}} \,(y - x)\Bigg)\,. }$$
(38)

The hopping phases from Eq. (38) are:

$$\displaystyle{ \phi _{\mathbf{r}+\hat{j},\mathbf{r}} = \frac{2\pi } {a}\,\Bigg(\Big(\frac{m_{y}} {n_{y}} -\frac{m_{x}} {n_{x}} \Big)\,\Big(z - x -\frac{a} {2}\Big), \frac{m_{z}} {n_{z}} \,\Big(x - y -\frac{a} {2}\Big), \frac{m_{x}} {n_{x}} \,(y - x)\Bigg)\,. }$$
(39)

The gauge in Eq. (38), similarly to the previous case, ensures the appearance of the minimum number of gauge-dependent sublattices. In particular, due to the simultaneous x dependence of all the components of A AB and following the same logic as in the Sect. 3.1, we obtain

$$\displaystyle{ n_{s} = \text{l. c. m. }(n_{x},n_{y},n_{z}) }$$
(40)

inequivalent sublattices (obtained varying y and z at fixed x) and corresponding subbands. Again each sublattice is then further divided in equivalent subsublattices.

More in detail, the counting of these subsublattices proceeds as follows. Starting from a point (x 0, y 0, z 0) belonging to a certain sublattice, they are obtained by adding 1 to each components: (x 0, y 0, z 0) → (x 0 + 1, y 0 + 1, z 0 + 1). The variable z has periodicity given by l. c. m. (n x , n y ) possible inequivalent values, y has periodicity l. c. m. (n x , n z ) and finally x has l. c. m. (n x , n y , n z ) inequivalent values. For this reason each inequivalent sublattice divides in

$$\displaystyle\begin{array}{rcl} n_{d} =\mathrm{ min}\Big(\text{l. c. m. }(n_{x},n_{y})\,,\,\text{l. c. m. }(n_{x},n_{z})\,,\,\text{l. c. m. }(n_{x},n_{y},n_{z})\Big) = & & \\ =\mathrm{ min}\Big(\text{l. c. m. }(n_{x},n_{y})\,,\,\text{l. c. m. }(n_{x},n_{z})\Big)& &{}\end{array}$$
(41)

equivalent subsublattices.

Correspondingly, we find \(\frac{N} {n_{s}\times n_{d}}\) quasi-momenta defining each subband: \(\mathbf{k} =\{ \frac{2\pi } {aL_{x}}\,p_{x}, \frac{2\pi } {aL_{y}}\,p_{y}, \frac{2\pi } {aL_{z}}\,p_{z}\}\), \(p_{\hat{x}} = 0,\ldots,L - 1\), \(p_{\hat{y}} = 0,\ldots, \frac{L} {n_{s}} - 1\), \(p_{\hat{z}} = 0,\ldots, \frac{L} {n_{d}} - 1\), or permutations in the pairs of the restricted momentum directions. The Hamiltonian in Eq. (1) can be then rewritten, in terms of these quasi-momenta and in the basis of the n s sublattices as in Eq. (31), by means of three n s × n s matrices similar to the ones in Eq. (32).

4 Two Applications of Synthetic Gauge Potentials in 1D Rings

The possibilities offered by ultracold atoms in optical lattices to engineer tight-binding models in tunable magnetic potential open as well new possibilities also in the field of quantum information in the sense that they could be used in perspective to perform quantum information tasks and control the amount of entanglement of the system. Here, as two examples we believe paradigmatic of such potentialities, we want to shortly address two specific applications showing how tuning a gauge potential could modify the capability of a system to share quantum information. We consider one-dimensional models of free fermions on a ring geometry in the presence of a synthetic magnetic field piercing the ring. We first analyze for short-range lattice models how a topological phase helps to enhance the fidelity in a quantum state transfer (QST) process between different sites of the lattice [7, 62]. Then we study a long-range model to see how the presence of a topological phase can lead to the a volume-law behavior of the entanglement entropy (EE) for the ground state of the system.

4.1 Quantum State Transfer in a Ring Pierced by a Magnetic Flux

We consider a one-dimensional tight-binding model for free fermions with nearest-neighbors hopping in a ring geometry embedded in a magnetic field. Such magnetic field determines the boundary conditions of the problem: its role is to induce an Aharonov-Bohm phase in the transport of a particle along a full circle around the ring geometry. The Hamiltonian of the system reads

$$\displaystyle{ H = -w\sum _{j}e^{i\phi }c_{ j}^{\dag }c_{ j+1} + h.c.\,, }$$
(42)

where \(\phi = \frac{2\pi } {N_{S}}\varPhi\) (Φ being the Abelian magnetic flux piercing the ring chain in units of 2 π), N S is the number of sites, and the site coordinate is \(r = aj\bmod N_{S}\).

The single-particle energy dispersion is

$$\displaystyle{ E_{k}(\phi ) = -2w\cos \left (ak-\phi \right ) = 2t\cos \left ( \frac{2\pi } {N_{S}}(n_{k}-\varPhi )\right )\,, }$$
(43)

with \(k = \frac{2\pi } {aN_{S}}\,n_{k}\). Due to the nontrivial phase e iϕ, the single-particle dispersion is shifted, as well as the points corresponding to the Fermi surface. For a single fermion, the introduction of this topological phase affects the wave-packet diffusion, giving a useful tool to optimize the quantum state transfer of a certain state from a part of the chain to another one.

One can consider a fermion initially localized at the time t = 0 around the site j = 0:

$$\displaystyle{ \mathinner{\vert \psi _{0}(0)\rangle } =\sum _{j}g_{j}c_{j}^{\dag }\mathinner{\vert 0\rangle }\,, }$$
(44)

with a square wave packet distribution extended over λ = 2M + 1 sites:

$$\displaystyle{ g_{l} = \left \{\begin{array}{cc} \frac{1} {\sqrt{2M+1}} & \text{ If } - M \leq l \leq M \\ 0 & \text{ elsewhere}\,.\\ \end{array} \right. }$$
(45)

After the state evolution | ψ 0(t)〉 = e −iHt | ψ 0(0)〉, the capacity for the channel to produce QST from the site j = 0 to site j = d can be measured by the square projection of the evolved state on the initial state localized on the site d:

$$\displaystyle{ F_{d}(t) = \left \vert \mathinner{\langle \psi _{d}(0)\vert \psi _{0}(t)\rangle }\right \vert ^{2} \simeq A(t)\,e^{-\frac{\left [d+2wt\sin \phi \right ]^{2}} {2\sigma _{F}^{2}(t)} }\,, }$$
(46)

with

$$\displaystyle{ A(t) = \frac{3\lambda ^{2}} {\pi \sqrt{(\lambda ^{2 } - 1)^{2 } + 144w^{2 } t^{2 } \cos ^{2}\phi }}\,\,, }$$
(47)

and

$$\displaystyle{ \sigma _{F}^{2}(t) = \frac{(\lambda ^{2} - 1)^{2} + 144w^{2}t^{2}\cos ^{2}\phi } {12(\lambda ^{2} - 1)} \,. }$$
(48)

For ϕ = −π∕2, the dispersion becomes approximately linear and the wave-packet does not diffuse. Moreover, it propagates with velocity v = 2w causing an enhancement in the fidelity (see Fig. 2). In particular, F d (t) assumes its maximum value at the approximate time

$$\displaystyle{ t^{{\ast}} = \frac{d} {2w}. }$$
(49)
Fig. 2
figure 2

Time evolution of the fidelity F d (t) in the square packet preparation (M = 5), with phase ϕ = −π∕2, different values for the final site d = 10, 30, 60, 90 and N = 500. The thick line indicates the maxima of fidelity reached by each site at different times

Full size image

4.2 Violation of the Area-Law in Long-Range Systems

The study of the ground-state entanglement properties plays an essential role in the characterization of a quantum many-body system. In this Section, we show how the introduction of a gauge potential in a free-fermion model with a long-range hopping can qualitatively change the scaling behavior of the ground state entanglement. The amount of entanglement of a pure state is well quantified by the so-called Entanglement Entropy (EE), defined as follows. Partitioning a given system in two subsystems A and its complement \(\bar{A}\), the EE is the Von Neumann entropy S of one of the two subsystems (say A) calculated from its reduced density matrix ρ A :

$$\displaystyle{ S = -Tr\left (\rho _{A}\ln \rho _{A}\right )\,. }$$
(50)

Typically for gapped short-range quantum systems (where gapped means with a finite energy difference of the first excited level, compared to the ground state energy), the EE grows as the boundary of the subsystem A, i.e., for a system in d dimensions the EE scales as S ∝ ∂L d−1. This is commonly known as the area law [26]. The physical origin of this law is that entanglement is appreciably nonvanishing only between parts of the system very close each others, since the quantum correlation functions between two points decay exponentially with their distance, with a finite decay constant ξ that increases as the mass gap decreases. At variance, for short-range free fermionic systems at a critical (gapless) point it has been shown that the divergence of ξ (resulting in an algebraic decay of quantum correlations) produces a logarithmic correction of the area law, S ∝ L d−1lnL [30, 76], so that in one dimension one expects to find S ∝ lnL. A more relevant, non-logarithmic, violation of the area law is obtained when S ∝ L β with d − 1 < β < d. When β = d one has a volume law.

Referring to free fermions on a lattice, in order to find violation to the area law in gapped regimes, one has to introduce longer-range connections, changing the Fermi surface in a suitable way. In one-dimensional short-range systems, the Fermi surface is typically composed by a finite set of points. This is what happens also in the simplest long-range models when, despite of the long-range hoppings, strong entanglement is created only between closed lattice sites. At variance, if the Fermi surface is a set of points with finite dimension, it can occurs that antipodal sites of the lattice becomes maximally entangled (Bell pairs). As a consequence, a bipartition into two connected complementary parts would cut a number of Bell pairs of the order of the volume of the smaller subsystem, giving rise to a violation of the area law. To this aim, a long-range connection appears useful but not sufficient.

A possible way to create a nontrivial Fermi surface is to introduce a gauge potential [34]. Let us consider a model with long-range hopping with periodic boundary conditions:

$$\displaystyle{ H = -\sum _{j}w_{i,j}c_{i}^{\dag }c_{ j} + h.c. }$$
(51)

with

$$\displaystyle{ w_{i,j} = w\frac{e^{i\,\phi \,d_{i,j}}} {\vert d_{i,j}\vert ^{\alpha }}, }$$
(52)

where \(\phi = \frac{2\pi } {N_{S}}\varPhi\), being Φ a constant, N S the number of sites. The filling f is defined to be f = N∕N S , where N is the number of sites. d i, j is the oriented distance between the sites i and j,

$$\displaystyle{ d_{i,j} = \left \{\begin{array}{c} (i - j)\quad \mathrm{if}\:\left \vert i - j\right \vert \leq N_{S} -\left \vert i - j\right \vert \\ - N_{S} + \left \vert i - j\right \vert \quad \mathrm{otherwise}. \end{array} \right. }$$
(53)

Due to the translational invariance, the eigenstates are plane waves, and, for finite N S , the spectrum is given by:

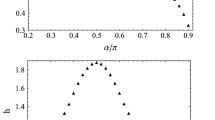
$$\displaystyle{ E_{k} = -2w\left \{\begin{array}{cc} \mbox{ $\sum _{m=1}^{\frac{N-1} {2} } \frac{1} {m^{\alpha }}\cos \left ((k+\phi )m\right )$} & \text{for odd}\:N_{S}\,,\\ \\ \sum _{m=1}^{\frac{N} {2} -1}\frac{1}{j^{\alpha }}\cos \left (\left (k+\phi \right )m\right ) + \frac{\cos \left (\pi n_{k}\right )} {2\left (\frac{N_{S}} {2} \right )^{\alpha }} & \text{for even}\:N_{S}\,. \end{array} \right. }$$
(54)

For ϕ = 0, the single-particle spectrum is always monotonous in the interval k ∈ [0, π], while for ϕ ≠ 0 the spectrum can split in two branches for α < α c < 1, where the critical value α c depends both on N and ϕ. This means that at fixed ϕ and N S ≫ 1 at half-filling, all the momenta k are occupied in an alternating way, as shown in Fig. 3. Thus, for α < α c and at half-filling, the ground-state is a Bell-paired state, and the EE grows linearly with N s (with slope ln2), resulting in a volume law and the Fermi surface has a fractal counting box dimension d box = 1. On the contrary, when α > α c only a fraction of the momenta are occupied in an alternating way, since the “zig-zag” structure of the dispersion relation is partially lost. As a result, the slope of the EE decreases.

Fig. 3
figure 3

Spectrum of the Hamiltonian in Eq. (51) with Φ = 0. 1, α = 0. 1, filling factor f = 0. 5 and N S = 100. Left inset: detail of the main plot showing the alternating occupation of the modes k, the Fermi energy corresponding to the dashed line. Right inset: decrease of the alternating occupation with increasing α. We set Φ = 0. 1, α = 0. 4, f = 0. 5 and N S = 100

Full size image

We conclude by observing that as long as the dispersion is such that the half-filling occupation is alternate in k, entanglement is created between antipodal sites and the system violates the area law behavior, in favour of a volume law.