Harnessing Butterflies: Theory and Practice of the Stochastic Seasonal to Interannual Prediction System (StocSIPS)

Lovejoy, S.; Del Rio Amador, L.; Hébert, R.

doi:10.1007/978-3-319-58895-7_17

S. Lovejoy²,
L. Del Rio Amador² &
R. Hébert²

1804 Accesses
11 Citations
1 Altmetric

Abstract

The atmosphere is governed by continuum mechanics and thermodynamics yet simultaneously obeys statistical turbulence laws. Up until its deterministic predictability limit (τ _w ≈ 10 days), only general circulation models (GCMs) have been used for prediction; the turbulent laws being still too difficult to exploit. However, beyond τ _w—in macroweather—the GCMs effectively become stochastic with internal variability fluctuating about the model—not the real world—climate and their predictions are poor. In contrast, the turbulent macroweather laws become advantageously notable due to (a) low macroweather intermittency that allows for a Gaussian approximation, and (b) thanks to a statistical space-time factorization symmetry that (for predictions) allows much decoupling of the strongly correlated spatial degrees of freedom. The laws imply new stochastic predictability limits. We show that pure macroweather—such as in GCMs without external forcings (control runs)—can be forecast nearly to these limits by the ScaLIng Macroweather Model (SLIMM) that exploits huge system memory that forces the forecasts to converge to the real world climate.

To apply SLIMM to the real world requires pre-processing to take into account anthropogenic and other low frequency external forcings. We compare the overall Stochastic Seasonal to Interannual Prediction System (StocSIPS, operational since April 2016) with a classical GCM (CanSIPS) showing that StocSIPS is superior for forecasts 2 months and further in the future, particularly over land. In addition, the relative advantage of StocSIPS increases with forecast lead time.

In this chapter we review the science behind StocSIPS and give some details of its implementation and we evaluate its skill both absolute and relative to CanSIPS.

Access provided by CONRICYT-eBooks. Download chapter PDF

Predicting the global temperature with the Stochastic Seasonal to Interannual Prediction System (StocSIPS)

Article 22 May 2019

Using regional scaling for temperature forecasts with the Stochastic Seasonal to Interannual Prediction System (StocSIPS)

Article 05 April 2021

The Global/Regional Integrated Model System (GRIMs): an Update and Seasonal Evaluation

Article 10 October 2022

Keywords

1 Introduction

1.1 Deterministic, Stochastic, Low Level, High Level Laws

L. F. Richardson’s “Weather forecasting by numerical process” (1922) opened the era numerical weather prediction. Richardson not only wrote down the modern equations of atmospheric dynamics, but he also pioneered numerical techniques for their solution and even laboriously attempted a manual integration. Yet this work also contained the seed of an alternative: buried in the middle of a paragraph, he slyly inserted the now iconic poem: “Big whirls have little whirls that feed on their velocity, little whirls have smaller whirls and so on to viscosity (in the molecular sense)”. Soon afterwards, this was followed by the Richardson 4/3 law of turbulent diffusion (Richardson 1926), which today is celebrated as the starting point for modern theories of turbulence including the key idea of cascades and scale invariance. Unencumbered by later notions of meso-scale, with remarkable prescience, he even proposed that his scaling law could hold from dissipation up to planetary scales, a hypothesis that has been increasingly confirmed in recent years. Today, he is simultaneously honoured by the Royal Meteorological Society’s Richardson prize as the father of numerical weather prediction, and by the Nonlinear Processes division the European Geosciences Union’s Richardson medal as the grandfather of turbulence approaches.

Richardson was not alone in believing that in the limit of strong nonlinearity (high Reynolds number, Re), that fluids would obey new high level turbulent laws. Since then, Kolmogorov, Corrsin, Obhukhov, Bolgiano and others proposed analogous laws, the most famous of which is the Kolmogorov law for velocity fluctuations (it is nearly equivalent to Richardson’s law). While the laws of continuum mechanics and thermodynamics are deterministic, the classical turbulent laws characterize the statistics of fluctuations as a function of space-time scale; they are stochastic. Just as the laws of statistical mechanics are presumed to be compatible with those of continuum mechanics—and even though no proof (yet) exists—the latter are also presumed to be compatible with the higher level turbulence laws, see the comprehensive review (Lovejoy and Schertzer 2013).

If both continuum mechanics and turbulent laws are valid, then both are potentially exploitable for making forecasts. Yet for reasons that we describe below, for forecasting, only the brute force integration of the equations of continuum mechanics—general circulation models (GCMs)—have been developed to any degree. In this paper we review an early attempt to directly exploit the turbulent laws for macroweather forecasting, i.e. for forecasts beyond the deterministic predictability limit (≈10 days).

1.2 The Status of the Turbulent Laws

The classical turbulent laws are of the scaling form: fluctuation ≈ (turbulent flux) × (scale)^H where H is the fluctuation exponent (for the Kolmogorov law, H = 1/3, see below). The scaling form is a consequence of the scale invariance of the governing laws; symbolically, (laws) ⟶ (scale change by factor λ) ⟶ λ ^H (laws), (note that the scale change must be anisotropic, see Schertzer et al. (2012)). The atmosphere has structures spanning the range of scales from planetary to submillimetric with Re ≈ 10¹²: making it in principle an ideal place to test such high Re theories. However, the classical laws were based on very restrictive assumptions, they used unrealistic notions of turbulent flux and scale. In particular, the fluxes (which are actually in Fourier space and typically go from small to large wavenumbers) were assumed to be homogeneous or at least quasi-Gaussian. However a basic feature of atmospheric dynamics is that almost all of the energy and other fluxes are sparsely distributed in storms—and in their centres—and this enormous turbulent intermittency was not taken into account. In addition, the classical notion of scale was naïve: it was taken to be the usual Euclidean distance between two points, i.e. it was isotropic, the same in all directions.

To be realistic, Schertzer and Lovejoy (1985) argued that the classical laws needed to be generalized precisely to take into account intermittency and anisotropy (especially stratification) and they introduced the main tools: multifractal cascade processes and Generalized Scale Invariance. Profiting from the golden age of geophysical data (remotely sensed, in situ and airborne), models and reanalyses (model–data hybrids), a growing body of work has largely vindicated this view, and has resulted in a quantitative characterization of the relevant multifractal hierarchy of exponents over wide ranges of space and time scales. While the laws are indeed of the (generalized) scaling form indicated above, with only a few exceptions the values of the exponents still have not been derived theoretically. They are nevertheless robust with quite similar values being found in diverse empirical data sets as well as in GCM outputs.

While large scale boundary conditions clearly affect the largest scales of flows, at small enough scales, the latter become unimportant so that, for example, in the atmosphere for scales below about 5000 km, the predictions of turbulent cascade theories are accurate to within typically ±0.5% (see, e.g., Chap. 4 of Lovejoy and Schertzer (2013), although at larger scales, deviations are important. If the turbulent laws are insensitive to driving mechanisms and boundary conditions, then they should be “universal”, operating, for example, in other planetary atmospheres. This prediction was largely confirmed in a quantitative comparison of turbulent laws on Earth and on Mars. It turns out with the exception of the largest factor of five or so in scale that statistically, we are twins with our sister planet (Chen et al. 2016), see Fig. 1a, b!

1.3 Status of Forecasts Based on the Classical Laws and their Prospects with Turbulence Laws

Over the last decades, conventional numerical approaches have developed to the point where they are now skilful up until nearly their theoretical (deterministic) predictability limits—itself close to the lifetimes of planetary structures (about 10 days, see below). Actually—due to stochastic parametrizations—state of the art ensemble GCM forecasts are stochastic–deterministic hybrids, but this limit is still fundamental. At the same time, the strong intermittency (multifractality) over this range has meant that stochastic forecasts based on the turbulent laws must be mathematically treated as (state) vector anisotropic multifractal cascade processes, the mathematical understanding of which is still in its infancy (see, e.g., Schertzer and Lovejoy (1995)), GCMs are the only alternative. However, if we consider scales of many lifetimes of planetary structures—the macroweather regime—then the situation is quite different. On the one hand, because of the butterfly effect (sensitive dependence on initial conditions), in macroweather even fully deterministic GCMs become stochastic. On the other hand, as pointed out in Lovejoy and Schertzer (2013) (Lovejoy and de Lima 2015; Lovejoy et al. 2015) in their macroweather limit, the turbulence laws become much simpler and—as we review below—can already be used to yield monthly, seasonal, annual and decadal forecasts that are comparable or better than the GCM alternatives. The stochastic forecasts that we describe here thus effectively harness the butterfly effect. Significantly, their forecasts already appear to be close to new—stochastic—predictability limits.

As we review below, there are two principal reasons that macroweather turbulent laws are tractable for forecasts. The first is that macroweather intermittency is generally low enough that a Gaussian model is a workable approximation (although not for the extremes)—and the corresponding prediction problem has been mathematically solved. This is the basis of the ScaLIng Macroweather Model (SLIMM (Lovejoy et al. 2015)) that is the core of the Stochastic Seasonal and Annual Prediction System (StocSIPS) that we describe in this review paper. The second macroweather simplification is that the usual size-lifetime relations breakdown, being replaced by new ones and an important new property called “statistical space-time factorization” (SSTF) holds (at least approximately). It turns out that the SSTF effectively transforms the forecast problem from a familiar deterministic nonlinear PDE initial value problem into a stochastic, fractional order linear ODE past value problem. In contrast at macroweather time scales, a fundamental GCM limitation comes to the fore: each GCM converges to its own model climate, not to the real world climate. While this was not important at shorter weather scales, now it becomes a fundamental obstacle. We conclude that for macroweather forecasting, the turbulent approach becomes attractive while the GCM approach becomes unattractive. Below, we compare the skills of the two different approaches and underline the advantages of exploiting the turbulent laws.

This review is structured as follows: we first discuss and summarize macroweather statistics (Sect. 2). In Sect. 3, we describe the forecast model and its skill, and in Sect. 4, we compare stochastic hindcasts with GCMs both with and without external forcings. In Sect. 5 we conclude.

2 Macroweather Statistics

2.1 The Transition from Weather to Macroweather

Ever since the first atmospheric spectra (Panofsky and Van der Hoven 1955; Van der Hoven 1957), it has been known that there is a drastic change in atmospheric statistics at time scales of several days. At first ascribed to “migratory pressure systems”, termed a “synoptic maximum” (Kolesnikov and Monin 1965), it was eventually theorized as baroclinic instability (Vallis 2010). However, its presence in all the atmospheric fields (Fig. 1c), its true origin and its fundamental implications could not be appreciated until the turbulent laws were extended to planetary scales.

The key point is that the horizontal dynamics are controlled by the energy flux ε to smaller scales (units W/Kg, also known as the “energy rate density”). Although this is the same dimensional quantity upon which the Kolmogorov law is based (Δv = ε ^1/3 L ^1/3 for the velocity difference Δv across a distance L), it had not been suggested that it hold up to planetary scales; Kolmogorov himself believed that it would not hold to more than several hundred metres (Fig. 2). Indeed as pointed out in Lovejoy et al. (2007) on the basis of state-of-the-art dropsonde data, the original Kolmogorov law is isotropic and doesn’t appear to hold anywhere in the atmosphere (at least at scales above ≈5 m)! However, the recognition that an anisotropic generalization of the Kolmogorov law could account for the horizontal statistics (with the vertical being controlled by buoyancy force variance fluxes and Bolgiano–Obhukhov statistics) explains how it is possible for the horizontal Kolmogorov law to hold up to planetary scales (see Fig. 1a, for the space-time scaling up to planetary scales, see also Fig. 3 for IR radiances). The classical lifetime–size (L) relation is then obtained by using dimensional analysis on ε: τ ≈ ε ^−1/3 L ^2/3 where L is the horizontal extent of a structure (no longer an isotropic 3D estimate of its size). This law has been validated in both Lagrangian and Eulerian frames, see Radkevitch et al. (2008) (Pinel et al. 2014, Fig. 3).

If one estimates ε by dividing the total tropospheric mass by the total solar power that is transformed into mechanical energy (about 4% of the total this is the thermodynamic efficiency of the atmospheric heat engine; see e.g. Pauluis (2011)), then one finds ε ≈ 1 mW/Kg which is close to the directly estimated empirical value (it even explains regional variations, see Fig. 2). Using ε ≈ 1 mW/Kg, L = 20,000 km (the largest great circle distance) this value implies that the lifetime of planetary structures and hence the weather–macroweather transition is τ _w ≈ 5–10 days. When the theory is applied to the ocean (which is similarly turbulent with ε ≈ 10⁻⁸ W/Kg), one obtains a transition at about 1–2 years (also observed, Lovejoy and Schertzer (2010), Fig. 1b). Finally, it can be used to accurately estimate ε ≈ 40 mW/Kg on Mars and hence the corresponding Martian transition scale at about 1.8 sols (Fig. 1b, Lovejoy et al. 2014).

From the point of view of turbulent laws, the transition from weather to macroweather is a “dimensional transition” since at time scales longer than τ _w, the spatial degrees of freedom are essentially “quenched” so that the system’s dimension is effectively reduced from 1 + 3 to 1 (Lovejoy and Schertzer 2010). Using spectral analysis Fig. 4 shows that simple multifractal turbulence models reproduce the transition. GCM control runs, i.e. with constant external forcings (see Sect. 2.2 and Fig. 5c)—also reproduce realistic macroweather variability, justifying the term “macroweather”. However in forced GCMs—as with instrumental and multiproxy data beyond a critical time scale τ _c, the variability starts to increase again (as in the weather regime) and the true climate regime begins; τ _c ≈ 10 years in the anthropocene, and τ _c ≳ 100 years in the pre-industrial epoch, (see Sect. 2.2, Fig. 5).

In order to understand the key difference between weather, macroweather and the climate, rather than spectra, it is useful to consider typical fluctuations. Classically—for example, in the Kolmogorov law—fluctuations were taken to be differences, i.e. ΔT(Δt):

$$ {\left(\Delta T\left(\Delta t\right)\right)}_{\mathrm{diff}}=T(t)-T\left(t-\Delta t\right) $$

(1)

While this is fine for weather fluctuations—these typically increase with scale Δt—it is not adequate for those that typically decrease with Δt, and as we shall see this includes macroweather fluctuations. For these, we often consider “anomalies”; for example, for the temperature anomaly T(t) is the temperature with both the annual cycle and the overall mean of the series removed so that $ \langle $ T $ \rangle $ = 0 where “$ \langle $.$ \rangle $” indicates averaging. For such zero mean anomaly series T(t), define the Δt resolution anomaly fluctuation by:

$$ {\left(\Delta T\left(\Delta t\right)\right)}_{\mathrm{anom}}\approx \frac{1}{\Delta t}\underset{t-\Delta t}{\overset{t}{\int }}T\left({t}^{\prime}\right)d{t}^{\prime } $$

(2)

(as for differences, in ΔT(Δt) we suppressed the t dependence since we assume that the fluctuations are statistically stationary). Since T(t) fluctuates around zero, averaging it at larger and larger Δt tends to decrease the fluctuations so that the decreasing classical anomaly fluctuations and the increasing difference fluctuations will each have restricted and incompatible ranges of validity.

In general, average fluctuations may either increase or decrease depending on the range of Δt considered so that we must define fluctuations in a more general way; wavelets provide a fairly general framework for this. A simple expedient combines averaging and differencing while overcoming many of the limitations of each: the Haar fluctuation (from the Haar wavelet). It is simply the difference of the mean over the first and second halves of an interval:

$$ {\left(\Delta T\left(\Delta t\right)\right)}_{\mathrm{Haar}}=\frac{2}{\Delta t}\underset{t-\Delta t/2}{\overset{t}{\int }}T\left({t}^{\prime}\right)d{t}^{\prime }-\frac{2}{\Delta t}\underset{t-\Delta t}{\overset{t-\Delta t/2}{\int }}T\left({t}^{\prime}\right)d{t}^{\prime } $$

(3)

(see Lovejoy and Schertzer (2012) for these fluctuations in a wavelet formalism). In words, the Haar fluctuation is the difference fluctuation of the anomaly fluctuation, it is also equal to the anomaly fluctuation of the difference fluctuation. In regions where the fluctuations decrease with scale we have:

$$ \begin{array}{l}{\left(\Delta T\left(\Delta t\right)\right)}_{\mathrm{Haar}}\approx {\left(\Delta T\left(\Delta t\right)\right)}_{\mathrm{anom}}\kern2.5em \left(\mathrm{decreasing}\kern0.5em \mathrm{with}\kern0.5em \Delta t\right)\\ {}{\left(\Delta T\left(\Delta t\right)\right)}_{\mathrm{Haar}}\approx {\left(\Delta T\left(\Delta t\right)\right)}_{\mathrm{diff}}\kern2.5em \left(\mathrm{increasing}\kern0.5em \mathrm{with}\kern0.5em \Delta t\right)\end{array} $$

(4)

In order for Eq. (4) to be reasonably accurate, the Haar fluctuations in Eq. (3) need to be multiplied by a calibration factor; here, we use the canonical value 2 although a more optimal value could be tailored to individual series.

Over ranges where the dynamics have no characteristic time scale, the statistics of the fluctuations are power laws so that:

$$ \left\langle {\left|\Delta T\left(\Delta t\right)\right|}^q\right\rangle \propto \Delta {t}^{\xi (q)} $$

(5)

the left-hand side is the qth order structure function and ξ(q) is the structure function exponent. “< >” indicates ensemble averaging; for individual series this is estimated by temporal averaging (over the disjoint fluctuations in the series). The first order (q = 1) case defines the “fluctuation exponent” ξ(1) = H:

$$ \left\langle \left|\Delta T\left(\Delta t\right)\right|\right\rangle \propto \Delta {t}^H $$

(6)

In the special case where the fluctuations are quasi-Gaussian, ξ(q) = qH and the Gaussian white noise case corresponds to H = −1/2. More generally, there will be “intermittency corrections” so that:

$$ K(q)= qH-\xi (q) $$

(7)

where K(q) is a convex function with K(1) = 0. K(q) characterizes the multifractality associated with the intermittency.

Equation (6) shows that the distinction between increasing and decreasing mean fluctuations corresponds to the sign of H. It turns out that the anomaly fluctuations are adequate when −1 < H < 0 whereas the difference fluctuations are adequate when 0 < H < 1. In contrast, the Haar fluctuations are useful over the range −1 < H < 1 which encompasses virtually all geoprocesses, hence its more general utility. When H is outside the indicated ranges, then the corresponding statistical behaviour depends spuriously on either the extreme low or extreme high frequency limits of the data.

2.2 The low Frequency Macroweather Limit and the Transition to the Climate

We have argued that there is a drastic statistical transition in all the atmospheric fields at time scales of 5–10 days, and that the basic equations have no characteristic time scale. However, it was noted since (Lovejoy and Schertzer 1986) (Fig. 5a) that global temperature differences tend to increase in a scaling manner right up to the ice age scales: the glacial-interglacial “window” at about 50 kyrs (a half cycle) over which fluctuations are typically of the order ±2 to ±4 K.

Figure 5a shows the root mean square second order structure function defined by difference fluctuations $ {\left\langle \Delta T{\left(\Delta t\right)}_{\mathrm{diff}}^2\right\rangle}^{1/2} $ for both local and hemispherically averaged temperatures. From the above discussion, we anticipate that it will give spurious results in the regions where the true fluctuations decrease with scale; indeed, the local (central England) series (upper left in Fig. 5a and ocean cores beyond ≈100 kyrs, upper right) are spuriously flat (i.e., the differences do not reflect the underlying scaling of the fluctuations that are in fact decreasing over these ranges). This is confirmed using more modern data as well as Haar rather than difference fluctuations, in Fig. 5b that shows a composite of temperature variability over the range of scales of hours to nearly a million years. From Fig. 5b, it can be seen that the drastic weather–macroweather spectral transition corresponds to a change in the sign of H for H > 0 to H < 0, i.e. from fluctuations increasing to fluctuations decreasing with scale. The bottom of the figure shows extracts of typical data at the corresponding resolutions, when H > 0, the signal “wanders” like a drunkard’s walk, when H < 0, successive fluctuations tend to cancel out.

Moving to the longer time scales, one may also note that beyond a decade or two, the fluctuations again increase with scale. In reality, as one averages from weeks to months to years, the temperature fluctuations are indeed averaged out, appearing to converge to a fixed climate. However, starting at decades, this apparent fixed climate actually starts to fluctuate, varying up to ice age scales in much the same way as the weather varies (with nearly the same exponent H ≈ 0.4, see Fig. 5b). While the adage says “The climate is what you expect, the weather is what you get”, the actual data indicate that “Macroweather is what you expect, the climate is what you get”.

The annual and decadal scales in Fig. 5a, b are from the anthropocene, it is important to compare this with the pre-industrial variability. This comparison is shown in detail in Fig. 5c, d that includes comparisons with GCM outputs. From the figures we see that in the anthropocene, macroweather ends (scale τ _c) at around a decade or so; Fig. 6 gives estimates of τ _c averaged over fixed latitudes showing that it is a little shorter in the low latitudes. We have seen (Fig. 4) that without external forcing, turbulence models when taken to their low frequency limit reproduce macroweather statistics; the same is true of GCMs in their “control run” mode (Fig. 5c). These results are important for macroweather forecasting since they represent a potential calculable climate perturbation to the otherwise (pure internal variability) macroweather behaviour.

In order to reproduce the low frequency climate regime characterized by increasing fluctuations, we therefore need something new: either a new source of internal variability or external forcings. Figure 5d shows that whereas in the anthropocene, the GCMs with Green House Gas (GHG) forcings do a good job of reproducing the variability, in the pre-industrial period (Fig. 5c), their centennial and millennial scale variability seems to be too weak (at least when using current estimates of “reconstructed” solar and volcanic forcings (Lovejoy et al. 2013)).

The usual way to understand the low frequencies is to consider them as responses to small perturbations, indeed, even the strong anthropogenic forcing is less than 1% of the mean solar flux and may be considered this way. This smallness is the usual justification for making the approximation that the external forcings (whether of natural or anthropogenic origin) yield a roughly linear response, indeed, this is the basis of linearized energy balance models and it can also be supported from a dynamical systems point of view (Ragone et al. 2015).

In order to avoid confusion, it is worth making these notions more precise. For simplicity, consider the atmosphere with fixed external radiative forcing F(r) at location r, (e.g. corresponding to GCM control runs). For this fixed forcing, the (stochastic) temperature field is:

$$ {T}_F\left(\underline{r},t\right)=\left\langle {T}_F\left(\underline{r}\right)\right\rangle +{T}_F^{\prime}\left(\underline{r},t\right) $$

(8)

where the ensemble average is independent of time (since the past forcing is fixed) and T’ (with $ \langle $ T’$ \rangle $ = 0) is the random deviation. If we identify $ F\left(\underline{r}\right)\to F\left(\underline{r}\right)+\Delta F\left(\underline{r},t\right) $ so that the climate part increases from $ \left\langle {T}_F\left(\underline{r}\right)\right\rangle \to \left\langle {T}_{F+\Delta F}\left(\underline{r},t\right)\right\rangle $ i.e. $ {T}_{F,\mathrm{clim}}\left(\underline{r}\right)\to {T}_{F+\Delta F,\mathrm{clim}}\left(\underline{r},t\right) $ and:

$$ \Delta {T}_{\Delta F,\mathrm{clim}}\left(\underline{r},t\right)={T}_{F+\Delta F,\mathrm{clim}}\left(\underline{r},t\right)-{T}_{F,\mathrm{clim}}\left(\underline{r}\right) $$

(9b)

is the change in the climate response to the changed forcing. The generalized climate sensitivity λ can then be defined as:

$$ \lambda \left(\underline{r},t\right)=\frac{\partial {T}_{F,\mathrm{clim}}\left(\underline{r},t\right)}{\partial F\left(\underline{r},t\right)}\approx \frac{\Delta {T}_{F,\mathrm{clim}}\left(\underline{r},t\right)}{\Delta F\left(\underline{r},t\right)} $$

(10)

GCMs make many realizations (sometimes from many models—“multimodel ensembles”) and this equation may be used to determine the climate response and generalized sensitivity (the more common equilibrium and transient climate sensitivities are discussed momentarily). If t is a future time, then $ {T}_{F+\Delta F}\left(\underline{r},t\right) $ is a prediction of the future state of the atmosphere including the internal variability and the changed forcing, whereas $ {T}_{F+\Delta F,\mathrm{clim}}\left(\underline{r},t\right) $ is called a climate “projection”. Sometimes climate projections and sensitivities are estimated from single GCM model runs by estimating the ensemble averages by temporal averages over decadal time scales.

We can now state the linear response assumption:

$$ \Delta {T}_{\mathrm{clim}}\left(\underline{r},t\right)=G\left(\underline{r},t\right)\ast \Delta F\left(\underline{r},t\right) $$

(11)

where G(r,t) is the system Green’s function, in this context, it is also known as the Climate Response Function (CRF), “_*” means convolution. Equation (11) is the most general statement of linearity for systems whose physics is the same at all times and locations (it assumes that only the differences in times and locations between the forcing and the responses are important). To date, applications of CRFs have been limited to globally averaged temperatures and forcings so that the spatial (r) dependence is averaged out; for simplicity, below we drop the spatial dependence.

The CRF is only meaningful if the system is linear, in which case it is the response of the system to a Dirac function forcing. The simplest CRF is itself a Dirac function possibly with a lag Δt ≥ 0, i.e. G(t) = λδ(t − Δt), (sensitivity λ). Such CRFs have been used with some success by Lean and Rind (2008) and Lovejoy (2014a) to account for both anthropogenic and natural forcings. Rather than characterize the system by a response to Dirac forcing, it is more usual to characterize it by its responses to a step function F(t) (the Equilibrium Climate Sensitivities, ECS) or to a linearly increasing F(t) (“ramps”; Transient Climate Responses, TCR). Since step functions and ramps are simply the first and second integrals of the Dirac function, if the response is linear (Eq. 11), then knowledge of these responses as functions of time is equivalent to the CRF (note that usually the ECS is defined as the response after an infinite time, and TCR after a finite conventional period of 70 years).

Traditionally, Green’s functions are deduced from linear differential operators arising from linear differential equations. For example, by treating the ocean as a homogeneous slab, the linearized energy balance equation may be used to determine the CRF, but the latter is an integer ordered ordinary differential equation for the mean global temperature which leads to exponential CRFs (e.g. Schwartz 2012; Zeng and Geil 2017). Such CRFs are unphysical since they break the scaling symmetry of the dynamics; the dynamical ocean is better modelled as a hierarchy of slabs each with its own time constant (rather than a unique slab with a unique constant). To model this in the linear energy balance framework requires introducing differential terms of fractional order; these generally lead to the required scaling CRFs (SCRF) and will be investigated elsewhere.

Rather than determine the CRF from differential operators, they can be determined directly from the symmetries of the problem. In this case (considering only the temporal CRF, G(t)), the three relevant symmetries are: (a) that the physics is stationary in time, (b) that the system is causal, (c) that there is no characteristic time scale. From these three symmetries we obtain $ G(t)\propto {t}^{H_R-1}\Theta (t) $ where H _R is the SCRF response exponent and Θ(t) is the Heaviside function (=0 for t < 0, =1 for t ≥ 0), necessary to ensure causality of the response.

Before continuing, we must note that such pure power law SCRFs are unusable due to either high or low frequency divergences; in this context, the divergences are aptly called “runaway Green’s function effect” (Hébert and Lovejoy 2015) so that truncations are needed. For forcings that have infinite “impulses” (such as step functions or ramps whose temporal integrals diverge), when H _R > 0 low frequency temperature divergences will occur, unless G(t) has a low frequency cutoff whereas whenever H _R < 0, the cutoff must be at high frequencies. For example, Rypdal (2015) and Rypdal and Rypdal (2014) use an SCRF with exponent H _R > 0 (without cutoff) so that low frequency temperature divergences occur unless all the forcings return to zero quickly enough. This is why Hebert et al. (2017) use H _R < 0 but introduce a high frequency cutoff τ in order to avoid the divergences: $ G(t)={\lambda}_H{\left(t/\tau +1\right)}^{H_R-1}\Theta (t) $; λ _Η is a generalized sensitivity. In this case, the cutoff should correspond to the smallest time scale over which the linear approximation is valid. While the most general (space-time) linear approximation (i.e. with G(r,t)) may be valid at shorter time scales, if we reduce the problem to a “zero dimensional” (globally averaged) series T(t), then clearly a linear response is only possible at scales over which the ocean and atmosphere are strongly coupled. The breakthrough in understanding and quantifying this was to use Haar fluctuations to show that the coupling of air temperature fluctuations over land and SST fluctuations abruptly change from very low to very high at the ocean weather-ocean macroweather transition scale of τ = 1–2 years (see Fig. 7). A truncated SCRF with this τ and with H _R ≈ −0.5 allows (Hebert et al. 2017) to make future projections based on historical forcings as well as to accurately project the forced response of GCM models.

2.3 Climate Zones and Intermittency: In Space and Time

We have argued that macroweather is the dynamical regime of fluctuations with time scales between the lifetimes of planetary structures (τ _w) and the climate regime where either new (slow) internal processes or external forcings begin to dominate (τ _c). We have seen that a key characteristic is that mean fluctuations tend to decrease with time scale so that the macroweather fluctuation exponent H < 0. However in general, fluctuations require an infinite hierarchy of exponents for their characterization (the entire function K(q) in Eq. (7)). In particular, when K(q) is large, the process is typically “spikey” with the spikes distributed in a hierarchical manner over various fractal sets.

To see this, consider the data shown in Fig. 8a (macroweather time series and spatial transects, top and bottom, respectively). Fig. 8b compares the root mean square (RMS, exponent ξ(2)/2) and mean fluctuation (exponent H = ξ(1)) of macroweather temperature temporal data (bottom) and for the transect (top). When the system is Gaussian, ξ(q) = qH so that K(q) = 0) and we obtain ξ(2)/2 = ξ(1) so that the lines in the figure will be parallel. We see that to a good approximation this is indeed true of the nonspikey temporal series (Fig. 8a, top). However, the spatial transect is highly spikey (Fig. 8a, bottom) and the corresponding statistics (the top lines in Fig. 8b) tend to converge at large Δt. To a first approximation, it turns out that ξ(2)/2 – ξ(1) ≈ K′(1) = C ₁ which characterizes the intermittency near the mean. However, there is a slightly better characterization of C ₁ (described in Lovejoy and Schertzer (2013), Chap. 11), using the intermittency function (see Fig. 8c and caption) whose theoretical slope (for ensemble averaged statistics) is exactly K′(1) = C ₁. As a point of comparison, recall that fully developed turbulence in the weather regime typically has C₁ ≈ 0.09, (see Lovejoy and Schertzer (2013), Table 4.5). The temporal macroweather intermittency (C₁ ≈ 0.01) is indeed small whereas the spatial intermittency is large (C ₁ ≈ 0.12).

The strong spatial intermittency is the statistical expression of the existence of climate zones (Lovejoy and Schertzer 2013). However we shall see that due to space-time statistical factorization (next subsection), each region may be forecast separately. In addition, a low intermittency (Gaussian) approximation can be made for the temporal statistics. Note that in spite of this Gaussian approximation for forecasts, there is evidence that the 5th and higher moments of the temperature fluctuations diverge (i.e. power probability distributions) so that the Gaussian approximation fails badly for the extreme 3% or so of the fluctuations (see Lovejoy and Schertzer (1986) and Lovejoy (2014a)).

2.4 Scaling, Space-Time Statistical Factorization and Size-Lifetime Relations

In the previous section we saw that there was evidence for scaling separately both in space and in time with the former being highly intermittent (multifractal) and the latter being nearly Gaussian (Fig. 8). However, in order to make stochastic macroweather forecasts, we need to understand the joint space-time macroweather statistics and these turn out to be quite different from those in the weather regime. For the latter, recall that there exist well-defined statistical relations between weather structures (“meso-scale complexes”, “storms”, “turbulence”, etc.) of a given size L and their lifetimes τ. Indeed, the textbook space-time “Stommel” diagrams that adorn introductory meteorology textbooks show log spatial scale versus log temporal scale plots with boxes or circles corresponding to different morphologies and phenomenologies and these typically occupy the diagonals. These diagrams are usually interpreted as implying that each factor of two or so in spatial scale corresponds to fundamentally different dynamical processes, each with its own typical spatial extent and corresponding lifetime. However, as pointed out in Schertzer et al. (1997), the part of the diagram occupied by realistic structures and processes are typically not only on diagonals (implying a scaling space-time relation), but are on the precise diagonal whose slope has the value 2/3, theoretically predicted by the (Lagrangian, co-moving) size-lifetime relation discussed above: τ = ε ^−1/3 L ^2/3. The usual interpretation is an example of the “phenomenological fallacy” (Lovejoy and Schertzer 2007): rather than refute the scaling hypothesis, the Stommel diagrams support it.

As usual, the Eulerian (fixed frame) space-time relations are much easier to determine empirically, although theoretically their relation to Lagrangian statistics is not trivial. In a series of papers based on high resolution lidar data (Lilley et al. 2008; Lovejoy et al. 2008; Radkevitch et al. 2008) and then geostationary IR data (Fig. 3, Pinel et al. (2014)), an argument by Tennekes (1975) about the small structures being “swept” by larger ones was extended to the (atmospheric) case assuming that there was no scale separation between small and large horizontal scales. It was concluded that the corresponding Eulerian (i.e. fixed frame) space-time relation generally had space-time spectra of the form:

$$ {P}_{xyt}\left({k}_x,{k}_y,\omega \right)={\left [\kern-0.15em[ \left({k}_x,{k}_y,\omega \right)\right ]\kern-0.15em] }^{-s} $$

(12)

where P _xyt is the space-time spectra density:

$$ {P}_{xyt}\left({k}_x,{k}_y,\omega \right)\propto \left\langle {\left|\tilde{T}\left({k}_x,{k}_y,\omega \right)\right|}^2\right\rangle $$

(13)

and 〚(k _x, k _y, ω)〛 is the wavenumber (k _x ,k _y)–frequency (ω) scale function nondimensionalized by the large scale turbulent velocities (i.e. using ε and the size of the earth). The analogous (real space) second order joint space-time structure function statistics:

$$ {S}_{xyt}\left(\Delta x,\Delta y,\Delta t\right)=\left\langle \Delta T{\left(\Delta x,\Delta y,\Delta t\right)}^2\right\rangle $$

(14)

were of the form:

$$ {S}_{xyt}\left(\Delta x,\Delta y,\Delta t\right)={\left [\kern-0.15em[ \left(\Delta x,\Delta y,\Delta t\right)\right ]\kern-0.15em] }^{\xi (2)} $$

(15)

where 〚(Δx, Δy, Δt)〛 is the real space (nondimensional) scale function for horizontal lag (Δx,Δy) and temporal lag Δt. The scale functions relevant here satisfy the isotropic scaling: 〚λ ⁻¹(Δx, Δy, Δt)〛 = λ ⁻¹〚(Δx, Δy, Δt)〛 and 〚λ(k _x, k _y, ω)〛 = λ〚(k _x, k _y, ω)〛 where λ is a scale reduction factor. This is directly confirmed in Fig. 3 for IR radiances.

In the simplest cases (with no mean advection and ignoring weak scaling singularities associated with waves (Pinel and Lovejoy 2014)), and retaining only a single spatial lag Δx, and wavenumber k _x, the nondimensional scale functions reduce to the usual vector norms, i.e. they are of the form:

$$ \left [\kern-0.15em[ \left(\Delta x,\Delta t\right)\right ]\kern-0.15em] ={\left(\Delta {x}^2+\Delta {t}^2\right)}^{1/2} $$

(16)

$$ \left [\kern-0.15em[ \left({k}_x,\omega \right)\right ]\kern-0.15em] ={\left({k}_x^2+{\omega}^2\right)}^{1/2} $$

(17)

With s = d + ξ(2) with d = the dimension of space-time, in this example d = 2.

In order to define a relationship between a structure of extent L with the lifetime τ, we can use S _xt. For example, if we wait at a fixed location (Δx = 0) for a time τ, we may ask what distance L must we go at a given instant (Δt = 0) in order to expect the same typical fluctuation? This gives us an implicit relation between L and τ: S _xt(0, τ) = S _xt(L, 0); in this simple case (Eqs. 15 and 16) this implies τ = L for the nondimensional variables so that the dimensional relationship would correspond to a constant speed relating space and time. A similar relation would be obtained by using the same argument in Fourier space on the spectral density P.

What is the space-time relation in macroweather where we consider temporal averages over periods >τ _w, typically months or longer? In this case, we average over many lifetimes of structures of all sizes, so clearly size-lifetime relations valid in the weather regime must break down. Lovejoy and Schertzer (2013) and Lovejoy and de Lima (2015) argued on theoretical, numerical and empirical grounds that—at least to a good approximation—the result is statistical space-time factorization (SSTF). The application of the SSTF to the second order statistics means:

$$ \begin{array}{c}\hfill {P}_{xt}\left({k}_x,\omega \right)={P}_x\left({k}_x\right){P}_t\left(\omega \right)\hfill \\ {}\hfill \begin{array}{cc}\hfill {R}_{xt}\left(\Delta x,\Delta t\right)={R}_x\left(\Delta x\right){R}_t\left(\Delta t\right);\hfill & \hfill \hfill \end{array}\hfill \end{array} $$

(18)

Note that in real space we have used correlation functions R _xt(Δx, Δt) = $ \langle $ T(t, x) T(t − Δt, x − Δx)$ \rangle $ rather than Haar structure functions S; in macroweather (H < 0), they are essentially equivalent. However for small lags in time, one effectively goes outside the macroweather regime and Δt = 0 is problematic. When both H _t < 0 and H _x < 0 we can avoid issues that arise at small Δt, Δx by using correlation functions (Fig. 9a) (for the case H _t < 0, H _x > 0, see Sect. 10.3 of Lovejoy and Schertzer (2013)).

Using the autocorrelations to obtain space-time macroweather relations, we obtain R _xt(0, τ) = R _xt(L, 0) so that using factorization and the identity R _t(0) = R _x(0) the implicit τ-L relation is:

$$ {R}_t\left(\tau \right)={R}_x(L) $$

(19)

This is valid if both space and time have H < 0; if there is scaling, we have $ {R}_t\left(\tau \right)\propto {\tau}^{H_t} $ and $ {R}_x(L)\propto {L}^{H_x} $ with exponents H _t < 0, H _x < 0. The lifetime of a macroweather structure of size L is thus:

$$ \tau \propto {L}^{H_x/{H}_t} $$

(20)

which—unless H _x = H _t —is quite different from the lifetime-size relationship in the weather regime; Fig. 9a shows that τ ∝ L ^0.65, for macroweather temperature and precipitation. Fig. 9a, shows that empirically the factorization works well for both temperature and precipitation data, and Fig. 9b shows that it is also (even better) obeyed by the GISS E2R GCM; Del Rio Amador 2017 shows that it holds very accurately for 36 CMIP5 control runs.

It turns out that the SSTF is important for macroweather forecasting. This is because, using means square estimators, it implies that no matter how strong the correlations (teleconnections), if one has long time series at each point, pixel or region, that no further improvement can be made in the forecast by adding co-predictors such as the temperature data at other locations (Del Rio Amador 2017). This effectively means that the original nonlinear initial value PDE problem has been effectively transformed into a linear but fractional ordered ODE “past value” problem, we pursue this in the next sections.

3 Macroweather Forecasting

3.1 The Fractional Gaussian Noise Model and some of Its Characteristics

We have argued that macroweather is scaling but with low intermittency, so that a Gaussian forecasting model may be an acceptable approximation. The simplest such model is fractional Gaussian noise (fGn). We now give a brief summary of some useful properties of fGn; for a longer review, see Lovejoy et al. (2015) and for an extensive mathematical treatment see (Biagini et al. 2008).

Over the parameter range of interest −1/2 < H < 0, fGn is essentially a smoothed Gaussian white noise and its mathematical definition raises similar issues. For our purposes, it is most straightforward to use the framework of generalized functions and start with the unit Gaussian white noise γ(t) which has $ \langle $ γ $ \rangle $ = 0 and is “δ correlated”:

$$ \left\langle \gamma (t)\gamma \left({t}^{\prime}\right)\right\rangle =\delta \left(t-{t}^{\prime}\right) $$

(21)

where “δ” is the Dirac function. The H parameter fGn G _H(t) is thus:

$$ \begin{array}{cc}\hfill {G}_H(t)=\frac{c_H}{\Gamma \left(1/2+H\right)}\underset{-\infty }{\overset{t}{\int }}{\left(t-{t}^{\prime}\right)}^{-\left(1/2-H\right)}\gamma \left({t}^{\prime}\right)d{t}^{\prime };\hfill & \hfill -1<H<0\hfill \end{array} $$

(22)

The constant c _H is a constant chosen so as to make the expression for the statistics particularly simple, see below. Mathematically γ(t) is thus the density of the Wiener process W(t), often written γ(t)dt = dW: just as the Dirac function is only meaningful when integrated, the same is true of γ(t). For fGn, we shall see below that G _H(t)dt = dB _H’ where B _H’ is a generalization of the Wiener process, fractional Brownian motion (fBm, parameter H′ = 1 + H) and B _H’ reduces to a Wiener process when H′ = 1/2. G _H(t) is thus the (singular) density of an fBm measure. In practice, we will always consider G _H(t) smoothed over finite resolutions so that whether we define G _H(t) indirectly via fBm or directly as a smoothing of Eq. (22) the result is equivalent.

We can see by inspection of Eq. (22) that G _H(t) is statistically stationary and by taking ensemble averages of both sides of Eq. (22) we see that the mean vanishes: $ \langle $ G _H(t)$ \rangle $ = 0. When H = −1/2, the process G _−1/2(t) itself is simply a Gaussian white noise. Although we justified the use of fGn as the simplest scaling process, it could also be introduced as the solution of a stochastic fractional ordered differential equation:

$$ \frac{d^{H+1/2}T}{dt^{H+1/2}}=\gamma (t) $$

(23)

the solution of which is T(t) ∝ G _H(t).

Now, take the average of G _H over τ, the “τ resolution anomaly fluctuation”:

$$ {G}_{H,\tau }(t)=\frac{1}{\tau}\underset{t-\tau }{\overset{t}{\int }}{G}_H\left({t}^{\prime}\right)d{t}^{\prime } $$

(24)

If c _H is now chosen such that:

$$ {c}_H={\left(\frac{\boldsymbol{\pi}}{2\operatorname{cos}\left(\boldsymbol{\pi} H\right)\Gamma \left(-2H-2\right)}\right)}^{1/2} $$

(25)

then we have:

$$ \begin{array}{cc}\hfill \left\langle {G}_{H,\tau }{(t)}^2\right\rangle ={\tau}^{2H};\hfill & \hfill -1<H<0\hfill \end{array} $$

(26)

This shows that a fundamental property of fGn is that in the small scale limit (τ → 0), the variance diverges and H is scaling exponent of the root mean square (RMS) value. This singular small scale behaviour is responsible for the strong power law resolution effects in fGn. Since $ \langle $ G _H(t)$ \rangle $ = 0, sample functions G _H,τ(t) fluctuate about zero with successive fluctuations tending to cancel each other out; this is the hallmark of macroweather.

3.1.1 Anomalies

An anomaly is the average deviation from the long-term average and since $ \langle $ G _H(t)$ \rangle $ = 0, the anomaly fluctuation over interval Δt is simply G _H at resolution Δt rather than τ:

$$ \begin{array}{cc}\hfill {\left(\Delta {G}_{H,\tau}\left(\Delta t\right)\right)}_{\mathrm{anom}}=\frac{1}{\Delta t}\underset{t-\Delta t}{\overset{t}{\int }}{G}_{H,\tau}\left({t}^{\prime}\right)d{t}^{\prime }=\frac{1}{\Delta t}\underset{t-\Delta t}{\overset{t}{\int }}{G}_H\left({t}^{\prime}\right)d{t}^{\prime }={G}_{H,\Delta t}(t);\hfill & \hfill \Delta t>\tau \hfill \end{array} $$

(27)

Hence using Eq. (26):

$$ \begin{array}{cc}\hfill \left\langle {\left(\Delta {G}_{H,\tau}\left(\Delta t\right)\right)}_{\mathrm{anom}}^2\right\rangle =\Delta {t}^{2H};\hfill & \hfill -1<H<0\hfill \end{array} $$

(28)

3.1.2 Differences

In the large Δt limit we have:

$$ \left\langle {\left(\Delta {G}_{H,\tau}\left(\Delta t\right)\right)}_{\mathrm{diff}}^2\right\rangle \approx 2{\tau}^{2H}\left(1-\left(H+1\right)\left(2H+1\right){\left(\frac{\Delta t}{\tau}\right)}^{2H}\right) $$

(29)

Since H < 0, the differences asymptote to the value 2τ ^2H (double the variance). Notice that since H < 0, the differences are not scaling with Δt.

3.1.3 Haar Fluctuations

For the Haar fluctuation we obtain:

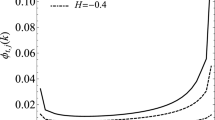
$$ \begin{array}{cc}\hfill \left\langle {\left(\Delta {G}_{H,\tau}\left(\Delta t\right)\right)}_{\mathrm{Haar}}^2\right\rangle =4\Delta {t}^{2H}\left({2}^{-2H}-1\right);\hfill & \hfill \Delta t\ge 2\tau \hfill \end{array} $$

(30)

this scales as Δt ^2H and does not depend on the resolution τ. This relation can be used to estimate the spatial variation of H, Fig. 10 gives the spatial distribution using 20CR data. It can be seen that H is near zero over the oceans and is lower over land, typical values being −0.1 and −0.3, respectively. Below, we see that this corresponds to large memory (and hence forecast skill) over oceans and lower memory and skill over land.

3.1.4 Autocorrelations

$$ \vspace*{-1pc}\begin{aligned}[b] \left\langle {G}_{\tau, H}(t){G}_{\tau, H}\left(t{-}\Delta t\right)\right\rangle & {=}R\left(\widehat{\Delta t}\right)\\ &{=}\frac{\tau^{2H}}{2}\left[{\left(\widehat{\Delta t}{+}1\right)}^{2H{+}2}{+}{\left(\widehat{\Delta t}{-}1\right)}^{2H{+}2}{-}2{\widehat{\Delta t}}^{2H{+}2}\right]; \kern0.5em \widehat{\Delta t}{=}\frac{\Delta t}{\tau }\end{aligned} $$

(31)

3.1.5 Spectra

Since fGn is stationary, its spectrum is given by the Fourier transform of the autocorrelation function. Note that in the above, Δt > 0; since the autocorrelation is symmetric for the Fourier transform with respect to Δt, we use the absolute value of Δt. We obtain:

$$ \begin{array}{cc}\hfill E\left(\omega \right)=\frac{\Gamma \left(3+2H\right)\operatorname{sin}\pi H}{\sqrt{2\pi }}{\left|\omega \right|}^{-\beta };\hfill & \hfill \beta =1+2H\hfill \end{array} $$

(32)

3.1.6 Relation to fBm

It is more common to treat fBm whose differential dB _H’(t) is given by:

$$ \begin{array}{ccc}\hfill {dB}_{H^{\prime }}={G}_H(t) dt;\hfill & \hfill {H}^{\prime }=H+1;\hfill & \hfill 0<{H}^{\prime }<1\hfill \end{array} $$

(33)

so that:

$$ \Delta {B}_{H^{\prime }}\left(\tau \right)={B}_{H^{\prime }}(t)-{B}_{H^{\prime }}\left(t-\tau \right)=\underset{t-\tau }{\overset{t}{\int }}{G}_{H^{\prime }}\left({t}^{\prime}\right)d{t}^{\prime }=\tau {G}_{H^{\prime },\tau }(t) $$

(34)

with the property:

$$ \left\langle \Delta {B}_{H^{\prime }}{\left(\Delta t\right)}^2\right\rangle =\Delta {t}^{2{H}^{\prime }} $$

(35)

While this defines the increments of B _H’(t) and shows that they are stationary, it does not completely define the process. For this, one conventionally imposes B _H’(0) = 0, and this leads to the usual definition:

$$ \begin{aligned}[b]{B}_{H^{\prime }}(t)&=\frac{c_{H^{\prime }}}{\Gamma \left({H}^{\prime }+1/2\right)}\underset{-\infty }{\overset{0}{\int }}\left({\left(t-s\right)}^{H^{\prime }-1/2}-{\left(-s\right)}^{H^{\prime }-1/2}\right)\gamma (s) ds\\[-3pt]&\quad+\frac{c_{H^{\prime }}}{\Gamma \left({H}^{\prime }+1/2\right)}\underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{H^{\prime }-1/2}\gamma (s) ds \end{aligned}\vspace*{-3pt} $$

(36)

(Mandelbrot and Van Ness 1968). Whereas fGn has a small scale divergence that can be eliminated by averaging over a finite resolution τ, the fGn integral $ \underset{-\infty }{\overset{t}{\int }}{G}_H\left({t}^{\prime}\right)d{t}^{\prime } $ on the contrary has a low frequency divergence. This is the reason for the introduction of the second term in the first integral in Eq. (36): it eliminates this divergence at the price of imposing B _H′(0) = 0 so that fBm is nonstationary (although its increments are stationary, Eq.(34)).

A comment on the parameter H is now in order. In treatments of fBm, it is usual to use the parameter H confined to the unit interval, i.e. to characterize the scaling of the increments of fBm. However, fBm (and fGn) are very special scaling processes, and even in low intermittency regimes such as macroweather—they are at best approximate models of reality. Therefore, it is better to define H more generally as the fluctuation exponent (Eq. 6); with this definition, H is also useful for more general (multifractal) scaling processes although the interpretation of H as the “Hurst exponent” is only valid for fBm). When −1 < H < 0, the mean at resolution τ (Eq. 24) defines the anomaly fluctuation, so that H is equal to the fluctuation exponent for fGn, in contrast, for processes with 0 < H < 1, the fluctuations scale as the mean differences and Eq. (35) shows that H′ is the fluctuation exponent for fBm. In other words, as long as an appropriate definition of fluctuation is used, H and H′ = 1 + H are fluctuation exponents of fGn, fBm, respectively. The relation H′ = H + 1 follows because fBm is an integral order 1 of fGn. Therefore, since the macroweather fields of interest have fluctuations with mean scaling exponent −1/2 < H < 0, we use H for the fGn exponent and ½ < H′ < 1 for the corresponding integrated fBm process.

We can therefore define the resolution τ temperature as:

$$ {T}_{\tau }(t)={\sigma}_T{G}_{H,\tau }(t)={\sigma}_T\frac{B_{H^{\prime }}(t)-{B}_{H^{\prime }}\left(t-\tau \right)}{\tau } \vspace*{-3pt}$$

(37)

Using Eq. (26), the τ resolution temperature variance is thus:

$$ \left\langle {T}_{\tau}^2\right\rangle ={\sigma}_T^2{\tau}^{2H}\vspace*{-3pt} $$

(38)

From this and the relation T _τ(t) = σ _T G _H , τ(t), we can trivially obtain the statistics of T _τ(t) from those of G _H , τ(t).

3.2 Mean Square (MS) Estimators for fGn and the ScaLIng Macroweather Model (SLIMM)

The Mean Square (MS) estimator framework is a general framework for predicting stochastic processes, it determines predictors that minimize the prediction error variance, see, e.g., Papoulis (1965). Since Gaussian processes are completely determined by their second order statistics, the MS framework therefore gives optimum forecasts for fGn.

Our problem is to use data T _τ(s) at times s < 0 (or equivalently, the innovations γ(s)) to predict the future temperature T _τ(t) at times t > 0. Denoting this predictor by $ {\widehat{T}}_{\tau }(t) $ MS theory then shows that the latter is given by a linear combination of data, i.e. either the T _τ(s) or equivalently by a linear combination of past white noise “innovations” γ(s):

$$ \begin{array}{c}\hfill {\widehat{T}}_{\tau }(t)=\underset{-{\tau}_0<s\le 0}{\int }{M}_T\left(t,s\right){T}_{\tau }(s) ds\hfill \\ {}\hfill {\widehat{T}}_{\tau }(t)=\underset{-{\tau}_0<s\le 0}{\int }{M}_{\gamma}\left(t,s\right)\gamma (s) ds\hfill \end{array} $$

(39)

where M _T, M _γ are the predictor kernels based on past temperatures and past innovations, respectively, and the range of integration is over all available data, the range –τ ₀ < s ≤ 0. The simplest problems are those where the range extends to the infinite past (τ ₀ → ∞), but practical predictions require the solution for finite τ ₀.

The prediction error is thus:

$$ {E}_T(t)={T}_{\tau }(t)-{\widehat{T}}_{\tau }(t) $$

(40)

and from MS theory, the basic condition imposed by minimizing the error variance $ \left\langle {E}_T^2(t)\right\rangle $ is:

$$ \begin{array}{ccc}\hfill \left\langle {E}_T(t){\widehat{T}}_{\tau }(t)\right\rangle =\left\langle {E}_T(t){T}_{\tau }(s)\right\rangle =\left\langle {E}_T(t)\gamma (s)\right\rangle =0;\hfill & \hfill t>0;\hfill & \hfill s\le 0\hfill \end{array} $$

(41)

This equation states that the (future) prediction error E _T(t) is statistically independent of the predictor $ {\widehat{T}}_{\tau }(t) $ or, equivalently, it is independent of the past data T _τ(s), γ(s) upon which the predictor is based. This makes intuitive sense: if there was a nonzero correlation between the available data and the prediction error, then there would still information in the data that could be used to improve the predictor and reduce the error. Since GCM forecasts are not MS, they do not satisfy this orthogonality condition. On the one hand, this explains how they can have negative skill (see below), on the other, it justifies complex GCM post-processing that exploit past data to reduce the errors. Indeed, a condition used to optimize post-processing corrections is actually close to the orthogonality condition.

In Lovejoy et al. (2015), the mathematically simplest predictor was given in the case of infinite past data but using the innovations γ(s):

$$ \begin{array}{c}\hfill {\widehat{T}}_{\tau }(t)=\underset{-\infty }{\overset{0}{\int }}{M}_{\gamma}\left(t,s\right)\gamma (s) ds\hfill \\ {}\hfill {M}_{\gamma}\left(t,s\right)=\frac{c_H{\sigma}_T}{\tau \Gamma \left(H+3/2\right)}\left[{\left(t-s\right)}^{H+1/2}-{\left(t-\tau -s\right)}^{H+1/2}\right]\hfill \end{array} $$

(42)

The error is:

$$ \begin{aligned}[b]{E}_T&={T}_{\tau }(t)-{\widehat{T}}_{\tau }(t)\\&=\frac{c_H{\sigma}_T}{\tau \Gamma \left(H+3/2\right)}\left[\underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{H+1/2}\gamma (s) ds-\underset{0}{\overset{t-\tau }{\int }}{\left(t-\tau -s\right)}^{H+1/2}\gamma (s) ds\right]\end{aligned} $$

(43)

Since $ \widehat{T}(t) $ depends only on γ(s) for s < 0 and E _T on γ(s) for s > 0, it can be seen by inspection that the orthogonality condition (Eq. 41) holds. Using this MS predictor, we can define the Mean Square Skill Score (MSSS) or “skill” for short:

$$ \mathrm{MSSS}={S}_k(t)=1-\frac{\left\langle {E}_T{(t)}^2\right\rangle }{\left\langle {T}_{\tau }{(t)}^2\right\rangle }\vspace*{-3pt} $$

(44)

For MS forecasts, we can use the orthogonality condition to obtain equivalently;

$$ {S}_k(t)=\frac{\left\langle {\widehat{T}}_{\tau}^2(t)\right\rangle }{\left\langle {T}_{\tau}^2(t)\right\rangle }\vspace*{-3pt} $$

(45)

which shows that for MS forecasts, the skill is the same as the fraction of the variance explained by the predictor.

Using the predictor (Eq. 42) we can easily obtain the skill for fGn forecasts:

$$ \begin{array}{cc}\hfill {S}_k\left(\lambda \right)=\left[\frac{F_H\left(\infty \right)-{F}_H\left(\lambda \right)}{F_H\left(\infty \right)+\frac{1}{2H+2}}\right];\hfill & \hfill \begin{array}{cc}\hfill \lambda =t/\tau; \hfill & \hfill \lambda \ge 1\hfill \end{array}\hfill \end{array} $$

(46)

where the auxiliary function F _H is given by:

$$ \begin{array}{cc}\hfill {F}_H\left(\lambda \right)=\underset{0}{\overset{\lambda -1}{\int }}{\left({\left(1+u\right)}^{H+1/2}-{u}^{H+1/2}\right)}^2 du;\hfill & \hfill \lambda \ge 1\hfill \end{array} $$

(47)

with:

$$ {F}_H\left(\infty \right)={\pi}^{-1/2}{2}^{-\left(2H+2\right)}\Gamma \left(-1-H\right)\Gamma \left(3/2+H\right) $$

(48)

and the asymptotic expression:

$$ {F}_H\left(\lambda \right)={F}_H\left(\infty \right)-\frac{{\left(H+1/2\right)}^2}{-2H}{\lambda}^{2H}+\dots $$

(49)

(Lovejoy et al. 2015). For any system that has quasi-Gaussian statistics and scaling fluctuations with −1/2 < H < 0 the theoretical skill, Eq. (46) represents a stochastic predictability limit, of similar fundamental significance to the usual deterministic predictability limits arising from sensitive dependence on initial conditions. In Sect. 4.2, we show that CMIP5 GCMs can indeed be predicted to nearly this limit using the MS approach outlined here.

Although the MSSS is commonly used for evaluating forecasts, the correlation coefficient between the hindcast and the temperature is occasionally used:

$$ {\rho}_{\overset{\frown}{T},T}\left(t,\tau \right)=\frac{\left\langle {\overset{\frown }{T}}_{\tau }(t){T}_{\tau }(t)\right\rangle -\left\langle {\overset{\frown }{T}}_{\tau }(t)\right\rangle \left\langle {T}_{\tau }(t)\right\rangle }{{\left\langle {\overset{\frown }{T}}_{\tau }{(t)}^2\right\rangle}^{1/2}{\left\langle {T}_{\tau }{(t)}^2\right\rangle}^{1/2}} $$

(50)

Since $ \langle $ T $ \rangle $ = 0, the upper right cross term vanishes and using orthogonality $ \left\langle {T}_{\tau }(t){\overset{\frown }{T}}_{\tau }(t)\right\rangle =\left\langle {\overset{\frown }{T}}_{\tau }{(t)}^2\right\rangle $ we obtain:

$$ {\rho}_{\overset{\frown }{T},T}\left(t,\tau \right)={S}_k{\left(t,\tau \right)}^{1/2} $$

(51)

Therefore, MS forecast skill can equivalently be quantified using either correlations or MSSS.

Figure 11a shows the theoretical skill as a function of H for different forecast horizons. To underscore the huge memory implied by the power law kernel M _γ, we can compare the fGn kernel with that of the exponential kernels that arise in auto-regressive (AR) type processes. This is relevant here since the main existing stochastic macroweather forecasts techniques (“Linear Inverse Modelling”, LIM, see the next subsection) are vector AR processes that reduce to scalar AR processes in an appropriately (diagonalized) frame. If for simplicity we consider only forecasts one time step into the future (i.e. horizon τ, for a process resolution τ), then the fraction f(λ) of the predictor variance that is due to innovations at times λτ or further in the past can be written in the same form as for fGn:

$$ \begin{array}{cc}\hfill f\left(\lambda \right)=\frac{I\left(\lambda \right)}{I(0)};\hfill & \hfill I\left(\lambda \right)=\underset{-\infty }{\overset{-\lambda }{\int }}{\left(g(s)-g\left(s-1\right)\right)}^2 ds\hfill \end{array} $$

(52)

where g(s) = (−s)^1/2 + H for fGn (for SLIMM predictions) and g(s) = e ^s for AR processes. The comparison is shown in Fig. 11b, it can be seen that almost all the information needed to forecast an AR process is in the most recent three steps, whereas for SLIMM, with H = −0.1 (appropriate for forecasting the globally averaged temperature), roughly 20% comes from innovations more than 1000 steps in the past. Significantly, we will see that this does not mean that we need such long series to make good forecast; this is because even relatively short series with H = −0.1 have information from the distant past; this is discussed below.

3.3 SLIMM Prediction Skill and Alternative Stochastic Macroweather Prediction Systems

Following Hasselmann (1976) who proposed the use of stochastic differential equations to understand low frequency weather (i.e. macroweather), attempts have been made to use this for monthly, Seasonal to Interannual forecasts. The basic idea is to model the atmosphere as an Ornstein-Uhlenbeck process, i.e. the solution of $ \frac{dT}{dt}+T/\tau =\gamma (t) $ where τ is the basic time scale and γ is a white noise forcing. The idea is that the weather acts essentially as a random white noise perturbation to the temperature T. Fourier analysis shows that the spectrum is E(ω) ∝ 1/(ω ² + τ ⁻²) so that at high frequencies, E(ω) ∝ ω ⁻² whereas at low frequencies, E(ω) ≈ constant. The process is thus an (unpredictable) white noise; this can be seen directly by taking the low frequency limit dT/dt ≈ 0 in the equation. From an empirical point of view, there are two scaling regimes (exponents β = 0, 2), corresponding to H = (β−1)/2 = −1/2 and H = ½, respectively, but neither is realistic: for example, the true values for the temperature are closer to ≈−0.1, ≈0.4 for macroweather, weather respectively with the former showing significant spatial variations, see Fig. 10. The key point is that models based on integer order differential equations implicitly assume that the low frequencies are unpredictable whereas on the contrary, the temporal scaling implies long range dependencies, a large memory. From the point of view of differential equations, we thus require terms of fractional order (see Eq. (22)).

Over the decades, the Hasselman inspired approach has been significantly developed, in the framework of “Linear Inverse Modelling” (LIM), sometimes also called the “Stochastic Linear Framework” (SLF), although the latter is somewhat a misnomer since it restrictively excludes fractional ordered (but still linear) terms (for LIM, SLF see, e.g., Penland (1996), Penland and Sardeshmuhk (1995), Sardeshmukh et al. (2000), and Newman (2013)). The essential development is the extension of scalar Ornstein-Uhlenbeck processes to vector processes with each component being a significant macroweather variable (e.g. an El Nino index, an ocean temperature at a particular grid point, etc.). Typical implementations such as described in Newman (2013) involve 20 components (implying hundreds of empirical parameters). When diagonalized, the system reduces to decoupled Ornstein-Uhlenbeck processes whose longest characteristic times are about 1 year, and beyond this, the system has little skill, see Fig. 12a.

Because its theoretical basis is weak and it involves a large number of empirical parameters, LIM is an example of what is commonly termed an “empirically based” approach. Other such approaches have been proposed, notably by Suckling et al. (2016) and they have had some success by using carefully chosen climate indices that are linearly related to macroweather variables of interest and using empirically determined time delays. In contrast, SLIMM is based on fundamental space-time scale symmetries that we argue are respected by the dynamical equations.

In order to use SLIMM for forecasts, it is important to first remove the low frequency responses to anthropogenic forcings, failure to do so (Baillie and Chung 2002) leads to poor results. For annually, globally averaged temperatures, it turns out that reasonable results can be obtained using the CO₂ radiative forcing (proportional to logCO₂ concentration) as a linear surrogate for all anthropogenic forcings (Fig.12b). SLIMM then forecasts the internal variability: the residuals. The reason that this works so well is presumably that all anthropogenic effects are linked through the economy and the economy is well characterized by energy use and hence by CO₂ emissions.

When SLIMM hindcasts are made for hemispheric and global scales (Lovejoy et al. 2015), they are generally better than LIM and GCM forecasts (Fig. 12a). In addition, Lovejoy (2015b) made global scale SLIMM forecasts and showed that they could accurately (to within about ±0.05 °C for three year anomalies) forecast the so-called “pause” in the warming (1998–2015). In comparison, CMIP3 GCM predictions were about 0.2 °C too high. While the cause of the GCM over-prediction is currently debated (e.g., Schmidt et al. 2014; Guemas et al. 2013; Steinman et al. 2015), the SLIMM prediction was successful large because as Fig. 12b shows, the pause was simply a natural cooling event that followed the enormous “pre-pause” 1992–1998 warming, with all of this superposed on a rising anthropogenic warming trend.

The SLIMM forecast technique showed that the fGn model was worth pursuing. However, the original technique was based on M _γ, i.e. finding the optimum predictor using the innovations γ(s) directly (obtained by numerically inverting Eq. (22)) and assuming that the available data extended into the infinite past. It is much more convenient to use the past data T(s) and to take into account the fact that the past data are only finite in extent. Since an fGn process at resolution τ is the average of the increments of an fBm, process, it suffices to forecast fBm so that in the operational version of SLIMM described below, we therefore availed ourselves of the mathematical solution of the prediction problem of finding the kernel M _T(t,s) in Eq. (39) for both finite and infinite past data. Gripenberg and Norros (1996) mathematically solved the fBm solution with ½ < H′ < 1 and this was numerically investigated by Hirchoren and D’attellis (1998).

We saw that the (infinite past) innovation kernel M_γ (Eq. 42) gave a strong (even singular) weight to the recent past, forecasting AR processes has an analogous strong weighting of the recent data. However, Gripenberg and Norros (1996) found something radically new in the case of finite data: the most ancient available data also had a singular weighting! In their words, this was because “the closest witnesses to the unobserved past have special weight”, see Fig. 12d for a graphical example.

4 Stochastic Predictability Limits and Forecast Skill

4.1 Stochastic Predictability Limits: StocSIPS Hindcasting Skill Demonstrated on CMIP5 Control Runs

We are used to the deterministic predictability limits that arise from the “butterfly effect”—sensitive dependence on initial conditions—we argued that this limit (the inverse Lyapunov exponent of the largest structures) was roughly given by the lifetime of planetary structures: τ _w = ε ^−1/3 L ^2/3 (Schertzer and Lovejoy 2004). However, we also argued that when taken way beyond this limit, that both the GCMs and the atmosphere should be considered stochastic. More precisely, we argued that fGn provides a good approximation for the temporal variability, and that due to SSTF, attempting to use spatial correlations for co-predictors may not lead to an improvement when compared to direct predictions that exploit the huge memory of the system. However, SSTF does not necessarily extend from temperatures to other series such as climate indices. It is possible that use of the latter as co-predictors may yield larger skills.

Since fGn has stochastic predictability limits that determine its skill, Eq. (46), these should therefore be relevant in both GCMs and in real macroweather. However, in the latter and in externally forced GCMs, as discussed in Sect. 4.2 there are low frequency responses to climate forcings, and these must be forecast separately (using linearity Eq. (11)) from the internal macroweather variability modelled by fGn processes. This means that the best place to test our predictors is on unforced GCMs, i.e. on control runs. For this purpose we used 36 globally and monthly averaged CMIP5 model control runs. For each, we estimated the relevant exponent H by determining the value that made the predictor best satisfy the orthogonality condition (Eq. 41); this was slightly more accurate than using either spectra or Haar fluctuation analysis (Del Rio Amador 2017). While each model had somewhat different exponents, we found a mean H = −0.11 ± 0.09 theoretically implying a huge memory (see, e.g., Fig. 11a, b). We used the discrete M _T kernel (following (Hirchoren and Arantes 1998)) and produced 12-month hindcasts comparing both the theoretical skill and the actual hindcast skill, see Fig. 13a. Figure 13b shows that the control runs were hindcast very nearly to their theoretical limits. It is thus quite plausible that the theoretical stochastic predictability limit Eq. (46) really is an upper bound on the skill of macroweather forecasts.

4.2 Regional Forecasting

In the previous section, we saw that without external forcings, we can make global scale macroweather forecasts that nearly attain their theoretical limits, and in Sect. 3.3 (the pause), we already indicated that by appropriately removing the low frequencies (in that case, the anthropogenic forcings), we could also make accurate global scale real world forecasts. Due to SSTF, we argued that if at a given location long series were available, they could be forecast directly, that using information at other locations as co-predictors would not increase the overall skill. In this section, we therefore discuss regional forecasts at 5° resolution. This resolution was chosen because it is the smallest that is available from both historical data and reanalysis data sets that we used.

The various steps in the forecast are illustrated in Fig. 14 using the pixel over Montreal as an example. The first step is to remove the low frequencies that are not due to internal macroweather variability; failure to remove them will lead to serious biases since the SLIMM forecast assumes a long-term mean equal to 0 and the ensemble forecast is always towards this mean. The low frequencies have both a mean component (mostly anthropogenic in origin but also one due to internal variability) and a strong annual cycle that slowly evolves from one year to the next. Using the knowledge (Fig. 5d) that the scaling is broken at decadal scales, we can use a high pass filter to separate out these from the internal variability. Similarly, the annual cycle can be forecast by using the past thirty years of data in order to make running estimates of the relevant Fourier coefficients (only keeping those for the annual cycle and 6, 4 and 3 month harmonics). The various steps are shown in Fig.14. Finally the anomalies (lower right) were forecast using SLIMM. The regional variation of the skill of the resulting StocSIPS hindcasts is shown in Fig.15a, we can see that it is close to the theoretical maximum.

4.3 StocSIPS-CanSIPS Comparison

The previous section reminded us that real world forecasts must estimate, remove and separately forecast the nonmacroweather low frequencies, the higher frequency internal fGn-like component. The overall model, including this “pre-processing” is called the Stochastic Seasonal to Interannual Prediction System (StocSIPS, see the website: http://www.physics.mcgill.ca/StocSIPS/), it is comparable in scope to the Canadian Seasonal to Interannual Prediction System (CanSIPS (Merryfield et al. 2011)) and the European Seasonal to Interannual Prediction System (EuroSIPS, http://www.ecmwf.int/en/forecasts/documentation-and-support/long-range/seasonal-forecast-documentation/eurosip-user-guide/multi-model), but of course is based directly on a stochastic rather than a deterministic-stochastic (GCM) model. Indeed, according to the World Meteorological Organization (WMO) site (http://www.wmo.int/pages/prog/wcp/wcasp/gpc/gpc.php), there are 12 international “producing” centres; StocSIPS based at McGill would be the 13th. Although completely unfunded, since April 2016, it has provided operational monthly, seasonal and annual temperature forecasts at 5° resolution.

As the previous section showed, SLIMM can forecast GCM control runs to nearly their theoretical stochastic predictability limits. However, we must evaluate the full StocSIPS system (pre-processing plus SLIMM) and compare it with conventional approaches. We singled out CanSIPS, which since 2010 is the institutional product of Environment Canada, for particularly close comparisons. Every month, CanSIPS makes monthly through annual temperature and precipitation forecasts; the publically available maps are only over Canada, but we accessed the global products and made global hindcast comparisons since 1980. The CanSIPS products are based on “multimodel ensemble” consisting of 10 realizations of the CanCM3 and 10 realizations of the CanCM4 GCM.

Before continuing, recall the method by which GCMs currently produce macroweather forecasts. The first step is the initialization; when CanSIPS is initialized it uses reanalyses from the European Centre for Medium-range Weather Forecasts (ECMWF) and these are data-model “hybrids” obtained by assimilating meteorological observations into the ECMWF GCM. The problem is that both the reanalyses and CanSIPS have their own different climatologies so that the latter cannot directly ingest the ECMWF reanalyses, instead, the ECMWF initial values must be converted into ECMWF anomalies. These anomalies are used to determine the CanSIPS initial values, the “actuals”. The process can be symbolically written as:

$$ \begin{array}{c}\hfill {T}_{\mathrm{CanSIPS}}\left(\underline{r},t\right)={\overline{T}}_{i(t),\mathrm{CanSIPS}}\left(\underline{r}\right)+{T}_{\mathrm{CanSIPS}}^{\prime}\left(\underline{r},t\right)\hfill \\ {}\hfill {T}_{\mathrm{ECMWF}}\left(\underline{r},t\right)={\overline{T}}_{i(t),\mathrm{ECMWF}}\left(\underline{r}\right)+{T}_{\mathrm{ECMWF}}^{\prime}\left(\underline{r},t\right)\hfill \end{array} $$

(53)

where the overbar represents the climatological temperature $ {\overline{T}}_i\left(\underline{r}\right) $ at position r, for the month number i = 1, 2, …, 12 and the primes indicate the anomalies which are functions of both position and time (i(t) denotes the month number of time t). The conventional way to define $ {\overline{T}}_i\left(\underline{r}\right) $ is to use the averages over the previous 30 i^th months (at each location/pixel r). Aside from the annual cycle (that was deliberately ignored in Sect. 2.2), the anomalies differ from the internal variability because they are based on temporal rather than ensemble averages and they have contributions from external forcings.

CanSIPS is thus initialized $ {T}_{\mathrm{CanSIPS}}\left(\underline{r},0\right) $ using the ECMWF anomaly at time t = 0:

$$ {T}_{\mathrm{CanSIPS}}\left(\underline{r},0\right)={\overline{T}}_{i(0),\mathrm{CanSIPS}}\left(\underline{r}\right)+{T}_{\mathrm{ECMWF}}^{\prime}\left(\underline{r},0\right) $$

(54)

The forecasts $ {\widehat{T}}_{\mathrm{CanSIPS}}\left(\underline{r},t\right) $ (at t > 0, indicated with circonflex) are then made using the 20 member CanSIPS ensemble followed by complex (and time consuming) post-processing that primarily correct for the “model drift” and poor climate sensitivity. “Model drift” refers to the tendency of model temperatures (even in control runs) to display low frequency variations that are usually attributed to slow (mostly ocean) processes, artefacts that are not fully “balanced” when the model is initialized. Since the model does not have perfect representation of the sensitivity to anthropogenic effects, the corresponding systematic errors also contribute a further low frequency “drift”. Both are removed (to some extent) using hindcasts over the previous 5-year period in an attempt to estimate (and remove) spurious linear trends (Merryfield et al. 2011). Unfortunately, 5 years is too short to properly estimate the trend (the true trends are buried in the macroweather noise until a decade or so in scale, see Fig. 5d) so that the internal 5-year variability is thus spuriously removed in the post-processing.

In spite of these manipulations, the final result $ {\widehat{T}}_{\mathrm{CanSIPS}}\left(\underline{r},t\right) $—i.e. an “actual”—is seriously in error as can be seen in Fig. 15b: which shows that the actuals’ error variance is typically several times larger than the anomaly variance. Due to this, the publically available macroweather forecasts are of the anomalies $ {{\widehat{T}}^{\prime}}_{\mathrm{CanSIPS}}\left(\underline{r},t\right)={\widehat{T}}_{\mathrm{CanSIPS}}\left(\underline{r},t\right)-{\overline{T}}_{i(t),\mathrm{CanSIPS}}\left(\underline{r},t\right) $. For these anomalies, the comparison with StocSIPS is much closer, see Fig. 16. The figure shows that even for anomalies over most of the globe, for 2 months and longer, StocSIPS has higher skill. StocSIPS’ increased skill is particularly noticeable over land, probably due to the fact that the CanSIPS ocean model is still within its deterministic predictability limit of 1–2 years making its ocean forecast reasonably accurate. This impression is bolstered in Fig. 17 which compares CanSIPS at 6 months and StocSIPS at 2 years (the skill is comparable), and also in Fig. 18 that shows that StocSIPS’ relative advantage grows with lead time and is particularly strong over land.

Although we have not discussed it in this review, StocSIPS actually provides forecasts of the probability distributions (both mean, discussed up until now, and the standard deviation about the mean). This can be used for various probabilistic forecasts. For example, Fig. 19a, b shows a typical seasonal forecast and its validation. In Fig. 19a we see that the StocSIPS anomaly forecasts generally follow the data better than CanSIPS. In Fig. 19b, we see that for this location and date, that the StocSIPS forecast was both more accurate and less uncertain than the CanSIPS forecast. This was true for both the actuals and the anomalies. This can be seen since not only is the dashed red StocSIPS mean closer to the NCEP validation (dashed black) than the CanSIPS dashed blue, but the uncertainties (the spreads in the probability densities) is narrower for the StochSIPS forecast. Other probabilistic forecasts that can readily be produced by StocSIPS include tercile forecasts: i.e. the probabilities of the forecast temperature being below, above or equal to the local climatology; see the StocSIPS site for examples.

5 Conclusions

Over the last decades, it has become increasingly clear that at weather scales, atmospheric dynamics are governed by both deterministic laws of continuum mechanics and by stochastic turbulence laws. Although the GCM equations do not acknowledge the existence of atoms or molecules, they are nevertheless compatible with statistical mechanics. Similarly they are also believed to be compatible with the turbulence laws and indeed, they obey them quite accurately. Over the same period, the GCM approach has—with the development of ensemble forecasting and stochastic parametrizations—itself evolved into a stochastic one, making it tempting to make weather forecasts directly using the turbulence laws. However the weather regime is highly intermittent, and it involves vector multifractal processes, whose corresponding mathematical prediction problem has yet to be solved. The GCM approach to weather prediction is thus the only one currently available.

The situation is radically different at time scales beyond the GCM deterministic predictability limit—in macroweather. On the one hand, GCMs have large errors associated with unrealistic model climatologies, especially poor representations of the annual cycle, and they also display model drift and unrealistic sensitivities to anthropogenic effects. On the other hand, macroweather “turbulence” (the extension of turbulence models to the macroweather regime) has low intermittency so that Gaussian models are useable approximations (fractional Gaussian noise, fGn). In addition, a new symmetry: statistical space-time factorization essentially decouples space and time so that mean square predictions can conveniently be made for each spatial location independently. Physically this means that even though strong spatial correlations exist (including “teleconnections”), if one has a long enough history at a given point, this spatial information is also implicit in the series so that using data at other spatial locations as co-predictors does not necessarily improve the forecast. The factorization is not exact and does not necessarily apply to other series such as climate indices so that there may be future scope for finding co-predictors and improve the skill.

The ideal testing ground for this approach is in GCM control runs since this is closest to pure fGn. We found that the ScaLIng Macroweather Model (SLIMM) based on an fGn model applied to temperatures from GCM control runs (i.e. pure macroweather processes, no changes in external forcings) is nearly able to attain the maximum theoretical stochastic predictability limit, verifying that GCMs well obey the macroweather laws upon which SLIMM is based and raising the possibility that these stochastic predictability limits are true GCM limits. With respect to usual stochastic forecasts based on exponential correlations (Auto Regressive, or Linear Inverse Modelling), the radically new feature of SLIMM is its exploitation of the huge long range memory. The SLIMM prediction kernel thus has singular weighting to both the most recent data and the most ancient data since the latter contain the maximum information of the distant past.

Applying SLIMM to real data requires pre-processing to remove nonmacroweather processes in particular to remove low frequency anthropogenic effects and—for regional forecasts—the annual cycle. The overall resulting system (i.e. pre-processing plus SLIMM) is the STOChastic Seasonal to Interannual Prediction System (StocSIPS). We compared StocSIPS with one of the leading GCM macroweather products: CanSIPS. Even without any co-predictors or other use of spatial correlations, we showed that StocSIPS was much superior to CanSIPS for forecasting “actuals”: this was due to StocSIPS’ ability to essentially forecast the climatology (especially the annual cycle). However, even for anomaly forecasts, StoSIPS was superior to CanSIPS for lead times of 2 months or longer and its relative advantage grew with the forecast lead time, the advantage was particularly important over land where for 2 months and longer StocSIPS was superior over more than ≈80% the earth’s land surface.

Aside from its increased skill, StocSIPS has other advantages. For example, at the moment, seasonal forecasts for the city of Montreal (or other localized region) are highly indirect. First data from all atmospheric fields from all over the world must be assimilated. Then the model—on grids typically several hundred kilometres across—is integrated forward in time. Anomalies are calculated, and post-processing is performed to make low frequency corrections for some of the known biases. Finally, the Montreal temperature anomaly is estimated by “downscaling” from the large pixel scale to the local city scale. This can be done either using sophisticated (but complex) nested regional models (of GCM type) or via ad hoc statistical methods based on local climatology. In contrast, if long enough (preferably several decades) of monthly or seasonal data are available, StocSIPS simply removes the low frequencies (including the annual cycle), separately forecasts the anomalies and low frequencies and adds them to produce the forecast. The overall saving in computational speed is estimated to be of the order of 10⁷ (about 10⁵ to 10⁶ for global forecasts on 5^o × 5^o grids). Finally, StocSIPS directly forecasts the conditional ensemble average, i.e. effectively the results of an infinite ensemble whereas CanSIPS uses only 20 members.

StocSIPS can be directly extended to other fields such as wind or precipitation which instead are known to have macroweather statistics roughly satisfying the SLIMM requirements (low intermittency temporal macroweather scaling with −1/2 < H < 0 and space-time statistical factorization (SSTF), Lovejoy and de Lima (2015) and Fig. 9a). But StocSIPS’ main advantage may be its ability to directly forecast other fields, such as insolation, wind power or degree-days, that can currently only be very indirectly forecast by GCMs. Other future extensions of StocSIPS could include drought indices and the prediction of extremes.

References

Baillie, R.T., and S.-K. Chung. 2002. Modeling and forecasting from trend-stationary long memory models with applications to climatology. International Journal of Forecasting 18: 215–226.
Article Google Scholar
Biagini, F., Y. Hu, B. Øksendal, and T. Zhang. 2008. Stochastic calculus for fractional Brownian motion and applications. London: Springer-Verlag.
Book Google Scholar
Chen, W., S. Lovejoy, and J.P. Muller. 2016. Mars’ atmosphere: The sister planet, our statistical twin. Journal of Geophysical Research—Atmospheres 121: 11968–11988. doi:10.1002/2016JD025211.
Article Google Scholar
Compo, G.P., et al. 2011. The twentieth century reanalysis project. Quarterly J. Roy. Meteorol. Soc. 137: 1–28. doi:10.1002/qj.776.
Article Google Scholar
Del Rio Amador, L. 2017. The stochastic seasonal to interannual prediction system. Montreal: McGill University.
Google Scholar
Garcıa-Serrano, J., and F. J. Doblas-Reyes (2012), On the assessment of near-surface global temperature and North Atlantic multi-decadal variability in the ENSEMBLES decadal hindcast, Climate Dynamics, 39, 2025–2040 doi: 10.1007/s00382-012-1413-1.
Gripenberg, G., and I. Norros. 1996. On the Prediction of Fractional Brownian Motion. Journal of Applied Probability 33: 400–410.
Article Google Scholar
Guemas, V., F.J. Doblas-Reyes, I. Andreu-Burillo, and M. Asif. 2013. Retrospective prediction of the global warming slowdown in the past decade. Nature Climate Change 3: 649–653.
Article Google Scholar
Hasselmann, K. 1976. Stochastic climate models, part I: Theory. Tellus 28: 473–485.
Article Google Scholar
Hébert, R., and S. Lovejoy. 2015. The runaway Green’s function effect: Interactive comment on “Global warming projections derived from an observation-based minimal model” by K. Rypdal. Earth System Dynamics Discovery 6: C944–C953.
Google Scholar
Hebert, R., S. Lovejoy, and A. de Vernal. 2017. A scaling model for the forced climate variability in the anthropocene. Climate Dynamics. (in preparation).
Google Scholar
Hirchoren, G.A., and D.S. Arantes. 1998. Predictors for the discrete time fractional Gaussian processes. In Telecommunications symposium. ITS '98 proceedings, SBT/IEEE international, 49–53. Sao Paulo: IEEE.
Chapter Google Scholar
Hirchoren, G.A., and C.E. D’attellis. 1998. Estimation of fractal signals, using wavelets and filter banks. IEEE Transactions on Signal Processing 46 (6): 1624–1630.
Article Google Scholar
Kolesnikov, V.N., and A.S. Monin. 1965. Spectra of meteorological field fluctuations. Izvestiya, Atmospheric and Oceanic Physics 1: 653–669.
Google Scholar
Lean, J.L., and D.H. Rind. 2008. How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006. Geophysical Research Letters 35: L18701. doi:10.1029/2008GL034864.
Article Google Scholar
Lilley, M., S. Lovejoy, D. Schertzer, K.B. Strawbridge, and A. Radkevitch. 2008. Scaling turbulent atmospheric stratification. Part II: Empirical study of the the stratification of the intermittency. Quarterly Journal of the Royal Meteorological Society 134: 301–315. doi:10.1002/qj.1202.
Article Google Scholar
Lovejoy, S. 2014a. Scaling fluctuation analysis and statistical hypothesis testing of anthropogenic warming. Climate Dynamics 42: 2339–2351. doi:10.1007/s00382-014-2128-2.
Article Google Scholar
———. 2014b. Return periods of global climate fluctuations and the pause. Geophysical Research Letters 41: 4704–4710. doi:10.1002/2014GL060478.
Article Google Scholar
———. 2015a. A voyage through scales, a missing quadrillion and why the climate is not what you expect. Climate Dynamics 44: 3187–3210. doi:10.1007/s00382-014-2324-0.
Article Google Scholar
———. 2015b. Using scaling for macroweather forecasting including the pause. Geophysical Research Letters 42: 7148–7155. doi:10.1002/2015GL065665.
Article Google Scholar
———. 2017. How accurately do we know the temperature of the surface of the earth? Climate Dynamics. (in press).
Google Scholar
Lovejoy, S., and M.I.P. de Lima. 2015. The joint space-time statistics of macroweather precipitation, space-time statistical factorization and macroweather models. Chaos 25: 075410. doi:10.1063/1.4927223.
Article Google Scholar
Lovejoy, S., and D. Schertzer. 1986. Scale invariance in climatological temperatures and the local spectral plateau. Annales Geophysicae 4B: 401–410.
Google Scholar
———. 2007. Scale, scaling and multifractals in geophysics: Twenty years on. In Nonlinear dynamics in geophysics, ed. J.E.A.A. Tsonis. New York, NY: Elsevier.
Google Scholar
———. 2010. Towards a new synthesis for atmospheric dynamics: Space-time cascades. Atmospheric Research 96: 1–52. doi:10.1016/j.atmosres.2010.01.004.
Article Google Scholar
———. 2012. Haar wavelets, fluctuations and structure functions: Convenient choices for geophysics. Nonlinear Processes in Geophysics 19: 1–14. doi:10.5194/npg-19-1-2012.
Article Google Scholar
———. 2013. The weather and climate: Emergent laws and multifractal cascades., 496 pp. Cambridge: Cambridge University Press.
Book Google Scholar
Lovejoy, S., A.F. Tuck, S.J. Hovde, and D. Schertzer. 2007. Is isotropic turbulence relevant in the atmosphere? Geophysical Research Letters 34: L14802. doi:10.1029/2007GL029359.
Article Google Scholar
Lovejoy, S., D. Schertzer, M. Lilley, K.B. Strawbridge, and A. Radkevitch. 2008. Scaling turbulent atmospheric stratification. Part I: Turbulence and waves. Quarterly Journal of the Royal Meteorological Society 134: 277–300. doi:10.1002/qj.201.
Article Google Scholar
Lovejoy, S., D. Schertzer, and D. Varon. 2013. Do GCM’s predict the climate…. or macroweather? Earth System Dynamics 4: 1–16. doi:10.5194/esd-4-1-2013.
Article Google Scholar
Lovejoy, S., J.P. Muller, and J.P. Boisvert. 2014. On Mars too, expect macroweather. Geophysical Research Letters 41: 7694–7700. doi:10.1002/2014GL061861.
Article Google Scholar
Lovejoy, S., L. del Rio Amador, and R. Hébert. 2015. The ScaLIng Macroweather Model (SLIMM): Using scaling to forecast global-scale macroweather from months to decades. Earth System Dynamics 6: 1–22. http://www.earth-syst-dynam.net/6/1/2015/. doi:10.5194/esd-6-1-2015.
Article Google Scholar
Mandelbrot, B.B., and J.W. Van Ness. 1968. Fractional Brownian motions, fractional noises and applications. SIAM Review 10: 422–450.
Article Google Scholar
Merryfield, W.J., B. Denis, J.-S. Fontecilla, W.-S. Lee, S. Kharin, J. Hodgson, and B. Archambault. 2011. The Canadian Seasonal to Interannual Prediction System (CanSIPS): An overview of its design and operational implementationRep., 51pp. Environment Canada.
Google Scholar
Newman, M. 2013. An empirical benchmark for decadal forecasts of global surface temperature anomalies. Journal of Climate 26: 5260–5269. doi:10.1175/JCLI-D-12-00590.1.
Article Google Scholar
Panofsky, H.A., and I. Van der Hoven. 1955. Spectra and cross-spectra of velocity components in the mesometeorlogical range. Quarterly Journal of the Royal Meteorological Society 81: 603–606.
Article Google Scholar
Papoulis, A. 1965. Probability, random variables and stochastic processes. New York, NY: Mc Graw Hill.
Google Scholar
Pauluis, O. 2011. Water vapor and mechanical work: a comparison of carnot and steam cycles. Journal of the Atmospheric Sciences 68: 91–102. doi:10.1175/2010JAS3530.1.
Article Google Scholar
Penland, C. 1996. A stochastic model of IndoPacific sea surface temperature anomalies. Physica D 98: 534–558.
Article Google Scholar
Penland, C., and P.D. Sardeshmuhk. 1995. The optimal growth of tropical sea surface temperature anomalies. Journal of Climate 8: 1999–2024.
Article Google Scholar
Pinel, J., and S. Lovejoy. 2014. Atmospheric waves as scaling, turbulent phenomena. Atmospheric Chemistry and Physics 14: 3195–3210. doi:10.5194/acp-14-3195-2014.
Article Google Scholar
Pinel, J., S. Lovejoy, and D. Schertzer. 2014. The horizontal space-time scaling and cascade structure of the atmosphere and satellite radiances. Atmospheric Research 140–141: 95–114. doi:10.1016/j.atmosres.2013.11.022.
Article Google Scholar
Radkevitch, A., S. Lovejoy, K.B. Strawbridge, D. Schertzer, and M. Lilley. 2008. Scaling turbulent atmospheric stratification. Part III: Empirical study of space-time stratification of passive scalars using lidar data. Quarterly Journal of the Royal Meteorological Society 134: 317–335. doi:10.1002/qj.1203.
Article Google Scholar
Ragone, F., V. Lucarini, and F. Lunkeit. 2015. A new framework for climate sensitivity and prediction: A modelling perspective. Climate Dynamics 46: 1459–1471. doi:10.1007/s00382-015-2657-3.
Article Google Scholar
Richardson, L.F. 1926. Atmospheric diffusion shown on a distance-neighbour graph. Proceedings of the Royal Society A110: 709–737.
Article Google Scholar
Rypdal, K. 2015. Global warming projections derived from an observation-based minimal model. Earth System Dynamics Discussions 6: 1789–1813. doi:10.5194/esdd-6-1789-2015.
Article Google Scholar
Rypdal, M., and K. Rypdal. 2014. Long-memory effects in linear response models of Earth's temperature and implications for future global warming. Journal of Climate 27 (14): 5240–5258. doi:10.1175/JCLI-D-13-00296.1.
Article Google Scholar
Sardeshmukh, P., G.P. Compo, and C. Penland. 2000. Changes in probability assoicated with El Nino. Journal of Climate 13: 4268–4286.
Article Google Scholar
Schertzer, D., and S. Lovejoy. 1985. The dimension and intermittency of atmospheric dynamics. In Turbulent shear flow, ed. L.J.S. Bradbury et al., 7–33. Berlin: Springer-Verlag.
Chapter Google Scholar
———. 1995. From scalar cascades to Lie cascades: Joint multifractal analysis of rain and cloud processes. In Space/time variability and interdependance for various hydrological processes, ed. R.A. Feddes, 153–173. New York, NY: Cambridge University Press.
Chapter Google Scholar
———. 2004. Uncertainty and predictability in geophysics: Chaos and multifractal insights. In State of the planet, frontiers and challenges in geophysics, ed. R.S.J. Sparks and C.J. Hawkesworth, 317–334. Washington, DC: American Geophysical Union.
Chapter Google Scholar
Schertzer, D., S. Lovejoy, F. Schmitt, Y. Chigirinskaya, and D. Marsan. 1997. Multifractal cascade dynamics and turbulent intermittency. Fractals 5: 427–471.
Article Google Scholar
Schertzer, D., I. Tchiguirinskaia, S. Lovejoy, and A.F. Tuck. 2012. Quasi-geostrophic turbulence and generalized scale invariance, a theoretical reply. Atmospheric Chemistry and Physics 12: 327–336. doi:10.5194/acp-12-327-2012.
Article Google Scholar
Schmidt, G.A., D.T. Shindell, and K. Tsigaridis. 2014. Reconciling warming trends. Nature Geoscience 7: 158–160.
Article Google Scholar
Schwartz, S.E. 2012. Determination of Earth’s transient and equilibrium climate sensitivities from observations over the twentieth century: Strong dependence on assumed forcing. Surveys in Geophysics 33: 745–777.
Article Google Scholar
Steinman, B.A., M.E. Mann, and S.K. Miller. 2015. Atlantic and Pacific multidecadal oscillations and Northern Hemisphere temperatures. Science 347: 988–991. doi:10.1126/science.1257856.
Article Google Scholar
Suckling, E.B., E. Hawkins, G. Jan van Oldenborgh, and J.M. Eden. 2016. An empirical model for probabilistic decadal prediction: A global analysis. Climate Dynamics (submitted).
Google Scholar
Tennekes, H. 1975. Eulerian and Lagrangian time microscales in isotropic turbulence. Journal of Fluid Mechanics 67: 561–567.
Article Google Scholar
Vallis, G. 2010. Mechanisms of climate variaiblity from years to decades. In Stochastic physics and climate modelliing, ed. P.W.T. Palmer, 1–34. Cambridge: Cambridge University Press.
Google Scholar
Van der Hoven, I. 1957. Power spectrum of horizontal wind speed in the frequency range from 0.0007 to 900 cycles per hour. Journal of Meteorology 14: 160–164.
Article Google Scholar
Zeng, X., and K. Geil. 2017. Global warming projection in the 21st Century based on an observational data driven model. Geophysical Research Letters. (in press).
Google Scholar

Download references

Acknowledgements

We thank Lydia Elias, Hannah Wakeling and Weylan Thompson for undergraduate summer contributions in developing StocSIPS. We thank OURANOS for funding Lydia Elias’s summer work. We thank Dave Clark, Norberto Majlis and Yosvany Martinez (Environment Canada) for regular discussions. Hydro Quebec is thanked for partial support of L. Del Rio Amador during his PhD. The project itself was unfunded, there were no conflicts of interest.

Author information

Authors and Affiliations

Department of Physics, McGill University, 3600 University St., Montreal, QC, H3A 2T8, Canada
S. Lovejoy, L. Del Rio Amador & R. Hébert

Authors

S. Lovejoy
View author publications
You can also search for this author in PubMed Google Scholar
L. Del Rio Amador
View author publications
You can also search for this author in PubMed Google Scholar
R. Hébert
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Lovejoy .

Editor information

Editors and Affiliations

Department Mathematical Sciences, Atmospheric Sciences Group, University of Wisconsin - Milwaukee, Milwaukee, Wisconsin, USA
Anastasios A. Tsonis

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Cite this chapter

Lovejoy, S., Del Rio Amador, L., Hébert, R. (2018). Harnessing Butterflies: Theory and Practice of the Stochastic Seasonal to Interannual Prediction System (StocSIPS). In: Tsonis, A. (eds) Advances in Nonlinear Geosciences. Springer, Cham. https://doi.org/10.1007/978-3-319-58895-7_17

Download citation

DOI: https://doi.org/10.1007/978-3-319-58895-7_17
Published: 11 October 2017
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-58894-0
Online ISBN: 978-3-319-58895-7
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)

Publish with us

Policies and ethics