Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Many decision-making problems, such as portfolio selection, capital budgeting, production planning, resource allocation, and computer networks, etc., can often be formulated as quadratic programming problems with discrete variables. See for examples, [4, 5, 9, 24]. In engineering applications, the decision variables can not have arbitrary values. Instead, either some or all of the variables must be selected from a list of integer or discrete values for practical reasons. For examples, structural members may have to be selected from selections available in standard sizes, member thicknesses may have to be selected from the commercially available ones, the number of bolts for a connection must be an integer, the number of reinforcing bars in a concrete member must be an integer, etc. [23]. However, these integer programming problems are computationally highly demanding. Nevertheless, some numerical methods are now available.

Several review articles on nonlinear optimization problems with discrete variables are available [1, 4, 28, 33, 37, 38], and some popular methods have been discussed, including branch and bound methods, a hybrid method that combines a branch and bound method with a dynamic programming technique [29], sequential linear programming, rounding-off techniques, cutting plane techniques [2], heuristic techniques, penalty function approaches, simulated annealing [25], and genetic algorithms, etc. The relaxation methods have also been proposed recently, leading to second order cone programming (SOC) [21] and improved linearization strategy [35].

Branch and bound is perhaps the most widely known and used deterministic method for discrete optimization problems. When applied to linear problems, this method can be implemented in a way to yield a global minimum point. However for nonlinear problems there is no such guarantee, unless the problem is convex. The branch and bound method has been used successfully to deal with problems with discrete design variables. However for the problem with a large number of discrete design variables, the number of subproblems (nodes) becomes large, making the method inefficient.

Simulated annealing (SA) and genetic algorithms (GA) belong to the category of stochastic search methods [22] which based on an element of random choice. Because of this, one has to sacrifice the possibility of an absolute guarantee of success within a finite amount of computation.

Canonical duality theory provides a new and potentially useful methodology for solving a large class of nonconvex/nonsmooth/discrete problems (see the review articles [13, 19]). It was shown in [8, 12] that the Boolean integer programming problems are actually equivalent to certain canonical dual problems in continuous space without duality gap, which can be solved deterministically under certain conditions. This theory has been generalized for solving multi-integer programming [39] and the well-known max cut problems [40]. It is also shown in [13, 16] that by the canonical duality theory, the NP-hard quadratic integer programming problem is identical to a continuous unconstrained Lipschitzian global optimization problem, which can be solved via deterministic methods (but not in polynomial times) (see [20]). The canonical duality theory has been used successfully for solving a large class of challenging problems not only in global optimization, but also in nonconvex analysis and continuum mechanics [17].

In this paper, our goal is to solve a general quadratic programming problem with its decision variables taking values from discrete sets. The elements from these discrete sets are not required to be binary or uniformly distributed. An effective numerical method is developed based on the canonical duality theory [10]. The rest of the paper is organized as follows. Section 2 presents a mathematical statement of the general discrete value quadratic programming problem and how it can be transformed into a standard 0–1 programming problem in higher dimensional space. Section 3 presents a brief review on the canonical duality theory. Detailed canonical dual transformation procedure is presented in Sect. 4 to show how the integer programming problem can be converted to a concave maximization in a convex space. A perturbed computational method is developed in Sect. 5. Some numerical examples are illustrated in Sect. 6 to demonstrate the effectiveness and efficiency of the proposed method. The paper is ended with some concluding remarks.

2 Primal Problem and Equivalent Transformation

The discrete programming problem to be addressed is given below:

$$\begin{aligned}&({\mathscr {P}}_{a})\;\;&\mathrm{\min }\;\;P(\mathbf{x})=\frac{1}{2}\mathbf{x}^T {Q}\mathbf{x}-\mathbf{c}^T \mathbf{x}\end{aligned}$$
(1)
$$\begin{aligned}&\mathrm{s.t. }\;\;\mathbf{g}(\mathbf{x})=\mathbf{A}\mathbf{x}- \mathbf{b}\le 0,\\&\;\; \;\;\;\;\; \mathbf{x}=[x_1, x_2, \cdots , x_n]^T, \;x_i \in U_i,\;i=1,\cdots ,n, \nonumber \end{aligned}$$
(2)

where \({Q}= \{ q_{ij} \} \in {\mathbb R}^{n\times n}\) is a symmetric matrix, \(\mathbf{A}=\{ a_{ij} \} \in {\mathbb R}^{m \times n}\) is a matrix with \(rank(\mathbf{A})=m<n\), \(\mathbf{c}=[c_1,\cdots ,c_n]^T \in {\mathbb R}^n\) and \(\mathbf{b}= [b_1, \cdots , b_m]^T \in {\mathbb R}^m\) are given vectors. Here, for each \(i=1, \cdots , n\),

$$\begin{aligned} U_i=\{ u_{i,1}, \cdots , u_{i, K_i}\}, \end{aligned}$$

where \(u_{i,j}, j=1, \cdots , K_i\), are given real numbers. In this paper, we let \({K}=\sum _{i=1}^n K_i\).

Problem \(({\mathscr {P}}_a)\) arises in many real-world applications, say, the pipe network optimization problems in water distribution systems, where the choices of pipelines are discrete values. Such problems have been studied extensively by traditional direct approaches (see [41]). Due to the constraint of discrete values, this problem is considered to be NP-hard and the traditional methods can only provide upper bound results. In this paper, we will show that the canonical duality theory will provide either a lower bound approach to this challenging problem, or the global optimal solution under certain conditions.

In order to convert the discrete value problem \(({\mathscr {P}}_a)\) to the standard 0–1 programming problem, we introduce the following transformation,

$$\begin{aligned} x_i=\sum _{j=1}^{K_i} u_{i,j} y_{i,j},\; i=1, \cdots , n, \end{aligned}$$
(3)

where, for each \(i=1, \cdots ,n \), \(u_{i,j} \in U_i,\; j=1, \cdots , K_i\). Then, the discrete programming problem \(({\mathscr {P}}_{a})\) can be written as the following 0–1 programming problem:

$$\begin{aligned}&({\mathscr {P}}_{b})\;\;&\mathrm{\min }\;\;P(\mathbf{y})=\frac{1}{2}\mathbf{y}^T B \mathbf{y}-\mathbf{h}^T \mathbf{y}\end{aligned}$$
(4)
$$\begin{aligned}&\mathrm{s.t.}\;\;\mathbf{g}(\mathbf{y}) = {D}\mathbf{y}- \mathbf{b}\le 0, \end{aligned}$$
(5)
$$\begin{aligned}&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum _{j=1}^{K_i} y_{i,j} - 1 = 0,\; i=1, \cdots , n, \end{aligned}$$
(6)
$$\begin{aligned}&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;y_{i,j} \in \{0, 1 \}, ~i=1,\ldots ,n;\; j=1,\cdots , K_i, \end{aligned}$$
(7)

where

$$\begin{aligned} \mathbf{y}=[y_{1,1}, \cdots , y_{1, K_1},\cdots , y_{n,1}, \cdots ,y_{n, K_n}]^T \in {\mathbb R}^{K}, \end{aligned}$$
$$\begin{aligned} \mathbf{h}=[c_1 u_{1,1},\cdots , c_1 u_{1, K_1}, \cdots , c_n u_{n,1}, \cdots , c_n u_{n, K_n}]^T \in {\mathbb R}^{K}, \end{aligned}$$
$$\begin{aligned} {B}= \left[ \begin{array}{ccccc} q_{1,1} u_{1,1}^2 &{} \cdots &{} q_{1,1} u_{1,1} u_{1, K_1}&{} \cdots &{} q_{1,n} u_{1,1}u_{n, K_n} \\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ q_{1,1}u_{1, K_1} u_{1,1}&{}\cdots &{} q_{1,1}u_{1, K_1}^2 &{} \cdots &{} \cdots \\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ q_{n,1} u_{n, K_n} u_{1,1}&{} \cdots &{} \cdots &{} \cdots &{} q_{n,n}u_{n, K_n}^2 \end{array} \right] \;\in {\mathbb R}^{{K}\times {K}}, \end{aligned}$$
$$\begin{aligned} {D}= \left[ \begin{array}{ccccc} a_{1,1} u_{1,1} &{} \cdots &{} a_{1,1} u_{1, K_1}&{}\cdots &{} a_{1,n} u_{n, K_n}\\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ a_{m,1} u_{1,1} &{} \cdots &{} a_{m,1} u_{1, K_1}&{}\cdots &{} a_{m,n} u_{n, K_n} \end{array} \right] \;\in {\mathbb R}^{m \times {K}}. \end{aligned}$$

Theorem 1

Problem \(({\mathscr {P}}_{b})\) is equivalent to Problem \(({\mathscr {P}}_{a})\).

Proof

For any \(i=1,2, \cdots , n\), it is clear that constraints (6) and (7) are equivalent to the existence of only one \(j \in \{ 1, \cdots , K_i\}\), such that \(y_{i,j}=1\) while \(y_{i,j}=0\) for all other j. Thus, from the definition of \( \mathbf{y}\), the conclusion follows readily. \(\square \)

Problem \(({\mathscr {P}}_b)\) is a standard 0–1 quadratic programming problem with both equality and inequality constraints. Let

$$\begin{aligned} {H}= \left[ \begin{array}{cccccccccc} 1 &{} \cdots &{} 1 &{} 0 &{}\cdots &{} 0 &{}\cdots &{} 0 &{}\cdots &{}0\\ 0 &{} \cdots &{} 0 &{} 1&{}\cdots &{} 1 &{}\cdots &{} 0 &{}\cdots &{}0\\ \vdots &{}\ddots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ 0 &{} \cdots &{} 0 &{} 0 &{}\cdots &{} 0 &{}\cdots &{} 1 &{}\cdots &{}1 \end{array} \right] \in {\mathbb R}^{n \times {K}} \end{aligned}$$

and, for a given integer K, let

$$\begin{aligned} \mathbf{e}_{K}=[1, \cdots , 1,\cdots , 1, \cdots ,1]^T \in {\mathbb R}^{K}. \end{aligned}$$

Thus, on the feasible space

$$\begin{aligned} {\mathscr {Y}}=\{\mathbf{y}\in {\mathbb R}^{K} :{D}\mathbf{y}\le \mathbf{b}, \;\; {H}\mathbf{y}=\mathbf{e}_n, \;\; \mathbf{y}\in \{ 0,1\}^K\}, \end{aligned}$$
(8)

the integer constrained problem \(({\mathscr {P}}_b)\) can be reformulated as a standard constrained 0–1 programming problem:

$$\begin{aligned}&({\mathscr {P}}_c):\;\;&{ \min }\left\{ P(\mathbf{y})=\frac{1}{2}\mathbf{y}^T B \mathbf{y}-\mathbf{h}^T \mathbf{y}| \;\; \mathbf{y}\in {\mathscr {Y}}\right\} . \end{aligned}$$
(9)

3 Canonical Duality Theory: A Brief Review

The basic idea of the canonical duality theory can be demonstrated by solving the following general nonconvex problem (the primal problem \(({\mathscr {P}})\) in short)

$$\begin{aligned} ({\mathscr {P}}): \; \min _{ \mathbf{x}\in {\mathscr {X}}_a} \left\{ {P}(\mathbf{x}) = \frac{1}{2}\langle \mathbf{x}, \mathbf{A}\mathbf{x}\rangle - \langle \mathbf{x}, \mathbf{f}\rangle + {W}( \mathbf{x}) \right\} , \end{aligned}$$
(10)

where \( \mathbf{A}\in {\mathbb R}^{n\times n} \) is a given symmetric indefinite matrix, \(\mathbf{f}\in {\mathbb R}^n\) is a given vector (input), \(\langle \mathbf{x}, \mathbf{x}^* \rangle \) denotes the bilinear form between \(\mathbf{x}\) and its dual variable \(\mathbf{x}^*\), \({\mathscr {X}}_a \subset {\mathbb R}^n\) is a given feasible space, and \(W: {\mathscr {X}}_a \rightarrow {\mathbb R}\cup \{\infty \}\) is a general nonconvex objective function.

It must be emphasized that, different from the objective function extensively used in mathematical optimization, a real-valued function \(W(\mathbf{x})\) is called to be objective in continuum physics and the canonical duality theory only if (see [10] Chap. 6, p. 288)

$$ W(\mathbf{x}) = W(\mathbf{Q}\mathbf{x}) \;\; \; \forall \; \mathbf{x}\in {\mathscr {X}}_a , \;\; \forall \mathbf{Q}\in {\mathscr {Q}} , $$

where \({\mathscr {Q}} = \{ \mathbf{Q}\in {\mathbb R}^{n\times n} | \;\; \mathbf{Q}^{-1} = \mathbf{Q}^T \;\; \det \mathbf{Q}= 1 \}\) is a special rotation group.

Geometrically speaking, an objective function does not depend on the rotation, but only on certain measure of its variable. In Euclidean space \( {\mathbb R}^n\), the simplest objective function is the \(\ell _2\)-norm \(\Vert \mathbf{x}\Vert \) in \({\mathbb R}^n\) since \(\Vert \mathbf{Q} \mathbf{x}\Vert ^2 = \mathbf{x}^T \mathbf{Q}^T \mathbf{Q} \mathbf{x}= \Vert \mathbf{x}\Vert ^2 \;\; \forall \mathbf{Q}\in {\mathscr {Q}}\). By Cholesky factorization, any positive definite matrix has a unique decomposition \(C = D^* D\). Thus, any convex quadratic function is objective. Physically, an objective function does not depend on observers [7], which is essential for any real-world mathematical modeling.

The key step in the canonical duality theory is to choose a nonlinear operator

$$\begin{aligned} \varvec{\xi }= {\varLambda }(\mathbf{x}):{\mathscr {X}}_a \rightarrow {\mathscr {E}}_a \subset {\mathbb R}^p \end{aligned}$$
(11)

and a canonical function \({V}: {\mathscr {E}}_a \rightarrow {\mathbb R}\) such that the nonconvex objective function \({W}( \mathbf{x})\) can be recast by adopting a canonical form \({W}( \mathbf{x}) = {V}({\varLambda }(\mathbf{x}))\). Thus, the primal problem \(({\mathscr {P}})\) can be written in the following canonical form:

$$\begin{aligned} ({\mathscr {P}}): \; \min _{\mathbf{x}\in {\mathscr {X}}_a} \left\{ {P}(\mathbf{x}) = {V}({\varLambda }(\mathbf{x})) - {U}(\mathbf{x})\right\} , \end{aligned}$$
(12)

where \({U}(\mathbf{x}) = \langle \mathbf{x}, \mathbf{f}\rangle - \frac{1}{2}\langle \mathbf{x}, \mathbf{A}\mathbf{x}\rangle \). By the definition introduced in [10], a differentiable function \({V}(\varvec{\xi })\) is said to be a canonical function on its domain \({\mathscr {E}}_a\) if the duality mapping \(\varvec{\varsigma }= \nabla {V}(\varvec{\xi })\) from \({\mathscr {E}}_a\) to its range \( {\mathscr {S}}_a \subset {\mathbb R}^p \) is invertible. Let \(\langle \varvec{\xi }; \varvec{\varsigma }\rangle \) denote the bilinear form on \({\mathscr {E}}_a \times {\mathscr {S}}_a\). Thus, for the given canonical function \({V}(\varvec{\xi })\), its Legendre conjugate \({V}^*(\varvec{\varsigma })\) can be defined uniquely by the Legendre transformation (cf. Gao [10])

$$\begin{aligned} {V}^*(\varvec{\varsigma }) = \mathrm{sta}\{ \langle \varvec{\xi }; \varvec{\varsigma }\rangle - {V}(\varvec{\xi }) \; | \; \; \varvec{\xi }\in {\mathscr {E}}_a \}, \end{aligned}$$
(13)

where the notation \(\mathrm{sta}\{ g(\varvec{\xi }) | \; \varvec{\xi }\in {\mathscr {E}}_a\}\) stands for finding stationary point of \(g(\varvec{\xi })\) on \({\mathscr {E}}_a\). It is easy to prove that the following canonical duality relations hold on \( {\mathscr {E}}_a \times {\mathscr {S}}_a\):

$$\begin{aligned} \varvec{\varsigma }=\nabla {V}(\varvec{\xi }) \; \Leftrightarrow \; \varvec{\xi }= \nabla {V}^*(\varvec{\varsigma }) \; \Leftrightarrow {V}(\varvec{\xi }) + {V}^*(\varvec{\varsigma }) = \langle \varvec{\xi }; \varvec{\varsigma }\rangle . \end{aligned}$$
(14)

By this one-to-one canonical duality, the nonconvex term \(W( \mathbf{x})={V}({\varLambda }(\mathbf{x}))\) in the problem \(({\mathscr {P}})\) can be replaced by \(\langle {\varLambda }(\mathbf{x}) ; \varvec{\varsigma }\rangle - {V}^*(\varvec{\varsigma })\) such that the nonconvex function \({P}(\mathbf{x})\) is reformulated as the Gao-Strang total complementary function [10]:

$$\begin{aligned} \varXi (\mathbf{x}, \varvec{\varsigma }) = \langle {\varLambda }(\mathbf{x}) ; \varvec{\varsigma }\rangle - {V}^*(\varvec{\varsigma }) - {U}(\mathbf{x}) : \;\; {\mathscr {X}}_a \times {\mathscr {S}}_a \rightarrow {\mathbb R}. \end{aligned}$$
(15)

By using this total complementary function, the canonical dual function \({P}^d (\varvec{\varsigma })\) can be obtained as

$$\begin{aligned} {P}^d(\varvec{\varsigma })= & {} \mathrm{sta}\{ \varXi (\mathbf{x}, \varvec{\varsigma }) \; | \; \mathbf{x}\in {\mathscr {X}}_a \} \nonumber \\= & {} {U}^{\varLambda }(\varvec{\varsigma }) - {V}^*(\varvec{\varsigma }), \end{aligned}$$
(16)

where \({U}^{\varLambda }(\mathbf{x})\) is defined by

$$\begin{aligned} {U}^{\varLambda }(\varvec{\varsigma }) = \mathrm{sta}\{ \langle {\varLambda }(\mathbf{x}) ; \varvec{\varsigma }\rangle - {U}(\mathbf{x}) \; | \;\; \mathbf{x}\in {\mathscr {X}}_a \}. \end{aligned}$$
(17)

In many applications, the geometrically nonlinear operator \({\varLambda }(\mathbf{x})\) is usually a quadratic function [3, 34]

$$\begin{aligned} {\varLambda }(\mathbf{x})=\frac{1}{2}\langle \mathbf{x}, D_k \mathbf{x}\rangle +\langle \mathbf{x}, \mathbf{b}_k \rangle , \end{aligned}$$
(18)

where \(D_k \in {\mathbb R}^{n \times n}\) and \(\mathbf{b}_k\in {\mathbb R}^n (k = 1, \cdots , p)\). Let \(\varvec{\varsigma }= [\varsigma _1,\cdots , \varsigma _p]^T\). In this case, the canonical dual function can be written in the following form:

$$\begin{aligned} P^d(\varvec{\varsigma })=-\frac{1}{2}\langle \mathbf{F}(\varvec{\varsigma }), \mathbf{G}^{-1}(\varvec{\varsigma }) \mathbf{F}(\varvec{\varsigma }) \rangle - V^{*}(\varvec{\varsigma }), \end{aligned}$$
(19)

where

$$ \mathbf{G}(\varvec{\varsigma }) = \mathbf{A}+\sum _{k=1}^p \varsigma _k D_k , \;\;\; \mathbf{F}(\varvec{\varsigma })=\mathbf{f}-\sum _{k=1}^p \varsigma _k \mathbf{b}_k . $$

Let

$$ {\mathscr {S}}^+_a = \{\varvec{\varsigma }\in {\mathbb R}^p|\;\; G(\varvec{\varsigma }) \succ 0 \} . $$

It is easy to prove that \({\mathscr {S}}_a^+\) is convex. Moreover, \({\mathscr {S}}_a^+\) is nonempty as long as there exists one \(D_k \succ 0\).

Therefore, the canonical dual problem can be proposed as

$$\begin{aligned} ({\mathscr {P}}^d): \;\; \max \{ P^d(\varvec{\varsigma }) | \;\; \varvec{\varsigma }\in {\mathscr {S}}^+_a\}. \end{aligned}$$
(20)

which is a concave maximization problem over a convex set \({\mathscr {S}}^+_a \subset {\mathbb R}^p\).

Theorem 2

([10]). Problem \(({\mathscr {P}}^d)\) is canonically dual to \(({\mathscr {P}})\) in the sense that if \(\varvec{\bar{\varsigma }}\) is a critical point of \(P^d(\varvec{\varsigma })\), then

$$\begin{aligned} \bar{\mathbf{x}}= \mathbf{G}^{-1}(\varvec{\bar{\varsigma }}) \mathbf{F}(\varvec{\bar{\varsigma }}) \end{aligned}$$
(21)

is a critical point of \(\varPi (\mathbf{x})\) and

$$\begin{aligned} {P}(\bar{\mathbf{x}}) = \varXi (\bar{\mathbf{x}}, \varvec{\bar{\varsigma }}) = {P}^d(\varvec{\bar{\varsigma }}). \end{aligned}$$
(22)

If \(\varvec{\bar{\varsigma }}\) is a solution to \(({\mathscr {P}}^d)\), then \(\bar{\mathbf{x}}\) is a global minimizer of \(({\mathscr {P}}) \) and

$$\begin{aligned} \min _{\mathbf{x}\in {\mathscr {X}}_a} {P}(\mathbf{x}) = \varXi (\bar{\mathbf{x}}, \varvec{\bar{\varsigma }})= \max _{\varvec{\varsigma }\in {\mathscr {S}}_a^+} {P}^d(\varvec{\varsigma }). \end{aligned}$$
(23)

Conversely, if \(\bar{\mathbf{x}}\) is a solution to \(({\mathscr {P}})\), it must be in the form of (21) for critical solution \(\varvec{\bar{\varsigma }}\) of \(P^d(\varvec{\varsigma })\).

To help explaining the theory, we consider a simple nonconvex optimization in \({\mathbb R}^n\):

$$\begin{aligned} \min P(\mathbf{x})=\frac{1}{2}\alpha (\frac{1}{2}\Vert \mathbf{x}\Vert ^2-{\lambda })^2-\mathbf{x}^T \mathbf{f}, \; \forall \mathbf{x}\in {\mathbb R}^n, \end{aligned}$$
(24)

where \({\alpha }, {\lambda }> 0\) are given parameters. The criticality condition \(\nabla P(\mathbf{x})=0\) leads to a nonlinear algebraic equation system in \({\mathbb R}^n\)

$$\begin{aligned} \alpha (\frac{1}{2}\Vert \mathbf{x}\Vert ^2-{\lambda })\mathbf{x}=\mathbf{f}. \end{aligned}$$
(25)

Clearly, to solve this n-dimensional nonlinear algebraic equation directly is difficult. Also traditional convex optimization theory can not be used to identify global minimizer. However, by the canonical dual transformation , this problem can be solved. To do so, we let \(\xi ={\varLambda }(u)=\frac{1}{2}\Vert \mathbf{x}\Vert ^2-{\lambda }\in {\mathbb R}\). Then, the nonconvex function \(W(\mathbf{x}) = \frac{1}{2}\alpha (\frac{1}{2}\Vert \mathbf{x}\Vert ^2 -{\lambda })^2\) can be written in canonical form \(V(\xi ) = \frac{1}{2}\alpha \xi ^2\). Its Legendre conjugate is given by \(V^{*}(\varsigma )=\frac{1}{2}\alpha ^{-1}\varsigma ^2\), which is strictly convex. Thus, the total complementary function for this nonconvex optimization problem is

$$\begin{aligned} \varXi (\mathbf{x},\varsigma )=(\frac{1}{2}\Vert \mathbf{x}\Vert ^2 - {\lambda }) \varsigma -\frac{1}{2}\alpha ^{-1}\varsigma ^2 - \mathbf{x}^T \mathbf{f}. \end{aligned}$$
(26)

For a fixed \(\varsigma \in {\mathbb R}\), the criticality condition \(\nabla _{\mathbf{x}} \varXi (\mathbf{x}, \varsigma )=0\) leads to

$$\begin{aligned} \varsigma \mathbf{x}-\mathbf{f}=0. \end{aligned}$$
(27)

For each \(\varsigma \ne 0 \), the Eq. (27) gives \(\mathbf{x}=\mathbf{f}/\varsigma \) in vector form. Substituting this into the total complementary function \(\varXi \), the canonical dual function can be easily obtained as

$$\begin{aligned} P^d(\varsigma )= & {} \{\varXi (\mathbf{x},\varsigma )| \nabla _{\mathbf{x}} \varXi (\mathbf{x},\varsigma ) =0\}\nonumber \\= & {} -\frac{ \Vert \mathbf{f}\Vert ^2 }{2 \varsigma }-\frac{1}{2}\alpha ^{-1} \varsigma ^2 -{\lambda }\varsigma , \;\;\; \forall \varsigma \ne 0. \end{aligned}$$
(28)

The critical point of this canonical function is obtained by solving the following dual algebraic equation

$$\begin{aligned} (\alpha ^{-1} \varsigma +{\lambda })\varsigma ^2=\frac{1}{2}\Vert \mathbf{f}\Vert ^2 . \end{aligned}$$
(29)

For any given parameters \(\alpha \), \({\lambda }\) and the vector \(\mathbf{f}\in {\mathbb R}^n\), this cubic algebraic equation has at most three roots satisfying \(\varsigma _1 \ge 0 \ge \varsigma _2\ge \varsigma _3\), and each of these roots leads to a critical point of the nonconvex function \(P(\mathbf{x})\), i.e., \(\mathbf{x}_i=\mathbf{f}/\varsigma _i\), \(i=1,2,3\). By the fact that \(\varsigma _ 1 \in {\mathscr {S}}^+_a = \{ \varsigma \in {\mathbb R}\; |\; \varsigma > 0 \}\), then Theorem 1 tells us that \(\mathbf{x}_1\) is a global minimizer of \({P}(\mathbf{x})\).

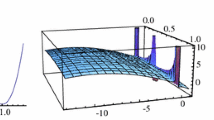
Consider one dimension problem with \(\alpha = 1\), \({\lambda }=2\), \(f= \frac{1}{2}\), the primal function and canonical dual function are shown in Fig. 1, where, \(x_1= 2.11491\) is a global minimizer of P(x), \(\varsigma _1=0.236417\) is a global maximizer of \({P}^d(\varsigma )\), and \({P}(x_1)=-1.02951={P}^d(\varsigma _1)\) (See the two black dots).

Fig. 1
figure 1

Graphs of \( P (\mathbf{x})\) (solid) and \({P}^d(\varsigma )\) (dashed)

Full size image

If we let \(\mathbf{f}= 0\), the graph of \({P}(\mathbf{x})\) is symmetric (i.e., the so-called double-well potential or the Mexican hat for \(n=2\) [11]) with infinite number of global minimizers satisfying \(\Vert \mathbf{x}\Vert ^2 = 2 {\lambda }\). In this case, the canonical dual \({P}^d (\varsigma ) = - \frac{1}{2}{\alpha }^{-1} \varsigma ^2 - {\lambda }\varsigma \) is strictly concave with only one critical point (local maximizer) \(\varsigma _3 = - {\alpha }{\lambda }< 0 \) (for \({\alpha }, {\lambda }> 0\)). The corresponding solution \(\mathbf{x}_3 = \mathbf{f}/\varsigma _3 = 0\) is a local maximizer. By the canonical dual equation (29) we have \(\varsigma _1 = \varsigma _2 = 0\) located on the boundary of \({\mathscr {S}}^+_a\), which corresponding to the two global minimizers \(x_{1,2} = \pm \sqrt{2 {\lambda }}\) for \(n=1\), see Fig. 1b.

This simple example shows a fundamental issue in global optimization, i.e., the optimal solutions of a nonconvex problem depends sensitively on the linear term (input) \(\mathbf{f}\). Geometrically speaking , the objective function \({W}( \mathbf{x})\) in \({P}(\mathbf{x})\) possesses certain symmetry. If there is no linear term, i.e., the subjective function in \({P}(\mathbf{x})\), the nonconvex problem usually has more than one global minimizer due to the symmetry. Traditional direct approaches and the popular SDP method are usually failed to deal with this situation. By the canonical duality theory, we understand that in this case the canonical dual function has no critical point in its open set \({\mathscr {S}}^+_a\). Therefore, by adding a linear perturbation \(\mathbf{f}\) to break this symmetry, the canonical duality theory can be used to solve the nonconvex problems to obtain one of global optimal solutions. This idea was originally from Gao’s work (1996) on post-buckling analysis of large deformed beam. The potential energy of this beam model is a double-well function, similar to this example, without the force \(\mathbf{f}\), the beam could have two buckling states (corresponding to two minimizers) and one un-buckled state (local maximizer). Later on (2008) in the Gao and Ogden work on analytical solutions in phase transformation [14], they further discovered that the nonconvex system has no phase transition unless the force distribution f(x) vanished at certain points. They also discovered that if force field f(x) changes dramatically, all the Newton type direct approaches failed even to find any local minimizer. This discovery is fundamentally important for understanding NP-hard problems in global optimization and chaos in nonconvex dynamical systems. The linear perturbation method has been used successfully for solving global optimization problems [16, 18, 32, 40]. Comprehensive reviews of the canonical duality theory and its applications in nonconvex analysis and global optimization can be found in [11, 13, 15].

4 Canonical Dual Problem

Now we are ready to apply the canonical duality theory for solving the integer programming problem \(({\mathscr {P}}_c)\) presented in Sect. 2. As indicated in [12, 13], the key step for solving this NP-hard problem is to use a so-called canonical measure \(\varvec{\rho }= \{y_i (y_i -1)\} \in {\mathbb R}^K\) such that the integer constraint \(y_{i} \in \{ 0, 1 \}\) can be equivalently written in the canonical form

$$ \varvec{\rho }= \mathbf{y}\circ (\mathbf{y}-\mathbf{e}_K) = \{ y_i (y_i -1)\} = 0 \in {\mathbb R}^K $$

where the notation \(\mathbf{s}\circ \mathbf{t}:=[s_1 t_1,s_2 t_2,\ldots ,s_K t_K]^T\) denotes the Hadamard product for any two vectors \(\mathbf{s}, \mathbf{t} \in {\mathbb R}^K\). Thus, the so-called geometrically admissible measure \(\varLambda \) can be defined as

$$\begin{aligned} \varvec{\xi }= & {} \varLambda (\mathbf{y})= \{ {D}\mathbf{y}-\mathbf{b}, \; {H}\mathbf{y}-\mathbf{e}_{n} , \;\; \mathbf{y}\circ (\mathbf{y}-\mathbf{e}_K) \} \\= & {} \{ \varvec{\varepsilon }, \;\; \varvec{\delta }, \;\; \varvec{\rho }\} \in {\mathscr {E}}= {\mathbb R}^{m + n + K} . \end{aligned}$$

Let

$$\begin{aligned} U(\mathbf{y}) = - P(\mathbf{y}) = \mathbf{h}^T \mathbf{y}-\frac{1}{2}\mathbf{y}^T {B}\mathbf{y}, \end{aligned}$$

and define

$$\begin{aligned} {V}(\varvec{\xi }) = \left\{ \begin{array}{ll} 0 &{} \text{ if } \varvec{\varepsilon }\le 0, \varvec{\delta }= 0, \varvec{\rho }= 0, \\ + \infty &{} \text{ otherwise }. \end{array} \right. \end{aligned}$$

Clearly, the constraints in \({\mathscr {Y}}\) can be replaced by the canonical transformation \({V}(\varLambda (\mathbf{y}))\) and the primal problem \(({\mathscr {P}}_c)\) can be equivalently written in the standard canonical form [13]

$$\begin{aligned} ({\mathscr {P}}): \;\; \min \left\{ \varPi (\mathbf{y}) = {V}(\varLambda (\mathbf{y})) - {U}(\mathbf{y}) : \; \; \mathbf{y}\in {\mathbb R}^{K} \right\} . \end{aligned}$$
(30)

By the fact that \({V}(\varvec{\xi })\) is convex, lower, semi-continuous on \( {\mathscr {E}}\), its sub-differential leads to the canonical dual variable \( \varvec{\varsigma }= ( \varvec{\sigma }, \varvec{\tau }, \varvec{\mu }) \in \partial {V}(\varvec{\xi }) \in {\mathscr {E}}^* = {\mathbb R}^{m + n + {K}}\), and its Fenchel super-conjugate (cf. Rockafellar [30])

$$\begin{aligned} {V}^{\sharp }(\varvec{\varsigma })= & {} \sup \{ \langle \varvec{\xi }; \varvec{\varsigma }\rangle - {V}(\varvec{\xi }):\; \varvec{\xi }\in {\mathscr {E}}\}\nonumber \\= & {} \left\{ \begin{array}{ll} 0 &{} \text{ if } \varvec{\sigma }\ge 0, \;\; \varvec{\tau }\ne 0, \;\; \varvec{\mu }\ne 0 \\ + \infty &{} \text{ otherwise } \end{array} \right. \end{aligned}$$
(31)

is also convex, l.s.c. on \({\mathscr {E}}^*\). By convex analysis, the following generalized canonical duality relations

$$\begin{aligned} \varvec{\varsigma }\in \partial {V}(\varvec{\xi }) = {\mathscr {E}}^*_a \;\; \Leftrightarrow \;\; \varvec{\xi }\in \partial {V}^\sharp (\varvec{\varsigma }) = {\mathscr {E}}_a \;\; \Leftrightarrow \;\; {V}(\varvec{\xi }) + {V}^\sharp (\varvec{\varsigma }) = \langle \varvec{\xi }; \varvec{\varsigma }\rangle \end{aligned}$$
(32)

hold on \({\mathscr {E}}\times {\mathscr {E}}^*\), where

$$ {\mathscr {E}}_a = \{ \varvec{\xi }= \{ \varvec{\varepsilon }, \varvec{\delta }, \varvec{\rho }\} \in {\mathscr {E}}| \; \varvec{\varepsilon }\le 0, \; \varvec{\delta }= 0, \; \varvec{\rho }= 0 \}, $$
$$ {\mathscr {E}}_a^* = \{ \varvec{\varsigma }= \{ \varvec{\sigma }, \varvec{\tau }, \varvec{\mu }\} \in {\mathscr {E}}^* | \; \; \varvec{\sigma }\ge 0, \;\; \varvec{\tau }\ne 0, \;\; \varvec{\mu }\ne 0 \} $$

are effective domains of \({V}\) and \({V}^\sharp \), respectively. The last equality in (32) is equivalent to the following KKT complementarity conditions:

$$\begin{aligned} \varvec{\varepsilon }^T \varvec{\sigma }= 0, \;\; \varvec{\delta }^T \varvec{\tau }= 0, \;\; \varvec{\rho }^T \varvec{\mu }= 0. \end{aligned}$$
(33)

Clearly, the condition \(\varvec{\mu }\ne 0\) leads to the integer condition \(\varvec{\rho }= \{ y_i(y_i -1) \} = 0 \in {\mathbb R}^K\). Let

$$\begin{aligned} \mathbf{F}(\varvec{\varsigma })= & {} \mathbf{h}- {D}^T \varvec{\sigma }-{H}^T \varvec{\tau }+ \varvec{\mu }, \end{aligned}$$
(34)
$$\begin{aligned} \mathbf{G}(\varvec{\mu })= & {} {B}+2 {\text{ Diag } }(\varvec{\mu }) . \end{aligned}$$
(35)

Thus, on \({\mathbb R}^K \times {\mathscr {E}}^*_a\), the total complementary function \(\varXi \) associated with \(\varPi (\mathbf{y}) \) can be written as

$$\begin{aligned} \varXi (\mathbf{y},\varvec{\varsigma })= & {} \langle \varLambda (\mathbf{y}) ; \varvec{\varsigma }\rangle - {V}^{\sharp } (\varvec{\varsigma })-U(\mathbf{y}) \\= & {} \frac{1}{2}\mathbf{y}^T \mathbf{G}(\varvec{\mu }) \mathbf{y}- \mathbf{F}^T(\varvec{\varsigma }) \mathbf{y}-\varvec{\sigma }^T \mathbf{b}-\varvec{\tau }^T \mathbf{e}_{n}. \end{aligned}$$

The criticality condition \(\nabla _{\mathbf{y}} \varXi (\mathbf{y}, \varvec{\varsigma }) = 0\) leads to the canonical equilibrium equation

$$\begin{aligned} \mathbf{G}(\varvec{\mu }) \mathbf{y}- \mathbf{F}(\varvec{\varsigma }) = 0 . \end{aligned}$$
(36)

Let \({\mathscr {S}}_a \subset {\mathscr {E}}^*_a\) be a canonical dual space:

$$\begin{aligned} {\mathscr {S}}_a = \{ \varvec{\varsigma }= ( \varvec{\sigma }, \varvec{\tau }, \varvec{\mu }) \in {\mathscr {E}}^*_a : \;\; \det \mathbf{G}(\varvec{\varsigma }) \ne 0 \; \} . \end{aligned}$$
(37)

Then on \({\mathscr {S}}_a\), the canonical dual function can be finally formulated as

$$\begin{aligned} \varPi ^d(\varvec{\varsigma })= & {} \mathrm{sta}\{ \varXi (\mathbf{y}, \varvec{\varsigma })\; : \;\; \mathbf{y}\in {\mathbb R}^K \} \nonumber \\= & {} -\frac{1}{2}\mathbf{F}^T(\varvec{\varsigma }) \mathbf{G}^{-1} (\varvec{\mu }) \mathbf{F}(\varvec{\varsigma }) -\varvec{\sigma }^T \mathbf{b}-\varvec{\tau }^T \mathbf{e}_{n} . \end{aligned}$$
(38)

Theorem 3

(Complementary-Dual Principle). If \(\varvec{\bar{\varsigma }}= (\varvec{\bar{\sigma }}, \bar{\varvec{\tau }}, \bar{\varvec{\mu }}) \) is a KKT point of \(\varPi ^d(\varvec{\varsigma })\) on \({\mathscr {S}}_a\), then the vector

$$\begin{aligned} \bar{\mathbf{y}}(\varvec{\bar{\varsigma }})= \mathbf{G}^{-1}(\bar{\varvec{\mu }}) \mathbf{F}(\varvec{\bar{\varsigma }}) \end{aligned}$$
(39)

is a KKT point of Problem \(({\mathscr {P}})\) and

$$\begin{aligned} \varPi (\bar{\mathbf{y}}) = \varPi ^d(\varvec{\bar{\varsigma }}). \end{aligned}$$
(40)

Proof

By introducing the Lagrange multiplier vectors \( \varvec{\xi }= \{ \varvec{\varepsilon }, \varvec{\delta }, \varvec{\rho }\} \in {\mathscr {E}}_a\) to relax the inequality constraintsFootnote 1 in \({\mathscr {E}}^*_a\), the Lagrangian function associated with the dual function \(\varPi ^d(\varvec{\sigma }, \varvec{\tau },\varvec{\mu }) \) becomes

$$\begin{aligned} L(\varvec{\sigma }, \varvec{\tau },\varvec{\mu }, \varvec{\varepsilon }, \varvec{\rho }) = \varPi ^d(\varvec{\sigma }, \varvec{\tau },\varvec{\mu })- \varvec{\varepsilon }^T \varvec{\sigma }- \varvec{\delta }^T \varvec{\tau }- \varvec{\rho }^T \varvec{\mu }. \end{aligned}$$

Then, in terms of \(\mathbf{y}= {G}^{-1} (\varvec{\mu }) \mathbf{F}(\varvec{\sigma }, \varvec{\tau }, \varvec{\mu }) \), the criticality condition \(\nabla _{\varvec{\varsigma }} L(\varvec{\varsigma }, \varvec{\xi }) = 0\) leads to

$$\begin{aligned} \frac{\partial L(\varvec{\sigma }, \varvec{\tau },\varvec{\mu }, \varvec{\varepsilon }, \varvec{\delta }, \varvec{\rho })}{\partial \varvec{\sigma }}= & {} {D}\mathbf{y}-\mathbf{b}- \varvec{\varepsilon }= 0,\\ \frac{\partial L(\varvec{\sigma }, \varvec{\tau },\varvec{\mu }, \varvec{\varepsilon }, \varvec{\delta }, \varvec{\rho })}{\partial \varvec{\tau }}= & {} {H}\mathbf{y}-\mathbf{e}_n - \varvec{\delta }= 0,\\ \frac{\partial L(\varvec{\sigma }, \varvec{\tau },\varvec{\mu }, \varvec{\varepsilon }, \varvec{\delta }, \varvec{\rho })}{\partial \varvec{\mu }}= & {} \mathbf{y}\circ (\mathbf{y}-\mathbf{e}_K)-\varvec{\rho }=0, \end{aligned}$$

as well as the KKT conditions

$$\begin{aligned} \varvec{\sigma }\ge 0,\;\; \varvec{\varepsilon }\le 0, \;\; \varvec{\sigma }^T \varvec{\varepsilon }= & {} 0,\end{aligned}$$
(41)
$$\begin{aligned} \varvec{\tau }\ne 0,\;\; \varvec{\delta }= 0 , \;\; \varvec{\delta }^T \varvec{\tau }= & {} 0.\end{aligned}$$
(42)
$$\begin{aligned} \varvec{\mu }\ne 0,\;\; \varvec{\rho }= 0, \;\; \varvec{\rho }^T \varvec{\mu }= & {} 0. \end{aligned}$$
(43)

They can be written as:

$$\begin{aligned} {D}\mathbf{y}- \mathbf{b}\le 0 ,\end{aligned}$$
(44)
$$\begin{aligned} {H}\mathbf{y}- \mathbf{e}_n= 0,\end{aligned}$$
(45)
$$\begin{aligned} \mathbf{y}\circ (\mathbf{y}-\mathbf{e}_K) = 0, \end{aligned}$$
(46)

This proves that if \((\varvec{\bar{\sigma }}, \bar{\varvec{\tau }}, \bar{\varvec{\mu }}) \) is a KKT point of \(\varPi ^d(\varvec{\varsigma })\), then the vector

$$\begin{aligned} \bar{\mathbf{y}}(\varvec{\bar{\sigma }}, \bar{\varvec{\tau }}, \bar{\varvec{\mu }})= \mathbf{G}^{-1} (\bar{\varvec{\mu }}) \mathbf{F}(\varvec{\bar{\sigma }}, \bar{\varvec{\tau }}, \bar{\varvec{\mu }}) \end{aligned}$$

is a KKT point of Problem \(({\mathscr {P}})\).

Again, by the complementary conditions (41)–(43) and (39), we have

$$\begin{aligned} \varPi ^d(\varvec{\bar{\sigma }}, \bar{\varvec{\tau }},\bar{\varvec{\mu }})= & {} -\frac{1}{2}\mathbf{F}(\varvec{\bar{\sigma }}, \bar{\varvec{\tau }}, \bar{\varvec{\mu }})^T \mathbf{G}(\bar{\varvec{\mu }})^{-1} \mathbf{F}(\varvec{\bar{\sigma }}, \bar{\varvec{\tau }}, \bar{\varvec{\mu }}) -\varvec{\bar{\sigma }}^T \mathbf{b}-\bar{\varvec{\tau }}^T \mathbf{e}_n\nonumber \\= & {} \frac{1}{2}\bar{\mathbf{y}}^T {B}\bar{\mathbf{y}}- \mathbf{h}^T \bar{\mathbf{y}}+ \varvec{\bar{\sigma }}^T ({D}\bar{\mathbf{y}}-\mathbf{b}) +\bar{\varvec{\tau }}^T ({H}\bar{\mathbf{y}}-\mathbf{e}_n) +\bar{\varvec{\mu }}^T (\bar{\mathbf{y}}\circ (\bar{\mathbf{y}}-\mathbf{e}_K))\nonumber \\= & {} \frac{1}{2}\bar{\mathbf{y}}^T {B}\bar{\mathbf{y}}- \mathbf{h}^T \bar{\mathbf{y}}= \varPi (\bar{\mathbf{y}}). \end{aligned}$$

Therefore, the theorem is proved. \(\square \)

Theorem 3 shows that the strong duality (40) holds for all KKT points of the primal and dual problems. In continuum mechanics, this theorem solved a 50-year-old problem and is known as the Gao principle [27]. In nonconvex analysis, this theorem can be used for solving a large class of fully nonlinear partial differential equations.

Remark 1.

As we have demonstrated that by the generalized canonical duality (32), all KKT conditions can be recovered for both equality and inequality constraints. Generally speaking, the nonzero Lagrange multiplier condition for the linear equality constraint is usually ignored in optimization textbooks. But it can not be ignored for nonlinear constraints. It is proved recently [26] that the popular augmented Lagrange multiplier method can be used mainly for linear constrained problems. Since the inequality constraint \(\varvec{\mu }\ne 0 \) produces a nonconvex feasible set \({\mathscr {E}}^*_a\), this constraint can be replaced by either \(\varvec{\mu }< 0\) or \(\varvec{\mu }> 0 \). But the condition \(\varvec{\mu }< 0\) is corresponding to \(\mathbf{y}\circ (\mathbf{y}-\mathbf{e}_{{K}}) \ge 0\), this leads to a nonconvex open feasible set for the primal problem. By the fact that the integer constraints \(y_i (y_i- 1) = 0\) are actually a special case (boundary) of the boxed constraints \( 0 \le y_i \le 1\), which is corresponding to \(\mathbf{y}\circ (\mathbf{y}-\mathbf{e}_{{K}}) \le 0\), we should have \(\varvec{\mu }> 0\) (see [8] and [12, 16]). In this case, the KKT condition (43) should be replaced by

$$\begin{aligned} \varvec{\mu }> 0, \;\; \mathbf{y}\circ (\mathbf{y}-\mathbf{e}_{{K}}) \le 0 , \;\; \varvec{\mu }^T [ \mathbf{y}\circ (\mathbf{y}-\mathbf{e}_{{K}})] = 0 . \end{aligned}$$
(47)

Therefore, as long as \(\varvec{\mu }\ne 0\) is satisfied, the complementarity condition in (47) leads to the integer condition \(\mathbf{y}\circ (\mathbf{y}-\mathbf{e}_{{K}}) = 0\). Similarly, the inequality \(\varvec{\tau }\ne 0 \) can be replaced by \(\varvec{\tau }> 0\).

By this remark, we can introduce a convex subset of the dual feasible space \({\mathscr {S}}_a\):

$$\begin{aligned} {\mathscr {S}}_a^+ = \{\varvec{\varsigma }= (\varvec{\sigma }, \varvec{\tau }, \varvec{\mu }) \in {\mathscr {E}}^*: \;\; \varvec{\sigma }\ge 0 , \;\; \varvec{\tau }> 0, \; \; \varvec{\mu }> 0 , \;\; \mathbf{G}(\varvec{\mu }) \succ 0 \}. \end{aligned}$$
(48)

Then the canonical dual problem can be eventually proposed as the following

$$\begin{aligned}&({\mathscr {P}}^{d})\;\;&\mathrm{\max } \left\{ \varPi ^d(\varvec{\varsigma }) =-\frac{1}{2}\mathbf{F}^T(\varvec{\varsigma }) \mathbf{G}^{-1} (\varvec{\mu }) \mathbf{F}(\varvec{\varsigma }) -\varvec{\sigma }^T \mathbf{b}-\varvec{\tau }^T \mathbf{e}_{n} | \;\; \varvec{\varsigma }\in {\mathscr {S}}_a^+ \right\} . \end{aligned}$$
(49)

It is easy to check that \( \varPi ^d(\varvec{\varsigma })\) is concave on the convex open set \({\mathscr {S}}^+_a\). Therefore, if \( {\mathscr {S}}^+_a\) is not empty, this canonical dual problem can be solved easily by convex minimization techniques.

Theorem 4

Assume that \(\varvec{\bar{\varsigma }}= (\varvec{\bar{\sigma }},\bar{\varvec{\tau }}, \bar{\varvec{\mu }})\) is a KKT point of \(\varPi ^d(\varvec{\varsigma })\) and \(\bar{\mathbf{y}}= \mathbf{G}^{-1} (\bar{\varvec{\mu }}) \mathbf{F}(\varvec{\bar{\varsigma }})\). If \( \varvec{\bar{\varsigma }}\in {\mathscr {S}}_a^+\), then \(\bar{\mathbf{y}}\) is a global minimizer of \(\varPi (\mathbf{y})\) and \(\varvec{\bar{\varsigma }}\) is a global maximizer of \(\varPi ^d(\varvec{\varsigma })\) with

$$\begin{aligned} \varPi (\bar{\mathbf{y}})=\min _{\mathbf{y}\in {\mathbb R}^K} \varPi (\mathbf{y})=\max _{\varvec{\varsigma }\in {\mathscr {S}}_a^+} \varPi ^d(\varvec{\varsigma }) = \varPi ^d(\varvec{\bar{\varsigma }}) \end{aligned}$$
(50)

Proof

It is easy to check that the total complementary function \(\varXi (\mathbf{y}, \varvec{\varsigma })\) is a saddle function on the open set \({\mathbb R}^K \times {\mathscr {S}}^+_a\), i.e., convex (quadratic) in \(\mathbf{y}\in {\mathbb R}^K\) and concave (linear) in \(\varvec{\varsigma }\in {\mathscr {S}}^+_a\). Therefore, if \((\bar{\mathbf{y}},\varvec{\bar{\varsigma }})\) is a critical point of \(\varXi (\mathbf{y}, \varvec{\varsigma })\), we must have

$$\begin{aligned}&\varPi ^d(\varvec{\bar{\varsigma }}) = \max _{\varvec{\varsigma }\in {\mathscr {S}}_a^+} P^d(\varvec{\varsigma }) = \max _{\varvec{\varsigma }\in {\mathscr {S}}_a^+} \min _{\mathbf{y}\in {\mathbb R}^K}\varXi (\mathbf{y},\varvec{\varsigma }) =\min _{\mathbf{y}\in {\mathbb R}^K} \max _{\varvec{\varsigma }\in {\mathscr {S}}_a^+}\varXi (\mathbf{y},\varvec{\varsigma })\nonumber \\= & {} \min _{\mathbf{y}\in {\mathbb R}^K} \max _{ \varvec{\varsigma }\in {\mathscr {S}}_a^+} \left\{ \frac{1}{2}\mathbf{y}^T \mathbf{G}(\varvec{\mu }) \mathbf{y}-(\mathbf{h}-{D}^T \varvec{\sigma }-{H}^T \varvec{\tau }+\varvec{\mu })^T \mathbf{y}-\varvec{\sigma }^T \mathbf{b}-\varvec{\tau }^T \mathbf{e}_n \right\} \nonumber \\= & {} \min _{\mathbf{y}\in {\mathbb R}^K } \max _{\varvec{\varsigma }\in {\mathscr {S}}_a^+} \left\{ \frac{1}{2}\mathbf{y}^T {B}\mathbf{y}-\mathbf{h}^T \mathbf{y}+\varvec{\sigma }^T({D}\mathbf{y}- \mathbf{b}) +\varvec{\tau }^T ({H}\mathbf{y}-\mathbf{e}_n) +\varvec{\mu }^T [\mathbf{y}\circ (\mathbf{y}- \mathbf{e}_{{K}})] \right\} \nonumber \\= & {} \min _{\mathbf{y}\in {\mathbb R}^K } \max _{\varvec{\varsigma }\in {\mathscr {S}}_a^+} \{\frac{1}{2}\mathbf{y}^T {B}\mathbf{y}-\mathbf{h}^T \mathbf{y}+ \langle \varLambda (\mathbf{y}) ; \varvec{\varsigma }\rangle \} \end{aligned}$$
(51)

Note that

$$\begin{aligned} \min _{\varvec{\varsigma }\in {\mathscr {E}}^*} \{ {V}^{\sharp }(\varvec{\varsigma })\}= {V}^{\sharp }(\varvec{\bar{\varsigma }}) = 0 , \;\; \min _{\varvec{\xi }\in {\mathscr {E}}} \{ {V}(\varvec{\xi })\} = {V}(\bar{\varvec{\xi }} ) =0 . \end{aligned}$$

Thus, it follows from (51) that

$$\begin{aligned} \varPi ^d(\varvec{\bar{\varsigma }})= & {} \min _{\mathbf{y}\in {\mathbb R}^K} \max _{\varvec{\varsigma }\in {\mathscr {E}}^*} \{\frac{1}{2}\mathbf{y}^T {B}\mathbf{y}-\mathbf{h}^T \mathbf{y}+ \langle \varLambda (\mathbf{y}) ; \varvec{\varsigma }\rangle -{V}^{\sharp } (\varvec{\varsigma })\}\\= & {} \min _{\mathbf{y}\in {\mathbb R}^K } \{\frac{1}{2}\mathbf{y}^T {B}\mathbf{y}-\mathbf{h}^T \mathbf{y}\} + \max _{\varvec{\varsigma }\in {\mathscr {E}}^* } \{ \langle \varLambda (\mathbf{y}) ; \varvec{\varsigma }\rangle - {V}^{\sharp } (\varvec{\varsigma })\}\nonumber \\= & {} \min _{\mathbf{y}\in {\mathbb R}^K}\{ \frac{1}{2}\mathbf{y}^T {B}\mathbf{y}-\mathbf{h}^T \mathbf{y}+ {V}(\varLambda (\mathbf{y})) \}\nonumber \\= & {} \min _{\mathbf{y}\in {\mathbb R}^K} \varPi (\mathbf{y}) = \min _{\mathbf{y}\in {\mathscr {Y}}} {P}(\mathbf{y}). \end{aligned}$$

This completes the proof. \(\square \)

Remark 2.

By the fact that \({\mathscr {S}}^+_a\) is an open convex set, if the problem \(({\mathscr {P}})\) has multiple global minimizers, then its canonical dual solutions could be located on the boundary of \({\mathscr {S}}^+_a\) as illustrated in Sect. 3 and in [12, 31]. In order to solve this problem, we let

$$ {\mathscr {S}}^+_c = \{ \varvec{\varsigma }= (\varvec{\sigma }, \varvec{\tau }, \varvec{\mu }) \in {\mathscr {S}}^+_a : \;\; \varvec{\mu }\ge 0 , \; \; \varvec{\tau }\ge 0 , \;\; \mathbf{G}(\varvec{\mu }) \succeq 0\}. $$

Then on this closed convex domain, the relaxed concave maximization problem

$$\begin{aligned} ({\mathscr {P}}^\sharp ) \;\; \max \{ \varPi ^d(\varvec{\varsigma }) : \; \; \varvec{\varsigma }\in {\mathscr {S}}_c^+ \} \end{aligned}$$
(52)

has at least one solution \(\varvec{\bar{\varsigma }}= (\varvec{\bar{\sigma }}, \bar{\varvec{\tau }}, \bar{\varvec{\mu }})\). If the corresponding \(\bar{\mathbf{y}}= \mathbf{G}^{-1} (\bar{\varvec{\mu }}) \mathbf{F}(\varvec{\bar{\varsigma }})\) is feasible, then \(\bar{\mathbf{y}}\) is a global minimizer of the primal problem \(({\mathscr {P}})\). If \(\mathbf{G}(\bar{\varvec{\mu }})\) is singular, than \(\mathbf{G}^{-1} (\bar{\varvec{\mu }})\) can be replaced by the Moore–Penrose generalized inverse \(\mathbf{G}^{\dagger }\) (see [31]). Otherwise, the relaxed canonical dual \(({\mathscr {P}}^\sharp )\) provides a lower bound approach to the primal problem \(({\mathscr {P}})\), i.e.,

$$ \min _{ \mathbf{y}\in {\mathscr {Y}}} {P}(\mathbf{y}) \ge \max _{\varvec{\varsigma }\in {\mathscr {S}}_c^+ } \varPi ^d(\varvec{\varsigma }). $$

This is one of the main advantages of the canonical duality theory.

5 Canonical Perturbation Method

In fact, Problem \(({\mathscr {P}}^d)\) can be rewritten as a convex minimization problem:

$$\begin{aligned}&\mathrm{\min }\;\; \frac{1}{2}\mathbf{F}^T(\varvec{\varsigma }) \mathbf{G}^{-1} (\varvec{\mu }) \mathbf{F}(\varvec{\varsigma }) + \varvec{\sigma }^T \mathbf{b}+ \varvec{\tau }^T \mathbf{e}_{n} , \nonumber \\&\mathrm{s.t.}\;\; \varvec{\varsigma }\in {\mathscr {S}}_a^+ .\nonumber \end{aligned}$$

If the primal problem has a unique global minimal solution, this canonical dual problem may have a unique critical point in \({\mathscr {S}}^+_a\) which can be obtained easily by well-developed nonlinear minimization techniques. Otherwise, the canonical dual function \(\varPi ^d(\varvec{\varsigma })\) may have critical point \(\varvec{\bar{\varsigma }}\) located on the boundary of \({\mathscr {S}}_a^+\), where the matrix \(\mathbf{G}(\varvec{\mu }) \) is singular. In order to handle this issue, \(({\mathscr {P}}^d)\) can be relaxed to a semi-definite programming problem:

$$\begin{aligned}&\mathrm{\min }\;\; g + \varvec{\sigma }^T \mathbf{b}+ \varvec{\tau }^T \mathbf{e}_{n},\nonumber \\&\mathrm{s.t.}\;\; g \ge \frac{1}{2}\mathbf{F}^T(\varvec{\varsigma }) \mathbf{G}^\dagger (\varvec{\mu }) \mathbf{F}(\varvec{\varsigma }),\end{aligned}$$
(53)
$$\begin{aligned}&\;\;\;\;\;\;\;\; \mathbf{G}(\varvec{\mu })\succeq 0,\end{aligned}$$
(54)
$$\begin{aligned}&\;\;\;\;\;\;\;\;\varvec{\varsigma }\in {\mathscr {E}}^*, \;\; \varvec{\sigma }\ge 0 , \;\; \varvec{\mu }> 0 , \end{aligned}$$
(55)

where the parameter g is actually the Gao-Strang pure complementary gap function [19], and \(\mathbf{G}^{\dagger }\) represents the Moore–Penrose generalized inverse of \(\mathbf{G}\). Since \(\varvec{\tau }\) is a Lagrange multiplier for the linear equality \(H\mathbf{y}= \mathbf{e}_n\), the condition \(\varvec{\tau }\ne 0\) can be ignored in this section as long as the final solution \(\mathbf{y}\) is feasible.

Lemma 1

(Schur Complementary Lemma). Let

$$\begin{aligned} A=\left[ \begin{array}{cc} B &{}C^T\\ C &{}D \end{array} \right] , \end{aligned}$$

If \(B \succ 0\), then A is positive (semi) definite if and only if the matrix \(D-CB^{-1} C^T \) is positive (semi) definite. If \(B\succeq 0\), then, A is positive semi-definite if and only if the matrix \(D-CB^{-1} C^T\) is positive semi-definite and \((I - B B^{-1}) C=0\).

According to Lemma 1, (53) is equivalent to

$$\begin{aligned} \left[ \begin{array}{cc} \mathbf{G}(\varvec{\mu }) &{} \mathbf{F}(\varvec{\varsigma })\\ \mathbf{F}^T (\varvec{\varsigma }) &{} 2 g \end{array} \right] \succeq 0. \end{aligned}$$

Thus, the canonical dual problem \(({\mathscr {P}}^d)\) can be further relaxed to the following stardard semi-definite problem (SDP):

$$\begin{aligned}&\mathrm{\min }\;\; g + \varvec{\sigma }^T \mathbf{b}+ \varvec{\tau }^T \mathbf{e}_{n},\\&\mathrm{s.t.}\;\; \left[ \begin{array}{cc} \mathbf{G}(\varvec{\mu }) &{} \mathbf{F}(\varvec{\varsigma })\\ \mathbf{F}^T (\varvec{\varsigma }) &{} 2 g \end{array} \right] \succeq 0, \;\; \mathbf{G}(\varvec{\mu })\succeq 0,\\&\;\;\;\;\;\;\;\;\varvec{\varsigma }\in {\mathscr {E}}^*, \;\; \varvec{\sigma }\ge 0 , \;\; \varvec{\mu }> 0 . \end{aligned}$$

Although the SDP relaxation can be used theoretically to solve the canonical dual problem for the case that \(\varPi ^d\) has critical points on the boundary \(\partial {\mathscr {S}}_a^+\), in practice, the matrix \(\mathbf{G}(\varvec{\mu })\) will be ill-conditioning when the dual solution approaches to \(\partial {\mathscr {S}}_a^+\). In order to solve this type of challenging problems, a canonical perturbation method has been suggested [16, 32]. Let

$$\begin{aligned} \varXi _{\delta _k} (\mathbf{y}, \varvec{\varsigma })= & {} \varXi (\mathbf{y}, \varvec{\varsigma }) + \frac{\delta _k}{2} \Vert \mathbf{y}-\mathbf{y}_k \Vert ^2 \\= & {} \frac{1}{2}\mathbf{y}^T \mathbf{G}_{\delta _k}(\varvec{\mu }) \mathbf{y}- \mathbf{F}_{\delta _k}^T(\varvec{\varsigma }) \mathbf{y}-\varvec{\sigma }^T \mathbf{b}-\varvec{\tau }^T \mathbf{e}_{n}+ \frac{\delta _k}{2} \mathbf{y}_k^T \mathbf{y}_k, \end{aligned}$$

where, \(\{\delta _k\}\) is a bounded sequence of positive real numbers, \(\{\mathbf{y}_k \} \in {\mathbb R}^K\) is a set of given vectors, \(\mathbf{G}_{\delta _k}(\varvec{\mu }) = \mathbf{G}(\varvec{\mu })+\delta _{k} I\), \(\mathbf{F}_{\delta _k}^T(\varvec{\varsigma }) = \mathbf{F}^T(\varvec{\varsigma }) +\delta _{k} \mathbf{y}_k\). Let

$$ {\mathscr {S}}_{\delta _k}^+ =\{ \varvec{\varsigma }\in {\mathscr {S}}_a : \;\; \mathbf{G}_{\delta _k}(\varvec{\mu }) \ge 0\}. $$

Clearly, we have \({\mathscr {S}}_a^+ \subset {\mathscr {S}}_{\delta _k}^+ \). Therefore, the perturbed canonical dual problem can be expressed as

$$\begin{aligned}&({\mathscr {P}}_{\delta _k}^{d})\;&\mathrm{\max }\;\; \varPi _{\delta _k}^d(\varvec{\varsigma }) =-\frac{1}{2}\mathbf{F}_{\delta _k}^T(\varvec{\varsigma }) \mathbf{G}_{\delta _k}^\dagger (\varvec{\mu }) \mathbf{F}_{\delta _k}(\varvec{\varsigma }) -\varvec{\sigma }^T \mathbf{b}-\varvec{\tau }^T \mathbf{e}_{n} , \nonumber \\&\;\;&\mathrm{s.t.}\;\; \varvec{\varsigma }\in {\mathscr {S}}_{\delta _k}^+ .\nonumber \end{aligned}$$

Based on this perturbed problem, the following canonical primal-dual algorithm can be proposed for solving the nonconvex problem \(({\mathscr {P}})\).

Algorithm 1

(Canonical Primal-Dual Algorithm)

Given initial data \(\delta _0 > 0, \;\; \mathbf{y}_0 \in {\mathbb R}^K\), and error allowance \(\varepsilon > 0\), let \(k = 0\).

  1. 1.

    Solve the perturbed canonical dual problem \(({\mathscr {P}}^d_{\delta _k})\) to obtain \(\varvec{\varsigma }_k \in \mathcal {S}^{+}_{\delta _k}\).

  2. 2.

    Compute \(\widetilde{\mathbf{y}}_{k+1} = [\mathbf{G}_{\delta _k}( \varvec{\varsigma }_k)]^\dag \mathbf{F}_{\delta _k}(\varvec{\varsigma }_k)\) and let

    \( \mathbf{y}_{k+1} = \mathbf{y}_k + \beta _k (\widetilde{\mathbf{y}}_{k+1} - \mathbf{y}_k), \;\; \beta _k \in [0,1] .\)

  3. 3.

    If \( | P(\mathbf{y}_{k+1} - P(\mathbf{y}_{k}) | \le \varepsilon \), then stop, \(\mathbf{y}_{k+1}\) is the optimal solution. Otherwise, let \(k = k + 1\), go back to step 1.

In this algorithm, \(\{\beta _k\} \in [ 0, 1]\) are given parameters, which change the search directions. Clearly, if \( \beta _k = 1 \), we have \(\mathbf{y}_{k+1} = \widetilde{\mathbf{y}}_{k+1}\).

The key step in this algorithm is to solve the perturbed canonical dual problem \(({\mathscr {P}}_{\delta _k}^d)\), which is equivalent to

$$\begin{aligned}&\mathrm{\min }\;\; g + \varvec{\sigma }^T \mathbf{b}+ \varvec{\tau }^T \mathbf{e}_{n},\\&\mathrm{s.t.}\;\; \left[ \begin{array}{cc} \mathbf{G}(\varvec{\mu })+\delta _k I &{} \mathbf{F}(\varvec{\varsigma })+\delta _k \mathbf{y}_k\\ \mathbf{F}^T (\varvec{\varsigma })+\delta _k \mathbf{y}_k &{} 2 g \end{array} \right] \succeq 0,\\&\;\;\;\;\;\;\;\; \mathbf{G}(\varvec{\mu })\succeq 0,\\&\;\;\;\;\;\;\;\;\varvec{\varsigma }\in {\mathscr {S}}, \;\; \varvec{\sigma }\ge 0 , \;\; \varvec{\mu }> 0 . \end{aligned}$$

This problem can be solved by a well-known software package named SeDuMi [36].

6 Numerical Experience

All data and computational results presented in this section are produced by Matlab. In order to save space and fit the matrix in the paper, we round our these results up to two decimals.

Example 1. 5-dimensional problem.

Consider Problem \(({\mathscr {P}}_a)\) with \(\mathbf{x}{=}[x_1,\cdots ,x_5]^T\), while \(x_i \in \{ 2,3,5 \} \), \(i{=}1, \cdots , 5\),

$$\begin{aligned} {Q}=\left[ \begin{array}{ccccc} 3.43&{}0.60&{}0.39&{}0.10&{}0.60\\ 0.60&{}2.76&{}0.32&{}0.65&{}0.49\\ 0.39&{}0.32&{}2.07&{}0.59&{}0.39\\ 0.10&{}0.65&{}0.59&{}2.62&{}0.30\\ 0.60&{}0.49&{}0.39&{}0.30&{}3.34 \end{array} \right] , \end{aligned}$$
$$\begin{aligned} \mathbf{c}=[38.97,-24.17,40.39,-9.65,13.20]^T, \end{aligned}$$
$$\begin{aligned} \mathbf{A}=\left[ \begin{array}{ccccc} 0.94&{}0.23&{}0.04&{}0.65&{}0.74\\ 0.96&{}0.35&{}0.17&{}0.45&{}0.19\\ 0.58&{}0.82&{}0.65&{}0.55&{}0.69\\ 0.06&{}0.02&{}0.73&{}0.30&{}0.18 \end{array} \right] , \end{aligned}$$
$$\begin{aligned} \mathbf{b}=[11.49,9.32,14.43,5.66]^T. \end{aligned}$$

Under the transformation (3), this problem is transformed into the 0–1 programming Problem \(({\mathscr {P}})\), where

$$\begin{aligned} \mathbf{y}=[y_{1,1}, y_{1,2}, y_{1, 3},\cdots , y_{5,1}, y_{5,1},y_{5,3}]^T \in {\mathbb R}^{15}, \end{aligned}$$
$$\begin{aligned} B= \left[ \begin{array}{ccccccccccccccc} 13.71&{}20.56&{}34.27&{}2.40 &{}3.61 &{}6.01 &{}1.58 &{}2.37 &{}3.95 &{}0.39 &{}0.58 &{}0.97 &{}2.38 &{}3.57 &{}5.95\\ 20.56&{}30.84&{}51.41&{}3.61 &{}5.41 &{}9.01 &{}2.37 &{}3.55 &{}5.92 &{}0.58 &{}0.88 &{}1.46 &{}3.57 &{}5.36 &{}8.93\\ 34.27&{}51.41&{}85.68&{}6.01 &{}9.01 &{}15.02&{}3.95 &{}5.92 &{}9.87 &{}0.97 &{}1.46 &{}2.43 &{}5,95 &{}8.93 &{}14.88\\ 2.40 &{}3.61 &{}6.01 &{}11.05&{}16.57&{}27.61&{}1.27 &{}1.91 &{}3.18 &{}2.61 &{}3.91 &{}6.52 &{}1.95 &{}2.93 &{}4.88\\ 3.61 &{}5.41 &{}9.01 &{}16.57&{}24.85&{}41.42&{}1.91 &{}2.86 &{}4.77 &{}3.91 &{}5.87 &{}9.78 &{}2.93 &{}4.39 &{}7.32\\ 6.01 &{}9.01 &{}15.02&{}27.61&{}41.42&{}69.03&{}3.18 &{}4.77 &{}7.96 &{}6.52 &{}9.78 &{}16.31&{}4.88 &{}7.32 &{}12.20\\ 1.58 &{}2.37 &{}3.95 &{}1.27 &{}1.91 &{}3.18 &{}8.27 &{}12.40&{}20.67&{}2.37 &{}3.55 &{}5.92 &{}1.57 &{}2.36 &{}3.93\\ 2.37 &{}3.55 &{}5.92 &{}1.91 &{}2.86 &{}4.77 &{}12.40 &{}18.60&{}31.00&{}3.55 &{}5.33 &{}8.89 &{}2.36 &{}3.53 &{}5.90\\ 3.95 &{}5.92 &{}9.87 &{}3.18 &{}4.77 &{}7.96 &{}20.67 &{}31.00&{}51.67&{}5.92 &{}8.86 &{}14.81&{}3.93 &{}5.90 &{}9.83\\ 0.39 &{}5.58 &{}0.97 &{}2.61 &{}3.91 &{}6.52 &{}2.37 &{}3.55 &{}5.92 &{}10.50&{}15.74&{}26.24&{}1.20 &{}1.80 &{}3.00\\ 0.58 &{}0.88 &{}1.46 &{}3.91 &{}5.87 &{}9.78 &{}3.55 &{}5.33 &{}8.89 &{}15.74&{}23.62&{}39.36&{}1.80 &{}2.70 &{}4.50\\ 0.97 &{}1.46 &{}2.43 &{}6.52 &{}9.78 &{}16.31&{}5.92 &{}8.89 &{}14.81&{}26.24&{}39.36&{}65.60&{}3.00 &{}4.50 &{}7.51\\ 2.38 &{}3.57 &{}5.95 &{}1.95 &{}2.93 &{}4.88 &{}1.57 &{}2.36 &{}3.93 &{}1.20 &{}1.80 &{}3.00 &{}13.35&{}20.02&{}33.37\\ 3.57 &{}5.36 &{}8.93 &{}2.93 &{}4.39 &{}7.32 &{}2.36 &{}3.54 &{}5.90 &{}1.80 &{}2.70 &{}4.50 &{}20.02&{}30.04&{}50.06\\ 5.95 &{}8.93 &{}14.88&{}4.88 &{}7.32 &{}12.20&{}3.93 &{}5.90 &{}9.83 &{}3.00 &{}4.50 &{}7.51 &{}33.37&{}50.06&{}83.43 \end{array} \right] , \end{aligned}$$
$$\begin{aligned} \mathbf{h}= & {} [77.95,116.92,194.87,-48.34,-72.51,-120.85,80.78,121.17\\&201.96,-19.29,-28.94, -48.23,26.39,39.59,65.99]^T, \end{aligned}$$
$$\begin{aligned} D=\left[ \begin{array}{ccccccccccccccc} \;1.88\;\;2.83\;\;4.71\;\;0.47\;\;0.70\;\;1.17\;\;0.09\;\;0.12\;\;0.22\;\;1.30\;\;1.94\;\;3.24\;\;1.49\;\;2.23\;\;3.72\\ \;1.91\;\;2.87\;\;4.78\;\;0.71\;\;1.06\;\;1.77\;\;0.34\;\;0.51\;\;0.85\;\;0.90\;\;1.35\;\;2.25\;\;0.38\;\;0.57\;\;0.94\\ \;1.15\;\;1.72\;\;2.88\;\;1.64\;\;2.46\;\;4.11\;\;1.30\;\;1.95\;\;3.25\;\;1.09\;\;1.64\;\;2.74\;\;1.37\;\;2.06\;\;3.43\\ \;0.12\;\;0.18\;\;0.30\;\;0.03\;\;0.05\;\;0.08\;\;1.46\;\;2.20\;\;3.66\;\;0.59\;\;0.89\;\;1.48\;\;0.37\;\;0.55\;\;0.92 \end{array} \right] , \end{aligned}$$
$$\begin{aligned} H = \left[ \begin{array}{cccccccccc} 1 &{} \cdots &{} 1 &{} 0 &{}\cdots &{} 0 &{}\cdots &{} 0 &{}\cdots &{}0\\ 0 &{} \cdots &{} 0 &{} 1&{}\cdots &{} 1 &{}\cdots &{} 0 &{}\cdots &{}0\\ \vdots &{}\ddots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ 0 &{} \cdots &{} 0 &{} 0 &{}\cdots &{} 0 &{}\cdots &{} 1 &{}\cdots &{}1 \end{array} \right] \in {\mathbb R}^{5 \times 15}. \end{aligned}$$

The canonical dual problem can be stated as follows:

$$\begin{aligned}&({\mathscr {P}}^{d})\mathrm{Maximize}\;\;\varPi ^d(\varvec{\varsigma }) =-\frac{1}{2}\mathbf{F}(\varvec{\varsigma })^T \mathbf{G}^\dagger (\varvec{\mu }) \mathbf{F}(\varvec{\varsigma }) -\varvec{\sigma }^T \mathbf{b}-\varvec{\tau }^T \mathbf{e}_{5} \\&\qquad \mathrm{subject \; to}\;\; \varvec{\varsigma }= (\varvec{\sigma }, \varvec{\tau }, \varvec{\mu }) \in {\mathbb R}^{4+ 5 +15}, \;\; \varvec{\sigma }\ge 0, \varvec{\mu }>0. \end{aligned}$$

By solving this dual problem with the sequential quadratic programming method in the optimization Toolbox within the Matlab environment, we obtain

$$\begin{aligned} \varvec{\bar{\sigma }}=[0,0,0,0]^T, \end{aligned}$$
$$\begin{aligned} \bar{\varvec{\tau }}=[73.90,-106.70,111.95,-59.27,-0.01]^T, \end{aligned}$$

and

$$\begin{aligned} \bar{\varvec{\mu }}= & {} [39.34,22.07,12.49,33.56,3.01,76.14,61.00,35.52\\&18.78,1.47,41.96, 0.001,0.001,0.006]^T. \end{aligned}$$

It is clear that \(\varvec{\bar{\varsigma }}= (\varvec{\bar{\sigma }},\bar{\varvec{\tau }},\bar{\varvec{\mu }}) \in \mathcal {S}_a^{+}\). Thus, from Theorem 4,

$$\begin{aligned} \bar{\mathbf{y}}= & {} ({B}+2 {\text{ Diag } }(\bar{\varvec{\mu }}))^\dagger (\mathbf{h}- {D}^T \varvec{\bar{\sigma }}-{H}^T \bar{\varvec{\tau }}+ \bar{\varvec{\mu }})\\= & {} [0,0,1,1,0,0,0,0,1,1,0,0,1,0,0]^T \end{aligned}$$

is the global minimizer of Problem \(({\mathscr {P}})\) with \(\varPi ^d(\varvec{\bar{\varsigma }})=-227.87=\varPi (\bar{\mathbf{y}})\). The solution to the original primal problem can be calculated by using the transformation

$$\begin{aligned} \bar{x}_i=\sum _{j=1}^{K_i} u_{i,j} \bar{y}_{i,j},\; i=1,2,3,4,5, \end{aligned}$$

to give

$$\begin{aligned} \bar{\mathbf{x}}=[5,2,5,2,2]^T \end{aligned}$$

with \(P(\bar{\mathbf{x}})=-227.87\).

Example 2. 10-dimensional problem. Consider Problem \(({\mathscr {P}}_a)\), with \(\mathbf{x}=[x_1, \cdots , x_{10}]^T \), while \(x_i \in \{1,2,4,7,9\},\;i=1,\cdots ,10\),

$$\begin{aligned} {Q}=\left[ \begin{array}{cccccccccc} 6.17&{}0.62&{}0.46&{}0.37&{}0.56&{}0.66&{}0.67&{}0.85&{}0.57&{}0.44\\ 0.62&{}5.63&{}0.29&{}0.56&{}0.79&{}0.29&{}0.43&{}0.69&{}0.49&{}0.39\\ 0.46&{}0.29&{}5.81&{}0.55&{}0.22&{}0.55&{}0.36&{}0.27&{}0.51&{}0.91\\ 0.37&{}0.56&{}0.55&{}6.10&{}0.28&{}0.42&{}0.44&{}0.34&{}0.75&{}0.44\\ 0.56&{}0.79&{}0.22&{}0.28&{}4.75&{}0.40&{}0.55&{}0.42&{}0.49&{}0.44\\ 0.66&{}0.29&{}0.55&{}0.42&{}0.40&{}5.71&{}0.32&{}0.57&{}0.65&{}0.70\\ 0.67&{}0.43&{}0.36&{}0.44&{}0.55&{}0.32&{}5.27&{}0.56&{}0.37&{}0.85\\ 0.85&{}0.69&{}0.27&{}0.34&{}0.42&{}0.57&{}0.56&{}5.91&{}0.15&{}0.62\\ 0.57&{}0.49&{}0.51&{}0.75&{}0.49&{}0.65&{}0.37&{}0.15&{}4.51&{}0.46\\ 0.44&{}0.39&{}0.91&{}0.44&{}0.44&{}0.70&{}0.85&{}0.62&{}0.46&{}5.73 \end{array} \right] , \end{aligned}$$
$$\begin{aligned} \mathbf{f}=[0.89,0.03, 0.49, 0.17, 0.98, 0.71, 0.50, 0.47, 0.06, 0.68]^T, \end{aligned}$$
$$\begin{aligned} \mathbf{A}=\left[ \begin{array}{cccccccccc} 0.04&{}0.82&{}0.97&{}0.83&{}0.83&{}0.42&{}0.02&{}0.20&{}0.05&{}0.94\\ 0.07&{}0.72&{}0.65&{}0.08&{}0.80&{}0.66&{}0.98&{}0.49&{}0.74&{}0.42\\ 0.52&{}0.15&{}0.80&{}0.13&{}0.06&{}0.63&{}0.17&{}0.34&{}0.27&{}0.98\\ 0.10&{}0.66&{}0.45&{}0.17&{}0.40&{}0.29&{}0.11&{}0.95&{}0.42&{}0.30\\ 0.82&{}0.52&{}0.43&{}0.39&{}0.53&{}0.43&{}0.37&{}0.92&{}0.55&{}0.70 \end{array} \right] , \end{aligned}$$
$$\begin{aligned} \mathbf{b}=[33.76, 37.07, 26.75, 25.46, 37.36]^T. \end{aligned}$$

By solving the canonical dual problem of Problem \(({\mathscr {P}}_a)\), we obtain

$$\begin{aligned} \varvec{\bar{\sigma }}=[0,0,0,0,0]^T, \end{aligned}$$
$$\begin{aligned} \bar{\varvec{\tau }}= & {} [-19.99, -20.12, -18.13, -18.37, -14.32,\\&-17.13, -18.46, -19.73, -17.65, -16.55]^T, \end{aligned}$$

and

$$\begin{aligned} \bar{\varvec{\mu }}= & {} [9.51,0.97,21.93,53.36,74.34,9.95,0.21,20.53,51.01,71.35\\&8.68,0.77,19.68,48.03,66.94,8.30,1.77,21.91,52.13,72.27\\&6.40,1.54,17.39,41.19,57.04,7.57,1.98,21.10,49.77,68.90\\&9.15,0.16,18.79,46.72,65.34,9.82,0.09,19.90,49.63,69.45\\&8.76,0.13,17.92,44.60,62.39,6.26,4.03,24.60,55.48,76.04]^T, \end{aligned}$$

It is clear that \(\varvec{\bar{\varsigma }}= (\varvec{\bar{\sigma }},\bar{\varvec{\tau }},\bar{\varvec{\mu }}) \in \mathcal {S}_a^{+}\). Therefore,

$$\begin{aligned}&\bar{\mathbf{y}}=[1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,\\&1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0]^T \end{aligned}$$

is the global minimizer of the problem \(({\mathscr {P}})\) with \(\varPi ^d(\varvec{\bar{\varsigma }})=45.54=\varPi (\bar{\mathbf{y}})\). The solution to the original primal problem is

$$\begin{aligned} \bar{\mathbf{x}}=[1,1,1,1,1,1,1,1,1,1]^T \end{aligned}$$

with \({P}(\bar{\mathbf{x}})=45.54\).

Example 3. Relatively large size problems.

Consider Problem \(({\mathscr {P}}_a)\) with \(n=20\), 50, 100, 200, and 300. Let these five problems be referred to as Problem (1), \(\cdots \), Problem (5), respectively. Their coefficients are generated randomly with uniform distribution. For each problem, \(q_{ij} \in (0,1)\), \( a_{ij} \in (0,1)\), for \(i=1, \cdots , n\); \(j=1, \cdots , n\), and \(c_i \in (0,1)\), \(x_i \in \{1,2,3,4,5 \}\), for \(i=1, \cdots n\). Without loss of generality, we ensure that the constructed \({Q}\) is a symmetric matrix. Otherwise, we let \({Q}= \frac{{Q}+{Q}^T }{2}\). Furthermore, let \({Q}\) be diagonally dominated. For each \(x_i\), its lower bound is \(l_i=1\), and its upper bound is \(u_i=5\). Let \(l=[l_1, \cdots , l_n]^T\) and \(u=[u_1,\cdots ,u_n]^T \). The right-hand sides of the linear constraints are chosen such that the feasibility of the test problem is satisfied. More specifically, we set \(\mathbf{b}=\sum _{j} a_{ij} l_j + 0.5\cdot (\sum _j a_{ij}u_j-\sum _j a_{ij} l_j)\).

We then construct the canonical problem of each of the five problems. It is solved by using the sequential quadratic programming method with active set strategy from the Optimization Toolbox within the Matlab environment. The specifications of the personal notebook computer used are: Window 7 Enterprise, Intel(R), Core(TM)(2.50 GHZ). Table 1 presents the numerical results, where m is number of linear constraints in Problem \(I({\mathscr {P}}_a)\).

Table 1 Numerical results for large scale integer programming problems
Full size table

From Table 1, we see that the algorithm based on the canonical dual method can solve large scale problems with reasonable computational time. Furthermore, for each of the five problems, the solution obtained is a global optimal solution. For the case of \(n=300\), the equivalent problem in the form of Problem \(({\mathscr {P}}_b)\) has 1500 variables. For such a problem, there are \(2^{1500}\) possible combinations.

7 Conclusion

We have presented a canonical duality approach for solving a general quadratic discrete value selection problem with linear constraints. Our results show that this NP-hard problem can be converted to a continuous concave dual maximization problem over a convex space without duality gap. For certain given data, if this canonical dual has a KKT point in the dual feasible space \({\mathscr {S}}^+_a\), the problem can be solved easily by well-developed convex optimization methods. Otherwise, a canonical perturbation method is proposed, which can be used to deal with challenging cases when the primal problem has multiple global minimizers. Several examples, including some relatively large scale ones, were solved effectively by using the method proposed.

Remanning open problems include how to solve the canonical dual problem \(({\mathscr {P}}^d)\) more efficiently instead of using the SDP approximation. Also, for the given data \({Q}, \mathbf{c}, \mathbf{A}, \mathbf{b}\), the existence condition for the canonical dual problem having KKT point in \({\mathscr {S}}^+_a\) is fundamentally important for understanding NP-hard problems . If the canonical dual \(({\mathscr {P}}^d)\) has no KKT point in the closed set \( {{\mathscr {S}}}^+_c = {\mathscr {S}}^+_a \cup \partial {\mathscr {S}}^+_a\), the primal problem is equivalent to the following canonical dual problem (see Eq. (67) in [16])

$$\begin{aligned} \min \mathrm{sta}\{ \varPi ^d(\varvec{\varsigma }) | \;\; \varvec{\varsigma }\in {\mathscr {S}}_a \}, \end{aligned}$$
(56)

i.e., to find the minimal stationary value of \(\varPi ^d\) on \({\mathscr {S}}_a\). Since the feasible set \({\mathscr {S}}_a\) is nonconvex, to solve this canonical dual problem is very difficult. Therefore, it is a conjecture that the primal problem \(({\mathscr {P}})\) could be NP-hard if its canonical dual \(({\mathscr {P}}^d)\) has no KKT point in the closed set \( \mathcal {S}_a^{+} \) [12]. In this case, one alternative approach for solving \(({\mathscr {P}})\) is the canonical dual relaxation \(({\mathscr {P}}^\sharp )\). Although the relaxed problem \(({\mathscr {P}}^\sharp )\) is convex, by Remark 2 we know that there exists a duality gap between the primal problem \(({\mathscr {P}})\). It turns out that the associated SDP method provides only a lower bound approach for solving the primal problem. Further researches are needed to know how big is this duality gap, how much does this relaxation lose, and how to solve the nonconvex canonical dual problem (56).