Canonical Primal–Dual Method for Solving Nonconvex Minimization Problems

Abstract

A new primal–dual algorithm is presented for solving a class of nonconvex minimization problems. This algorithm is based on canonical duality theory such that the original nonconvex minimization problem is first reformulated as a convex–concave saddle point optimization problem, which is then solved by a quadratically perturbed primal–dual method. Numerical examples are illustrated. Comparing with the existing results, the proposed algorithm can achieve better performance.

1 Problems and Motivations

The nonconvex minimization problem to be studied is proposed as the following:

$$\begin{aligned} (\mathscr {P}_o): \;\; \min \left\{ P\left( \mathbf{x}\right) = W(\mathbf{x}) + \frac{1}{2}\langle \mathbf{x}, \mathbf {A}\mathbf{x}\rangle - \langle \mathbf{x}, \varvec{f}\rangle \; | \; \mathbf{x}\in \mathscr {X}_a \right\} , \end{aligned}$$

(1)

where $\mathbf{x}= \{ x_i \} \in \mathbb {R} ^{n}$ is a decision vector, $\mathbf {A}=\left\{ A_{ij}\right\} \in \mathbb {R}^{n\times n}$ is a given real symmetrical matrix, $\varvec{f}=\{ f_i \} \in \mathbb {R}^{n}$ is a given vector, $\langle * , * \rangle$ denotes a bilinear form in ${\mathbb R}^n \times {\mathbb R}^n$; the feasible space $\mathscr {X}_a$ is an open convex subset of ${\mathbb R}^n$ such that on which the nonconvex function $W:\mathscr {X}_a\rightarrow {\mathbb R}$ is well-defined.

Due to the nonconvexity, Problem ($\mathscr {P}_o$) may admit many local minima and local maxima [4]. It is not an easy task to identify or numerically compute its global minimizer. Therefore, many numerical methods have been developed in literature, including the extended Gauss-Newton method (see [22]), the proximal method (see [21]), as well as the popular semi-definite programming (SDP) relaxation (see [18]). Generally speaking, Gauss–Newton type methods are local-based such that only local optimal solutions can be expected. To find global optimal solution often relies on the branch-and-bound [2] as well as the moment matrix-based SDP relaxation [20, 36]. However, these methods are computationally expensive which can be used for solving mainly small or medium size problems. The main goal of this paper is to develop an efficient algorithm for solving the nonconvex problem ($\mathscr {P}_o$).

Generally speaking, a powerful algorithm should based on a precise theory. Canonical duality theory is a newly developed, powerful methodological theory that has been used successfully for solving a large class of global optimization problems in both continuous and discrete systems [4, 6, 8]. The main feature of this theory is that, which depends on the objective function $W(\mathbf{x})$, the nonconvex/nonsmooth/discrete primal problems can be transformed into a unified concave maximization problem over a convex continuous space, which can be solved easily using well-developed convex optimization techniques (see review articles [6, 8] for details). This powerful theory was developed from Gao and Strang’s original work [7] where the nonconvex function $W(\mathbf{x})$ is the so-called stored energy, which is required, by the concept (see [24], p. 8), to be an objective function. In mathematical physics, a real-valued function $W(\mathbf{x})$ is said to be objective if $W(\mathbf{Q}\mathbf{x}) = W(\mathbf{x})$ for all rotation matrix $\mathbf{Q}$ such that $\mathbf{Q}^{-1} = \mathbf{Q}^T$ and det$\mathbf{Q}= 1$ (see Chap. 6 in [4]), i.e., an objective function $W(\mathbf{x})$ should be an invariant under certain coordinate transformations. In continuum mechanics, the objectivity is also referred as the frame-indifference (see [1, 24]). Therefore, instead of the decision variables directly, an objective function usually depends on certain measure (norm) of $\mathbf{x}$, say, the Euclidean norm $\Vert \mathbf{x}\Vert$ as we have $\Vert \mathbf{Q}\mathbf{x}\Vert ^2 = \mathbf{x}^T\mathbf{Q}^T \mathbf{Q}\mathbf{x}= \Vert \mathbf{x}\Vert ^2$. In this paper, we shall need only the following weak assumptions for the nonconvex function $W(\mathbf{x})$ in $(\mathscr {P}_o)$.

Assumption 1

 

(A1).:

There exits a geometrical operator $\varLambda (\mathbf{x}): \mathscr {X}_a \rightarrow \mathscr {V}_a \subset {\mathbb R}^m$ and a strictly convex differentiable function $V: \mathscr {V}_a \subset {\mathbb R}^m \rightarrow {\mathbb R}$ such that

$$\begin{aligned} W(\mathbf{x}) = V(\varLambda (\mathbf{x})) \;\; \forall \mathbf{x}\in \mathscr {X}_a . \end{aligned}$$

(2)

(A2).:

The geometrical operator $\varLambda (\mathbf{x})$ is a vector-valued quadratic mapping in the form of

$$\begin{aligned} \varLambda (\mathbf{x}) = \left\{ \frac{1}{2}\langle \mathbf{x}, \mathbf {A}_1\mathbf{x}\rangle - \langle \mathbf{x},\varvec{b}_1\rangle ,\cdots , \frac{1}{2}\langle \mathbf{x}, \mathbf {A}_m\mathbf{x}\rangle - \langle \mathbf{x},\varvec{b}_m\rangle \right\} , \end{aligned}$$

(3)

where $\mathbf {A}_i,i=1,\cdots ,m$, are symmetrical matrices with appropriate dimensions and $\varvec{b}_i,i=1,\cdots ,m,$ are given vectors such that the range $\mathscr {V}_a$ is a closed convex set in ${\mathbb R}^m$.

 

Actually, Assumption (A1) is the so-called canonical transformation. Particularly, if $\mathbf {A}_i \succeq 0, \; \; \varvec{b}_i = 0 \;\; \forall i=1,\cdots ,m,$ then $\varLambda (\mathbf{x})$ is an objective (Cauchy–Riemann type) measure (see [4]). Based on this assumption, the proposed nonconvex problem ($\mathscr {P}_o$) can be reformulated in the following canonical form:

$$\begin{aligned} (\mathscr {P}): \;\; \min \left\{ P\left( \mathbf{x}\right) = V(\varLambda (\mathbf{x})) + \frac{1}{2}\langle \mathbf{x}, \mathbf {A}\mathbf{x}\rangle - \langle \mathbf{x}, \varvec{f}\rangle \; : \; \mathbf{x}\in \mathscr {X}_a \right\} . \end{aligned}$$

(4)

The canonical primal problem $(\mathscr {P})$ arises naturally from a wide range of applications in engineering and sciences. For instance, the canonical function $V(\varvec{\xi })$ is simply a quadratic function of $\varvec{\xi }=\varLambda (\mathbf{x})$ in the least squares methods for solving systems of quadratic equations $\varLambda (\mathbf{x}) = \mathbf{d} \in {\mathbb R}^m$ (see [32]), chaotic dynamical systems [31], wireless sensor network localization [11], general Euclidean distance geometry [26], and computational biology [38]. In computational physics and networks optimization, the position variable $\mathbf{x}$ is usually a matrix (second-order tensor) and the geometrical operator $\varvec{\xi }=\varLambda (\mathbf{x})$ is a positive semi-definite (discredited Cauchy–Riemann measure) tensor (see [11]), the convex function $V(\varvec{\xi })$ is then an objective function, which is the instance studied by Gao and Strang [4, 7]. Particularly, if $W(\mathbf{x})$ is a quadratic function, the canonical dual problem is equivalent to a SDP problem (see [11]). By the facts that the geometrical operator defined in Assumption (A2) is a general quadratic mapping, the nonconvex function $W(\mathbf{x})$ studied in this paper is not necessary to be “objective”, which certainly has extensive applications in complex systems.

The rest of this paper is divided into six sections. The canonical dual problem is formulated in the next section, where some existing difficulties are addressed. The associated canonical min-max duality theory is discussed in Sect. 3. A proximal point method is proposed in Sect. 4 to solve this canonical min-max problem. Section 5 presents some numerical experiments. Applications to sensor network optimization are illustrated in Sect. 6. The paper is ended by some concluding remarks.

2 Canonical Duality Theory

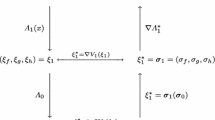
By Assumption (A1), the canonical function $V(\cdot )$ is strictly convex and differentiable on $\mathscr {V}_a$, therefore, the canonical dual mapping $\varvec{\varsigma }= \nabla V(\varvec{\xi }) : \mathscr {V}_a \rightarrow \mathscr {V}_a^* \subset {\mathbb R}^m$ is one-to-one onto the convex set $\mathscr {V}_a^* \subset {\mathbb R}^m$ such that the following canonical duality relations hold on $\mathscr {V}_a \times \mathscr {V}^*_a$

$$\begin{aligned} \varvec{\varsigma }= \nabla V(\varvec{\xi }) \Leftrightarrow \varvec{\xi }= \nabla V^{*}(\varvec{\varsigma }) \Leftrightarrow V(\varvec{\xi }) + V^{*}(\varvec{\varsigma }) = \langle \varvec{\xi }; \varvec{\varsigma }\rangle , \end{aligned}$$

(5)

where $\langle * ; * \rangle$ is a bilinear form on ${\mathbb R}^m \times {\mathbb R}^m$, and $V^{*}(\varvec{\varsigma })$ is the Legendre conjugate of $V(\varvec{\xi })$ defined by

$$\begin{aligned} V^*(\varvec{\varsigma }) =\max \left\{ \langle \varvec{\xi }; \varvec{\varsigma }\rangle - V(\varvec{\xi }) \; | \; \varvec{\xi }\in \mathscr {V}_a \right\} . \end{aligned}$$

(6)

By convex analysis, we have

$$\begin{aligned} V(\varLambda (\mathbf{x})) =\max \left\{ \langle \varLambda (\mathbf{x}) ; \varvec{\varsigma }\rangle - V^*(\varvec{\varsigma }) \; | \; \varvec{\varsigma }\in \mathscr {V}^*_a \right\} . \end{aligned}$$

(7)

Substituting (7) into (4), Problem ($\mathscr {P}$) can be equivalently written as

$$\begin{aligned} \min _{\mathbf{x}}\max _{\varvec{\varsigma }} \left\{ \Xi (\mathbf{x}, \varvec{\varsigma }) \; | \; (\mathbf{x},\varvec{\varsigma }) \in \mathscr {X}_a \times \mathscr {V}^*_a \right\} , \end{aligned}$$

(8)

where $\Xi : \mathscr {X}_a \times \mathscr {V}^*_a \rightarrow {\mathbb R}$ is the total complementary function defined by

$$\begin{aligned} \Xi (\mathbf{x},\varvec{\varsigma })= & {} \langle \varLambda (\mathbf{x}) ; \varvec{\varsigma }\rangle - V^{*}(\varvec{\varsigma }) + \frac{1}{2}\langle \mathbf{x}, \mathbf {A}\mathbf{x}\rangle - \langle \mathbf{x}, \varvec{f}\rangle \nonumber \\= & {} \frac{1}{2}\langle \mathbf{x},\mathbf {G}(\varvec{\varsigma })\mathbf{x}\rangle - V^{*}(\varvec{\varsigma }) -\langle \mathbf{x},\varvec{\tau }(\varvec{\varsigma })\rangle , \end{aligned}$$

(9)

in which

$$\begin{aligned} \mathbf {G}(\varvec{\varsigma }) = \mathbf {A}+ \sum _{k=1}^m \varsigma _k \mathbf {A}_k, \end{aligned}$$

(10)

and

$$\begin{aligned} \varvec{\tau }(\varvec{\varsigma }) = \varvec{f}+ \sum _{k=1}^m {\varsigma }_k \varvec{b}_k. \end{aligned}$$

(11)

For a given $\varvec{\varsigma }\in \mathscr {V}^*_a$, the stationary condition $\nabla _{\mathbf{x}} \Xi (\mathbf{x}, \varvec{\varsigma }) = 0$ leads to the following canonical equilibrium equation

$$\begin{aligned} \mathbf {G}(\varvec{\varsigma }) \mathbf{x}= \varvec{\tau }(\varvec{\varsigma }). \end{aligned}$$

(12)

Let

$$ \mathscr {S}_a = \left\{ \varvec{\varsigma }\in \mathscr {V}^*_a \;| \; \exists \; \mathbf{x}\in \mathscr {X}_a , \text { such that } \mathbf {G}(\varvec{\varsigma }) \mathbf{x}= \varvec{\tau }(\varvec{\varsigma }) \right\} $$

be the dual feasible space, in which, the canonical dual function is defined by

$$\begin{aligned} P^d(\varvec{\varsigma }) = \text {sta}\left\{ \Xi (\mathbf{x},\varvec{\varsigma }) \;| \; \mathbf{x}\in \mathscr {X}_a \right\} = - \frac{1}{2}\langle \mathbf {G}^\dag (\varvec{\varsigma }) \varvec{\tau }(\varvec{\varsigma }) , \varvec{\tau }(\varvec{\varsigma }) \rangle - V^*(\varvec{\varsigma }) , \end{aligned}$$

(13)

where $\text {sta}\left\{ f(\mathbf{x}) | \mathbf{x}\in \mathscr {X}_a \right\}$ stands for finding stationary points of $f(\mathbf{x})$ on $\mathscr {X}_a$, and $\mathbf {G}^\dag$ represents the generalized inverse of $\mathbf {G}$. Particularly, let

$$\begin{aligned} \mathscr {S}_a^+ = \left\{ \varvec{\varsigma }\in \mathscr {V}^*_a\; | \; \mathbf {G}(\varvec{\varsigma }) \succeq 0 \right\} , \end{aligned}$$

(14)

where $\mathbf {G}(\varvec{\varsigma })\succeq 0$ means that the matrix $\mathbf {G}(\varvec{\varsigma })$ is positive semi-definite. Clearly, $\mathscr {S}_a^+$ is a convex set of $\mathscr {S}_a$ and the total complementary function $\Xi (\mathbf{x},\varvec{\varsigma })$ is convex–concave on $\mathscr {X}_a\times \mathscr {S}_a^+$, by which, the canonical dual problem can be proposed as the following:

$$\begin{aligned} (\mathscr {P}^d): \;\;\;\;\;\;\; \max \{ P^d(\varvec{\varsigma }) \; | \; {\varvec{\varsigma }\in \mathscr {S}^+_a} \}. \end{aligned}$$

(15)

The following result is due to the canonical duality theory.

Theorem 1.

(Gao [6]). Problem $(\mathscr {P}^d)$ is canonically dual to $(\mathscr {P})$ in the sense that if $\bar{\varvec{\varsigma }}$ is a stationary solution to $(\mathscr {P}^d)$, then the vector

$$\begin{aligned} \bar{\varvec{x}}= \mathbf {G}^\dag (\bar{\varvec{\varsigma }})\varvec{\tau }(\bar{\varvec{\varsigma }}) \end{aligned}$$

(16)

is a stationary point to $(\mathscr {P})$ and $P(\bar{\varvec{x}}) = P^d(\bar{\varvec{\varsigma }}).$

Moreover, if $\bar{\varvec{\varsigma }}\in \mathscr {S}^+_a$, then $\bar{\varvec{x}}$ is a global minimizer of $(\mathscr {P})$ if and only if $\bar{\varvec{\varsigma }}$ is a global maximizer of $(\mathscr {P}^d)$, i.e.,

$$\begin{aligned} P(\bar{\varvec{x}}) = \min _{\mathbf{x}\in \mathscr {X}_a} P(\mathbf{x}) \;\; \Leftrightarrow \;\; \max _{\varvec{\varsigma }\in \mathscr {S}^+_a} P^d(\varvec{\varsigma }) = P^d(\bar{\varvec{\varsigma }}). \end{aligned}$$

(17)

This theorem shows that if the canonical dual problem $(\mathscr {P}^d)$ has a stationary solution on $\mathscr {S}^+_a$, then the nonconvex primal problem $(\mathscr {P})$ is equivalent to a concave maximization dual problem $(\mathscr {P}^d)$ without duality gap. If we further assume that $\mathscr {X}_a = {\mathbb R}^n$ and the optimal solution $\bar{\varvec{\varsigma }}$ to Problem ($\mathscr {P}^d$) is an interior point of $\mathscr {S}^+_a$, i.e., $\mathbf {G}(\bar{\varvec{\varsigma }})\succ 0$, then the optimal solution $\bar{\varvec{x}}$ of Problem ($\mathscr {P}$) can be obtained uniquely by $\bar{\varvec{x}}=\mathbf {G}^{-1} (\bar{\varvec{\varsigma }}) \varvec{\tau }(\varvec{\varsigma })$ (see [10]).

However, our experiences show that for a class of “difficult” global optimization problems, the canonical dual problem has no stationary solution in $\mathscr {S}^+_a$ such that $\mathbf {G}(\bar{\varvec{\varsigma }})\succ 0$. In this paper, we propose a computational scheme to solve the case in which the solution is located on the boundary of $\mathscr {S}_a^+$. To continue, we need an additional mild assumption:

 

(A3):

There exists an optimal solution $\bar{\varvec{x}}$ of Problem ($\mathscr {P}$) such that $\mathbf {G}(\bar{\varvec{\varsigma }})\succeq 0$, where $\bar{\varvec{\varsigma }}= \nabla V(\varvec{\xi })|_{\varvec{\xi }= \varLambda (\bar{\varvec{x}})}$.

 

In fact, Assumption (A3) is easily satisfied by many real-world problems. To see this, let us first examine the following examples.

Example 1

Suppose that $\mathscr {X}_a$ is a bounded convex polytope subset of ${\mathbb R}^n$. Since $\mathscr {X}_a$ contains only linear constraints, both $\mathscr {V}_a$ and $\mathscr {S}_a$ are also close and bounded. Let $\chi$ be the smallest eigenvalue of $\sum _{k=1}^m \varsigma _k \mathbf {A}_k$, where $\varvec{\varsigma }=[\varsigma _1,\ldots ,\varsigma _m]^T \in \mathscr {S}_a$. Since $\mathscr {S}_a$ is bounded, $\chi >-\infty$. Let $\bar{\chi }$ be the smallest eigenvalue of $\mathbf {A}$. If $\bar{\chi }+\chi \ge 0$, then Assumption (A3) is satisfied.¹

This example shows that if the quadratic function $\frac{1}{2}\langle \mathbf{x}, \mathbf {A}\mathbf{x}\rangle$ is sufficiently convex, the nonconvexity of $V(\varLambda (\mathbf{x}))$ becomes insignificant. Thus, the combination of them is still convex. However, this is a special case in nonconvex systems. The following example has a wide applications in network optimization.

Example 2

Euclidean distance optimization problem:

$$\begin{aligned} \min \left\{ \sum _{i,j} \left( \Vert \mathbf{x}_i - \mathbf{x}_j \Vert ^2 -d_{i,j}^2\right) ^2 + \sum _{k} \left( \Vert \mathbf{x}_k - \varvec{a}_k \Vert ^2 -d_k^2 \right) ^2 | \; \mathbf{x}_i \in {\mathbb R}^{ d} \; \forall i = 1, \dots , n \right\} , \nonumber \\ \end{aligned}$$

(18)

where $\mathbf{x}_i$ is the location vector in Euclidean space ${\mathbb R}^d$, $d_{i j}$ and $d_k$ are given distance values, the vectors $\{\varvec{a}_k \}$ are pre-fixed locations. Problem (18) has many applications, such as wireless sensor network localization and molecular design, etc. For this nonconvex problem, we can choose $\varLambda (\mathbf{x})$ to be the collection of all $\varLambda _{i j}(\mathbf{x}) = \Vert \mathbf{x}_i - \mathbf{x}_j \Vert ^2$ and $\varLambda _k(\mathbf{x}) = \Vert \mathbf{x}_k - \varvec{a}_k \Vert ^2$. In this case, $V(\varvec{\xi })=\sum _{i,j}( \xi _{i j} -d_{i j}^2)^2 + \sum _k (\xi _k-d_k^2)^2$. If (18) has the optimal function value of 0, then $\xi _{ij} = d_{i j}^2$ and $\xi _k = d_k^2$, where $\varvec{\xi }=\varLambda (\bar{\varvec{x}})$ and $\bar{\varvec{x}}$ is an optimal solution of problem (18). It is easy to check that the dual variable $\bar{\varvec{\varsigma }}=0$. Thus, $\det \mathbf {G}(\bar{\varvec{\varsigma }})=0$. Therefore, Assumption (A3) holds.

This example shows that Assumption (A3) is satisfied in the least squares method for solving a large class of nonlinear systems [31, 32]. It is known that for the conventional SDP relaxation methods, the solution of problem (18) can be exactly recovered if and only if the SDP solution of Problem (18) is a relative interior and the optimal function value of problem (18) is 0 [29]. If the problem (18) has more than one solution, the conventional SDP relaxation does not produce any solution. The goal of this paper is to overcome this difficulty by proposing a canonical primal–dual iterative scheme.

3 Saddle Point Problem

Based on Assumption (A1–A3), the primal problem ($\mathscr {P}$) is relaxed to the following canonical saddle point problem:

$$\begin{aligned} (\mathscr {S}_p): \;\; \min _{\mathbf{x}}\max _{\varvec{\varsigma }} \left\{ \Xi (\mathbf{x}, \varvec{\varsigma }) = \frac{1}{2}\langle \mathbf{x},\mathbf {G}(\varvec{\varsigma })\mathbf{x}\rangle - V^{*}(\varvec{\varsigma }) -\langle \mathbf{x},\varvec{\tau }(\varvec{\varsigma })\rangle \; | \; (\mathbf{x},\varvec{\varsigma }) \in \mathscr {X}_a \times \mathscr {S}_a^+ \right\} . \nonumber \\ \end{aligned}$$

(19)

Suppose that $(\bar{\varvec{x}},\bar{\varvec{\varsigma }})$ is a saddle point of Problem ($\mathscr {S}_p$). If $\det (\mathbf {G}(\bar{\varvec{\varsigma }}))\ne 0$, we call Problem ($\mathscr {S}_p$) is non-degenerate. Otherwise, we call it degenerate.

3.1 Non-degenerate Problem ($\mathscr {S}_p$)

Theorem 2.

Suppose that Problem ($\mathscr {S}_p$) is non-degenerate. Then, $\bar{\varvec{x}}$ is a unique solution of Problem ($\mathscr {P}$) if and only if ($\bar{\varvec{x}},\bar{\varvec{\varsigma }}$) is a solution of Problem ($\mathscr {S}_p$).

Proof.  Suppose that ($\bar{\varvec{x}},\bar{\varvec{\varsigma }}$) is the solution of Problem ($\mathscr {S}_p$). Since Problem ($\mathscr {S}_p$) is non-degenerate, $\mathbf {G}(\bar{\varvec{\varsigma }})\succ 0$, i.e., $\bar{\varvec{\varsigma }}\in \text {int}\mathscr {S}_a^+$. Thus, $\nabla _{\varvec{\varsigma }}\Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) =\bar{\varvec{\varsigma }}- \varLambda (\bar{\varvec{x}}) = 0$. For any $\mathbf{x}\in \mathscr {X}_a$, we have

$$ \min _{\mathbf{x}\in \mathscr {X}_a}P(\mathbf{x}) =\min _{\mathbf{x}\in \mathscr {X}_a} \max _{\varvec{\varsigma }\in \mathscr {V}^*_a} \Xi (\mathbf{x},\varvec{\varsigma }) = \min _{\mathbf{x}\in \mathscr {X}_a} \max _{\varvec{\varsigma }\in \mathscr {S}_a^+} \Xi (\mathbf{x},\varvec{\varsigma }) = \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) = P(\bar{\varvec{x}}). $$

Thus, $\bar{\varvec{x}}$ is the optimal solution of Problem ($\mathscr {P}$).

On the other hand, we suppose that $\bar{\varvec{x}}$ is the optimal solution of Problem ($\mathscr {P}$). Let $\bar{\varvec{\varsigma }}= \nabla V(\varLambda (\bar{\varvec{x}}))$. Then,

$$ P(\bar{\varvec{x}}) = \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }})= \max _{\varvec{\varsigma }\in {\mathbb R}^m} \Xi (\bar{\varvec{x}},\varvec{\varsigma }). $$

Since $V(\cdot )$ is strictly convex, we have

$$\begin{aligned} \Xi (\bar{\varvec{x}},\varvec{\varsigma }) \le \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) \;\;\forall \; \varvec{\varsigma }\in \mathscr {V}^*_a \subset {\mathbb R}^m . \end{aligned}$$

(20)

The equality holds in (20) if and only if $\varvec{\varsigma }= \bar{\varvec{\varsigma }}$ since $\Xi (\bar{\varvec{x}},\varvec{\varsigma })$ is strictly concave in terms of $\varvec{\varsigma }$. Suppose that ($\mathbf{x}_1,\varvec{\varsigma }_1$) is also a saddle point of Problem ($\mathscr {S}_p$). By a similar induction as above, we can show that $\mathbf{x}_1$ is an optimal solution of Problem ($\mathscr {P}$). Furthermore, $P(\mathbf{x}_1) = \Xi (\mathbf{x}_1,\varvec{\varsigma }_1)$. Since $\mathbf{x}_1\in \mathscr {X}_a$, we have

$$ P(\mathbf{x}_1) = \Xi (\mathbf{x}_1,\varvec{\varsigma }_1) \le \Xi (\bar{\varvec{x}},\varvec{\varsigma }_1) \le \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) = P(\bar{\varvec{x}}). $$

The first equality holds only when $\mathbf{x}_1 = \bar{\varvec{x}}$ since $\mathbf {G}(\varvec{\varsigma }_1)\succ 0$. The second inequality becomes equality if and only if $\varvec{\varsigma }_1= \bar{\varvec{\varsigma }}$ since $V(\cdot )$ is strictly convex. By the fact that $\bar{\varvec{x}}$ is an optimal solution of Problem ($\mathscr {P}$) and $\mathbf{x}_1\in \mathscr {X}_a$, $P(\mathbf{x}_1) = P(\bar{\varvec{x}})$, $\mathbf{x}_1 = \bar{\varvec{x}}$ and $\varvec{\varsigma }_1= \bar{\varvec{\varsigma }}$. Thus, ($\bar{\varvec{x}},\bar{\varvec{\varsigma }}$) is the solution of Problem ($\mathscr {S}_p$). We complete the proof. $\blacksquare$

If $\mathscr {X}_a = {\mathbb R}^n$, the saddle point Problem ($\mathscr {S}_p$) can be further recast as a convex semi-definite programming problem.

Proposition 1.

Suppose that Problem ($\mathscr {S}_p$) is non-degenerate and $\mathscr {X}_a ={\mathbb R}^n$. Let $\bar{\varvec{\varsigma }}$ be the solution of the following convex SDP problem:

$$\begin{aligned} (SDP): \;\;\; \min \left\{ V^{*}(\varvec{\varsigma }) + g \right\} \;\;\;\; \text {s.t.} \;\; \left[ \begin{array}{cc} \mathbf {G}(\varvec{\varsigma }) &{} \varvec{\tau }(\varvec{\varsigma }) \\ \varvec{\tau }^T(\varvec{\varsigma }) &{} 2 g \\ \end{array} \right] \succeq 0. \end{aligned}$$

(21)

Then, the SDP problem defined by (21) has a unique solution ($\bar{g},\bar{\varvec{\varsigma }}$) such that $\mathbf {G}(\bar{\varvec{\varsigma }}) \succ 0$. Furthermore, $\bar{\varvec{x}}= \mathbf {G}^{-1}(\bar{\varvec{\varsigma }})\varvec{\tau }(\bar{\varvec{\varsigma }})$ is the unique solution of Problem ($\mathscr {P}$).

Proof.  By Schur complement lemma [15], the SDP problem (21) has a unique solution ($\bar{g},\bar{\varvec{\varsigma }}$) such that $\mathbf {G}(\bar{\varvec{\varsigma }}) \succ 0$ if and only if the following convex minimization problem

$$\begin{aligned} \min \left\{ V^{*}(\varvec{\varsigma }) + \frac{1}{2}\langle \mathbf {G}^{-1}(\varvec{\varsigma })\varvec{\tau }(\varvec{\varsigma }), \varvec{\tau }(\varvec{\varsigma })\rangle | \; \mathbf {G}(\varvec{\varsigma }) \succeq 0 \right\} \end{aligned}$$

(22)

has a unique solution $\bar{\varvec{\varsigma }}$ such that $\mathbf {G}(\bar{\varvec{\varsigma }}) \succ 0$. Since $\mathscr {X}_a = {\mathbb R}^n$, the convex minimization problem (22) is equivalent to Problem ($\mathscr {S}_p$) by Theorem 3.1 in [10]. $\blacksquare$

Remark 1.

Theorem 2 is actually a special case of the general result obtained by Gao and Strang in finite deformation theory [7]. Indeed, if we let $\bar{W}(\mathbf{x}) = W(\mathbf{x}) + \frac{1}{2}\langle \mathbf{x}, \mathbf {A}\mathbf{x}\rangle$ and $\bar{\varLambda }(\mathbf{x}) = \{ \varLambda (\mathbf{x}), \frac{1}{2}\langle \mathbf{x}, \mathbf {A}\mathbf{x}\rangle \}$, then, the Gao–Strang complementary gap function is simply defined as

$$ G (\mathbf{x}, \varvec{\varsigma }) = \frac{1}{2}\langle \mathbf{x}, \mathbf{G}(\varvec{\varsigma }) \mathbf{x}\rangle . $$

Clearly, this gap function is strictly positive for any nonzero $\mathbf{x}\in \mathscr {X}_a$ if and only if $\mathbf{G}(\varvec{\varsigma }) \succ 0$. Then by Theorem 2 in [7] we know that the primal problem has a unique solution if the problem ($\mathscr {S}_p$) is non-degenerate. By Theorem 2 and Proposition 1 we know that the nonconvex problem ($\mathscr {P}$) can be solved easily either by solving a sequence of strict convex–concave saddle point problems, or via solving a convex semi-definite programming problem if Problem ($\mathscr {S}_p$) is non-degenerate. By the fact that $g = \frac{1}{2}\langle \mathbf {G}^{-1}(\varvec{\varsigma })\varvec{\tau }(\varvec{\varsigma }), \varvec{\tau }(\varvec{\varsigma })\rangle$ is actually the pure complementary gap function (see Eq. (19) in [6]), the convex SDP problem (21) is indeed a special case of the canonical dual problem $(\mathscr {P}^d)$ defined by (15). Moreover, the canonical duality theory can also be used to find the biggest local extrema of the nonconvex problem $(\mathscr {P})$ (see [10]).

3.2 Degenerate Problem ($\mathscr {S}_p$) and Linear Perturbation

If Problem ($\mathscr {S}_p$) is degenerate, i.e., $\mathbf {G}(\bar{\varvec{\varsigma }})\succeq 0$ and $\det (\mathbf {G}(\bar{\varvec{\varsigma }})) = 0$ or $\bar{\varvec{\varsigma }}\in \partial \mathscr {S}_a^+$, it has multiple saddle points. The following theorem reveals the relations between Problem ($\mathscr {P}$) and Problem ($\mathscr {S}_p$).

Theorem 3.

Suppose that Problem ($\mathscr {S}_p$) is degenerate.

1):

If $\bar{\varvec{x}}$ is a solution of Problem ($\mathscr {P}$) and $\bar{\varvec{\varsigma }}= \nabla V(\varLambda (\bar{\varvec{x}}))$, then ($\bar{\varvec{x}},\bar{\varvec{\varsigma }}$) is a saddle point of Problem ($\mathscr {S}_p$).

2):

If ($\bar{\varvec{x}},\bar{\varvec{\varsigma }}$) is a saddle point of Problem ($\mathscr {S}_p$), then $\bar{\varvec{x}}$ is a solution of Problem ($\mathscr {P}$).

3):

If ($\mathbf{x}_1,\varvec{\varsigma }_1$) and ($\mathbf{x}_2,\varvec{\varsigma }_2$) are two saddle points of Problem ($\mathscr {S}_p$), then $\varvec{\varsigma }_1 = \varvec{\varsigma }_2$.

Proof.  1). Since $\bar{\varvec{x}}$ is a solution of Problem ($\mathscr {P}$) and $\bar{\varvec{\varsigma }}= \nabla V(\varLambda (\bar{\varvec{x}}))\in \mathscr {S}_a^+$ (by Assumption (A3)),

$$ \Xi (\bar{\varvec{x}},\varvec{\varsigma }) \le \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}), \;\;\forall \varvec{\varsigma }\in \mathscr {S}_a^+. $$

Furthermore,

$$\begin{aligned} \langle \nabla P(\bar{\varvec{x}}), \mathbf{x}-\bar{\varvec{x}}\rangle \ge 0,\;\; \forall \mathbf{x}\in \mathscr {X}_a. \end{aligned}$$

(23)

Substituting $\nabla P(\bar{\varvec{x}}) = \mathbf {G}(\bar{\varvec{\varsigma }})\bar{\varvec{x}}- \varvec{\tau }(\bar{\varvec{\varsigma }}) = \nabla _{\mathbf{x}}\Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }})$ into (23), we obtain

$$ \langle \nabla _{\mathbf{x}}\Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}), \mathbf{x}-\bar{\varvec{x}}\rangle \ge 0,\;\; \forall \; \mathbf{x}\in \mathscr {X}_a. $$

Thus,

$$ \min _{\mathbf{x}\in \mathscr {X}_a} \Xi (\mathbf{x},\bar{\varvec{\varsigma }}) = \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}). $$

Therefore,

$$ \Xi (\bar{\varvec{x}},\varvec{\varsigma })\le \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) \le \Xi (\mathbf{x},\bar{\varvec{\varsigma }}),\;\;\forall \; (\mathbf{x},\varvec{\varsigma })\in \mathscr {X}_a\times \mathscr {S}_a^+. $$

This implies that ($\bar{\varvec{x}},\bar{\varvec{\varsigma }}$) is a saddle point of Problem ($\mathscr {S}_p$).

2). Suppose that ($\bar{\varvec{x}},\bar{\varvec{\varsigma }}$) is a saddle point of Problem ($\mathscr {S}_p$) and $\nabla _{\varvec{\varsigma }} \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) = 0$. Then,

$$ P(\bar{\varvec{x}}) = \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) \le \Xi (\mathbf{x},\bar{\varvec{\varsigma }}),\;\;\forall \; (\mathbf{x},\varvec{\varsigma })\in \mathscr {X}_a\times \mathscr {S}_a^+. $$

On the other hand,

$$ \Xi (\mathbf{x},\bar{\varvec{\varsigma }}) = \langle \varLambda (\mathbf{x}) ; \bar{\varvec{\varsigma }}\rangle - V^{*}(\bar{\varvec{\varsigma }}) - U(\mathbf{x}) \le V(\varLambda (\mathbf{x})) - U(\mathbf{x}) = P(\mathbf{x}). $$

Combining the above two inequalities, $\bar{\varvec{x}}$ is a solution Problem ($\mathscr {P}$).

3). This result follows directly from the strict convexity of both $V(\cdot )$ and $V^{*}(\cdot )$. The proof is completed. $\blacksquare$

Theorem 3 shows that the nonconvex minimization Problem ($\mathscr {P}$) is equivalent to the canonical saddle min-max Problem ($\mathscr {S}_p$). What we should emphasize is that the solutions set of Problem ($\mathscr {P}$) is in general nonconvex, while the set of saddle points of Problem ($\mathscr {S}_p$) is convex. For example, let us consider the following optimization problem:

$$\begin{aligned} \min \left\{ \frac{1}{2}\left( (x_1+x_2)^2 -1 \right) ^2 + \frac{1}{2}\left( (x_1-x_2)^2 -1 \right) ^2 | \; \; (x_1, x_2) \in {\mathbb R}^2 \right\} . \end{aligned}$$

(24)

Let $\xi =\varLambda (\mathbf{x}) = [(x_1+x_2)^2 -1, (x_1-x_2)^2 -1]^T$. Then,

$$ \mathbf {G}(\varvec{\varsigma }) = \left[ \begin{array}{cc} \varsigma _1 + \varsigma _2 &{} \varsigma _1 - \varsigma _2 \\ \varsigma _1 - \varsigma _2 &{} \varsigma _1 + \varsigma _2 \\ \end{array} \right] , $$

$V^{*}(\varvec{\varsigma }) = \frac{1}{2}\varvec{\varsigma }^T\varvec{\varsigma }$. Thus, $\mathbf {G}(\varvec{\varsigma })\succeq 0 \Leftrightarrow \varsigma _1\ge 0$ and $\varsigma _2\ge 0$. Clearly, ($\bar{\varvec{x}},\bar{\varvec{\varsigma }}$) is a saddle point of Problem ($\mathscr {S}_p$) if and only if ($\bar{\varvec{x}},\bar{\varvec{\varsigma }}$) is the solution of the following variational inequality:

$$\begin{aligned}&\mathbf {G}(\bar{\varvec{\varsigma }})\bar{\varvec{x}}=0 ,\end{aligned}$$

(25)

$$\begin{aligned}&\langle \nabla V^{*}(\bar{\varvec{\varsigma }}) - \varLambda (\bar{\varvec{x}}) ; \varvec{\varsigma }- \bar{\varvec{\varsigma }}\rangle \ge 0,\; \forall \varvec{\varsigma }\ge 0. \end{aligned}$$

(26)

It is easy to verify that the optimization problem (24) has four solutions (1, 0), (0, 1), $(-1,0)$ and $(0,-1)$. Clearly, its solution set is nonconvex. On the other hand, by the statement 3) in Theorem 3, we have $\bar{\varvec{\varsigma }}= 0$. Thus, $(\bar{\varvec{x}},\bar{\varvec{\varsigma }})$ is a saddle point of Problem ($\mathscr {S}_p$) if and only if $\bar{\varvec{\varsigma }}= 0$ and $\bar{\varvec{x}}$ satisfies

$$\begin{aligned} (x_1+x_2)^2\le & {} 1,\\ (x_1-x_2)^2\le & {} 1. \end{aligned}$$

Denote $\varOmega = \text {convhull} \{(1,0), (0,1), (-1,0), (0,-1)\}$, where convhull means convex hull. Therefore, the saddle point set of Problem ($\mathscr {S}_p$) is $\varOmega \times 0$ which is a convex set. This example also shows that the solutions of Problem ($\mathscr {P}$) are the vertex points of the saddle points set of Problem ($\mathscr {S}_p$).

Now we turn our attention to the saddle point problem ($\mathscr {S}_p$). For some simple optimization problems, we can simply use linear perturbation method to solve it. To illustrate it, let us consider a simple optimization problem given as below:

$$\begin{aligned} (\mathscr {P}_1): \;\;\min _{\mathbf{x}}P_1(\mathbf{x}) = \frac{1}{2}\left( \frac{1}{2}\mathbf{x}^T \mathbf {A}_1 \mathbf{x}-b_1 \right) ^2 + \frac{1}{2}\left( \frac{1}{2}\mathbf{x}^T \mathbf {A}_2 \mathbf{x}-b_2 \right) ^2-\langle \mathbf{x},\varvec{f}\rangle . \end{aligned}$$

(27)

Proposition 2.

Suppose that there exists $(\varsigma _1,\varsigma _2)$ such that $\varsigma _1 \mathbf {A}_1 +\varsigma _2 \mathbf {A}_2 \succ 0$. If the saddle point $(\bar{\varvec{x}},\bar{\varvec{\varsigma }})$ of the associated Problem (${\mathscr {S}_p}_1$) is on the boundary of $\mathscr {S}_a^+$, then for any given $\varepsilon >0$, there exists a $\varDelta \varvec{f}\in {\mathbb R}^n$ such that $\Vert \varDelta \varvec{f}\Vert \le \varepsilon$ and the perturbed saddle point Problem (${\mathscr {S}_p}_1$)

$$\begin{aligned} ({\mathscr {S}_p}_1): \;\; \min _{\mathbf{x}}\max _{\varvec{\varsigma }} \left\{ \frac{1}{2}\langle \mathbf{x},\mathbf {G}(\varvec{\varsigma })\mathbf{x}\rangle -\frac{1}{2}\varvec{\varsigma }^T\varvec{\varsigma }-\langle \mathbf{x},\varvec{f}+\varDelta \varvec{f}\rangle \; : \; (\mathbf{x},\varsigma ) \in {\mathbb R}^n \times \mathscr {S}_a^+ \right\} \end{aligned}$$

has a unique saddle point $(\bar{\varvec{x}}_p,\bar{\varvec{\varsigma }}_p)$ such that $\mathbf {G}(\bar{\varvec{\varsigma }}_p)\succ 0$. Furthermore, $\bar{\varvec{x}}_p$ is the unique solution of

$$ (\mathscr {P}^{\text {ptb}}_1): \;\;\min _{\mathbf{x}}P_1(\mathbf{x}) = \frac{1}{2}\left( \frac{1}{2}\mathbf{x}^T \mathbf {A}_1 \mathbf{x}-b_1 \right) ^2 + \frac{1}{2}\left( \frac{1}{2}\mathbf{x}^T \mathbf {A}_2 \mathbf{x}-b_2 \right) ^2 -\langle \mathbf{x},\varvec{f}+\varDelta \varvec{f}\rangle , $$

where $\mathbf {G}(\varvec{\varsigma }) = \varsigma _1\mathbf {A}_1 + \varsigma _2\mathbf {A}_2$.

Proof.  Since $\mathbf{x}\in {\mathbb R}^n$, Problem (${\mathscr {S}_p}_1$) is equivalent to the following optimization problem:

$$\begin{aligned} \max _{\varvec{\varsigma }}&- V^{*}(\varvec{\varsigma }) - \frac{1}{2}(\varvec{f}+\varDelta \varvec{f})^T(\varvec{\varsigma })\mathbf {G}^{-1}(\varvec{\varsigma })(\varvec{f}+\varDelta \varvec{f}) \nonumber \\ \text {s.t.}&\mathbf {G}(\varvec{\varsigma }) \succeq 0. \end{aligned}$$

(28)

By the assumption that there exists $(\varsigma _1,\varsigma _2)$ such that $\varsigma _1 \mathbf {A}_1 +\varsigma _2 \mathbf {A}_2 \succ 0$, $\mathbf {A}_1$ and $\mathbf {A}_2$ are simultaneously diagonalizable via congruence. More specifically, there exists an invertible matrix C such that

$$\begin{aligned} \mathbf {C}^T \mathbf {A}_1 \mathbf {C}= & {} \text {diag}(a_1^1,\cdots ,a_n^1),\\ \mathbf {C}^T \mathbf {A}_2 \mathbf {C}= & {} \text {diag}(a_1^2,\cdots ,a_n^2). \end{aligned}$$

Under this condition, it is easy to show that for any given $\varepsilon >0$, there exists a $\varDelta \varvec{f}\in {\mathbb R}^n$ such that $\Vert \varDelta \varvec{f}\Vert \le \varepsilon$ and

$$ \lim _{\varvec{\varsigma }\rightarrow \partial \mathscr {S}_a^+} \frac{1}{2}(\varvec{f}+\varDelta \varvec{f})^T(\varvec{\varsigma })\mathbf {G}^{-1}(\varvec{\varsigma })(\varvec{f}+\varDelta \varvec{f}) = + \infty . $$

Thus, the solution of the optimization problem (28) cannot be located in the boundary of $\mathscr {S}_a^+$ for this $\varDelta \varvec{f}$. The results follow readily. We complete the proof. $\blacksquare$

From Proposition 1 we know that if the solution $\bar{\varvec{x}}$ of Problem ($\mathscr {P}_1$) satisfies $\mathbf {G}(\bar{\varvec{\varsigma }})\succ 0$, then it can be obtained by simply solving the concave maximization dual problem $(\mathscr {P}^d)$. Otherwise, Proposition 2 shows that this solution can be obtained under a small perturbation. Thus, the nonconvex optimization problem ($\mathscr {P}_1$) can be completely solved by either the convex SDP or the canonical duality. However, for general optimization problems, the linear perturbation method may not produce an interior saddle point of Problem ($\mathscr {S}_p$). To overcome this difficulty, we shall introduce a nonlinear perturbation method in the next section.

4 Quadratic Perturbation Method

We now focus on solving the degenerated Problem ($\mathscr {S}_p$). Clearly, Problem ($\mathscr {S}_p$) is strictly concave with respect to $\varvec{\varsigma }$. However, if Problem ($\mathscr {S}_p$) is degenerate, i.e., $\bar{\varvec{\varsigma }}\in \partial \mathscr {S}_a^+$, then Problem ($\mathscr {S}_p$) is convex but not strictly in terms of $\mathbf{x}$. In this case, Problem ($\mathscr {S}_p$) has multiple solutions. To stabilize such kind of optimization problems, nonlinear perturbation methods can be used (see [9]). Thus, using the quadratic perturbation method to Problem ($\mathscr {S}_p$), a regularized saddle point problem can be proposed as

$$\begin{aligned} \min _{\mathbf{x}}\max _{\varvec{\varsigma }\in \mathscr {S}_a^+}\Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma }) = \Xi (\mathbf{x},\varvec{\varsigma }) + \frac{\rho _k}{2}\Vert \mathbf{x}-\mathbf{x}_k\Vert ^2, \end{aligned}$$

(29)

where both $\mathbf{x}_k$ and $\rho _k$, $k=1,2,\cdots ,$ are given. In practical computation, the canonical dual feasible space $\mathscr {S}_a^+$ can also be relaxed as

$$ \mathscr {S}_{\mu _k}^+=\{ \varvec{\varsigma }\in \mathscr {V}^*_a \subset {\mathbb R}^m\; | \; \mathbf {G}(\varvec{\varsigma })+\mu _k I\succeq 0\}, $$

where $\mu _k<\rho _k$. Note that

$$ \Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma }) = \frac{1}{2}\langle \mathbf{x},(\mathbf {G}(\varvec{\varsigma })+\rho _k I)\mathbf{x}\rangle -V^{*}(\varvec{\varsigma }) - \langle \mathbf{x},\rho _k\mathbf{x}_k+\varvec{\tau }(\varvec{\varsigma }) \rangle +\frac{\rho _k}{2}\langle \mathbf{x}_k,\mathbf{x}_k\rangle . $$

Thus, $\Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma })$ is strictly convex–concave in ${\mathbb R}^n\times \mathscr {S}_{\mu _k}^+$ and

$$ \min _{\mathbf{x}}\max _{\varvec{\varsigma }\in \mathscr {S}_{\mu _k}^+}\Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma }) = \max _{\varvec{\varsigma }\in \mathscr {S}_{\mu _k}^+}\min _{\mathbf{x}}\Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma }). $$

For each given $\varvec{\varsigma }\in \mathscr {S}_{\mu _k}^+$, denote

$$ \mathbf{x}(\varvec{\varsigma }) = \arg \min _{\mathbf{x}}\Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma }). $$

Then, $\mathbf{x}(\varvec{\varsigma }) = (\mathbf {G}(\varvec{\varsigma })+\rho _k I)^{-1}(\rho _k\mathbf{x}_k+\varvec{\tau }(\varvec{\varsigma }))$. Substituting this $\mathbf{x}(\varvec{\varsigma })$ into $\Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma })$, we obtain the perturbed canonical dual function

$$ P_{\rho _k}^d(\varvec{\varsigma }) = -\frac{1}{2}\langle (\mathbf {G}(\varvec{\varsigma })+\rho _k I)^{-1}(\rho _k\mathbf{x}_k+\varvec{\tau }(\varvec{\varsigma })), \rho _k\mathbf{x}_k+\varvec{\tau }(\varvec{\varsigma })\rangle - V^{*}(\varvec{\varsigma }) +\frac{\rho _k}{2}\langle \mathbf{x}_k,\mathbf{x}_k\rangle . $$

Now our canonical primal–dual algorithm can be proposed as follows.

Algorithm 1

 

Step 1:

Initialization $\mathbf{x}_0$, $\rho _0$, N and the error tolerance $\varepsilon$. Set $k=0$.

Step 2:

Set $\varvec{\varsigma }_{k+1} = \arg \max _{\varvec{\varsigma }\in \mathscr {S}_{\mu _k}^+}P_{\rho _k}^d(\varvec{\varsigma })$ and $\mathbf{x}_{k+1} = (\mathbf {G}(\varvec{\varsigma }_{k+1})+\rho _{k} I)^{-1}(\rho _k\mathbf{x}_k+\varvec{\tau }(\varvec{\varsigma }_{k+1}))$.

Step 3:

If $\Vert \varvec{\varsigma }_{k+1} -\varvec{\varsigma }_{k} \Vert \le \varepsilon$, stop. Otherwise, set $k=k+1$ and go to Step 2.

 

Theorem 4.

Suppose that

1):

$\bar{\rho }\ge \rho _k >0$, $\sigma _k = \sum _{i=1}^k\rho _i \rightarrow +\infty$, $\rho _k\downarrow 0$, $\mu _k \downarrow 0$ and $0< \mu _k<\rho _k$;

2):

For any given $\mathbf{x}$, $\lim _{\Vert \varvec{\varsigma }_k\Vert \rightarrow \infty }\Xi (\mathbf{x},\varvec{\varsigma }_k)=-\infty$;

3):

The sequence $\{\mathbf{x}_k \}$ is a bounded;

Then, there exists a $(\bar{\varvec{x}},\bar{\varvec{\varsigma }})\in {\mathbb R}^n\times \mathscr {S}_a^+$ such that $\{\mathbf{x}_k,\varvec{\varsigma }_k\}\rightarrow (\bar{\varvec{x}},\bar{\varvec{\varsigma }})$. Furthermore, $(\bar{\varvec{x}},\bar{\varvec{\varsigma }})$ is a saddle point of Problem ($\mathscr {S}_p$).

Proof.  Note that $0< \mu _k<\rho _k$, the perturbed total complementary function $\Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma })$ is strictly convex–concave with respect to $(\mathbf{x},\varvec{\varsigma })$ in ${\mathbb R}^n\times \mathscr {S}_{\mu _k}^+$. Since $(\mathbf{x}_{k},\varvec{\varsigma }_k)$ is generated by Algorithm 1, we have

$$\begin{aligned} (\mathbf{x}_{k},\varvec{\varsigma }_k) = \arg \min _{\mathbf{x}}\max _{\varvec{\varsigma }\in \mathscr {S}_{\mu _k}^+}\Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma }) = \arg \min _{\mathbf{x}}\max _{\varvec{\varsigma }\in \mathscr {S}_{\mu _k}^+} \left\{ \Xi (\mathbf{x},\varvec{\varsigma }) + \frac{\rho _{k-1}}{2}\Vert \mathbf{x}-\mathbf{x}_{k-1}\Vert ^2 \right\} . \end{aligned}$$

(30)

That is

$$ \Xi _{\rho _k}(\mathbf{x}_k,\varvec{\varsigma }) \le \Xi _{\rho _k}(\mathbf{x}_k,\varvec{\varsigma }_k)\le \Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma }_k),\;\;\forall (\mathbf{x},\varvec{\varsigma })\in {\mathbb R}^n\times \mathscr {S}_{\mu _k}^+. $$

By the fact that $\mu _k \downarrow 0$ and $\mathscr {S}_{\mu _k}^+=\{ \varvec{\varsigma }\in \mathscr {V}^*_a \;|\; \mathbf {G}(\varvec{\varsigma })+\mu _k I\succeq 0\}$, we have $\mathscr {S}_{\mu _k}^+\supseteq \mathscr {S}_{\mu _{k+1}}^+$ and $\bigcap _{k}\mathscr {S}_{\mu _k}^+ = \mathscr {S}_a^+$.

To continue, we suppose that $(\bar{\varvec{x}},\bar{\varvec{\varsigma }})$ is a saddle point of Problem ($\mathscr {S}_p$), i.e.,

$$ \Xi (\bar{\varvec{x}},\varvec{\varsigma }) \le \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }})\le \Xi (\mathbf{x},\bar{\varvec{\varsigma }}),\;\;\forall (\mathbf{x},\varvec{\varsigma })\in {\mathbb R}^n\times \mathscr {S}_a^+. $$

Now we adopt the following steps to prove our results.

1):

The sequence $\{\mathbf{x}_k\}$ is convergent, i.e., there exists a $\bar{\varvec{x}}$ such that $\mathbf{x}_k\rightarrow \bar{\varvec{x}}$. From (30), we have

$$\begin{aligned} \Xi _{\rho _{k-1}}(\mathbf{x}_k,\varvec{\varsigma }_k) = \Xi (\mathbf{x}_k,\varvec{\varsigma }_k)+ \frac{\rho _{k-1}}{2}\Vert \mathbf{x}_k -\mathbf{x}_{k-1}\Vert ^2\le \Xi _{\rho _{k-1}}(\mathbf{x}_{k-1},\varvec{\varsigma }_k) = \Xi (\mathbf{x}_{k-1},\varvec{\varsigma }_k). \end{aligned}$$

(31)

Clearly,

$$\begin{aligned} \Xi (\mathbf{x}_{k-1},\varvec{\varsigma }_k) + \frac{\rho _{k-2}}{2}\Vert \mathbf{x}_{k-1} -\mathbf{x}_{k-2}\Vert ^2 = \Xi _{\rho _{k-2}}(\mathbf{x}_{k-1},\varvec{\varsigma }_k). \end{aligned}$$

(32)

Since $\varvec{\varsigma }_k\in \mathscr {S}_{\mu _k}^+\subset \mathscr {S}_{\mu _{k-1}}^+$ and $(\mathbf{x}_{k-1},\varvec{\varsigma }_{k-1})$ is the saddle point of $\Xi _{\rho _{k-1}}(\mathbf{x},\varvec{\varsigma })$ in ${\mathbb R}^n\times \mathscr {S}_{\mu _{k-1}}^+$, we obtain

$$\begin{aligned} \Xi _{\rho _{k-2}}(\mathbf{x}_{k-1},\varvec{\varsigma }_k) \le \Xi _{\rho _{k-2}}(\mathbf{x}_{k-1},\varvec{\varsigma }_{k-1})= \Xi (\mathbf{x}_{k-1},\varvec{\varsigma }_{k-1})+ \frac{\rho _{k-2}}{2}\Vert \mathbf{x}_{k-1} -\mathbf{x}_{k-2}\Vert ^2. \end{aligned}$$

(33)

Combining (32) and (33), we obtain

$$ \Xi (\mathbf{x}_{k-1},\varvec{\varsigma }_k) \le \Xi (\mathbf{x}_{k-1},\varvec{\varsigma }_{k-1}). $$

Thus,

$$\begin{aligned} \Xi (\mathbf{x}_{k},\varvec{\varsigma }_k) + \frac{\rho _{k-1}}{2}\Vert \mathbf{x}_{k} -\mathbf{x}_{k-1}\Vert ^2 \le \Xi (\mathbf{x}_{k-1},\varvec{\varsigma }_{k-1}). \end{aligned}$$

(34)

Repeating the above process, we get

$$\begin{aligned} \Xi (\mathbf{x}_{k},\varvec{\varsigma }_k) + \sum _{i=1}^{k-1}\frac{\rho _{i-1}}{2}\Vert \mathbf{x}_{i} -\mathbf{x}_{i-1}\Vert ^2 \le \Xi (\mathbf{x}_{1},\varvec{\varsigma }_{1}). \end{aligned}$$

(35)

On the other hand,

$$\begin{aligned}&\Xi _{\rho _{k-1}}(\mathbf{x}_{k},\varvec{\varsigma }_k) =\Xi (\mathbf{x}_{k},\varvec{\varsigma }_k) + \frac{\rho _{k-1}}{2}\Vert \mathbf{x}_k -\mathbf{x}_{k-1}\Vert ^2 \nonumber \\&\ge \Xi _{\rho _{k-1}}(\mathbf{x}_{k},\bar{\varvec{\varsigma }}) = \Xi (\mathbf{x}_{k},\bar{\varvec{\varsigma }}) + \frac{\rho _{k-1}}{2}\Vert \mathbf{x}_k -\mathbf{x}_{k-1}\Vert ^2\nonumber \\&\ge \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) + \frac{\rho _{k-1}}{2}\Vert \mathbf{x}_k -\mathbf{x}_{k-1}\Vert ^2. \end{aligned}$$

(36)

Substituting (36) into (35) gives rise to

$$ \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) + \sum _{i=1}^{k-2}\frac{\rho _{i-1}}{2}\Vert \mathbf{x}_{i} -\mathbf{x}_{i-1}\Vert ^2 \le \Xi (\mathbf{x}_{1},\varvec{\varsigma }_{1}),\;\;\forall \;k\in \mathbb {N}. $$

Since $\{\mathbf{x}_k\}$ is a bounded sequence, $\sigma _k \rightarrow +\infty$ and $\rho _k\downarrow 0$, the sequence $\mathbf{x}_k$ is convergent, i.e., there exists a $\bar{\varvec{x}}$ such that $\mathbf{x}_k\rightarrow \bar{\varvec{x}}$.

2):

The sequence $\{\varvec{\varsigma }_k\}$ is convergent. We first show that $\varvec{\varsigma }_k$ is a bounded sequence. In a similar argument to the inequality (34), we can show that

$$ \Xi (\mathbf{x}_{k+1},\varvec{\varsigma }_{k+1}) \ge \Xi (\mathbf{x}_{k+1},\bar{\varvec{\varsigma }})\ge \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}). $$

On the other hand,

$$\begin{aligned}&\Xi _{\rho _k}(\mathbf{x}_{k+1},\varvec{\varsigma }_{k+1}) = \Xi (\mathbf{x}_{k+1},\varvec{\varsigma }_{k+1}) + \frac{\rho _{k}}{2}\Vert \mathbf{x}_{k+1} -\mathbf{x}_{k}\Vert ^2 \\&\le \Xi _{\rho _k}(\bar{\varvec{x}},\varvec{\varsigma }_{k+1}) = \Xi (\bar{\varvec{x}},\varvec{\varsigma }_{k+1}) + \frac{\rho _{k}}{2}\Vert \bar{\varvec{x}}-\mathbf{x}_{k}\Vert ^2. \end{aligned}$$

Summing the above inequalities together yields that

$$\begin{aligned}&\Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) -\frac{\bar{\rho }}{2}\Vert \bar{\varvec{x}}-\mathbf{x}_{k}\Vert ^2\le \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) -\frac{\rho _{k}}{2}\Vert \bar{\varvec{x}}-\mathbf{x}_{k}\Vert ^2\\&\le \Xi (\mathbf{x}_{k+1},\bar{\varvec{\varsigma }}) - \frac{\rho _{k}}{2}\Vert \bar{\varvec{x}}-\mathbf{x}_{k}\Vert ^2 \le \Xi (\bar{\varvec{x}},\varvec{\varsigma }_{k+1}). \end{aligned}$$

By Assumption (2) and $\mathbf{x}^k\rightarrow \bar{\varvec{x}}$, we know that $\varvec{\varsigma }_k$ is a bounded sequence. Now we suppose that there are two subsequences $\{\varvec{\varsigma }_k^1\}$ and $\{\varvec{\varsigma }_k^2\}$ of $\{\varvec{\varsigma }_k\}$ such that $\{\varvec{\varsigma }_k^1\}\rightarrow \varvec{\varsigma }^1$ and $\{\varvec{\varsigma }_k^2\}\rightarrow \varvec{\varsigma }^2$. Denote $\{\mathbf{x}_k^1\}$ and $\{\mathbf{x}_k^2\}$ are two subsequences of $\{\mathbf{x}_k\}$ associated with $\{\varvec{\varsigma }_k^1\}$ and $\{\varvec{\varsigma }_k^2\}$. Clearly, $\varvec{\varsigma }^1,\varvec{\varsigma }^2\in \mathscr {S}_a^+$. Note that

$$\begin{aligned}&\Xi (\mathbf{x}_{k+1}^1,\varvec{\varsigma }^2) + \frac{\rho _{k}^1}{2}\Vert \mathbf{x}_{k+1}^1 -\mathbf{x}_{k}^1\Vert ^2 = \Xi _{\rho _k^1}(\mathbf{x}_{k+1}^1,\varvec{\varsigma }^2) \nonumber \\&\le \Xi _{\rho _k^1}(\mathbf{x}_{k+1}^1,\varvec{\varsigma }_{k+1}^1) = \Xi (\mathbf{x}_{k+1}^1,\varvec{\varsigma }_{k+1}^1) + \frac{\rho _{k}^1}{2}\Vert \mathbf{x}_{k+1}^1 -\mathbf{x}_{k}^1\Vert ^2 . \end{aligned}$$

(37)

Thus,

$$ \Xi (\mathbf{x}_{k+1}^1,\varvec{\varsigma }^2)\le \Xi (\mathbf{x}_{k+1}^1,\varvec{\varsigma }_{k+1}^1). $$

Taking limit on both sides of the above inequality yields to

$$ \Xi (\bar{\varvec{x}},\varvec{\varsigma }^2) \le \Xi (\bar{\varvec{x}},\varvec{\varsigma }^1). $$

In a similar way, we can show that

$$ \Xi (\bar{\varvec{x}},\varvec{\varsigma }^1) \le \Xi (\bar{\varvec{x}},\varvec{\varsigma }^2). $$

Therefore,

$$ \Xi (\bar{\varvec{x}},\varvec{\varsigma }^1) = \Xi (\bar{\varvec{x}},\varvec{\varsigma }^2) $$

which implies that $\varvec{\varsigma }^1 = \varvec{\varsigma }^2$. Hence, $\{\varvec{\varsigma }_k\}$ is a convergent sequence.

3):

We show that if $\{\mathbf{x}_k,\varvec{\varsigma }_k\}\rightarrow (\bar{\varvec{x}},\bar{\varvec{\varsigma }})$, then $(\bar{\varvec{x}},\bar{\varvec{\varsigma }})$ is a saddle point of Problem ($\mathscr {S}_p$). In a similar argument to 2), it is easy to show that for any $\varvec{\varsigma }\in \mathscr {S}_a^+$, we have

$$ \Xi (\bar{\varvec{x}},\varvec{\varsigma }) \le \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}). $$

So we only need to show that for any $\mathbf{x}$,

$$\begin{aligned} \Xi (\bar{\varvec{x}},\bar{\varvec{\varsigma }}) \le \Xi (\mathbf{x},\bar{\varvec{\varsigma }}). \end{aligned}$$

(38)

Indeed, by the fact that

$$ \Xi _{\rho _k}(\mathbf{x}_{k+1},\varvec{\varsigma }_{k+1})\le \Xi _{\rho _k}(\mathbf{x},\varvec{\varsigma }_{k+1}),\;\;\forall \mathbf{x}. $$

Passing limit to the above inequality yields to the inequality (38). We complete the proof. $\blacksquare$

In Theorem 4, there are three assumptions. Assumption (1) is on the selection of the parameters and Assumption (2) is always satisfied for strictly convex functions. Assumption (3) is important to ensure the convergence of Algorithm 1. In fact, from our numerical experiments, we found that $\mathbf{x}_k$ might become unbound for certain cases. Therefore, a modified algorithm for solving Problem ($\mathscr {P}$) is suggested as the following.

Algorithm 2

 

Step 1:

Adopt Algorithm 1 to solve Problem ($\mathscr {S}_p$). Denote the obtained solution as $(\bar{\varvec{x}},\bar{\varvec{\varsigma }})$.

Step 2:

If $\Vert \varLambda (\bar{\varvec{x}})- \nabla V^*(\bar{\varvec{\varsigma }}) \Vert \le \varepsilon$, output $\bar{\varvec{x}}$ is a global minimizer of Problem ($\mathscr {P}$), where $\varepsilon$ is the tolerance. Otherwise, a gradient-based optimization method is used to refine Problem ($\mathscr {P}$) with initial condition $\bar{\varvec{x}}$.

 

Remark 2.

Since Problem ($\mathscr {S}_p$) is a convex–concave saddle point problem, many exact and inexact proximal point methods can be adapted [12, 14, 30]. In fact, solving Problem ($\mathscr {S}_p$) is an easy task since it is essentially a convex optimization problem. However, to obtain a solution of Problem ($\mathscr {P}$) from the solution set of Problem ($\mathscr {S}_p$) is a difficult task since the identification of degenerate indices in the nonlinear complementarity problem is hard [37]. Unlike the classical proximal point methods, our proposed Algorithm 1 is based on a sequence of exterior point approximation. In this case, the gradient operator $[\nabla _{\mathbf{x}}\Xi (\mathbf{x},\varvec{\varsigma }),-\nabla _{\varvec{\varsigma }}\Xi (\mathbf{x},\varvec{\varsigma })]$ in ${\mathbb R}^n\times \mathscr {S}_a^+$ is not a monotone operator, but $[\nabla _{\mathbf{x}}\Xi (\mathbf{x},\varvec{\varsigma })+\mu _k I,-\nabla _{\varvec{\varsigma }}\Xi (\mathbf{x},\varvec{\varsigma })]$ is monotone in ${\mathbb R}^n\times \mathscr {S}_{a}^+$. By the fact that $\bigcap _k \mathscr {S}_{\mu _k}^+ =\mathscr {S}_a^+$, our algorithm generates a convergent sequence and its clustering point is a saddle point of Problem ($\mathscr {S}_p$) under certain conditions. Since $[\nabla _{\mathbf{x}}\Xi (\mathbf{x},\varvec{\varsigma }),-\nabla _{\varvec{\varsigma }}\Xi (\mathbf{x},\varvec{\varsigma })]$ in ${\mathbb R}^n\times \mathscr {S}_a^+$ is not monotone for each subproblem, it is natural to approximate an optimal solution of Problem ($\mathscr {P}$) under the perturbation of the regularized term $\frac{1}{2} \rho _k \Vert \mathbf{x}-\mathbf{x}_k\Vert ^2$. This illustrates why our perturbed (exterior penalty-type) algorithm usually produces an optimal solution of Problem ($\mathscr {P}$), while the existing proximal point methods based on the interior point algorithm do not.

Remark 3.

In our proof of Theorem 4, we require that $\rho _k\rightarrow 0$. For classical proximal point methods, this condition was not required. In fact, this condition is adopted for simple proof that of clustering point $(\bar{\varvec{x}},\bar{\varvec{\varsigma }})$ of the sequence $\{\mathbf{x}_k,\varvec{\varsigma }_k\}$ being a saddle point of Problem ($\mathscr {P}$). Our simulations show that $\rho _k\rightarrow 0$ can be relaxed. Indeed, in our test simulations, we found that the convergence for the case of $\rho _k$ being chosen as a proper constant parameter is faster than that one of $\rho _k\rightarrow 0$.

5 Numerical Experiments

This section presents some numerical results by proposed canonical primal–dual method. In our simulations, the involved SDP is solved by YALMIP [23] and SeDuMi [34].

Example 5.1

Let us first consider the optimization problem (24). Taking $\rho _k = \frac{1}{k}$ and $\mu _k = 0.1\rho _k$, the initial condition is randomly generated. Table 1 reports the results obtained by our method.

Table 1 Numerical results for optimization problem (24)

From Table 1, we can see that all the four solutions $(0,1), (1,0), (0,-1)$, and $(-1,0)$ can be detected by our algorithm with different (randomly generated) initial conditions. The corresponding $\mathbf {G}(\bar{\varvec{\varsigma }}) \approx 0$, as we shown in Proposition 2, can also be solved by perturbation method under any given tolerance. However, the following optimization problem

$$\begin{aligned} \min _{\mathbf{x}} P(\mathbf{x}) =\frac{1}{2}\sum _{i=1}^m(\mathbf{x}^T\mathbf {A}_i\mathbf{x}-d_i)^2 \end{aligned}$$

(39)

cannot be solved by perturbation method in general, where $\mathbf {A}_i, i=1,\cdots ,m,$ are randomly generated semi-definite matrix and $d_i,i=1,\cdots ,m,$ are chosen such that the optimal function value of $P(\mathbf{x})$ is 0. In fact, $\mathbf {G}(\bar{\varvec{\varsigma }}) = 0$ since the optimal cost function value of the optimization problem (39) is 0. Suppose that m is not too small (for example $m\ge 20$), for any given small perturbation $\varDelta \varvec{f}$, the corresponding saddle point problem ($\mathscr {S}_p$) has no solution ($\bar{\varvec{x}}, \bar{\varvec{\varsigma }}$) such that $\mathbf {G}(\bar{\varvec{\varsigma }})\succ 0$ by our numerical experiences. Thus, the linear perturbation method cannot be applied. Now we use our proposed algorithm to solve (39) with different $\rho _k$ and $\mu _k$. In about $80\%$ cases, our method can capture a solution of Problem ($\mathscr {P}$). The corresponding numerical results are reported in Table 2.

Table 2 Numerical results for optimization problem (39) after 50 iterations

During our numerical computation, we observe that for very few steps (for example, less than 20 iterations), the numerical solution by our method is very close to one solution of Problem ($\mathscr {P}$). In fact, for all the cases in Table 2, if we set $\varepsilon = 10^{-4}$, then all the obtained results are satisfied with $\max _i |\bar{x}_i^{*}-x^{true}_i| \le \varepsilon$, $i=1,\cdots , n$, where $\mathbf{x}^{true}=[x^{true}_1,\cdots ,x^{true}_n]^T$ is one of exact optimal solutions of Problem ($\mathscr {P}$). However, it suffers from slow convergence . Table 2 shows it clearly for the last two cases. If a gradient-based optimization method is applied, then the optimal function value is $P(\bar{\varvec{x}})\approx 10^{-8}$ for all cases in Table 2.

It is obvious that Problem (39) has at least two solutions because of its symmetry, i.e., if $\bar{\varvec{x}}$ is its solution, so is $-\bar{\varvec{x}}$. Thus, classical SDP-based relaxation methods in [18, 33, 36] cannot produce an exact solution. However, our method can produce one at the expense of iterative computation of a sequence of SDPs in most cases.

6 Applications to Sensor Networks

In this section, we apply our proposed method for sensor network localization problems.

Consider N sensors and M anchors, both located in the d-dimensional Euclidean space $\mathbb {R}^d$, where d is 2 or 3. Let the locations of M anchor points be given as $a_1$, $a_2$, $\cdots$, $a_M\in \mathbb {R}^d$. The locations of N sensor points $x_1$, $x_2$, $\cdots$, $x_N\in \mathbb {R}^d$ are to be determined. Let $N_x$ be a subset of $\{(i,j):1\le i < j \le N\}$ in which the distance between the ith and the jth sensor point is given as $d_{ij}$ and $N_a$ be a subset of $\{(i,k):1\le i \le N, 1\le k \le M\}$ in which the distance between the ith sensor point and the kth anchor point is given as $e_{ik}$. Then, a sensor network localization problem is to find vector $x_i\in \mathbb {R}^d$ for all $i=1,2,\cdots ,N,$ such that

$$\begin{aligned} \Vert x_i - x_j\Vert ^2= & {} d_{ij}^2,\;\; \forall (i,j) \in N_x, \end{aligned}$$

(40)

$$\begin{aligned} \Vert x_i - a_k\Vert ^2= & {} e_{ik}^2,\;\; \forall (i,k) \in N_a. \end{aligned}$$

(41)

When the given distances $d_{ij}, (i,j)\in N_x,$ and $e_{ik}, (i,k)\in N_a,$ contain noise, the equalities (40) and (41) may become infeasible. Thus, instead of solving (40) and (41), we formulate it as a nonconvex optimization as given below:

$$\begin{aligned} \min _{x_1,\cdots ,x_N}\sum _{(i,j) \in N_x}(\Vert x_i-x_j\Vert ^2-d_{ij}^2)^2 + \sum _{(i,k) \in N_a}(\Vert x_i-a_k\Vert ^2-e_{ik}^2)^2. \end{aligned}$$

(42)

Denote $\mathbf{x}= [x_1^T,\cdots ,x_N^T ]^T\in \mathbb {R}^{dN}$. Then, (42) can be rewritten as

$$\begin{aligned} \min _{\mathbf{x}}\left\{ P(\mathbf{x}) = \sum _{ij\in N_x}(\mathbf{x}^T \mathbf {A}_{ij}\mathbf{x}- d_{ij}^2)^2 + \sum _{ik\in N_a}(\mathbf{x}^T \mathbf {B}_{ii}\mathbf{x}-2\varvec{f}_{ik}^T \mathbf{x}- (e_{ik}^2 -\varvec{f}_{ik}^T\varvec{f}_{ik}) )^2\right\} , \nonumber \\ \end{aligned}$$

(43)

where $\mathbf {A}_{ij} = (\mathbf {E}_i - \mathbf {E}_j) (\mathbf {E}_i - \mathbf {E}_j)^T$, $\mathbf {B}_{ii} = \mathbf {E}_i \mathbf {E}_i^T$,

$$ \mathbf {E}_i =\left( \begin{array}{c} 0_{d\times d} \\ \cdots \\ 0_{d\times d} \\ I_{d\times d} \leftarrow i\\ 0_{d\times d} \\ \cdots \\ 0_{d\times d} \\ \end{array} \right) \text { and } \varvec{f}_{ik} =\left( \begin{array}{c} 0_{d} \\ \cdots \\ 0_{d} \\ a_k \leftarrow i\\ 0_{d} \\ \cdots \\ 0_{d} \\ \end{array} \right) . $$

As in [17, 33], the root mean square distance

$$\begin{aligned} RMSD=\left( \frac{1}{N}\sum _{i=1}^{N}\Vert \widehat{x}_{i}-x^{*}_{i}\Vert _{2}^{2}\right) \nonumber \end{aligned}$$

is adopted to measure the accuracy of the locations of the sensor i, $i=1,\cdots ,N$, where $\widehat{x}_{i}$ and $x^*_i$ are the estimated position and true positions, respectively, $i=1,\cdots ,N$. The software package SFSDP [17] is applied for generating test problems and comparison. During our simulation, all of sensors are placed in [0, 1]$\times$[0, 1] randomly and four anchors are fixed at (0.125, 0.125), (0.125, 0.875),(0.875, 0.125), and (0.875, 0.875), respectively.

For the conventional SDP relaxation methods, the computed sensor locations match its true locations if and only if the corresponding sensor network is uniquely localizable [33, 36]. Thus, if the localized sensor network has multiple solutions, the conventional SDP relaxation methods [17, 33] fail to produce a good solution of the optimization problem defined by (43). Let us consider the following network with multiple solutions:

Example 6.1

Consider a sensor network containing six sensors and four anchors depicted in Fig. 1. From Fig. 1, we can see that the sensors $x^{*}_{2}$, $x^{*}_{3}$, and $x^{*}_{5}$ have two positions.

Fig. 1

Network topology of six sensors and four anchors

More specifically, $x_{2}$ can be either (0.0791, 0.0091) or (0.0091, 0.1709), $x_{3}$, $x_{5}$ can be either the pair of [(0.7342, 0.8470), (0.8506, 0.7257)] or the pair of $[(1.0158, 0.9030), (0.8994, 1.0243)]$. Let $x^{*}$, $\check{x}$, and $\hat{x}$ be the true sensor locations, sensor locations computed by the SDP method ([18]), and sensor locations computed by Algorithm 1, respectively. The results are depicted in Fig. 2a, c. The true sensor locations (denoted by circles) and the computed locations (denoted by stars) are connected by solid lines. From the two figures, we can clearly see that our method produce better estimations than the SDP relaxation method in [18]. However, we need to solve a sequence of SDPs, but in [18], only one SDP is involved (Table 3). To achieve a higher accuracy, we apply the gradient-based optimization method in SFSDP to refine the solutions obtained by our method and that obtained by SDP method in [18]. After refinement, RMSD obtained by SFSDP is $4.91\times 10^{-5}$ and $2.07\times 10^{-8}$ is obtained by our method. The refined results are depicted in Fig. 2b, d. From Fig. 2b, we observe that there are still big errors for the sensor 3 and sensor 5 obtained by the refinement of SDP method in [18]. Figure 2d shows that our method produces one of the exact solutions of the optimization problem defined by (43). Thus, our method achieves better performance no matter before or after refinement.

Fig. 2

Computed locations information of six sensors and four anchors

In practical circumstances, the exact distances $d_{ij}$ and $e_{ik}$ are unavailable because of the presence of noise during the measurement. To model such a case, we perturb the distances as

$$\begin{aligned} \widehat{d}_{ij}= \max \{(1 + \xi _{ij}), 0.1\}d_{ij} \quad ((i, j)\in N_x),\end{aligned}$$

(44)

$$\begin{aligned} \widehat{e}_{ik}= \max \{(1 + \xi _{ik}), 0.1\}e_{ik} \quad ((i, k)\in N_a), \end{aligned}$$

(45)

where $\xi _{ij}$, $\xi _{ik}$ are random variables and chosen from the standard normal distribution $N(0, \sigma )$, where $\sigma$ is the noisy parameter. By substituting (44) and (45) into (43), the corresponding optimization problem involved in noisy distance is obtained.

Table 3 Numerical results for six sensors and four anchors

Example 6.2

Consider a sensor network localization problem with 20 sensors and 4 anchors. Let the radio range be 0.3 and the noisy parameter be 0.001, respectively. A sensor network generated randomly by these parameters is depicted in Fig. 3.

Fig. 3

Network topology of 20 sensors and 4 anchors

Table 4 Numerical results for 20 sensors and 4 anchors

From Fig. 3, we can verify that for this sensor network, it has a unique solution.

We apply Algorithm 2 and the SDP method in [18] in conjunction with a gradient-based refinement method to solve it. The computed results are listed in Table 4. The RMSD computed by SFSDP in conjunction with a gradient-based refinement method is $9.95\times$10$^{-2}$ while that computed by our method is $4.1041\times 10^{-7}$. The computed results by Algorithm 2 and by SDP in conjunction with a gradient-based refinement method in [18] are depicted in Fig. 4. From Fig. 4 and the values of RMSD, we know that our method achieves better performance than that by SFSDP in conjunction with a gradient-based refinement method. This is because if the distances are inexact, the SDP-based methods in [18] are not ensured to produce a good solution. However, our method is based on the global solution of the optimization problem defined by (43). Thus, the inexact measurements do not deteriorate the performance of our method.

Fig. 4

Computed locations information of 20 sensors and 4 anchors

Fig. 5

Network topology of 50 sensors and 4 anchors

Fig. 6

Computed locations information of 50 sensors and 4 anchors

Example 6.3

Consider a sensor network localization problem with 50 sensors, 4 anchors, and noisy perturbation being 0.001. The corresponding connections between sensors and sensors and sensors and anchors are depicted in Fig. 5.

The computed results by Algorithm 2 and by SFSDP in conjunction with a gradient-based refinement method are depicted in Fig. 6. The RMSD computed by SFSDP in conjunction with a gradient-based refinement method is $1.07\times 10^{-1}$, while that by our method is $1.9956\times 10^{-5}$. Both Fig. 6 and the values of RMSD show that our method achieves better performance.

7 Conclusion

This paper presented an effective method and algorithms for solving a class of nonconvex optimization problems. Using the canonical duality theory, the original nonconvex optimization problem is first relaxed to a convex–concave saddle point optimization problem. Depending on the singularity of the matrix $\mathbf {G}$, this relaxed saddle point problem is classified in two cases: degenerate or non-degenerate. For the non-degenerate case, the solution of the primal problem can be recovered exactly through solving a convex SDP problem. Otherwise, a quadratic perturbed primal–dual scheme is proposed to solve the corresponding degenerate saddle point problem. We proved that, under certain conditions, the sequence generated by our proposed scheme converges to a solution of the corresponding saddle point problem. If this saddle point satisfies the condition of $\Vert \varLambda (\bar{\varvec{x}})- \nabla V^*(\bar{\varvec{\varsigma }}) \Vert \le \varepsilon$ within a given error tolerance, then the solution of the primal problem is also recovered exactly. Otherwise, $\bar{\varvec{x}}$ is taken as a starting point and a gradient-based optimization method is applied to refine the primal solution. Numerical simulations show that our method can achieve better performance than the conventional SDP-based relaxation methods.