Keywords

1 Introduction

Control of robot manipulators is difficult in general, because robot dynamics is usually strongly non-linear. Although the influence of non-linear terms in the arm motion equations can be suppressed by using high-ratio gears in the actuators, is such cases the friction in the gears and bearings often degrades the actuator performance for high-velocity motions. Especially in the case of light-weight, high-velocity robot arms for pure manipulating purposes, the arm dynamics cannot be neglected to achieve optimal performance.

In this paper the problem of tracking a trajectory, provided by the motion planning layer of the robot control system, is discussed. It is assumed that the trajectory, defined in the robot operational space, is transformed into the robot joint space by the algorithm of inverse kinematics [1], before the motion task is performed. The motion control layer then works with the information on the robot joint positions, i.e. the relative positions of the robot links.

Multiple approaches to design of the feedback control system of robot manipulator are described in literature [1, 2]. The simplest approach, suitable only for low-velocity motions, works with the actuators as with velocity generators and the effects of the robot dynamics are considered as unknown disturbances [2]. The feedback control can be then based on PI or PID controllers. To enhance the performance, cascade configuration with additional velocity or even acceleration feedback can be used. It is also possible to use a partial feed-forward compensation of non-linearities, if a partial knowledge of the robot mathematical model is available [1].

More advanced robot control architectures use actuators as torque generators [1, 2]. This approach is utilized in centralized control systems, viewing the robot dynamics in full complexity as a high-order, coupled and non-linear one. The centralized methods utilize some special features of the robot dynamics. In particular, dynamic inversion method transforms the controller design problem into a linear one by means of additional interior loop. However, applicability of this approach depends on precision of the mathematical model available, which often cannot be guaranteed due to unknown influences, such as backslashes and flexibilities in the gears or saturations of the action forces. Therefore, practical usability requires some extensions, guaranteeing at least closed-loop asymptotical stability [1]. Among alternative approaches e.g. the non-linear PID control based on Lyapunov stability theory or passive systems theory can be mentioned [1, 2].

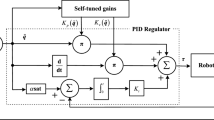
An advantage of the decentralized control approach is that for the controller tuning only rough robot mathematical model is sufficient, describing approximate inertial effect on individual axes and damping effects. If we assume that terms in the robot model depend only on position, it is possible to improve the performance by dividing the joint space into segments with constant controller settings. The controller parameters can be changed during motion when the trajectory goes across the segment boundary. Within each segment the robot then can be controlled as a decoupled linear system by means of conventional PID controllers. It is possible to use initially the same settings in all the segments and to adapt the controller parameters in each segment automatically by processing past measurements of the kinematic and control variables. Such an algorithm adapts the controller parameters also when the robot manipulated load changes.

In this paper an extension of the decentralized robot control approach is proposed, based on the idea outlined above, including some additional enhancements. Practical implementation is indeed more complex than in the case of conventional decentralized control. Partitioning of the joint space into segments brings increased requirements on the control system hardware, as regards both performance and memory capacity. However, it reveals that these requirements can be fulfilled by using current 32-bit microcontroller-based platforms.

2 The Robot Mathematical Model

The mathematical model of a robot arm consisting of \( n \) links in an open kinematic chain, moving freely in the operation space, can be considered in the form

$$ {\mathbf{B}}\left( {\mathbf{q}} \right){\mathbf{\ddot{q}}} + {\mathbf{C}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}}} \right){\dot{\mathbf{q}}} + {\mathbf{g}}\left( {\mathbf{q}} \right) = {\mathbf{f}} $$
(1)

where \( {\mathbf{q}} \) is the vector of joint positions and \( {\mathbf{f}} \) the vector of total force effects of actuators. If \( K \) and \( P \) denote the total kinetic and potential energy, \( {\mathbf{B}}\left( {\mathbf{q}} \right) = \partial^{2} K/\partial {\dot{\mathbf{q}}}^{2} \) is a positive definite position-dependent inertia matrix,

$$ {\mathbf{C}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}}} \right){\dot{\mathbf{q}}} = \frac{{\partial^{2} K}}{{\partial {\mathbf{q}}\partial {\dot{\mathbf{q}}}}}{\dot{\mathbf{q}}} - \frac{\partial K}{{\partial {\mathbf{q}}}} $$
(2)

is a non-linear function corresponding to the effects of centrifugal and Coriolis forces and \( {\mathbf{g}}\left( {\mathbf{q}} \right) = \partial P/\partial {\mathbf{q}} \) is the vector function corresponding to the gravity-force effects [1]. If we assume only electrical DC actuators, by neglecting the winding inductance and mechanical friction, we obtain

$$ {\mathbf{M}} \approx {\mathbf{K}}_{u} {\mathbf{u}} - {\mathbf{K}}_{v} {\varvec{\upomega}} $$
(3)

where \( {\mathbf{M}} \) is the vector of motor output torques, \( {\mathbf{u}} \) the input voltages, \( {\varvec{\upomega}} \) the vector of motor angular velocities and \( {\mathbf{K}}_{u} > 0 \), \( {\mathbf{K}}_{v} > 0 \) constant diagonal matrices. In principle, (3) allows using the motors as velocity generators, where the connected load is represented as a disturbance. Alternatively, the motor can play the role of a torque generator, where the term \( {\mathbf{K}}_{v} {\varvec{\upomega}} \), corresponding to induced voltage in winding, is considered as electromagnetic friction. In this case, the motor is usually equipped with inner current feedback, which reduces the effect of \( {\mathbf{K}}_{v} {\varvec{\upomega}} \) and protects from overload [1]. Although this paper is based on the idea of decentralized control, the motors are considered as torque generators, like at most centralized control methods. In this case

$$ {\mathbf{f}} = {\mathbf{K}}_{r} \left( {{\mathbf{K}}_{u} {\mathbf{u}} - {\mathbf{K}}_{v} {\varvec{\upomega}}} \right) - {\mathbf{F\dot{q}}} $$
(4)

where \( {\mathbf{K}}_{r} > 0 \) and \( {\mathbf{F}} > 0 \) are diagonal matrices. The term \( {\mathbf{F\dot{q}}} \) corresponds to viscous friction in bearings and gears and \( {\mathbf{K}}_{r} \) is the mechanical gear ratio. Coulomb friction is not considered. Since \( {\dot{\mathbf{q}}} = {\mathbf{K}}_{r}^{ - 1} {\varvec{\upomega}} \),

$$ {\mathbf{f}} = {\mathbf{K}}_{r} {\mathbf{K}}_{u} {\mathbf{u}} - {\mathbf{F}}_{r} {\dot{\mathbf{q}}},\,{\mathbf{F}}_{r} = {\mathbf{K}}_{r} {\mathbf{K}}_{v} {\mathbf{K}}_{r} + {\mathbf{F}}. $$
(5)

The Eq. (1) then can be rewritten as

$$ {\mathbf{B}}\left( {\mathbf{q}} \right){\mathbf{\ddot{q}}} + \left( {{\mathbf{C}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}}} \right) + {\mathbf{F}}_{r} } \right){\dot{\mathbf{q}}} + {\mathbf{g}}\left( {\mathbf{q}} \right) = {\mathbf{Ku}} $$
(6)

where \( {\mathbf{K}} = {\mathbf{K}}_{r} {\mathbf{K}}_{u} \). Since the dependence of \( {\mathbf{F}}_{r} \) on \( {\mathbf{K}}_{r} \) is quadratic, the term \( {\mathbf{C}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}}} \right) \) has low influence in the case of higher mechanical gear ratios and the model depends predominantly only on \( {\mathbf{q}} \).

3 The Decentralized Control with Partial Knowledge of \( {\mathbf{B}}\left( {\mathbf{q}} \right) \)

One possible version of the decentralized robot control algorithm uses partial knowledge of the inertia matrix \( {\mathbf{B}}\left( {\mathbf{q}} \right) \), which is decomposed as

$$ {\mathbf{B}}\left( {\mathbf{q}} \right) = {\bar{\mathbf{B}}} + \Delta {\mathbf{B}}\left( {\mathbf{q}} \right) $$
(7)

where \( {\bar{\mathbf{B}}} \) is a constant diagonal positive definite matrix, corresponding to approximate average inertial effects on individual axes [1]. The robot model for the controller design is in the form

$$ {\mathbf{\bar{B}\ddot{q}}} + {\mathbf{F}}_{r} {\dot{\mathbf{q}}} = {\mathbf{Ku}} - {\mathbf{d}} $$
(8)

where

$$ {\mathbf{d}} = \Delta {\mathbf{B}}\left( {\mathbf{q}} \right){\mathbf{\ddot{q}}} + {\mathbf{C}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}}} \right){\dot{\mathbf{q}}} + {\mathbf{g}}\left( {\mathbf{q}} \right) $$
(9)

is disturbance. Since all matrices in (8) are diagonal, it is possible to write (8) as

$$ b_{i} \ddot{q}_{i} + f_{ri} \dot{q} = k_{i} u_{i} - d_{i} ,\,\,i = 1,..,n $$
(10)

where \( b_{i} \), \( f_{ri} \) and \( k_{i} \) denote the diagonal terms of \( {\bar{\mathbf{B}}} \), \( {\mathbf{F}}_{r} \) and \( {\mathbf{K}} \), respectively. Equation (10) can be rewritten as

$$ T_{i} \ddot{q}_{i} + \dot{q} = K_{i} u_{i} - \delta_{i} $$
(11)

where \( T_{i} = b_{i} /f_{ri} \), \( K_{i} = k_{i} /f_{ri} \) and \( \delta_{i} = d_{i} /f_{ri} \). The corresponding axis transfer function is in the form

$$ F_{i} \left( s \right) = \frac{{K_{i} }}{{s\left( {T_{i} s + 1} \right)}}. $$
(12)

To compensate the effect of persistent input-type disturbance \( d_{i} \) of the system (10) and to achieve zero tracking error in the case of ramp reference trajectory, a controller with additional zero pole is needed. If we use the PID controller with the transfer function in Laplace transform

$$ R_{i} \left( s \right) = r_{i} \left( {1 + \frac{1}{{T_{Ii} s}} + T_{Di} s} \right) = \frac{{r_{i} }}{{T_{Ii} s}}\left( {T_{Ii} T_{Di} s^{2} + T_{Ii} s + 1} \right) $$
(13)

for generating the control signals \( u_{i} \left( t \right) \), the characteristic polynomial of the i-th axis is in the form

$${ Q_{i} \left( s \right) = \frac{{T_{Ii} s^{2} \left( {T_{i} s + 1} \right)}}{{r_{i} K_{i} }} + \left( {T_{Ii} T_{Di} s^{2} + T_{Ii} s + 1} \right) = \frac{{T_{Ii} T_{i} }}{{r_{i} K_{i} }}s^{3} + \frac{{T_{Ii} + r_{i} K_{i} T_{Di} T_{Ii} }}{{r_{i} K_{i} }}s^{2} + T_{Ii} s + 1. }$$
(14)

The PID controller parameters can be determined so that poles of \( Q_{i} \left( s \right) \) are placed at desired locations [6]. If we assume \( Q_{i} \left( s \right) = \left( {T_{1i} s + 1} \right)\left( {T_{2i}^{2} s^{2} + 2\xi_{i} T_{2i} s + 1} \right) \), where \( T_{1i} ,T_{2i} \) are chosen closed-loop response time constants and \( \xi_{i} \) is the relative damping ratio, by comparison of the coefficients we obtain

$$ r_{i} = \frac{{\left( {T_{1i} + 2\xi_{i} T_{2i} } \right)T_{i} }}{{T_{1i} T_{2i}^{2} K_{i} }},\,T_{Ii} = T_{1i} + 2\xi_{i} T_{2i} ,\,T_{Di} = \frac{{2\xi_{i} T_{1i} T_{2i} + T_{2i}^{2} }}{{T_{Ii} }} - \frac{1}{{r_{i} K_{i} }}. $$
(15)

If the disturbance \( d_{i} \) is partially known, its effect can be compensated in part by adding \( K_{i}^{ - 1} \delta_{i} \) to the i-th axis controller output, where \( \delta_{i} = d_{i} /f_{ri} \).

4 The Extended Decentralized Robot Control Algorithm

Consider that the robot joint space \( S \), i.e. the space of all possible joint positions \( {\mathbf{q}} = \left[ {q_{1} , \ldots ,q_{n} } \right]^{T} \), is partitioned into m segments \( S_{k} \), \( k = 1,..,m \), such that

$$ \bigcup\limits_{k = 1}^{m} {S_{k} } = S,\bigcap\limits_{k = 1}^{m} {S_{k} = } \,\emptyset . $$
(16)

Since the diagonal parts of \( {\mathbf{B}}\left( {\mathbf{q}} \right) \) and \( {\mathbf{g}}\left( {\mathbf{q}} \right) \) are position-dependent, it is possible to approximate the robot dynamics in each segment by a different linear model. Then the tracking performance can be enhanced if to each segment there correspond different controller settings.

A basic approach is that the controller parameters are rewritten during motion when the trajectory goes across the segment boundary. Within each segment the robot is controlled as a decoupled linear system by means of conventional PID controllers. This extension is rather straightforward and can be efficiently implemented, although a sufficient amount of memory in the control system hardware is needed. If a space of each generalized coordinate is divided into \( d \) sub-intervals, the joint space will be divided into \( m = d^{n} \) segments. To each segment \( S_{k} \) there corresponds a matrix of the parameters \( {\mathbf{P}}_{k} = \left[ {{\mathbf{K}}_{k} ,\,{\mathbf{T}}_{k} ,\,{\varvec{\updelta}}_{k} } \right] \) describing the plant dynamics as described in the previous section. The columns in \( {\mathbf{P}}_{k} \) are vectors of n components, e.g. \( {\mathbf{K}}_{k} = \left[ {K_{k1} , \ldots ,K_{kn} } \right]^{T} \). The corresponding PID controlled settings can be obtained directly by substitution into (15).

However, this concept has an important drawback, consisting in discontinuity of the action variables \( u_{i} \left( t \right) \) caused by changes of the controller settings at the segments boundaries. Such discontinuities are undesirable, since they can lead to oscillations of the mechanical structure.

One possible solution is replacing the segments \( S_{k} \) by the fuzzy sets \( \tilde{S}_{k} = \left\{ {R^{n} ,\mu_{k} \left( {\mathbf{q}} \right)} \right\} \), where the membership functions \( \mu_{k} \left( {\mathbf{q}} \right) \) are chosen continuous and so that \( \mu_{k} \left( {\mathbf{q}} \right) \in \left[ {0,1} \right] \) and \( \mu_{k} \left( {{\mathbf{c}}_{k} } \right) = 1 \), where \( {\mathbf{c}}_{k} \) denotes the centre of the segment \( S_{k} \). The matrix of the plant parameters is then computed at each control step as

$$ {\mathbf{P}} = \sum\limits_{k = 1}^{m} {\mu_{k} \left( {\mathbf{q}} \right){\mathbf{P}}_{k} }/\sum\limits_{k = 1}^{m} {\mu_{k} \left( {\mathbf{q}} \right)} . $$
(17)

The expression (17) is usually used as an inference rule in Takagi-Sugeno-type fuzzy modeling [4]. However, the computation of (17) at each control step can be time-consuming due to rather large number of segments m. It can be considered that the segments are for given parameter \( h \) defined by means of their centers \( {\mathbf{c}}_{k} \) as

$$ S_{k} = \left\{ {{\mathbf{q}}\,|\,\,\left\| {{\mathbf{q}} - {\mathbf{c}}_{k} } \right\|_{\infty } \le h} \right\}, $$
(18)

where \( \,\left\| {\mathbf{x}} \right\|_{\infty } = \hbox{max} \left| {x_{i} } \right| \) denotes the \( L_{\infty } \)-norm. Then it is possible to define

$$ \mu_{k} \left( {\mathbf{q}} \right) = \mu \left( {{\mathbf{q}} - {\mathbf{c}}_{k} } \right) $$
(19)

where \( \mu \left( {\mathbf{q}} \right) \in \left[ {0,1} \right] \) is a chosen continuous function, such that \( \mu \left( {\mathbf{0}} \right) = 1 \). Computation of (17) can be made much more efficient if \( \mu \left( {\mathbf{q}} \right) \) is chosen as a function with compact support, see e.g. [5]. A simple possibility is to choose

$$ \mu \left( {\mathbf{q}} \right) = \hbox{max} \left\{ {1 - \left\| {\mathbf{q}} \right\|_{\infty } /\left( {\left( {1 + \lambda } \right)h} \right),\,\,0} \right\} $$
(20)

where \( \lambda > 0 \), typically \( \lambda \in \left[ {0.5,\,2} \right] \). In this case the values of \( \mu_{k} \left( {\mathbf{q}} \right) \) are zero, except for the \( k \)-the segment, where \( \mu_{k} \left( {\mathbf{q}} \right) \) has the largest value, and several neighboring segments. This fact can be utilized for efficient implementation of the controller, although such a realization is more complex. A disadvantage of the choice (20) is that this function is not smooth, which will produce non-smooth histories of the control signals. Therefore, it might be preferable to construct \( \mu \left( {\mathbf{q}} \right) \) as at least continuously differentiable. The compact-support choice of \( \mu \left( {\mathbf{q}} \right) \) brings the risk of unbounded values in (17) for trajectories exceeding the boundaries of \( S \), but this problem can be easily avoided, e.g. by increasing \( \lambda \) in the cases when \( \sum\nolimits_{k = 1}^{m} {\mu_{k} \left( {\mathbf{q}} \right)} = 0 \).

5 Adaptation of the Controller Settings

Since the number of segments can be rather large, it is necessary that the controller settings are computed automatically. Initially, the settings in all the segments are set to the same values corresponding to the decentralized PID controller design described in Sect. 3. During the robot operation the settings in the segments can be adapted by processing the measured values of \( {\mathbf{q}}\left( {t_{k} } \right) \) and \( {\mathbf{u}}\left( {t_{k} } \right) \), at the instants \( t_{k} = k\Delta \), where \( \Delta \) is the identification scan period. During motion in each segment it is needed to estimate the parameters \( K_{i} \), \( T_{i} \) and \( \delta_{i} \). The index of segment is omitted below for simplicity, i.e. e.g. \( K_{i} \) should be written as \( K_{ki} \) in the k-th segment to be precise.

The continuous transfer function (12) has the corresponding transfer function in Z-transform

$$ \begin{aligned} F_{i} (z) & = {\mathcal{Z}}\left\{ {K_{i} T_{i} \left( { - 1 + t/T_{i} + e^{{ - t/T_{i} }} } \right);\,\,t = k\Delta } \right\} \\ & = K_{i} T_{i} \left( { - 1 + \frac{\Delta }{{T_{i} }}\frac{1}{z - 1} + \frac{z - 1}{{z - e^{ - \Delta /T} }}} \right) = K_{i} \left( {\frac{\Delta }{z - 1} + T_{i} \frac{{e^{{ - \Delta /T_{i} }} - 1}}{{z - e^{{ - \Delta /T_{i} }} }}} \right). \\ \end{aligned} $$
(21)

If \( \Delta /T_{i} \) is sufficiently low, \( e^{{ - \Delta /T_{i} }} \approx 1 - \Delta /T_{i} \), so

$$ F_{i} (z) \approx K_{i} \Delta \left( {\frac{1}{z - 1} - \frac{1}{{z - e^{{ - \Delta /T_{i} }} }}} \right) = K_{i} \Delta \frac{{1 - \alpha_{i} }}{{z^{2} - \left( {1 + \alpha_{i} } \right)z + \alpha_{i} }} $$
(22)

where \( \alpha_{i} = e^{{ - \Delta /T_{i} }} \). Equation (22) corresponds to the data model

$$ q_{i}^{{\left[ {k + 2} \right]}} - \left( {1 + \alpha_{i} } \right)q_{i}^{{\left[ {k + 1} \right]}} + \alpha_{i} q_{i}^{\left[ k \right]} = K_{i} \Delta \left( {1 - \alpha_{i} } \right)\,u_{i}^{\left[ k \right]} + \varepsilon^{\left[ k \right]} $$
(23)

where \( q_{i}^{\left[ k \right]} \) denotes the value of \( q_{i} \) at \( k \)-th instant and \( \varepsilon^{\left[ k \right]} \) is the error process. After including the disturbance \( \delta_{i} \), defined by (11), (23) can be rewritten as

$$ \Delta^{ - 1} \left( {q_{i}^{\left[ k \right]} - q_{i}^{{\left[ {k + 1} \right]}} } \right)\alpha_{i} - u_{i}^{\left[ k \right]} \tilde{K}_{i} + \tilde{\delta }_{i} = \Delta^{ - 1} \left( {q_{i}^{{\left[ {k + 1} \right]}} - q_{i}^{{\left[ {k + 2} \right]}} } \right) + \varepsilon^{\left[ k \right]} $$
(24)

where \( \tilde{K}_{i} = K_{i} \left( {1 - \alpha_{i} } \right) \) and \( \tilde{\delta }_{i} = \delta_{i} \left( {1 - \alpha_{i} } \right) \). From (24) the value of \( {\varvec{\uptheta}}_{i} = \left[ {\alpha_{i} ,\tilde{K}_{i} ,\tilde{\delta }_{i} } \right]^{T} \) can be estimated by means of the least-squares method. Then, \( \alpha_{i} \) determines the value of \( T_{i} \). The parameters \( K_{i} \) and \( \delta_{i} \) can be computed directly from \( {\varvec{\uptheta}}_{i} \).

Note that to each segment there corresponds one data model (24) and a corresponding data structure have to exist in the control system for storing the measurements. It is advantageous to use the recursive version of the LS estimator [3], which need not store all the data, but only a 3 × 3 matrix and the vector \( {\varvec{\uptheta}}_{i} \) in each segment and for each axis. It is assumed that the settings are updated after a single task is performed, but the same approach can be used when the controller is updated during motion. Let

$$ {\mathbf{x}}_{i}^{[k]} = w_{j} \left( {{\mathbf{q}}^{[k]} } \right)\left[ {\Delta^{ - 1} \left( {q_{i}^{\left[ k \right]} - q_{i}^{{\left[ {k + 1} \right]}} } \right), - u_{i}^{\left[ k \right]} ,1} \right]^{T} ,\,y_{i}^{[k]} = w_{j} \left( {{\mathbf{q}}^{[k]} } \right)\Delta^{ - 1} \left( {q_{i}^{{\left[ {k + 1} \right]}} - q_{i}^{{\left[ {k + 2} \right]}} } \right) $$
(25)

where \( w_{j} \left( {\mathbf{q}} \right) \) is the weight of the measurement in the j-th segment, computed as

$$ w_{j} \left( {\mathbf{q}} \right) = \mu_{j} \left( {\mathbf{q}} \right)\,/\,\sum\limits_{l = 1}^{m} {\mu_{l} \left( {\mathbf{q}} \right)} . $$
(26)

The \( \left( {k + 1} \right) \)-th estimate of \( {\varvec{\uptheta}}_{i} \) for the j-th segment is obtained as follows:

$$ {\varvec{\uptheta}}_{i}^{{\left[ {k + 1} \right]}} = {\varvec{\uptheta}}_{i}^{\left[ k \right]} + \frac{{{\mathbf{C}}_{i}^{\left[ k \right]} {\mathbf{x}}_{i}^{\left[ k \right]} }}{{\gamma + {\mathbf{x}}_{i}^{\left[ k \right]T} \,{\mathbf{C}}_{i}^{\left[ k \right]} {\mathbf{x}}_{i}^{\left[ k \right]} }}\left( {y_{i}^{\left[ k \right]} - {\mathbf{x}}_{i}^{\left[ k \right]T} {\varvec{\uptheta}}_{i}^{\left[ k \right]} } \right) $$
(27)
$$ {\mathbf{C}}_{i}^{{\left[ {k + 1} \right]}} = \frac{1}{\gamma }\left( {{\mathbf{I}} - \frac{{{\mathbf{C}}_{i}^{\left[ k \right]} {\mathbf{x}}_{i}^{\left[ k \right]} {\mathbf{x}}_{i}^{\left[ k \right]T} }}{{\gamma + {\mathbf{x}}_{i}^{\left[ k \right]T} \,{\mathbf{C}}_{i}^{\left[ k \right]} {\mathbf{x}}_{i}^{\left[ k \right]} }}} \right){\mathbf{C}}_{i}^{\left[ k \right]} $$
(28)

where \( \gamma \) is the forgetting coefficient, equal or very close to 1. In the considered case it seems to be necessary to require that \( T_{i} > T_{i\text{min} } > 0 \) and \( K_{i} > K_{i\text{min} } > 0 \), where the constants \( T_{i\text{min} } \), \( K_{i\text{min} } \) are suitably chosen. The recursive form of the estimator (27) enables to keep the values of the components of \( {\varvec{\uptheta}}_{i} \) in the corresponding range by updating only with feasible values. The matrix \( {\mathbf{C}}_{i}^{\left[ 0 \right]} \) is set as \( {\mathbf{C}}_{i}^{\left[ 0 \right]} = {\text{diag}}\left( {\sigma_{1} ,\sigma_{2} ,\sigma_{3} } \right) \), where \( \sigma_{k} > 0 \) are chosen. Total memory requirements can be estimated as \( 12\,m\,n \) real numbers, which can occupy from tens to hundreds of kbytes of the control system memory.

6 Simulated Results

Consider the 3-DOF anthropomorphic robot arm approximate model in Fig. 1, where \( m_{1} = m_{2} = 1\,\,{\text{kg}} \), \( l_{1} = l_{2} = 0.5\,{\text{m}} \) and \( h = 1\,{\text{m}} \). The terms of the diagonal matrices \( {\mathbf{K}}_{u} ,\,{\mathbf{K}}_{v} ,\,{\mathbf{K}}_{r} \) and \( {\mathbf{F}} \) were chosen as \( k_{ui} = 1 \), \( k_{vi} = 0 \), \( k_{ri} = 10 \) and \( f_{i} = 3 \), \( i = 1,..,3 \). The mathematical model for simulation, which is strongly non-linear, was obtained by expressing the terms \( {\mathbf{B}}\left( {\mathbf{q}} \right) \), \( {\mathbf{C}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}}} \right){\dot{\mathbf{q}}} \) and \( {\mathbf{g}}\left( {\mathbf{q}} \right) \) in (1), where \( {\mathbf{q}} = \left[ {\varphi ,\,\psi ,\,\vartheta } \right]^{T} \), from the expressions for kinetic and potential energy. Since the mathematical model is rather complex, the details had to be omitted due to paper length limitations.

Fig. 1.
figure 1

The robot arm approximate model

Full size image

First, the fixed axes PID controllers (13) were used. The diagonal matrix \( {\bar{\mathbf{B}}} \) for setting-up the PID controllers, with the meaning of rough estimate of the inertia matrix, was chosen as

$$ {\bar{\mathbf{B}}} = {\text{diag}}\left( {\frac{{m_{1} l_{1}^{2} + m_{2} \left( {l_{1} + l_{2} } \right)^{2} }}{ 2},\,\,\left( {m_{1} + m_{2} } \right)l_{1}^{2} ,\,\,m_{2} l_{2}^{2} } \right). $$
(29)

The reference trajectory was chosen as the step function, which can be viewed as the worst-case situation, since the robot will usually track a continuous trajectory. The controller parameters were computed so that \( T_{1i} = T_{2i} = 0.075\,{\text{s}} \) and \( \xi_{i} = 0.8 \) in (15). The joint initial and target positions are considered as

$$ {\mathbf{q}}_{0} = \left[ { - 1.5,\,2,\,3} \right],{\mathbf{q}}_{f} = \left[ {1.5,\, - 2,\, - 1} \right]. $$
(30)

Figure 2 shows the corresponding histories of the robot joint positions.

Fig. 2.
figure 2

The joint step responses - fixed axes PID controllers

Full size image

Further, the proposed adaptive controller has been used. The joint space has been divided into \( m\, = \,8^{3} \) segments, \( \lambda = 1 \) has been chosen in (20). The controller has been initialized to the same settings as in the previous case and executed 20 times the same trajectory with the scan period \( \Delta = 0.002 \) s to adapt. The desired closed-loop settings \( T_{1i} = T_{2i} = 0.075\;{\text{s}} \) and \( \xi_{i} = 0.8 \) were preserved. The matrices \( {\mathbf{C}}_{i}^{{}} \) have been initialized as \( {\mathbf{C}}_{i}^{\left[ 0 \right]} = 0.01\, \times {\text{diag}}\left( {1,0.3,1} \right) \) and \( \gamma = 0.9^{\Delta } \), \( T_{i\text{min} } = 0.03 \) and \( K_{i\text{min} } = 0.05 \) has been chosen. Figure 3 shows the final simulated histories. It can be seen that significant enhancement has been achieved. Similar results were obtained also for lower values of \( m \). In these cases the convergence was faster, but it seems that it is necessary to use higher values of \( T_{i\text{min} } \) and \( K_{i\text{min} } \) and the responses are a little slower.

Fig. 3.
figure 3

The joint step responses - adaptive control system, \( m = 8^{3} \)

Full size image

7 Conclusions

The proposed adaptive control system is based on the principles of the PID controller-based decentralized control, where the joint space is divided into segments with different controller settings. To ensure continuity of the control signal at the segment boundaries, the segments are represented as fuzzy sets with a special choice of the membership function. Simulated results show that the approach can be used in the cases when the conventional decentralized control fails to produce good responses, although such situations seem to occur mainly in the cases of long-range and high-velocity movements. The control system memory requirements are large in comparison with conventional control algorithms, but can be fulfilled by using current 32-bit microcontrollers. Thus the worst problem from practical point of view seems to be proper initial settings of \( {\mathbf{C}}_{i}^{{}} \), \( T_{i\text{min} } \), \( K_{i\text{min} } \) and other parameters that influence convergence of the sequence of estimates (27).