Multi-Objective Resource Allocation Optimization for SWIPT in Small-Cell Networks

Abstract

In this chapter we consider time switching (TS) simultaneous wireless information and power transfer (SWIPT) for a small-cell network consisting of multiple multi-antenna access points (APs) that serve multiple single antenna user equipments (UEs). In this scenario, we address the jointly optimized design of spatial precoding and TS ratios under a multi-objective optimization (MOO) framework. Our goal is to maximize a utility vector including the data rates and harvested energies of all UEs simultaneously. This problem is a non-convex rank-constrained MOO problem which is transformed into a non-convex semidefinite program using the weighted Chebyshev method. We propose an algorithm based on majorization–minimization approach to solve this problem. Numerical results are provided to demonstrate the performance of the proposed beamforming and TS algorithm in terms of harvested energy-data rate trade-off. The effect of different parameters on this trade-off is also investigated to get a general overview for the practical design of the network.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The rapid development of mobile internet and internet of things (IoTs) has given rise to a serious concern about the highly growing traffic and the support of a massive number of connected devices. Therefore, the energy storage, power management and increase of the battery life of these devices are major issues to be considered in realizing the upcoming networks successfully. While many energy efficient strategies aim at expanding the system’s battery life by reducing the energy consumption, the others propose to recycle the ambient energy associated with the energy harvesting (EH) sources such as vibration, heat and electromagnetic waves. Among these different EH techniques, radiofrequency (RF) EH via RF electromagnetic waves is one of the most appealing techniques. In this context, the idea of using the same electromagnetic field for transferring both information and power to wireless devices, called simultaneous wireless information and power transfer (SWIPT) has recently attracted significant attention. It is predicted that SWIPT will become an essential part for many commercial and industrial wireless systems in the future, including the IoT, wireless sensor networks and small-cell networks [1].

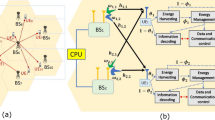
The ideal SWIPT receiver is the one which is able to extract energy from the same signal as that used for information decoding (ID) [2]. However, this extraction is not possible with the current circuit designs, since the energy carried by the RF signal is lost during the ID process. Hence, a considerable effort has been devoted to investigate different practical SWIPT receiver architectures. These architectures can be classified into two groups of: parallel and co-located receivers [3]. In a parallel receiver architecture, also referred to as antenna switching, energy harvester and information receiver are equipped with independent antennas for EH and ID. As shown in Fig. 3.1, the antenna array is divided into two subsets, one for EH and the other for ID. In a co-located receiver architecture, the energy harvester and the information receiver share the same antennas. Two practical methods to design the co-located receiver architecture for SWIPT are time switching (TS) and power splitting (PS). As shown in Fig. 3.2a, in a TS design, each reception time frame is divided into two orthogonal time slots, one for ID and the other for EH and the receiver switches in time between EH and ID modes. However, in PS design the receiver splits the received signal into two streams of different power levels for EH and ID, as shown in Fig. 3.2b.

Fig. 3.1

Antenna switching SWIPT receiver

Fig. 3.2

Practical designs for the co-located SWIPT receiver. (a) Time switching (TS). (b) Power splitting (PS)

To realize SWIPT, the available resources such as transmit power, subcarriers and beamforming vectors should be allocated properly among both information and energy transfer functionalities. In [4–6], the authors address the problem of designing TS/PS SWIPT receivers in a point-to-point wireless environment to achieve various trade-offs between wireless information transfer and EH. In multi-user environments, however, most of the researches focus on the power and subcarrier allocation among different users such that some criteria (throughput, harvested power, fairness, etc.) are met. Various policies have been proposed for single input-single output (SISO) and multiple input-single output (MISO) configurations in a multi-user downlink channel [7–12].

Resource allocation algorithm design aiming at maximization of the energy efficiency of data transmission in a SISO PS SWIPT multi-user system is considered in [7] with an orthogonal frequency division multiple access (OFDMA).

In MISO configuration, there exists an additional degree of freedom of beamforming vector optimization at the transmitter. In [11], a joint beamforming and PS ratio allocation scheme was designed to minimize the power cost under the constraints of throughput and harvested energy. The problem of joint power control and TS in MISO SWIPT systems by considering the long-term power consumption and heterogeneous quality of service (QoS) requirements for different types of traffics is also studied in [9]. In [10] resource allocation algorithm design for SWIPT is addressed in a multi-user coordinated multipoint (CoMP) network which includes multiple multi-antenna remote radio heads (RRHs) and separate single antenna EH and ID receivers. A MISO femtocell co-channel overlaid with a macro-cell is considered in [12] to exploit the advantages of SWIPT while promoting the energy efficiency. The femto base station sends information to ID femto users (FUs) and transfers energy to EH FUs simultaneously, and also suppresses its interference to macro users. A novel EH balancing technique for robust beamformers design in MISO SWIPT system is also proposed in [8] considering imperfect channel state information (CSI) at the transmitter.

SWIPT in multi-user MIMO interference channel is studied in [13, 14]. In [13] a MIMO interference channel with two transmitter–receiver pairs is considered. When both receivers are set in ID mode or EH mode, the achievable rate obtained with iterative water-filling and without CSI sharing is studied. Strategies are proposed for the mixed case of one ID receiver and one EH receiver, in order to maximize the energy transfer to the EH receiver and minimize the interference to the ID receiver. PS SWIPT in a multi-user MIMO interference channel scenario is also studied in [14]. The objective is to minimize the total transmit power of all transmitters by jointly designing the transmit beamformers, power splitters and receiver filters, subject to the signal-to-interference-plus-noise ratio (SINR) constraint for ID and the harvested power constraint for EH at each receiver.

In this chapter, we address SWIPT from the following points of view:

• First, based on the literature review conducted, most of the existing works in SWIPT consider single cell cases with one base station (BS) and single or multiple mobile users. In a multi-cell case the system becomes interference limited, since reuse of subcarriers from users in different cells produce interference that degrades the system performance in terms of throughput and spectral efficiency, particularly for cell edge users. In this perspective, important features such as inter-cell interference coordination (ICIC) and CoMP communication have been introduced for cellular communication networks. However, while interference links are always harmful for information decoding, constructive interferences are useful for energy harvesting. This already shows the dualistic nature of interference in SWIPT networks. On the other hand, it is worth remarking that the signal strength of far-field RF transmission is greatly impaired by the path loss when the separation between the transmitter and the RF energy harvester increases. From an architectural point of view, a potential solution that could ensure ubiquitous SWIPT is the avoidance of the high signal attenuation due to path loss. This can be achieved, thanks to densification of network nodes. Therefore, the concept of ICIC relying on a cloud-based centralized digital processing can be the basis to SWIPT technologies ensuring large energy transfer efficiency and reduced costs. In this scenario, a large number of low-cost RRHs, also referred to as access points (APs), are randomly deployed and connected to the baseband unit (BBU) pool through the fronthaul links. This concept has generally been applied to macro-cells, i.e. large outdoor tower-based systems. However, it can also be applied to small-cells that provide distributed coverage across a large space such as a stadium, airport or office building. Such an architecture would permit an integrated control of power and data transfer while keeping the RF front ends relatively close to the associated devices.

• Second, we consider TS SWIPT technique, which is practically feasible and can be implemented using simple switches, while PS receivers require highly complex hardware due to the different power sensitivity levels of ID and EH parts in each receiver. In this perspective, it is worth mentioning that TS SWIPT receivers can be considered as a special case of dynamic PS SWIPT receivers with on–off power splitting factor. Hence, since realistic values of the ID and EH receivers’ sensitivities may differ by more than 30dB, TS and dynamic PS SWIPT will have similar performance in practical scenarios.

• Third, existing SWIPT works have considered single objective optimization (SOO) framework to formulate the problem of resource allocation or beamforming optimization. Popular objectives are classical performance metrics such as sum rate/ throughput (to be maximized), or transmit power (to be minimized), or sum of energy harvested (to be maximized). However, SWIPT has a multi-objective nature, i.e. both throughput and the amount of harvested energy are desirable objectives in designing SWIPT systems. In SOO one of these objectives is selected as the sole objective while the others are considered as constraints. This approach assumes that one of the objectives is of dominating importance and also it requires prior knowledge about the accepted values of the constraints related to the other objectives. Therefore, the fundamental approach used in our study is the multi-objective optimization (MOO) which investigates the optimization of the vector of objectives, for nontrivial situations, where there is a conflict between objectives. This approach has been proposed lately for wireless information systems [15] and is only considered in [16, 17] very recently for a parallel SWIPT system which consists of a multi-antenna transmitter, a single-antenna information receiver and multiple EH receivers equipped with multiple antennas. In this scenario, the trade-off between the maximization of the energy efficiency of information transmission and the maximization of the wireless power transfer efficiency is studied by means of resource allocation using an MOO framework.

2 System Model

We consider a small-cell network consisting of several APs which may overlay the existing macro-cell network as in Fig. 3.3. Small-cells are realized using multiple RRHs which are connected to a central BBU through the fronthaul links [18]. Macro BS and RRHs are equipped with multiple antennas and serve multiple single antenna users. We assume that each cell in Fig. 3.3 consists of N _AP APs which are equipped with $N_{A_{j}},j = 1,\ldots,N_{\mathrm{AP}}$ antennas and serve N _UE single antenna user equipments (UEs). The term UE in this chapter refers to the broader range of devices from the ones directly used by the end-users to the autonomous sensors. The sets of all UEs and all APs are denoted by $\mathscr{N}_{\mathrm{UE}}$ and $\mathscr{N}_{\mathrm{AP}}$, respectively. Each user is assumed to be served by multiple transmitters but with different beamforming vectors. Therefore, the received signal in the ith UE can be modelled as:

$$\displaystyle{ y_{i} =\sum _{ j=1}^{N_{\mathrm{AP}} }\boldsymbol{h_{ij}^{H}}\sum _{ l=1}^{N_{\mathrm{UE}} }\boldsymbol{x_{lj}}s_{l} + n_{i}, }$$

(3.1)

where $i,l \in \mathscr{N}_{\mathrm{UE}},j \in \mathscr{N}_{\mathrm{AP}}$, s _l is the information symbol from APs to the lth UE which originates from independent Gaussian codebooks, $s_{l} \sim \mathscr{CN}(\boldsymbol{0},1)$ and $\boldsymbol{x_{lj}} \in \mathbb{C}^{N_{A_{j}}\times 1}$ is the beamforming vector from the jth AP to the lth UE. We assume quasi-static flat fading channel for all UEs and denote by $\boldsymbol{h_{ij}} \in \mathbb{C}^{N_{A_{j}}\times 1}$ the complex channel vector from the jth AP to the ith UE. Also $n_{i} \sim \mathscr{CN}(0,\sigma _{i}^{2})$ is the circularly symmetric complex Gaussian receiver noise which includes the antenna noise and the ID processing noise in the ith user. According to (3.1), the achievable data rate R _i (bits/s/Hz) for the ith UE can be found from the following equation:

$$\displaystyle{ \begin{array}{l} R_{i} =\log _{2}\left (1 + \frac{\sum _{j=1}^{N_{\mathrm{AP}}}\text{trace}(\boldsymbol{H_{ ij}}\boldsymbol{X_{ij}})} {\sigma _{i}^{2}+\sum _{j=1}^{N_{\mathrm{AP}}}\sum _{l=1,l\neq i}^{N_{\mathrm{UE}}}\text{trace}(\boldsymbol{H_{ij}}\boldsymbol{X_{lj}})}\right ), \end{array} }$$

(3.2)

where $\boldsymbol{X_{ij}} =\boldsymbol{ x_{ij}}\boldsymbol{x_{ij}^{H}}$, $\boldsymbol{H_{ij}} =\boldsymbol{ h_{ij}}\boldsymbol{h_{ij}^{H}}$ and therefore $\boldsymbol{X_{ij}},\boldsymbol{H_{ij}} \in \mathbb{C}^{N_{A_{j}}\times N_{A_{j}} }$ are rank-one matrices for $i \in \mathscr{N}_{\mathrm{UE}},j \in \mathscr{N}_{\mathrm{AP}}$. This information data rate is achieved by treating the interference as noise.

Fig. 3.3

Small-cell network with TS scheme in MISO SWIPT system

Besides, the received energy per channel use E _i (assuming normalized energy unit of Joule/(channel use) or W) in the ith UE is given by:

$$\displaystyle{ \begin{array}{l} E_{i} =\sum \limits _{ j=1}^{N_{\mathrm{AP}}}\sum \limits _{l=1}^{N_{\mathrm{UE}}}\text{trace}(\boldsymbol{H_{ij}}\boldsymbol{X_{lj}}), \end{array} }$$

(3.3)

in which the antenna noise power is neglected. However, this amount of energy cannot be harvested in practice due to the technical issues of RF-to-DC energy conversion. The efficiency of the RF energy harvester depends on the efficiency of the antenna, the accuracy of the impedance matching between the antenna and the voltage multiplier, and the power efficiency of the voltage multiplier that converts the received RF signals to DC voltage [19].

In this scenario, the UEs are assumed to use TS design for implementing SWIPT. As stated before, in a TS scheme each reception time frame is divided into two orthogonal time slots, one for ID and the other for EH. Consequently, denoting by α _i the fraction of time devoted to ID in the ith UE, the average data rate in this scheme can be written as:

$$\displaystyle{ \begin{array}{l} R_{i}^{\mathrm{TS}}(\boldsymbol{X},\alpha _{i}) = \alpha _{i}R_{i}(\boldsymbol{X}),\end{array} }$$

(3.4)

where $R_{i}(\boldsymbol{X})$ can be found from (3.2). Also we have the following equation for the amount of harvested energy at the ith UE:

$$\displaystyle{ \begin{array}{l} E_{h_{i}}^{\mathrm{TS}}(\boldsymbol{X},\alpha _{ i}) = (1 -\alpha _{i})\eta _{i}E_{i}(\boldsymbol{X}), \end{array} }$$

(3.5)

in which $E_{i}(\boldsymbol{X})$ can be found from (3.3) and η _i denotes the energy harvesting efficiency factor of the ith UE.

3 Resource Allocation Optimization for TS SWIPT

In this section, we study the resource allocation optimization problem for our TS SWIPT system in a multi-objective manner. First we formulate the problem of designing the optimal transmit strategies $\boldsymbol{X} = [\boldsymbol{X_{lj}}]_{l\in \mathscr{N}_{\mathrm{UE}},j\in \mathscr{N}_{\mathrm{AP}}}$ and time switching ratios $\boldsymbol{\alpha }= [\alpha _{l}]_{l\in \mathscr{N}_{\mathrm{UE}}}$ jointly to maximize the performance of all users simultaneously and then we propose an algorithm based on the majorization–minimization approach [20] to solve this problem.

3.1 Problem Formulation

As mentioned earlier, the data rate and harvested energy are both desirable for each user in SWIPT scenarios. Therefore, in our problem formulation, we define the utility vector of the ith UE by $\boldsymbol{u}_{i}(\boldsymbol{X},\alpha _{i}) = [R_{i}^{\mathrm{TS}}(\boldsymbol{X},\alpha _{i}),E_{h_{i}}^{\mathrm{TS}}(\boldsymbol{X},\alpha _{ i})]$ which includes both the data rate and the harvested energy values of the ith TS SWIPT UE. Our optimization objective is then to maximize the utility vector of the whole system defined by $\boldsymbol{u}(\boldsymbol{X},\boldsymbol{\alpha }) = [\boldsymbol{u}_{1}(\boldsymbol{X},\alpha _{1}),\boldsymbol{u}_{2}(\boldsymbol{X},\alpha _{2}),\ldots,\boldsymbol{u}_{N_{\mathrm{UE}}}(\boldsymbol{X},\alpha _{N_{\mathrm{UE}}})]$ jointly via the multi-objective problem formulation. This problem can be written as:

$$\displaystyle{ \begin{array}{llll} &\mathop{\text{Maximize}}\limits_{\boldsymbol{X},\boldsymbol{\alpha }}&&\boldsymbol{u}(\boldsymbol{X},\boldsymbol{\alpha }) \\ &\text{subject to} &&\mbox{ (1)}\ \sum _{j=1}^{N_{\mathrm{AP}}}\sum _{l=1}^{N_{\mathrm{UE}}}\text{trace}(\boldsymbol{X_{lj}}) \leq P_{\max } \\ & &&\mbox{ (2)}\ \boldsymbol{X_{lj}}\succeq 0,\ \text{Rank}(\boldsymbol{X_{lj}}) = 1,\ \forall l,j \\ & &&\mbox{ (3)}\ \alpha _{l} \in [0,1],\ \forall l, \end{array} }$$

(3.6)

where constraint (1) denotes the average power constraint for APs across all transmitting antennas with upper limit of P _max, constraint (2) considers the rank-one property of X _lj s and constraint (3) is due to definition of TS rates.

The design problem for the ideal SWIPT case in which energy is assumed to be extracted simultaneously while information decoding is the same as problem (3.6) but with utility vectors of $\boldsymbol{u}_{i}(\boldsymbol{X}) = [R_{i}(\boldsymbol{X}),\eta _{i}E_{i}(\boldsymbol{X})]$, where $R_{i}(\boldsymbol{X})$ and $E_{i}(\boldsymbol{X})$ can be found from (3.2) and (3.3), respectively. As already stated, this ideal receiver is not feasible in practice; however, for theoretical benchmarking, its performance can be used as an upper bound for the performance of the TS SWIPT.

3.2 Resource Allocation Algorithm

Our approach to solve problem (3.6) is to relax the rank constraints on X _lj s. It is proved in [21] that the optimal solution of the relaxed problem satisfies Rank(X _lj ) = 1, ∀l ∈ N _UE, ∀j ∈ N _AP. As the objectives in problem (3.6) are conflicting, this problem cannot be solved in a globally optimal way and the Pareto optimality of the resource allocation will be adopted as the optimality criterion. Pareto optimality is a state of allocating the resources in which none of the objectives can be improved without degrading the other objectives [22]. As there usually exists multiple Pareto optimal solutions for MOO problems, it is generally converted into a SOO problem involving possibly some parameters or additional constraints to compute each Pareto optimal point. This conversion is called scalarization and examples of it are the weighted sum, weighted product and the weighted Chebyshev methods [15].

To solve the relaxed version of MOO problem (3.6), we use the weighted Chebyshev method, which provides the complete Pareto optimal set by varying predefined preference parameters. The weighted Chebyshev goal function is

$$\displaystyle{ \begin{array}{l} f_{\mathrm{ch}}(.) =\mathop{ \text{Minimum}}\limits_{\boldsymbol{i \in \mathscr{N}_{\mathrm{UE}},m = 1,2}}\frac{\boldsymbol{u}_{i}^{(m)}} {v_{i}^{(m)}},\end{array} }$$

(3.7)

where $\boldsymbol{u}_{i}^{(m)}$ denotes the mth element of $\boldsymbol{u}_{i}(\boldsymbol{X},\alpha _{i})$ and $v_{i}^{(1)},v_{i}^{(2)}\ \forall i \in \mathscr{N}_{\mathrm{UE}}$ are the predefined preference parameters that specify the priority of each objective. Therefore, introducing the new parameter λ, weighted Chebyshev scalarization is equivalent to the following problem:

$$\displaystyle{ \begin{array}{llll} &\mathop{\text{Maximize}}\limits_{\boldsymbol{X},\boldsymbol{\alpha },\lambda }&&\lambda \\ &\text{subject to} &&\mbox{ (1)}\ \alpha _{i}R_{i}(\boldsymbol{X}) \geq \lambda v_{i}^{(1)},\ \forall i \\ & &&\mbox{ (2)}\ (1 -\alpha _{i})\eta _{i}E_{i}(\boldsymbol{X}) \geq \lambda v_{i}^{(2)},\ \forall i \\ & &&\mbox{ (3)}\ \sum _{j=1}^{N_{\mathrm{AP}}}\sum _{l=1}^{N_{\mathrm{UE}}}\text{trace}(\boldsymbol{X_{lj}}) \leq P_{\max } \\ & &&\mbox{ (4)}\ \boldsymbol{X_{lj}}\succeq 0,\ \forall l,j \\ & &&\mbox{ (5)}\ \alpha _{i} \in [0,1],\ \forall i,\end{array} }$$

(3.8)

The above problem is a non-convex semidefinite program (SDP) due to not only the coupled TS ratios and R _i , E _i in the first and second constraints but also the definition of $R_{i}(\boldsymbol{X})$ as presented in (3.2). Introducing the new variables R _i , E _i , I _i and β _i , problem (3.8) can be represented as:

$$\displaystyle{ \begin{array}{llll} &\mathop{\text{Maximize}}\limits_{\boldsymbol{X},\alpha _{i},\beta _{i},R_{i},E_{i},I_{i},\lambda,\ \forall i}&&\lambda \\ &\mathrm{\ \ \ \ \ subject\ to} &&\mbox{ (C1)}\ \alpha _{i}R_{i} \geq \lambda v_{i}^{(1)},\ \forall i \\ & &&\mbox{ (C2)}\ \beta _{i}\eta _{i}E_{i} \geq \lambda v_{i}^{(2)},\ \forall i \\ & &&\mbox{ (C3)}\ E_{i} =\sum _{ j=1}^{N_{\mathrm{AP}}}\sum _{l=1}^{N_{\mathrm{UE}}}\text{trace}(\boldsymbol{H_{ij}}\boldsymbol{X_{lj}}),\ \forall i \\ & &&\mbox{ (C4)}\ I_{i} =\sum _{ j=1}^{N_{\mathrm{AP}}}\sum _{l=1,l\neq i}^{N_{\mathrm{UE}}}\text{trace}(\boldsymbol{H_{ij}}\boldsymbol{X_{lj}}),\ \forall i \\ & &&\mbox{ (C5)}\ R_{i} = \log (E_{i} + \sigma _{i}^{2}) -\log (I_{i} + \sigma _{i}^{2}),\ \forall i \\ & &&\mbox{ (C6)}\ \sum _{j=1}^{N_{\mathrm{AP}}}\sum _{l=1}^{N_{\mathrm{UE}}}\text{trace}(\boldsymbol{X_{lj}}) \leq P_{\max } \\ & &&\mbox{ (C7)}\ \boldsymbol{X_{lj}}\succeq 0,\ \forall l,j \\ & &&\mbox{ (C8)}\ \alpha _{i} +\beta _{i} = 1,\ \forall i \\ & &&\mbox{ (C9)}\ \alpha _{i} \in [0,1], \end{array} }$$

(3.9)

where E _i and I _i defined in (C3) and (C4) are the received energy and the interference level in the ith UE, respectively. Also (C5) is directly obtained from substituting the definition of E _i and I _i in the definition of R _i given by Eq. (3.2). It is shown in [21] that the constraint (C5) in problem (3.9) can be relaxed to $(\overline{\mbox{ C5}})$ defined below:

$$\displaystyle{ \begin{array}{l} (\overline{\mbox{ C5}})\ R_{i} \leq \log (E_{i} + \sigma _{i}^{2}) -\log (I_{i} + \sigma _{i}^{2}). \end{array} }$$

(3.10)

We define $\hat{\lambda }=\log (\lambda )$, and use the monotonicity and concavity properties of the logarithm function to reformulate the above problem as below:

$$\displaystyle{ \begin{array}{llll} &\mathop{\text{Maximize}}\limits_{\boldsymbol{X},\alpha _{i},\beta _{i},R_{i},E_{i},I_{i},\hat{\lambda },\ \forall i}&&\hat{\lambda } \\ &\mathrm{\ \ \ \ \ subject\ to} &&(\overline{\mbox{ C1}})\ \log (\alpha _{i}) +\log (R_{i}) \geq \hat{\lambda }+\log (v_{i}^{(1)}) \\ & &&(\overline{\mbox{ C2}})\ \log (\beta _{i}) +\log (\eta _{i}E_{i}) \geq \hat{\lambda }+\log (v_{i}^{(2)}) \\ & &&\mbox{ (C3)\textendash (C4)} \\ & &&(\overline{\mbox{ C5}})\ R_{i} \leq \log (E_{i} + \sigma _{i}^{2}) -\log (I_{i} + \sigma _{i}^{2}) \\ & &&\mbox{ (C6)\textendash (C9)},\\ \end{array} }$$

(P)

in which the nonconvexity of problem (3.9) is concentrated in inequality $(\overline{\mbox{ C5}})$. Now problem (P) can be considered as a DC (difference of convex) programming [23] since $(\overline{\mbox{ C5}})$ is the difference of two convex functions (R _i − log(E _i + σ _i ²), − log(I _i + σ _i ²)). Therefore, it can be solved using local optimization method of convex–concave procedure (CCP) [24]. CCP is a majorization–minimization algorithm [20] that solves DC programs as a sequence of convex programs by linearizing the concave part, log(I _i + σ _i ²), around the current iteration solution of I _i . To this end, we use the first order Taylor expansion and replace problem (P) in the kth step by the following subproblem:

This problem is a convex SDP and it can be solved by standard optimization techniques such as Interior-Point Method. In this paper, we have used the CVX package to solve (P _k ). The linearization point is updated with each iteration until it satisfies the termination criterion as described in Algorithm 1. It can be easily verified that if I _i ^k is the stationary point of subproblem (P _k ), i.e. fulfilling the KKT conditions of subproblem (P _k ), it is also a stationary point of problem (P) [25]. The conditions under which the constrained CCP algorithm converges to a stationary point of the original problem are studied in [26] using Zangwill’s global convergence theory [27] of iterative algorithms. These conditions are shown to be satisfied for Algorithm 1 in [21].

Algorithm 1: CCP Algorithm for TS SWIPT

  1:    Define a step size $\gamma \in \mathbb{R}$ and a given tolerance ɛ > 0.

  2:    Initialize: choose a value for I _i ⁰ inside the convex set defined by (C1)-(C4), (C6)-(C9).

  3:    Set k: = 0.

  4:    For the given I _i ^k, solve the convex SDP of (P _k ) to obtain the solution $\hat{I}_{i}(I_{i}^{k})$.

  5:    if $\|\hat{I}_{i}(I_{i}^{k}) - I_{i}^{k}\|\leqslant \varepsilon$ then

  6:        stop.

  7:    else

  8:        update $I_{i}^{k} = I_{i}^{k} +\gamma (\hat{I_{i}}(I_{i}^{k}) - I_{i}^{k})$.

  9:        update iteration, k = k + 1.

10:        go back to line 4.

11:    end if

4 Numerical Results

In this section, we provide numerical results to demonstrate the performance of the proposed beamforming and TS algorithm in terms of harvested energy-data rate trade-off. We investigate the effect of different parameters on this trade-off to get a general overview for the practical design of the network.

4.1 Experimental Setup

We consider two small-cells as shown in Fig. 3.4, consisting of N _AP = 2 APs equipped with $N_{A_{1}}$, $N_{A_{2}}$ antennas and N _UE TS SWIPT sensors. Sensors are distributed uniformly in a region bounded by two concentric circles with radius of d _min and d _max. The distance of APs from each other is denoted by D as shown in Fig. 3.4. Transmission channel gains, $\boldsymbol{h}_{ij},\forall i \in \mathscr{N}_{\mathrm{UE}},j = 1,2$, depend on the location of sensors with respect to APs and the channel fading model. At each sensor location, channel gains are generated with Rayleigh fading and path loss exponent of 3. Noise powers are assumed to be σ _i ² = −90 dBm, $\forall i \in \mathscr{N}_{\mathrm{UE}}$ and the maximum total power budget is set to P _max = 1 W. Parameter assumptions in this section (unless they are clearly stated with different values) are summarized in Table 3.1.

Fig. 3.4

Simulation scheme

Table 3.1 Parameter assumptions

4.2 Discussion

In this section, we illustrate the Pareto boundary of TS and ideal SWIPT systems to investigate the trade-off between the harvested energy and the data rate. To plot the Pareto boundaries, we solve the optimization problems (3.6) using Algorithm 1 in several directions by changing the preference weights of $v_{i}^{(1)},v_{i}^{(2)},\forall i$. To have a general view of the Pareto boundary, we first consider a setup which includes two UEs served by two coordinated APs. The first UE is assumed to be a SWIPT sensor while the second UE is assumed to be an ID receiver such as smartphone. Therefore, we set v ₁ ⁽¹⁾ = θ ₂ θ ₁, v ₁ ⁽²⁾ = θ ₂, v ₂ ⁽¹⁾ = θ ₁ and search for the optimal solutions in different directions by changing the values of θ ₁ and θ ₂. In this setup, θ ₁ changes the trade-off between the harvested energy and the data rate in the first UE and θ ₂ changes the data rate preference between the first and second UE.

Figure 3.5 depicts the 3D Pareto boundary and its three 2D projections for one channel realization. As can be seen in Fig. 3.5a, the maximum harvested energy occurs when both the data rate of the first and second UEs are almost zero. By decreasing the amount of desired harvested energy, we can achieve higher data rates. In this scenario, the first UE (SWIPT sensor) desires high amount of harvested energy. Achieving high data rate is not required by this sensor while it is desired for the second UE. The desired trade-off is therefore the boundary marked in pink colour in Fig. 3.5d. The corresponding counterparts are also shown in Fig. 3.5b,c. To explain the behaviour of the Pareto boundary in this area, we study the performance in three different regions shown in Fig. 3.5d. At point A, we have the maximum data rate for the second UE, i.e. R ₂ ^TS = 33 bits/s/Hz, R ₁ ^TS = 2 bits/s/Hz and E ₁ ^TS = 0. 08 mW. At this point, the whole power is assigned to the AP which is closest to the second UE (it should be noted that we have assumed global power constraint for the APs in our system model). A small part of this power is only devoted to the sensor and therefore we will have such a low data rate and harvested energy in the first UE. By adapting the TS ratio of the sensor we can increase the harvested energy to a certain point B in which we have E ₁ ^TS = 0. 5 mW with the data rate of R ₁ ^TS = 1. 8 bits/s/Hz in this case. As a result while we are increasing the harvested energy, data rate of the second UE decreases only slightly to R ₂ ^TS = 30 bits/s/Hz. However, to further increase the harvested energy, the beamformers should be aligned toward the first UE and this yields to an interference which suddenly decreases the data rate of the second UE to R ₂ ^TS = 10 bits/s/Hz at point C. As a result, region 2 is the region in which both APs are active. In region 3, we are willing to harvest more energy and therefore the power will be assigned to the AP which is closer to the first UE. Therefore by transferring the power to the first AP and adapting the TS ratio we could harvest up to E ₁ ^TS = 0. 9 mW (point D).

Fig. 3.5

3D Pareto boundary of TS SWIPT and its projections. (a) R ₁ ^TS∕E ₁ ^TS∕R ₂ ^TS. (b) R ₁ ^TS∕E ₁ ^TS. (c) R ₁ ^TS∕R ₂ ^TS. (d) E ₁ ^TS∕R ₂ ^TS

Now we consider a symmetric setup which includes $N = \frac{N_{\mathrm{UE}}} {2} = 1$ UE with the same priority in each small-cell. Therefore we set $v_{i}^{(1)} =\theta _{1},v_{i}^{(2)} = 1\ \forall i$ and search for the optimal solutions by changing the value of θ ₁ only. Figure 3.6 shows the average Pareto boundary of the first TS SWIPT UE. As it can be seen, the average harvested energy is a monotonically decreasing function of the achievable data rate. This result shows that these two objectives are generally conflicting and any resource allocation algorithm that maximizes the harvested energy cannot maximize the data rate. In this plot, as the amount of harvested energy increases from 0.45 μW to 1.8 mW, the average data rate reduces from 29.13 to 0.2657 bits/s/Hz.

Fig. 3.6

Pareto boundary of TS SWIPT and ideal SWIPT

Pareto boundary of the infeasible ideal SWIPT is also shown in this figure as an upper bound. It can be observed that the maximum value of the harvested energy $E_{h_{\max }}$ and the achievable data rates R _max are the same for ideal and TS SWIPT. However, as expected, the minimum value of the harvested energy and the achievable data rates are not zero in this case since the ideal SWIPT is assumed to be able to harvest energy while decoding the information. It should be noticed that if the AP is able to change its beamforming vector for EH and ID, the optimal strategy would be to use the beamforming vectors related to the two extreme points of the ideal SWIPT Pareto boundary in each time slot. In this case, the optimal TS Pareto boundary would simply be the dashed linear line in Fig. 3.6. However, since in our scenario the same beamforming vector is used for EH and ID, the optimal TS Pareto boundary is the envelope of all linear lines connecting the projection of ideal Pareto boundary points (R ^∗, E _h ^∗) on two axes, i.e. (0, E _h ^∗) and (R ^∗, 0). Besides, as it is evident from Fig. 3.6, the Pareto boundary of TS SWIPT generated from the objectives in our problem formulation is non-convex. This is due to the multiple AP schemes and joint optimization of TS ratios and the beamforming vectors considered in this problem. In the following, we study the effect of the network parameters such as the number of UEs, distance of the APs from each other and the maximum possible distance of UEs from the APs on the Pareto boundary of the TS SWIPT UE.

4.2.1 Effect of the Number of UEs

To study the effect of the number of UEs, we consider a symmetric setup which includes $N = \frac{N_{\mathrm{UE}}} {2} = 1,2,3$ UEs in each small-cell with the same user preference weights as in previous plot. Figure 3.7 shows the Pareto boundary of the first TS SWIPT UE in this setup.

Fig. 3.7

Pareto boundary of TS SWIPT and ideal SWIPT

As can be seen, increasing the number of UEs highly affects the possible amount of harvestable energy at each UE, while the maximum data rate changes very slightly by increasing the number of UEs. For example, the maximum harvested energy in Fig. 3.7 reduces approximately from 1.8 mW to 0.5 mW and 0.3 mW by increasing the number of UEs at each small-cell from N = 1 to N = 2 and N = 3, respectively. This result is expectable, due to the fixed total power consumption assumption and the direct impact of transmit power on the received energy.

In Fig. 3.7 we have also plotted the Pareto boundaries of ideal SWIPT for N = 1, 2, 3 UEs in each small-cell. Comparing the results of ideal and TS SWIPT for different number of UEs shows that the harvested energy loss of TS SWIPT with respect to the ideal SWIPT for a fixed required data rate reduces with increasing the number of UEs. As can be seen in Fig. 3.7, to achieve R ₁ = 5 bits/s/Hz in the first UE, we lose approximately 1 mW in TS SWIPT with respect to the ideal SWIPT in N = 1 UE per small-cell. However, this amount reduces to nearly 0.3 mW and 0.2 mW in N = 2 and N = 3, respectively.

4.2.2 Effect of the Distance D Between APs

The effect of multi-user interference on the harvested energy-data rate trade-off is shown in Fig. 3.8. In this figure, we have plotted the Pareto boundaries for the first UE for different AP distances of D = 10, 15, 20 m for two cases of d _max = 5, 10 m. As can be seen in Fig. 3.8a, in d _max = 5 m, the Pareto boundaries are quite close to each other for different values of D. The maximum harvested energy is slightly higher in D = 10 m because of the higher level of interference in this case. However, by increasing the demand for the data rate, this interference will degrade the performance. In the case of d _max = 10 m, as plotted in Fig. 3.8b, Pareto boundaries for D = 15, 20 m are very close to each other. However, by decreasing the distance to D = 10 m the harvested energy increases in a fixed desired data rate. This is due to the fact that in higher d _maxs the probability of utilizing both APs increases while in lower d _maxs the UEs are mostly fed with their nearest AP.

Fig. 3.8

Pareto boundary of TS SWIPT for different D and d _max = 5, 10 m. (a) d _max = 5 m. (b) d _max = 10 m

4.2.3 Effect of Maximum UE Distance d _max from the AP

The effect of small-cell size is investigated in this section by plotting the Pareto boundaries for different maximum distance of UEs from the APs. Figure 3.9 shows the harvested energy-data rate trade-off for N = 1, d _max = 5, 7. 5, 10 m. As can be seen, by decreasing the maximum distance of the UEs from the AP, in the same number of UEs, the system can benefit from less path loss and harvest more energy. This superior performance is mostly seen in the region when harvested energy has a higher preference weight. By decreasing the d _max further to 5 m, the system can also benefit from less interference due to the farther distance of UEs in each cell from the AP of the other cell and therefore, this better performance can also be observed in the data-rate preference region.

Fig. 3.9

Pareto boundary of TS SWIPT for different d _max

4.2.4 Effect of Inter-User Trade-Off

To study the trade-off between users in different small-cells, we choose different preference weights for N _UE = 2 UEs by setting v ₁ ² = θ ₁ θ ₂, v ₁ ² = θ ₂ and v ₂ ¹ = θ ₁, v ₂ ² = 1. As a result, the trade-off between harvested energy and data rate is changing with θ ₁ for both UEs the same as previous plots, but the priority of the first UE is θ ₂ times the second UE.

Figure 3.10a,b show the Pareto boundaries of these two UEs for θ ₂ = 1, 5, 10, 15. As can be seen, both UEs have the same Pareto boundaries for θ ₂ = 1. To benefit from better performance in the first UE, we increase the θ ₂. It can be inferred from Fig. 3.10 that this superior performance is not achievable by only adapting the TS ratio. Consequently beamformers will be aligned toward the first UE by allocating more power to the first AP which results in increasing the $E_{h_{1}}^{\mathrm{TS}}$ without increasing the interference on the first UE. Hence the maximum data rate and harvested energy both decrease in the second UE. Therefore, improving the performance of one user by increasing its preference weight will be at the expense of decreasing the performance of the other user drastically.

Fig. 3.10

Pareto boundary of (a) first and (b) second TS SWIPT UEs with different priorities

4.2.5 Effect of the TS Ratios α _i

In this section, we study the effect of the TS ratios on harvested energy-data rate trade-off. Specifically, we compare the Pareto boundaries of the optimal TS SWIPT with the Pareto boundaries of the TS SWIPT which uses fixed predefined switching rate. We consider a symmetric scenario with N = 1 and for the fixed switching rate case, we assume the same TS rate for both users. Figure 3.11 illustrates the Pareto boundaries for fixed switching rates of α ₁ = 0. 1, …, 0. 9. As can be seen, for lower switching rates, we have higher maximum harvested energy and lower maximum achievable data rates. However, the optimal TS SWIPT leverages the best possible harvested energy and data rate by optimizing $\alpha _{i},\forall i$ jointly with the beamforming strategy.

Fig. 3.11

Pareto boundary of TS SWIPT with fixed and adaptive TS ratios

5 Conclusion

In this chapter, we studied the resource allocation optimization for SWIPT in small-cell networks. We considered a small-cell network with MISO SWIPT system model and we addressed the problem of joint transmit beamforming and receiver time switching design in an MOO manner. The design problem was formulated as a non-convex MOO problem with the goal of maximizing the harvested energy and information data rates for all users simultaneously. The proposed MOO problem was scalarized employing the weighted Chebyshev method. This problem is a non-convex SDP which is relaxed and solved using convex–concave procedure based on the majorization–minimization algorithm. The trade-off between energy harvested and information data rate and the effect of network parameters on this trade-off was investigated by means of numerical results. The numerical results showed that:

• For TS SWIPT receiver, the energy performance loss with respect to ideal case increases when the number of UEs decreases.

• Interference is beneficial in case of low-rate devices operating in a very dense network.

• Cooperation among multiple transmitters can be used to drastically increase the achievable trade-off of one UE but the effect on the trade-off of other UEs could be detrimental.

In this work, we have considered perfect CSI. However, channel estimation is not possible during energy harvesting phase which may lead to out-dated CSI if the harvesting phase is too long. Reliability of CSI estimation also depends on TS ratio. Analysing this dependence and its associated trade-off which implies robust beamforming and SWIPT strategy can be considered as an interesting future work. Also generalization of this work can be applied in distributed massive MIMO scenario which has the potential to increase the harvested energy.