Abstract
Private-key functional encryption enables fine-grained access to symmetrically-encrypted data. Although private-key functional encryption (supporting an unbounded number of keys and ciphertexts) seems significantly weaker than its public-key variant, its known realizations all rely on public-key functional encryption. At the same time, however, up until recently it was not known to imply any public-key primitive, demonstrating our poor understanding of this extremely-useful primitive.
Recently, Bitansky et al. [TCC ’16B] showed that sub-exponentially-secure private-key function encryption bridges from nearly-exponential security in Minicrypt to slightly super-polynomial security in Cryptomania, and from sub-exponential security in Cryptomania to Obfustopia. Specifically, given any sub-exponentially-secure private-key functional encryption scheme and a nearly-exponentially-secure one-way function, they constructed a public-key encryption scheme with slightly super-polynomial security. Assuming, in addition, a sub-exponentially-secure public-key encryption scheme, they then constructed an indistinguishability obfuscator.
We show that quasi-polynomially-secure private-key functional encryption bridges from sub-exponential security in Minicrypt all the way to Cryptomania. First, given any quasi-polynomially-secure private-key functional encryption scheme, we construct an indistinguishability obfuscator for circuits with inputs of poly-logarithmic length. Then, we observe that such an obfuscator can be used to instantiate many natural applications of indistinguishability obfuscation. Specifically, relying on sub-exponentially-secure one-way functions, we show that quasi-polynomially-secure private-key functional encryption implies not just public-key encryption but leads all the way to public-key functional encryption for circuits with inputs of poly-logarithmic length. Moreover, relying on sub-exponentially-secure injective one-way functions, we show that quasi-polynomially-secure private-key functional encryption implies a hard-on-average distribution over instances of a PPAD-complete problem.
Underlying our constructions is a new transformation from single-input functional encryption to multi-input functional encryption in the private-key setting. The previously known such transformation [Brakerski et al., EUROCRYPT ’16] required a sub-exponentially-secure single-input scheme, and obtained a scheme supporting only a slightly super-constant number of inputs. Our transformation both relaxes the underlying assumption and supports more inputs: Given any quasi-polynomially-secure single-input scheme, we obtain a scheme supporting a poly-logarithmic number of inputs.
I. Komargodski—Supported by a Levzion fellowship and by a grant from the Israel Science Foundation.
G. Segev—Supported by the European Union’s 7th Framework Program (FP7) via a Marie Curie Career Integration Grant, by the European Union’s Horizon 2020 Framework Program (H2020) via an ERC Grant (Grant No. 714253), by the Israel Science Foundation (Grant No. 483/13), by the Israeli Centers of Research Excellence (I-CORE) Program (Center No. 4/11), by the US-Israel Binational Science Foundation (Grant No. 2014632), and by a Google Faculty Research Award.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Functional encryption [16, 49, 51] allows tremendous flexibility when accessing encrypted data: Such encryption schemes support restricted decryption keys that allow users to learn specific functions of the encrypted data without leaking any additional information. We focus on the most general setting where the functional encryption schemes support an unbounded number of functional keys in the public-key setting, and an unbounded number of functional keys and ciphertexts in the private-key setting. In the public-key setting, it has been shown that functional encryption is essentially equivalent to indistinguishability obfuscation [6, 7, 12, 33, 54], and thus it currently seems somewhat challenging to base its security on standard cryptographic assumptions (especially given the various attacks on obfuscation schemes and their underlying building blocks [21, 25,26,27,28,29, 40, 47, 48] – see [5, Appendix A] for a summary of these attacks).
Luckily, when examining the various applications of functional encryption (see, for example, the survey by Boneh et al. [17]), it turns out that private-key functional encryption suffices in many interesting scenarios.Footnote 1 However, although private-key functional encryption may seem significantly weaker than its public-key variant, constructions of private-key functional encryption schemes are currently known based only on public-key functional encryption.Footnote 2
Minicrypt, Cryptomania, or Obfustopia? For obtaining a better understanding of private-key functional encryption, we must be able to position it correctly within the hierarchy of cryptographic primitives. Up until recently, private-key functional encryption was not known to imply any cryptographic primitives other than those that are essentially equivalent to one-way functions (i.e., Minicrypt primitives [42]). Moreover, Asharov and Segev [8] proved that as long as a private-key functional encryption scheme is invoked in a black-box manner, it cannot be used as a building block to construct any public-key primitive (i.e., Cryptomania primitives [42]).Footnote 3 This initial evidence hinted that private-key functional encryption may belong to Minicrypt, and thus may be constructed based on extremely well-studied cryptographic assumptions.
Recently, Bitansky et al. [10] showed that private-key functional encryption is more powerful than suggested by the above initial evidence. They proved that any sub-exponentially-secure private-key functional encryption scheme and any (nearly) exponentially-secure one-way function can be used to construct a public-key encryption scheme.Footnote 4 Although their underlying building blocks are at least sub-exponentially secure, the resulting public-key scheme is only slightly super-polynomially secure. In addition, Bitansky et al. proved that any sub-exponentially-secure private-key functional encryption scheme and any sub-exponentially-secure public-key encryption scheme can be used to construct a full-fledged indistinguishability obfuscator. Overall, their work shows that sub-exponentially-secure private-key functional encryption bridges from nearly-exponential security in Minicrypt to slightly super-polynomial security in Cryptomania, and from sub-exponential security in Cryptomania to Obfustopia (see Fig. 1).
1.1 Our Contributions
We show that quasi-polynomially-secure private-key functional encryption bridges from sub-exponential security in Minicrypt all the way to Cryptomania. First, given any quasi-polynomially-secure private-key functional encryption scheme, we construct a (quasi-polynomially-secure) indistinguishability obfuscator for circuits with inputs of poly-logarithmic length and sub-polynomial size. We prove the following theorem:
Theorem 1.1
(Informal). Assuming a quasi-polynomially-secure private-key functional encryption scheme for polynomial-size circuits, there exists an indistinguishability obfuscator for the class of circuits of size \({2^{(\log \lambda )^\epsilon }}\) with inputs of length \({(\log \lambda )^{1+\delta }}\) bits, for some positive constants \(\epsilon \) and \(\delta \).
Underlying our obfuscator is a new transformation from single-input functional encryption to multi-input functional encryption in the private-key setting. The previously known such transformation of Brakerski et al. [22] required a sub-exponentially-secure single-input scheme, and obtained a multi-input scheme supporting only a slightly super-constant number of inputs. Our transformation both relaxes the underlying assumption and supports more inputs: Given any quasi-polynomially-secure single-input scheme, we obtain a multi-input scheme supporting a poly-logarithmic number of inputs.
We demonstrate the wide applicability of our obfuscator by observing that it can be used to instantiate many natural applications of (full-fledged) indistinguishability obfuscation for polynomial-size circuits. We exemplify this observation by constructing a public-key functional encryption scheme (based on [54]), and a hard-on-average distribution of instances of a PPAD-complete problem (based on [11]).
Theorem 1.2
(Informal). Assuming a quasi-polynomially-secure private-key functional encryption scheme for polynomial-size circuits, and a sub-exponentially-secure one-way function, there exists a public-key functional encryption scheme for the class of circuits of size \({2^{(\log \lambda )^\epsilon }}\) with inputs of length \({(\log \lambda )^{1+\delta }}\) bits, for some positive constants \(\epsilon \) and \(\delta \).
Theorem 1.3
(Informal). Assuming a quasi-polynomially-secure private-key functional encryption scheme for polynomial-size circuits, and a sub-exponentially-secure injective one-way function, there exists a hard-on-average distribution over instances of a PPAD-complete problem.
Compared to the work of Bitansky at el. [10], Theorem 1.2 shows that private-key functional encryption implies not just public-key encryption but leads all the way to public-key functional encryption. Furthermore, in terms of underlying assumptions, whereas Bitansky et al. assume a sub-exponentially-secure private-key functional encryption scheme and a (nearly) exponentially-secure one-way function, we only assume a quasi-polynomially-secure private-key functional encryption scheme and a sub-exponentially-secure one-way function.
In addition, recall that average-case PPAD hardness was previously shown based on compact public-key functional encryption (or indistinguishability obfuscation) for polynomial-size circuits and one-way permutations [35]. We show average-case PPAD hardness based on quasi-polynomially-secure private-key functional encryption and sub-exponentially-secure injective one-way function. In fact, as shown by Hubáček and Yogev [41], our result (as well as [11, 35]) implies average-case hardness for CLS, a proper subclass of PPAD and PLS [32]. See Fig. 1 for an illustration of our results.
1.2 Overview of Our Constructions
In this section we provide a high-level overview of our constructions. First, we recall the functionality and security requirements of multi-input functional encryption (MIFE) in the private-key setting, and explain the main ideas underlying our new construction of a multi-input scheme. Then, we describe the obfuscator we obtain from our multi-input scheme, and briefly discuss its applications to public-key functional encryption and to average-case PPAD hardness.
Multi-input Functional Encryption. In a private-key t-input functional encryption scheme [37], the master secret key \({\mathsf {msk}}\) of the scheme is used for encrypting any message \(x_i\) to the \({i^{th}}\) coordinate, and for generating functional keys for t-input functions. A functional key \(\mathsf {sk}_f\) corresponding to a function f enables to compute \(f(x_1,\dots ,x_t)\) given \(\mathsf {Enc}(x_1,1),\dots ,\mathsf {Enc}(x_t,t)\). Building upon the previous notions of security for private-key multi-input functional encryption schemes [13, 37], we consider a strengthened notion of security that combines both message privacy and function privacy (as in [2, 23] for single-input schemes and as in [6, 22] for multi-input schemes), to which we refer as full security. Specifically, we consider adversaries that are given access to “left-or-right” key-generation and encryption oracles.Footnote 5 These oracles operate in one out of two modes corresponding to a randomly-chosen bit b. The key-generation oracle receives as input pairs of the form \((f_0, f_1)\) and outputs a functional key for the function \(f_b\). The encryption oracle receives as input triples of the form \((x^0,x^1,i)\), and outputs an encryption of the message \(x^b\) with respect to coordinate i. We require that no efficient adversary can guess the bit b with probability noticeably higher than 1 / 2, as long as for each such \(t+1\) queries \((f_0, f_1)\), \((x^0_1, x^1_1),\dots ,(x^0_t, x^1_t)\) it holds that \(f_0(x^0_1, \dots , x_t^0) = f_1(x^1_1, \dots , x_t^1)\).
The BKS Approach. Given any private-key single-input functional encryption scheme for all polynomial-size circuits, Brakerski et al. [22] constructed a \(t(\lambda )\)-input scheme for all circuits of size \({s(\lambda ) = 2^{(\log \lambda )^\epsilon }}\), where \({t(\lambda ) = \delta \cdot \log \log \lambda }\) for some fixed positive constants \(\epsilon \) and \(\delta \), and \(\lambda \in \mathbb {N}\) is the security parameter.
Their transformation is based on extending the number of inputs the scheme supports one by one. That is, for any \(t \ge 1\), given a t-input scheme they construct a \((t+1)\)-input scheme. Relying on the function privacy of the underlying scheme, Brakerski et al. observed that ciphertexts for one of the coordinates can be treated as a functional key for a function that has the value of the input hardwired. In terms of functionality, this idea enabled them to support \(t+1\) inputs using a scheme that supports t inputs. The transformation is implemented such that every step of it incurs a polynomial blowup in the size of the ciphertexts and functional keys.Footnote 6 Thus, applying this transformation t times, the size of a functional key for a function of size s is roughly \({(s\cdot \lambda )^{O(1)^t}}\). Therefore, Brakerski et al. could only apply their transformation \({t(\lambda ) = \delta \cdot \log \log \lambda }\) times, and this required assuming that their underlying single-input scheme is sub-exponentially secure, and that \({s(\lambda ) = 2^{(\log \lambda )^\epsilon }}\).
Our Construction. We present a new transformation that constructs a 2t-inputs scheme directly from any t-input scheme. Our transformation shares the same polynomial efficiency loss as in [22], so applying the transformation t times makes a functional key be of size \({(s\cdot \lambda )^{O(1)^{t}}}\). But now, since each transformation doubles the number of inputs, applying the transformation t times gets us all the way to a scheme that supports \({2^t = (\log \lambda )^{\delta }}\) inputs, as required. We further observe, by a careful security analysis, that for the resulting scheme to be secure it suffices that the initial scheme is only quasi-polynomially secure (and the resulting scheme can be made quasi-polynomially secure as well).
Doubling the Number of Inputs via Dynamic Key Encapsulation. As opposed to the approach of [22] (and the similar idea of [6]), it is much less clear how to combine the ciphertexts and functional keys of a t-input scheme to satisfy the required functionality (and security) of a 2t-input scheme.
Our high-level idea is as follows. Given a 2t-input function f, we will generate a functional key for a function \(f^*\) that gets t inputs each of which is composed of two inputs: \(f^*(x_1\mathbin {\Vert }x_{1+t}, \dots , x_t\mathbin {\Vert }x_{2t}) = f(x_1,\dots ,x_{2t})\). We will encrypt each input such that it is possible to compute an encryption of each pair \((x_\ell , x_{\ell +t})\), and evaluate the function in two steps. First, we concatenate each such pair to get an encryption of \(x_\ell \mathbin {\Vert }x_{\ell +t}\). Then, given such t ciphertexts, we will apply a functional key that corresponds to \(f^*\). By the correctness of the underlying primitives, the output must be correct. There are three main issues that we have to overcome: (1) We need to be able to generate the encryption of \(x_\ell \mathbin {\Vert }x_{\ell +t}\), (2) we need to make sure all of these ciphertexts are with respect to the same master secret key and that the functional key for \(f^*\) is also generated with respect to the same key, and (3) we need to prove the security of the resulting scheme. We now describe our solution.
The master secret key for our scheme is a master secret key for a t-input scheme \({\mathsf {msk}}\) and a PRF key K. We split the 2t input coordinates into two parts: (1) the first t coordinates \(1,\dots , t\) which we call the “master coordinates” and (2) the last t coordinates \(1+t,\dots ,2t\) which we call the “slave coordinates”. Our main idea is to let each combination of the master coordinates implicitly define a master secret “encapsulation” key \({\mathsf {msk}}_{x_1\dots ,x_t}\) for a t-input scheme. Details follow.
To encrypt a message \(x_\ell \) with respect to a master coordinate \(1\le \ell \le t\), we encrypt \(x_\ell \) with respect to coordinate \(\ell \) under the key \({\mathsf {msk}}\). To encrypt a message \(x_{\ell +t}\) with respect to a slave coordinate \(1\le \ell \le t\), we generate a functional key for a t-input function \(\mathsf {AGG}_{x_{\ell +t}, K}\) under the key \({\mathsf {msk}}\). To generate a functional key for a 2t-input function f, we generate a functional key for a t-input function \(\mathsf {Gen}_{f,K}\) under \({\mathsf {msk}}\). Both \(\mathsf {AGG}_{x_{\ell +t}, K}\) and \(\mathsf {Gen}_{f,K}\) first compute a pseudorandom master secret key \({\mathsf {msk}}_{x_1 \dots x_{t}}\) using randomness generated via the PRF key K on input \(x_1\dots x_t\). Then, \(\mathsf {AGG}_{x_{\ell +t}, K}\) computes an encryption of \((x_{\ell }\mathbin {\Vert }x_{\ell +t})\) to coordinate \(\ell \) under this master secret key, and \(\mathsf {Gen}_{f,K}\) computes a functional key for \(f^*\) (described above) under this master secret key (see Fig. 2).
It is straightforward to verify that the above scheme indeed provides the required functionality of a 2t-input scheme. Indeed, given t ciphertexts corresponding to the master coordinates \(\mathsf {ct}_{x_1},\dots ,\mathsf {ct}_{x_t}\), t ciphertexts corresponding to the slave coordinates \(\mathsf {ct}_{{x_{1+t}}},\dots ,\mathsf {ct}_{{x_{2t}}}\), and a functional key \(\mathsf {sk}_f\) for a 2t-input function f, we first combine \(\mathsf {ct}_{x_1},\dots ,\mathsf {ct}_{x_t}\) with each \(\mathsf {ct}_{{x_{\ell +t}}}\) to get \(\mathsf {ct}_{x_{\ell }\mathbin {\Vert }x_{\ell +t}}\), which is an encryption of \(x_{\ell }\mathbin {\Vert }x_{\ell +t}\) under \({\mathsf {msk}}_{x_1\dots x_t}\). Then, we combine \(\mathsf {ct}_{x_1},\dots ,\mathsf {ct}_{x_t}\) with \(\mathsf {sk}_f\) to get a functional key \(\mathsf {sk}_{f^*}\) for \(f^*\) under the same \({\mathsf {msk}}_{x_1\dots x_t}\). Finally, we combine \(\mathsf {ct}_{x_{1}\mathbin {\Vert }x_{1+t}},\dots ,\mathsf {ct}_{x_{t}\mathbin {\Vert }x_{2t}}\) with \(\mathsf {sk}_{f^*}\) to get \(f^*(x_{1}\mathbin {\Vert }x_{1+t},\dots ,x_{t}\mathbin {\Vert }x_{2t}) = f(x_1,\dots ,x_{2t})\), as required.
The security proof is done by a sequence of hybrid experiments, where we “attack” each possible sequence of master coordinates separately, namely, we handle each \({\mathsf {msk}}_{x_1\dots x_t}\) separately so that it will not be explicitly needed. A typical approach for such a security proof is to embed all possible encryptions and key-generation queries under \({\mathsf {msk}}_{x_1\dots x_t}\) in the ciphertexts that are generated under \({\mathsf {msk}}\). Handling the key-generation queries using \({\mathsf {msk}}_{x_1\dots x_t}\) is rather standard: whenever a key-generation query is requested we compute the corresponding functional key under \({\mathsf {msk}}_{x_1\dots x_t}\) and embed it into the functional key. Handling encryption queries under \({\mathsf {msk}}_{x_1\dots x_t}\) is significantly more challenging since for every \(x_1\dots x_t\) sequence, there are many possible ciphertexts \(x_{\ell +t}\) of slave coordinates that will be paired with it to get the encryption of \(x_{\ell }\mathbin {\Vert }x_{\ell +t}\). It might seem as if there is not enough space to embed all these possible ciphertexts, but we observe that we can embed each ciphertext \(\mathsf {ct}_{x_{\ell }\mathbin {\Vert }x_{\ell +t}}\) in the ciphertext corresponding to \(x_{\ell +t}\) (for each such \(x_{\ell +t}\)). This way, \({\mathsf {msk}}_{x_1\dots x_t}\) is not explicitly needed in the scheme and we can use the security of the underlying t-input scheme. In total, the number of hybrids is roughly \(T^t\), where T is an upper bound on the running time of the adversary. Thus, since t is roughly logarithmic in the security parameter, we have to start with a quasi-polynomially-secure scheme.
From MIFE to Obfuscation. Goldwasser et al. [37] observed that multi-input functional encryption is tightly related to indistinguishability obfuscation [9, 33]. Specifically, a multi-input scheme that supports a polynomial number of inputs (i.e., \({t(\lambda ) = {\mathsf {poly}}(\lambda )}\)) readily implies an indistinguishability obfuscator (and vice-versa). We use a more fine-grained relationship (as observed by [10]) that is useful when \({t(\lambda )}\) is small compared to \({\lambda }\): A multi-input scheme that supports all circuits of size \({s(\lambda )}\) and \({t(\lambda )}\) inputs implies an indistinguishability obfuscator for all circuits of size \({s(\lambda )}\) that have at most \({t(\lambda )\cdot \log \lambda }\) input bits.
This transformation works as follows. An obfuscation of a function f of circuit-size at most \({s(\lambda )}\) that has at most \({t(\lambda )\cdot \log \lambda }\) bits as input, is composed of \({t(\lambda )\cdot \lambda }\) ciphertexts and one functional key. We think of f as a function \(f^*\) that gets \({t(\lambda )}\) inputs each of which is of length \({\log \lambda }\) bits. The obfuscation now consists of a functional key for the circuit \(f^*\), denoted by \(\mathsf {sk}_f = \mathsf {KG}(f^*)\), and a ciphertext \(\mathsf {ct}_{x,i} = \mathsf {Enc}(x,i)\) for every \({(x, i) \in \{ 0,1 \}^{\log \lambda }\times [t(\lambda )]}\). To evaluate C at a point \({x=(x_1\dots x_{t(\lambda )})\in (\{ 0,1 \}^{\log \lambda })^{t(\lambda )}}\) one has to compute and output \({\mathsf {Dec}(\mathsf {sk}_f, \mathsf {ct}_{x_1,1},\dots ,\mathsf {ct}_{x_{t(\lambda )},t(\lambda )})= f(x)}\). Correctness and security of the obfuscator follow directly from the correctness and security of the multi-input scheme.
Given the relationship described above and given our multi-input scheme that supports circuits of size at most \({s(\lambda ) = 2^{(\log \lambda )^\epsilon }}\) that have \({t(\lambda ) = (\log \lambda )^{\delta }}\) inputs for some fixed positive constants \(\epsilon \) and \(\delta \), we obtain Theorem 1.1.
Applications of our Obfuscator. One of the main conceptual contributions of this work is the observation that an indistinguishability obfuscator as described above (that supports circuits with a poly-logarithmic number of input bits) is in fact sufficient for many of the applications of indistinguishability obfuscation for all polynomial-size circuits. We exemplify this observation by showing how to adapt the construction of Waters [54] of a public-key functional encryption scheme and the construction of Bitansky et al. [11] of a hard-on-average distribution for PPAD, to our obfuscator. Such an adaptation is quite delicate and involves a careful choice of the additional primitives that are involved in the construction. In a very high level, since the obfuscator supports only a poly-logarithmic number of inputs, a primitive that has to be secure when applied on (part of) the input (say a one-way function), must be sub-exponentially secure. We believe that this observation may find additional applications beyond the scope of our work.
Using the Multi-input Scheme of [22]. Using the multi-input scheme of [22], one can get that sub-exponentially-secure private-key functional encryption implies indistinguishability obfuscation for inputs of length slightly super-logarithmic. However, using such an obfuscator as a building block seems to inherently require to additionally assume nearly-exponentially-secure primitives and the resulting primitives are (at most) slightly super-polynomially-secure.
Our approach, on the other hand, requires quasi-polynomially-secure private-key functional encryption. In addition, our additional primitives are only sub-exponentially-secure and the resulting primitives are quasi-polynomially secure.
1.3 Additional Related Work
Constructions of FE Schemes. Private-key single-input functional encryption schemes that are sufficient for our applications are known to exist based on a variety of assumptions, including indistinguishability obfuscation [33, 54], differing-input obfuscation [3, 19], and multilinear maps [34]. Restricted functional encryption schemes that support either a bounded number of functional keys or a bounded number of ciphertexts can be based on the Learning with Errors (LWE) assumption (where the length of ciphertexts grows with the number of functional-key queries and with a bound on the depth of allowed functions) [38], and even based on pseudorandom generators computable by small-depth circuits (where the length of ciphertexts grows with the number of functional-key queries and with an upper bound on the circuit size of the functions) [39].
In the work of Bitansky et al. [10, Proposition 1.2 & Footnote 1] it has been shown that, assuming weak PRFs in \(\mathsf {NC}^1\), any public-key encryption scheme can be used to transform a private-key functional encryption scheme into a public-key functional encryption scheme (which can be used to get PPAD-hardness [35]). This gives a better reduction than ours in terms of security loss, but requires a public-key primitive to begin with.
Constructions of MIFE Schemes. There are several constructions of private-key multi-input functional encryption schemes. Mostly related to our work is the construction of Brakerski et al. [22] which we significantly improve (see Sect. 1.2 for more details). Other constructions [6, 13, 37] are incomparable as they either rely on stronger assumptions or could be proven secure only in an idealized generic model. Goldwasser et al. [37] constructed a multi-input scheme that supports a polynomial number of inputs assuming indistinguishability obfuscation for all polynomial-size circuits. Ananth and Jain [6] constructed a multi-input functional encryption scheme that supports a polynomial number of inputs assuming any sub-exponentially-secure (single-input) public-key functional encryption scheme. Boneh et al. [13] constructed a multi-input scheme that supports a polynomial number of inputs based on multilinear maps, and was proven secure in the idealized generic multilinear map model.
Proof Techniques. Parts of our proof rely on two useful techniques from the functional encryption literature: key encapsulation (also known as “hybrid encryption”) and function privacy.
Key encapsulation is an extremely useful approach in the design of encryption schemes, both for improved efficiency and for improved security. Specifically, key encapsulation typically means that instead of encrypting a message m under a fixed key \(\mathsf {sk}\), one can instead sample a random key \(\mathsf{k}\), encrypt m under \(\mathsf{k}\) and then encrypt \(\mathsf{k}\) under \(\mathsf {sk}\). The usefulness of this technique in the context of functional encryption was demonstrated by [4, 22]. Our constructions incorporate key encapsulation techniques, and exhibit additional strengths of this technique in the context of functional encryption schemes. Specifically, as discussed in Sect. 1.2, we use key encapsulation techniques for our dynamic key-generation technique, a crucial ingredient in our constructions and proofs of security.
The security guarantees of functional encryption typically focus on message privacy that ensures that a ciphertext does not reveal any unnecessary information on the plaintext. In various cases, however, it is also useful to consider function privacy [2, 14, 15, 23, 53], asking that a functional key \(\mathsf {sk}_f\) does not reveal any unnecessary information on the function f. Brakerski and Segev [23] (and the follow-up of Ananth and Jain [6]) showed that any private-key (multi-input) functional encryption scheme can be generically transformed into one that satisfies both message privacy and function privacy. Function privacy was found useful as a building block in the construction of several functional encryption schemes [4, 22, 46]. In particular, functional encryption allows to successfully apply proof techniques “borrowed” from the indistinguishability obfuscation literature (including, for example, a variant of the punctured programming approach of Sahai and Waters [52]).
1.4 Paper Organization
The remainder of this paper is organized as follows. In Sect. 2 we provide an overview of the notation, definitions, and tools underlying our constructions. In Sect. 3 we present our construction of a private-key multi-input functional encryption scheme based on any single-input scheme. In Sect. 4 we present our construction of an indistinguishability obfuscator for circuits with inputs of poly-logarithmic length, and its applications to public-key functional encryption and average-case PPAD hardness.
2 Preliminaries
In this section we present the notation and basic definitions that are used in this work. For a distribution X we denote by \(x \leftarrow X\) the process of sampling a value x from the distribution X. Similarly, for a set \(\mathcal {X}\) we denote by \(x \leftarrow \mathcal {X}\) the process of sampling a value x from the uniform distribution over \(\mathcal {X}\). For a randomized function f and an input \(x\in \mathcal X\), we denote by \(y\leftarrow f(x)\) the process of sampling a value y from the distribution f(x). For an integer \(n \in \mathbb {N}\) we denote by [n] the set \(\{1,\ldots , n\}\).
Throughout the paper, we denote by \({\lambda }\) the security parameter. A function \({\mathsf {neg}}:\mathbb N\rightarrow \mathbb R^+\) is negligible if for every constant \(c > 0\) there exists an integer \(N_c\) such that \({{\mathsf {neg}}(\lambda ) < \lambda ^{-c}}\) for all \({\lambda > N_c}\). Two sequences of random variables \({X = \{ X_\lambda \}_{\lambda \in \mathbb N}}\) and \({Y = \{Y_\lambda \}_{\lambda \in \mathbb N}}\) are computationally indistinguishable if for any probabilistic polynomial-time algorithm \({\mathcal {A}}\) there exists a negligible function \({\mathsf {neg}}(\cdot )\) such that \({\left| \Pr [{\mathcal {A}}(1^{\lambda }, X_\lambda ) = 1] - \Pr [{\mathcal {A}}(1^{\lambda },Y_\lambda ) = 1] \right| \le {\mathsf {neg}}(\lambda )}\) for all sufficiently large \(\lambda \in \mathbb N\).
2.1 One-Way Functions and Pseudorandom Generators
We rely on the standard (parameterized) notions of one-way functions and pseudorandom generators.
Definition 2.1
(One-way function). An efficiently computable function \(f:\{ 0,1 \}^{*}\rightarrow \{ 0,1 \}^{*}\) is (t, \(\mu )\) -one-way if for every probabilistic algorithm \({\mathcal {A}}\) that runs in time \(t=t(\lambda )\) it holds that
for all sufficiently large \(\lambda \in \mathbb N\), where the probability is taken over the choice of \(x\in \{ 0,1 \}^\lambda \) and over the internal randomness of \({\mathcal {A}}\).
Whenever \(t = t(\lambda )\) is a super-polynomial function and \(\mu = \mu (\lambda )\) is a negligible function, we will often omit t and \(\mu \) and simply call the function one-way. In case \(t(\lambda ) = 1/ \mu (\lambda ) = 2^{\lambda ^\epsilon }\), for some constant \(0< \epsilon < 1\), we will say that f is sub-exponentially one-way.
Definition 2.2
(Pseudorandom generator). Let \(\ell (\cdot )\) be a function. An efficiently computable function \(\mathsf {PRG}:\{ 0,1 \}^{\ell (\lambda )}\rightarrow \{ 0,1 \}^{2\ell (\lambda )}\) is a \((t,\mu )\) -secure pseudorandom generator if for every probabilistic algorithm \({\mathcal {A}}\) that runs in time \(t=t(\lambda )\) it holds that
for all sufficiently large \(\lambda \in \mathbb N\).
Whenever \(t = t(\lambda )\) is a super-polynomial function and \(\mu = \mu (\lambda )\) is a negligible function, we will often omit t and \(\mu \) and simply call the function a pseudorandom generator. In case \(t(\lambda ) = 1/ \mu (\lambda ) = 2^{\lambda ^\epsilon }\), for some constant \(0< \epsilon < 1\), we will say that \(\mathsf {PRG}\) is sub-exponentially secure.
2.2 Pseudorandom Functions
Let \(\{\mathcal K_\lambda , \mathcal X_\lambda , \mathcal Y_\lambda \}_{\lambda \in \mathbb N}\) be a sequence of sets and let \(\mathsf {PRF}= (\mathsf {PRF.Gen}, \mathsf {PRF.Eval})\) be a function family with the following syntax:
-
\(\mathsf {PRF.Gen}\) is a probabilistic polynomial-time algorithm that takes as input the unary representation of the security parameter \(\lambda \), and outputs a key \(K\in \mathcal K_\lambda \).
-
\(\mathsf {PRF.Eval}\) is a deterministic polynomial-time algorithm that takes as input a key \(K\in \mathcal K_\lambda \) and a value \(x\in \mathcal X_\lambda \), and outputs a value \(y\in \mathcal Y_\lambda \).
The sets \(\mathcal K_\lambda \), \(\mathcal X_\lambda \), and \(\mathcal Y_\lambda \) are referred to as the key space, domain, and range of the function family, respectively. For easy of notation we may denote by \(\mathsf {PRF.Eval}_K(\cdot )\) or \(\mathsf {PRF}_K(\cdot )\) the function \(\mathsf {PRF.Eval}(K,\cdot )\) for \(K\in \mathcal K_\lambda \). The following is the standard definition of a pseudorandom function family.
Definition 2.3
(Pseudorandomness). A function family \(\mathsf {PRF}= (\mathsf {PRF.Gen}, \mathsf {PRF.Eval})\) is \((t,\mu )\) -secure pseudorandom if for every probabilistic algorithm \({\mathcal {A}}\) that runs in time \(t(\lambda )\), it holds that

for all sufficiently large \(\lambda \in \mathbb N\), where \(F_\lambda \) is the set of all functions that map \(\mathcal X_\lambda \) into \(\mathcal Y_\lambda \).
In addition to the standard notion of a pseudorandom function family, we rely on the seemingly stronger (yet existentially equivalent) notion of a puncturable pseudorandom function family [18, 20, 43, 52]. In terms of syntax, this notion asks for an additional probabilistic polynomial-time algorithm, \(\mathsf {PRF.Punc}\), that takes as input a key \(K \in \mathcal K_\lambda \) and a set \(S \subseteq \mathcal X_\lambda \) and outputs a “punctured” key \(K_S\). The properties required by such a puncturing algorithm are captured by the following definition.
Definition 2.4
(Puncturable PRF). A \((t,\mu )\)-secure pseudorandom function family \(\mathsf {PRF}= (\mathsf {PRF.Gen}, \mathsf {PRF.Eval})\) is puncturable if there exists a probabilistic polynomial-time algorithm \(\mathsf {PRF.Punc}\) such that the following properties are satisfied:
-
1.
Functionality: For all sufficiently large \(\lambda \in \mathbb {N}\), for every set \(S \subseteq \mathcal X_\lambda \), and for every \(x \in \mathcal X_\lambda \setminus S\) it holds that

-
2.
Pseudorandomness at punctured points: Let \({\mathcal {A}}=({\mathcal {A}}_1,{\mathcal {A}}_2)\) be any probabilistic algorithm that runs in time at most \(t(\lambda )\) such that \({\mathcal {A}}_1(1^\lambda )\) outputs a set \(S \subseteq \mathcal X_\lambda \), a value \(x \in S\), and state information \(\mathsf {state}\). Then, for any such \({\mathcal {A}}\) it holds that
$$\begin{aligned}&\mathsf {Adv}_{\mathsf {PRF}, {\mathcal {A}}}(\lambda ) \mathop {=}\limits ^\mathsf{def} \\&\quad \left| \Pr \left[ {\mathcal {A}}_2(K_S,\mathsf {PRF.Eval}_K(x), \mathsf {state}) = 1\right] -\Pr \left[ {\mathcal {A}}_2(K_S, y, \mathsf {state})=1\right] \right| \le \mu (\lambda ) \end{aligned}$$for all sufficiently large \(\lambda \in \mathbb N\), where \((S, x, \mathsf {state}) \leftarrow {\mathcal {A}}_1(1^{\lambda })\), \(K\leftarrow \mathsf {PRF.Gen}(1^\lambda )\), \(K_S = \mathsf {PRF.Punc}(K,S)\), and \(y \leftarrow \mathcal Y_\lambda \).
For our constructions we rely on pseudorandom functions that need to be punctured only at one point (i.e., in both parts of Definition 2.4 it holds that \(S = \{x\}\) for some \(x \in \mathcal X_\lambda \)). As observed by [18, 20, 43, 52] the GGM construction [36] of PRFs from any one-way function can be easily altered to yield such a puncturable pseudorandom function family.
2.3 Private-Key Multi-Input Functional Encryption
In this section we define the functionality and security of private-key t-input functional encryption. For \(i\in [t]\) let \(\mathcal X_i = \{(\mathcal X_i)_{\lambda }\}_{\lambda \in \mathbb N}\) be an ensemble of finite sets, and let \(\mathcal F= \{\mathcal F_{\lambda }\}_{\lambda \in \mathbb N}\) be an ensemble of finite t-ary function families. For each \(\lambda \in \mathbb {N}\), each function \(f\in \mathcal F_{\lambda }\) takes as input t strings, \(x_1\in (\mathcal X_1)_\lambda ,\dots ,x_t\in (\mathcal X_t)_\lambda \), and outputs a value \(f(x_1,\dots ,x_t) \in \mathcal Z_{\lambda }\).
A private-key t-input functional encryption scheme \(\varPi \) for \(\mathcal F\) consists of four probabilistic polynomial time algorithm \(\mathsf {Setup}\), \(\mathsf {Enc}\), \(\mathsf {KG}\) and \(\mathsf {Dec}\), described as follows. The setup algorithm \(\mathsf {Setup}(1^\lambda )\) takes as input the security parameter \(\lambda \), and outputs a master secret key \({\mathsf {msk}}\). The encryption algorithm \(\mathsf {Enc}({\mathsf {msk}}, m, \mathsf {\ell })\) takes as input a master secret key \({\mathsf {msk}}\), a message m, and an index \(\mathsf {\ell }\in [t]\), where \(m\in (\mathcal X_\mathsf {\ell })_\lambda \), and outputs a ciphertext \(\mathsf {ct}_\mathsf {\ell }\). The key-generation algorithm \(\mathsf {KG}({\mathsf {msk}}, f)\) takes as input a master secret key \({\mathsf {msk}}\) and a function \(f\in \mathcal F_\lambda \), and outputs a functional key \(\mathsf {sk}_f\). The (deterministic) decryption algorithm \(\mathsf {Dec}\) takes as input a functional key \(\mathsf {sk}_f\) and t ciphertexts, \(\mathsf {ct}_1,\dots ,\mathsf {ct}_t\), and outputs a string \(z\in \mathcal Z_\lambda \cup \{ \bot \}\).
Definition 2.5
(Correctness). A private-key t-input functional encryption scheme \(\varPi = (\mathsf {Setup}, \mathsf {Enc}, \mathsf {KG}, \mathsf {Dec})\) for \(\mathcal F\) is correct if there exists a negligible function \({\mathsf {neg}}(\cdot )\) such that for every \(\lambda \in \mathbb {N}\), for every \(f\in \mathcal F_\lambda \), and for every \((x_1,\dots ,x_t) \in (\mathcal X_1)_\lambda \times \dots \times (\mathcal X_t)_\lambda \), it holds that
where \({\mathsf {msk}}\leftarrow \mathsf {Setup}(1^{\lambda })\), \(\mathsf {sk}_f \leftarrow \mathsf {KG}({\mathsf {msk}}, f)\), and the probability is taken over the internal randomness of \(\mathsf {Setup}, \mathsf {Enc}\) and \(\mathsf {KG}\).
In terms of security, we rely on the private-key variant of the standard indistinguishability-based notion that considers both message privacy and function privacy [2, 22, 23]. Intuitively, we say that a t-input scheme is secure if for any two t-tuples of messages \((x^0_{1},\ldots ,x^0_{t})\) and \((x^1_{1},\dots , x^1_{t})\) that are encrypted with respect to indices \(\mathsf {\ell }=1\) through \(\mathsf {\ell }=t\), and for every pair of functions \((f_0, f_1)\), the triplets \((\mathsf {sk}_{f_0}, \mathsf {Enc}({\mathsf {msk}}, x^0_1, 1),\ldots ,\mathsf {Enc}({\mathsf {msk}}, x_t^0, t))\) and \((\mathsf {sk}_{f_1}, \mathsf {Enc}({\mathsf {msk}}, x^1_1, 1), \ldots ,\mathsf {Enc}({\mathsf {msk}}, x_t^1, t))\) are computationally indistinguishable as long as \(f_0(x^0_{1},\ldots ,x^0_t) = f_1(x^1_{1},\ldots ,x^1_t)\) (note that this captures both message privacy and function privacy). The formal notions of security build upon this intuition and capture the fact that an adversary may in fact hold many functional keys and ciphertexts, and may combine them in an arbitrary manner. We formalize our notions of security using left-or-right key-generation and encryption oracles. Specifically, for each \(b\in \{ 0,1 \}\) and \(\mathsf {\ell }\in \{1,\ldots ,t\}\) we let the left-or-right key-generation and encryption oracles be \(\mathsf {KG}_b({\mathsf {msk}}, f_0, f_1)\mathop {=}\limits ^\mathsf{def} \mathsf {KG}({\mathsf {msk}}, f_b)\) and \(\mathsf {Enc}_b({\mathsf {msk}},(m_0,m_1),\mathsf {\ell }) \mathop {=}\limits ^\mathsf{def} \mathsf {Enc}({\mathsf {msk}},m_b,\mathsf {\ell })\). Before formalizing our notions of security we define the notion of a valid t-input adversary. Then, we define selective security.
Definition 2.6
(Valid adversary). A probabilistic polynomial-time algorithm \({\mathcal {A}}\) is called valid if for all private-key t-input functional encryption schemes \(\varPi = (\mathsf {Setup},\mathsf {KG},\mathsf {Enc},\mathsf {Dec})\) over a message space \(\mathcal X_1\times \cdots \times \mathcal X_t= \{(\mathcal X_1)_\lambda \}_{\lambda \in \mathbb N}\times \dots \times \{(\mathcal X_t)_\lambda \}_{\lambda \in \mathbb N}\) and a function space \(\mathcal F= \{\mathcal F_\lambda \}_{\lambda \in \mathbb N}\), for all \(\lambda \in \mathbb N\) and \(b\in \{ 0,1 \}\), and for all \((f_0,f_1)\in \mathcal F_\lambda \) and \(((x^0_{i}, x^1_{i}),i)\in \mathcal X_i\times \mathcal X_i\times [t]\) with which \({\mathcal {A}}\) queries the left-or-right key-generation and encryption oracles, respectively, it holds that \(f_0(x^0_1,\dots ,x^0_t) = f_1(x^1_1,\dots ,x^1_t)\).
Definition 2.7
(Selective security). Let \(t = t(\lambda )\), \(T= T(\lambda )\), \(Q_\mathsf {key}= Q_\mathsf {key}(\lambda )\), \(Q_\mathsf {enc}= Q_\mathsf {enc}(\lambda )\) and \(\mu = \mu (\lambda )\) be functions of the security parameter \(\lambda \in \mathbb {N}\). A private-key t-input functional encryption scheme \(\varPi = (\mathsf {Setup}, \mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})\) over a message space \(\mathcal X_1\times \cdots \times \mathcal X_t= \{(\mathcal X_1)_\lambda \}_{\lambda \in \mathbb N}\times \dots \times \{(\mathcal X_t)_\lambda \}_{\lambda \in \mathbb N}\) and a function space \(\mathcal F= \{\mathcal F_\lambda \}_{\lambda \in \mathbb N}\) is \((T, Q_\mathsf {key}, Q_\mathsf {enc}, \mu )\) -selectively-secure if for any valid adversary \({\mathcal {A}}\) that on input \(1^{\lambda }\) runs in time \(T(\lambda )\) and issues at most \(Q_\mathsf {key}(\lambda )\) key-generation queries and at most \(Q_\mathsf {enc}(\lambda )\) encryption queries for each index \(i \in [t]\), it holds that
for all sufficiently large \(\lambda \in \mathbb {N}\), where the random variable \(\mathsf {Exp}^{\mathsf {selFE_t}}_{\varPi , \mathcal F, {\mathcal {A}}}(\lambda )\) is defined via the following experiment:
-
1.
\(\left( \vec {x_1},\dots ,\vec {x_t},\mathsf {state}\right) \leftarrow {\mathcal {A}}_1^{}\left( 1^{\lambda }\right) \), where \(\vec {x_i} = ((x^0_{i, 1},x^1_{i, 1}), \dots , (x^0_{i, T},x^1_{i, T}))\) for \(i\in [t]\).
-
2.
\({\mathsf {msk}}\leftarrow \mathsf {Setup}(1^{\lambda })\), \(b\leftarrow \{ 0,1 \}\).
-
3.
\(\mathsf {ct}_{i, j} \leftarrow \mathsf {Enc}({\mathsf {msk}}, x^{b}_{i, j}, 1)\) for \(i\in [t]\) and \(j\in [T]\).
-
4.
\(b' \leftarrow {\mathcal {A}}_2^{\mathsf {KG}_b({\mathsf {msk}},\cdot ,\cdot )}\left( 1^{\lambda }, \{\mathsf {ct}_{i,j}\}_{i\in [t], j\in [T]},\mathsf {state}\right) \).
-
5.
If \(b' = b\) then output 1, and otherwise output 0.
Known Constructions for \(\varvec{t=1}\) . Private-key single-input functional encryption schemes that satisfy the above notion of full security and support circuits of any a-priori bounded polynomial size are known to exist based on a variety of assumptions.
Ananth et al. [4] gave a generic transformation from selective security to full security. Moreover, Brakerski and Segev [23] showed how to transform any message-private functional encryption scheme into a functional encryption scheme which is fully secure, and the resulting scheme inherits the security guarantees of the original one. Therefore, based on [4, 23], given any selectively-secure message-private functional encryption scheme we can generically obtain a fully secure scheme. This implies that schemes that are fully secure for any number of encryption and key-generation queries can be based on indistinguishability obfuscation [33, 54], differing-input obfuscation [3, 19], and multilinear maps [34]. In addition, schemes that are fully secure for a bounded number of key-generation queries \(Q_\mathsf {key}\) can be based on the Learning with Errors (LWE) assumption (where the length of ciphertexts grows with \(Q_\mathsf {key}\) and with a bound on the depth of allowed functions) [38], and even based on pseudorandom generators computable by small-depth circuits (where the length of ciphertexts grows with \(Q_\mathsf {key}\) and with an upper bound on the circuit size of the functions) [39].
Known Constructions for \(\varvec{t > 1}\) . Private-key multi-input functional encryption schemes are much less understood than single-input ones. Goldwasser et al. [37] gave the first construction of a selectively-secure multi-input functional encryption scheme for a polynomial number of inputs relying on indistinguishability obfuscation and one-way functions [9, 33, 44]. Following the work of Goldwasser et al., a fully-secure private-key multi-input functional encryption scheme for a polynomial number of inputs based was constructed based on multilinear maps [13]. Later, Ananth, Jain, and Sahai, and Bitasnky and Vaikuntanathan [6, 7, 12] showed a selectively-secure multi-input functional encryption scheme for a polynomial number of inputs based on any sub-exponentially secure single-input public-key functional encryption scheme. Brakerski et al. [22] showed that a fully-secure single-input private-key scheme implies a fully-secure multi-input scheme for any constant number of inputs. Furthermore, Brakerski et al. observed that their construction can be used to get a fully-secure t-input scheme for \(t = O(\log \log \lambda )\) inputs, where \(\lambda \) is the security parameter, if the underlying single-input scheme is sub-exponentially secure.
2.4 Public-Key Functional Encryption
In this section we define the functionality and security of public-key (single-input) functional encryption. Let \(\mathcal X= \{\mathcal X_{\lambda }\}_{\lambda \in \mathbb N}\) be an ensemble of finite sets, and let \(\mathcal F= \{\mathcal F_{\lambda }\}_{\lambda \in \mathbb N}\) be an ensemble of finite function families. For each \(\lambda \in \mathbb {N}\), each function \(f\in \mathcal F_{\lambda }\) takes as input a string, \(x\in \mathcal X_\lambda \), and outputs a value \(f(x) \in \mathcal Z_{\lambda }\).
A public-key functional encryption scheme \(\varPi \) for \(\mathcal F\) consists of four probabilistic polynomial time algorithm \(\mathsf {Setup}\), \(\mathsf {Enc}\), \(\mathsf {KG}\) and \(\mathsf {Dec}\), described as follows. The setup algorithm \(\mathsf {Setup}(1^\lambda )\) takes as input the security parameter \(\lambda \), and outputs a master secret key \({\mathsf {msk}}\) and a master public key  . The encryption algorithm
. The encryption algorithm  takes as input a master public key
takes as input a master public key  and a message \(m\in \mathcal X_\lambda \), and outputs a ciphertext \(\mathsf {ct}\). The key-generation algorithm \(\mathsf {KG}({\mathsf {msk}}, f)\) takes as input a master secret key \({\mathsf {msk}}\) and a function \(f\in \mathcal F_\lambda \), and outputs a functional key \(\mathsf {sk}_f\). The (deterministic) decryption algorithm \(\mathsf {Dec}\) takes as input a functional key \(\mathsf {sk}_f\) and t ciphertexts, \(\mathsf {ct}_1,\dots ,\mathsf {ct}_t\), and outputs a string \(z\in \mathcal Z_\lambda \cup \{ \bot \}\).
and a message \(m\in \mathcal X_\lambda \), and outputs a ciphertext \(\mathsf {ct}\). The key-generation algorithm \(\mathsf {KG}({\mathsf {msk}}, f)\) takes as input a master secret key \({\mathsf {msk}}\) and a function \(f\in \mathcal F_\lambda \), and outputs a functional key \(\mathsf {sk}_f\). The (deterministic) decryption algorithm \(\mathsf {Dec}\) takes as input a functional key \(\mathsf {sk}_f\) and t ciphertexts, \(\mathsf {ct}_1,\dots ,\mathsf {ct}_t\), and outputs a string \(z\in \mathcal Z_\lambda \cup \{ \bot \}\).
Definition 2.8
(Correctness). A public-key functional encryption scheme \(\varPi = (\mathsf {Setup}, \mathsf {Enc}, \mathsf {KG}, \mathsf {Dec})\) for \(\mathcal F\) is correct if there exists a negligible function \({\mathsf {neg}}(\cdot )\) such that for every \(\lambda \in \mathbb {N}\), for every \(f\in \mathcal F_\lambda \), and for every \(x \in \mathcal X_\lambda \), it holds that

where  , \(\mathsf {sk}_f \leftarrow \mathsf {KG}({\mathsf {msk}}, f)\), and the probability is taken over the internal randomness of \(\mathsf {Setup}, \mathsf {Enc}\) and \(\mathsf {KG}\).
, \(\mathsf {sk}_f \leftarrow \mathsf {KG}({\mathsf {msk}}, f)\), and the probability is taken over the internal randomness of \(\mathsf {Setup}, \mathsf {Enc}\) and \(\mathsf {KG}\).
In terms of security, we rely on the public-key variant of the existing indistinguishability-based notions for message privacy.Footnote 7 Intuitively, we say that a scheme is secure if the encryption of any pair of messages  and
and  cannot be distinguished as long as for any function f for which a functional key is queries, it holds that \(f(m_0) = f(m_1)\). The formal notions of security build upon this intuition and capture the fact that an adversary may in fact hold many functional keys and ciphertexts, and may combine them in an arbitrary manner. We formalize our notions of security using left-or-right key-generation (similarly to the private-key setting). Specifically, for each \(b\in \{ 0,1 \}\) we let the left-or-right key-generation and encryption oracles be \(\mathsf {KG}_b({\mathsf {msk}}, f_0, f_1)\mathop {=}\limits ^\mathsf{def} \mathsf {KG}({\mathsf {msk}}, f_b)\) and \(\mathsf {Enc}_b({\mathsf {msk}},(m_0,m_1)) \mathop {=}\limits ^\mathsf{def} \mathsf {Enc}({\mathsf {msk}},m_b)\), respectively. Before formalizing our notions of security we define the notion of a valid adversary. Then, we define selective security.Footnote 8.
cannot be distinguished as long as for any function f for which a functional key is queries, it holds that \(f(m_0) = f(m_1)\). The formal notions of security build upon this intuition and capture the fact that an adversary may in fact hold many functional keys and ciphertexts, and may combine them in an arbitrary manner. We formalize our notions of security using left-or-right key-generation (similarly to the private-key setting). Specifically, for each \(b\in \{ 0,1 \}\) we let the left-or-right key-generation and encryption oracles be \(\mathsf {KG}_b({\mathsf {msk}}, f_0, f_1)\mathop {=}\limits ^\mathsf{def} \mathsf {KG}({\mathsf {msk}}, f_b)\) and \(\mathsf {Enc}_b({\mathsf {msk}},(m_0,m_1)) \mathop {=}\limits ^\mathsf{def} \mathsf {Enc}({\mathsf {msk}},m_b)\), respectively. Before formalizing our notions of security we define the notion of a valid adversary. Then, we define selective security.Footnote 8.
Definition 2.9
(Valid adversary). A probabilistic polynomial-time algorithm \({\mathcal {A}}\) is called valid if for all public-key functional encryption schemes \(\varPi = (\mathsf {Setup},\mathsf {KG},\mathsf {Enc},\mathsf {Dec})\) over a message space \(\mathcal X= \{\mathcal X_\lambda \}_{\lambda \in \mathbb N}\) and a function space \(\mathcal F= \{\mathcal F_\lambda \}_{\lambda \in \mathbb N}\), for all \(\lambda \in \mathbb N\) and \(b\in \{ 0,1 \}\), and for all \(f\in \mathcal F_\lambda \) and \(((x^0, x^1)\in (\mathcal X)^2\) with which \({\mathcal {A}}\) queries the left-or-right encryption oracle, it holds that \(f(x^0) = f(x^1)\).
Definition 2.10
(Selective security). Let \(t = t(\lambda )\), \(T= T(\lambda )\), \(Q_\mathsf {key}= Q_\mathsf {key}(\lambda )\) and \(\mu = \mu (\lambda )\) be functions of the security parameter \(\lambda \in \mathbb {N}\). A public-key functional encryption scheme \(\varPi = (\mathsf {Setup}, \mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})\) over a message space \(\mathcal X= \{\mathcal X_\lambda \}_{\lambda \in \mathbb N}\) and a function space \(\mathcal F= \{\mathcal F_\lambda \}_{\lambda \in \mathbb N}\) is \((T, Q_\mathsf {key}, \mu )\) -selectively secure if for any valid adversary \({\mathcal {A}}\) that on input \(1^{\lambda }\) runs in time \(T(\lambda )\) and issues at most \(Q_\mathsf {key}(\lambda )\) key-generation queries, it holds that
for all sufficiently large \(\lambda \in \mathbb {N}\), where the random variable \(\mathsf {Exp}^{\mathsf {sel}\text {-}\mathsf {pkFE}}_{\varPi , \mathcal F, {\mathcal {A}}}(\lambda )\) is defined via the following experiment:
-
1.
\(\left( x^0,x^1,\mathsf {state}\right) \leftarrow {\mathcal {A}}_1^{}\left( 1^{\lambda }\right) \).
-
2.
 , \(b\leftarrow \{ 0,1 \}\).
, \(b\leftarrow \{ 0,1 \}\). -
3.
 .
. -
4.
If \(b' = b\) then output 1, and otherwise output 0.
2.5 Indistinguishability Obfuscation
We consider the standard notion of indistinguishability obfuscation [9, 33]. We say that two circuits, \(C_0\) and \(C_1\) are functionally equivalent, and denote it by \(C_0 \equiv C_1\), if for every x it holds that \(C_0(x)=C_1(x)\).
Definition 2.11
(Indistinguishability obfuscation). Let \(\mathcal C = \{\mathcal C_n\}_{n\in \mathbb N}\) be a class of polynomial-size circuits operating on inputs of length n. An efficient algorithm \(i\mathcal {O}\) is called a \((t,\mu )\) -indistinguishability obfuscator for the class \(\mathcal C\) if it takes as input a security parameter \(\lambda \) and a circuit in \(\mathcal C\) and outputs a new circuit so that following properties are satisfied:
-
1.
Functionality: For any input length \(n\in \mathbb N\), any \(\lambda \in \mathbb N\), and any \(C\in \mathcal C_n\) it holds that
$$\begin{aligned} \Pr \left[ C \equiv i\mathcal {O}(1^\lambda ,C) \right] = 1, \end{aligned}$$where the probability is taken over the internal randomness of \(i\mathcal {O}\).
-
2.
Indistinguishability: For any probabilistic adversary \({\mathcal {A}}=({\mathcal {A}}_1,{\mathcal {A}}_2)\) that runs in time \(t=t(\lambda )\), it holds that
$$\begin{aligned} \mathsf {Adv}^{i\mathcal {O}}_{i\mathcal {O},\mathcal C,{\mathcal {A}}} \mathop {=}\limits ^\mathsf{def} \left| \Pr \left[ \mathsf {Exp}^{i\mathcal {O}}_{i\mathcal {O}, \mathcal C, {\mathcal {A}}}(\lambda ) = 1 \right] - \frac{1}{2} \right| \le \mu (\lambda ), \end{aligned}$$for all sufficiently large \(\lambda \in \mathbb {N}\), where the random variable \(\mathsf {Exp}^{i\mathcal {O}}_{i\mathcal {O}, \mathcal C, {\mathcal {A}}}(\lambda )\) is defined via the following experiment:
-
(a)
\((C_0, C_1, \mathsf {state}) \leftarrow {\mathcal {A}}_1(1^\lambda )\) such that \(C_0, C_1 \in \mathcal {C}\) and \(C_0 \equiv C_1\).
-
(b)
\(\widehat{C} \leftarrow i\mathcal {O}(C_b)\), \(b\leftarrow \{ 0,1 \}\).
-
(c)
\(b' \leftarrow {\mathcal {A}}_2\left( 1^{\lambda },\widehat{C},\mathsf {state}\right) \).
-
(d)
If \(b' = b\) then output 1, and otherwise output 0.
-
(a)
3 Private-Key MIFE for a Poly-Logarithmic Number of Inputs
In this section we present our construction of a private-key multi-input functional encryption scheme. The main technical tool underlying our approach is a transformation from a t-input scheme to a 2t-input scheme which is described in Sect. 3.1. Then, in Sects. 3.2 and 3.3 we show that by iteratively applying our transformation \(O(\log \log \lambda )\) times, and by carefully controlling the security loss and the efficiency loss by adjusting the security parameter appropriately, we obtain a t-input scheme, where \(t = (\log \lambda )^\delta \) for some constant \(0< \delta < 1\) (recall that \(\lambda \in \mathbb {N}\) denotes the security parameter).
3.1 From \(\varvec{t}\) Inputs to \(\varvec{2t}\) Inputs
Let \(\mathcal F= \{ \mathcal F_{\lambda } \}_{\lambda \in \mathbb {N}}\) be a family of 2t-input functionalities, where for every \(\lambda \in \mathbb {N}\) the set \(\mathcal F_{\lambda }\) consists of functions of the form \(f:(\mathcal X_1)_{\lambda }\times \cdots \times (\mathcal X_{2t})_{\lambda } \rightarrow \mathcal Z_{\lambda }\). Our construction relies on the following building blocks:
-
1.
A private-key t-input functional encryption scheme \(\mathsf {FE}_t= ({\mathsf {FE}_t\mathsf {.S}}, {\mathsf {FE}_t\mathsf {.KG}}, {\mathsf {FE}_t\mathsf {.E}}, {\mathsf {FE}_t\mathsf {.D}})\).
-
2.
A puncturable pseudorandom function family \(\mathsf {PRF}= (\mathsf {PRF.Gen},\mathsf {PRF.Eval})\).
Our scheme \(\mathsf {FE}_{2t}= ({\mathsf {FE}_{2t}\mathsf {.S}}, {\mathsf {FE}_{2t}\mathsf {.KG}}, {\mathsf {FE}_{2t}\mathsf {.E}}, {\mathsf {FE}_{2t}\mathsf {.D}})\) is defined as follows.
-
The setup algorithm. On input the security parameter \(1^{\lambda }\) the setup algorithm \({\mathsf {FE}_{2t}\mathsf {.S}}\) samples a master secret key for a t-input scheme \(\mathsf {msk_{in}}\leftarrow {\mathsf {FE}_t\mathsf {.S}}(1^{\lambda })\), and a PRF key \(K^\mathsf {msk}\leftarrow \mathsf {PRF.Gen}(1^\lambda )\), and outputs \({\mathsf {msk}}= (\mathsf {msk_{in}},K^\mathsf {msk})\).
-
The key-generation algorithm. On input the master secret key \({\mathsf {msk}}\) and a function \(f \in \mathcal F_{\lambda }\), the key-generation algorithm \({\mathsf {FE}_{2t}\mathsf {.KG}}\) samples a PRF key \(K^\mathsf {key}\leftarrow \mathsf {PRF.Gen}(1^\lambda )\) and outputs \(\mathsf {sk}_{f} \leftarrow {\mathsf {FE}_t\mathsf {.KG}}(\mathsf {msk_{in}}, {\mathsf {Gen}_{f,\bot ,K^\mathsf {msk},K^\mathsf {key},\bot }})\), where \(\mathsf {Gen}_{f,\bot ,K^\mathsf {msk},K^\mathsf {key},\bot }\) is the t-input function that is defined in Fig. 3.
-
The encryption algorithm. On input the master secret key \({\mathsf {msk}}\), a message x and an index \(\mathsf {\ell }\in [2t]\), the encryption algorithm \({\mathsf {FE}_{2t}\mathsf {.E}}\) distinguished between the following three cases:
-
If \(\mathsf {\ell }= 1\), it samples a random string \(\tau \in \{ 0,1 \}^\lambda \), and then outputs \(\mathsf {ct}_\mathsf {\ell }\) defined as follows:
$$\begin{aligned} \mathsf {ct}_\mathsf {\ell }\leftarrow & {} {\mathsf {FE}_t\mathsf {.E}}(\mathsf {msk_{in}}, (x, \bot , \tau , 1, \underbrace{1,\dots ,1,0}_{t \text { slots}}), \mathsf {\ell }). \end{aligned}$$ -
If \(1<\mathsf {\ell }\le t\), it samples a random string \(\tau \in \{ 0,1 \}^\lambda \), and then outputs \(\mathsf {ct}_\mathsf {\ell }\) defined as follows:
$$\begin{aligned} \mathsf {ct}_\mathsf {\ell }\leftarrow & {} {\mathsf {FE}_t\mathsf {.E}}(\mathsf {msk_{in}}, (x, \bot , \tau , 1), \mathsf {\ell }). \end{aligned}$$ -
If \(t < \mathsf {\ell }\le 2t\), it samples a PRF key \(K^\mathsf {enc}\leftarrow \mathsf {PRF.Gen}(1^\lambda )\) and outputs \(\mathsf {sk}_\mathsf {\ell }\) defined as follows:
$$\begin{aligned} \mathsf {sk}_\mathsf {\ell }\leftarrow & {} {\mathsf {FE}_t\mathsf {.KG}}(\mathsf {msk_{in}}, \mathsf {AGG}_{x, \bot , \mathsf {\ell }, K^\mathsf {msk}, K^\mathsf {enc}, \bot }), \end{aligned}$$where \(\mathsf {AGG}_{x, \bot , \mathsf {\ell }, K^\mathsf {msk}, K^\mathsf {enc},\bot }\) is the t-input function that is defined in Fig. 4.
-
-
The decryption algorithm. On input a functional key \(\mathsf {sk}_f\) and ciphertexts \(\mathsf {ct}_1, \ldots , \mathsf {ct}_{t}, \mathsf {sk}_{t+1},\dots ,\mathsf {sk}_{2t}\), the decryption algorithm \({\mathsf {FE}_t\mathsf {.D}}\) computes
$$\begin{aligned} \forall i \in \{t+1,\dots ,2t\} :\mathsf {ct}'_i&= {\mathsf {FE}_t\mathsf {.D}}(\mathsf {sk}_i, \mathsf {ct}_1, \ldots , \mathsf {ct}_{t}) \\ \mathsf {sk}'&= {\mathsf {FE}_t\mathsf {.D}}(\mathsf {sk}_f, \mathsf {ct}_1,\dots ,\mathsf {ct}_{t}), \end{aligned}$$and outputs \({\mathsf {FE}_t\mathsf {.D}}(\mathsf {sk}', \mathsf {ct}'_{t+1},\dots , \mathsf {ct}'_{2t})\).
Correctness. For any \(\lambda \in \mathbb {N}\), \(f \in \mathcal F_{\lambda }\) and \((x_1, \ldots , x_{2t}) \in (\mathcal X_1)_{\lambda }\times \cdots \times (\mathcal X_{2t})_{\lambda }\), let \(\mathsf {sk}_f\) denote a functional key for f and let \(\mathsf {ct}_1, \ldots , \mathsf {ct}_t, \mathsf {sk}_{t+1},\dots ,\mathsf {sk}_{2t}\) denote encryptions of \(x_1, \ldots , x_{2t}\). Then, for every \(i \in \{1,\dots ,t\}\), it holds that
and
where \({\mathsf {msk}}_{\tau _1,\dots ,\tau _{t}} = {\mathsf {FE}_t\mathsf {.S}}(1^\lambda , \mathsf {PRF.Eval}(K^\mathsf {msk}, \tau _1\dots \tau _{t}))\). Therefore,
Security. The following theorem captures the security our transformation. The proof can be found in the full version [45].
Theorem 3.1
Let \(t = t(\lambda )\), \(T= T(\lambda )\), \(Q_\mathsf {key}= Q_\mathsf {key}(\lambda )\), \(Q_\mathsf {enc}= Q_\mathsf {enc}(\lambda )\) and \(\mu = \mu (\lambda )\) be functions of the security parameter \(\lambda \in \mathbb {N}\), and assume that \(\mathsf {FE}_t\) is a \((T, Q_\mathsf {key}, Q_\mathsf {enc}, \mu )\)-selectively-secure t-input functional encryption scheme and that \(\mathsf {PRF}\) is a \((T,\mu )\)-secure puncturable pseudorandom function family. Then, \(\mathsf {FE}_{2t}\) is \((T', Q_\mathsf {key}', Q_\mathsf {enc}', \mu ')\)-selectively-secure, where
-
\(T'(\lambda ) = T(\lambda ) - Q_\mathsf {key}(\lambda ) \cdot {\mathsf {poly}}(\lambda )\), for some fixed polynomial \({\mathsf {poly}}(\cdot )\).
-
\(Q_\mathsf {key}'(\lambda ) = Q_\mathsf {key}(\lambda ) - t(\lambda ) \cdot Q_\mathsf {enc}(\lambda ) \).
-
\(Q_\mathsf {enc}'(\lambda ) = Q_\mathsf {enc}(\lambda )\).
-
\(\mu '(\lambda ) = 8 t(\lambda ) \cdot (Q_\mathsf {enc}(\lambda ))^{t(\lambda )+1}\cdot Q_\mathsf {key}(\lambda ) \cdot \mu (\lambda )\).
3.2 Efficiency Analysis
In this section we analyze the overhead incurred by our transformation. Specifically, for a message space \(\mathcal X_1\times \dots \times \mathcal X_{2t}\) and a function space \(\mathcal F\) that consists of 2t-input functions, we instantiate our scheme (by applying our transformation \(\log t\) times) and analyze the size of a master secret key, the size of a functional-key, the size of a ciphertext and the time it takes to evaluate a functional-key with 2t ciphertexts.
Let \(\lambda \in \mathbb N\) be a security parameter with which we instantiate the 2t-input scheme, let us assume that \(\mathcal F\) consists of functions of size at most \(s=s(\lambda )\) and that each \(\mathcal X_i\) consists of messages of size at most \(m=m(\lambda )\). Assuming that \(\log t\le {\mathsf {poly}}(\lambda )\) (to simplify notation), we show that there exists a fixed constant \(\mathsf {c}\in \mathbb N\) such that:
-
the setup procedure takes time \(\lambda ^{\mathsf {c}}\),
-
the key-generation procedure takes time \((s\cdot \lambda )^{t^{\log \mathsf {c}}}\),
-
the encryption procedure takes time \((m\cdot \lambda )^{t^{\log \mathsf {c}}}\), and
-
the decryption procedure takes time \(t^{\log t} \cdot \lambda ^{\mathsf {c}}\).
In Sect. 3.3 we will choose s, m, t and \(\lambda \) to satisfy Lemma 3.2.
For a circuit A that receives inputs of lengths \(x_1\dots ,x_m\), we denote by \(\mathsf {Time}(A, x_1,\dots ,x_m)\) the size of the circuit when applied to inputs of length \(\sum _{i=1}^{m} x_i\). For a function family \(\mathcal F\), we denote by \(\mathsf {Size}(\mathcal F)\) the maximal size of the circuit that implements a function from \(\mathcal F\).
We analyze the overhead incurred by our transformation
The Setup Procedure. The setup procedure of \(\mathsf {FE}_{2t}\) is composed of sampling a key for a scheme \(\mathsf {FE}_t\) and generating a PRF key. Iterating this, we see that a master secret key in our final scheme consists of a single master secret key for a single-input scheme and \(\log t\) additional PRF keys. Namely,
where \(p_1\) is a fixed polynomial that depends on the key-generation time of the PRF, and thus
The Key-Generation Procedure. The key-generation procedure of \(\mathsf {FE}_{2t}\) depends on the complexity of the key-generation procedure of the \(\mathsf {FE}_t\) scheme. Let \(\mathcal F^{2t}\) be the function family that is supported by the scheme \(\mathsf {FE}_{2t}\).
where \(p_2\) subsumes the size of the embedded PRF keys and the complexity of the simple operations that are done in \(\mathsf {Gen}\), and \(p_3\) subsumes the running time of the generation of the PRF key \(K^\mathsf {key}\).
The dominant part in the above equation is that the time it takes to generate a key with respect to \(\mathsf {FE}_{2t}\) for a function whose size is \(\mathsf {Size}(\mathcal F^{2t})\) depends on the circuit size of key-generation in the scheme \(\mathsf {FE}_t\) for a function whose size is \(\mathsf {Time}({\mathsf {FE}_t\mathsf {.KG}}, \mathsf {Size}(\mathcal F^{2t}))\) (namely, it is a function that outputs a functional key for a function whose size is \(\mathsf {Size}(\mathcal F^{2t})\)). Thus, applying this equation recursively, we get that for large enough \(c\in \mathbb N\) (that depends on the exponents of \(p_2\) and \(p_3\)), it holds that
The Encryption Procedure. The encryption procedure of \(\mathsf {FE}_{2t}\) depends on the complexity of encryption and key-generation of the \(\mathsf {FE}_t\) scheme. Let m be the length of a message to encrypt. For \(\ell \le t\), the complexity is at most
For \(t+1 \le \ell \le 2t\), the complexity of encryption is
where \(p_4\) subsumes the running time of the key-generation procedure of the PRF and the various other simple operations made by \(\mathsf {AGG}\).
The dominant part is that an encryption of a message with respect to the scheme \(\mathsf {FE}_{2t}\) requires generating a key with respect to the scheme \(\mathsf {FE}_t\) for a function whose size is \(\mathsf {Time}({\mathsf {FE}_t\mathsf {.E}}, 2m)\). Thus, similarly to the analysis of the key-generation procedure, we get that for some fixed \(c\in \mathbb N\) (that depends on the exponents of \(p_4\) and the time it takes to encrypt a message with respect to \(\mathsf {FE}_1\)), we get that
The Decryption Procedure. Decryption in the scheme \(\mathsf {FE}_{2t}\) requires \(t+2\) decryption operations with respect to the scheme \(\mathsf {FE}_t\). Let \(\mathsf {ct}(t)\) and \(\mathsf {sk}(t)\) be the length of a ciphertext and a key in the scheme \(\mathsf {FE}_t\), respectively. We get that
where \(p_5\) is a polynomial that subsumes the complexity of decryption in \(\mathsf {FE}_1\).
3.3 Iteratively Applying Our Transformation
In this section we show that by iteratively applying our transformation \(O(\log \log \lambda )\) times we obtain a t-input scheme, where \(t = (\log \lambda )^\delta \) for some constant \(0< \delta < 1\). We prove the following two theorems:
Lemma 3.2
Let \(T= T(\lambda )\), \(Q_\mathsf {key}= Q_\mathsf {key}(\lambda )\), \(Q_\mathsf {enc}= Q_\mathsf {enc}(\lambda )\) and \(\mu = \mu (\lambda )\) be functions of the security parameter \(\lambda \in \mathbb N\) and let \(\epsilon \in (0,1)\). Assume any \(\left( T, Q_\mathsf {key},Q_\mathsf {enc}, \mu \right) \)-selectively-secure single-input private-key functional encryption scheme with the following properties:
-
1.
it supports circuits and messages of size \({\mathsf {poly}}(2^{(\log \lambda )^{2\epsilon }})\) and
-
2.
the size of a ciphertext and a functional key is bounded by \({\mathsf {poly}}(2^{(\log \lambda )^{2\epsilon }})\),
then for some constant \(\delta \in (0,1)\), there exists a \(\left( T', Q_\mathsf {key}',Q_\mathsf {enc}', \mu '\right) \)-selectively-secure \((\log \lambda )^{\delta }\)-input private-key functional encryption scheme with the following properties:
-
1.
it supports circuits and messages of size \({\mathsf {poly}}(2^{(\log \lambda )^{\epsilon }})\),
-
2.
\(T'(\lambda )\ge T(\lambda )- (\log \log \lambda ) \cdot p(\lambda )\),
-
3.
\(Q_\mathsf {key}'(\lambda ) \ge Q_\mathsf {key}(\lambda ) - (2\log \lambda ) \cdot Q_\mathsf {enc}(\lambda )\),
-
4.
\(Q_\mathsf {enc}'(\lambda ) = Q_\mathsf {enc}(\lambda )\), and
-
5.
\(\mu '(\lambda ) \le 2^{(3\log \log \lambda )^2} \cdot (Q_\mathsf {enc}(\lambda ))^{2(\log \lambda )^\delta +2}\cdot (Q_\mathsf {key}(\lambda ))^{\log \log \lambda } \cdot \mu (\lambda )\).
Proof
Let \(\mathsf {FE}_1\) be a \(\left( T, Q_\mathsf {key},Q_\mathsf {enc}, \mu \right) \)-selectively-secure single-input scheme with the properties from the statement.
Let us analyze the complexity of the t-input scheme where \(t(\lambda ) = (\log \lambda )^\delta \), where \(\delta >0\) is some fixed constant that we fix later. In terms of complexity, using the properties of the single-input scheme and our efficiency analysis from Sect. 3.2, we have that setup takes a polynomial time in \(\lambda \), key-generation for a function of size s takes time at most \({(s\cdot \lambda )}^{t^{\log c}}\) and encryption of a message of length m takes time \({(m\cdot \lambda )}^{t^{\log c}}\) for some large enough constant \(c>1\) (recall that c is an upper bound on the exponents of the running time of key generation and encryption procedures of the underlying single-input scheme). Plugging in \(\delta = 2\epsilon /(3\log c)\), \(t = (\log \lambda )^{\delta }\) and \(s,m \le 2^{c'\cdot (\log \lambda )^{\epsilon }}\) for any \(c'\in \mathbb N\), we get that key-generation and encryption take time at most \(2^{c'\cdot (\log \lambda )^{2\epsilon /3} \cdot (\log \lambda )^{\epsilon }} = 2^{c'\cdot (\log \lambda )^{5\epsilon /3}}\). Notice that for large enough \(\lambda \), decryption of such a key-message pair takes time at most \({\mathsf {poly}}(2^{(\log \lambda )^{5\epsilon /3}}) \cdot (t+2)^{\log t} \le 2^{(\log \lambda )^{2\epsilon }}\).
In terms of security, by Theorem 3.1, we have that if \(\mathsf {FE}_t\) is \((T^{(t)}, Q_\mathsf {key}^{(t)}, Q_\mathsf {enc}^{(t)}, \mu ^{(t)})\)-selectively-secure and \(\mathsf {PRF}\) is a \((T^{(t)}, \mu ^{(t)})\)-secure puncturable pseudorandom function family, then \(\mathsf {FE}_{2t}\) is \((T^{(2t)}, Q_\mathsf {key}^{(2t)}, Q_\mathsf {enc}^{(2t)}, \mu ^{(2t)})\)-selectively-secure, where
-
1.
\(T^{(2t)}(\lambda ) = T^{(t)}(\lambda )- p(\lambda )\),
-
2.
\(Q_\mathsf {key}^{(2t)}(\lambda ) = Q_\mathsf {key}^{(t)}(\lambda ) - t\cdot Q_\mathsf {enc}^{(t)}\),
-
3.
\(Q_\mathsf {enc}^{(2t)}(\lambda ) = Q_\mathsf {enc}^{(t)}(\lambda )\), and
-
4.
\(\mu ^{(2t)}(\lambda ) = 2^{(3\log \log \lambda )^2}\cdot (Q_\mathsf {enc}(\lambda ))^{2(\log \lambda )^\delta +2}\cdot (Q_\mathsf {key}(\lambda ))^{\log \log \lambda } \cdot \mu (\lambda )\).
Iterating these recursive equations, using the fact that \(Q_\mathsf {key}^{(2t)} \le Q_\mathsf {key}^{(t)}\), and plugging in our initial scheme parameters, we get that
\(\blacksquare \)
Claim 3.3
Let \(\lambda \in \mathbb N\) be a security parameter and fix any constant \(\epsilon \in (0,1)\). Assuming any \(( 2^{2 \cdot (\log \lambda )^{1/\epsilon }}, 2^{2\cdot (\log \lambda )^{1/\epsilon }},2^{(\log \lambda )^{1/\epsilon }}, 2^{-(\log \lambda )^{1.5/\epsilon }})\)-selectively-secure single-input private-key functional encryption scheme supporting polynomial-size circuits, there exists a \(( 2^{2 \cdot (\log \lambda )^{2}}, 2^{2\cdot (\log \lambda )^{2}},2^{(\log \lambda )^{2}}, 2^{-(\log \lambda )^{3}})\)-selectively-secure single-input private-key functional encryption scheme with the following properties
-
1.
it supports circuits and messages of size \({\mathsf {poly}}(2^{(\log \lambda )^{2\epsilon }})\) and
-
2.
the size of a ciphertext and a functional key is bounded by \({\mathsf {poly}}(2^{(\log \lambda )^{2\epsilon }})\).
Proof
We instantiate the given scheme with security parameter \(\tilde{\lambda }= 2^{(\log \lambda )^{2\epsilon }}\). The resulting scheme is \(\left( 2^{2 \cdot (\log \lambda )^{2}}, 2^{2\cdot (\log \lambda )^{2}},2^{(\log \lambda )^{2}}, 2^{-(\log \lambda )^{3}} \right) \)-selectively-secure and for a circuit (resp., message) of size \(\tilde{\lambda }\), the size of a functional key (resp., ciphertext) is bounded by \({\mathsf {poly}}(\tilde{\lambda })\). \(\blacksquare \)
Combining Theorem 3.3 and Lemma 3.2 we get the following theorem.
Theorem 3.4
Let \(\lambda \in \mathbb N\) be a security parameter and fix any constant \(\epsilon \in (0,1)\). Assuming any \(( 2^{2 \cdot (\log \lambda )^{1/\epsilon }}, 2^{1\cdot (\log \lambda )^{2/\epsilon }},2^{(\log \lambda )^{1/\epsilon }}, 2^{-(\log \lambda )^{1.5/\epsilon }})\)-selectively-secure single-input private-key functional encryption scheme supporting polynomial-size circuits, then for some \(\delta \in (0,1)\), there exists a \(( 2^{(\log \lambda )^2}, 2^{(\log \lambda )^2},2^{(\log \lambda )^2}, 2^{-(\log \lambda )^2} )\)-selectively-secure \((\log \lambda )^{\delta }\)-input private-key functional encryption scheme supporting circuits of size \(2^{(\log \lambda )^\epsilon }\).
Proof
Assuming any \(\left( 2^{2 \cdot (\log \lambda )^{1/\epsilon }}, 2^{2\cdot (\log \lambda )^{1/\epsilon }},2^{(\log \lambda )^{1/\epsilon }}, 2^{-(\log \lambda )^{1.5/\epsilon }} \right) \)-selectively-secure single-input private-key functional encryption scheme supporting polynomial-size circuits. By 3.3, it implies a \(\left( 2^{2 \cdot (\log \lambda )^{2}}, 2^{2\cdot (\log \lambda )^{2}},2^{(\log \lambda )^{2}},\right. \left. 2^{-(\log \lambda )^{3}} \right) \)-selectively-secure single-input private-key functional encryption scheme with the following properties:
-
1.
it supports circuits and messages of size \({\mathsf {poly}}(2^{(\log \lambda )^{2\epsilon }})\) and
-
2.
the size of a ciphertext and a functional key is bounded by \({\mathsf {poly}}(2^{(\log \lambda )^{2\epsilon }})\).
Using Lemma 3.2, we get that for some constant \(\delta \in (0,1)\), there exists a \(\left( T', Q_\mathsf {key}',Q_\mathsf {enc}', \mu '\right) \)-selectively-secure \((\log \lambda )^{\delta }\)-input private-key functional encryption scheme with the following properties:
-
1.
it supports circuits and messages of size at most \({\mathsf {poly}}(2^{(\log \lambda )^{\epsilon /2}})\),
-
2.
\(T'(\lambda )\ge 2^{2 \cdot (\log \lambda )^{2}}- (\log \log \lambda ) \cdot p(\lambda ) \ge 2^{(\log \lambda )^{2}}\),
-
3.
\(Q_\mathsf {key}'(\lambda ) \ge 2^{2 \cdot (\log \lambda )^{2}} - (2\log \lambda ) \cdot 2^{(\log \lambda )^{2}} \ge 2^{(\log \lambda )^{2}}\),
-
4.
\(Q_\mathsf {enc}'(\lambda ) = 2^{(\log \lambda )^{2}}\), and
-
5.
\(\mu '(\lambda ) \le 2^{(3\log \log \lambda )^2} \cdot (2^{(\log \lambda )^{2}})^{2(\log \lambda )^\delta +2}\cdot (2^{(\log \lambda )^{2}})^{\log \log \lambda } \cdot 2^{-(\log \lambda )^{3}} \le 2^{-(\log \lambda )^{2}} \). \(\blacksquare \)
4 Applications of Our Construction
In this section we present our construction of an indistinguishability obfuscator for circuits with inputs of poly-logarithmic length, and its applications to public-key functional encryption and average-case PPAD hardness.
4.1 Obfuscation for Circuits with Poly-Logarithmic Input Length
We show that any selectively-secure t-input private-key functional encryption scheme that supports circuits of size s can be used to construct an indistinguishability obfuscator that supports circuits of size s that have at most \(t\cdot \log \lambda \) inputs, where \(\lambda \in \mathbb {N}\) is the security parameter. This is similar to the proof of Goldwasser et al. [37] that showed that private-key multi-input functional encryption for a polynomial number of inputs implies indistinguishability obfuscation (and a follow-up refinement of Bitansky et al. [10]).
We consider the following restricted class of circuits:
Definition 4.1
Let \(\lambda \in \mathbb N\) and let \(s(\cdot )\) and \(t'(\cdot )\) be functions. Let \(\mathcal C^{s,t'}_\lambda \) denoet the class of all circuits of size at most \(s(\lambda )\) that get as input \(t'(\lambda )\) bits.
Lemma 4.2
Let \(t = t(\lambda )\), \(s = s(\lambda )\), \(T= T(\lambda )\), \(Q_\mathsf {key}= Q_\mathsf {key}(\lambda )\), \(Q_\mathsf {enc}= Q_\mathsf {enc}(\lambda )\) and \(\mu = \mu (\lambda )\) be functions of the security parameter \(\lambda \in \mathbb {N}\), and assume a \((T,Q_\mathsf {key},Q_\mathsf {enc},\mu )\)-selectively-secure t-input private-key functional encryption scheme for functions of size at most s, where \(Q_\mathsf {key}(\lambda ) \ge 1\) and \(Q_\mathsf {enc}(\lambda ) \ge \lambda \). Then, there exists a \((T(\lambda ) - \lambda \cdot t(\lambda )\cdot p(\lambda ), \mu (\lambda ))\)-secure indistinguishability obfuscator for the circuit class \(\mathcal C^{s,t'}_{\lambda }\), where \(p(\cdot )\) is some fixed polynomial and \(t'(\lambda )=t(\lambda )\cdot \log \lambda \).
Proof
Let \(\mathsf {FE}_t\) be a t-input scheme as in the statement of the lemma. We construct an obfuscator for circuits of size at most \(s(\lambda )\) that receive \(t(\lambda )\cdot \log \lambda \) bits as input. On input a circuit \(C\in \mathcal C^{s,t'}_\lambda \), the obfuscator works as follows:
-
1.
Sample a master secret key \({\mathsf {msk}}\leftarrow {\mathsf {FE}_t\mathsf {.S}}(1^\lambda )\).
-
2.
Compute \(\mathsf {ct}_{i,j} = {\mathsf {FE}_t\mathsf {.E}}({\mathsf {msk}}, i, j)\) for every \(i\in \{ 0,1 \}^{\log \lambda }\) and \(j\in [t(\lambda )]\).
-
3.
Compute \(\mathsf {sk}_C = {\mathsf {FE}_t\mathsf {.KG}}({\mathsf {msk}}, C)\)
-
4.
Output \(\widehat{C} = \{\mathsf {sk}_C\} \cup \{\mathsf {ct}_{i,j}\}_{i\in \{ 0,1 \}^{\log \lambda }, j\in [t(\lambda )]}\).
Evaluation of an obfuscated circuit \(\widehat{C}\) on an input \(x\in (\{ 0,1 \}^{\log \lambda })^t\), where we view x as \(x=x_1\dots x_t\) and \(x_i\in \{ 0,1 \}^{\log \lambda }\), is done by outputting the result of a single execution of the decryption procedure of the t-input scheme \({\mathsf {FE}_t\mathsf {.D}}(\mathsf {sk}_C, \mathsf {ct}_{x_1,1},\dots ,\mathsf {ct}_{x_t,t})\). Notice that the description size of the obfuscated circuit is upper bounded by some fixed polynomial in \(\lambda \).
For security, notice that a single functional key is generated and it is for a circuit of size at most \(s(\lambda )\). Moreover, the number of ciphertexts is bounded by \(\lambda \) ciphertexts per coordinate. Thus, following [37], one can show that an adversary that can break the security of the above obfuscator can be used to break the security of the \(\mathsf {FE}_t\) scheme with the same success probability (it can even break \(\mathsf {FE}_t\) that satisfies a weaker security notion in which the functional keys are also fixed ahead of time, before seeing any ciphertext). \(\blacksquare \)
Applying Lemma 4.2 with the t-input scheme from Theorem 3.4 we obtain the following corollary.
Corollary 4.3
Let \(\lambda \in \mathbb N\) be a security parameter and fix any constant \(\epsilon \in (0,1)\). Assume a \((2^{2(\log \lambda )^{1/\epsilon }}, 2^{2(\log \lambda )^{1/\epsilon }},2^{(\log \lambda )^{1/\epsilon }}, 2^{-(\log \lambda )^{1.5/\epsilon }})\)-selectively-secure single-input private-key functional encryption scheme for all functions of polynomial size. Then, for some constant \(\delta \in (0,1)\), there exists a \((2^{(\log \lambda )^{2}},2^{-(\log \lambda )^{2}})\)-secure indistinguishability obfuscator for the circuit class \(\mathcal C^{2^{O((\log \lambda )^\varepsilon )},(\log \lambda )^{1+\delta }}_\lambda \).
4.2 Public-Key Functional Encryption
In this section we present a construction of a public-key functional encryption scheme based on our multi-input private-key scheme.
Theorem 4.4
Let \(\lambda \in \mathbb N\) be a security parameter and fix any \(\epsilon \in (0,1)\). There exists a constant \(\delta >0\) for which the following holds. Assume a \((2^{2(\log \lambda )^{1/\epsilon }}, 2^{2(\log \lambda )^{1/\epsilon }},2^{(\log \lambda )^{1/\epsilon }}, 2^{-(\log \lambda )^{1.5/\epsilon }})\)-selectively-secure single-input private-key functional encryption scheme for all functions of polynomial size, and that \((2^{2\lambda ^{\epsilon '}},2^{-2\lambda ^{\epsilon '}})\)-secure one-way functions exist for \(\epsilon ' > 1/(1+\delta )\). Then, for some constant \(\zeta >1\), there exists a \((2^{(\log \lambda )^{\zeta }}, 2^{(\log \lambda )^{\zeta }}, 2^{-(\log \lambda )^{\zeta }})\)-selectively-secure public-key encryption scheme for the circuit class \(\mathcal C^{2^{O((\log \lambda )^\epsilon )},(\log \lambda )^{1+\delta }}_\lambda \).
Our construction is essentially the construction of Waters [54], who showed how to construct a public-key functional encryption scheme for the set of all polynomial-size circuits assuming indistinguishability obfuscation for all polynomial-size circuits. We make a more careful analysis of his scheme and show that for a specific range of parameters, it suffices to use the obfuscator we have obtained in Corollary 4.3. The proof of Theorem 4.4 can be found in the full version [45].
4.3 Average-Case PPAD Hardness
We present a construction of a hard-on-average distribution of Sink-of-Verifiable-Line (SVL) instances assuming any quasi-polynomially-secure private-key (single-input) functional encryption scheme and sub-exponentially-secure one-way function. Following the work of Abbot et al. [1] and Bitansky et al. [11], this shows that the complexity class PPAD [24, 30, 31, 50] contains complete problems that are hard on average (we refer the reader to [11] for more details). In what follows we first recall the SVL problem, and then state our hardness result. The proof can be found in the full version [45].
Definition 4.5
(Sink-of-Verifiable-Line). An SVL instance \((\mathsf {S}, \mathsf {V}, x_s, T)\) consists of a source \(x_s\in \{ 0,1 \}^\lambda \), a target index \(T\in [2^\lambda ]\), and a pair of circuits \(\mathsf {S}:\{ 0,1 \}^\lambda \rightarrow \{ 0,1 \}^\lambda \) and \(\mathsf {V}:\{ 0,1 \}^\lambda \times [T]\rightarrow \{ 0,1 \}\), such that for \((x,i)\in \{ 0,1 \}^\lambda \times [T]\), it holds that \(\mathsf {V}(x,i)=1\) if and only if \(x=x_i=\mathsf {S}^{i-1}(x_s)\), where \(x_1=x_s\). A string \(w\in \{ 0,1 \}^\lambda \) is a valid witness if and only if \(\mathsf {V}(w,T)=1\).
Theorem 4.6
Let \(\lambda \in \mathbb N\) be a security parameter and fix any constant \(\epsilon \in (0,1)\). Assume a \((2^{2(\log \lambda )^{1/\epsilon }}, 2^{2(\log \lambda )^{1/\epsilon }},2^{(\log \lambda )^{1/\epsilon }}, 2^{-(\log \lambda )^{1.5/\epsilon }})\)-selectively-secure single-input private-key functional encryption scheme for all functions of polynomial size, and that \((2^{\lambda ^{2\epsilon '}},2^{-\lambda ^{2\epsilon '}})\)-secure injective one-way functions exist for some large enough constant \(\epsilon '\in (0,1)\). Then, there exists a distribution with an associated efficient sampling procedure that generates instances of sink-of-verifiable-line which are hard to solve for any polynomial-time algorithm.
Notes
- 1.
As a concrete (yet quite general) example, consider a user who stores her data on a remote server: The user uses the master secret key both for encrypting her data, and for generating functional keys that will enable the server to offer her various useful services.
- 2.
This is not true in various restricted cases, for example, when the functional encryption scheme has to support an a-priori bounded number of functional keys or ciphertexts [39]. However, as mentioned, we focus on schemes that support an unbounded number of functional keys and ciphertexts.
- 3.
This holds even if the construction is allowed to generate functional keys (in a non-black-box manner) for any circuit that invokes one-way functions in a black-box manner.
- 4.
- 5.
In this work we focus on selectively-secure schemes, where an adversary first submits all of its encryption queries, and can then adaptively interact with the key-generation oracle (see Definition 2.7). This notion of security suffices for the applications we consider in this paper.
- 6.
A similar strategy was also employed by Ananth and Jain [6], that showed how to use any t-input private-key scheme to get a private-key \((t+1)\)-input scheme under the additional assumption that a public-key functional encryption scheme exists. Their construction, however, did not incur the polynomial blowup and could be applied all the way to get a scheme that supports a polynomial number of inputs.
- 7.
We note that the notion of function privacy is very different from the one in the private-key setting, and in particular, natural definitions already imply obfuscation.
- 8.
We focus on selective securiy and do not define full security since there is a generic transfomation [4].
References
Abbot, T., Kane, D., Valiant, P.: On algorithms for Nash equilibria (2004). http://web.mit.edu/tabbott/Public/final.pdf
Agrawal, S., Agrawal, S., Badrinarayanan, S., Kumarasubramanian, A., Prabhakaran, M., Sahai, A.: Function private functional encryption and property preserving encryption: new definitions and positive results. Cryptology ePrint Archive, Report 2013/744 (2013)
Ananth, P., Boneh, D., Garg, S., Sahai, A., Zhandry, M.: Differing-inputs obfuscation and applications. Cryptology ePrint Archive, Report 2013/689 (2013)
Ananth, P., Brakerski, Z., Segev, G., Vaikuntanathan, V.: From selective to adaptive security in functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 657–677. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_32
Ananth, P., Jain, A., Naor, M., Sahai, A., Yogev, E.: Universal constructions and robust combiners for indistinguishability obfuscation and witness encryption. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 491–520. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_17
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_15
Ananth, P., Jain, A., Sahai, A.: Achieving compactness generically: indistinguishability obfuscation from non-compact functional encryption. Cryptology ePrint Archive, Report 2015/730 (2015)
Asharov, G., Segev, G.: Limits on the power of indistinguishability obfuscation and functional encryption. In: Proceedings of the 56th Annual IEEE Symposium on Foundations of Computer Science, pp. 191–209 (2015)
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6 (2012)
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 391–418. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53644-5_15
Bitansky, N., Paneth, O., Rosen, A.: On the cryptographic hardness of finding a Nash equilibrium. In: Proceedings of the 56th Annual IEEE Symposium on Foundations of Computer Science, pp. 1480–1498 (2015)
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: Proceedings of the 56th Annual IEEE Symposium on Foundations of Computer Science, pp. 171–190 (2015)
Boneh, D., Lewi, K., Raykova, M., Sahai, A., Zhandry, M., Zimmerman, J.: Semantically secure order-revealing encryption: multi-input functional encryption without obfuscation. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 563–594. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_19
Boneh, D., Raghunathan, A., Segev, G.: Function-private identity-based encryption: hiding the function in functional encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 461–478. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_26
Boneh, D., Raghunathan, A., Segev, G.: Function-private subspace-membership encryption and its applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 255–275. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42033-7_14
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_16
Boneh, D., Sahai, A., Waters, B.: Functional encryption: a new vision for public-key cryptography. Commun. ACM 55(11), 56–64 (2012)
Boneh, D., Waters, B.: Constrained pseudorandom functions and their applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 280–300. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42045-0_15
Boyle, E., Chung, K.-M., Pass, R.: On extractability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 52–73. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_3
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54631-0_29
Brakerski, Z., Gentry, C., Halevi, S., Lepoint, T., Sahai, A., Tibouchi, M.: Cryptanalysis of the quadratic zero-testing of GGH. Cryptology ePrint Archive, Report 2015/845 (2015)
Brakerski, Z., Komargodski, I., Segev, G.: Multi-input functional encryption in the private-key setting: stronger security from weaker assumptions. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 852–880. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_30
Brakerski, Z., Segev, G.: Function-private functional encryption in the private-key setting. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 306–324. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_12
Chen, X., Deng, X., Teng, S.: Settling the complexity of computing two-player Nash equilibria. J. ACM 56(3) (2009). http://doi.acm.org/10.1145/1516512.1516516
Cheon, J.H., Fouque, P.A., Lee, C., Minaud, B., Ryu, H.: Cryptanalysis of the new CLT multilinear map over the integers. Cryptology ePrint Archive, Report 2016/135 (2016)
Cheon, J.H., Han, K., Lee, C., Ryu, H., Stehlé, D.: Cryptanalysis of the multilinear map over the integers. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 3–12. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46800-5_1
Cheon, J.H., Jeong, J., Lee, C.: An algorithm for NTRU problems and cryptanalysis of the GGH multilinear map without an encoding of zero. Cryptology ePrint Archive, Report 2016/139 (2016)
Cheon, J.H., Lee, C., Ryu, H.: Cryptanalysis of the new CLT multilinear maps. Cryptology ePrint Archive, Report 2015/934 (2015)
Coron, J.-S., et al.: Zeroizing without low-level zeroes: new MMAP attacks and their limitations. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 247–266. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_12
Daskalakis, C., Goldberg, P.W., Papadimitriou, C.H.: The complexity of computing a Nash equilibrium. Commun. ACM 52(2), 89–97 (2009)
Daskalakis, C., Goldberg, P.W., Papadimitriou, C.H.: The complexity of computing a Nash equilibrium. SIAM J. Comput. 39(1), 195–259 (2009)
Daskalakis, C., Papadimitriou, C.H.: Continuous local search. In: Proceedings of the 22nd Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 790–804 (2011)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: Proceedings of the 54th Annual IEEE Symposium on Foundations of Computer Science, pp. 40–49 (2013)
Garg, S., Gentry, C., Halevi, S., Zhandry, M.: Functional encryption without obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 480–511. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_18
Garg, S., Pandey, O., Srinivasan, A.: Revisiting the cryptographic hardness of finding a nash equilibrium. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 579–604. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_20
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Goldwasser, S., et al.: Multi-input functional encryption. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 578–602. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_32
Goldwasser, S., Kalai, Y., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Proceedings of the 45th Annual ACM Symposium on Theory of Computing, pp. 555–564 (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_11
Hu, Y., Jia, H.: Cryptanalysis of GGH map. Cryptology ePrint Archive, Report 2015/301 (2015)
Hubácek, P., Yogev, E.: Hardness of continuous local search: query complexity and cryptographic lower bounds. In: Proceedings of the 28th Annual ACM-SIAM Symposium on Discrete Algorithms, SODA, pp. 1352–1371 (2017)
Impagliazzo, R.: A personal view of average-case complexity. In: Proceedings of the 10th Annual Structure in Complexity Theory Conference, pp. 134–147 (1995)
Kiayias, A., Papadopoulos, S., Triandopoulos, N., Zacharias, T.: Delegatable pseudorandom functions and applications. In: Proceedings of the 20th Annual ACM Conference on Computer and Communications Security, pp. 669–684 (2013)
Komargodski, I., Moran, T., Naor, M., Pass, R., Rosen, A., Yogev, E.: One-way functions and (im)perfect obfuscation. In: Proceedings of the 55th Annual IEEE Symposium on Foundations of Computer Science, pp. 374–383 (2014)
Komargodski, I., Segev, G.: From Minicrypt to Obfustopia via private-key functional encryption. Cryptology ePrint Archive, Report 2017/080
Komargodski, I., Segev, G., Yogev, E.: Functional encryption for randomized functionalities in the private-key setting from minimal assumptions. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 352–377. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_14
Miles, E., Sahai, A., Zhandry, M.: Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13. Cryptology ePrint Archive, Report 2016/147 (2016)
Minaud, B., Fouque, P.A.: Cryptanalysis of the new multilinear map over the integers. Cryptology ePrint Archive, Report 2015/941 (2015)
O’Neill, A.: Definitional issues in functional encryption. Cryptology ePrint Archive, Report 2010/556 (2010)
Papadimitriou, C.H.: On the complexity of the parity argument and other inefficient proofs of existence. J. Comput. Syst. Sci. 48(3), 498–532 (1994)
Sahai, A., Waters, B.: Slides on functional encryption (2008). http://www.cs.utexas.edu/bwaters/presentations/files/functional.ppt
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Proceedings of the 46th Annual ACM Symposium on Theory of Computing, pp. 475–484 (2014)
Shen, E., Shi, E., Waters, B.: Predicate privacy in encryption systems. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 457–473. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00457-5_27
Waters, B.: A punctured programming approach to adaptively secure functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 678–697. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_33
Acknowledgments
We thank Zvika Brakerski and the anonymous referees for many valuable comments. The first author thanks his advisor Moni Naor for his support and guidance.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Komargodski, I., Segev, G. (2017). From Minicrypt to Obfustopia via Private-Key Functional Encryption. In: Coron, JS., Nielsen, J. (eds) Advances in Cryptology – EUROCRYPT 2017. EUROCRYPT 2017. Lecture Notes in Computer Science(), vol 10210. Springer, Cham. https://doi.org/10.1007/978-3-319-56620-7_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-56620-7_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-56619-1
Online ISBN: 978-3-319-56620-7
eBook Packages: Computer ScienceComputer Science (R0)


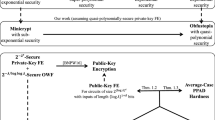




 ,
,  .
.
