Ultrafast Manipulation of Excitons and Spins in Quantum Dots

Abstract

This chapter reviews the coherent manipulation of excitons and spins in self-assembled InGaAs quantum dots by ultrafast laser pulses. We begin with a review of the basic theory of coherent control of two-level systems, followed by a discussion of the beneficial features of quantum dots. Experiments on ultrafast coherent control of excitons in neutral dots and spins in charged dots are then presented, before concluding with a comparison of the two different approaches in the context of applications in quantum information processing.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The coherent manipulation of quantum systems lies at the heart of most quantum information processing (QIP) schemes. Many of the techniques for coherent control were originally developed in the fields of nuclear magnetic resonance (NMR) and atomic physics, and have only recently been applied to semiconductor systems. The reason for this is the problem of decoherence: the coherence times of optical transitions in most semiconductors are extremely short, making the task of observing coherent phenomena particularly challenging. It is in this context that quantum dots, with their long dephasing times, come into their own. The subject of this chapter is precisely on the coherent control experiments that are facilitated by the long coherence times of quantum dots.

An appreciation of coherent control experiments first requires that the basic concepts should be well understood. The chapter therefore starts in Sect. 10.2 with a summary of the main concepts of two-level systems interacting with resonant laser pulses. The second part of the chapter then focuses on the observation of coherent phenomena in quantum dots. After discussing the reasons why quantum dots are good for coherent control experiments (Sect. 10.3), two different approaches are considered, namely the control of excitons in neutral dots (Sect. 10.4), and of spins in charged dots (Sect. 10.5). The chapter concludes by comparing the two approaches and giving an outlook for further work.

2 Concepts of Coherent Control Experiments

This section gives a tutorial review of the coherent manipulation of two-level systems by resonant laser pulses, starting from first principles. Readers who are familiar with this text-book material may skip ahead to the specific sections on quantum dots, beginning in Sect. 10.3.

2.1 The Two-Level Atom Approximation and the Bloch Sphere

The starting point for understanding the coherent interaction between laser light and quantum dots is the two-level atom approximation. A real atom has many quantised energy levels, giving rise to a rich spectrum of optical transitions, and the two-level approximation applies when the laser frequency is close to resonance with one of them. As we shall see, the interaction depends very strongly on the detuning $\varDelta$ of the laser relative to the transition frequency, and becomes negligibly small when $\varDelta$ is much larger than the line width. We can then neglect the other transitions, and focus exclusively on the one transition that is resonant with the laser.

In applying the two-level approximation to quantum dots, we make use of their discrete energy level spectrum that follows from the three-dimensional confinement of the electrons and holes. The optical transitions consist of sharp lines, corresponding to neutral exciton, biexciton, charged exciton, etc. transitions. The laser can be tuned close to resonance with one of these, while being many line widths away from the others, justifying the use of the two-level approximation. The fact that the model works well is a clear confirmation of the well-used description of quantum dots as “solid-state atoms”.

An arbitrary superposition state of a two-level system has a wave function of the form:

$$\begin{aligned} | \psi \rangle = c_1 | 1 \rangle + c_2 | 2 \rangle \, , \end{aligned}$$

(10.1)

where $c_1$ and $c_2$ are the amplitude coefficients for the two states. The normalization condition requires that:

$$\begin{aligned} |c_1|^2 + |c_2|^2 = 1 \, , \end{aligned}$$

(10.2)

which suggests that we can represent the state by a vector of unit length starting at the origin. This geometric interpretation of coherent superposition states is called the Bloch representation. The vector that describes the state is called the Bloch vector, and the sphere it defines is the Bloch sphere.

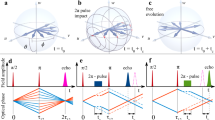
The Bloch representation was originally developed by Felix Bloch in 1946 to model NMR phenomena, and was adapted to two-level atoms by Feynman, Vernon, and Hellwarth in 1957, where they showed that a two-level atom can be regarded as a pseudo-spin 1/2 system [1]. The corresponding optical Bloch equations were derived by Arecchi and Bonifacio in 1965 [2]. This analogy with a spin 1 / 2 particle in a magnetic field is shown schematically in Fig. 10.1.

Fig. 10.1

a Spin 1 / 2 system in a magnetic field B interacting resonantly with microwaves. b Two-level atom interacting resonantly with a laser. c Bloch sphere for representing the state of a two-level system. For historical reasons, we usually consider nuclear spin systems in a, in which case the Zeeman splitting is equal to $g_{I} \mu _\mathrm{N} B$, where $g_I$ is the gyromagnetic ratio and $\mu _\mathrm{N}$ is the nuclear Bohr magneton

The direction of the Bloch vector $\varvec{s}$ can be specified either in Cartesian co-ordinates (x, y, z) or spherical polar co-ordinates $(r,\theta ,\varphi )$. The requirement that the vector has unit length implies that $r^2 = (x^2 + y^2 + z^2) = 1$, so that only two independent variables are required to define an arbitrary state, for example the angles $(\theta ,\varphi )$. This allows us to make a unique mapping between the wave function amplitudes $(c_1, c_2)$ and the direction of the Bloch vector.

The connection between the Bloch sphere and a two-level system may be made by defining the poles to correspond to the $| 1 \rangle$ and $| 2 \rangle$ states respectively, as shown in Fig. 10.1c. The ground state at the south pole with $| \psi \rangle = | 1 \rangle$ thus corresponds to $(0,0,-1)$ in Cartesian co-ordinates or $\theta = \pi$ in polar co-ordinates. Similarly, the pure excited state $| 2 \rangle$ corresponds to (0, 0, 1) or $\theta = 0$. An arbitrary state is given in Cartesian co-ordinates as:

$$\begin{aligned} x= & {} 2 \, \mathrm{Re} \langle c_1 c_2 \rangle \nonumber \, ,\\ y= & {} 2 \, \mathrm{Im} \langle c_1 c_2 \rangle \, , \\ z= & {} | c_2|^2 - |c_1|^2 \nonumber \, , \end{aligned}$$

(10.3)

where the notation $\langle \cdots \rangle$ indicates that we take the average of repeated measurements on identical systems. In polar co-ordinates this simplifies to:

$$\begin{aligned} c_1= & {} \sin (\theta /2) \nonumber \, ,\\ c_2= & {} \mathrm{e}^{\mathrm{i} \varphi } \cos (\theta /2) \, . \end{aligned}$$

(10.4)

This one-to-one mapping allows us to visualize an arbitrary superposition state of a two-level atom in a geometric way, which is very useful when considering the resonant interaction with an intense optical field.

The coherence of a two-level system relies on having a definite phase relationship between $c_1$ and $c_2$, leading to non-zero x and y components of the Bloch vector. By contrast, in a completely incoherent system (i.e. a statistical mixture) we only know the probability that the atom is in the upper or lower level, i.e. the z component of the Bloch vector. The phase relationship between $c_1$ and $c_2$ is random, so that $\langle c_1 c_2 \rangle = 0$, and the x and y components are zero. Statistical mixtures thus correspond to points inside the Bloch sphere with $r < 1$. The system is completely incoherent if both the x and y components are zero, and partially coherent for non-zero x and y but $r<1$. In the equivalent language of the density matrix $\rho _{ij} = \langle c_i c_j^* \rangle$, the coherence is determined by the off-diagonal elements $\rho _{12}$ and $\rho _{21}$, while statistical mixtures only contain information about the diagonal elements $\rho _{11}$ and $\rho _{22}$. Note, however, that there is no difference between superposition states and statistical mixtures for the pure states $|i\rangle$ at the poles of the Bloch sphere with $c_i=1$.

2.2 Rabi Oscillations

The effect of a resonant laser on a two-level atom can understood by solving the time-dependent Schrödinger equation:

$$\begin{aligned} \hat{H} \varPsi = \mathrm{i} \hbar \frac{\partial \varPsi }{\partial t} \, . \end{aligned}$$

(10.5)

We start by splitting the Hamiltonian into a time-independent part $\hat{H}_0$ which describes the atom in the dark, and a perturbation term $\hat{V}(t)$ which accounts for the light-atom interaction:

$$\begin{aligned} \hat{H} = \hat{H}_0(\varvec{r}) + \hat{V}(t) \, . \end{aligned}$$

(10.6)

Since we are dealing with a two-level atom, there will be two solutions for the unperturbed system:

$$\begin{aligned} \hat{H}_0 \varPsi _i = \mathrm{i} \hbar \frac{\partial \varPsi _i}{\partial t} \, , \end{aligned}$$

(10.7)

with

$$\begin{aligned} \varPsi _i({\varvec{r}},t) = \psi _i(\varvec{r}) \exp (-\mathrm{i}E_i t / \hbar ) \; \; \; \; \{i=1,2 \} \, , \end{aligned}$$

(10.8)

and

$$\begin{aligned} \hat{H}_0(\varvec{r}) \psi _i(\varvec{r}) = E_i \, \psi _i(\varvec{r}) \; \; \; \; \{i=1,2 \} \, . \end{aligned}$$

(10.9)

The general solution for a two-level atom is:

$$\begin{aligned} \varPsi (\varvec{r},t) = c_1(t) \psi _1(\varvec{r}) \mathrm{e}^{-\mathrm{i}E_1 t / \hbar } + c_2(t) \psi _2(\varvec{r}) \mathrm{e}^{-\mathrm{i}E_2 t / \hbar } \, . \end{aligned}$$

(10.10)

On substituting (10.10) into (10.5) with $\hat{H}$ given by (10.6), we obtain:

$$\begin{aligned}&{(\hat{H}_0 + \hat{V}) \left( c_1 \psi _1 \mathrm{e}^{-\mathrm{i}E_1 t / \hbar } + c_2 \psi _2 \mathrm{e}^{-\mathrm{i}E_2 t / \hbar } \right) } \nonumber \\&\,\, = \mathrm{i} \hbar \left( (\dot{c}_1 - \mathrm{i} E_1 c_1/\hbar ) \psi _1 \mathrm{e}^{-\mathrm{i}E_1 t / \hbar } + (\dot{c}_2 - \mathrm{i} E_2 c_2 /\hbar )\psi _2 \mathrm{e}^{-\mathrm{i}E_2 t / \hbar } \right) \, . \end{aligned}$$

(10.11)

On using (10.9), and cancelling several terms, this becomes:

$$\begin{aligned} c_1 \hat{V} \psi _1 \mathrm{e}^{-\mathrm{i}E_1 t / \hbar } + c_2 \hat{V} \psi _2 \mathrm{e}^{-\mathrm{i}E_2 t / \hbar } = \mathrm{i} \hbar \dot{c}_1 \psi _1 \mathrm{e}^{-\mathrm{i}E_1 t / \hbar } + \mathrm{i} \hbar \dot{c}_2 \psi _2 \mathrm{e}^{-\mathrm{i}E_2 t / \hbar } \, . \end{aligned}$$

(10.12)

On multiplying by $\psi _i^*$, integrating over space, and making use of the orthonormality of the eigenfunctions, we find that:

$$\begin{aligned} \dot{c}_1(t)= & {} -{\mathrm{i}\over \hbar } \left( c_1(t) V_{11} + c_2(t) V_{12} \mathrm{e}^{-\mathrm{i}\omega _0 t } \right) \, , \nonumber \\ \dot{c}_2(t)= & {} -{\mathrm{i}\over \hbar } \left( c_1(t) V_{21} \mathrm{e}^{\mathrm{i} \omega _0 t}+ c_2(t) V_{22} \right) \, , \end{aligned}$$

(10.13)

where $\omega _0 = (E_2-E_1)/\hbar$ is the transition frequency, and

$$\begin{aligned} V_{ij}(t) \equiv \langle i | \hat{V}(t) | j \rangle = \int \psi _i^* \hat{V}(t) \psi _j \, \mathrm{d}^3 \varvec{r} \, . \end{aligned}$$

(10.14)

To proceed further we must consider the explicit form of the perturbation $\hat{V}$. In the semi-classical approach, the light-atom interaction is given by the energy shift of the atomic dipole in the electric field of the light:

$$\begin{aligned} \hat{V}(t) = e \varvec{r} \cdot \varvec{E}(t) \, . \end{aligned}$$

(10.15)

We arbitrarily choose the x axis as the direction of the polarization so that we can write $\varvec{E}(t) = (E_0, 0,0) \cos {\omega t}$, where $E_0$ is the amplitude of the light wave, and $\omega$ is its angular frequency. The perturbation then simplifies to:

$$\begin{aligned} \hat{V}(t) = e x E_0 \cos {\omega t} = \frac{e x E_0}{2} \left( \mathrm{e}^{\mathrm{i}\omega t} + \mathrm{e}^{-\mathrm{i}\omega t} \right) \, , \end{aligned}$$

(10.16)

and the perturbation matrix elements are given by:

$$\begin{aligned} V_{ij}(t) = \frac{e E_0}{2} \left( \mathrm{e}^{\mathrm{i}\omega t} + \mathrm{e}^{-\mathrm{i}\omega t} \right) \int \psi _i^* x \psi _j \, \mathrm{d}^3 \varvec{r} \, . \end{aligned}$$

(10.17)

We now introduce the dipole matrix element $\mu _{ij}$ given by:

$$\begin{aligned} \mu _{ij} = -e \int \psi _i^* x \psi _j \, \mathrm{d}^3 \varvec{r} \equiv -e \langle i | x|j \rangle \, . \end{aligned}$$

(10.18)

Since x is an odd parity operator and atomic states have well-defined parities, it follows that $\mu _{11} = \mu _{22} =0$. Moreover, $\mu _{ij}$ represents a measurable quantity and must therefore be real, implying $\mu _{21}=\mu _{12}$, because $\mu _{21} = \mu _{12}^*$. With these simplifications, (10.13) reduces to:

$$\begin{aligned} \dot{c}_1 (t)= & {} \mathrm{i} \frac{E_0 \mu _{12}}{2 \hbar } \left( \mathrm{e}^{\mathrm{i}(\omega -\omega _0)t} + \mathrm{e}^{-\mathrm{i}(\omega +\omega _0) t} \right) c_2(t) \, , \nonumber \\ \dot{c}_2 (t)= & {} \mathrm{i} \frac{E_0 \mu _{12}}{2 \hbar } \left( \mathrm{e}^{-\mathrm{i}(\omega -\omega _0)t} + \mathrm{e}^{\mathrm{i}(\omega +\omega _0) t} \right) c_1(t) \, . \end{aligned}$$

(10.19)

We now introduce the Rabi frequency defined by:

$$\begin{aligned} \varOmega _\mathrm{R} = | \mu _{12} E_0 / \hbar | \, . \end{aligned}$$

(10.20)

We then finally obtain:

$$\begin{aligned} \dot{c}_1 (t)= & {} \frac{\mathrm{i}}{2} \varOmega _\mathrm{R} \left( \mathrm{e}^{\mathrm{i}(\omega -\omega _0)t} + \mathrm{e}^{-\mathrm{i}(\omega +\omega _0) t} \right) c_2(t) \, , \nonumber \\ \dot{c}_2 (t)= & {} \frac{\mathrm{i}}{2} \varOmega _\mathrm{R} \left( \mathrm{e}^{-\mathrm{i}(\omega -\omega _0)t} + \mathrm{e}^{\mathrm{i}(\omega +\omega _0) t} \right) c_1(t) \, . \end{aligned}$$

(10.21)

These are the equations that must be solved to understand the behaviour of the atom in the light field. The solutions in the weak-field limit (i.e. low light intensity) correspond to the incoherent Einstein B coefficient analysis of transition rates. In what follows, we focus instead on the strong-field limit.

The equations can be simplified by applying the rotating wave approximation in which we move to a rotating frame at frequency $\omega _0$. The term at $(\omega +\omega _0)$ oscillates very rapidly in this frame, while the one at $(\omega -\omega _0)$ is nearly stationary. We therefore neglect the former and focus on the latter to obtain:

$$\begin{aligned} \dot{c}_1 (t)= & {} \frac{\mathrm{i}}{2} \varOmega _\mathrm{R} \mathrm{e}^{\mathrm{i}\varDelta t} c_2(t) \, , \nonumber \\ \dot{c}_2 (t)= & {} \frac{\mathrm{i}}{2} \varOmega _\mathrm{R} \mathrm{e}^{-\mathrm{i}\varDelta t} c_1(t) \, , \end{aligned}$$

(10.22)

where $\varDelta = \omega -\omega _0$ is the detuning. For exact resonance with $\varDelta = 0$, we find

$$\begin{aligned} \ddot{c}_1 = \frac{\mathrm{i}}{2} \varOmega _\mathrm{R} \dot{c}_2 = \left( \frac{\mathrm{i}}{2} \varOmega _\mathrm{R} \right) ^2 c_1 \, . \end{aligned}$$

(10.23)

We then obtain the equation of motion:

$$\begin{aligned} \ddot{c}_1 + \left( {\varOmega _\mathrm{R} \over 2} \right) ^2 c_1 = 0 \, , \end{aligned}$$

(10.24)

which describes oscillatory motion at angular frequency $\varOmega _\mathrm{R}/2$. If the particle is in the lower level at $t=0$ so that $c_1(0) = 1$ and $c_2(0) = 0$, the solution is:

$$\begin{aligned} c_1(t)= & {} \cos {(\varOmega _\mathrm{R} t /2) } \, , \nonumber \\ c_2(t)= & {} \mathrm{i} \sin {(\varOmega _\mathrm{R}t/2)} \, . \end{aligned}$$

(10.25)

The probabilities for finding the electron in the upper or lower levels are then:

$$\begin{aligned} |c_1(t)|^2= & {} \cos ^2 {(\varOmega _\mathrm{R}t/2) } \, , \nonumber \\ |c_2(t)|^2= & {} \sin ^2 {(\varOmega _\mathrm{R}t/2)} \, . \end{aligned}$$

(10.26)

The time dependence of these probabilities is shown in Fig. 10.2. At $t = \pi / \varOmega _\mathrm{R}$ the electron is in the upper level, whereas at $t = 2\pi / \varOmega _\mathrm{R}$ it is back in the lower level. The process then repeats itself with a period equal to $2\pi / \varOmega _\mathrm{R}$. The electron thus oscillates back and forth between the lower and upper levels at a frequency equal to $\varOmega _\mathrm{R}/2 \pi$. This oscillatory behaviour in response to the strong light field is called Rabi oscillation or Rabi flopping. It has been observed in many systems, and, as we shall see in Sect. 10.2.4, can be given a geometric interpretation in terms of rotations of the Bloch vector. Observations of Rabi flopping in quantum dots will be discussed in Sect. 10.4.2.

Fig. 10.2

Rabi oscillations for a two-level atom interacting with a resonant laser in the absence of damping. The electron oscillates back and forth between the two levels at the Rabi frequency, $\varOmega _\mathrm{R}$

For the more general case where $\varDelta \ne 0$, it can be shown that:

$$\begin{aligned} |c_2(t)|^2 = \frac{\varOmega _\mathrm{R}^2}{\varOmega ^2} \sin ^2 {(\varOmega t/2)} \, , \end{aligned}$$

(10.27)

where $\varOmega = \sqrt{\varDelta ^2 + \varOmega _\mathrm{R}^2}$ is the generalised Rabi frequency. This shows that the frequency of the Rabi oscillations increases but their amplitude decreases as the light is tuned away from resonance, which explains why we can neglect off-resonant transitions.

The observation of Rabi flopping often requires powerful, pulsed lasers, so that the electric field amplitude $E_0$, and hence $\varOmega _\mathrm{R}$, varies with time. It is then useful to define the pulse area $\varTheta$ according to:

$$\begin{aligned} \varTheta = \left| {\mu _{12} \over \hbar } \int _{-\infty }^{+\infty } E_0 (t) \, \mathrm{d} t \right| \, . \end{aligned}$$

(10.28)

This is a dimensionless parameter that serves the same purpose as $\varOmega _\mathrm{R}t$ in the analysis above. A pulse with $\varTheta = \pi$ is called a $\pi$-pulse , etc. An atom in the ground state with $c_1 = 1$ at $t=0$ will thus be promoted to the excited state by a $\pi$-pulse, but will end up back in the ground state if it interacts with a $2\pi$-pulse. Note, however, that additional geometric phase shifts can be picked up by fermionic particles during Rabi rotations. These are important in the spin control experiments described in Sect. 10.5.

2.3 Damping

We have assumed so far that the wave functions remain completely coherent while being driven by the laser. In reality, collisions, or interactions with the environment, randomize the phases, leading to a loss of coherence. The damping mechanisms that cause decoherence are generally determined by two time constants, $T_1$ and $T_2$ , originally introduced in NMR theory.

The $T_1$ time characterizes the spontaneous decay rate of the population from the upper state, for example, by a radiative transition:

$$\begin{aligned} \frac{\text {d} N_2}{\text {d}t} = - \frac{N_2}{T_1} \, , \end{aligned}$$

(10.29)

where $N_2 = |c_2(t)|^2 N$ is the population of the upper level in an ensemble of N identical systems. Solution of (10.29) gives exponential decay with $N_2(t) = N_2(0) \exp (-t/T_1)$, which shows that $T_1$ is the lifetime of the upper level, and characterises the decay of the z component of the Bloch vector, as shown in Fig. 10.3a. Since radiative transitions occur spontaneously (i.e. at random times, triggered by vacuum fluctuations), they destroy all phase information in the system. Non-radiative process can also contribute to $T_1$. An example of particular relevance to quantum dot physics is the tunnelling of electrons and holes out of a dot in an electric field.

The $T_2$ time gives the timescale over which coherence is maintained. It is related to $T_1$ through the following relationship:

$$\begin{aligned} \frac{1}{T_2} = \frac{1}{2T_1} + \frac{1}{T_2^*} \, . \end{aligned}$$

(10.30)

The first term accounts for the loss of coherence due to population decay. The second is the pure dephasing rate $(T_2^*)^{-1}$. The $T_2^*$ time quantifies pure dephasing processes in which z is unchanged, for example: elastic scattering by phonons or by fluctuating fields from impurities. This difference is illustrated in Fig. 10.3a. The $T_2^*$ processes cause a coherent state on the surface of the Bloch sphere to relax to a mixed state on the z axis, and is therefore called transverse relaxation This contrasts with the longitudinal $T_1$ processes that causes changes in z as well as x and y.

Fig. 10.3

a Damping processes in the Bloch representation: $T_2^*$ processes conserve z but $T_1$ processes do not. b Damped Rabi oscillations for two values of the ratio of the damping rate $\gamma$ to the Rabi oscillation frequency $\varOmega _\mathrm{R}$. The dotted curve shows the oscillations when no damping is present

The overall coherence time is given by $T_2$. In a system with negligible pure dephasing (i.e. $T_2^* \gg T_1$), the coherence time is $2T_1$. This means that the ultimate limit on $T_2$ is set by the lifetime of the upper level. The factor of two between $T_2$ and $T_1$ in this limit arises from the fact that coherence is sensitive to the wave function amplitude (i.e. $c_2$), whereas population depends on $|c_2|^2$. For a system with simple exponential dynamics following (10.29), $c_2$ decays at half the rate as the population: $|c_2(t)| \propto \exp (-t/2T_1)$.

The probability that a damped two-level system is in the upper level when driven on resonance is given by [3]:

$$\begin{aligned} |c_2(t)|^2 = \frac{1}{2(1 + 2 \xi ^2)} \left[ 1 - \left( \cos {\varOmega ' t} + \frac{3\xi }{(4-\xi ^2)^{1/2}} \sin {\varOmega ' t} \right) \exp \left( -{3\gamma t \over 2} \right) \right] \, , \end{aligned}$$

(10.31)

where $\xi = \gamma / \varOmega _R$ and $\varOmega ' = \varOmega _R \sqrt{ 1 -\xi ^2/4 }$. The parameter $\gamma$ that enters here is the damping rate $1/T_2$. It is easily verified that this formula reduces to the undamped case given in (10.26) when $\gamma = 0$. The effect of damping on Rabi oscillations is illustrated in Fig. 10.3b. The dotted line shows the undamped case with $\gamma = 0$ shown previously in Fig. 10.2. The two other graphs demonstrate the effect of increasing damping. With light damping ($\gamma / \varOmega _\mathrm{R} = 0.1$), the system performs a few damped oscillations and then approaches the asymptotic limit with $|c_1|^2 = |c_2|^2 = 1/2$. This asymptotic limit is exactly the behaviour predicted by the incoherent analysis based on the Einstein B coefficients, where the rates of stimulated emission and absorption eventually equal out at high pumping rates, leading to identical upper and lower level populations. With stronger damping ($\gamma / \varOmega _\mathrm{R} = 1$), no oscillations are observed, and we recover the fully incoherent picture where $|c_2(\infty )|^2$ is proportional to the laser power, independent of time. This asymptotic limit is best seen by setting $\xi \gg 1$, in which case the probability of occupation of the upper level at long times is equal to $\xi ^{-2} /4 = \mu _{12}^2 E_0^2 / 4 \hbar ^2 \gamma ^2$, i.e. proportional to the Einstein B coefficient via $\mu _{12}^2$ and the laser power via $E_0^2$.

The conclusion of this analysis is that Rabi oscillations can only be observed in highly coherent systems where the damping rate is significantly smaller than the Rabi frequency. In atomic gases, the damping rate depends on the collision rate and the radiative lifetime, which gives $\gamma \sim 10^7 - 10^9$ s$^{-1}$. In semiconductors the dephasing times are often much shorter due to phonon scattering, scattering by free charge carriers, or tunnelling. This makes the task of demonstrating Rabi oscillations somewhat difficult, which explains why they are not routinely observed. The art of coherent control experiments thus entails reducing the damping rate as much as possible (e.g. by working with very pure samples at low temperatures) and using lasers with pulses that are shorter than the coherence time.

2.4 Coherent Rotations on the Bloch Sphere

The previous sub-sections have established the basic principles for the main focus of this chapter, namely the coherent manipulation of a two-level system by a resonant laser pulse with duration shorter than $T_2$. This process is best visualised by considering the Bloch vector $\varvec{s}$. If damping is negligible, the system remains coherent, and the pulse only changes the direction of $\varvec{s}$ without altering its length. This means that the pulse acts as a rotation operator. We showed previously that a $\pi$-pulse can convert a system in the ground state $|1\rangle$ to the excited state $|2\rangle$, and vice versa. This corresponds to a change of the Bloch vector angle $\theta$ by $\pi$ radians, and explains the origin of the name ‘$\pi$-pulse’. In general, it can be shown that the rotation angle is equal to the pulse area defined in (10.28). Hence a pulse of area $\varTheta$ causes a rotation of $\varvec{s}$ by $\varTheta$ radians.

In analysing coherent manipulations of Bloch vectors, we can usually assume that the system is initially in the ground state. The azimuthal angle of the Bloch sphere is then undefined, which means that the azimuthal angle of the rotation axis is also undefined. It is therefore convenient to choose the x and y axis directions so that the first pulse in a sequence produces a rotation about, say, the y axis, leaving the Bloch vector in x–z plane at the end of the pulse. The axis about which subsequent rotations take place is then determined by the phases of the pulses relative to the first one. Combinations of pulses of the appropriate area and phase can then be used to move the Bloch vector to any particular point on the Bloch sphere.

Figure 10.4 illustrates how this works in Ramsey interference experiments. The system is initially in the ground state as shown in Fig. 10.4a. A resonant $\pi /2$ pulse is incident and rotates the Bloch vector by $90^\circ$ to a point on the equator, as shown in Fig. 10.4b. The system is then interrogated with a second $\pi /2$ pulse with phase $\varDelta \varPhi$ relative to the first one. If the second pulse is in phase ($\varDelta \varPhi = 2 m \pi$, $m = \text {integer}$, Fig. 10.4c, top half), the second $90^\circ$ rotation takes place about the same axis as the first, and the system ends up at the north pole. However, if the second pulse is out of phase ($\varDelta \varPhi = (2 m+1) \pi$, Fig. 10.4c, bottom half), the rotation takes place about an axis pointing in the opposite direction to the first, leaving the system at the south pole. Figure 10.4d illustrates the equivalent picture when dephasing is included. The system ends up in a mixed state along the z axis, either in the upper or lower half of the Bloch sphere, depending on the relative phase of the second pulse.

Fig. 10.4

Ramsey interference experiment illustrated on the Bloch sphere. a The system is initially in the ground state. b A resonant pulse of area $\pi /2$ rotates the system to a point on the equator. c A second resonant $\pi /2$ pulse with relative phase $\varDelta \varPhi$ rotates the system to the north or south pole respectively when $\varDelta \varPhi = 2 m \pi$ or $(2m+1) \pi$, m being an integer. d Same as c, but with dephasing included

A final mention should be made of the case of off-resonant pulses. Equation (10.27) implies that an off-resonant pulse with detuning $\varDelta$ induces Rabi oscillations at a slightly different frequency, and with reduced amplitude. This can be visualised as rotations about an axis with polar angle $\alpha$ relative to the equatorial plane, where $\tan \alpha = \varDelta /\varOmega _\mathrm{R}$ [4]. As with resonant pulses, the azimuthal angle is determined by the phase. This off-equatorial rotation for finite $\varDelta$ accounts for the reduced amplitude of the Rabi flopping. Note that $\alpha = 0$ for $\varDelta =0$, and that $\alpha = \pi /2$ for $\varOmega _\mathrm{R} =0$.

3 Quantum Dots as Coherent Systems

In the sections that follow, coherent control experiments on quantum dots (QDs) will be reviewed in detail. However, it is first useful to make some general remarks that explain the interest in QDs for coherent state manipulation.

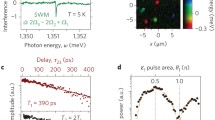
The observation of intense, discrete lines in the emission spectra of individual dots in 1994 [5] immediately pointed to the 3-D confinement of the electrons and holes. A particularly striking feature was the sharpness of the lines: see, for example, Fig. 10.5c. Since the width $\varDelta E$ of spectral lines is determined by the dephasing time of the emitters, a sharp line implies a long $T_2$ time. At the time when single-dot spectra were first observed, the state-of-the-art in semiconductor optics was set by quantum-well samples in GaAs-related materials. The very best samples showed $\varDelta E \sim 0.1$ meV, which implied $T_2 \sim 10$ ps at best. While very impressive results were demonstrated (see e.g. [6,7,8]), the short dephasing time made long-term applications difficult. With InGaAs quantum dots, by contrast, it is relatively straight forward to get $\varDelta E \sim 0.01$ meV, with the best samples showing $\varDelta E \sim 1 \, \upmu$eV, limited only by the ${\sim } 1$ ns radiative lifetime [9]. From this we can deduce that, in the right conditions, pure dephasing can effectively be eliminated, leading to ${\sim } 1$ ns coherence times. Such long $T_2$ times were indeed verified from four-wave mixing experiments on QD ensembles in 2001 [10].

Fig. 10.5

Data from E.A. Chekhovich and M.N. Makhonin

a Energy level spectrum of the exciton and biexciton in a neutral dot in the linearly-polarized basis. The two eigenstates $|X_x\rangle$ and $|X_y\rangle$ are split by the fine-structure splitting (FSS) ($\hbar \delta$). b Circularly-polarized basis with excitation bandwidth ${>} \hbar \delta$. The FSS causes precession between the two eigenstates, indicated by the green arrows. The exciton and biexciton energies are given respectively by $\hbar \omega _X$ and $\hbar \varDelta _{XX}$. For clarity, the splittings are not to scale, as $\hbar \delta \ll \hbar \varDelta _{XX} \ll \hbar \omega _X$. c Emission spectrum of a typical dot. The neutral exciton and biexciton lines are identified. The $X^+$ line arise from a positively charged exciton. The inset gives a high resolution spectrum of the $X^0$ line of a similar dot, from which the FSS can be deduced.

Another very striking feature of QDs is the absence of phonon side-bands. Most localized emitters in solid-state hosts (e.g. NV centres in diamond, Ti$^{3+}$ ions in sapphire) are strongly coupled to phonons, giving rise to vibronic sidebands in their emission and absorption spectra. In the case of NV centres, for example, the coupling is so strong that only a few percent of the emission occurs in the zero-phonon line, with most of the photons emitted from the sidebands [11]. The relatively weak intensity of the zero-phonon line has serious consequences for practical applications in optical QIP.

The reason for the strong phonon sidebands in materials like diamond NV centres and Ti:sapphire is that both the electronic and vibrational modes are localized on length scales similar to the unit cell size. This means that the overlap between the electronic wave functions and the phonon modes is large. By contrast, InGaAs quantum dots (QDs) have envelope wave functions localized on much larger length scales that are determined by the size of the dot, i.e. ${\sim } 10$ nm. This means that the coupling to phonons is relatively weak, with the dominant interaction being to longitudinal-acoustic (LA) phonons via deformational potential scattering. The weak vibronic coupling gives rise to very strong emission in the zero-phonon line, with only ${\sim }$8% in the sideband at cryogenic temperature [12, 13]. This makes InGaAs QDs excellent single-photon sources [14]. It also gives a small phonon dephasing rate, and hence explains the long $T_2$ time discussed above.

It should be noted that the actual coherence times measured in QDs are still shorter than those obtained in atomic systems. This follows immediately from the short (${\sim } 1$ ns) radiative lifetime of InGaAs QDs, compared to atomic transitions (e.g. 16 ns for sodium D lines at ${\sim } 589$ nm). However, this is not necessarily a drawback provided we work in the regime where $T_2$ is limited by the radiative lifetime. As discussed in Sect. 10.2.3, the key parameter is the ratio of the Rabi frequency to the damping rate. The Rabi frequency is determined by the dipole moment of the transition (see (10.20)), which also determines the radiative lifetime. Hence a system with a large dipole moment automatically has a short coherence time, but the ratio $\varOmega _\mathrm{R}/\gamma$ is not necessarily adversely affected. In fact, InGaAs QDs typically have dipole moments of ${\sim } 30$ Debye (${\sim } 1 \times 10^{-28}$ C m) [15], which is at least an order of magnitude larger than atoms. The larger dipole moment means that the light-matter coupling is stronger, enabling efficient driving at relatively low powers. Overall, InGaAs QDs represent a good compromise between strong light-matter coupling and freedom from dephasing (at least compared to bulk and quantum well semiconductors.) These properties, combined with their compatibility with advanced technological device processing, makes QDs very attractive for QIP applications.

There are several different types of quantum dots, but this chapter focusses on the self-assembled InGaAs QDs grown by epitaxial methods such as molecular beam epitaxy (MBE) or metal-organic chemical vapour deposition (MOCVD). QDs can also be formed during MBE growth of pure GaAs layers at interface islands due to monolayer fluctuations [16]. In fact, the first coherent control experiment on single III-V QDs was performed on these types of dots [17], and this was soon followed by two other key ‘firsts’: Rabi flopping [18] and a two-qubit quantum gate [19]. However, the electrons and holes in these interface dots are only weakly confined, making them very sensitive to temperature, and also to scattering form free carriers, which can come from either impurities or optical excitation. This means that their $T_2$ times, although substantially better than bulk or quantum well semiconductors, are shorter than those of InGaAs dots. There are also colloidal quantum dots, but these are hard to incorporate into photonic devices. For these reasons, InGaAs dots are best suited for most applications in QIP.

We should also clarify that everything considered in this section so far refers to the excitons created when electron and hole pairs are excited in QDs by absorption of photons. These excitons have radiative lifetimes of ${\sim } 1$ns, which sets a similar upper limit on $T_2$. At the same time, they interact very strongly with light, which facilitates their coherent manipulation (see Sect. 10.4 below). An alternative approach involving the coherent control of spins in charged QDs will be discussed in Sect. 10.5. Charged dots contain electrons or holes before the laser is incident, and the goal is to rotate the carrier spins with the laser. Since the resident carriers cannot recombine, $T_2$ is no longer limited by the radiative lifetime. On the other hand, light does not interact directly with electron or hole spins, which makes the coherent manipulation techniques more challenging. There are therefore advantages and disadvantages of working with spins, as will be discussed in Sect. 10.5.

4 Coherent Control of Excitons

The relatively long coherence times of excitons in QDs facilitate their use in ultrafast coherent control experiments. The DiVincenzo checklist for QIP requires that we demonstrate complete control of single excitonic qubits, and establish at least one excitonic two-qubit gate [20]. We therefore begin this section by considering the coherent control of single excitons, which can be visualized as single qubit rotations, and finish with two-exciton systems. We focus exclusively on bright excitons, leaving the discussion of dark excitons to Chap. 4.

In this chapter we restrict our discussion of QD coherence to the time domain. There is an equivalent approach that investigates QD coherence in the frequency domain through high-resolution spectroscopy. Examples include the observation of the Mollow triplet [21], and the Autler–Townes doublet [22, 23]. Phenomena such as these are discussed elsewhere in this book (see e.g. Chaps. 2 and 3).

4.1 Level Structure of Excitons in Neutral Quantum Dots

Before considering the principles of coherent control experiments on QDs, we must first review the excitonic level structure of a typical dot. We assume here that the dot is neutral: i.e. that it contains no free electrons or holes before the laser pulse arrives. (Charged dots will be considered in Sect. 10.5.) Furthermore, we neglect the light-hole (LH) bands, since they have significantly larger confinement energies than heavy-hole (HH) bands.

Absorption of a photon creates an electron in the conduction band and a hole in the valence band, which then bind together to form an exciton through their mutual Coulomb attraction. The exciton state in a neutral dot containing one electron and hole, both in their lowest confined energy states (i.e. the s-shell), is typically notated as $X^{0}$. Since heavy holes have $m_{z}^{hh} = \pm 3/2$, the possible z-axis spin projections of the exciton are given by:

$$\begin{aligned} S_{z}=m_{z}^{hh}+m_{z}^{e}=\pm \frac{3}{2}\pm \frac{1}{2}=-2,\,-1,\,1,\,2 \, . \end{aligned}$$

(10.32)

Absorption/emission of a single circularly-polarized photon may only impart a change in angular momentum of $\pm 1$. Hence $S_{z}=\pm 1$ “bright excitons” with circular polarization $\left| \uparrow \Downarrow \right\rangle$ and $\left| \downarrow \Uparrow \right\rangle$ are optically allowed whilst $S_{z}=\pm 2$ “dark excitons” are optically forbidden. Here, and throughout the whole of this chapter, the notation $|$ $\uparrow$ $\rangle$ and $|$ $\Uparrow$ $\rangle$ refers to electron and heavy-hole spin states respectively.

An ideal QD exhibits radial symmetry in the growth (x–y) plane. However, the self-assembly process typically leads to QDs with some degree of asymmetry. In this case the two bright exciton states become coupled by the electron-hole exchange interaction [24], causing a precession between the $S_{z}=\pm 1$ states with angular frequency $\delta$ [25]. As a result, the eigenstates are linearly polarized and split by the fine-structure splitting (FSS) $\hbar \delta$ as shown in Fig. 10.5a, with:

$$\begin{aligned} \left| X_{x}\right\rangle= & {} \frac{1}{\sqrt{2}}\left\{ \left| \downarrow \Uparrow \right\rangle +\left| \uparrow \Downarrow \right\rangle \right\} \nonumber \\ \left| X_{y}\right\rangle= & {} \frac{1}{\sqrt{2}}\left\{ \left| \downarrow \Uparrow \right\rangle -\left| \uparrow \Downarrow \right\rangle \right\} \, , \end{aligned}$$

(10.33)

where the axes x and y are defined by the asymmetry of the dot, often coinciding with the [111] and $[1\overline{1}1]$ crystal axes. The magnitude of $\hbar \delta$ varies significantly from dot to dot, as it originates from the randomness of the self-assembly process [26]. Its value is a very important parameter in the coherent control of excitons (see Sect. 10.4.3), and also in the initialisation of spin states in charged dots (see Sect. 10.5.2). Moreover, its minimisation is highly important for the generation of entangled photons [27, 28]. The control of the fine-structure splitting is therefore an important research field (see Chap. 7).

The s-shells of a QD can be occupied by two carriers with opposite spins. It is therefore possible for both of the $S_{z}=\pm 1$ neutral excitons to exist simultaneously, forming a biexciton (generally denoted as either XX or 2X). The Coulomb interaction between the excitons results in a binding energy ($E_{XX}=\hbar \varDelta _{XX}$) that reduces the biexciton energy to less than that of two excitons. The resulting energy level structure is illustrated in Fig. 10.5. Figure 10.5a shows the linearly polarised basis, where the two $X^0$ eigenstates defined in (10.33) are split by the FSS energy $\hbar \delta$. For circular excitation ($\varvec{\sigma }^\pm = \varvec{\hat{x}} \pm I\varvec{\hat{y}}$) as shown in Fig. 10.5b, both $X^0$ spin states are excited and the energy splitting is zero. However, as the eigenstates of the system are linear, the exciton spin precesses with a frequency $\delta$.

Figure 10.5c shows a typical emission spectrum of a single InGaAs quantum dot at 4 K. The neutral exciton and biexciton states are labelled. The energy shift between the $X^0$ and XX states is equal to 2.37 meV, which equates with the biexciton binding energy $\hbar \varDelta _{XX}$ for this dot. The FSS of the $X^0$ line is clearly shown in the high-resolution spectrum for another dot in the inset. A value of $\hbar \delta = 9.9 \, \upmu$eV is deduced, together with an exciton linewidth of $4.3 \, \upmu$eV, corresponding to a coherence time $T_2 \sim 150$ ps. This linewidth is smaller than the resolution limit of most spectrometers, and its measurement usually requires the use of a scanning Fabry–Perot interferometer. The lines do, of course, broaden with temperature, implying a reduction in $T_2$. For this reason, the best coherent control results are generally obtained at 4 K.

A third strong line labelled $X^+$ is also clearly visible in Fig. 10.5c. This line is due to a positively-charged exciton state and will be discussed in Sect. 10.5. Charged excitons can be observed in “neutral” dots through the capture of free electrons or holes from the wetting layer.

4.2 Rabi Flopping

The first observation of Rabi flopping for excitons in a single quantum dot was obtained for GaAs interface dots in 2001 [18]. Similar observations were soon obtained for single InGaAs/AlGaAs dots [29] and for ensembles of self-assembled InGaAs/GaAs dots [30, 31]. In these experiments, the exciton population was measured as a function of increasing pulse area, as in Fig. 10.3b. The Rabi oscillations were subsequently observed directly in the time domain by measuring the second-order correlation of the photons emitted [32] or by performing pump-probe experiments using two pulses [33]. Rabi flopping has also been observed for biexcitons by tuning the laser to the two-photon resonance midway between the $X^0$ and XX transition frequencies [34].

In 2002, Zrenner et al. established the photocurrent technique that has been used extensively for the experimental work reviewed in this chapter [35]. A schematic of the method is given in Fig. 10.6a. The self-assembled InGaAs quantum dots are embedded within a reverse-biassed Schottky diode, and are excited through a nano-aperture within a metal shadow mask. With nano-apertures in the sub-$\upmu$m range, the number of dots interrogated by the laser is reduced to ${\sim } 10$ for dot densities of ${\sim } 10^9\, \mathrm {cm}^{-2}$. The randomness of the self-assembly leads to fluctuations in the size and shape, and hence confinement energies, so that individual QDs can be addressed by tuning the laser. Coherent effects from single dots can then be observed when excited resonantly by a laser pulse with duration shorter than the coherence time.

An attractive feature of the photocurrent technique is that the final state of the dot can be deduced very easily from the photocurrent measured in the external circuit. With negative bias applied to the diode, the dots experience a strong electric field, and tunnel out towards the contacts, as shown schematically in Fig. 10.6a. A $\pi$-pulse leaves the dot containing a single exciton, which then generates one electron in the external circuit. For a laser repetition rate of f, the current is equal to fe, where e is the electron charge. This gives a current of around 13 pA for a typical laser repetition rate of ${\sim } 80$ MHz, which is easily measurable with a precision pico-ammeter. The actual current measured is typically lower than this, due to competition with radiative recombination before tunnelling occurs.

Fig. 10.6

a Schematic of experiment to observe Rabi rotations in a quantum dot photodiode. The laser pulse width must be shorter than the exciton coherence time. b Rabi rotation of the neutral exciton transition of a single InAs/GaAs quantum dot at 4 K. The photocurrent (final exciton population) oscillates according to the pulse area $\varTheta$ (which is proportional to the square root of the applied laser power). The red line shows a damped sinusoidal fit to the data

Figure 10.6b shows a typical Rabi oscillation measurement on a single self-assembled InGaAs/GaAs quantum dot at 4 K. Six oscillatory periods are clearly visible, but with substantial damping as the pulse area $\varTheta$ increases. This damping is mainly caused by the way the measurements are made. In NMR experiments, the pulse area defined in (10.28) is varied by changing the pulse duration while keeping its amplitude constant. This is not practical for ultrafast laser experiments, since the pulse length cannot be changed easily. Moreover, since the pulse length changes the laser bandwidth, the excitation conditions are also changed by varying the pulse width. For these reasons, the pulse area is varied by keeping the pulse duration constant, and increasing its amplitude. This means that the laser driving power P is varying as $\sqrt{P}$ along the x axis in Fig. 10.6b, and the damping at high pulse areas is related to this increase in the excitation intensity. The damping is therefore termed Excitation Induced Dephasing (EID). It is important to point out that qubit control experiments on QDs are typically carried out at pulse areas of ${\sim } \pi$ (see Sect. 10.4.3), where EID is small.

Ramsay et al. performed careful studies of the effect of temperature on Rabi flopping, and demonstrated that EID arises from phonon interactions [36, 37]. The dominant coupling is to longitudinal-acoustic (LA) phonons via deformation potential scattering, which is quantified by the function $J (\omega )$:

$$\begin{aligned} J(\omega ) =\frac{\omega ^{3}}{4\pi ^{2}\rho \hbar v_{c}^{5}} \left[ D_{\mathrm {e}}\, \mathrm{{e}}^{ \left( -\omega ^{2}a_{\mathrm {e}}^{2}/4v_{c}^{2} \right) } -D_{\mathrm {h}}\, \mathrm{{e}}^{\left( -\omega ^{2}a_{\mathrm {h}}^{2}/4v_{c}^{2} \right) } \right] ^{2} \, . \end{aligned}$$

(10.34)

The parameters that enter here are the mass density $\rho$, the sound velocity $v_{c}$, the deformation potential constants for electrons and holes $D_{\mathrm {e/h}}$, and the electron/hole confinement lengths inside the dot, $a_{\mathrm {e/h}}$. The function $J(\omega )$ increases at first with $\omega$ due to the $\omega ^3$ factor from the LA-phonon density of states. It passes through a peak, and then rolls off rapidly above the “cut-off frequency” due to the exponential form-factors that characterize the physical size of the dot. For typical InGaAs dots, values of $a_{\mathrm {e}}=4.5$ nm and $a_{\mathrm {h}}=1.8$ nm are obtained [38], and $J(\omega )$ peaks at about 1–2 meV. The significance is that the damping rate for Rabi rotations is governed by $J(\varOmega _\mathrm{R})$, i.e. the electron-phonon coupling at the Rabi frequency. For the data shown in Fig. 10.6b, the largest Rabi frequency is still smaller than the cut-off frequency, and so the damping gets stronger at higher pulse areas. In principle, the damping rate should weaken for very strong driving when $\varOmega _\mathrm{R}$ exceeds the cut-off frequency [39]. This phenomenon is sometimes called phonon revival, but not yet been observed experimentally.

4.3 Manipulation of Exciton States

The demonstration of Rabi flopping confirms the possibility of moving the exciton state around the Bloch sphere in a coherent way. However, a single rotation does not give access to all points on the Bloch sphere, as required for full single-qubit control: two rotations are needed, about different axes. In this sub-section, we shall see how this is done.

The simplest way to achieve full Bloch sphere control is to use two resonant pulses with a well-defined phase difference. This works because the azimuthal angle for the second pulse is determined by its phase relative to the first. A key demonstration of this principle is the observation of Ramsey interference, as explained in Fig. 10.4. Such Ramsey interference was first observed for InGaAs dots within a Schottky photodiode by using two phase-locked excitation pulses of area $\pi /2$ [40, 41]. The time between the pulses had to be less than the exciton coherence time, which was determined by the loss of electrons out of the dot by electric-field-induced tunnelling.

While proving the principle, the Ramsey method suffers from the need to keep the phases of the pulses locked together over long periods, which requires an actively-stabilised interferometer. For this reason, simpler methods have been employed that exploit the fine-structure splitting of the dot. As noted in Sect. 10.4.1, a typical neutral InGaAs dot has two linearly polarized excitons split by the FSS $\hbar \delta$, as shown in Fig. 10.5a. If the dot is excited with a $\varvec{\sigma }^+ \equiv \varvec{\hat{x}} + I\varvec{\hat{y}}$ pulse with bandwidth $> \delta$ at time $t=0$, both eigenstates are excited, and the wave function evolves as:

$$\begin{aligned} \varPsi (t) = \frac{1}{\sqrt{2}} \left( |X_x\rangle + I|X_y\rangle \mathrm{{e}}^{I\delta t} \right) \, , \end{aligned}$$

(10.35)

where the phase factor accounts for the frequency difference between $|X_x\rangle$ and $|X_y\rangle$. This evolves to a linear state [$(|X_x\rangle - |X_y\rangle )/ \sqrt{2}$] at $t= \pi /2\delta$, through to an opposite circular state [$(|X_x\rangle - I|X_y\rangle )/ \sqrt{2}$] at $t= \pi /\delta$, to an opposite linear state [$(|X_x\rangle + |X_y\rangle )/ \sqrt{2}$] at $t=3 \pi /2\delta$, and finally back to the original circular state at $t= 2\pi /\delta$. On realizing that the polarization Poincaré sphere maps directly to the exciton spin Bloch sphere, with the $\sigma ^\pm$ and diagonal linear states at the four cardinal points of the equator, it is apparent that the FSS causes a precession about the $\varvec{\hat{z}}$ axis at a rate $\delta$. This can then be combined with a single x-axis rotation by a resonant optical pulse to reach arbitrary points on the exciton Bloch sphere [42]. A second “control” pulse can also be added to achieve optical rotation of the exciton spin while it is precessing [43,44,45].

Fig. 10.7

After [46], data from J.H. Quilter

Fine-structure beats from a single InGaAs dot measured by the photocurrent (PC) technique. a Raw data for co- and cross-polarized probe pulses. b Difference of the two signals in a.

The fine-structure beats were first observed for single GaAs interface QDs in 1998 [17], and then for an ensemble of InGaAs dots in 2004 [25]. Recent results on fine-structure beating from a single InGaAs dot are shown in Fig. 10.7 [46]. The dot was in a Schottky diode as in Fig. 10.6a, and was excited with a resonant $\sigma ^+$ pulse of area $\pi$ at $t=0$. The dot was then probed by a second $\pi$ pulse with either $\sigma ^+$ or $\sigma ^-$ polarization at varying time delay. When the spin of the exciton is co-polarized with the probe, the probe de-excites the exciton and reduces the photocurrent (PC) signal. When the spin of the exciton is cross-polarized with the probe, the probe does nothing. Hence the photocurrent signal oscillates at the same rate as the spin precession, as clearly seen in Fig. 10.7a. Note that the signals for opposite polarizations are in anti-phase. The difference between the co- and cross-polarized signals, which is proportional to $\langle S_z \rangle$, is shown in Fig. 10.7b. At least four oscillations can be observed, with the period of 145 ps implying an FSS of 28 $\upmu$eV. The damping of the oscillations is mainly caused by electron tunnelling out of the dot within the photodiode.

The final state of the exciton qubit in the experiments described above is highly sensitive to changes in the laser pulse area, which means that precise control on the pulse intensity is required. Several authors have explored alternative methods that are less sensitive to the exact pulse area. One such approach is to use adiabatic rapid passage with chirped optical pulses [47, 48]. In these experiments, the frequency of the laser is swept during the pulse, giving a time-varying detuning relative to the transition frequency. In the right conditions, the final state of the dot is relatively insensitive to the exact pulse area. Another method is to pump the dot within the LA-phonon sideband [49]. Pumping via phonon-assisted transitions is, of course, incoherent. However, if the pumping is hard enough, near perfect inversion of the dot is possible, producing a final state very close to the north pole of the Bloch sphere, which is insensitive to phase variations. Such phonon-sideband pumping was recently observed by three groups [38, 50, 51].

4.4 Two-Qubit Gates

The DiVincenzo check-list for QIP [20] requires at least one two-qubit gate in addition to the full control of single qubits. One way to achieve this is via coupling between two excitons of opposite spins inside a single dot. As noted in the discussion of Fig. 10.5, the biexciton state does not have twice the energy of the individual excitons, which indicates coupling via the Coulomb interaction. This allows a two-qubit conditional rotation gate (CROT) to be performed by using two laser pulses tuned respectively to the exciton and biexciton transitions of the dot. The method was initially demonstrated for a GaAs interface dot by Li et al. in 2003 [19]. Below, we describe the equivalent experiment on a self-assembled InGaAs dot reported by Boyle et al. in 2008 [52].

Fig. 10.8

CROT gate in an InGaAs dot using the exciton and biexciton transitions. a Level scheme showing the transitions involved. b Experimental results. Note that the data were collected in the linear polarization basis, where the conditional Rabi rotation is expected for co-polarized pulses, rather than the cross-polarized configuration indicated in a. After [52]

A simplified version of the levels used in the CROT gate is given in Fig. 10.8a. The control qubit $|q_1 \rangle$ is the $S_z=-1$ exciton, while the target qubit $|q_2 \rangle$ corresponds to $S_z=+1$. The combined state of the system $|q_1q_2 \rangle$ is denoted by the number of excitons (either 0 or 1) in the respective qubit states. The aim of the experiment is to demonstrate a rotation of the target qubit conditional on the state of $|q_1 \rangle$: i.e. we need to show that we rotate $|q_2\rangle$ only when $q_1 = 1$.

The state of the control qubit is determined by a $\pi$ pulse with $\sigma ^-$ polarization tuned to the $X^0$ transition. If this pulse is present, we have $q_1=1$; if not, $q_1=0$. The conditional rotation of $|q_2 \rangle$ is performed by a $\sigma ^+$ pulse of variable area tuned to the XX transition. The rotation can only occur if $q_1=1$, since a pulse tuned to the biexciton only drives the dot when an exciton of the opposite spin is already present. If the dot is empty, no exciton can be created, as the laser has the wrong frequency. The key result is to therefore to demonstrate Rabi rotation of the biexciton conditional on the state of $|q_1\rangle$.

The results of the experiment are presented in Fig. 10.8b. For technical reasons, the experiment was performed in the linear polarization basis rather than the more natural circular one. In this linear basis, we expect to excite the biexciton when the CROT pulse is co-polarized with the control pulse, and not when it is cross-polarized. This is exactly what is observed: the biexciton Rabi rotation is only observed when the co-polarized control pulse has acted first on the dot. If the control pulse has the wrong polarization, or is not present at all, the initial state of the dot is $|01\rangle$ or $|00\rangle$ respectively, and no Rabi oscillation is observed. On the other hand, when the control pulse has the right polarization, the initial state of the dot is $|10\rangle$. A CROT pulse of area $\pi$ then drives the system to the $|11\rangle$ state (i.e. the biexciton state), while a $2\pi$ pulse leaves the system in the $-|10\rangle$ state, where the − sign originates from the geometric phase of $\pi$ that is accumulated on completing a $2\pi$ rotation of the Bloch sphere. The data in Fig. 10.8b thus establishes the four outcomes of the CROT truth table. The gate fidelity deduced from the data was $0.87 \pm 0.04$, which was significantly higher than that obtained for interface dots in [19], mainly due to the longer dephasing time of InGaAs dots.

A more scalable QIP architecture would require that the excitons should be localized in separate dots. In the short term, however, the results in [19, 52] prove the principle that QD excitons can be used to demonstrate two-qubit gates, laying the foundations for further work.

5 Coherent Control of Spins

Single carriers (electrons or holes) confined within charged QDs may also be manipulated by ultrafast laser pulses. A number of different approaches are used to obtain charged dots. Typically, QDs embedded within diode structures are employed either to ionize a photoexcited exciton [46, 53,54,55] or to deterministically charge the QDs [56,57,58,59,60,61]. Alternatively, dopant layers may be added during sample growth; by tuning the doping concentration, it is possible to produce a mean QD carrier occupation of unity at equilibrium [62, 63]. Since resident carriers do not recombine, the $T_2$ time of their spins is no longer limited by the radiative lifetime. The coherence times can therefore be much longer than for excitons, which motivates their use in coherent control experiments.

5.1 Energy Level Structure of Charged Dots

The ground state of a charged dot consists of a dot containing a single electron or hole in their respective s-shells. Absorption of a photon adds an additional electron-hole pair to the system, leading to the formation of a charged exciton called a trion. The trion is split from the neutral exciton line by a binding energy typically ${\sim }2\,\mathrm {meV}$ (see $X^+$ peak in Fig. 10.5). A single electron leads to a negatively charged trion (e.g. $\left| X^{-}\right\rangle =\left| \uparrow \Uparrow \downarrow \right\rangle$) whilst a single hole leads to a positively charged trion (e.g. $\left| X^{+}\right\rangle =\left| \Uparrow \uparrow \Downarrow \right\rangle$). The trion transitions for opposite spins have orthogonal circular polarizations, which can be exploited for spin-readout, as discussed in Sect. 10.5.5.

The application of a magnetic field (B) splits the electron and hole levels by the Zeeman effect into their two $m_{j}$ states. The splitting is given by:

$$\begin{aligned} E_{Z}=g\mu _{B}B \, , \end{aligned}$$

(10.36)

where g is the Landé g-factor and $\mu _{B}$ is the Bohr magneton. The hole is regarded as having a pseudo-spin of $\pm 1/2$, with the factor of three from the $m_{j}=\pm 3/2$ states included in its g-factor. The splitting of the ground and trion states of a positive dot in a Faraday geometry field (i.e. $\varvec{B}$ parallel to the growth (z) axis) is shown in Fig. 10.9a. Note that the circular polarization selection rules decouple the states of opposite spin.

Fig. 10.9

Energy level spectrum of a positively charged dot in a magnetic field, with the Zeeman splittings exaggerated for clarity. a Faraday geometry with $\varvec{B}$ directed along the growth (z) axis. b Voigt geometry with $\varvec{B}$ directed along the x-axis. x/$\bar{x}$ and $\Downarrow$/$\Uparrow$ represents opposite hole spin states along the magnetic field. For negative dots, the charges and Zeeman splittings are reversed

A Voigt geometry field (i.e. $\varvec{B}$ oriented within the sample x-y plane) can mix the bright ($S_{z}=\pm 1$) and dark ($S_{z}=\pm 2$) exciton states.. The exciton eigenstates are no longer well defined and it is simpler to consider single carrier states, as shown for a positive dot in Fig. 10.9b. The hole and trion states are defined in terms of their orientation with respect to the magnetic field and are split by the hole and electron Zeeman energies respectively. The hole-trion transitions are linearly polarized, with a pair of cross-polarized diagonal transitions coupling the hole states to the orthogonal trion state. The up and down hole spin states ($\left| h_{\Uparrow /\Downarrow }\right\rangle$) are superpositions of x-axis eigenstates, and spins initialised along z therefore precess about the in-plane field at the Larmor frequency $\omega _{Z}=E_{Z}/\hbar$. This implements a coherent rotation about the field axis on the Bloch sphere, and is widely used for coherent control of single carrier spins (see Sects. 10.5.3 and 10.5.4).

5.2 Spin Initialization

The DiVincenzo checklist for QIP [20] includes the requirement to begin with a well-defined qubit state. To achieve this, single carrier spins are generally initialised to either up or down. A widely used method is optical pumping, in which one of the trion transitions is continuously driven by a laser [59, 60]. Over time, the population becomes shelved in the undriven state, as any population that relaxes into the driven state is immediately re-pumped. These methods have reached fidelities as high as 99.8% in Faraday geometry [59], with ${\sim } \upmu$s initialization times that rely on weak spin-flip processes in the trion state. Faster (ns) initialization times have been observed in Voigt geometry on account of the allowed diagonal transitions (see Fig. 10.9b) to the opposite spin state [60]. The fidelity, however, is slightly lower. Coherent population trapping methods can also be employed [61, 64].

A fault-tolerant QIP implementation [65, 66] requires rapid initialization compared to decoherence, and this prompts research into faster schemes such as exciton ionization in a QD photodiode [53,54,55, 67]. In this method, an exciton with well defined spin is prepared in a neutral dot with circularly-polarised light. In reverse bias, the electric field causes fast electron tunnelling, leaving a hole behind with its spin determined by the polarization of the laser, as shown schematically in Fig. 10.10a. (Electron initialization is also possible if suitable tunnel barriers are included to reduce the electron tunnelling rate below that of the holes.) The strong circular selection rules for the trion transitions (see right of Fig. 10.10a) underpin methods to measure the fidelity of the initialisation mechanism. The dot is excited with a circularly-polarized $\pi$ pulse tuned to the neutral exciton and probed by a co- or cross-polarized $\pi$ pulse of variable frequency at a delay time longer than the electron tunnelling time, as shown in Fig. 10.10b. The negative signal at zero detuning identifies the $X^0$ transition, since the second $\pi$ pulse moves the system back to the ground state, leading to a reduction in the photocurrent. The strongly polarization-sensitive signal at the $X^+$ line confirms the high fidelity of the ionization method.

Fig. 10.10

The figure is adapted from [46]

a Initialisation of a single hole spin by exciton ionization. On the left are the exciton energy levels of a neutral dot in the circular basis as in Fig. 10.5. After electron tunnelling only a single hole remains. The spin of the hole can be measured by exciting with circularly polarized light to create a positively charged trion as illustrated on the right. b Two-color pump-probe photocurrent spectra of QDs exhibiting negligible ($2.01\, \upmu$eV) FSS. The probe is delayed by longer than the electron tunnelling time. Black (red) line corresponds to a co- (cross-) polarized probe laser.

Exciton ionization schemes can offer both picosecond initialization times and on-demand operation. Unfortunately, the anisotropic exchange interaction [24, 68] typically reduces fidelity by causing spin precession during the exciton lifetime [54, 69, 70]: see Fig. 10.10a and discussion of Fig. 10.7. Speeding up the ionisation process minimizes this effect [67, 71] but also significantly reduces the qubit lifetime due to faster tunnelling rates. The best solution is to select or tune QDs such that the exchange interaction becomes negligible [46, 72]. Figure 10.10b illustrates that a fidelity ${>}99\%$ can be obtained in this way for a dot with FSS close to zero. This approach has allowed the demonstration of fast, high-fidelity initialisation with long qubit lifetimes. Modulation of the sample electric field to suppress tunnelling after initialisation [73] has the potential to lead to further increases in lifetime.

5.3 Coherent Control of Single Electron Spins

Coherent control of a single electron spin is based on the electron-trion system discussed in Sect. 10.5.1. In Voigt geometry, the energy levels may be considered as a pair of independent $\varLambda$ systems incorporating the two electron spin states and one of the trion states (see Fig. 10.11a). Under circular excitation, the probability amplitudes from the two systems add. By using a large detuning, unwanted population in excited states is minimised and the upper states may be adiabatically eliminated as shown in Fig. 10.11b. Hence a single broadband circularly-polarised pulse will produce coherent rotations via Stimulated Raman Adiabatic Passage (STIRAP). The rotation angle is given by:

$$\begin{aligned} \phi _{z}=\int \lambda _{-}(t)\, \mathrm{{d}}t \, , \end{aligned}$$

(10.37)

where $\lambda _{-}(t)$ is the eigenenergy of the dressed states given by:

$$\begin{aligned} \lambda _{\pm }=\frac{1}{2}\sqrt{\varDelta ^{2}\pm \left| \varOmega _{R}\right| ^{2}} \, . \end{aligned}$$

(10.38)

The rotations are about the z axis on the Bloch sphere and may also be interpreted in terms of the AC Stark effect [75]. Full spin control can be achieved by combining with x axis rotations caused by Larmor precession about the $\varvec{B}$ field (see Sect. 10.5.1)  [74] optical rotations of electron spins have also been demonstrated by using the geometric phase approach (see Fig. 10.11c) [76, 77]. The principles of this method will be explained in Sect. 10.5.4 below in the context of hole spin control.

Fig. 10.11

Optical spin rotation methods for electrons in Voigt geometry. The dot is excited with circularly polarized laser pulses of energy $\hbar \omega$ and bandwidth broader than the electron/hole Zeeman energies $E_Z^{e/h}$. a Energy levels of the electron-trion system in the z basis. Note that this contrasts with Fig. 10.9b, which would correspond to the x basis. The system has four linearly-polarised transitions with the diagonal transitions carrying a $\pi /2$ phase factor. b For large laser detuning $\varDelta$, the trion levels may be adiabatically eliminated and the laser drives a stimulated Raman transition with Rabi frequency $\varOmega _\mathrm{eff} \approx \frac{\varOmega _{H} \varOmega _{V}}{\varDelta }$ between the two spin states where $\varOmega _\mathrm{{H}/\mathrm {V}}$ are the Rabi frequencies of the H/V transitions shown in a. Changing the laser power allows control of the Rabi rotation angle. c For $\varDelta =0$, a $2\pi$ laser pulse drives a spin state (selected by the choice of $\sigma ^{+/-}$ polarisation) to the trion state and back. The driven spin state acquires a “geometric phase” of $\pi$. Control of the geometric phase is achieved by varying $\varDelta$

A two-qubit spin register with similar possibilities to the biexciton approach discussed in Sect. 10.4.4 may be realized with a QD molecule comprising two vertically stacked QDs [78]. The interaction between the two QDs is facilitated by coherent tunnelling and may be controlled by the applied electric field. Coherent control of an electron spin weakly coupled to an L3 photonic crystal cavity has also been demonstrated [79]. Using a scheme similar to that of [74], the spin rotation is performed by pulses that are detuned from both the trion transitions and the cavity mode. Theoretical work has proposed a more complex scheme whereby two transitions of the electron-trion system are coupled to two non-degenerate cavity modes [80]. This scheme has the potential both to increase initialisation fidelity and reduce the rotation time. Other experiments on electron spin control in nanocavities are discussed in Chap. 11.

5.4 Coherent Control of Single Hole Spins

Optical coherent control of a single hole spin may be achieved by similar methods to those for electrons. Schemes using the AC Stark shift for z-axis rotation [81, 82] are the direct equivalent of those for electrons discussed in Sect. 10.5.3, with x-axis rotations again implemented by Larmor precession. In addition, Greilich et al. successfully demonstrated control of a two hole-spin state for two dots interacting through tunnel coupling [81].

Fig. 10.12

The figure is adapted from [83]

Coherent control of a single hole spin in a Voigt geometry field $B_x$. a Schematic of the method. The hole spin is initialised to $\left| \Uparrow \right\rangle$ by the exciton ionization method. Full Bloch sphere control is achieved by combining z axis rotations induced by the geometric phase shift from a detuned $2\pi$ pulse as in Fig. 10.11c, with x axis rotations by Larmor precession about the field. b Experimental geometry. c Optical rotation angle $\phi _z$ versus laser detuning $\varDelta$. The red line is a fit according to (10.40).

An alternative approach was employed by Godden et al. [83] in which a single hole spin was initialised by the exciton ionization method discussed in Sect. 10.5.2, and then z-axis rotations were implemented via the geometric phase previously established for electrons [76, 77]. Excitation by a laser pulse with bandwidth larger than the Zeeman splittings simplifies the hole-trion system to a pair of independent two-level systems that may be selected by orthogonal circular polarisations (see Fig. 10.11c for a schematic of the equivalent level scheme for electrons). A resonant $\sigma ^+$ pulse of area $\varTheta$ then drives a Rabi rotation between the spin-down hole and the corresponding trion state, so that an arbitrary initial hole state $| \varPsi \rangle = h_{\Uparrow }\left| \Uparrow \right\rangle +h_{\Downarrow }\left| \Downarrow \right\rangle$ evolves as [84]:

$$\begin{aligned} | \varPsi \rangle \rightarrow | \varPsi ^\prime \rangle = h_{\Uparrow }\left| \Uparrow \right\rangle +h_{\Downarrow }\left[ \cos \left( \frac{\varTheta }{2}\right) \left| \Downarrow \right\rangle +I\sin \left( \frac{\varTheta }{2}\right) \left| \Downarrow \Uparrow \downarrow \right\rangle \right] . \end{aligned}$$

(10.39)

For $\varTheta = 2 \pi$, we obtain $| \varPsi ^\prime \rangle = h_{\Uparrow }\left| \Uparrow \right\rangle -h_{\Downarrow }\left| \Downarrow \right\rangle$ when trion dephasing is negligible, which is equivalent to a $\pi$ rotation about z. Arbitrary rotation angles $\phi _z$ about $\hat{\varvec{z}}$ are implemented by detuning the laser [83, 84]:

$$\begin{aligned} \phi _z = 2 \arctan (\beta _z/\varDelta ) \, , \end{aligned}$$

(10.40)

where $\beta _z$ is the pulse bandwidth and $\varDelta$ the detuning from the hole-trion transition. Figure 10.12 shows a schematic of the method and experimental geometry, together with a fit to the experimental results showing excellent agreement with (10.40). Theoretical proposals indicate that rotations about an arbitrary axis are possible, thereby eliminating the need for Larmor precession, and potentially reducing the gate time [84].

5.5 Spin Readout

In the experiments described above, measurement of the spin is performed by averaging over many experimental cycles. For QIP it is desirable to perform “single-shot” readout where the state of the qubit is determined faster than the back-action of the measurement. In Faraday geometry, the trion transitions are spin-selective and have a very weak coupling to the orthogonal spin state. Single-shot spin readout may then be accomplished by driving one transition continuously and collecting the spin-sensitive resonance fluorescence. This approach has been realised experimentally with a fidelity of $82.3\%$ for a measurement time of $800\,\mathrm {ns}$ [85].

A drawback to this approach is the Faraday geometry, as coherent spin control requires Voigt geometry. A recent theoretical proposal envisions spin initialisation and manipulation in Voigt geometry, before applying a detuned laser to AC Stark-shift the energy levels into a pseudo-Faraday configuration to perform single-shot readout [86]. Significant potential exists to increase the readout performance by exploiting photonic nanostructures to enhance both the collection efficiency and the emission rate.

6 Dephasing: Comparison of Qubits

A critical parameter for any qubit is its coherence time, since this determines how many gate operations can be performed. Table 10.1 compares measurements of $T_1$, $T_2^*$ and $T_2$ for exciton and single carrier spin qubits. The basic concepts of these three time constants were outlined in Sect. 10.2.3.

Table 10.1 Table of dephasing timescales for different single qubit implementations in InGaAs self-assembled QDs. The coherence of neutral excitons has been observed to be lifetime-limited and thus the limit $T_{2}=2T_{1}$ is taken here. In the case of single electrons and holes, the $T_{2}$ values reported here are measured by spin echo methods to suppress pure dephasing ($T_2^*$)

Single exciton qubits have been observed to have lifetime-limited coherence [87, 88], i.e. $T_2 = 2T_1$, where $T_1$ is typically around $1\,\mathrm {ns}$ owing to radiative recombination [88]. Single spins cannot undergo radiative recombination and therefore generally have far longer $T_1$ times. For InGaAs QDs, electron spin dephasing times ($T_2^*$) of the order of 1–2 ns are typically measured [89,90,91] with values of around 10 ns measured for holes [61, 81,82,83]. The primary source of electron spin dephasing is postulated to be hyperfine interactions with the nuclear spins within the dot [9, 90]. The longer $T_2^*$ time for holes is related to its ${\sim } 10 \times$ smaller hyperfine constant due to the primarily p-type orbital structure [93]. The dominant source of hole dephasing is instead attributed to charge noise [81, 82, 94], most probably originating from charges trapped at the capping layer interface [95, 96]. Further discussion of the exciton and spin dephasing mechanisms may be found in Chap. 9.

The use of spin echo techniques [97] can suppress pure dephasing, allowing longer coherence times ($T_2$) to be measured. For both electrons [90, 91] and holes [82], this has resulted in $T_2$ times of the order of $\upmu$s. It is worth noting that these values are still orders of magnitude below the lifetime ($T_1$) limit. Recent studies [98] have shown that strain in the sample wafer acts to reduce fluctuations of the nuclear spin bath, potentially offering a route to increasing both $T_2$ and $T_2^*$ for electron spins. Meanwhile, improvements in sample quality should lead to reduced charge fluctuations for hole spins (see Chap. 9). In addition, a recent theoretical proposal envisions using the AC Stark shift to oppose changes in the Zeeman energy, suppressing charge noise dephasing for holes [99].

7 Outlook

The experiments described in Sects. 10.4 and 10.5 show that ultrafast coherent control techniques for single excitons and spins in QDs are now well established. The primary need for future QIP applications is to increase the coherence time. Significant progress has already been made here, with studies clarifying the origins of the dephasing and proposing strategies to reduce it (see Sect. 10.6).

The development of quantum processors based on spin networks will require scaling to multiple qubits. The approaches based on biexcitons (Sect. 10.4.4) or vertically stacked QDs do not scale easily beyond two qubits, and it is therefore necessary to consider spins confined in separate QDs, as discussed in Chap. 12. Entanglement has been observed between QD spins and emitted photons [100,101,102], illustrating conversion between stationary and flying qubits. The complementary process of transferring a quantum state from a photonic qubit to a QD spin qubit was also demonstrated [103]. Combining these two concepts has recently led to the demonstration of entanglement between two hole spins separated by 5 m [104], a critical development for any spin-based QIP architecture.

The methods described in this chapter are also applicable to other QIP applications. For example, current state-of-the-art single [105, 106] and entangled [107] photon sources are driven by resonant $\pi$-pulses acting on the neutral exciton or biexciton. Moving beyond this simple case, coherent control of single spins has been proposed as a means to generate more complex photonic states for QIP such as cluster states [108], and these have recently been observed using dark excitons as the qubits [109] (see Chap. 4). Coherent control methods are also of significant interest for controlling light-matter interactions in cavity-QD systems, as discussed in Chap. 11. Examples include polarization shifts of light that are conditional on the state of a spin [110, 111] and controlling the coherent energy transfer between an emitter and a cavity [112].