Global Stabilization of Nonlinear Systems via Novel Second Order Sliding Mode Control with an Application to a Novel Highly Chaotic System

Abstract

Sliding mode control is an important method used to solve various problems in control systems engineering. In robust control systems, the sliding mode control is often adopted due to its inherent advantages of easy realization, fast response and good transient performance as well as insensitivity to parameter uncertainties and disturbance. In this work, we derive a novel second order sliding mode control method for the global stabilization of any nonlinear system. The global stabilization result is derived using novel second order sliding mode control method and established using Lyapunov stability theory. Chaos in nonlinear dynamics occurs widely in physics, chemistry, biology, ecology, secure communications, cryptosystems and many scientific branches. Synchronization of chaotic systems is an important research problem in chaos theory. As an application of the general result, the problem of global chaos control of a novel highly chaotic system is studied and a new sliding mode controller is derived. The Lyapunov exponents of the novel chaotic system are obtained as $L_1 = 12.8393$, $L_2 = 0$ and $L_3 = -33.1207$. The large value of the maximal Lyapunov exponent (MLE) shows that the novel chaotic system is highly chaotic. The Kaplan-Yorke dimension of the novel chaotic system is obtained as $D_{KY} = 2.3877$. We show that the novel highly chaotic system has three unstable equilibrium points. Numerical simulations using MATLAB have been shown to depict the phase portraits of the novel highly chaotic system and the global chaos control of the state trajectories of the novel highly chaotic system.

1 Introduction

Chaos theory describes the quantitative study of unstable aperiodic dynamic behavior in deterministic nonlinear dynamical systems. For the motion of a dynamical system to be chaotic, the system variables should contain some nonlinear terms and the system must satisfy three properties: boundedness, infinite recurrence and sensitive dependence on initial conditions [4,5,6, 125,126,127].

Chaos theory has applications in several fields such as memristors [28, 30, 31, 34,35,36, 137, 140, 142], fuzzy logic [7, 49, 111, 146], communication systems [13, 14, 143], cryptosystems [10, 12], electromechanical systems [15, 58], lasers [8, 21, 145], encryption [22, 23, 147], electrical circuits [1, 2, 16, 120, 138], chemical reactions [75, 76, 78, 79, 81, 83, 85,86,87, 90, 92, 96, 112], oscillators [93, 94, 97, 98, 139], tokamak systems [91, 99], neurology [80, 88, 89, 95, 105, 141], ecology [77, 82, 106, 108], etc.

The problem of global control of a chaotic system is to device feedback control laws so that the closed-loop system is globally asymptotically stable. The problem of global chaos synchronization of chaotic systems is to find feedback control laws so that the master and slave systems are globally and asymptotically synchronized with respect to their states. There are many techniques available in the control literature for the regulation and synchronization of chaotic systems such as active control [17, 44, 45, 54, 118, 129], adaptive control [46,47,48, 51, 53, 64, 104, 115, 119, 120], backstepping control [37,38,39,40,41, 57, 122, 130, 135, 136], sliding mode control [19, 26, 56, 63, 65, 66, 73, 103, 107, 123], etc.

Some classical paradigms of 3-D chaotic systems in the literature are Lorenz system [24], Rössler system [42], ACT system [3], Sprott systems [50], Chen system [11], Lü system [25], Cai system [9], Tigan system [60], etc.

Many new chaotic systems have been discovered in the recent years such as Zhou system [148], Zhu system [149], Li system [20], Sundarapandian systems [52, 55], Vaidyanathan systems [67,68,69,70,71,72, 74, 84, 100, 102, 109, 110, 113, 114, 116, 117, 121, 124, 128, 131,132,133,134], Pehlivan system [27], Sampath system [43], Tacha system [59], Pham systems [29, 32, 33, 35], Akgul system [2], etc.

In this research work, we derive a general result for the global stabilization of nonlinear systems using second order sliding mode control (SMC) [61, 62]. The sliding mode control approach is recognized as an efficient tool for designing robust controllers for linear or nonlinear control systems operating under uncertainty conditions.

A major advantage of sliding mode control is low sensitivity to parameter variations in the plant and disturbances affecting the plant, which eliminates the necessity of exact modeling of the plant. In the sliding mode control, the control dynamics will have two sequential modes, viz. the reaching mode and the sliding mode. Basically, a sliding mode controller design consists of two parts: hyperplane design and controller design. A hyperplane is first designed via the pole-placement approach and a controller is then designed based on the sliding condition. The stability of the overall system is guaranteed by the sliding condition and by a stable hyperplane.

This work is organized as follows. In Sect. 2, we discuss the problem statement for the global stabilization of nonlinear systems. Then we derive a general result for the global stabilization of nonlinear systems using novel second order sliding mode control. In Sect. 3, we describe the novel highly chaotic system and its phase portraits. In Sect. 4, we describe the qualitative properties of the novel highly chaotic system. The Lyapunov exponents of the novel chaotic system are obtained as $L_1 = 12.8393$, $L_2 = 0$ and $L_3 = -33.1207$. The Kaplan-Yorke dimension of the novel chaotic system is obtained as $D_{KY} = 2.3877$. We show that the novel highly chaotic system has three unstable equilibrium points. In Sect. 5, we describe the second order sliding mode controller design for the global chaos control of the novel highly chaotic system and its numerical simulations. Section 6 contains the conclusions of this work.

2 Second Order Sliding Mode Control for Nonlinear Systems

We consider a general nonlinear system given by

$$\begin{aligned} \dot{\mathbf {x}} = A \mathbf {x} + f(\mathbf {x}) + \mathbf {u} \end{aligned}$$

(1)

where $\mathbf {x} \in {\mathbf R}^n$ denotes the state of the system, $A \in {\mathbf R}^{n \times n}$ denotes the matrix of system parameters and $f(\mathbf {x}) \in {\mathbf R}^n$ contains the nonlinear parts of the system. Also, $\mathbf {u}$ represents the sliding mode controller to be designed.

Then the global stabilization problem for the system (1) can be stated as follows: Find a controller $\mathbf {u}(\mathbf {x})$ so as to render the state $\mathbf {x}(t)$ to be globally asymptotically stable for all values of $\mathbf {x}(0) \in {\mathbf R}^n$, i.e.

$$\begin{aligned} \lim \limits _{t \rightarrow \infty } \Vert \mathbf {x}(t) \Vert = 0 \ \ \text{ for } \text{ all } \ \ \mathbf {x}(0) \in {\mathbf R}^n \end{aligned}$$

(2)

We start the controller design by setting

$$\begin{aligned} \mathbf {u}(t) = - f(\mathbf {x}) + B v(t) \end{aligned}$$

(3)

In Eq. (3), $B \in {\mathbf R}^n$ is chosen such that (A, B) is completely controllable.

By substituting (3) into (1), we get the closed-loop system dynamics

$$\begin{aligned} \dot{\mathbf {x}} = A \mathbf {x} + B v \end{aligned}$$

(4)

Next, we start the sliding controller design by defining the sliding variable as

$$\begin{aligned} s(\mathbf {x}) = C \mathbf {x} = c_1 x_1 + c_2 x_2 + \cdots + c_n x_n, \end{aligned}$$

(5)

where $C \in {\mathbf R}^{1 \times n}$ is a constant vector to be determined.

The sliding manifold S is defined as the hyperplane

$$\begin{aligned} S = \left\{ \mathbf {x} \in {\mathbf R}^n \ : \ s(\mathbf {x}) = C \mathbf {x} = 0 \right\} \end{aligned}$$

(6)

We shall assume that a sliding motion occurs on the hyperplane S.

In the second order sliding mode control, the following equations must be satisfied:

$$\begin{aligned} s&= 0 \end{aligned}$$

(7a)

$$\begin{aligned} \dot{s}&= C A \mathbf {x} + C B v = 0 \end{aligned}$$

(7b)

We assume that

$$\begin{aligned} C B \ne 0 \end{aligned}$$

(8)

The sliding motion is influenced by equivalent control derived from (7b) as

$$\begin{aligned} v_{\text{ eq }}(t) = - (C B)^{-1} \, C A \mathbf {x}(t) \end{aligned}$$

(9)

By substituting (9) into (4), we obtain the equivalent error dynamics in the sliding phase as follows:

$$\begin{aligned} \dot{\mathbf {x}} = A \mathbf {x} - (C B)^{-1} C A \mathbf {x} = E \mathbf {x}, \end{aligned}$$

(10)

where

$$\begin{aligned} E = \left[ I - B (C B)^{-1} C \right] A \end{aligned}$$

(11)

We note that E is independent of the control and has at most $(n - 1)$ non-zero eigenvalues, depending on the chosen switching surface, while the associated eigenvectors belong to $\text{ ker }(C)$.

Since (A, B) is controllable, we can use sliding control theory [61, 62] to choose B and C so that E has any desired $(n - 1)$ stable eigenvalues.

This shows that the dynamics (10) is globally asymptotically stable.

Finally, for the sliding controller design, we apply a novel sliding control law, viz.

$$\begin{aligned} \dot{s} = - k s - q s^2 \mathop {\mathrm {sgn}}(s) \end{aligned}$$

(12)

In (12), $\mathop {\mathrm {sgn}}(\cdot )$ denotes the sign function and the SMC constants $k> 0, q > 0$ are found in such a way that the sliding condition is satisfied and that the sliding motion will occur.

By combining Eqs. (7b), (9) and (12), we finally obtain the sliding mode controller v(t) as

$$\begin{aligned} v(t) = - (C B)^{-1} \left[ C (k I + A) \mathbf {x} + q s^2 \mathop {\mathrm {sgn}}(s) \right] \end{aligned}$$

(13)

Next, we establish the main result of this section.

Theorem 1

The second order sliding mode controller defined by (3) achieves global stabilization for all the states of the system (1) where v is defined by the novel sliding mode control law (13), $B \in {\mathbf R}^{n \times 1}$ is such that (A, B) is controllable, $C \in {\mathbf R}^{1 \times n}$ is such that $C B \ne 0$ and the matrix E defined by (11) has $(n - 1)$ stable eigenvalues.

Proof

Upon substitution of the control laws (3) and (13) into the state dynamics (1), we obtain the closed-loop system dynamics as

$$\begin{aligned} \dot{\mathbf {x}} = A \mathbf {x} - B (C B)^{-1} \left[ C (k I + A) \mathbf {x} + q s^2 \mathop {\mathrm {sgn}}(s) \right] \end{aligned}$$

(14)

We shall show that the error dynamics (14) is globally asymptotically stable by considering the quadratic Lyapunov function

$$\begin{aligned} V(\mathbf {x}) = {1 \over 2} \, s^2(\mathbf {x}) \end{aligned}$$

(15)

The sliding mode motion is characterized by the equations

$$\begin{aligned} s(\mathbf {x}) = 0 \ \ \text{ and } \ \ \dot{s}(\mathbf {x}) = 0 \end{aligned}$$

(16)

By the choice of E, the dynamics in the sliding mode given by Eq. (10) is globally asymptotically stable.

When $s(\mathbf {x}) \ne 0$, $V(\mathbf {x}) > 0$.

Also, when $s(\mathbf {x}) \ne 0$, differentiating V along the error dynamics (14) or the equivalent dynamics (12), we get

$$\begin{aligned} \dot{V}(\mathbf {x}) = s \dot{s} = - k s^2 - q s^3 \mathop {\mathrm {sgn}}(s) < 0 \end{aligned}$$

(17)

Hence, by Lyapunov stability theory [18], the error dynamics (14) is globally asymptotically stable for all $\mathbf {x}(0) \in {\mathbf R}^n$.

This completes the proof. $\blacksquare$

3 A Novel Highly Chaotic System

In this work, we propose a novel highly chaotic system described by

$$\begin{aligned} \left. \begin{array}{ccl} \dot{x}_1 &{} = &{} a (x_2 - x_1) + d x_2 x_3 \\ \dot{x}_2 &{} = &{} b x_1 - x_2 - x_1 x_3 \\ \dot{x}_3 &{} = &{} x_1 x_2 - c x_3 + p x_2^2 \\ \end{array} \right. \end{aligned}$$

(18)

where $x_1, x_2, x_3$ are the states and a, b, c, d, p are constant, positive, parameters.

In this chapter, we show that the system (18) is chaotic when the parameters take the values

$$\begin{aligned} a = 14, \ \ b = 18, \ \ c = 6, \ \ d = 98, \ \ p = 12 \end{aligned}$$

(19)

For numerical simulations, we take the initial state of the system (18) as

$$\begin{aligned} x_1(0) = 0.2, \ \ x_2(0) = 0.2, \ \ x_3(0) = 0.2 \end{aligned}$$

(20)

The Lyapunov exponents of the system (18) for the parameter values (19) and the initial state (20) are determined by Wolf’s algorithm [144] as

$$\begin{aligned} L_1 = 12.8393, \ \ L_2 = 0, \ \ L_3 = -33.1207 \end{aligned}$$

(21)

Since $L_1 > 0$, we conclude that the system (18) is chaotic.

Since $L_1 + L_2 + L_3 < 0$, we deduce that the system (18) is dissipative.

Hence, the limit sets of the system (18) are ultimately confined into a specific limit set of zero volume, and the asymptotic motion of the novel highly chaotic system (18) settles onto a strange attractor of the system.

From (21), we see that the maximal Lyapunov exponent (MLE) of the chaotic system (18) is $L_1 = 12.8393$, which is very large.

Thus, we conclude that the proposed novel system (18) is highly chaotic.

Also, the Kaplan-Yorke dimension of the novel highly chaotic system (18) is calculated as

$$\begin{aligned} D_{KY} = 2 + {L_1 + L_2 \over | L_3 |} = 2.3877, \end{aligned}$$

(22)

which shows the high complexity of the system (18).

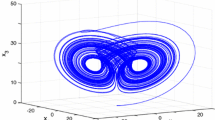
Figure 1 shows the 3-D phase portrait of the highly chaotic system (18) in ${\mathbf R}^3$.

Figures 2, 3 and 4 show the 2-D projections of the highly chaotic system (18) in $(x_1, x_2)$, $(x_2, x_3)$ and $(x_1, x_3)$ planes, respectively.

Fig. 1

3-D phase portrait of the novel highly chaotic system in ${\mathbf R}^3$

Fig. 2

2-D phase portrait of the novel highly chaotic system in $(x_1, x_2)$ plane

Fig. 3

2-D phase portrait of the novel highly chaotic system in $(x_2, x_3)$ plane

Fig. 4

2-D phase portrait of the novel highly chaotic system in $(x_1, x_3)$ plane

4 Qualitative Properties of the Novel Highly Chaotic System

4.1 Dissipativity

In vector notation, the novel highly chaotic system (18) can be expressed as

$$\begin{aligned} \dot{\mathbf {x}} = f(\mathbf {x}) = \left[ \begin{array}{c} f_1(x_1, x_2, x_3) \\ f_2(x_1, x_2, x_3) \\ f_3(x_1, x_2, x_3) \\ \end{array} \right] , \end{aligned}$$

(23)

where

$$\begin{aligned} \left\{ \begin{array}{ccl} f_1(x_1, x_2, x_3) &{} = &{} a (x_2 - x_1) + d x_2 x_3 \\ f_2(x_1, x_2, x_3) &{} = &{} b x_1 - x_2 - x_1 x_3 \\ f_3(x_1, x_2, x_3) &{} = &{} x_1 x_2 - c x_3 + p x_2^2 \\ \end{array} \right. \end{aligned}$$

(24)

We take the parameter values as in the chaotic case (19).

Let $\varOmega$ be any region in ${\mathbf R}^3$ with a smooth boundary and also, $\varOmega (t) = \varPhi _t(\varOmega ),$ where $\varPhi _t$ is the flow of f. Furthermore, let V(t) denote the volume of $\varOmega (t)$.

By Liouville’s theorem, we know that

$$\begin{aligned} \dot{V}(t) = \int \limits _{\varOmega (t)} \ (\nabla \cdot f) \, dx_1 \, dx_2 \, dx_3 \end{aligned}$$

(25)

The divergence of the novel chaotic system (23) is calculated as

$$\begin{aligned} \nabla \cdot f = {\partial f_1 \over \partial x_1} + {\partial f_2 \over \partial x_2} + {\partial f_3 \over \partial x_3} = - (a + c + 1) = - \mu < 0 \end{aligned}$$

(26)

where $\mu = a + c + 1 = 21 > 0$.

Inserting the value of $\nabla \cdot f$ from (26) into (25), we get

$$\begin{aligned} \dot{V}(t) = \int \limits _{\varOmega (t)} \ (- \mu ) \, dx_1 \, dx_2 \, dx_3 = - \mu V(t) \end{aligned}$$

(27)

Integrating the first order linear differential equation (27), we get

$$\begin{aligned} V(t) = \exp (- \mu t) V(0) \end{aligned}$$

(28)

Since $\mu > 0$, it follows from Eq. (28) that $V(t) \rightarrow 0$ exponentially as $t \rightarrow \infty$.

This shows that the novel chaotic system (18) is dissipative. Hence, the limit sets of the system (18) are ultimately confined into a specific limit set of zero volume, and the asymptotic motion of the novel chaotic system (18) settles onto a strange attractor of the system.

4.2 Equilibrium Points

The equilibrium points of the novel highly chaotic system (18) are obtained by solving the equations

$$\begin{aligned} \left\{ \begin{array}{ccccr} f_1(x_1, x_2, x_3) &{} = &{} a (x_2 - x_1) + d x_2 x_3 &{} = &{} 0 \\ f_2(x_1, x_2, x_3) &{} = &{} b x_1 - x_2 - x_1 x_3 &{} = &{} 0\\ f_3(x_1, x_2, x_3) &{} = &{} x_1 x_2 - c x_3 + p x_2^2 &{} = &{} 0\\ \end{array} \right. \end{aligned}$$

(29)

We take the parameter values as in the chaotic case (19).

Solving the system (29), we find that the system (18) has three equilibrium points given by

$$\begin{aligned} E_0 = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right] , \ \ E_1 = \left[ \begin{array}{c} 111.8950 \\ 0.8814 \\ 17.9921 \\ \end{array} \right] , \ \ E_2 = \left[ \begin{array}{c} - 111.8950 \\ - 0.8814 \\ 17.9921 \\ \end{array} \right] \end{aligned}$$

(30)

To test the stability type of the equilibrium points, we calculate the Jacobian of the system (18) at any $\mathbf {x} \in {\mathbf R}^3$ as

$$\begin{aligned} J(\mathbf {x}) = \left[ \begin{array}{ccccc} -a &{}&{} a + d x_3 &{}&{} d x_2 \\ b - x_3 &{}&{} - 1 &{}&{} - x_1 \\ x_2 &{}&{} x_1 + 2 p x_2 &{}&{} - c \\ \end{array} \right] = \left[ \begin{array}{ccccc} -14 &{}&{} 14 + 98 x_3 &{}&{} 98 x_2 \\ 18 - x_3 &{}&{} - 1 &{}&{} - x_1 \\ x_2 &{}&{} x_1 + 24 x_2 &{}&{} - 6 \\ \end{array} \right] \end{aligned}$$

(31)

The matrix $J_0 = J(E_0)$ has the eigenvalues

$$\begin{aligned} \lambda _1 = -24.6537, \ \ \lambda _2 = -6, \ \ \lambda _3 = 9.6537 \end{aligned}$$

(32)

This shows that the equilibrium point $E_0$ is a saddle point, which is unstable.

The matrix $J_1 = J(E_1)$ has the eigenvalues

$$\begin{aligned} \lambda _1 = -25.54, \ \ \lambda _{2, 3} = 2.27 \pm 122.52 i \end{aligned}$$

(33)

This shows that the equilibrium point $E_1$ is a saddle-focus, which is unstable.

The matrix $J_2 = J(E_2)$ has the same eigenvalues as $J_1 = J(E_1)$. Hence, we conclude that the equilibrium point $E_2$ is also a saddle-focus, which is unstable.

Thus, all three equilibrium points of the novel highly chaotic system (18) are unstable.

4.3 Rotation Symmetry About the $x_3$-Axis

It is easy to see that the system (18) is invariant under the change of coordinates

$$\begin{aligned} (x_1, x_2, x_3) \mapsto (- x_1, - x_2, x_3) \end{aligned}$$

(34)

Thus, the 3-D novel chaotic system (18) has rotation symmetry about the $x_3$-axis. Hence, it follows that any non-trivial trajectory of the system (18) must have a twin trajectory

4.4 Invariance

It is easy to see that the $x_3$-axis is invariant under the flow of the 3-D novel highly chaotic system (18). The invariant motion along the $x_3$-axis is characterized by

$$\begin{aligned} \dot{x}_3 = - c x_3, \ \ (c > 0) \end{aligned}$$

(35)

which is globally exponentially stable.

4.5 Lyapunov Exponents and Kaplan-Yorke Dimension

We take the parameters of the system (18) as

$$\begin{aligned} a = 14, \ \ b = 18, \ \ c = 6, \ \ d = 98, \ \ p = 12 \end{aligned}$$

(36)

Also, we take the initial state of the system (18) as

$$\begin{aligned} x_1(0) = 0.2, \ \ x_2(0) = 0.2, \ \ x_3(0) = 0.2 \end{aligned}$$

(37)

The Lyapunov exponents of the system (18) for the parameter values (36) and the initial state (37) are determined by Wolf’s algorithm [144] as

$$\begin{aligned} L_1 = 12.8393, \ \ L_2 = 0, \ \ L_3 = -33.1207 \end{aligned}$$

(38)

Figure 5 describes the MATLAB plot for the Lyapunov exponents of the novel chaotic system (18).

Fig. 5

Lyapunov exponents of the novel highly chaotic system

From (21), we see that the maximal Lyapunov exponent (MLE) of the chaotic system (18) is $L_1 = 12.8393$, which is very large. Thus, novel system (18) is highly chaotic. Also, the Kaplan-Yorke dimension of the novel highly chaotic system (18) is calculated as

$$\begin{aligned} D_{KY} = 2 + {L_1 + L_2 \over | L_3 |} = 2.3877, \end{aligned}$$

(39)

which shows the high complexity of the system (18).

5 Sliding Mode Controller Design for the Global Chaos Control of the Novel Highly Chaotic System

In this section, we describe the sliding mode controller design for the global chaos control of the novel highly chaotic system by applying the novel sliding mode control method described by Theorem 1 in Sect. 2.

Thus, we consider the controlled novel highly chaotic system given by

$$\begin{aligned} \left. \begin{array}{ccl} \dot{x}_1 &{} = &{} a (x_2 - x_1) + d x_2 x_3 + u_1 \\ \dot{x}_2 &{} = &{} b x_1 - x_2 - x_1 x_3 + u_2 \\ \dot{x}_3 &{} = &{} x_1 x_2 - c x_3 + p x_2^2 + u_3 \\ \end{array} \right. \end{aligned}$$

(40)

where $x_1, x_2, x_3$ are the states and u is the sliding mode control to be designed.

We take the parameter values as in the chaotic case (19), i.e.

$$\begin{aligned} a = 14, \ \ b = 18, \ \ c = 6, \ \ d = 98, \ \ p = 12 \end{aligned}$$

(41)

In matrix form, we can write the system dynamics (40) as

$$\begin{aligned} \dot{\mathbf {x}} = A \mathbf {x} + f(\mathbf {x}) + \mathbf {u} \end{aligned}$$

(42)

The matrices in (42) are given by

$$\begin{aligned} A = \left[ \begin{array}{rrrrr} -a &{}&{} a &{}&{} 0 \\ b &{}&{} -1 &{}&{} 0 \\ 0 &{}&{} 0 &{}&{} -c \\ \end{array} \right] \ \ \text{ and } \ \ f(\mathbf {x}) = \left[ \begin{array}{c} d x_2 x_3 \\ - x_1 x_3 \\ x_1 x_2 + p x_2^2 \\ \end{array} \right] \end{aligned}$$

(43)

We follow the procedure given in Sect. 2 for the construction of the novel sliding controller to achieve global chaos stabilization of the chaotic system (42).

First, we set $\mathbf {u}$ as

$$\begin{aligned} \mathbf {u}(t) = - f(\mathbf {x}) + B v(t) \end{aligned}$$

(44)

where B is selected such that (A, B) is completely controllable.

A simple choice of B is

$$\begin{aligned} B = \left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ \end{array} \right] \end{aligned}$$

(45)

It can be easily checked that (A, B) is completely controllable.

Next, we find a sliding variable $s = C \mathbf {x}$ such that the matrix $E = [ I - B (C B)^{-1} C ] A$ has two stable eigenvalues.

A simple calculation gives

$$\begin{aligned} s(\mathbf {x}) = C \mathbf {x} = \left[ \begin{array}{rrr} 1 &{} 8 &{} 1 \\ \end{array} \right] \mathbf {x} = x_1 + 8 x_2 + x_3 \end{aligned}$$

(46)

We also note that the matrix $E = [ I - B (C B)^{-1} C ] A$ has the eigenvalues

$$\begin{aligned} \lambda _1 = -28.6140, \ \ \lambda _2 = -4.3860, \ \ \lambda _3 = 0 \end{aligned}$$

(47)

Next, we take the sliding mode gains as

$$\begin{aligned} k = 6, \ \ q = 0.2 \end{aligned}$$

(48)

From Eq. (13) in Sect. 2, we obtain the novel sliding control v as

$$\begin{aligned} v(t) = - 13.6 x_1 - 5.4 x_2 - 0.02 s^2 \mathop {\mathrm {sgn}}(s) \end{aligned}$$

(49)

As an application of Theorem 1 to the novel highly chaotic system (40), we obtain the main result of this section as follows.

Theorem 2

The novel highly chaotic system (40) is globally and asymptotically stabilized for all initial conditions $\mathbf {x}(0) \in {\mathbf R}^3$ with the sliding controller $\mathbf {u}$ defined by (44), where $f(\mathbf {x})$ is defined by (43), B is defined by (45) and v is defined by (49). $\blacksquare$

For numerical simulations, we use MATLAB for solving the systems of differential equations using the classical fourth-order Runge-Kutta method with step size $h = 10^{-8}$.

The parameter values of the novel highly chaotic system (40) are taken as in the chaotic case (47).

The sliding mode gains are taken as $k = 6$ and $q = 0.2$.

We take the initial state of the chaotic system (40) as

$$\begin{aligned} x_1(0) = 14.4, \ \ x_2(0) = 10.7, \ \ x_3(0) = 6.8 \end{aligned}$$

(50)

Figure 6 shows the time-history of the controlled states $x_1, x_2, x_3$.

Fig. 6

Time-history of the controlled states $x_1, x_2, x_3$

6 Conclusions

In robust control systems, the sliding mode control is commonly used due to its inherent advantages of easy realization, fast response and good transient performance as well as insensitivity to parameter uncertainties and disturbance. In this work, we derived a novel second order sliding mode control method for the global stabilization of nonlinear systems. We proved the main result using Lyapunov stability theory. As an application of the general result, the problem of global chaos control of a novel highly chaotic system was studied and a new second order sliding mode controller has been derived. Numerical simulations using MATLAB were shown to depict the phase portraits of the novel highly chaotic system and the second order sliding mode controller design for the global chaos control of the novel highly chaotic system.