Keywords

32.1 Introduction

Flutter is a dangerous aeroelastic mechanism arising from the coalescence of two or more system modes in the presence of an airflow. The phenomenon can lead to a reduction of the aircraft’s flight envelope or even necessitate a re-design of the structure. In some cases, nonlinearities present in the aircraft’s structure or in the airflow can cause limit cycle oscillations (LCOs) at airspeeds much lower the flutter speed. Among these nonlinearities, freeplay, transonic buzz and store-induced limit cycle oscillations are the most common.

An alternative to aircraft re-design could be the use of mitigation techniques. Active control using control surface or piezoelectric patches can significantly delay these oscillations [1–5]. Alternatively, passive methods such as the nonlinear energy sink [6–9] or the linear tuned vibration absorber (LTVA) [10–12] and its nonlinear version, the nonlinear tuned vibration absorber (NLTVA) [11, 13], can also have a substantial beneficial effect.

In this paper, we study mechanical and electromechanical linear and nonlinear passive vibration absorbers in order to increase a nonlinear aeroelastic system’s linear flutter speed and LCO onset speed. The linear flutter speed, which is the linear equivalent of the Hopf bifurcation speed and is defined as the airspeed where the damping of one of the linearised system modes becomes negative, can be increased by means of a properly tuned linear absorber. Conversely, the LCO onset speed, defined as the first airspeed where LCOs can be observed, is equal to the flutter speed in a linear system but can be significantly smaller in the presence of nonlinearities. The LCO onset speed can be increased by means of properly tuned nonlinearities in the absorbers.

The mechanical linear and nonlinear tuned vibration absorbers (MLTVA and MNLTVA) are made of a mass-spring-dashpot subsystem that is attached to the primary structure. Previous studies showed that such a mechanical linear absorber can drastically increase the linear flutter speed of the system but can also lead to an area of bi-stability that would be dangerous in real life applications [10–13]. In this work, we demonstrate that adding nonlinearity to the absorber’s stiffness can suppress bi-stable phenomena. Malher et al. already demonstrated this beneficial effect of the nonlinear absorber however, they did not investigate the possible presence of isolated solutions [13].

The electrical linear and nonlinear tuned vibration absorbers (ELTVA and ENLTVA) are made of piezoelectric (PZT) patches glued to the primary system and connected to a circuit with an inductance and a resistance, forming a RLC circuit. The potential of these passive absorbers has been demonstrated for forced vibration mitigation [14, 15] (PZT shunting) but to the authors’ knowledge, none of the studies considered the case of flutter. Again, we demonstrate that the addition of a nonlinear capacitor to the absorber can suppress bi-stable phenomena caused by the linear absorber and the primary system’s nonlinearity.

The effect of these linear and nonlinear, mechanical and electrical tuned vibration absorbers is assessed numerically on a classical wing with pitch and plunge degrees-of-freedom (DOFs) and a hardening nonlinearity in the pitch DOF. The model used and all the parameter values are based on an experiment that is currently being built at the wind tunnel lab of the university of Liège (Belgium). The study is conducted in three parts. First, the optimal linear flutter speed of the aeroelastic system coupled to both types of linear absorbers is considered. Then, the effect of the optimal absorbers on the pre-critical response of the linearised system is assessed. Finally, nonlinear analysis is performed using linear and nonlinear absorbers in order to analyse their effect on the LCO onset speed of the system.

32.2 Aeroelastic System

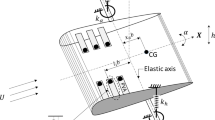
Figure 32.1 depicts the typical aeroelastic system, called the primary system, considered in this study. It consists of a rigid symmetric wing with chord c = 200 mm and span s = 1000 mm attached to springs and dashpots that provide elastic degrees of freedom in pitch (θ) and plunge (h). The system respectively features rotational and translational inertia I θ & m h , stiffness k θ & k h , damping c θ & c h and a static imbalance S. The flexural axis is located at a distance x f  = 0. 35c from the leading edge. All the system parameters are linear apart from the stiffness in pitch which follows a cubic hardening curve of coefficient k θ, 3 so that the total stiffness in pitch is given by k θ θ + k θ, 3 θ 3. This system, whose parameters values are given in Table 32.1, is an approximation of an experimental apparatus that is being built at the University of Liège. Without any mitigation device the flutter speed of the wing is U 0 ∗ = 17. 5 m/s.

Fig. 32.1
figure 1

Aeroelastic system with different absorbers. (a ) Mechanical LTVA. (b ) Electrical LTVA

Full size image
Table 32.1 Characteristics of the system
Full size table

The first vibration absorber considered is the mechanical absorber (Fig. 32.1a), which serves as a reference as its capabilities have already been demonstrated [10–12]. It consists of a mass m ltva attached to the wing at a distance x ltva from the flexural axis by means of a spring and a dashpot of stiffness and damping k ltva and c ltva respectively. The mass ratio \(\overline{m}_{ltva}\) of this absorber is varied from 1 to 8% of the mass of the primary system while the only position considered is x ltva  = 0 i.e. the absorber is located on the flexural axis of the wing and therefore only affects the plunge. This absorber configuration adds a DOF y that measures the displacement of the absorber’s mass. A nonlinear version of this absorber with a cubic stiffness of coefficient k nl, 3 is also considered so that the total absorber stiffness force is given by (y − h)k ltva + k nl, 3(y − h)3. Throughout the paper, the mechanical absorber is called MLTVA when the nonlinear coefficient k nl, 3 is equal to zero and MNLTVA when it is different from zero.

Alternatively, the electromechanical absorber (Fig. 32.1b) consists of a RL electrical circuit with resistance R and inductance L coupled to the plunge springs by up to eight PI255 piezoelectric patches of capacitance C pzt  = 87. 5 nF and coupling coefficient β pzt  = 7500 C/m per PZT patch. In this configuration, the LTVA capacitance C ltva  = N pzt × C pzt and the LTVA coupling coefficient β ltva  = N pzt ×β pzt of the absorber are the product of the number of patches N pzt and the individual capacitance and coupling coefficient of the patches. This absorber configuration adds a DOF q, the charge in the electrical circuit, to the system. A nonlinear version of this absorber with a cubic capacitive term C nl, 3 is also considered so that the capacitive tension in the circuit is given by \(\frac{1} {C_{ltva}}q + C_{nl,3}q^{3}\). Throughout the paper, the electromechanical absorber is called ELTVA when the nonlinear coefficient C nl, 3 is equal to zero and ENLTVA when it is different from zero.

Assuming small displacements, the structural equations of motion of the system coupled to a MNLTVA at x ltva  =  0 are given by

$$\displaystyle{ \left \{\begin{array}{ccccccccc} m\ddot{h}& + &S\ddot{\theta }&+&c_{h}\dot{h} + c_{ltva}(\dot{h} -\dot{ y})&+&k_{h}h + k_{ltva}(h - y) + k_{nl,3}(h - y)^{3} & =&F_{ext,h} \\ S\ddot{h} & + & I_{\theta }\ddot{\theta } &+& c_{\theta }\dot{\theta } &+& k_{\theta }\theta + k_{\theta,3}\theta ^{3} & =& F_{ext,\theta } \\ &m_{ltva}\ddot{y}& &+& c_{ltva}(\dot{y} -\dot{ h}) &+& k_{ltva}(y - h) + k_{nl,3}(y - h)^{3} & =& 0 \end{array} \right. }$$
(32.1)

and the equations of motion of the system coupled to a ENLTVA are written as

$$\displaystyle{ \left \{\begin{array}{ccccccccc} m\ddot{h}& + & S\ddot{\theta } &+&c_{h}\dot{h}&+& k_{h}h +\beta _{ltva}q & =&F_{ext,h} \\ I_{\theta }\ddot{\theta } & + &S\ddot{h}&+& c_{\theta }\dot{\theta } &+& k_{\theta }\theta + k_{\theta,3}\theta ^{3} & =& F_{ext,\theta } \\ &L\ddot{q}& &+& R\dot{q} &+& \frac{1} {C_{ltva}}q +\beta _{ltva}h + C_{nl,3}q^{3} & =& 0\end{array} \right. }$$
(32.2)

where F ext, h and F ext, θ correspond to plunge and pitch aerodynamic loads that can be computed using any unsteady aerodynamic formulation. In both cases, the linear absorber is recovered by setting C nl, 3 or k nl, 3 to zero. The equations of motion of the system with a mechanical and an electrical absorber are very similar as the inductance plays the role of the inertia, the resistance of the damping and the capacitance of the stiffness. The only difference between the two absorbers lies in their coupling to the primary system.

Assuming a linear attached airflow and unsteady aerodynamics based on the Wagner function [16], the aeroelastic equations of motion of the coupled system subject to an air stream of density ρ and airspeed U are given by

$$\displaystyle{ \mathbf{\dot{x}} = \mathbf{Q}\mathbf{x}+\mathbf{f}_{nl} = \left (\begin{array}{*{10}c} -\mathbf{M}^{-1}(\mathbf{C} +\rho U\mathbf{D})&-\mathbf{M}^{-1}(\mathbf{E} +\rho U^{2}\mathbf{F})&-\rho U^{3}\mathbf{M}^{-1}\mathbf{W} \\ \mathbf{I}_{3\times 3} & \mathbf{0}_{3\times 3} & \mathbf{0}_{4\times 3} \\ \mathbf{0}_{4\times 3} & \mathbf{W_{1}} & U\mathbf{W_{2}} \end{array} \right )\mathbf{x}+k_{\theta,3}\theta ^{3}\times \left (\begin{array}{*{10}c} -\mathbf{M}^{-1}\left (\begin{array}{*{10}c} 0\\ 1 \\ 0 \end{array} \right ) \\ \mathbf{0}_{7\times 1} \end{array} \right ) }$$

where \(\mathbf{x} = [\mathbf{\dot{z}}\ \mathbf{z}\ \mathbf{w}]^{T}\) is the state vector that comprises z, the structural DOFs of the system with an absorber, and w = [w 1 w 2 w 3 w 4], the aerodynamic state vector that models the memory effect of the wake. The structural DOFs of the system are written z = [h θ y] when a mechanical absorber is considered and z = [h θ q] when an electrical absorber is used. Matrix C is the structural damping matrix, ρ U D is the aerodynamic damping matrix, E is the structural stiffness matrix, ρ U 2 F is the aerodynamic stiffness matrix, W is the aerodynamic state matrix, W 1 and W 2 are the aerodynamic state matrices, A is the structural mass matrix, ρ B is the aerodynamic mass matrix and M is defined as M = A +ρ B. All those matrices are given in Appendix.

32.3 Effect of the Absorber on the Flutter Speed

Figure 32.2a plots the relative flutter speed of the system defined as U ∗∕U 0 ∗, the ratio between U ∗, the linear flutter speed of the system with an optimally tuned LTVA and U 0 ∗ = 17. 5 m/s, the flutter speed of the primary system alone. The mechanical absorber (blue) increases the flutter speed by 10 to 35% depending on the mass ratio while the electrical absorber (black) is ineffective if too few PZT patches are used but can increase the flutter speed by up to 80% with 8 patches. Figure 32.2a, b depict the optimal absorber frequency and damping as a function of the mass ratio or amount of PZT patches. The mechanical absorber’s optimal frequency decreases and its optimal damping increases as the absorber becomes heavier; the behaviour resembles Den Hartoog’s criterion for LTVA tuning in forced systems [17]. Conversely, with a ELTVA the optimum frequency increases while N pzt  ≤ 4 then decreases, while the damping increases monotonously. Absorbers with \(\overline{m}_{ltva} = 4.2\%\) and N pzt  = 4 are studied in detail in the rest of the study. In these configurations, both absorbers increase the flutter speed by 25% when optimally tuned.

Fig. 32.2
figure 2

Performance of different absorbers and their optimal tuning. The legend of subfigure (c ) applies to all three subfigures. (a ) Optimum flutter speed. (b ) Optimum absorber frequency. (c ) Optimum absorber damping

Full size image

Figure 32.3a plots the linear relative flutter speed of the system as a function of the absorber damping and frequency with a MLTVA with \(\overline{m}_{ltva} = 4.2\%\). Figure 32.3b depicts the same quantities for a ELTVA with N pzt  = 4. In this case, both absorbers increase the flutter speed by up to 25%. They lose their effectiveness smoothly as their damping is modified or when their frequency is increased but very abruptly when their frequency is decreased. This phenomenon, due to the damping variation with airspeed, is investigated in Sect. 32.4. The white line separates the area where the absorber has a detrimental effect on the system. Mechanical absorbers with small frequency and damping reduce the frequency gap between the system’s modes without providing any damping to the system, which reduces the flutter speed. Electrical absorbers without sufficient damping have a similar effect.

Fig. 32.3
figure 3

Flutter speed of the system as a function of the LTVA frequency and damping. The colorbar or subfigure (b ) applies to subfigures (a ) and (b ). (a ) MLTVA with \(\overline{m}_{ltva} = 4.2\%\). (b ) ELTVA with N pzt  = 4

Full size image

In the rest of this work, only the optimal absorbers are studied in detail. The optimal mechanical absorber with \(\overline{m}_{ltva} = 4.2\%\) is tuned at f ltva  = 8. 0732 Hz and ζ ltva  = 7. 9145% and the optimal electrical absorber with N pzt  = 4 is tuned at f ltva  = 8. 1878 Hz and ζ ltva  = 7. 8085%. These parameters are very finely tuned in order to study the optimal absorber but a detuning of 0.1 Hz in the absorber still leads to a significant increase in flutter speed and to detuning phenomena similar to those observed in the rest of this work. A fine frequency tuning of the absorber should be possible in the wind tunnel by slightly modifying the mass of the MLTVA or the inductance of the ELTVA.

32.4 Linear System Frequency and Damping Variation with Airspeed

Figure 32.4 depicts the frequency and damping variation with relative airspeed in the case where no LTVA is attached to the system (grey), with an optimally tuned MLTVA (blue) and with an optimally tuned ELTVA (black). Figure 32.4a corresponds to the frequency variation with airspeed, Fig. 32.4b plots the damping variation with airspeed while Fig. 32.4c is a zoom in the purple rectangle of Fig. 32.4b. These figures are computed from linear stability analysis after linearizing the system around the fixed point at the origin. The modes are named M 0i for the reference system, M ei for the system with the ELTVA and M mi for the system with the MLTVA. The wind-off mode shapes and frequencies are described in Table 32.2.

Fig. 32.4
figure 4

Frequency and damping variation with airspeed of the system without absorber and with mechanical and electrical linear tuned vibration absorbers. The legend in subfigure (a ) applies to all three subfigures. (a ) Frequency. (b ) Damping. (c ) Damping (zoom on the purple square)

Full size image
Table 32.2 Wind-off mode shapes of the system with and without absorber
Full size table

The primary system features two modes, M 01 and M 02. As the airspeed increases, the system frequencies approach each other while the damping of mode M 01 increases then decreases to cause flutter and the damping of mode M 02 increases monotonously. The addition of a MLTVA introduces a new mode with an intermediate wind-off frequency. In that case, the damping of mode M m3 increases monotonously, the damping of mode M m2 increases, decreases, becomes almost zero at point B then increases again while the damping of mode M m1 increases at first then decreases to cause flutter. Any small decrease in absorber frequency would make the mode M m2 flutter at point B, hence the abrupt detuning observed in Fig. 32.3a, while any small increase in absorber frequency would just reduce the flutter speed of mode M m1 (point C) and increase the damping of mode M m2 at point B. The behaviour of the system with a ELTVA is very similar to that of the system with a MLTVA. When optimally tuned, the coupled system has a mode M e2 whose damping nearly causes flutter at point A then increases and a mode M e1 whose damping becomes negative at point C. Again, any small decrease in ELTVA frequency would cause the system to flutter at point A, which explains the sensitivity of the system to a decrease in absorber frequency.

32.5 Bifurcation Analysis of the System with Linear Tuned Vibration Absorbers

The bifurcation diagrams in pitch amplitude of the system without absorber (grey), with an optimal MLTVA (blue) and with an optimal ELTVA (black) are depicted in Fig. 32.5. These diagrams plot limit cycle amplitude in pitch against relative airspeed and are computed using a numerical continuation technique based on finite differences [18]. Without absorber, the system undergoes a supercritical Hopf bifurcation at relative airspeed 1, then the LCO amplitude increases monotonously with airspeed. In this case, the linear flutter speed coincides with the LCO onset speed (smallest airspeed at which a LCO can be observed) and the pitch nonlinearity has a beneficial effect because it prevents the oscillation amplitude from becoming infinite at the flutter airspeed.

Fig. 32.5
figure 5

Bifurcation diagram of the system with and without linear absorbers

Full size image

The bifurcation branch with a MTLVA (blue) is significantly different than that without absorber. The coupled system undergoes a supercritical Hopf bifurcation at an airspeed of 1.25, then the amplitude increases with airspeed until 1.26 where the branch folds back and becomes unstable. At U∕U 0 ∗ = 1. 16, a second fold occurs, the branch becomes stable again and its amplitude increases monotonously with airspeed. As a result, the relative LCO onset speed is only 1.16 and it no longer coincides with the linear flutter speed of the system. The bifurcation branch of the system with a ELTVA is very similar. The Hopf airspeed lies again at 1.25 but the two folds occur at 1.27 and 1.14. In this case, the LCO onset speed is only 1.14. For both absorbers, the region between the Hopf and first fold is bi-stable, as there are two possible stable limit cycle oscillations, one of low and of high amplitude. The region between the Hopf and the second fold is also bi-stable, as the system’s response trajectories can be attracted by either the stable fixed point or the stable limit cycle.

The bi-stability and the reduction in LCO onset speed are due to the detuning of the absorbers. The linear absorbers are only effective when the amplitude is small, i.e. when the effects of the structural nonlinearity can be neglected. In that case, they increase the relative Hopf speed of the coupled system to 1.25. If the oscillation amplitude is increased, the equivalent linear stiffness of the primary system increases, which detunes the absorbers. The detuning of the absorbers due to the structural nonlinearity in the primary system can cause limit cycle oscillations at airspeeds lower than the linear flutter speed, which leads to a bi-stable region where LCOs or static solutions can exist depending on the initial conditions. In many real-life applications, LCOs can not be tolerated. As a consequence, the performance of the systems with absorbers is determined by the LCO onset speed rather than the linear flutter speed. With that in mind, the MLTVA increases the performance of the system by only 16% while the ELTVA provides an improvement of only 14% while linear analysis predicted a performance gain of 25%.

32.6 Bifurcation Analysis of the System with Nonlinear Tuned Vibration Absorbers

The detuning of the linear absorbers that is causing the large bi-stable area can be countered by introducing a nonlinear stiffness (MNLTVA) or capacitance (ENLTVA) to the respective LTVAs. This nonlinearity added to the absorbers allows them to increase their equivalent stiffness to cancel the detuning. For the mechanical absorber, the stiffness force is given by F nl  = k ltva  (y − h) + k nl, 3 (y − h)3 with values of k nl, 3 ranging from 0 (linear absorber) to 800 × k ltva .

Figure 32.6 depicts bifurcation diagrams of the system with MNLTVAs of nonlinear coefficient between 0 and 800 × k ltva . These diagrams, computed using a numerical continuation algorithm based on a shooting method [18], are described as follows.

  • Figure 32.6a: k nl, 3 = 0 × k ltva . This figure plots the bifurcation behaviour of the linear absorber that was studied in detail in Sect. 32.5. The Hopf relative speed is increased to 1.25 however a large bi-stable area arises from the detuning of the absorber. As a result, the LCO onset speed is equal to only 1.16, the relative airspeed of the fold B.

    Fig. 32.6
    figure 6

    Bifurcation diagrams of the system with linear and nonlinear mechanical vibration absorbers. The legend in subfigure (a ) applies to all eight subfigures. (a ) k nl, 3 = 0 × k ltva . (b ) k nl, 3 = 20 × k ltva . (c ) k nl, 3 = 60 × k ltva . (d ) k nl, 3 = 70 × k ltva . (e ) k nl, 3 = 120 × k ltva . (f ) k nl, 3 = 130 × k ltva . (g ) k nl, 3 = 400 × k ltva . (h ) k nl, 3 = 800 × k ltva

    Full size image

  • Figure 32.6b: k nl, 3 = 20 × k ltva . This absorber increases the relative LCO onset speed (fold B) to 1.161 because its nonlinearity mitigates the detuning of the absorber to a certain extent but is not sufficiently large. At higher airspeeds, two new fold bifurcations C and D arise at high amplitudes.

  • Figure 32.6c: k nl, 3 = 60 × k ltva . Increasing the NLTVA nonlinear coefficient delays the LCO onset speed slightly further as the fold B is now located at an airspeed of 1.171. More importantly, the increased nonlinearity in the absorber reduces the airspeed and amplitude of the folds C and D and therefore the airspeed at which the lower amplitude LCO branch arises.

  • Figure 32.6d: k nl, 3 = 70 × k ltva . When the nonlinear coefficient reaches approximately 70 times the linear coefficient, the folds at points D and A merge and disappear. There are now two separate limit cycle branches, one that appears at the supercritical Hopf point and an isolated branch that closes in on itself. The folds B and C now lie on the isolated solution branch and the LCO onset speed reaches 1.175.

  • Figure 32.6e: k nl, 3 = 120 × k ltva . Increasing the nonlinear coefficient further has very little effect on the main branch however it reduces the span of the isolated solution branch. At this point, the relative LCO onset speed is equal to 1.201. This isolated solution is dangerous because it is rather narrow and can easily be missed when performing continuation without bifurcation tracking.

  • Figure 32.6f: k nl, 3 = 130 × k ltva . This nonlinear coefficient is sufficient to totally suppress the isolated solution branch. As a result, the system now features a smooth super-critical bifurcation diagram with a nonlinear LCO onset speed that coincides with the Hopf point and without any bi-stable regions. This is the optimal tuning of the nonlinear absorber.

  • Figure 32.6g: k nl, 3 = 400 × k ltva . Nonlinear absorber coefficients larger than the optimal turn the super-critical Hopf bifurcation into sub-critical, which reduces the LCO onset speed but also increases the LCO onset amplitude. The higher the nonlinear coefficient, the lower the LCO onset speed. Nevertheless, even at three times the optimal value, the relative LCO onset speed is equal to 1.230 for this absorber which is much better than a LTVA.

  • Figure 32.6h: k nl, 3 = 800 × k ltva . Even at about six times the optimal value, this nonlinear absorber still features a relative LCO onset speed of 1.203 which further proves the robustness of this absorber.

Similar phenomena are observed with an electromechanical vibration absorber. In this case, the capacitive tension is given by \(V _{C} = \frac{1} {C_{ltva}}q + C_{nl,3}q^{3}\). The values of the nonlinear coefficient C nl, 3 are varied from 0 to \(80 \times \ 10^{5} \times \frac{1} {C_{ltva}}\). Theses values of the nonlinear coefficient may seem extreme but in fact, they are not because the charge q in the absorber is very small. Figure 32.7 depicts mostly the same phenomena as Fig. 32.6 for an electromechanical nonlinear absorber.

  • Figure 32.7a–e: for nonlinear coefficients smaller than \(7 \times \ 10^{5} \times \frac{1} {C_{ltva}}\), the absorber’s nonlinearity causes the appearance of two additional folds at points C and D. As the nonlinear coefficient increases, the folds at points A and D merge, creating an isolated branch when the nonlinear coefficient is sufficiently large. Increasing the nonlinear coefficient increases the LCO onset speed and reduces the span of the isolated branch. Note that in Fig. 32.7e, the fold C has an airspeed smaller than that of the Hopf point which means that between relative airspeeds of 1.219 and 1.248, only static solutions exist.

    Fig. 32.7
    figure 7

    Bifurcation diagrams of the system with linear and nonlinear electromechanical vibration absorbers. The legend in subfigure (a) applies to all eight subfigures. (a ) \(C_{nl,3} = 0 \times \frac{1} {C_{ltva}}\). (b ) \(C_{nl,3} = 3 \times 10^{5} \times \frac{1} {C_{ltva}}\). (c ) \(C_{nl,3} = 6 \times 10^{5} \times \frac{1} {C_{ltva}}\). (d ) \(C_{nl,3} = 7 \times 10^{5} \times \frac{1} {C_{ltva}}\). (e ) \(C_{nl,3} = 12 \times 10^{5} \times \frac{1} {C_{ltva}}\). (f ) (\(C_{nl,3} = 13 \times 10^{5} \times \frac{1} {C_{ltva}}\). g ) (\(C_{nl,3} = 40 \times 10^{5} \times \frac{1} {C_{ltva}}\). h ) \(C_{nl,3} = 80 \times 10^{5} \times \frac{1} {C_{ltva}}\)

    Full size image

  • Figure 32.7f corresponds to a nonlinear coefficient of \(13 \times \ 10^{5} \times \frac{1} {C_{ltva}}\), which is the optimal value for this system. This nonlinearity is just sufficient to suppress the isola and the LCO onset speed coincides with the Hopf speed.

  • Figure 32.7g, h: when the nonlinear capacity is higher than the optimal, the super-critical Hopf bifurcation is turned into sub-critical, which leads to a large LCO onset amplitude. The system is not sensitive to the exact value of C nl, 3 as a nonlinear coefficient about six times higher than the optimal one leads to a relative LCO onset speed of 1.195, which is still much higher than the onset speed of the system with a linear absorber.

In summary, the addition of a properly tuned nonlinear stiffness term to the MLTVA or of a properly tuned nonlinear capacitive term to the ELTVA increases the LCO onset speed to the linear flutter speed of the system and suppresses a potentially dangerous bi-stable area. The LCO onset speed is quite sensitive to the absorber’s nonlinearity when it is smaller than the optimal value, i.e. when the absorber is not capable of suppressing the isolated branch, but not so sensitive when it is larger than the optimal value, which is encouraging for practical implementations.

32.7 Conclusions

This work shows numerically that an electrical linear tuned vibration absorber made of a RL circuit and PZT patches can perform at least as well as a mechanical linear tuned vibration absorber. Both linear absorbers have a similar effect on the system and lead to a substantial increase in linear flutter speed. On the other hand, a large bi-stable region, due to the structural nonlinearity of the primary system, greatly reduces the nonlinear LCO onset speed of the system.

The addition of a properly tuned nonlinear stiffness or capacity on the mechanical or electrical absorbers respectively totally suppresses the bi-stable area. Finally, it must be noted that unlike the linear absorber parameters that require a very fine tuning, the nonlinear parameters do not have a significant impact on the absorber performance provided they are sufficiently large.