Keywords

1 Introduction, Presentation of the SIR Model

The SIR model with vital dynamics, see e.g. [4, 11], is one of the most elementary compartmental models of epidemics. It describes the evolution of the relative proportions of three classes of a population of constant size, namely the susceptibles S, capable of contracting the disease and becoming infective; the infectives I, capable of transmitting the disease to susceptibles; and the recovered R, permanently immune after healing. This model is as follows:

$$\begin{aligned} \dot{S} = \mu - \mu S-\beta SI\end{aligned}$$
(3.1a)
$$\begin{aligned} \dot{I} = \beta SI - (\mu +\gamma )I \end{aligned}$$
(3.1b)

The natural birth and mortality rate is \(\mu \) (the disease is supposed not to induce supplementary death rate), \(\gamma \) is the recovery rate, while \(\beta \) represents the transmission rate per infective. All these parameters are positive. We consider here proportions of the population, and more precisely that \(S+I+R\equiv 1\). Notice that the dynamics of R (given by \(\dot{R} = \gamma I-\mu R\), that guarantees that \(\dot{S}+\dot{I}+\dot{R}\equiv 0\)) may be omitted, as the total population size is constant.

When the parameters are constant, the evolution of the solutions of system (3.1) depends closely upon the ratio \({\mathscr {R}}_0:=\frac{\beta }{\mu +\gamma }\) [4, 11]. The disease-free equilibrium (\(S=1\), \(I=R=0\)) always exists. When \({\mathscr {R}}_0 < 1\), it is the only equilibrium and it is globally asymptotically stable. It becomes unstable when \({\mathscr {R}}_0 > 1\), and an asymptotically stable endemic equilibrium then appears.

On the contrary, when the parameters are time-varying, complicated dynamics may occur [12]. We are interested here in estimating the value of the three populations, a first step paving the way for epidemic outbreak forecasting. We use techniques of interval observers, including output injection, in the spirit e.g. of [7, 8, 14]. The dynamics of the obtained error equation is seen as a linear uncertain time-varying positive system, whose asymptotic stability is ensured through the search of a common linear Lyapunov function and adequate choice of the gain as function of the state estimate.

The hypotheses on the model and some qualitative results are presented in Sect. 3.2. The considered class of observers is given in Sect. 3.3, with some a priori estimates and technical results. The main result is provided in Sect. 3.4, where the asymptotic error corresponding to certain gain choice is quantified. Last, illustrative numerical experiments are shown in Sect. 3.5.

2 Hypotheses on the Model and Preliminaries

We consider in the sequel that the transmission rate is subject to uncertain seasonal variations. It is known that relatively modest variations of this type have the capacity to induce large amplitude fluctuations in the observed disease incidence. This seems due to harmonic resonance, the seasonal forcing exciting frequencies close to the natural near-equilibrium oscillatory frequency [6].

One assumes that the transmission rate \(\beta \) is bounded by two functions \(\beta _\pm \), available in real-time (all functions are supposed locally integrable):

$$\begin{aligned} \beta _-(t) \le \beta (t) \le \beta _+(t) \quad \text {for a.e.} \ t\ge 0 \end{aligned}$$
(3.2)

(typically with \(\displaystyle 0< \liminf _{t\rightarrow +\infty }\beta _-(t) \le \limsup _{t\rightarrow +\infty } \beta _+(t) <+\infty \)).

Our goal is to estimate lower and upper bounds for the three subpopulations. The unique available measurement is supposed to be the incidence rate \(y= \beta SI\), i.e. the number of new infectives per time unit (accessible through epidemiological surveillance). With representation (3.1), y is not a state component, contrary e.g. to [3, 5]. One sees easily that with this output, the system is detectable, but not observable at the disease-free equilibrium (where \(I=0\)).

The following result provides qualitative estimates of its solutions.

Lemma 3.1

Assume \(S(0)\ge 0\), \(I(0)\ge 0\) and \(S(0)+I(0)\le 1\). Then the same properties hold for any \(t\ge 0\). The same is true with strict inequalities.

Proof

Integrating (3.1a), (3.1b) yields

$$\begin{aligned} I(t) = I(0) e^{\int _0^t (\beta (\tau )S(\tau )-(\mu +\gamma )).d\tau } \end{aligned}$$
$$\begin{aligned} S(t) = S(0) e^{-\int _0^t (\mu +\beta (\tau )I(\tau )).d\tau } + \mu \int _0^t e^{-\int _\tau ^t (\mu +\beta I)}.d\tau \end{aligned}$$

which show that \(S(t), I(t)\ge 0\) for any \(t\ge 0\); while integrating the differential inequality \(\dot{S} + \dot{I} \le \mu (1-S-I)\) shows that \(1-(S(t)+I(t))\ge 0\) for any \(t\ge 0\). The same formulas provide the demonstration in the strict inequality case.\(\square \)

3 A Class of Nonlinear Observer Models

As preparation for the upcoming study, we explore now the following class of observers for system (3.1):

$$\begin{aligned} \dot{\hat{S}} = \mu - \mu \hat{S}-y +k_S(t)(y-\beta _S \hat{S}\hat{I}) \end{aligned}$$
(3.3a)
$$\begin{aligned} \dot{\hat{I}} = y - (\mu +\gamma )h\hat{I}+k_I(t)(y-\beta _I \hat{S}\hat{I}) \end{aligned}$$
(3.3b)

where the time-varying gain components \(k_S(t), k_I(t)\) are yet to be defined.

Lemma 3.2

Suppose that for some \(\varepsilon >0\),

$$\begin{aligned} k_S(t)\ge 1\ \text { whenever }\ \hat{S}(t)\le \varepsilon ,\qquad k_I(t)\ge -1\ \text { whenever}\ \hat{I}(t)\le \varepsilon . \end{aligned}$$
(3.4)

Assume \(\hat{S}(0)\ge 0\), resp. \(\hat{I}(0)\ge 0\). Then, for any \(t\ge 0\), \(\hat{S}(t)\ge 0\), resp. \(\hat{I}(t)\ge 0\).

Proof

Verify directly that, under assumption (3.4), \(\dot{\hat{S}} \ge 0\), resp. \(\dot{\hat{I}} \ge 0\), in the neighborhood of a point where \(\hat{S}= 0\), resp. \(\hat{I}= 0\). This proves the result.\(\square \)

Last, the following technical result will be needed.

Lemma 3.3

Define \(e_S:= S-\hat{S}\), \(e_I:=I-\hat{I}\). Then,

$$\begin{aligned} \begin{pmatrix} \dot{e}_S \\ -\dot{e}_I \end{pmatrix} = \begin{pmatrix} -(\mu +k_S\beta _S h\hat{I}) &{} k_S\beta _S S\\ k_I\beta _I h\hat{I}&{} -(\mu +\gamma +k_I\beta _I S) \end{pmatrix} \begin{pmatrix} e_S \\ - e_I \end{pmatrix} + SI \begin{pmatrix} k_S(\beta _S-\beta ) \\ k_I(\beta -\beta _I) \end{pmatrix} \end{aligned}$$
(3.5)

Proof

One has \(\dot{e}_S = -\mu e_S +k_S(\beta _S \hat{S}\hat{I}-y)\) and \(\dot{e}_I = -(\mu +\gamma ) e_I +k_I(\beta _I \hat{S}\hat{I}-y)\). On the other hand, \(\beta _S \hat{S}\hat{I}-y = (\beta _S-\beta )SI+\beta _SS(\hat{I}-I)+\beta _S\hat{I}(\hat{S}-S)=-SI(\beta -\beta _S)-\beta _SSe_I-\beta _S\hat{I}e_S\), and similarly for \(\beta _I \hat{S}\hat{I}-y\). One deduces

$$\begin{aligned} \begin{pmatrix} \dot{e}_S \\ \dot{e}_I \end{pmatrix} = -\begin{pmatrix} \mu +k_S\beta _S \hat{I}&{} k_S\beta _S S\\ k_I\beta _I\hat{I}&{} k_I\beta _I S + \mu +\gamma \end{pmatrix} \begin{pmatrix} e_S \\ e_I \end{pmatrix} - SI \begin{pmatrix} k_S(\beta -\beta _S) \\ k_I(\beta -\beta _I) \end{pmatrix} \end{aligned}$$
(3.6)

and finally (3.5) when using \(-e_I\) instead of \(e_I\).\(\square \)

Observe that system (3.6) appears monotone for nonpositive gains, which is detrimental to its stability. This is not the case with system (3.5), which is used in the sequel to construct interval observers.

4 Error Estimates for Interval Observers

Notice first that system (3.1) is not evidently, or transformable into, a monotone system. The instances of (3.3) presented in the next result provide a class of interval observers with guaranteed speed of convergence.

Theorem 3.1

Consider the two independent systems

$$\begin{aligned} \dot{S}_+ = \mu - \mu S_+-y +k_{S+}(t)(y-\beta _-(t) S_+I_-)\end{aligned}$$
(3.7a)
$$\begin{aligned} \dot{I}_- = y - (\mu +\gamma )I_-+k_{I-}(t)(y-\beta _+(t) S_+I_-) \end{aligned}$$
(3.7b)
$$\begin{aligned} \dot{S}_- = \mu - \mu S_--y +k_{S-}(t)(y-\beta _+(t) S_-I_+)\end{aligned}$$
(3.8a)
$$\begin{aligned} \dot{I}_+ = y - (\mu +\gamma )I_++k_{I+}(t)(y-\beta _-(t) S_-I_+) \end{aligned}$$
(3.8b)

i. Assume that the gains are nonnegative functions of \(S_\pm , I_\pm \), that fulfill (3.4) for some \(\varepsilon >0\). If \(0\le S_-(t)\le S(t)\le S_+(t)\) and \(0\le I_-(t)\le I(t)\le I_+(t)\) for \(t=0\), then the same holds for any \(t\ge 0\).

ii. If in addition the gain components \(k_{S\pm }(t), k_{I\mp }(t)\) are chosen such that

$$\begin{aligned} \beta _-(t) k_{S+}(t)-\rho _+ \beta _+(t) k_{I-}(t) = \frac{\rho _+\gamma }{\rho _+I_-(t)+S_+(t)}\end{aligned}$$
(3.9a)
$$\begin{aligned} \beta _+(t) k_{S-}(t)-\rho _- \beta _-(t) k_{I+}(t) = \frac{\rho _-\gamma }{\rho _-I_+(t)+S_+(t)} \end{aligned}$$
(3.9b)

for fixed \(\rho _\pm >0\), then, writing \(V_+(t):= (S_+(t)-S(t))+\rho _+(I(t)-I_-(t))\), \(V_-(t):= (S(t)-S_-(t))+\rho _-(I_+(t)-I(t))\), the state functions \(V_\pm \) are positive definite when the trajectories are initialized according to point i., andFootnote 1

$$\begin{aligned} \begin{aligned} \forall t\ge 0,\ V_\pm (t) \le \int _0^t e^{-\int _\tau ^t\delta _\pm } \max \{k_{S\pm }(\tau ),\rho _\pm k_{I\mp }(\tau )\} S(\tau )I(\tau )(\beta _+(\tau )-\beta _-(\tau ))\ d\tau \\ + e^{-\int _0^t\delta _\pm (\tau ).d\tau }V_\pm (0),\quad \text { with }\ \delta _\pm (t):=\mu + \gamma \frac{\rho _\pm I_\mp (t)}{\rho _\pm I_\mp (t)+S_+(t)} \end{aligned} \end{aligned}$$
(3.10)

The proposed observers guarantee that the errors converge exponentially, with speeds \(\delta _\pm (t)\) that smoothly vary from \(\mu \) (in absence of infectives: \(I_\pm (t)=0\)) to at most \(\mu +\gamma \) (in case of outbreak, if \(\rho _\pm I_\mp (t)\gg S_+(t)\)). Recall that a positive linear time-invariant system is asymptotically stable iff it admits a linear Lyapunov function of the type \(V_\pm \) [1, 10, 13]. With this in mind, it may indeed be deduced from the proof (see in particular (3.11)) that the convergence speed of observer of type (3.7)–(3.8) is bound to be at most equal to \(\mu +\gamma \) in presence of epidemics, and cannot be larger than \(\mu \) in absence of infectives.Footnote 2 Recall that \(\mu \) is the inverse of the mean life duration, while \(\gamma \) is the inverse of the mean recovery time: typically \(\mu \ll \gamma \). Therefore, the observer takes advantage of epidemic bursts to reduce faster the estimation error. Notice that these convergence speeds do not depend upon the values of \(\beta _\pm \).

The trade-off between stability and precision is clear from formula (3.10): an intrinsic limitation is evident from the fact that the integral therein is at least equal to \(\int _0^t e^{-(\mu +\gamma )(t-\tau )} \max \{k_{S\pm }(\tau ),\rho _\pm k_{I\mp }(\tau )\} S(\tau )I(\tau ) (\beta _+(\tau )-\beta _-(\tau )) d\tau \) which is guaranteed to vanish only when both gains are zero. On the other hand, for zero gains, the error equation for the susceptibles is \(\dot{e}_{S\pm }+\mu e_{S\pm } = 0\) which converges slowly to zero.

Last, observe that, with the estimate-dependent choice of the gain defined in (3.9), the error equations may be non monotone. However they fulfill the positivity and stability properties mentioned in the statement.

Proof of Theorem 3.1. We show the results for system (3.7) only, system (3.8) is treated similarly.

\(\bullet \) Introduce the error terms \(e_{S+}:=S_+-S\) and \(e_{I-} := I-I_-\). Applying Lemma 3.3 to system (3.7) with \(\hat{S}=S_+, \hat{I}=I_-, k_S=k_{S+}, \beta _S=\beta _-, k_I=k_{I-}, \beta _I=\beta _+\) (and therefore \(e_S= -e_{S+}, e_I=e_{I-}\)) yields

$$\begin{aligned} \begin{aligned} \begin{pmatrix} \dot{e}_{S+} \\ \dot{e}_{I-} \end{pmatrix}&= - \begin{pmatrix} \dot{e}_S \\ -\dot{e}_I \end{pmatrix} \\&= -\begin{pmatrix} -(\mu +k_{S+}\beta _-I_-) &{} k_{S+}\beta _- S\\ k_{I-}\beta _+I_- &{} -(\mu +\gamma +k_{I-}\beta _+ S) \end{pmatrix} \begin{pmatrix} e_S \\ - e_I \end{pmatrix} - SI \begin{pmatrix} k_{S+}(\beta _--\beta ) \\ k_{I-}(\beta -\beta _+) \end{pmatrix}\\&= \begin{pmatrix} -(\mu +k_{S+}\beta _-I_-) &{} k_{S+}\beta _- S\\ k_{I-}\beta _+I_- &{} -(\mu +\gamma +k_{I-}\beta _+ S) \end{pmatrix} \begin{pmatrix} e_{S+} \\ e_{I-} \end{pmatrix} + SI \begin{pmatrix} k_{S+}(\beta -\beta _-) \\ k_{I-}(\beta _+-\beta ) \end{pmatrix}\ . \end{aligned} \end{aligned}$$

The previous system may thus be written \(\dot{X} = f(t,X)\), for \(X:=\begin{pmatrix} e_{S+}&e_{I-} \end{pmatrix}^{{\textsf {T}}}\) and where the dependence with respect to time comes indirectly through the presence of the other time-varying term. The off-diagonal terms of the Jacobian matrix are respectively \(k_{S+}(t)\beta _-(t) S_+(t)\) and \(k_{I-}(t)\beta _+(t) I_-(t)\), clearly nonnegative for a.e. \(t\ge 0\) due to the hypotheses on the gain components (see Lemma 3.2). The corresponding system is therefore monotone [9, 15], and any solution of (3.7) departing with \(e_{S+}(0), e_{I-}(0)\ge 0\) verifies \(e_{S+}(t), e_{I-}(t)\ge 0\) for any \(t\ge 0\). This proves i.

\(\bullet \) Writing \(X:=\begin{pmatrix} e_{S+}&\ e_{I-} \end{pmatrix}^{{\textsf {T}}}\), notice that \(V_+(X) := u^{{\textsf {T}}}X\), for \(u:= \begin{pmatrix} 1&\ \rho _+ \end{pmatrix}\), and \(V_+\) and \(\rho _+>0\) as in the statement. When X is initialized with nonnegative values, then this property is conserved (see point i.), so \(V_+\) is positive definite and may be considered as a candidate Lyapunov function.

Along the trajectories of (3.7), one has, using \(\delta _+\) defined in (3.10),

$$\begin{aligned}&\dot{V}_+(X) +\delta _+ V_+ (X)\nonumber \\&\, = u^{{\textsf {T}}}(\dot{X}+\delta _+ X)\nonumber \\&\, = u^{{\textsf {T}}}\begin{pmatrix} \delta _+-(\mu +k_{S+}\beta _-I_-) &{} k_{S+}\beta _- S\\ k_{I-}\beta _+I_- &{} \delta _+-(\mu +\gamma +k_{I-}\beta _+ S) \end{pmatrix} X + SI u^{{\textsf {T}}}\begin{pmatrix} k_{S+}(\beta -\beta _-) \\ k_{I-}(\beta _+-\beta ) \end{pmatrix}\nonumber \\&\, = \begin{pmatrix} \delta _+-\mu +(\rho _+ k_{I-}\beta _+-k_{S+}\beta _-)I_-&\ \rho _+ (\delta _+-\mu -\gamma ) -(\rho _+ k_{I-}\beta _+-k_{S+}\beta _-) S \end{pmatrix}X \nonumber \\&\quad \,\, + SI (k_{S+}(\beta -\beta _-)+\rho _+k_{I-}(\beta _+-\beta ))\ . \end{aligned}$$
(3.11)

Choosing the gain as in (3.9a) gives

$$\delta _+-\mu +(\rho _+ k_{I-}\beta _+-k_{S+}\beta _-)I_- = \frac{\gamma I_-}{I_-+\frac{S_+}{\rho _+}}- \frac{\gamma I_-}{I_-+\frac{S_+}{\rho _+}}= 0$$

and

$$ \rho _+ (\delta _+-\mu -\gamma ) -(\rho _+ k_{I-}\beta _+-k_{S+}\beta _-)S = -\frac{\gamma S_+}{I_-+\frac{S_+}{\rho _+}} + \frac{\gamma S}{I_-+\frac{S_+}{\rho _+}}\le 0. $$

Formula (3.11) then yields \(\dot{V}_+(X) +\delta _+ V_+ (X) \le SI (k_{S+}(\beta -\beta _-)+\rho _+k_{I-}(\beta _+-\beta ))\le \max \{k_{S+},\rho _+k_{I-}\} SI(\beta _+-\beta _-)\), which gives (3.10) by integration. This proves point ii. and achieves the proof of Theorem 3.1.\(\square \)

5 Numerical Experiments

We consider in the sequel the following parameter values. One takes \(\mu =0.02 \text {/year}\), \(\gamma =\frac{1}{20} \text {/day}=\frac{365}{20} \text {/year}\). The transmission rate \(\beta (t)\) is taken as \(\beta ^*(1+\eta \cos (\omega t))\), with nominal value \(\beta ^*\) such that \({\mathscr {R}}_0=\frac{\beta ^*}{\mu +\gamma }=17\), \(\eta =0.4\) and \(\omega = 2.4\,\text {rad/year}\), close to the pulsation of the near-equilibrium natural oscillations. Last, S and I are initialized at 0.06 and 0.001, close to the perturbation-free equilibrium (\(\eta =0\)), and the observer initial conditions as 0 and 1 (lower and upper values).

The gains were chosen as follows

$$ k_{S_+} = \frac{\gamma }{I_-+\frac{S_+}{\rho _+}} \frac{1}{\beta _-}, \qquad k_{I_-} = 0 $$
$$ k_{S_-} = \max \left( \frac{\gamma }{I_++\frac{S_+}{\rho _-}} \frac{1}{\beta _+},\frac{1}{1+\frac{S_-}{\varepsilon }} \right) \text { with } \varepsilon = 5 \times 10^{-3}, \qquad k_{I_+} = \frac{1}{\rho _- \beta _-} \left( \beta _+ k_{S_-} -\frac{\gamma }{I_++\frac{S_+}{\rho _-}} \right) $$

in accordance with (3.9). The small parameter \(\varepsilon \) is introduced in order to ensure that \(S_-\) remains positive, according to Lemma 3.2.

\(\bullet \) First, essays were realized in the absence of uncertainty on the transmission rate, that is taking \(\beta =\beta _-=\beta _+\). Figure 3.1 shows, for \(\rho _\pm =100\), the logarithm of the errors of \(S_\pm \), i.e., \(\log _{10}(e_{S+}) = \log _{10}(S_+ - S)\) and \(\log _{10}(e_{S-}) = \log _{10}(S - S_-)\). We see that it decays with a high speed, whose instantaneous values are between \(\mu \) and \(\mu +\gamma \), as proved in Theorem 3.1.

Fig. 3.1
figure 1

Decimal logarithm of the \(e_{S-}\) (left) and \(e_{S+}\) (right) as a function of time (in years)

Full size image

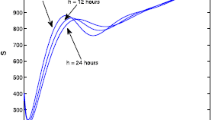
\(\bullet \) We now introduce uncertainty in the transmission rate. We use quite imprecise estimates, namely \(\beta _\pm (t)= (1\pm 0.6) \beta (t)\). Figure 3.2 shows results for \(\rho _\pm =10^2, 10^3, 10^4\).

Fig. 3.2
figure 2

Actual value (blue), lower estimates (green) and upper estimates (red) of S (left) and I (right) as functions of time (in years). The values at unperturbed equilibrium appear as dashed lines (color figure online)

Full size image

The convergence of \(I_\pm \) towards I is fast, with small residual errors. On the other hand, errors remain present in the estimates of S, illustrating the phenomenon mentioned right after Theorem 3.1.

6 Conclusion

A family of SIR model with time-varying transmission rate has been considered. For these models, a class of interval observers has been proposed, assuming that the rate of new infectives is continuously measured and that the transmission rate is uncertain and limited by (time-varying) known lower and upper bounds. It has been shown that these observers ensure fast convergence to the exact values in absence of uncertainty. For uncertain transmission rates, analytical bounds have been provided for the estimation errors.

To improve these results, we plan to consider in the future higher-order observers, and to apply the techniques of bundles of interval observers introduced in [2]. Also, processing real experimental data should allow to assess the interest of the proposed method.