Positive Stabilization of a Diffusion System by Nonnegative Boundary Control

Abstract

This chapter deals with the issue of considering nonnegative inputs in the positive stabilization problem. It is shown in two different ways why one cannot expect to positively stabilize a positive system by use of a nonnegative input, first by a classical approach with a formal proof, then by working on an extended system for which the new input corresponds to the time derivative of the nominal one, thus circumventing the sign restriction. However, it is shown via a classical example of positive system—the pure diffusion system—that positively stabilizing a positive system with a nonnegative input is in some way possible: using a boundary control, the input sign depends on whether the boundary control appears in the boundary conditions or in the dynamics. The chapter then provides a parameterization of all positively stabilizing feedbacks for a discretized model of the pure diffusion system, some numerical simulations and a convergence discussion which allows to extend the results to the infinite-dimensional case, where the system is described again by a parabolic partial differential equation and the input acts either in the dynamics or in the boundary conditions.

1 Introduction

Positive linear systems are linear systems whose state variables are nonnegative at all time whenever so are the initial state and the input. Studying this kind of systems is of great importance as the nonnegativity property can be found frequently in numerous fields like biology, chemistry, physics, ecology, economy or sociology (see e.g. [1, 4, 10, 11, 19] for particular examples).

It is known that positively stabilizing an unstable (lumped parameter) positive system by means of a nonnegative input is impossible [6]. This has to be taken into account while studying the positive stabilization problem. In this chapter, we show in two different ways that a positive linear system is exponentially positively stabilizable by a nonnegative input if and only if the system is already exponentially stable. Then we introduce a classical and relevant example—the pure diffusion (distributed parameter) system—for which the input nonnegativity issue is considered in two different ways, depending on whether the boundary control appears in the boundary conditions or in the dynamics [9]. The system is discretized and all positively stabilizing feedbacks are parameterized [7] by use of classical positive control theory [11, 15]. Finally, the discretized system is positively stabilized with a suitable feedback, and convergence issues are discussed.

2 Preliminaries

In the following subsections, we provide the reader with the notations, definitions and main concepts used in the chapter.

2.1 Terminology

In the sequel, we will use the sets $\mathbb {R}_+ := \{x \in \mathbb {R} \ | \ x \ge 0\}$, $\mathbb {R}_{0,+} := \{x \in \mathbb {R} \ | \ x > 0\}$, $\mathbb {R}^n_+ := \{(x_1,\ldots ,x_n) \in \mathbb {R}^n \ | \ x_i \in \mathbb {R}_+, \forall i=1,\ldots ,n\}$ and $\mathbb {R}^n_{0,+} := \{(x_1,\ldots ,x_n) \in \mathbb {R}^n \ | \ x_i \in \mathbb {R}_{0,+}, \forall i=1,\ldots ,n\}$. Similarly, $\mathbb {R}_-$, $\mathbb {R}_{0,-}$, $\mathbb {R}^n_-$ and $\mathbb {R}^n_{0,-}$ denote the sets $\{x \in \mathbb {R} \ | \ x \le 0\}$, $\{x \in \mathbb {R} \ | \ x < 0\}$, $\{(x_1,\ldots ,x_n) \in \mathbb {R}^n \ | \ x_i \in \mathbb {R}_-, \forall i=1,\ldots ,n\}$ and $\{(x_1,\ldots ,x_n) \in \mathbb {R}^n \ | \ x_i \in \mathbb {R}_{0,-}, \forall i=1,\ldots ,n\}$ respectively. For convenience, we use the notations $v \ge 0$ if $v \in \mathbb {R}^n_+$, $v > 0$ if $v \in \mathbb {R}^n_+$ and $v \ne 0$, $v \gg 0$ if $v \in \mathbb {R}^n_{0,+}$. The real part of a complex number $z \in \mathbb {C}$ will be denoted by $\mathscr {R}(z)$. A nonnegative vector v has all its components greater or equal to zero (i.e. $v_i \in \mathbb {R}_+$, for all i). The transpose of a matrix A will be denoted by $A^T$. The ijth entry of a matrix A will be denoted by $a_{ij}$. The spectrum of a matrix A is the set of its eigenvalues and will be denoted by $\sigma (A)$. A nonnegative matrix A (denoted by $A \ge 0$) has all its entries greater or equal to zero (i.e. $a_{ij} \in \mathbb {R}_+$, for all i, j). A Metzler matrix A has all its off-diagonal entries greater or equal to zero (i.e. $a_{ij} \in \mathbb {R}_+$, for all $i \ne j$). A stable matrix A has all its eigenvalues with negative real parts (i.e. $\mathscr {R}(\lambda ) < 0$, $\forall \lambda \in \sigma (A)$). For convenience, lower-case letters when used in an appropriate context will represent scalars or vectors, while upper-case letters will represent matrices.

2.2 Main Concepts

Consider a linear time-invariant system

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x} &{} = &{} Ax + Bu \\ y &{} = &{} Cx + Du \end{array} \right. \end{aligned}$$

where $A \in \mathbb {R}^{n \times n}$, $B \in \mathbb {R}^{n \times m}$, $C \in \mathbb {R}^{p \times n}$ and $D \in \mathbb {R}^{p \times m}$. We first recall the concept of positive linear system [10, 11, 13, 15].

Definition 14.1

A linear system $R = [A,B,C,D]$ is positive if for every nonnegative initial state $x_0 \in \mathbb {R}^n_+$ and for every admissible nonnegative input u (i.e. every piecewise continuous function $u : \mathbb {R}_+ \rightarrow \mathbb {R}_+^m$) the state trajectory x of the system and the ouput trajectory y are nonnegative (i.e. for all $t \ge 0$, $x(t) \in \mathbb {R}_+^n$ and $y(t) \in \mathbb {R}_+^p$).

It is possible to express the positivity of a system by use of the matrices A, B, C and D only [10, 11].

Theorem 14.1

A linear system $R = [A,B,C,D]$ is positive if and only if A is a Metzler matrix and B, C and D are nonnegative matrices.

Now we define the positive stabilizability of positive systems. For convenience, throughout the chapter the notion of stability will refer to asymptotic stability, which is equivalent to exponential stability as we deal with LTI systems.

Definition 14.2

A positive linear system $R = [A,B,C,D]$ is positively (exponentially) stabilizable if there exists a state feedback matrix $K \in \mathbb {R}^{m \times n}$ such that $A+BK$ is a stable Metzler matrix, i.e. such that there exist positive constants M and $\sigma$ such that for all $t \ge 0$

$$\left\| e^{(A+BK)t}\right\| \le Me^{-\sigma t}$$

and for all $t \ge 0$, $e^{(A+BK)t} \ge 0$. Such a feedback matrix K is called a positively stabilizing feedback for the system R.

The positive stabilization problem is concerned with existence conditions and the computation of such a matrix K. Finally, we introduce an important result from [4, 11, 15] which provides a necessary and sufficient condition for the stability of a Metzler matrix.

Lemma 14.1

A Metzler matrix $A \in \mathbb {R}^{n \times n}$ is stable if and only if there exists $v \gg 0$ in $\mathbb {R}^n$ such that $Av \ll 0$.

Remark 14.1

The sufficiency of the condition can be shown by considering the Lyapunov function $V(x) = v^Tx$ which leads to $\dot{V}(x) = v^TAx < 0$. The necessity follows from the fact that the opposite of the inverse of a stable Metzler matrix is nonnegative: it suffices to define $v = -A^{-1}\tau$ with $\tau \gg 0$. See [11, Lemma 2.2] or [16, Lemma 1.1].

3 Positive Stabilization by Nonnegative Input

One obvious way to ensure the nonnegativity of the state trajectory of a positive system is to force the input to remain nonnegative. However, it is impossible to positively stabilize an unstable positive system with such an input. The first subsection provides a classical approach of the problem, while the second one provides an alternative as we work on an extended system.

3.1 A Classical Approach

First, let us recall the Perron-Frobenius theorem for Metzler matrices [2, 12]:

Theorem 14.2

If A is a Metzler matrix, there exist a real number $\lambda$ and a real vector $v > 0$ such that $Av = \lambda v$ and for every eigenvalue $\mu$ of A, $\mathscr {R}(\mu ) \le \lambda$.

Remark 14.2

The result in [12] is actually shown for nonnegative matrices. However, a Metzler matrix is a nonnegative matrix up to a diagonal shift. It is easy to see that a diagonal shift just shifts the eigenvalues and leaves the eigenvectors unchanged, making the result valid for Metzler matrices.

In [6] it is stated without proof that, in view of [17], if the dominant eigenvalue of A is nonnegative one cannot stabilize the system with a nonnegative input. Then one can conclude that if a positive system is not already stable, it cannot be stabilized by use of a nonnegative input. For the sake of self-containedness, let us briefly formulate and prove that assertion.

Theorem 14.3

Consider the positive linear system $\dot{x} = Ax + bu$. The system is (exponentially) positively stabilizable by a state feedback $u = Kx$ such that $u \in \mathbb {R}_+$ if and only if it is already (exponentially) stable.

Proof

The sufficiency of the condition is trivial: it suffices to take $K = 0$, hence $u = 0$. Let us prove the necessity. Suppose that the system is unstable, then the dominant eigenvalue $\lambda$ of $A^T$ is nonnegative (see Theorem 14.2). By [10, 12] there exists an eigenvector $v > 0$ such that $A^Tv = \lambda v$. Now let us define $\rho = v^Tx$ and focus on the unstable part of the system relative to $\lambda$. We then have

$$\begin{aligned} \dot{\rho } = v^T\dot{x} = v^TAx + v^Tbu = (A^Tv)^Tx + v^Tbu = \lambda \rho + (v^Tb)u \end{aligned}$$

where $v^Tb \ge 0$. If $u = Kx$ was a state feedback such that $u \in \mathbb {R}_+$, then

$$\begin{aligned} \rho (t) = e^{\lambda t}\rho _0 + \int _0^t e^{\lambda (t-\tau )} (v^Tb) u(\tau ) d\tau \end{aligned}$$

would not tend to zero as $t \rightarrow \infty$, since $\lambda$, $e^{\lambda t}$, $\rho _0$, $(v^Tb)$ and u are all nonnegative (or positive), thus showing that the system cannot be positively stabilized in this way. $\square$

3.2 An Extended System

As we showed the issue of considering a nonnegative input, we try to circumvent the problem by working on an extended system. Consider

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x} &{} = &{} Ax + Bu \\ \dot{u} &{} = &{} v \end{array} \right. \end{aligned}$$

where A is a Metzler matrix, B is nonnegative and v is the new input. This leads to the positive extended system

$$ \dot{ \left[ \begin{matrix} x\\ u \end{matrix} \right] } = \left[ \begin{matrix} A &{} B\\ 0 &{} 0 \end{matrix} \right] \left[ \begin{matrix} x\\ u \end{matrix} \right] + \left[ \begin{matrix} 0\\ I \end{matrix} \right] v $$

that we will denote by $\dot{\tilde{x}} = \tilde{A}\tilde{x} + \tilde{B}v$ with initial condition

$$ \tilde{x}_0 = \left[ \begin{matrix} x(0)\\ u(0) \end{matrix} \right] = \left[ \begin{matrix} x_0\\ u_0 \end{matrix} \right] \ge 0 $$

and with state feedback control

$$\begin{aligned} v = \tilde{K}\tilde{x} = [K_x \ K_u] \left[ \begin{matrix} x\\ u \end{matrix}\right] = K_x x + K_u u \end{aligned}$$

where the new input v has no sign restriction as it represents the variation of u, which allows us to get rid of the input positivity problem. The resulting closed-loop extended system is therefore described by

$$\begin{aligned} \dot{\left[ \begin{matrix}x\\ u\end{matrix}\right] } = \left[ \begin{matrix}A &{} B\\ 0 &{} 0\end{matrix}\right] \left[ \begin{matrix} x\\ u \end{matrix}\right] + \left[ \begin{matrix}0\\ I\end{matrix}\right] [K_x \ K_u] \left[ \begin{matrix}x\\ u\end{matrix}\right] = \left[ \begin{matrix}A &{} B\\ K_x &{} K_u\end{matrix}\right] \left[ \begin{matrix}x\\ u\end{matrix}\right] . \end{aligned}$$

Note that if one considers a static feedback $v = \tilde{K}\tilde{x}$ for the extended system, it actually corresponds to a dynamic feedback controller $\dot{u} = K_uu + K_xx$ for the initial system. The extended system is positively stabilizable if and only if there exists a state feedback $\tilde{K} = [K_x \ K_u]$ such that

• 1. the matrix $\left[ \begin{matrix}A &{} B\\ K_x &{} K_u\end{matrix}\right]$ is Metzler, i.e. $K_u$ is Metzler and $K_x \ge 0$, and

• 2. the matrix $\left[ \begin{matrix}A &{} B\\ K_x &{} K_u\end{matrix}\right]$ is exponentially stable.

As a consequence of these conditions, the pair $(\tilde{A},\tilde{B})$ should be exponentially stabilizable. Now, [3, Sect. 10.3] provides necessary and sufficient conditions for the positive stabilizability of a positive system, using LMIs and a Lyapunov equation. We adapt this result to the extended system, leading to the following theorem.

Theorem 14.4

Consider a linear time-invariant system $\dot{x} = Ax + Bu$ and his extended system $\dot{\tilde{x}} = \tilde{A}\tilde{x} + \tilde{B}v$ as defined above. The extended system is positively stabilizable if and only if there exist a positive-definite diagonal matrix $Q =$ $\left[ \begin{matrix}Q_1 &{} 0\\ 0 &{} Q_2\end{matrix}\right]$ and a feedback $\tilde{K}$ such that, with $Y = [Y_1 \ Y_2] = \tilde{K}Q$, the matrix

$$ \left[ \begin{matrix}Q_1A^T+AQ_1 &{} Y_1^T+BQ_2\\ Q_2B^T+Y_1 &{} Y_2^T+Y_2\end{matrix}\right] $$

is negative-definite, $Y_1$ is nonnegative and $Y_2$ is Metzler.

Proof

By [3] the extended system is positively stabilizable if and only if there exist a positive-definite diagonal matrix Q and a feedback $\tilde{K}$ such that, with $Y = \tilde{K}Q$, $(\tilde{A}Q + \tilde{B}Y)$ is Metzler and $Q\tilde{A}^T + Y^T\tilde{B}^T + \tilde{A}Q + \tilde{B}Y$ is negative-definite. One easily sees that $(\tilde{A}Q + \tilde{B}Y)$ is Metzler if and only if the matrix

$$\left[ \begin{matrix}A &{} B\\ K_x &{} K_u\end{matrix}\right] $$

is Metzler, which means (as stated previously) that $K_x$ has to be nonnegative and $K_u$ has to be Metzler. Moreover, as $Y = \tilde{K}Q$,

$$ [Y_1 \ Y_2] = [K_x \ K_u] \left[ \begin{matrix}Q_1 &{} 0\\ 0 &{} Q_2\end{matrix}\right] $$

and then

$$\begin{aligned} \left\{ \begin{array}{rcl} K_x &{} = &{} Y_1Q_1^{-1}\\ K_u &{} = &{} Y_2Q_2^{-1} \end{array} \right. \end{aligned}$$

which implies that $Y_1$ has to be nonnegative and $Y_2$ has to be Metzler. Now, we can rewrite $Q\tilde{A}^T + Y^T\tilde{B}^T + \tilde{A}Q + \tilde{B}Y$ as

$$\begin{aligned} \left[ \begin{matrix}Q_1 &{} 0\\ 0 &{} Q_2\end{matrix}\right] \left[ \begin{matrix}A^T &{} 0\\ B^T &{} 0\end{matrix}\right] + \left[ \begin{matrix}Y_1^T\\ Y_2^T\end{matrix}\right] [0 \ I] + \left[ \begin{matrix}A &{} B\\ 0 &{} 0\end{matrix}\right] \left[ \begin{matrix}Q_1 &{} 0\\ 0 &{} Q_2\end{matrix}\right] + \left[ \begin{matrix}0\\ I\end{matrix}\right] [Y_1 \ Y_2] \end{aligned}$$

which is equal to

$$\left[ \begin{matrix}Q_1A^T+AQ_1 &{} Y_1^T+BQ_2\\ Q_2B^T+Y_1 &{} Y_2^T+Y_2\end{matrix}\right] .$$

$\square$

Remark 14.3

By the previous theorem, the matrix

$$\left[ \begin{matrix}Q_1A^T+AQ_1 &{} Y_1^T+BQ_2\\ Q_2B^T+Y_1 &{} Y_2^T+Y_2\end{matrix}\right] $$

has to be negative-definite in order to positively stabilize the extended system by means of a feedback $v = \tilde{K}\tilde{x}$. However, it is known that every principal submatrix of a negative-definite matrix is negative-definite. This means that $Q_1A^T+AQ_1$ is negative-definite and thus the initial system should be stable already. Thus the use of an extended system does not allow to circumvent the obstacle of using a nonnegative input as described in Sect. 14.3.1.

4 A Pure Diffusion System

Now we show that one can actually positively stabilize a pure diffusion system—which is a distributed parameter positive system—by use of a nonnegative boundary control, as long as the input appears in the boundary conditions.

4.1 Modelization

Consider a standard example of unstable positive distributed parameter system, namely the pure diffusion system described by the partial differential equation (PDE)

$$\begin{aligned} \frac{\partial x}{\partial t} = D_a \frac{\partial ^2 x}{\partial z^2} \end{aligned}$$

(14.1)

with Neumann boundary conditions

$$\begin{aligned} \left\{ \begin{array}{rcl} \frac{\partial x}{\partial z}(t,0) &{} = &{} v(t)\\ \frac{\partial x}{\partial z}(t,L) &{} = &{} 0 \end{array} \right. \end{aligned}$$

(14.2)

where v is the input, $D_a$ is the diffusion parameter and L is the domain length. By [9, Example 2.1], this boundary control system is equivalent to the system described by the PDE

$$\begin{aligned} \frac{\partial x}{\partial t} = D_a \frac{\partial ^2 x}{\partial z^2} + \delta _0 u(t) \end{aligned}$$

(14.3)

with the Dirac delta distribution $\delta _0$ as control operator and with homogeneous Neumann boundary conditions

$$\begin{aligned} \left\{ \begin{array}{rcl} \frac{\partial x}{\partial z}(t,0) &{} = &{} 0\\ \frac{\partial x}{\partial z}(t,L) &{} = &{} 0 \end{array} \right. \end{aligned}$$

(14.4)

where the input $u(t) = -v(t)$. This implies that considering a positive input v(t) in the boundary conditions leads to a negative input u(t) in the dynamics, and thus to a potential stabilization of the system.

4.2 Discretization

In order to stabilize the system, we discretize it by the finite difference method and we obtain the finite-dimensional system (considering n discretization points $z_i$, $i = 1,\ldots ,n$, with $z_1 = 0$, $z_n = L$ and $\varDelta z = L/(n-1)$ the discretization step)

$$\begin{aligned} \dot{x}^{(n)} = A^{(n)}x^{(n)} + b^{(n)}u \end{aligned}$$

(14.5)

where

$$ A^{(n)} = \left[ \begin{matrix} -p_2 &{} p_2 &{} 0 &{} \cdots &{} 0\\ p_2 &{} -2p_2 &{} p_2 &{} &{} \vdots \\ 0 &{} \ddots &{} \ddots &{} \ddots &{} 0\\ \vdots &{} &{} p_2 &{} -2p_2 &{} p_2 \\ 0 &{} \cdots &{} 0 &{} p_2 &{} -p_2 \end{matrix} \right] \in \mathbb {R}^{n \times n}, $$

$$ b^{(n)} = [p_1 \quad 0 \quad \cdots \quad 0]^T \in \mathbb {R}^n $$

and

$$ x^{(n)} = [x(z_1) \quad \cdots \quad x(z_n)]^T \in \mathbb {R}^n $$

where

$$p_1 = \frac{1}{\varDelta z} \quad \text {and} \quad p_2 = \frac{D_a}{\varDelta z^2}. $$

Clearly, this finite-dimensional system is positive (see Theorem 14.1). Moreover, the infinite-dimensional system (14.1)–(14.2) is not exponentially stable [1, 5] as zero is in the spectrum of its generator. Discretizing the system will perturb the spectrum though one easily sees that the finite-dimensional system (14.5) is not exponentially stable as zero is still in the spectrum of $A^{(n)}$. Also note that all eigenvalues are real, $A^{(n)}$ being symmetric.

4.3 Positive Stabilization of the System

Now we can provide the reader with a parameterization of all positively stabilizing feedbacks for the distributed pure diffusion system (14.5), using Lemma 14.1 and developing the resulting set of inequalities [7].

Theorem 14.5

A feedback $k = [k_1 \quad \cdots \quad k_n]$ is positively stabilizing for the discretized pure diffusion system (14.5) if and only if it is such that

$$\begin{aligned} k_1 = \frac{D_av_1-D_av_2-k_2v_2\varDelta z-\cdots -k_nv_n\varDelta z- \varDelta z^2\omega }{v_1\varDelta z}, \end{aligned}$$

$$\begin{aligned} k_2 \ge \frac{-D_a}{\varDelta z} \qquad \textit{and} \qquad k_i \ge 0 \quad i = 3,\ldots ,n, \end{aligned}$$

with $\omega > 0$ (free parameter) and such that $v \gg 0$ is a positive solution of the strict inequalities set

$$\begin{aligned} \begin{array}{rcl} -v_1 + 2v_2 - v_3 &{}> &{} 0\\ &{} \vdots &{}\\ -v_{n-2} + v_{n-1} - v_n &{}> &{} 0\\ -v_{n-1} + v_n &{} > &{} 0. \end{array} \end{aligned}$$

(14.6)

It is actually possible to parameterize all the solutions of the inequalities set (14.6), leading to a full parameterization of all the positively stabilizing feedbacks for the pure diffusion system (see [7]). In order to illustrate the theoretical results, let us design a particular feedback that falls in the class defined in Theorem 14.5. Let us set

$$\begin{aligned} k^{(n)}_1 = -\frac{1}{\varDelta z}\kappa \quad \text { and } \quad k^{(n)}_i = 0 \quad (i = 2,\ldots ,n) \end{aligned}$$

(14.7)

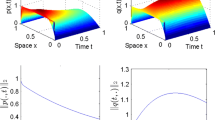
with $\kappa > 0$. Considering $L = 1$, $D_a = 1$, $\kappa = 0.2$ and $n = 11$ and choosing the initial condition $x_0 = 2z^3 - 3z^2 + 1$ (this polynomial respects the boundary conditions and the all-ones eigenvector corresponds to the Frobenius unstable eigenvalue $\lambda = 0$, so the initial condition excites the unstable mode) yields the open-loop state trajectory shown in Fig. 14.1, and the closed-loop state trajectory shown in Fig. 14.2. This illustrates that the closed-loop system is positive and that it is stable unlike the open-loop system. Figure 14.3 shows the nonnegative input trajectory v(t).

Fig. 14.1

Open-loop state trajectory $x^{(n)}(t)$ ($n = 11$). It converges to a constant non-null value

Fig. 14.2

Closed-loop state trajectory $x^{(n)}(t)$ ($n = 11$). It stabilizes to zero while staying nonnegative at all time

Fig. 14.3

Input trajectory $v(t) = -k^{(n)}x^{(n)}(t)$ ($n = 11$). The input—as it appears in the boundary conditions—is nonnegative at all time and decreases to zero

4.4 Convergence Analysis

Now we focus on convergence issues, whenever the finite difference step tends to zero. Let us introduce the following result (see [7]).

Theorem 14.6

Applying the feedback $k^{(n)}$ given by (14.7) to the approximate system (14.5) leads to the convergence of the resulting closed-loop system

$$\begin{aligned} \dot{x}^{(n)} = (A^{(n)} + b^{(n)}k^{(n)})x^{(n)}, \end{aligned}$$

(14.8)

as $\varDelta z$ tends to zero, to the system described by the PDE

$$\begin{aligned} \frac{\partial x}{\partial t} = D_a \frac{\partial ^2 x}{\partial z^2} \end{aligned}$$

(14.9)

with Neumann boundary conditions

$$\begin{aligned} \left\{ \begin{array}{rcl} \frac{\partial x}{\partial z}(0,t) &{} = &{} \kappa x(0,t)\\ \frac{\partial x}{\partial z}(L,t) &{} = &{} 0. \end{array} \right. \end{aligned}$$

(14.10)

Moreover, the approximate closed-loop system (14.8) is positive and (exponentially) stable for n sufficiently large, and the system (14.9)–(14.10) is positive and (exponentially) stable.

One can show the convergence of the system operators by a state space approach, setting the discretized operators in the appropriate spaces and using the related norms [9, Example 2.1]. Positivity of system (14.9)–(14.10) can be proved by standard arguments (positivity of the resolvent operator as in [14] or the maximum principle as in [18]). Also, as it is of Sturm-Liouville type, system (14.9)–(14.10) is a Riesz-spectral system [8]. Its spectrum is thus real and discrete: it is easy to compute all eigenvalues and to show that they are negative, implying the stability of the system. For a complete proof, refer to [7].

5 Conclusion

In this chapter, we have studied the issue of considering a nonnegative input while positively stabilizing a positive system, using a classical approach and working on an extended system. Then we have shown via a classical example that the boundary input sign may vary depending on whether it acts in the dynamics or in the boundary conditions, implying that it is technically possible to positively stabilize the system with a nonnegative input. Finally we have provided a convenient way to parameterize all the positively stabilizing feedbacks for a discretized model of the pure diffusion system, we have discussed the convergence of the results and we have produced some numerical simulations. Next steps in this work are—among others—to extend Theorem 14.3 and its proof to infinite-dimensional systems, to find conditions over any discretized feedback so that it converges to a positively stabilizing feedback for the nominal PDE system, to optimize the choice of a positively stabilizing feedback with respect to some given criterion, to design observer based compensators and to extend the results to a specific interesting application in biochemical engineering. These questions are currently under investigation.