Introduction

During the last decade, the isolation of a stable and truly two-dimensional (2D) system like graphene [1] has given the possibility to experimentally probe for the quantum mechanical nature of electronic transport in strongly confined systems, even at elevated temperatures. Characteristic examples are the measurement of ballistic transport for graphene systems on various substrates [2,3,4,5] and the manifestation of a half-integer quantum hall effect [6,7,8,9,10]. Moreover, when a 2D graphene sheet is further confined in a quasi one-dimensional (1D) structure through patterning and nanolithography (usually referred to as a graphene nanoribbon) , integer plateaus on the conductance appear, corresponding to the presence of 1D sub-bands in the electronic structure [11]. Finally, the signature of single defects or adatoms can be resolved through scanning tunneling microscopy measurements [12].

Such fully quantum mechanical picture necessitates for an adequate theoretical description of charge transport with an atomic accuracy, as alterations of the structural symmetry even in single lattice sites can induce significant modifications in the calculated conductance spectra [13]. A widespread paradigm of such methodology is the non-equilibrium Green’s function formalism [14], used for the calculation of transport in both ideal and defected/disordered graphene systems [13, 15,16,17]. Such formalism naturally incorporates the concept of electronic scattering either by structural defects or by the metallic contacts. It is by now well-consolidated that the presence of structural imperfections and the perturbations that these induce in the otherwise ideal electronic structure is one of the main origins for conductance degradation in graphene-based systems [15]. Hence, perturbation potentials can be considered as the cause for such scattering mechanisms, whereas conductance degradation (with respect to the ideal value) their immediate consequence. Within this picture, a key quantity for the determination of the current-carrying capacity of a single quantum channel is the transmission coefficient \(T(\varepsilon )\) [14], which can obtain values between zero and one, corresponding to complete reflection and perfect transmission of the propagated electrons, respectively. The latter can be only retrieved for ideal systems, whereas a lower value is usually calculated for strongly disordered structures.

In the last years, a group of methodologies have been developed that are particularly suited for the calculation of the electronic structure in systems with defects. They consist in using big supercells that contain the defects, calculating the electronic properties for such supercells and consequently unfolding the supercell band structure [18,19,20,21,22,23,24,25,26]. The resulting unfolded band structure contains information not only of the original unit-cell bands, but also on the impact of the induced perturbation on the robustness of the total band structure. The key quantity here is the spectral weight \(w(\varepsilon ,\mathbf {k})\) of each unfolded band, whose value ranges form zero to one, and indicates the degree of maintenance of the original bands in the defected supercell [26]. The \(0< w(\varepsilon ,\mathbf {k}) < 1\) range of the spectral weight with respect to the perturbation potential, unavoidably brings to mind the respective \( 0< T(\varepsilon ) < 1\) range of the transmission coefficient in quantum transport calculations of defected systems. In this article we attempt to explore the relationship between quantum transport and band structure unfolding using a graphene nanoribbon with a single-vacancy defect as a model system. We will show that strong qualitative similarities exist for the two methods, making them complementary for the study of the electronic and transport properties of systems with defects.

The article is organized as follows: In Sect. Methodology we will introduce the theoretical methodology for both quantum transport and band structure unfolding calculations. In Sect. Results we will confront the results obtained by the two formalisms. Finally, in Sect. Discussion we will discuss our results.

Methodology

The basis for the calculation of both electronic structure and quantum transport is an appropriate definition of the electronic Hamiltonian. For the case of graphene, the nearest-neighbor tight-binding (TB) model is sufficient for the description of the low-energy spectrum of the material, accounting only for the \(\pi \) atomic orbitals (as \(\sigma \) states are too far away from the Fermi level). Hence, the TB Hamiltonian can be written as

$$\begin{aligned} H=-t\sum _{\langle i,j \rangle ,s} c_{i,s}^{\dagger } c_{j,s} + H.c., \end{aligned}$$
(13.1)

where \(c_{i}\) (\(c_{i}^{\dagger }\)) is the annihilation (creation) operator for an electron with spin s at site i, and t is the hopping integral with a typical value \(t=2.7\) eV. We point out that the nearest-neighbor model gives a symmetric description of the valence and conduction bands of ideal graphene that can be only lifted with higher accuracy Hamiltonians, (e.g., by considering a second neighbor in the tight-binding scheme). Considering that graphene has two atoms per unit cell, the eigenstates can be approximated by a linear combination of the two atomic wavefunctions multiplied by a single phase factor, which denotes translation of the entire supercell in space [27]:

$$\begin{aligned} \Psi (\mathbf {k},\mathbf {r}) =&c_A(\mathbf {k}) \Psi _{A}(\mathbf {k},\mathbf {r}) + c_B(\mathbf {k}) \Psi _{B}(\mathbf {k},\mathbf {r}) = \nonumber \\&\qquad \quad \, = \frac{1}{\sqrt{\mathscr {N}}} \sum _j e^{i\mathbf {k}\cdot \mathbf {R}_j} \left[ c_A(K) \phi (\mathbf {r}-\mathbf {R}_j^A) + c_B(\mathbf {k}) \phi (\mathbf {r}-\mathbf {R}_j^B) \right] \end{aligned}$$
(13.2)

Here \(c_A\) and \(c_B\) are expansion coefficients of the \(\phi (\mathbf {r})\) wave function of atomic orbitals A and B, respectively, and \(\mathscr {N}\) is the number of elementary cells. The \(\mathbf {R}_j=n\mathbf {a}_1+m\mathbf {a}_2\) vectors specify the position of the graphene unit-cell, with \(\mathbf {a}_1\) and \(\mathbf {a}_2\) being the lattice vectors. Equation (13.2) derives directly from Bloch’s theorem [27].

For the calculation of quantum transport , two-terminal graphene devices are considered, where a single graphene nanoribbon is contacted by two semi-infinite leads. As the objective of the study is to comprehend the internal scattering mechanisms due to the presence of defects, here we consider ideal contacts, i.e., contacts made of graphene with the same lateral width as the channel material. According to the non-equilibrium Green’s function formalism [14], the single-particle retarded Green’s function matrix can be written as

$$\begin{aligned} \mathscr {G}^r(\varepsilon ) = [ \varepsilon S - H - \varSigma _{L} - \varSigma _{R} ]^{-1}, \end{aligned}$$
(13.3)

where \(\varepsilon \) is the energy, H the real-space Hamiltonian, and S the overlap matrix, which is identical with the unitary matrix I in the case of an orthonormal basis set. Moreover, \(\varSigma _{L,R}\) are self-energies that account for the effect of the contacts, calculated from the expression:

$$\begin{aligned} \varSigma _{L(R)} = \tau ^\dagger _{L(R)} g_{L(R)} \tau _{L(R)}. \end{aligned}$$
(13.4)

Here \(\tau _{L,R}\) are interaction Hamiltonians that describe the coupling between the contacts and the device, while \(g_{L,R}\) are the contact surface Green functions. The transmission coefficient of an incident Bloch state with energy \(\varepsilon \) can be thereon computed as the trace of the matrix product:

$$\begin{aligned} T(\varepsilon )=Tr \{ \varGamma _{L} \mathscr {G}^r \varGamma _{R} [ \mathscr {G}^r ]^\dagger \}, \end{aligned}$$
(13.5)

where

$$\begin{aligned} \varGamma _{L(R)}=i \{ \varSigma _{L(R)}- [\varSigma _{L(R)}] ^\dagger \} \end{aligned}$$
(13.6)

are the spectral functions of the two contacts. According to the Landauer–Buttiker theory [14], conductance can be calculated as:

$$\begin{aligned} G=\frac{2e^2}{h} T, \end{aligned}$$
(13.7)

where \(G_0=2e^2/h \approx 77.5\) \(\upmu \)S is the conductance quantum.

For the calculation of the unfolded band structure, we consider the same graphene nanorribon used in the quantum transport scheme. Such ribbon can be viewed as an integer multiple of the ribbon’s unit cell along the transport direction. Based on the TB Hamiltonian described above, the spectral weight of the unfolded bands on the unit-cell Brillouin zone can be defined as [26]:

$$\begin{aligned} w(\varepsilon ,\mathbf {k}) = \frac{1}{\mathscr {N}} \sum _{{a \in PC}} \left( \sum _j^{\mathscr {N}} \{ (c^{a+j} (\mathbf {k}))^* \cdot e^{-i\mathbf {k}\cdot \mathbf {R}_j}\} \right) \times \left( \sum _j^{\mathscr {N}} \{ c^{a+j} (\mathbf {k}) \cdot e^{-i\mathbf {k}\cdot \mathbf {R}_j} \} \right) , \end{aligned}$$
(13.8)

where a are the atoms that belong to the primitive cell. The important aspect of this formula is that the sum of the expansion coefficients c should involve only equivalent atoms within the elementary cells that comprise the supercell.

We consider single carbon vacancies as the origin of the structural/electronic perturbation for our graphene system. Vacancies can be modeled within the nearest-neighbor TB scheme by removing a \(\pi \) electron, either by switching to infinite the related on-site energy term \(\varepsilon _i\) in the Hamiltonian, or equivalently, by switching to zero the hopping \(t_{ij}\) terms between the vacancy and the neighboring sites. However, a more accurate treatment of the states introduced by such defect within the electronic spectrum has to take into account the structural reconstruction around the vacancy. This can be achieved through a multiscale approach, where first principles calculations are performed initially and the TB Hamiltonian is parameterized consequently, on the basis of the ab initio results. In our implementation, we calibrate the TB parameters from density functional theory computations of defected graphene quantum dots [28]. The optimized values for the on-site energy of the vacancy and the hopping integral between this and its neighboring sites are \(\varepsilon _i=10\) eV and \(t_{ij}=1.9\) eV, respectively.

Fig. 13.1
figure 1

Scheme of the armchair graphene nanoribbon with a width of 38 dimer lines and a length of 64 zigzag chains, used for the quantum transport and band structure calculations. A single vacancy is introduced in either the 27th (\(V_1\)) or the 29th (\(V_2\)) dimer line

Full size image

Results

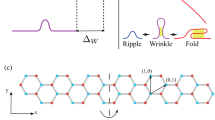
We consider a graphene nanoribbon with an armchair-type lateral confinement, having a width of \(N_a =38\) carbon dimer lines (\({\approx }4.5\) nm) and a length of \(N_z=64\) zigzag chains (\(l \approx 6.7\) nm), as seen in Fig. 13.1. By attaching two ideal semi-infinite contacts along the zigzag confinement (i.e., by considering the ribbon infinite along its length) we can calculate the quantum transport properties of this system using the non-equilibrium Green’s function formalism. According to the TB scheme (where ribbons with \(N_a=3p+2\) dimer lines are semi-metallic \(\forall p \in \mathbb {N}\) and the rest are semiconducting), the \(N_a=38\) ribbon presents a semi-metallic character with a secondary band-gap of few meV. Figure 13.2 shows the ideal transmission coefficient and the respective density of states as a function of the energy (black lines). The conductance is characterized by the presence of integer plateaus that correspond to the number of available conduction channels (i.e., the number of 1D subbands) at a given energy. Conductance steps take place at energies where van Hove singularities appear in the density of states spectrum (see Fig. 13.2). If we now consider a single vacancy defect, there are two plausible configurations that give rise to different conduction characteristics. In the first case, if the vacancy is introduced at a \(N_a=3q\) position (\(\forall q \in \mathbb {N}\), \(q\le p\)), the defect states do not perturb the first conductance plateau around the Fermi level [13] and the transmission coefficient is equal with the ideal value (see results for \(V_1\) in Fig. 13.2c). When the vacancy is introduced at a \(N_a \ne 3q\) site (as \(V_2\)), the defect perturbation influences the first conductance plateau (Fig. 13.2b) and a dip in the transmission coefficient appears at the resonance of the defect state, which is \(\sim 0.4\) eV below the Fermi level (Fig. 13.2d). It is important to point out that in both configurations the \(\sim -0.4\) eV defect state is present, but perturbs the ideal ribbon wave function only in the second case [13]. Above the first plateau, both vacancy configurations show similar characteristics, with a small reduction of the transmission probability mainly for the valence band, due to the presence of a higher number of defect states bellow the Fermi level (in accordance with the acceptor-type character of reconstructed single vacancies in graphene [28]).

Fig. 13.2
figure 2

a Density of states for the graphene nanoribbon with vacancy \(V_1\). b Density of states for the graphene nanoribbon with vacancy \(V_2\). c Transmission coefficient for the graphene nanoribbon with vacancy \(V_1\). d Transmission coefficient for the graphene nanoribbon with vacancy \(V_2\). Grey lines show the ideal values for the non-defected nanoribbon

Full size image
Fig. 13.3
figure 3

a Unfolded band structure in the primitive Brillouin zone for the non-defected graphene nanorribon of Fig. 13.1. b Unfolded band structure for the ribbon with \(V_1\). c Unfolded band structure for the ribbon with \(V_2\)

Full size image

We now turn into the band structure calculations for the same graphene nanoribbon as above. Considering the armchair-type lateral confinement and periodicity along its length (i.e., considering that the ribbon has no zig-zag confinement, in accordance with the quantum transport calculations), such ribbon can be described as a supercell with 16 repetitions of the unit cell (see Fig. 13.1). If we unfold the calculated band structure to the primitive Brillouin zone, we obtain the results shown in Fig. 13.3. For the non-defected ribbon, unfolding ideally recovers the unit-cell band structure, assigning a spectral weight value \(w=1\) for the original unit-cell bands, whereas \(w=0\) for the extra bands that are present due to the additional supercell atoms. When performing the same calculation for the defected structures, the spectral weight values range between zero and one also for the original bands, in proportion to the perturbation of the wave functions induced by the defects. We note that for the \(V_1\) vacancy (Fig. 13.2b), the bands around the Fermi level (\(-0.45 \mathrm {eV}< E_{\mathrm {F}} < 0.45 \mathrm {eV}\)) maintain the ideal \(w\approx 1\) value. On the contrary, the \(V_2\) vacancy (Fig. 13.3c) shows \(w \le 1\) also for the low-energy spectrum, with a minimum \(w\approx 0\) around \(-0.4\) eV that corresponds to the resonant energy of the defect state. Similarly as in the transport calculations, for energies above and below the \(-0.45\,\mathrm {eV}<E_{\mathrm {F}} < 0.45\, \mathrm {eV}\) range, both defects give rise to a reduction of the spectral weight value that depends both on the energy as well as on the wavenumber. Also here we note a bigger reduction trend for the valence than for the conduction band. However such reduction is stronger for the spectral weight with respect to the respective lowering of the transmission coefficient.

Based on the previous results, a critical analysis of the two computational methodologies shows strong similarities as well as some subtle differences. Band structure unfolding is a measure of the robustness of the intrinsic bands in the presence of structural/electronic perturbations. The spectral weight measures the resemblance between the unit-cell and the supercell wave functions. In this sense, each perturbative event automatically signals a reduction in the value of the spectral weight. On the other hand, the same perturbative events also give rise to the backscattering of the propagated electrons when calculating the quantum transport . The direct relationship between the cause (structural/electronic perturbation) and the result (diminishment of both the spectral weight and the transmission coefficient) is at the origin of the similarities for the two quantum mechanical methodologies. However, as noted above, a general trend shows that the reduction of the spectral weight in the unfolded band structure is stronger than the respective lowering of the transmission coefficient in quantum transport calculations. The most probable explanation of such quantitative misalignment reflects the fact that disordered states can still contribute in the propagation of electrons through hopping interactions between the perturbed states. This aspect should lower the negative impact of the perturbation even in the presence of moderate disorder. On the other hand, the spectral weight is a direct measure of the same disorder but does not account for tunneling or wave-function overlapping phenomena as the transport formalism does. Notwithstanding such difference, the two methodologies appear complementary, with band structure unfolding giving a robust interpretation of the motivations for electron back-scattering in quantum transport calculations.

Discussion

In this article we have compared the results obtained from two different computational methodologies that account for the effects of defects on the electronic and transport properties of graphene nanoribbons . The first one calculates the quantum transport properties within the non-equilibrium Green’s function formalism, whereas the second one computes the spectral weight of the ribbon’s unfolded band structure. Our analysis has evidenced clear qualitative similarities between the transmission coefficient of the propagated electrons and the spectral weight of the unfolded bands, as well as some quantitative divergences due to the intrinsic differences between the purely electronic and the quantum transport-related features. On the other hand, a strong complementary character has emerged, with the spectral weight giving a robust theoretical explanation for the origin of conductance degradation in the quantum transport calculations of defected/disordered systems.