Abstract
Big data is being generated by everything around us at all times. The massive amount and corresponding data of assets in the financial market naturally form a big data set. In this paper, we tackle the multi-period mean-variance portfolio of asset-liability management using the parameterized method addressed in Li et al. (SIAM J. Control Optim. 40:1540–1555, 2002) and the state variable transformation technique. By this simple yet efficient method, we derive the analytical optimal strategies and efficient frontiers accurately. A numerical example is presented to shed light on the results established in this work.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
Portfolio selection is concerned with finding the most desirable group of funds to hold. The mean-variance model proposed by Markowitz (1952) aims to seek a balance between the gain and the risk, which are expressed by expectation and variance of the investment return, respectively. In order to trace out the efficient frontier for this bi-objective optimization problem, one typically puts weights on the two criteria and transforms the problem into a single-objective optimization problem.
After Markowitz’s vanward work in a single-period setting, the mean-variance portfolio selection framework was extended to multi-period setting by Li and Ng (2000) using an embedding technique. Zhou and Li (2000) considered a continuous-time mean-variance problem while Li et al. (2002) investigated the problem with no short setting. As any nonlinear term of expectation operator, the term \((\mathbb{E}[x_{T}])^{2}\) in the mean-variance case, induces nonseparability, the spirit of both the embedding scheme proposed by Li and Ng (2000) and Zhou and Li (2000) and the parameterized method developed by Li et al. (2002) is to embed \((\mathbb{E}[x_{T}])^{2}\) into an auxiliary function or to replace \(\mathbb{E}[x_{T}]\) by an auxiliary variable in mean-variance models to deal with mean-variance problems in dynamic programming. Besides the above, Cui et al. (2014) presented another powerful tool named mean-field formulation to tackle the nonseparability of multi-period mean-variance portfolio selection problem and derived analytical optimal strategies and efficient frontiers. Yi et al. (2014) developed the mean-field formulation method to solve the multi-period mean-variance portfolio selection problem with an uncertain exit horizon.
Big data is being generated by everything around us at all times. The number of assets in the financial market and the corresponding data constitute a typical big data. Big data is also changing the way people investing. Insights from big data and extracting meaningful value from big data can enable all investors to make better profit. It is well known that the stability of financial institutions depends crucially on the matching of assets, and liabilities. Liability is being brought more and more into the limelight when investors establish their portfolios. The mean-variance framework of asset-liability management was first investigated by Sharp and Tint (1990) in a single-period setting. For the multi-period setting and by the embedding technique, Leippold et al. (2004) derived the closed form optimal policies and mean-variance frontiers under exogenous and endogenous liabilities using a geometric approach; Chiu and Li (2006) employed the stochastic optimal control theory to analytically solve the asset-liability management in a continuous time setting; Yi et al. (2008) considered the situation of uncertain investment horizon; Chen and Yang (2011) studied the case with regime switching; Zeng and Li (2011) investigated the model under benchmark and mean-variance criteria in a jump diffusion market; Li and Li (2012) took the risk control over bankruptcy into account; Yao et al. (2013) re-considered the uncertain time-horizon model of Yi et al. (2008) by adding an uncontrolled cash flow.
Most of the papers for multi-period mean-variance portfolio selection of asset-liability management mentioned above are based on the embedding technique. The embedding scheme is indeed an efficient way to deal with problems having the nonseparable property. However, it is prone to involve inefficient and complicated calculation during the derivation of the optimal strategies and efficient frontiers by embedding. Therefore, research is naturally required on developing a simple yet accurate method. In this paper, we study asset-liability management under a multi-period mean-variance portfolio selection framework using the parameterized method addressed in Li et al. (2002). We first deduce the case when the returns of assets and liability are correlated. Then we reduce it to the uncorrelated setting. One prominent feature of the dynamic mean-variance formulations is that the optimal portfolio policy is always linear with respect to the current wealth and liability. According to this feature, we derive the analytical optimal policies and efficient frontiers. The analytical form of the Lagrange multiplier is also given in expression of the expectation of the final surplus.
The rest of the paper is organized as follows. In Sect. 9.2, we present the mean-variance formulation of the multi-period portfolio selection model for asset-liability management. The optimal strategies and efficient frontiers are derived in Sect. 9.3. Section 9.4 provides some numerical examples to illustrate the results developed in this paper. Section 9.5 concludes this paper.
2 Mean-Variance Formulation
Assume that an investor joining the market at the beginning of period 0 with an initial wealth x 0 and initial liability l 0, plans to invest his/her wealth within a time horizon T. He/she can reallocate his/her portfolio at the beginning of each of the following T − 1 consecutive periods. The capital market consists of one risk-free asset, n risky assets and one liability. At time period t, the given deterministic return of the risk-free asset, the random returns of the n risky assets, and the random return of the liability are denoted by s t ( > 1), vector e t = [e t 1, ⋯ , e t n]′ and q t , respectively. The random vector e t = [e t 1, ⋯ , e t n]′ and the random variable q t are defined over the probability space \((\Omega,\mathcal{F},P)\) and are supposed to be statistically independent at different time periods.
Suppose that M and N are symmetric matrices with the same order. We denote M ≻ N (\(M \succcurlyeq N\)) if and only if M − N is positive definite (semidefinite). We assume that the only information known about e t and q t are their first two unconditional moments, \(\mathbb{E}[\mathbf{e}_{t}] =\big (\mathbb{E}[e_{t}^{1}],\cdots \,, \mathbb{E}[e_{t}^{n}]\big)^{{\prime}}\), \(\mathbb{E}[q_{t}]\) and (n + 1) × (n + 1) positive definite covariance
From the above assumptions, we have
We further define the excess return vector of risky assets P t = (P t 1, ⋯ , P t n)′ as (e t 1 − s t , ⋯ , e t n − s t )′. The following is then true for t = 0, 1, ⋯ , T − 1:
where 1 and 0 are the n-dimensional all-one and all-zero vectors, respectively, and I is the n × n identity matrix, which further implies, for t = 0, 1, ⋯ , T − 1,
and s t 2(1 − B t ) > 0, where \(B_{t}\stackrel{\Delta }{=}\mathbb{E}[\mathbf{P}_{t}^{{\prime}}]\mathbb{E}^{-1}[\mathbf{P}_{t}\mathbf{P}_{t}^{{\prime}}]\mathbb{E}[\mathbf{P}_{t}]\). This implies that 0 < B t < 1 for t = 0, 1, ⋯ , T − 1.
Let x t and l t be the wealth and liability of the investor at the beginning of period t, respectively, then x t − l t is the net wealth. At period t, if π t i, i = 1, 2, ⋯ , n is the amount invested in the ith risky asset, then x t − ∑ i = 1 n π t i is the amount invested in the risk-free asset. We assume in this paper that the liability is exogenous, which means it is uncontrollable and cannot be affected by the investor’s strategies. Denote the information set at the beginning of period t, t = 1, 2, ⋯ , T − 1, as \(\mathcal{F}_{t}\) = σ(P 0, P 1, ⋯ , P t−1, q 0, q 1, ⋯ , q t−1) and the trivial σ-algebra over \(\Omega\) as \(\mathcal{F}_{0}\). Therefore, \(\mathbb{E}[\cdot \vert \mathcal{F}_{0}]\) is just the unconditional expectation \(\mathbb{E}[\cdot ]\). We confine all admissible investment strategies to be the \(\mathcal{F}_{t}\)-adapted Markov controls, i.e., \(\pi _{t} = (\pi _{t}^{1},\;\pi _{t}^{2},\;\cdots \,,\;\pi _{t}^{n})^{{\prime}}\in \mathcal{F}_{t}\). Then, P t and π t are independent, {x t , l t } is an adapted Markovian process and \(\mathcal{F}_{t} =\sigma (x_{t},l_{t})\).
The multi-period mean-variance model of asset-liability management is to seek the best strategy, π t ∗ = [(π t 1)∗, (π t 2)∗, ⋯ , (π t n)∗]′, t = 0, 1, ⋯ , T − 1, which is the solution of the following dynamic stochastic optimization problem,
Introducing a Lagrange multiplier 2ω > 0 yields
which is equivalent to the following problem,
in the sense that the two problems have the same optimal strategy. It can be rewritten as
where γ = d +ω. Set
and denote ∏ k = T T−1 s k −1: = 1. Then the dynamic system of problem (9.1) turns to
where y 0 = x 0 −γ ∏ k = 0 T−1 s k −1. Problem (9.4) can be reformulated as
and it is the ‘same’ as the following problem:
The ‘same’ here means that they have the same optimal strategy. By studying problem (9.8), we can obtain the optimal strategy of the original problem (9.1).
3 The Optimal Strategies
3.1 The Optimal Strategy with Correlation of Assets and Liability
In this subsection, assume that the returns of assets and liability are correlated at every period, i.e., P t and q t are dependent on each other at period t = 0, 1, ⋯ , T − 1. Before we derive the optimal strategy, we denote
for t = 0, 1, 2, ⋯ , T − 1.
Theorem 1
Assume that the returns of assets and liability are correlated at every period. Then the optimal strategy of problem ( 9.1 ) is given by
where
Proof
We prove it by making use of the dynamic programming approach. For the information set \(\mathcal{F}_{t}\), the cost-to-go functional of problem (9.8) at period t is
where the terminal condition J T (y T , l T ) = y T 2 − 2l T y T . □
We start from the last stage T − 1. While t = T − 1, we have
Minimizing it with respect to π T−1 yields the optimal decision at period T − 1 as follows:
Substituting π T−1 ∗ to \(\mathbb{E}\big[J_{T}(y_{T},l_{T})\big\vert \mathcal{F}_{T-1}\big]\), we obtain
In order to derive the cost-to-go functional and the optimal decision at period t clearly, we patiently repeat the procedure at time T − 2. While t = T − 2, we have
We derive the following optimal decision at period T − 2 by minimizing the above functional with respect to π T−2
Then the cost-to-go functional at period T − 2 is
While t = T − 3, we can similarly get
Thus the optimal decision at period T − 3 is
and the cost-to-go functional at period T − 3 is
Inspired by the above three stages, we conjecture that the cost-to-go functional at period t can be expressed in the following form:
Next, we prove it in mathematical induction. Assume that the cost-to-go functional (9.11) holds at period t + 1. Then we shall prove that it still holds at time t. For the given information set \(\mathcal{F}_{t}\), we have
Minimizing the above functional with respect to π t , we get the optimal strategy decision at time t as follows:
Substituting it to \(\mathbb{E}\big[J_{t+1}(y_{t+1},l_{t+1})\big\vert \mathcal{F}_{t}\big]\) yields
which proves (9.11).
To derive the expression (9.10) of γ, we first consider the value of the optimal objective function in (9.8). In fact,
Then
Since
we have
and
Hence,
where
Since 0 < B t < 1 for t = 0, 1, ⋯ , T − 1,
This implies that the variance term Var(x T − l T ) in (9.12) is concave in ω. To obtain the minimum variance Var(x T − l T ) and the optimal strategy for the original portfolio selection problem (9.1), one needs to maximize the value in (9.12) over \(\omega \in \mathbb{R}\) according to the Lagrange duality theorem in Luenberger (1968). Taking the first order derivative for (9.12) with respect to ω yields
A simple calculation of γ ∗ = d +ω ∗ implies the desired result (9.10). □
3.2 Efficient Frontier
For any matrix M, we denote by M + the Moore-Penrose pseudoinverse of M satisfying
It can be proved that M + is unique for any matrix M and if the inverse M −1 of M exists, then M + = M −1.
Let M be a square matrix partitioned as
Then we have
Lemma 1
If M 22 is invertible, then \(\left \vert M\right \vert = \left \vert M_{22}\right \vert \left \vert M_{11} - M_{12}M_{22}^{-1}M_{21}\right \vert\) .
Suppose that the square matrix M is symmetrical and partitioned as (9.14), where M 11 and M 22 are also symmetrical square matrices, then the following two lemmas hold.
Lemma 2
The matrix \(M \succcurlyeq 0\) is equivalent to \(M_{22} \succcurlyeq 0,M_{22}M_{22}^{+}M_{21} = M_{21}\) and \(M_{11} - M_{12}M_{22}^{+}M_{21} \succcurlyeq 0\) , where M 21 = M 12 ′ .
Lemma 3
If \(M \succcurlyeq N \succcurlyeq 0\) , then \(\left \vert M\right \vert \geq \left \vert N\right \vert\) .
The proof of Lemmas 1 and 3 can be found in Zhang (2011). And the proof of Lemma 2 can be found in Albert (1969).
Before we analyze the efficient frontier, we prove the following important result.
Lemma 4
If \(\mathbb{E}\left [\left (\begin{array}{*{10}c} \mathbf{P}_{k}\\ q_{k } \end{array} \right )\left (\begin{array}{*{10}c} \mathbf{P}_{k}^{{\prime}}&q_{k} \end{array} \right )\right ]\) is positive definite for k = 0,1,⋯ ,T − 1, then
Proof
Let \(L_{k} = \left (\begin{array}{*{10}c} \mathbf{P}_{k}\\ 1 \end{array} \right )\) and \(Q_{k} = \left (\begin{array}{*{10}c} \mathbf{P}_{k}\\ q_{k } \end{array} \right ),\) then
Taking determinant on both sides for (9.16)–(9.18) and according to Lemma 1, we get
By the assumption of \(\mathbb{E}[Q_{k}Q_{k}^{{\prime}}] \succ 0\), the inverse \(\mathbb{E}^{-1}[Q_{k}Q_{k}^{{\prime}}]\) of \(\mathbb{E}[Q_{k}Q_{k}^{{\prime}}]\) exists. Then \(\mathbb{E}^{+}[Q_{k}Q_{k}^{{\prime}}] = \mathbb{E}^{-1}[Q_{k}Q_{k}^{{\prime}}]\). Since
it follows from Lemma 2 that
Obviously,
Consequently,
Then according to (9.23) and Lemma 3, it follows that
Notice that \(\left \vert \mathbb{E}[Q_{k}L_{k}^{{\prime}}]\right \vert = \left \vert \mathbb{E}[L_{k}Q_{k}^{{\prime}}]\right \vert\) and \(\left \vert \mathbb{E}^{-1}[Q_{k}Q_{k}^{{\prime}}]\right \vert = \left \vert \mathbb{E}[Q_{k}Q_{k}^{{\prime}}]\right \vert ^{-1}\), then (9.24) implies
By (9.19)–(9.21) and (9.25), we obtain
Namely,
Then
Therefore,
As a result, it follows from the above inequality that
This completes the proof of Lemma 4. □
It follows from Eq. (9.12) with ω ∗ that we have the following minimum variance theorem.
Theorem 2
Assume that the returns of assets and liability are correlated at every period. Then the efficient frontier is given by
Setting the expected terminal surplus \(d = x_{0}\prod \limits _{k=0}^{T-1}s_{k} - l_{0}\prod \limits _{k=0}^{T-1}\mathbb{E}[q_{k}]\), we obtain the global minimum variance as
By Lemma 4, it follows that the global minimum variance Varmin(x T − l T ) ≥ 0.
3.3 The Optimal Strategy with Uncorrelation of Assets and Liability
Assume that the returns of asset and liability are uncorrelated at every period. Then
Hence, we have the following results:
and
Therefore, we have the following two theorems.
Theorem 3
Assume that the returns of assets and liability are uncorrelated at every period. Then the optimal strategy of problem ( 9.1 ) is given by
where
Theorem 4
Assume that the returns of assets and liability are uncorrelated at every period. Then the efficient frontier is given by
4 Numerical Examples
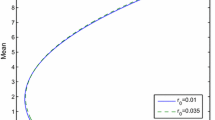
We consider an example of constructing a pension fund consisting of S&P 500 (SP), the index of Emerging Market (EM), Small Stock (MS) of the US market, and a bank account. Based on the data provided in Elton et al. (2007), Table 9.1 presents the expected values, variances, and correlation coefficients of the annual return rates of these indices.
Thus, for any time t, we have
We consider five time periods and an annual risk free rate 5% (s t = 1. 05). Assume that the investor has an initial wealth x 0 = 3 and an initial liability l 0 = 1. Furthermore, for t = 0, 1, 2, 3, 4, the correlation of assets and the liability is \(\boldsymbol{\rho }= (\rho _{1},\rho _{2},\rho _{3})\), where
is the correlation coefficient of the ith asset and the liability. This means
4.1 Correlation
In this subsection, assume that the returns of the assets and liability are correlated with \(\boldsymbol{\rho }= (\rho _{1},\rho _{2},\rho _{3}) = (-0.25,0.5,0.25)\). Hence,
Using the above formula of \(\mathbb{E}[q_{t}P_{t}^{i}]\), we have \(\mathbb{E}[q_{t}\mathbf{P}_{t}] = (0.0898,0.1510,0.1440)^{{\prime}}\). We seek for the expected terminal target with d = 3. 5. According to Theorem 1, we can derive γ ∗ = 4. 0470 and the optimal strategy of problem (9.1) is specified as follows:
where
The variance of the final optimal surplus is Var(x 5 − l 5) = 0. 7289.
4.2 Uncorrelation
In this subsection, assume that the returns of the assets and liability are uncorrelated. Hence,
We still seek to attain the same expected terminal target with d = 3. 5. According to Theorem 3, we can derive γ ∗ = 4. 0464 and the optimal strategy of problem (9.1) is specified as follows:
where K 1 is the same as in Sect. 9.4.1, and the variance of the final optimal surplus is Var(x 5 − l 5) = 1. 0043.
5 Conclusion
Using the parameterized method, the state variable transformation technique, and the dynamic programming approach, we obtain in this paper the closed-form expressions for the optimal investment strategy and the efficient frontier of our multi-period mean-variance asset-liability management problem. Compared with previous studies in the literature, our method is simpler yet more efficient, and the result is more concise and powerful since we do not need to solve an auxiliary problem and investigating the relationship of the auxiliary problem and the original one. Our method is hence especially useful in the big data era. In the future, we will try to use the parameterized method to solve the portfolio selection problem when the returns are correlated in every period, with probability constraint, with uncertain exit time and with Markov jumps.
References
A. Albert, Conditions for positive and nonnegative definiteness in terms of pseudoinverses. SIAM J. Appl. Math. 17, 434–440 (1969)
P. Chen, H.L. Yang, Markowitz’s mean-variance asset-liability management with regime switching: a multi-period model. Appl. Math. Financ. 18, 29–50 (2011)
M.C. Chiu, D. Li, Asset and liability management under a continuous-time mean-variance optimization framework. Insur. Math. Econ. 39, 330–355 (2006)
X.Y. Cui, X. Li, D. Li, Unified framework of mean-field formulations for optimal multi-period mean-variance portfolio selection. IEEE Trans. Autom. Control 59, 1833–1844 (2014)
E.J. Elton, M.J. Gruber, S.J. Brown, W.N. Goetzmann, Modern Portfolio Thoery and Investment Analysis (Wiley, New York, 2007)
M. Leippold, F. Trojani, P. Vanini, A geometric approach to multi-period mean-variance optimization of assets and liabilities. J. Econ. Dyn. Control. 28, 1079–1113 (2004)
C.J. Li, Z.F. Li, Multi-period portfolio optimization for asset-liability management with bankrupt control. Appl. Math. Comput. 218, 11196–11208 (2012)
D. Li, W.L. Ng, Optimal dynamic portfolio selection: multi-period mean-variance formulation. Math. Financ. 10, 387–406 (2000)
X. Li, X.Y. Zhou, A.E.B. Lim, Dynamic mean-variance portfolio selection with no-shorting constraints. SIAM J. Control. Optim. 40, 1540–1555 (2002)
D.G. Luenberger, Optimization by Vector Space Methods (Wiley, New York, 1968)
H.M. Markowitz, Portfolio selection. J. Financ. 7, 77–91 (1952)
W.F. Sharp, L.G. Tint, Liabilities–a new approach. J. Portf. Manag. 16, 5–10 (1990)
H.Y. Yao, Y. Zeng, S. Chen, Multi-period mean-variance asset-liability management with uncontrolled cash flow and uncertain time-horizon. Econ. Model. 30, 492–500 (2013)
L. Yi, D. Li, Z.F. Li, Multi-period portfolio selection for asset-liability management with uncertain investment horizon. J. Ind. Manag. Optim. 4, 535–552 (2008)
L. Yi, X.P. Wu, X. Li, X.Y. Cui, Mean-field formulation for optimal multi-period mean-variance portfolio selection with uncertain exit time. Oper. Res. Lett. 42 (8), 489–94 (2014)
Y. Zeng, Z.F. Li, Asset-liability management under benchmark and mean-variance criteria in a jump diffusion market. J. Syst. Sci. Complex. 24, 317–327 (2011)
F.Z. Zhang, Matrix Theory: Basic Results and Techniques, 2nd edn. (Springer, New York, 2011)
X.Y. Zhou, D. Li, Continuous-time mean-variance portfolio selection: a stochastic LQ framework. Appl. Math. Optim. 42, 19–33 (2000)
Acknowledgements
This work was partially supported by Research Grants Council of Hong Kong under grants 519913, 15209614 and 15224215, by National Natural Science Foundation of China (Nos. 71231008, 71471045), by China Postdoctoral Science Foundation (No. 2014M560658 and No. 2016M592505), and by Characteristic and Innovation Foundation of Guangdong Colleges and Universities (Humanity and Social Science Type).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Li, X., Li, Z., Wu, X., Yao, H. (2017). A Parameterized Method for Optimal Multi-Period Mean-Variance Portfolio Selection with Liability. In: Choi, TM., Gao, J., Lambert, J., Ng, CK., Wang, J. (eds) Optimization and Control for Systems in the Big-Data Era. International Series in Operations Research & Management Science, vol 252. Springer, Cham. https://doi.org/10.1007/978-3-319-53518-0_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-53518-0_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-53516-6
Online ISBN: 978-3-319-53518-0
eBook Packages: Business and ManagementBusiness and Management (R0)