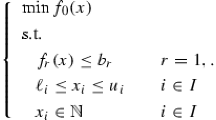Keywords

1 Introduction

Mixed-integer quadratically constrained quadratic programming (MIQCQP) problems are mathematical programming problems with continuous and discrete variables and quadratic functions in the objective function and constraints. The use of MIQCQP is a natural approach of formulating nonlinear problems where it is necessary to simultaneously optimize the system structure (discrete) and parameters (continuous).

MIQCQPs have been used in various applications, including the process industry and the financial, engineering, management science and operations research sectors. It includes problems such as the unit commitment problem (Frangioni and Gentile 2006; Frangioni et al. 2011), the Markowitz mean-variance mode with practical constraints (Mitra et al. 2007), the chaotic mapping of complete multipartite graphs (Fu et al. 2001), the material cutting problem (Cui 2005), the capacity planning problem (Hua and Banerjee 2000). More MIQCQP applications can be found in Grossmann and Sahinidis (2002). The MIQCQP problem is in general NP-hard. It also nests many NP-hard problems as its special cases, such as the binary quadratic programming problem, the integer quadratic programming problem, the semi-continuous quadratic programming problem, etc. All these problems are very difficult to solve and yet have many useful real-life applications such as the max-cut problem (Rendl et al. 2010), the portfolio lot sizing problem (Li et al. 2006), the cardinality constrained portfolio selection and control problems (Gao and Li 2011, 2013b; Zheng et al. 2014; Gao and Li 2013a). The needs in such diverse areas have motivated research and development in solving MIQCQP problems, as they become more and more challenging with larger problem sizes along with the “big data” era. Various methods to find local or global optimal solutions and good lower bounds for different classes of MIQCQP problems can be found in Li and Sun (2006), which is also an excellent survey for nonlinear integer programming.

The general form of an MIQCQP problem is:

$$\displaystyle\begin{array}{rcl} \mathrm{(P)}\ \ \ \min & & x^{T}Q_{ 0}x + c_{0}^{T}x {}\\ \mathrm{s.t.}& & x^{T}Q_{ i}x + c_{i}^{T}x \leq b_{ i},\ i = 1,\ldots,m, {}\\ & & x \in \mathbb{R}^{n}, {}\\ & & x_{i} \in \mathbb{Z},\ 0 \leq x_{i} \leq u_{i},\ i \in I \subset \{ 1,\ldots,n\}, {}\\ \end{array}$$

where we assume that, after fixing the values of x i ,  i ∈ I, the remaining problem is convex. The standard continuous relaxation of problem (P) resulting from removing the integral constraint \(x_{i} \in \mathbb{Z}\) is a convex problem. Thus, problem (P) can be directly plugged into and solved by many off-the-shelf solvers such as CPLEX and Gurobi, which use branch-and-bound schemes. The major issue is that the bound from the standard continuous relaxation is usually very loose, resulting in a large search tree in the branch-and-bound process.

One remedy is to find equivalent reformulations that have a tighter continuous relaxation. In this chapter, we review a general technique, the quadratic convex reformulation (QCR), that is used to find good equivalent reformulations for problem (P). When a better reformulation is solved by CPLEX or Gurobi, the computation time needed can be significantly reduced.

The QCR approach focuses on finding a tighter MIQCQP formulation that is equivalent to the original problem (P). It has the following characteristics:

  1. (a)

    Quadratic functions that vanish in the feasible region can be added to the objective function and the constraints.

  2. (b)

    These added quadratic functions can be characterized by a set of parameters.

  3. (c)

    A convex problem is solved to get the best parameters such that the continuous relaxation of the reformulation is convex and at the same time it provides a lower bound that is as tight as possible.

The process of QCR can be demonstrated by a simple example. The solid curve of Fig. 4.1 is the original objective function and the two dots are the feasible solutions. We can find a new objective curve, the dashed curve, that passes through the corresponding objective points of the feasible solutions and at the same time provides a better lower bound from its continuous relaxation. It is essential that the two curves coincide on the feasible region. The curvature of the dashed curve is smaller than that of the solid curve. That is why the QCR process is also called a “flattening” process in Plateau (2006) and Ahlatçıoğlu et al. (2012).

Fig. 4.1
figure 1

Equivalent reformulation that has a tighter lower bound

Full size image

We will explore the QCR technique on subclasses of problem (P) with simpler structures first and then generalize it step by step such that it can be applied to the general form of problem (P). In Sect. 4.2, we review QCR for binary quadratic programming problems. Two schemes are covered, with or without additional variables. In Sect. 4.3, we review QCR for linear equality constrained binary quadratic programming problems. In Sect. 4.4, we show step by step how we can apply QCR on the general from of problem (P). In Sect. 4.5, we extend the QCR on semi-continuous quadratic programming problems. We conclude the review in Sect. 4.6.

Notation

In remaining sections, we denote by v(⋅ ) the optimal value of problem (⋅ ), and \(\mathbb{R}_{+}^{n}\) the nonnegative orthant of \(\mathbb{R}^{n}\). For any \(a \in \mathbb{R}^{n}\), we denote by Diag(a) = Diag(a 1, …, a n ) the diagonal matrix with a i being its ith diagonal element. We denote by e the all-one vector. We denote by \(\mathbb{S}^{n}\) the set of n × n symmetric real matrix..

2 QCR for Binary Quadratic Programming

QCR is firstly applied on the following binary quadratic programming problem,

$$\displaystyle\begin{array}{rcl} \text{(BQP)}\ \ \ \min & & x^{T}Q_{ 0}x + c_{0}^{T}x {}\\ \text{s.t.}& & x \in \{ 0,1\}^{n}. {}\\ \end{array}$$

There are two main schemes, one with no additional variables and the other with additional variables.

2.1 QCR with No Additional Variables

The QCR scheme with no additional variables was pioneered by Hammer and Rubin (1970) and later improved by Plateau (2006) and Billionnet et al. (2008, 2009). Li et al. (2012) explored the geometry of QCR from another angle.

For any \(d \in \mathbb{R}^{n}\), the following problem is equivalent to problem (BQP):

$$\displaystyle\begin{array}{rcl} \text{(BQP}(d))\ \ \ \min & & x^{T}(Q_{ 0} -\text{Diag}(d))x + (c_{0} + d)^{T}x {}\\ \text{s.t.}& & x \in \{ 0,1\}^{n}. {}\\ \end{array}$$

By relaxing the binary constraint as continuous constraint and noting 0 ≤ x i  ≤ 1 is equivalent to x i 2 − x i  ≤ 0, we can represent problem \((\overline{\text{BQP}}(d))\) as

$$\displaystyle\begin{array}{rcl} (\overline{\text{BQP}}(d))\ \ \ \ \ \ & & \min _{x\in \mathbb{R}^{n}}\ \ x^{T}(Q_{ 0} -\text{Diag}(d))x + (c_{0} + d)^{T}x {}\\ & & \text{s.t.}\ \ x_{i}^{2} - x_{ i} \leq 0,\ i = 1,\ldots,n. {}\\ \end{array}$$

We want to choose d such that the continuous relaxation of (BQP(d)) is a convex problem and the lower bound from this relaxation is as tight as possible. This can be done by solving the following problem,

$$\displaystyle{ \mathrm{(BQP\_MAX\_d)}\ \ \max \{\text{v}(\overline{\text{BQP}}(d))\mid d \in \mathbb{R}^{n},\ Q_{ 0} -\text{Diag}(d)\succeq 0\}.\ \ \ }$$

Note that problem \((\overline{\text{BQP}}(d))\) is convex if and only if Q 0 −Diag(d)⪰0.

Theorem 1 (Billionnet et al. 2009)

Problem (BQP_MAX_d) is equivalent to the following semi-definite programming (SDP) problem,

$$\displaystyle\begin{array}{rcl} \mathrm{(BQP\_DSDP\_d)}\ \ \ \max \ \ & & \tau {}\\ \mathrm{s.t.}\ \ \ & & \left (\begin{array}{*{10}c} -\tau & 0.5(c_{0} + d)^{T} \\ 0.5(c_{0} + d)&Q_{0} -\mathrm{ Diag}(d)\\ \end{array} \right )\succeq 0,\ d \in \mathbb{R}^{n}.{}\\ \end{array}$$

Proof

The Lagrangian dual of \((\overline{\text{BQP}}(d))\) is

$$\displaystyle{ (\overline{\text{LBQP}}(d))\ \ \ \ \ \ \max _{\alpha \geq 0}\min _{x\in \mathbb{R}^{n}}\ x^{T}(Q_{ 0} -\text{Diag}(d))x + (c_{0} + d)^{T}x + x^{T}\text{ Diag}(\alpha )x -\alpha ^{T}x, }$$

which is equivalent to

$$\displaystyle\begin{array}{rcl} \max _{\alpha \geq 0}\min _{x\in \mathbb{R}^{n}}\ & & \tau +(1\ x^{T})\left (\begin{array}{*{10}c} -\tau & 0.5(c_{0} + d-\alpha )^{T} \\ 0.5(c_{0} + d-\alpha )&Q_{0} -\text{Diag}(d) + \text{Diag}(\alpha )\\ \end{array} \right )\left (\begin{array}{*{10}c} 1\\ x \end{array} \right ),{}\\ \end{array}$$

for any \(\tau \in \mathbb{R}\). By noting

$$\displaystyle\begin{array}{rcl} \min _{x\in \mathbb{R}^{n}}\ & & \tau +(1\ x^{T})\left (\begin{array}{*{10}c} -\tau & 0.5(c_{0} + d-\alpha )^{T} \\ 0.5(c_{0} + d-\alpha )&Q_{0} -\text{Diag}(d) + \text{Diag}(\alpha )\\ \end{array} \right )\left (\begin{array}{*{10}c} 1\\ x \end{array} \right ) {}\\ & =& \left \{\begin{array}{@{}l@{\quad }l@{}} \tau \quad &\text{ if }\left (\begin{array}{*{10}c} -\tau & 0.5(c_{0} + d-\alpha )^{T} \\ 0.5(c_{0} + d-\alpha )&Q_{0} -\text{Diag}(d) + \text{Diag}(\alpha )\\ \end{array} \right )\succeq 0, \\ -\infty \quad &\text{ otherwise},\\ \quad \end{array} \right. {}\\ \end{array}$$

we obtain that \((\overline{\text{LBQP}}(d))\) is equivalent to

$$\displaystyle\begin{array}{rcl} \max \ \ & & \tau {}\\ \text{s.t.}& & \left (\begin{array}{*{10}c} -\tau & 0.5(c_{0} + d-\alpha )^{T} \\ 0.5(c_{0} + d-\alpha )&Q_{0} -\text{Diag}(d) + \text{Diag}(\alpha )\\ \end{array} \right )\succeq 0,\ \alpha \geq 0.{}\\ \end{array}$$

Note that the constraints of \((\overline{\text{BQP}}(d))\) satisfy the Slater condition since (0. 5, …, 0. 5)T is an interior point. If Q 0 −diag(d)⪰0, then problem \((\overline{\text{BQP}}(d))\) is convex and from the no duality gap theory of convex programming (see, e.g., Proposition 6.5.6 in Bertsekas et al. 2003), we have \(\text{v}(\overline{\text{BQP}}(d)) = \text{v}(\overline{\text{LBQP}}(d))\). Thus (BQP_MAX_d) is equivalent to

$$\displaystyle{ \mathrm{(LBQP\_MAX\_d)}\ \ \max \{\text{v}(\overline{\text{LBQP}}(d))\mid d \in \mathbb{R}^{n},\ Q_{ 0} -\text{Diag}(d)\succeq 0\}, }$$

which is further equivalent to problem (BQP_DSDP_d) by eliminating the variable α. □ 

In fact, by rewriting the binary constraint x ∈ { 0, 1}n as x i 2 − x i  = 0,  i = 1, …, n, one can check that problem (BQP_DSDP_d) is the Lagrangian dual of problem (BQP).

Convex optimization shows that the conic dual of problem (BQP_DSDP_d) is equivalent to the following SDP relaxation of problem (BQP), which is well known as Shor’s relaxation (Shor 1987),

$$\displaystyle\begin{array}{rcl} \mathrm{(BQP\_PSDP\_d)}\ \ \ \min & & Q_{0}\bullet X + c_{0}^{T}x {}\\ \text{s.t.}& & X_{ii} = x_{i},\ i = 1,\ldots,n, {}\\ & & \quad \left (\begin{array}{*{10}c} 1 & x\\ x^{T } &X\\ \end{array} \right )\succeq 0.{}\\ \end{array}$$

2.2 QCR with Additional Variables

The QCR scheme with additional variables for binary quadratic programming problems can be found in Billionnet et al. (2012, 2013, 2015).

If we introduce new variables, the reformulation can be further strengthened. For any \(S \in \mathbb{S}^{n}\), the following problem is equivalent to (BQP),

$$\displaystyle\begin{array}{rcl} \text{(BQP}(S))\ \ \ \min & & x^{T}(Q_{ 0} - S)x + c_{0}^{T}x + S\bullet Y {}\\ \text{s.t.}& & Y _{ij} \leq x_{i},\ Y _{ij} \leq x_{j},\ Y _{ij} \geq x_{i} + x_{j} - 1,\ Y _{ij} \geq 0,\ \forall \ 0 \leq i < j \leq n, {}\\ & & Y _{ii} = x_{i},\ i = 1,\ldots,n, {}\\ & & x \in \{ 0,1\}^{n},\ Y \in [0,1]^{n\times n},\ Y \in \mathbb{S}^{n}. {}\\ \end{array}$$

By relaxing x ∈ { 0, 1}n, as 0 ≤ x i  ≤ 1,  i = 1…, n, we obtain the continuous relaxation of (BQP(S)) as follows:

$$\displaystyle\begin{array}{rcl} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \min & & x^{T}(Q_{ 0} - S)x + c_{0}^{T}x + S\bullet Y {}\\ \text{s.t.}& & Y _{ij} \leq x_{i},\ Y _{ij} \leq x_{j},\ Y _{ij} \geq x_{i} + x_{j} - 1,\ Y _{ij} \geq 0,\ \forall \ 0 \leq i < j \leq n, {}\\ & & Y _{ii} = x_{i},\ i = 1,\ldots,n, {}\\ & & x \in [0,1]^{n},\ Y \in [0,1]^{n\times n},\ Y \in \mathbb{S}^{n}, {}\\ \end{array}$$

which is equivalent to

$$\displaystyle\begin{array}{rcl} (\overline{\text{BQP}}(S))\ \ \ \min & & x^{T}(Q_{ 0} - S)x + c_{0}^{T}x + S\bullet Y \\ \text{s.t.}& & Y _{ij} \leq x_{i},\ Y _{ij} \leq x_{j},\ Y _{ij} \geq x_{i} + x_{j} - 1,\ Y _{ij} \geq 0,\ \forall \ 0 \leq i \leq j \leq n, \\ & & Y _{ii} = x_{i},\ i = 1,\ldots,n, \\ & & x \in \mathbb{R}^{n},\ Y \in \mathbb{S}^{n}, {}\end{array}$$
(4.1)

where the constraint (4.1) includes the case of i = j. Note that the constraint Y ≤ 1 is implicit in the above problem since Y ii  = x i and Y ii  ≥ x i + x i − 1 together imply Y ii  ≤ 1, thus Y ij  ≤ x i  = Y ii  ≤ 1. The constraint 0 ≤ x i  ≤ 1 is also implicit in the above problem since x i  = Y ii .

We want to choose S such that \((\overline{\text{BQP}}(S))\) is a convex problem and the lower bound from this relaxation is as tight as possible. This can be done by solving the following problem:

$$\displaystyle{ \mathrm{(BQP\_MAX\_S)}\ \ \max \{\text{v}(\overline{\text{BQP}}(S))\mid S \in \mathbb{S}^{n},\ Q_{ 0} - S\succeq 0\}. }$$

Theorem 2 (Billionnet et al. 2013)

Problem (BQP_MAX_S) is equivalent to the following semi-definite programming (SDP) problem,

$$\displaystyle\begin{array}{rcl} \mathrm{(BQP\_DSDP\_S)}\ \ \ \max & & -\tau + Y _{3}\bullet (ee^{T}) {}\\ \text{s.t.}& & \left (\begin{array}{*{10}c} \tau & 0.5y^{T} \\ 0.5y&Q_{0} - Y\\ \end{array} \right )\succeq 0, {}\\ & & y = c - Y ^{1}e - Y ^{2}e + 2Y ^{3}e - d, {}\\ & & Y = S + Y ^{1} + Y ^{2} - Y ^{3} - Y ^{4} + {\it \text{Diag}}(d), {}\\ & & Y ^{1},Y ^{2},Y ^{3},Y ^{4} \in \mathbb{N}^{n} \cap \mathbb{S}^{n},\ d \in \mathbb{R}^{n},Y \in \mathbb{S}^{n}, {}\\ & & S \in \mathbb{S}^{n},y \in \mathbb{R}^{n},\tau \in \mathbb{R}, {}\\ \end{array}$$

where e is a column vector with all entries being 1, and \(\mathbb{N}^{n}\) represents the set of n × n nonnegative matrices.

Proof

The Lagrangian dual of \((\overline{\text{BQP}}(S))\) is as follows:

$$\displaystyle\begin{array}{rcl} (\overline{\text{LBQP}}(S))\ \ \ \ \max \ & & \tau +Y _{3}\bullet (ee^{T}) {}\\ \text{s.t.}\ & & \left (\begin{array}{*{10}c} -\tau & 0.5y^{T} \\ 0.5y&Q_{0} - Y\\ \end{array} \right )\succeq 0 {}\\ & & y = c_{0} - Y ^{1}e - Y ^{2}e + 2Y ^{3}e - d, {}\\ & & Y = S + Y ^{1} + Y ^{2} - Y ^{3} - Y ^{4} + \text{Diag}(d), {}\\ & & Y ^{1},Y ^{2},Y ^{3},Y ^{4} \in \mathbb{N}^{n} \cap \mathbb{S}^{n},\ d \in \mathbb{R}^{n},Y \in \mathbb{S}^{n}, {}\\ & & y \in \mathbb{R}^{n},\tau \in \mathbb{R}. {}\\ \end{array}$$

Note that the constraints of \((\overline{\text{BQP}}(S))\) satisfy the Slater condition. If Q 0 − S ⪰0, then problem \((\overline{\text{BQP}}(S))\) is convex and from the no duality gap theory of convex programming, we have \(\text{v}(\overline{\text{BQP}}(S)) = \text{v}(\overline{\text{LBQP}}(S))\). Thus (BQP_MAX_S) is equivalent to

$$\displaystyle\begin{array}{rcl} \mathrm{(LBQP\_MAX\_S)}\ \ \max \{\text{v}(\overline{\text{LBQP}}(S))\mid S \in \mathbb{S}^{n},\ Q_{ 0} - S\succeq 0\}.& & {}\\ \end{array}$$

It is obvious that the above problem is further equivalent to (BQP_DSDP_S). □ 

The conic dual of problem (BQP_DSDP_S) is given as follows:

$$\displaystyle\begin{array}{rcl} \mathrm{(BQP\_PSDP\_S)}\ \min & & Q_{0}\bullet X + c_{0}^{T}x {}\\ \text{s.t.}& & X_{ij} \leq x_{i},\ X_{ij} \leq x_{j},\ X_{ij} \geq x_{i} + x_{j} - 1,X_{ij} \geq 0,\forall \ 0 \leq i \leq j \leq n, {}\\ & & X_{ii} = x_{i},\ i = 1,\ldots,n, {}\\ & & \left (\begin{array}{*{10}c} 1 &x^{T} \\ x& X\\ \end{array} \right )\succeq 0,{}\\ \end{array}$$

which is an SDP relaxation for problem (BQP) that is tighter than the Shor’s relaxation.

3 QCR for Linear Equality Constrained Binary Quadratic Programming

In this section, we extend the QCR to the following binary quadratic programming problems with linear equability constraints,

$$\displaystyle\begin{array}{rcl} \text{(EBQP)}\ \ \ \min & & x^{T}Q_{ 0}x + c_{0}^{T}x {}\\ \text{s.t.}& & Ax = b,\ x \in \{ 0,1\}^{n}, {}\\ \end{array}$$

where A is an m × n matrix and \(b \in \mathbb{R}^{n}\). We consider only the scheme with no additional variables, which was proposed by Plateau (2006) and Billionnet et al. (2008, 2009).

For any \(d \in \mathbb{R}^{n},s \in \mathbb{R}^{(m+1){\ast}m/2}\), the following problem is equivalent to problem (EBQP):

$$\displaystyle\begin{array}{rcl} \text{(EBQP}(d,s))\ \ \ \min & & x^{T}(Q_{ 0} -\text{Diag}(d))x + (c_{0} + d)^{T}x {}\\ & & \ \ \ +\sum _{1\leq i\leq j\leq m}s_{ij}(A_{i}x - b_{i})^{T}(A_{ j}x - b_{j}) {}\\ \text{s.t.}& & Ax = b,\ x \in \{ 0,1\}^{n}. {}\\ \end{array}$$

By relaxing the binary constraint as continuous constraint and noting 0 ≤ x i  ≤ 1 is equivalent to x i 2 − x i  ≤ 0, we can represent the continuous relaxation of (EBQP(d, s)) as

$$\displaystyle\begin{array}{rcl} (\overline{\text{EBQP}}(d))\ \ \ \min & & x^{T}(Q_{ 0} -\text{Diag}(d))x + (c_{0} + d)^{T}x {}\\ & & \ \ \ +\sum _{1\leq i\leq j\leq m}s_{ij}(A_{i}x - b_{i})^{T}(A_{ j}x - b_{j}) {}\\ \text{s.t.}& & Ax = b,\ x_{i}^{2} - x_{ i} \leq 0. {}\\ \end{array}$$

We want to choose d and s such that \((\overline{\text{EBQP}}(d,s))\) is a convex problem and the low bound from this relaxation is as tight as possible. This can be done by solving the following problem:

$$\displaystyle\begin{array}{rcl} & & \mathrm{(EBQP\_MAX\_ds)}\ \ \max \{\text{v}(\overline{\text{EBQP}}(d,s))\mid d \in \mathbb{R}^{n},\ s \in \mathbb{R}^{(m+1){\ast}m/2}, {}\\ & & \qquad \qquad \qquad \qquad \qquad \quad Q_{0} -\text{Diag}(d) +\sum _{1\leq i\leq j\leq m}s_{ij}A_{i}^{T}A_{ j}\succeq 0\}.\ \ \ {}\\ \end{array}$$

Using similar proofs as in Sect. 4.2, we can show that (EBQP_MAX_ds) is equivalent to the following SDP problem,

$$\displaystyle\begin{array}{rcl} \mathrm{(EBQP_PSDP\_ds)}\ \ \ \min & & Q_{0}\bullet X + c_{0}^{T}x {}\\ \text{s.t.}& & Ax = b, {}\\ & & X\bullet A_{i}^{T}A_{ j} - (b_{i}^{T}A_{ j} + b_{j}^{T}A_{ i})x + b_{i}^{T}b_{ j} = 0,\ 1 \leq i \leq j \leq n, {}\\ & & X_{ii} = x_{i},\ i = 1,\ldots,n, {}\\ & & \left (\begin{array}{*{10}c} 1 &x^{T} \\ x& X\\ \end{array} \right )\succeq 0.{}\\ \end{array}$$

The formulation (EBQP(d, s)) is parameterized by d and s. The dimension of s is (m + 1) ∗ m∕2. As the number of linear equalities grows, the number of parameters increases quadratically. In fact, we can achieve the same good reformulation with only one parameter.

For any \(d \in \mathbb{R}^{n},\ w \in \mathbb{R}\), the following problem is equivalent to (EBQP):

$$\displaystyle\begin{array}{rcl} \text{(EBQP}(d,w))\ \ \ \min & & x^{T}(Q_{ 0} -\text{Diag}(d))x + (c_{0} + d)^{T}x + w(Ax - b)^{T}(Ax - b) {}\\ \text{s.t.}& & Ax = b, {}\\ & & x \in \{ 0,1\}^{n}. {}\\ \end{array}$$

We want to choose d and w such that the continuous relaxation of (EBQP(d, w)) is a convex problem and the low bound from this relaxation is as tight as possible. This can be done by solving the following problem:

$$\displaystyle\begin{array}{rcl} & & \mathrm{(EBQP\_MAX\_dw)}\ \ \max \{\text{v}(\overline{\text{EBQP}}(d,w))\mid d \in \mathbb{R}^{n},\ w \in \mathbb{R} {}\\ & & \qquad \qquad \qquad \qquad \qquad \quad Q_{0} -\text{Diag}(d) + wA^{T}A\succeq 0\}.\ \ \ {}\\ \end{array}$$

Similar to the last section, we have the following theorem.

Theorem 3 (Billionnet et al. 2012)

Problem (EBQP_MAX_dw) is equivalent to the following SDP problem:

$$\displaystyle\begin{array}{rcl} \mathrm{(EBQP\_DSDP\_dw)}\ \ \ \max & & -\tau + wb^{T}b {}\\ \text{s.t.}& & \left (\begin{array}{*{10}c} \tau & 0.5(c_{0} + d - 2b^{T}A)^{T} \\ 0.5(c_{0} + d - 2b^{T}A)&Q_{0} -{\it \text{Diag}}(d) + wA^{T}A\\ \end{array} \right )\succeq 0, {}\\ & & d \in \mathbb{R}^{n},w \in \mathbb{R}. {}\\ \end{array}$$

The conic dual of problem (EBQP_DSDP_dw) is given as follows:

$$\displaystyle\begin{array}{rcl} \mathrm{(EBQP\_PSDP\_dw)}\ \ \ \min & & Q_{0}\bullet X + c_{0}^{T}x {}\\ \text{s.t.}& & Ax = b, {}\\ & & X\bullet (A^{T}A) - 2b^{T}Ax + b^{T}b = 0, {}\\ & & X_{ii} = x_{i},\ i = 1,\ldots,n, {}\\ & & \left (\begin{array}{*{10}c} 1 &x^{T} \\ x& X\\ \end{array} \right )\succeq 0.{}\\ \end{array}$$

which is also an SDP relaxation of (EBQP).

It is shown in Faye and Roupin (2007) that problem (EBQP_PSDP_dw) has the same optimal value with the SDP problem (EBQP_PSDP_ds). Thus the reformulation (EBQP(d, w)) with less parameters is as good as the reformulation (EBQP(d, s)).

4 Generalization of QCR to MIQCQP

In this section we extend QCR to general MIQCQP problems step by step using the techniques derived in Sects. 4.2 and 4.3.

4.1 QCR for Binary Quadratically Constrained Quadratic Programming

We first consider binary quadratic programming problems with quadratic constraints:

$$\displaystyle\begin{array}{rcl} \text{(BQCQP)}\ \ \ \min & & x^{T}Q_{ 0}x + c_{0}^{T}x {}\\ \text{s.t.}& & x^{T}Q_{ i}x + c_{i}^{T}x \leq b_{ i},\ i = 1,\ldots,m, {}\\ & & x \in \{ 0,1\}^{n}. {}\\ \end{array}$$

For any \(d_{0},d_{1},\ldots,d_{m} \in \mathbb{R}^{n}\), the following problem is equivalent to problem (BQCQP):

$$\displaystyle\begin{array}{rcl} \text{(BQCQP}(d))\ \ \ \min & & x^{T}(Q_{ 0} -\text{Diag}(d_{0}))x + (c_{0} + d_{0})^{T}x {}\\ \text{s.t.}& & x^{T}(Q_{ i} -\text{Diag}(d_{i}))x + (c_{i} + d_{i})^{T}x \leq b_{ i},\ i = 1,\ldots,m, {}\\ & & x \in \{ 0,1\}^{n}. {}\\ \end{array}$$

For any \(S_{0},S_{1},\ldots,S_{m} \in \mathbb{S}^{n}\), the following problem is equivalent to (BQCQP),

$$\displaystyle\begin{array}{rcl} \text{(BQCQP}(S))\ \ \ \min & & x^{T}(Q_{ 0}-S_{0})x+c_{0}^{T}x + S_{ 0}\bullet Y {}\\ \text{s.t.}& & Y _{ij} \leq x_{i},\ Y _{ij} \leq x_{j},\ Y _{ij} \geq x_{i}+x_{j} - 1,\ Y _{ij}=Y _{ji},\ \forall \ 0 \leq i < j \leq n, {}\\ & & Y _{ii}=x_{i},\ i=1,\ldots,n, {}\\ & & x^{T}(Q_{ i} - S_{i})x+c_{i}^{T}x+S_{ i}\bullet Y \leq b_{i},\ i = 1,\ldots,m, {}\\ & & x \in \{ 0,1\}^{n},\ Y \in \{ 0,1\}^{n\times n}. {}\\ \end{array}$$

Using the same methods as in Sects. 4.2 and 4.3, one can derive SDP problems to solve for the best parameters d for problem (BQCQP(d)) and S for problem (BQCQP(S)). Note that in this case we also need to maintain the convexity in the constraints.

4.2 QCR for Mixed-Binary Quadratic Programming

In this section we consider the following problem with continuous and binary variables,

$$\displaystyle\begin{array}{rcl} \text{(MBQP)}\ \ \ \min & & x^{T}Q_{ 0}x + c_{0}^{T}x {}\\ \text{s.t.}& & x \in \mathbb{R}^{n},\ x_{ i} \in \{ 0,1\},\ \ i \in I \subset \{ 1,\ldots,n\}, {}\\ \end{array}$$

where we assume that, after fixing the values of x i ,  i ∈ I, the remaining problem is convex.

For any \(s_{ij} \in \mathbb{R},\ (i,j) \in I \times \{ 1,\ldots,n\}\), the following problem is equivalent to (MBQP),

$$\displaystyle\begin{array}{rcl} \text{(BQP}(s))\ \ \ \min & & x^{T}Q_{ 0}x + c_{0}^{T}x -\sum _{ (i,j)\in I\times \{1,\ldots,n\}}s_{ij}(x_{i}x_{j} - y_{ij}) {}\\ \text{s.t.}& & y_{ij} \leq x_{i},\ y_{ij} \leq x_{j},\ y_{ij} \geq x_{i} + x_{j} - 1,\ y_{ij} \geq 0,\ (i,j) \in I \times \{ 1,\ldots,n\}, {}\\ & & y_{ii} = x_{i},\ i = 1,\ldots,n, {}\\ & & x \in \{ 0,1\}^{n},\ y_{ ij} \in \mathbb{R},\ (i,j) \in I \times \{ 1,\ldots,n\}. {}\\ \end{array}$$

Using the same methods as in Sects. 4.2 and 4.3, one can derive SDP problems to solve for the best parameters s for problem (MBQP(s)).

4.3 QCR for MIQCQP

The final step in extending QCR to the general form of problem (P) is to employ binary expansion of the integer variables. Each variable \(x_{i} \in \mathbb{Z},\ 0 \leq x_{i} \leq u_{i},\) can be replaced by its unique binary decomposition:

$$\displaystyle\begin{array}{rcl} & & x_{i} =\sum _{ k=0}^{\lfloor \log (u_{i})\rfloor }2^{k}t_{ ik}, {}\\ & & t_{ik} \in \{ 0,1\},\ k = 1,\ldots,\lfloor \log (u_{i})\rfloor. {}\\ \end{array}$$

Then we can apply all the results in previous sections to the “binarized” problem.

4.4 Compact QCR for MIQCQP

Using simple binary expansion as in Sect. 4.4.3 could blow up the problem size very quickly. This is especially true for problems driven by a massive amount of “big data”. Billionnet et al. (2012, 2013, 2015) proposed a relatively compact formulation. Consider the following integer quadratically constrained quadratic programming problem,

$$\displaystyle\begin{array}{rcl} \text{(IQCQP)}\ \ \ \min & & x^{T}Q_{ 0}x + c_{0}^{T}x {}\\ \text{s.t.}& & x^{T}Q_{ i}x + c_{i}^{T}x \leq b_{ i},\ i = 1,\ldots,m, {}\\ & & x_{i} \in \mathbb{Z},\ 0 \leq x_{i} \leq u_{i},\ i = 1,\ldots,n. {}\\ \end{array}$$

For any \(S_{0},S_{1},\ldots,S_{m} \in \mathbb{S}^{n}\), the following problem is equivalent to (IQCQP),

$$\displaystyle\begin{array}{rcl} \text{(IQCQP}(S))\ \ \ \min & & x^{T}(Q_{ 0} - S_{0})x + c_{0}^{T}x + S_{ 0}\bullet Y {}\\ \text{s.t.}& & x^{T}(Q_{ i} - S_{i})x + c_{i}^{T}x + S_{ i}\bullet Y \leq b_{i},\ i = 1,\ldots,m, {}\\ & & 0 \leq x_{i} \leq u_{i}.\ i = 1,\ldots,n, {}\\ & & x_{i} =\sum _{ k=0}^{\lfloor \log (u_{i})\rfloor }2^{k}t_{ ik},\ t_{ik} \in \{ 0,1\},\ k = 1,\ldots,\lfloor \log (u_{i})\rfloor, {}\\ & & i = 1,\ldots,m, {}\\ & & Y _{ij} =\sum _{ k=0}^{\lfloor \log (u_{i})\rfloor }2^{k}z_{ ijk},\ i,j = 1,\ldots,n, {}\\ & & z_{ijk} \leq u_{j}t_{jk},\ i,j = 1,\ldots,n,\ k = 1,\ldots,\lfloor \log (u_{i})\rfloor, {}\\ & & z_{ijk} \leq x_{j},\ i,j = 1,\ldots,n,\ k = 1,\ldots,\lfloor \log (u_{i})\rfloor, {}\\ & & z_{ijk} \geq x_{j} - u_{j}(1 - t_{ik}),\ i,j = 1,\ldots,n,\ k = 1,\ldots,\lfloor \log (u_{i})\rfloor, {}\\ & & z_{ijk} \geq 0,\ i,j = 1,\ldots,n,\ k = 1,\ldots,\lfloor \log (u_{i})\rfloor, {}\\ & & Y _{ii} = x_{i},\ i = 1,\ldots,n, {}\\ & & Y _{ij} = Y _{ji},\ i,j = 1,\ldots,n,\ i < j {}\\ & & Y _{ij} \geq u_{j}x_{i} + u_{i}x_{j} - u_{i}u_{j},\ i,j = 1,\ldots,n,\ i \leq j, {}\\ & & Y _{ij} \geq 0,\ i,j = 1,\ldots,n,\ i \leq j, {}\\ \end{array}$$

The method for extending this formulation to mixed-integer problems can be found in Billionnet et al. (2015).

4.5 With or Without Additional Variables

In Sect. 4.2, we presented two schemes, one with additional variables and the other without additional variables. In fact, all the reformulations we considered can have the corresponding two schemes. A natural question is: which scheme is better? The scheme with additional variables has tighter reformulations but involves more variables. The trade-off could be problem-specific. Billionnet et al. (2013) showed that the scheme without additional variables could be more efficient in terms of overall computation time for general problem (P).

5 QCR for Semi-Continuous Quadratic Programming

The QCR in previous sections exploits the structures of binary variables and linear equality constraints to derive tighter reformulations. In this section, we look at another structure involving semi-continuous variables.

When modeling real-world optimization problems, due to some managerial and technological consideration, the decision variables are often required to exceed certain threshold if they are set to be nonzero. Such variables are termed semi-continuous variables. Mathematically, semi-continuous variables can be defined as x i  ∈ { 0} ∪ [a i , b i ], where a i  < b i for i = 1, …, n. Using binary variables, semi-continuous variables can be expressed by a set of mixed-integer 0-1 linear constraints:

$$\displaystyle{a_{i}y_{i} \leq x_{i} \leq b_{i}y_{i},\ y_{i} \in \{ 0,1\},\ i = 1,\ldots,n.}$$

Let us consider the following semi-continuous quadratic programming problem,

$$\displaystyle\begin{array}{rcl} (\text{SQP})\ \ \min & & x^{T}Q_{ 0}x + c_{0}^{T}x + h_{ 0}^{T}y {}\\ \text{s.t.}& & Ax + By \leq d, {}\\ & & a_{i}y_{i} \leq x_{i} \leq b_{i}y_{i},\ y_{i} \in \{ 0,1\},\ i = 1,\ldots,n, {}\\ \end{array}$$

Wu et al. (2016) proposed the following equivalent reformulation,

$$\displaystyle\begin{array}{rcl} (\text{SQP}(u,v))\ \ \min & & \ \ f_{u,v}(x,y) \triangleq x^{T}Q_{ 0}x + c_{0}^{T}x + h_{ 0}^{T}y +\sum _{ i=1}^{n}(u_{ i}x_{i}y_{i} + v_{i}y_{i}^{2} - u_{ i}x_{i} - v_{i}y_{i}) {}\\ \text{s.t.}& & \ \ Ax + By \leq d, {}\\ & & \ \ a_{i}y_{i} \leq x_{i} \leq b_{i}y_{i},\ y_{i} \in \{ 0,1\},\ i = 1,\ldots,n, {}\\ \end{array}$$

for any \(u,v \in \mathbb{R}^{n}\). They showed that the quadratic function

$$\displaystyle{\sum _{i=1}^{n}(u_{ i}x_{i}y_{i} + v_{i}y_{i}^{2} - u_{ i}x_{i} - v_{i}y_{i})}$$

is the most general quadratic function that can be added to the objective function.

We want to choose u, v such that \((\overline{\text{SQP}}(u,v))\) is a convex problem and the lower bound from this relaxation is as tight as possible. This can be done by solving the following problem:

$$\displaystyle{ \mathrm{(SQP\_MAX\_uv)}\ \ \max \{\text{v}(\overline{\text{SQP}}(u,v))\mid u,v \in \mathbb{R}^{n},f_{ u,v}(x,y)\ is\ convex\}. }$$

Following the approaches in Sects. 4.2 and 4.3, we can derive an SDP problem to solve for the best parameters u, v for problem (SQP(u, v)).

Theorem 4 (Wu et al. 2016)

Problem (SQP_MAX_uv) is equivalent to the following SDP problem:

$$\displaystyle\begin{array}{rcl} (\mathrm{SDP}_{q})\ \ \max & & \ \ \tau \\ \mathrm{s.t.}& & \ \left (\begin{array}{ccc} Q & \frac{1} {2}\mathrm{diag}(u) & \frac{1} {2}\alpha (u,\eta,\mu,\sigma ) \\ \frac{1} {2}\mathrm{diag}(u) & \mathrm{diag}(v) & \frac{1} {2}\beta (v,\eta,\mu,\sigma,\lambda,\pi ) \\ \frac{1} {2}\alpha (u,\eta,\mu,\sigma )^{T}&\frac{1} {2}\beta (v,\eta,\mu,\sigma,\lambda,\pi )^{T}& -\eta ^{T}d - e^{T}\pi -\tau \\ \end{array} \right )\succeq 0,{}\end{array}$$
(4.2)
$$\displaystyle\begin{array}{rcl} & & \ \ (\eta,\mu,\sigma,\lambda,\pi ) \in \mathfrak{R}_{+}^{m} \times \mathfrak{R}_{ +}^{n} \times \mathfrak{R}_{ +}^{n} \times \mathfrak{R}_{ +}^{n} \times \mathfrak{R}_{ +}^{n}, \\ & & \ \ (u,v,\tau ) \in \mathfrak{R}^{n} \times \mathfrak{R}^{n} \times \mathfrak{R}, {}\end{array}$$
(4.3)

where

$$\displaystyle{ \alpha (u,\eta,\mu,\sigma ) = c - u + A^{T}\eta -\mu +\sigma, }$$
(4.4)
$$\displaystyle{ \beta (v,\eta,\mu,\sigma,\lambda,\pi ) = h - v + B^{T}\eta +\mathrm{ diag}(a)\mu -\mathrm{ diag}(b)\sigma -\lambda +\pi. }$$
(4.5)

6 Concluding Remark

The quadratic convex reformulation (QCR) approach for solving mixed-integer quadratically constrained quadratic programming (MIQCQP) problems is very effective. Its goal is to find a tight and efficient equivalent reformulation, by adding quadratic functions that vanish in the feasible region to the objective function and the constraints. We have reviewed recent advances in the QCR approach. By exploring the QCR technique on subclasses of MIQCQP problems with simpler structures first, we are able to generalize the approach step by step such that it can be applied to general MIQCQP problems. We have also covered the recent extension of QCR on semi-continuous quadratic programming problems. In a broad picture, the QCR approach provides a very effective solution framework for solving MIQCQP problems.

As the problem size of the NP-hard MIQCQP problems increases along with the “big data” era, the QCR approach would be more and more important. This is because finding the best reformulation in the QCR approach reduces to an SDP problem, which is a convex problem that can be solved in polynomial time. Armed with the optimized reformulation, better approximation and heuristics can be developed.

In the coming future, the QCR approach can be further generalized according to different practical structures in the objective function and the constraints. Also, the integration of the QCR approach with other solution techniques for MIQCQP problems is also an interesting research direction.