Spin Polarization and Small Size Effect in Bare Silver Nanoparticles

Abstract

In this chapter, we present the results of studies conducted on the magnetic properties that developed in ultrasmall bare Ag nanoparticles and the critical particle size for developing a sizable spontaneous magnetic moment in the nanoparticles. Seven sets of bare Ag nanoparticle assemblies, with diameters from 2 to 36 nm, were fabricated with the gas condensation method. Line profiles of the X-ray diffraction peaks were used to determine the mean particle diameters and size distributions of the assemblies. Lattice relaxation from the small size effect is clearly revealed in particles with a diameter smaller than 12 nm, where the electron charges are more extensively distributed toward the central regions of the two nearest neighbors. The extension of the electron charge distribution is not isotopic in all crystallographic directions, revealing that redistribution involves not only spherically distributed 5s electrons but also includes directional 4d electrons. The isothermal magnetization M(H _a) curves of the particle superspins reveal Langevin field profiles. Contributions to the magnetization from particles of different sizes in the assemblies were considered when analyzing the M(H _a) curves. The results show that the maximum superspin moment will appear in 2.6 nm Ag particles. The atoms on the surface and in the core of the bare Ag nanoparticles contribute to the superspin moment. Magnetic field–induced Zeeman magnetization from the quantum confined Kubo gap opening is revealed in Ag nanoparticles smaller than 8 nm in diameter. It is the disruptions of lattice periodicity that trigger the redistribution of electron charges for the development of spontaneous superspin in Ag nanoparticles.

6.1 Introduction

6.1.1 Magnetism of Noble Metals in Bulk Form

The term noble metal in chemistry refers to those transition-metal elements that are resistant to corrosion and oxidation in humid environments [1]. This class of elements includes the 3d, 4d, and 5d transition metals of ²⁹Cu, ⁴⁴Ru, ⁴⁵Rh, ⁴⁶Pd, ⁴⁷Ag, ⁷⁶Os, ⁷⁷Ir, ⁷⁸Pt, and ⁷⁹Au. Among these, the d bands of Ru, Rh, Pd, Os, Ir, and Pt are partially filled, giving rise to a nonzero atomic magnetic moment for each of these six elements. The atomic moments in these elements do not interact with each other but will respond to an external magnetic field, generating no spontaneous magnetic ordering but paramagnetic moments. In physics, the definition of a noble metal is restricted to those transition-metal elements with a completely filled d band [2]. From this perspective, only Cu, Ag, and Au are noble metals. The completely filled d bands give zero magnetic moments for Cu, Ag, and Au. In this chapter we follow the definition used in physics and focus on the magnetic properties of the noble metals Cu, Ag, and Au.

It is known that the magnetic behavior of a material is a direct consequence of the electron configuration. The band structures and Fermi surfaces of noble metals have been comprehensively studied both theoretically and experimentally. Generally speaking, the band structures of the 3d, 4d, and 5d transition metals are similar [3, 4]. Near the Fermi level, there is a broad, nearly free-electron-like s–p band that overlaps the relatively narrow d band in specific crystallographic directions [4]. The Fermi level of most transition metals falls into the d-band complex, but the completely filled d bands of Cu, Ag, and Au lie far below the Fermi energy, so that the s–d hybridization is negligibly small. The filled ion core and d bands give rise to a diamagnetic response to an applied magnetic field, whereas conduction electrons behave as a Pauli paramagnet. It appears that the diamagnetic responses are stronger than the Pauli paramagnetic ones in Cu, Ag, and Au, which gives rise to the diamagnetic character in their bulk forms.

6.1.2 Magnetism of Nanosized Noble Metals

Nanoparticle (NP) is a term used to indicate materials having sizes in the nanometer scale in all three spatial dimensions. Depending on their actual size, NPs may or may not exhibit properties that differ significantly from those observed in their bulk form [5]. Generally speaking, size-dependent properties will be revealed in NPs with diameters smaller than, say, 50 nm. The study of small NPs of various types is currently an area of intense scientific interest with regard to their fundamental properties as well as their practical applications for the next generation of devices [6, 7]. There are many ways to fabricate metal NPs, but the nucleation of atoms through chemical or physical processes is frequently employed for the fabrication of macroscopic amounts of small NPs. NPs fabricated through chemical processes are unavoidably capped by the organic molecules used as the reduction agents. These capping molecules not only stabilize the NP in the core but will also interact with the surface atoms. This interaction affects the physical properties of the NP. Studies conducted using surfactant-capped NPs reflect the physical properties of NP-surfactant complexes, rather than those of the NPs themselves. For example, it has been suggested [8] that the appearance of magnetic moments in thiol-capped Au NPs is associated with the 5d localized holes created through the covalent Au–S bonding between the surface Au ions and the S ions of the capping thiols. It is the strong affinity between Au and S ions, rather than the size effects themselves, that induces a noticeable charge transfer from the surface Au ions to the S ions that triggers the covalent Au–S bonding for the magnetism in Au NPs [9, 10]. Undoubtedly, NPs free from capping agents are needed for the investigation of the results of the size reduction itself. Metal NPs without capping agents may be fabricated by breaking down the bulk metal or building up from the atoms. The breakdown of bulk metals can be achieved by mechanical milling. This is a good way to fabricate particles with a high melting point, but it is difficult to control the particle size or produces particles smaller than 100 nm in diameter. The building-up method involves the assembly of atoms into small particles, which can be achieved through thermal evaporation coupled with cold condensation in an inner gas atmosphere [11].

An NP consists of a limited number of atoms, with a large fraction of them being on the surface where the coordinate number is much reduced. Obviously, the electronic properties of NPs will be affected by the broken symmetry and the disruption of lattice periodicity at the surface [12,13,14,15] and by the quantum confinement of the conduction electrons [16,17,18]. Many novel magnetic, electronic, optical, and catalytic properties have been found in NPs [19,20,21,22,23,24]. In particular, a great variety of magnetic phenomena, such as giant paramagnetism, superparamagnetism, spontaneous ferromagnetic moments, quantum-confined Brillouin magnetization, and thermally induced magnetization, have all been observed in noble-metal NPs [20, 25,26,27,28,29,30,31,32,33,34,35,36,37,38]. However, most studies conducted on the magnetic behavior of noble-metal NPs were performed using polymer-capped particles, with only a limited number of studies focusing on the magnetic properties of noble-metal NPs themselves.

6.1.3 Size Effects

It is known that the atomic environment of the atoms on the surface of a particle is different from those in the interior. Clearly, the physical and chemical behaviors of surface atoms will differ from those in the interior. In particular, surface atoms are relatively loosely bonded to the particle, which can be chemically very active with extrinsic stimulation. This surface effect is revealed in particles with sizes on the order of a few hundred nanometers, where the ratio between the number of surface and core atoms is no longer negligible [12]. The small size effect marks results from the disruption of the lattice periodicity at the particle surface. In addition to softening of the phonon modes from the weakening of the lattice rigidness at the surface, surface phonon modes will be revealed at low frequency when the total amount of surface atoms is not negligible [13,14,15]. Small size effects can be expected in particles a few dozen nanometers in diameter. Furthermore, a significant amount of electron charge redistribution will also occur if the lattice periodicity is severely limited. For example, there are 25 lattice periodicities along each crystallographic axis direction in a 10 nm Au NP, with two unit cells at the surface. Rearrangement of the electron charge distribution to accommodate the surface disruption can be anticipated. This electron charge redistribution can give rise to the significantly different physical characteristics of NPs compared to bulk materials.

Quantum confinement will be encountered if the spatial dimensions of the NPs are further reduced. Spatial confinement restricts the spatial motions of electrons, which results in a splitting of the electron energy bands near the Fermi energy into discrete narrow subbands [16,17,18]. The average electron band separation, known as the Kubo gap, is inversely proportional to the density of states at the Fermi energy D(E _F) [16, 18]. In the free electron approximation [16], it takes the form

$$ \varDelta =\frac{1}{D\left({E}_{\mathrm{F}}\right)}=\frac{2{\pi}^2{\hslash}^2}{m{\left(3{\pi}^2n\right)}^{1/3}V}, $$

(6.1)

where ħ is Planck’s constant divided by 2π, m is the electron mass, n is the free electron density, and V is the volume of the NP. Apparently, the size of the Kubo gap that opens up at the Fermi level depends very strongly on the diameter d of the NP and is inversely proportional to d ³. Quantum confinement governs the electronic behavior of particles smaller than 10 nm in diameter, but not larger. For example, the Kubo gap in a 10 nm Ag NP, estimated according to the Kubo formula, is only 0.23 meV, which corresponds to a thermal energy of 2.7 K, which will be barely visible at temperatures as low as 10 K. The Kubo gaps for other metals are even smaller as their free electron densities are lower.

In this study, we discuss the magnetic properties of capping-free noble-metal NPs, with an emphasis on the property changes originating from the reduction of particle size but avoiding the complications that might arise from the capping agents. Comprehensive discussion of the magnetic properties of bare Au NPs through magnetization studies are available in [11, 35], and confirmation of the existence of an intrinsic magnetic moment in 4 nm Au NPs using neutron diffraction can be found in [36]. Connections between the development of ferromagnetic superspins and the occurrence of electron charge redistribution in bare Cu NPs can be found in [37]. Here we focus on the magnetic properties of ultrasmall bare Ag NPs with diameters in a range of 2–35 nm. In the next section, we will present (a) details of the fabrication and characterization of the bare Ag NPs used in the present study, (b) the theoretical background for understanding the isofield and isothermal magnetization, (c) lattice relaxation and electron charge density, and (d) magnetic superspins in small Ag NPs a few nanometers in diameter.

6.2 Materials

6.2.1 Sample Fabrication

The Ag NPs used in the present study are fabricated using the gas condensation method. The basic concepts behind this method include (1) producing an atom vapor, (2) nucleation through collisions, (3) controlling the growth rate by introducing inner gas into the evaporation chamber, and (4) reducing the kinetic energies of the atoms to prevent interparticle fusion using a cold collector. Atom vapor can be produced by passing an electric current through bulk ingots until they reach their melting temperature. The source temperature and, hence, the evaporation rate can be controlled by adjusting the strength of the heating current. The kinetic energies of the evaporated atoms are reduced through collisions with the surrounding inert gas atoms. Argon gas is commonly used as the kinetic energy reducer. The cold collector acts as a cold trap for the collection of NPs. A collector maintained at 77 K can effectively prevent interparticle fusion for the formation of small NPs. Several physical parameters are important for controlling the mean size and size distribution of the resultant NPs: the strength of the electric current heating the metal ingots, the Ar pressure in the chamber during nucleation, the temperature of the collector, and the distance between source and collector. A schematic plot of a typical gas condensation chamber for the fabrication of small NPs may be found in Fig. 14 of [11].

The Ag NP powders used in the present study are fabricated using the gas condensation method. The mean particle size and size distribution are controlled by the proper choice of chamber pressure and source temperature. High-purity Ag spheres (approx. 0.5 g, 99.99% pure, and 2 mm in diameter) are heated by a current source (65–90 A) and are evaporated at a rate of 0.05 Å/s in an Ar atmosphere under various pressures (0.1–5 torr). The evaporated particles are collected on a nonmagnetic SS316 stainless-steel plate placed 20 cm above the evaporation source and maintained at 77 K. After restoration to room temperature, the NPs, which are only loosely attached to the collector, are stripped off. The samples thus fabricated are in powdered form and consist of macroscopic amounts of individual Ag NPs. There is no substrate or capping molecules on the NPs. The resultant powders are no longer sliver sheen but dark black, indicating that the absorption bands of the powders have blue shifted to the invisible region, as is the case with most metallic NPs. It appears that the samples are quite stable against exposure to air for a limited time since the X-ray diffraction patterns and magnetization curves of the as-grown sample and the sample exposed to the air for 5 days are indistinguishable. However, the samples used in the present study were kept in a vacuum at all times, after being stripped off from the collector and loaded into the sample holders for measurements.

6.2.2 Sample Characterization

X-ray diffraction is currently the most commonly used and most effective tool for the determination of the crystalline structure and chemical composition of powdered compounds. In the Bragg formulation, crystals are viewed as being made of many parallel planes of ions, known as the lattice planes. In general, many sets of parallel lattice planes may be identified in a crystalline structure. The Miller indices h, k, and l are used to label the interplanar spacing d _hkl for reflection from the (hkl) lattice planes. Constructive interference of the diffracted X-ray of wavelength λ will occur whenever Bragg’s law 2d _hkl sin θ = nλ is met, which gives the angle θ, known as the Bragg angle, for coherence scattering from crystal lattices. Identifying the d _hkl in the lattice allows for the construction of the crystalline structure. In addition, the width of the diffraction peak reflects the spatial extension of the lattice periodicity, which in the present case corresponds to the size of the NPs. The diffraction peaks from the NPs are broader than the instrumental width owing to the incomplete interference of the scattered waves. An easy way to extract the mean particle diameter of an NP assembly is to employ the Scherrer equation [39], which relates the peak width to the particle size but is formulated assuming a monodispersed particle assembly. The line profile of a diffraction peak from a size-dispersed assembly is the result of a superposition of the diffraction profiles from all the sizes in the assembly, which can be used to extract the size distribution of the assembly.

Atomic force microscopy (AFM) and transmission electron microscopy (TEM) images can reveal the shape and size of each individual NP, making them feasible to obtain the size distribution in an NP assembly, provided it has been properly sampled. In sampling the images, NPs must be very dispersedly deposited on a special sample holder for mapping of the morphology. The sampling must also be conducted over a substantial amount of individual NPs with no artificial preference to obtain a reliable signature of the size distribution. Stacking or aggregation of the NPs results in poor images for size or shape determination. The process is frequently troublesome and can be time consuming compared to the X-ray diffraction technique, in which a macroscopic amount of NPs in an assembly is automatically sampled. Proper analysis of the line profile of X-ray diffraction peaks allows one to extract the size distribution of the assembly.

6.2.3 Diffraction Profile of a Size-Dispersed Nanoparticle Assembly

The line profile of a diffraction peak from a size-dispersed NP assembly is produced from a combination of the diffraction profiles contributed from each individual NP in the assembly. It is clear that the resultant profiles will depart from the instrumental resolution function. Poor fits, especially at the tails and centers of the diffraction peaks, will emerge when the diffraction profiles of an NP assembly are fitted with the instrumental resolution function, as illustrated in Fig. 6.1. The intensities at the tails are contributed mainly from small particles, while those at the centers are from large particles. The diffraction profile contains information about the size distribution of the NP assembly. Unfortunately, it is not feasible to combine all the profiles from every individual NP since there are so many of them. However, the problem can be largely reduced by assuming that the size distribution of the assembly may be represented by an analytical expression that can be described by two parameters. Formulation of the line profiles of the diffraction peaks of a size-dispersed assembly is then feasible. Generally speaking, an analytical function that reflects the instrumental resolution and specifies the peak position, peak width, and peak height is needed to describe the diffraction peak from an assembly of monosized particles. The peak positions in the diffraction pattern are the scattering angles 2θ _hkl of the (hkl) Bragg reflection; in terms of the full width at half maximum, the peak width w _i of the (hkl) Bragg reflection for particles of diameter d _i can be formulated [39] as

$$ {w}_i=\frac{0.94\lambda }{d_i \cos \theta {}_{hkl}} $$

(6.2)

Fig. 6.1

X-ray diffraction peaks from representative Ag NP assembly. The solid curve indicates the results of fits of the diffraction peaks to Lorentizian profiles. Poor fits are obtained especially in the tail regions of the peaks

for spherical particles, and the peak height is proportional to the number n _i of particles of diameter d _i in the assembly. In many cases, the diffraction profile from a single particle can be satisfactorily described by a Lorentzian function:

$$ {L}_i\left(2\theta, {w}_i,{n}_i\right)=\frac{2{n}_i}{\pi}\left[\frac{w_i}{4{\left(2\theta -2{\theta}_{hkl}\right)}^2+{w}_i^2}\right]. $$

(6.3)

The diffraction intensity of the (hkl) Bragg reflection of a multidispersed NP assembly is the superposition of L _i (2θ,w _i ,n _i ) from all n _i in the assembly:

$$ {I}_{hkl}\left(2\theta \right)=C\sum_{n_i}{L}_i\left(2\theta, {w}_i,{n}_i\right), $$

(6.4)

where C is the instrumental scale factor that accounts for the setup of the diffractometer. In the case of an assembly consisting of quantum NPs, a log-normal size distribution is often found, so that

$$ {n}_i\left({d}_i\right)=\frac{1}{d_i\sqrt{2\pi}\sigma } \exp \left\{-\frac{{\left( \ln {d}_i- \ln {d}_{\mathrm{m}}\right)}^2}{2{\sigma}^2}\right\}, $$

(6.5)

where d _m represents the mean particle diameter for the size distribution of the assembly and σ is the standard deviation of the size distribution.

6.2.4 X-Ray Diffraction and AFM Measurements

The X-ray diffraction measurements were conducted on a Bruker D8 ADVANCE diffractometer with K _α radiation and source wavelengths of K _α1 = 1.5406 Å and K _α2 = 1.5443 Å from a copper target. An accelerating voltage of 40 kV and a beam current of 40 mA were employed. The Bruker LynxEye linear position-sensitive detector (PSD) captured a scattering angle of 4°, and a Ni filter was placed before the PSD to screen the K _β radiation. The diffraction patterns were taken in the reflection geometry, where a correct positioning of the sample to the zero-scattering-angle line is extremely important to avoid misjudgment of the diffraction angle. The sample temperature was controlled using a He-gas closed-cycle refrigeration system, equipped with a high-power heater. The AFM images were taken using a Digital Instruments Nanoscope III operated in tapping mode, with the cantilever oscillating to avoid trapping the NPs on the tip, at a scanning speed of three lines per second.

6.2.5 Size Distribution of Ag NP Assemblies

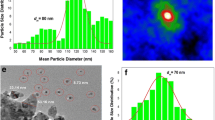
The size distributions and mean particle diameters of the Ag NP assemblies were determined by fitting the diffraction peaks to the diffraction profiles of finite size particles. Figure 6.2a shows an X-ray diffraction pattern of representative Ag NPs fabricated using a current source of 65 A and a chamber Ar pressure of 3 torr, taken at room temperature. As expected, the diffraction peaks appear to be much broader than the instrumental resolution, reflecting the broadening of the peak profiles owing to the finite size effect. The X-ray diffraction patterns can be associated with a face-centered cubic Ag structure. No traces of oxidation phases or elements other than Ag may be identified from the diffraction patterns. The solid curves in Fig. 6.2a indicate the fitted pattern, assuming a Lorentzian function for the diffraction profile (Eq. (6.3)), together with a log-normal size distribution (Eq. (6.5)), with the center at d _m = 2.5 nm and a standard deviation of σ = 0.55, as shown by the solid curve in Fig. 6.2b. This size distribution agrees well with that [bars in Fig. 6.2b] obtained from the AFM images, as illustrated in Fig. 6.2c.

Fig. 6.2

(a) X-ray diffraction pattern of Ag NP assembly at 300 K, revealing a face-centered cubic crystalline structure. The solid curves indicate the calculated profiles of the diffraction peaks, assuming a log-normal size distribution with a center at 2.5 nm and a standard deviation width of 0.55. (b) Size distributions obtained from X-ray diffraction profile (solid curve) and from AFM images (vertical bars). (c) Portion of AFM images of Ag NPs

6.3 Methods

6.3.1 Particle Superspin

Randomly oriented crystallized domains of sizes in the range of several hundred nanometers are frequently formed in bulk materials. The energy and stress buildup at the domain boundaries acts against the formation of a domain structure composed of domains smaller than a few hundred nanometers. Frequently, a single-domain structure is formed in an NP a few dozen nanometers in diameter. An isolated single-spin-domain NP can be treated as a superspin [40, 41], where the magnetic behavior is expressed by the net magnetic moment of the NP, namely, the particle magnetic moment μ _p, having several hundreds or thousands of Bohr magnetons. Thermal agitation will reduce the μ _p of each NP. The magnetic ordering temperature of the superspin, which frequently persists up to well above room temperature, depends strongly on the particle size.

Magnetization marks the density of the magnetic dipole moment of materials; it is the most commonly used parameter for revealing the magnetic character. An assembly of loosely packed magnetic NPs, where interparticle interactions are insignificant, is currently described as a superparamagnetic system that consists of a collection of many randomly oriented noninteracting superspins [42, 43]. The magnetization M at a finite temperature T of an NP assembly consisting of many individual well-separated (interaction-free) superspins will be zero when the NPs are naturally packed and the particle moments are randomly oriented, as illustrated in Fig. 6.3a. An applied magnetic field H _a drives the individual μ _p to align along the field direction. It is known that the magnetic field inside the NP that is experienced by the μ _p is a combination of the applied magnetic field, the magnetocrystalline anisotropy, and the molecular field. This effect is represented by the dimensionless permeability α such that αH _a indicates the net magnetic field inside the NP. It takes the form of $\alpha =1+\left({\mu}_0{M}_{\mathrm{P}}^2/2K\right)$ for uniaxial spheres [44], where K is the energy density associated with the magnetocrystalline anisotropy, μ ₀ is the magnetic permeability of the free space, and M _P is the spontaneous saturation magnetization. The Boltzmann statistics that balance the competition between the magnetic interaction energy μ _p αH _a and the thermal agitation energy k _B T give rise to a Langevin profile for the dependency of M on H _a and T [45]: M _L(H _a,T) = M _P(T)L(x), where M _P(T) indicates the saturation particle magnetization at temperature T

$$ L(x)\equiv \coth (x)-\frac{1}{x} $$

(6.6)

is known as the Langevin function with x ≡ αμ _p H _a/k _B T, and k _B is Boltzmann’s constant. The Langevin M _L(H _a,T) profile is understood to be a randomly oriented assembly of many interaction-free superspins, with an average magnetic moment μ _p at temperature T, that are being aligned by the applied magnetic field, as illustrated in Fig. 6.3b.

Fig. 6.3

Schematic illustration of configuration of superspins in NP assembly at finite temperature. Each NP carries a superspin moment μ _p (a) without and (b) with the presence of an applied magnetic field H _a

6.3.2 Quantum Confined Zeeman Condensation

An applied magnetic field will split the energy degenerate spin-up and spin-down bands into two separated spin-polarized bands, with a Zeeman splitting energy of gμ _B αH _a, where g is the Lande g-factor and μ _B is the Bohr magneton. Magnetization contributed from the condensation of electrons into the Zeeman split spin-polarized states will appear. This H _a-induced magnetization is contributed mainly from the conduction electrons. The effect can be substantial in NPs, where the discrete nature of the electron level spacing is significant. Under the assumption of an even band separation for all Kubo gaps, it is the available density of states for the thermal excitation that measures the contribution to the Zeeman magnetization since thermal excitation for the conduction electrons into the first excited band and for the valence electrons into the conduction band is equally probable. The Zeeman magnetization of quantum spins follows a Brillouin profile [45]: M _B(H _a,T) = M _Z(T)B _J (y), where M _Z(T) represents the induced saturation magnetization,

$$ {B}_J(y)\equiv \frac{2J+1}{2J}\mathrm{ctnh}\left[\frac{\left(2J+1\right)y}{2J}\right]-\frac{1}{2J}\mathrm{ctnh}\left(\frac{y}{2J}\right) $$

(6.7)

is the Brillouin function of order J, and y ≡ gμ _B αH _a/k _B T. Note that the Brillouin function reduces to a Langevin function when J = ∞, that is, B _∞(y) = L(y), and it reduces to a hyperbolic tangent function when J = 1/2, that is, B _1/2(y) = tanh(y). Competition between the thermal agitation and field alignment results in a Langevin profile for the magnetization M _L(H _a,T), whereas thermal excitation of valence and conduction electrons into the Zeeman split spin-polarized states gives rise to a Brillouin profile for the magnetization M _B(H _a,T).

6.3.3 Generalized Magnetization Profile for a Size-Dispersed Nanoparticle Assembly

It is very difficult to measure the physical properties of an individual NP at the currently available instrumental resolutions. Measurement is limited by the extremely weak signals that an NP can generate for detection. Thus measurement is nowadays performed on an assembly of NPs for signal enlargement. However, it is difficult to fabricate a monodispersed NP assembly. Consequently, the signals detected during measurement contain the responses from all sizes of NPs that appear in the assembly. It has been demonstrated that ignoring the influence of size dispersion in the NP assembly can result in unphysical conclusions [46]. When considering the magnetization profile for an NP assembly, the contributions from particles of different sizes must be taken into account. Assuming that there are n _i NPs having a particle magnetic moment μ _pi and a magnetic permeability α _i in the assembly, the Langevin magnetization then takes the form of the summation of contributions from all sizes of n _i :

$$ {M}_{\mathrm{L}}\left({H}_{\mathrm{a}},T\right)=\sum_i{n}_i{\mu}_{\mathrm{p}i}L\left(\frac{\mu_{\mathrm{p}i}{\alpha}_i{H}_{\mathrm{a}}}{k_{\mathrm{B}}T}\right)=\sum_i{n}_i{\mu}_{\mathrm{p}i}L\left(\frac{\mu_{\mathrm{p}i}\alpha {H}_{\mathrm{a}}}{k_{\mathrm{B}}T}\right) $$

(6.8)

taking the same value α for the magnetic permeability of all NPs in the assembly for simplicity. This simplified expression can be justified for narrowly dispersed assemblies. It is unphysical to extract all the parameters associated with the preceding expression from the observed M _L(H _a,T) unless the number of free parameters can be reduced further.

Even though the size distribution of an NP assembly can be determined from the diffraction profile, as discussed in Sect. 2.5, extraction of the size distribution from the magnetization data is also feasible by specifying a distribution function for the particle size. Specification of the distribution function reduces the free parameters associated with the size dispersity into two, the mean size and the distribution width. In the case of an assembly consisting of quantum NPs, a log-normal size distribution is often found, as expressed in Eq. (6.5). Cross examination of the size distributions obtained from the magnetization and from the diffraction can then be used to check the physical quality of the fits. Likewise, by taking an analytical expression for the dependency of the particle magnetic moment μ _pi on the particle diameter d _i , the free parameters associated with the moment dispersity reduce into three: the maximum particle moment μ _pm, the mean particle diameter for the moment distribution d _c , and the standard deviation of the moment distribution w. In the case of a log-normal type of size dependency for the particle moment, it can be expressed as

$$ {\mu}_{\mathrm{p}i}\left({d}_i\right)=\frac{\mu_{\mathrm{p}\mathrm{m}}}{d_i\sqrt{2\pi }w} \exp \left\{-\frac{{\left( \ln {d}_i- \ln {d}_c\right)}^2}{2{w}^2}\right\}. $$

(6.9)

A plot of n _i μ _pi against d _i using the parameters obtained from the fit gives the contribution from particles of each size to the saturation magnetization of the NP assembly.

6.3.4 Magnetization Measurements

The magnetization measurements were performed on a Physical Property Measurement System, manufactured by Quantum Design (San Diego, CA, USA), employing the standard setups. The magnetization M was measured by detecting the induced voltage in the detector coils as the sample moves through them. The NPs must be very loosely packed for these measurements, so that they reveal mainly the magnetic responses from individual NPs without significant contributions from interparticle interactions. To avoid any aggregation that might arise among the NPs, the assembly is shaken at 50 Hz for 5 min using a Vortex-Genie Mixer (Bohemia, NY, USA). The NPs (approximately 60 mg each) are packed into a nonmagnetic cylindrical holder provided by Quantum Design. The packing fraction f, which marks the ratio between the mass densities of the NP assembly in the holder and that of the bulk Ag, is used to quantify the average interparticle separation that signals the significance of interparticle interactions in the NP assembly. The packing fraction chosen for all NP assemblies used in the present studies is approximately 6%, which corresponds to an average interparticle separation, from edge to edge, of 1.25 times the particle diameter. The holder produces a smooth temperature curve and a background signal that is approximately 2% of the signal from samples.

6.4 Lattice Relaxation

6.4.1 Size Effect

The structural ordering of atoms within a solid is formed by the lattice interaction. Generally speaking, a stronger lattice interaction gives rise to a shorter lattice separation, specified by the lattice constants that indicate the spatial extension of the lattice unit cell. The formation of a face-centered cubic structure in noble metals is known to be driven by metallic bonding, where appreciable electrons are distributed throughout the interstitial regions and the atomic connection is not restricted to within the nearest neighbors but can extend to several unit cells. Larger lattice constants can be anticipated for ultrasmall NPs having sizes smaller than the lattice interaction can reach. The lattice constant of Ag NPs increases progressively when the size is reduced to below 20 nm in diameter, which is accompanied by a building up of negative stress in the NPs (Fig. 6.4). Interestingly, the enlargement of the lattice constant a and stress σ with the reduction in particle diameter d may be described using an exponential profile (solid curves in Fig. 6.4), with decay constants of d ₀ = 5.6(4) nm for the lattice constant and d _S = 3.9(4) nm for the stress. The a ₀ = 4.079(4) Å obtained from the fit indicates the lattice constant for large particles, which agree very well with the value known for bulk Ag. The lattice constant of 2.3 nm Ag NP at 300 K (a = 4.102 Å) is approximately 0.56% larger than that of bulk Ag (a ₀ = 4.079 Å). This 0.56% relaxation of the lattice constant corresponds to a temperature change of 298 K in thermal expansion, when estimated using the linear thermal expansion coefficient of 18.9×10⁻⁶ K⁻¹ at 300 K for bulk Ag. Note that a 298 K temperature change corresponds to a 25 meV change in thermal energy, which is significant when compared with the energy associated with lattice vibrations of Ag. Lattice relaxation is clearly revealed in the 12 and 16 nm Ag NPs. There are 30 unit cells in each crystallographic axis direction of the 12 nm Ag NP. The observation of a larger lattice constant for the 12 nm Ag NP than for the bulk Ag shows that lattice interaction in bulk Ag extends at least over 15 unit cells, which corresponds to a length of 6 nm. The effects from quantum confinement are insignificant for 12 nm Ag NPs at 300 K since the Kubo gap opening is only 0.13 meV, which is invisible at 300 K. It is the small size effect that governs the lattice relaxation in Ag NPs.

Fig. 6.4

Variations in lattice constant (open circles) and stress (open triangles) with particle diameter of Ag NPs. The solid curves indicate the results of fits to the expression listed in the plot

6.4.2 Electron Charge Density

It is remarkable to see that the small size effect significantly alters the distribution of the electron charge density (ECD) of silver. This is illustrated in the ECD contour plots of the (000) (Fig. 6.5) and (0, 0, 0.2) (Fig. 6.6) lattice planes for the 3.5 nm Ag NPs and 2 mm Ag ingots. These ECD maps were obtained by employing the GSAS program, starting with profile refinement of the X-ray diffraction patterns, followed by calculation of the inverse Fourier transforms of the structure factors to extract the ECD distribution. The ECD contour map of a specific plane was then obtained by slicing the electron density in the vicinity, including 0.025 Å below and above the lattice plane. The ECD along a specific crystallographic direction was then obtained by cutting the density map along the selective direction. The contour plots reveal an approximately spherically symmetric ECD around the lattice sites, but with distortion near the regions of contact between two neighboring atoms [Fig. 6.5b, d], reflecting the characteristics of metallic bonding in both 3.5 nm Ag NPs and 2 mm Ag ingots.

Fig. 6.5

Electron charge densities in (000) crystallographic plane of (a) 3.5 nm Ag NPs and (c) 2 mm Ag ingot, as inferred from X-ray diffraction data; the color bars are in units of e/ų. Contour plots of electron charge density in (000) crystallographic plane of (b) 3.5 nm Ag NPs and (d) 2 mm Ag ingot

Fig. 6.6

Electron charge densities in (0,0,0.2) crystallographic plane of (a) 3.5 nm Ag NPs and (c) 2 mm Ag ingot, as inferred from X-ray diffraction data. The color bars are in units of e/ų. Contour plots of electron charge density in (0,0,0.2) crystallographic plane of (b) 3.5 nm Ag NPs and (d) 2 mm Ag ingot

However, several distinct differences may be identified between the ECD of the 3.5 nm Ag NPs and the 2 mm Ag ingots. First, the ECDs around the lattice sites of the 3.5 nm Ag NPs are noticeably lower and less extensively distributed [Fig. 6.5a, c]. The amount of reduction is larger for smaller NPs; the reduction can be as large as 5% in the 3.5 nm NPs compared with that of the 2 mm Ag ingots [Fig. 6.7a, b]. In addition, the amount of change in the ECD upon reducing the particle size from 8 to 3.5 nm is significantly less than for a reduction from 2 mm to 8 nm, showing that quantum size effect plays a less important role than the small size effect does in renormalizing the electron charge distribution. This is understandable since quantum confinement renormalizes the band configuration near the Fermi level for the conduction electrons but has less of an effect for the core electrons. On the other hand, the ECD in the contact regions between two neighboring atoms of the NPs is considerably higher (Fig. 6.7). Apparently, a portion of the electron charges shifts from being near the lattice sites to the contact regions between two neighboring atoms. Second, the spherical ECD contours of the 3.5 nm Ag NPs extend from the lattice sites further into the contact regions of two neighboring atoms [Fig. 6.5b, d]. Third, the most pronounced differences appear near the regions of contact between two neighboring atoms. The dumbbell-shaped contours that appear in the contact regions of the two nearest neighboring atoms in the 2 mm Ag ingots [Fig. 6.5d] renormalize into elliptical contours in the 3.5 nm Ag NPs [Fig. 6.5b]. This characteristic is more clearly revealed in the ECD contours away from the lattice sites, as shown in Fig. 6.6. The ECD contours in the (0, 0, 0.2) lattice plane [Fig. 6.6b, d] of the 3.5 nm NPs are more densely distributed in the contact regions along the [110] crystallographic direction but much more loosely distributed in the contact regions along the [100] crystallographic direction. Fourth, the ECD distributions in the NPs are not evenly extended along all crystallographic directions but reveal less electronic connection with its neighbors along specific directions, such as along the [100] direction, while having a better connection along the others, such as along the [110] direction.

Fig. 6.7

Direct comparison of electron charge densities in (000) lattice plane along (a) [100] and (b) [110] crystallographic directions of 3.5 nm (dotted curve), 2 nm (dashed curve), and 8 nm (solid curve) Ag NPs at 7 K

6.4.3 Electron Charge Redistribution

It is clear that a reduction of the particle size to the nanometer scale can cause a significant change in the ECD distribution. These changes are better revealed in the difference density plots, where the electron density of the 2 mm ingot is subtracted from that of the 3.5 nm NP. Such difference density plots for the (000) and (0, 0, 0.2) crystallographic planes are illustrated in Figs. 6.8 and 6.9, respectively. The atomic positions with negative values of difference density represent the locations of lesser electron charges in the NP but are redistributed to the positions with positive values. The color-filled regions in Figs. 6.8 and 6.9 indicate the positions having a positive difference density. These positions can be more clearly seen in the projection of the difference density onto the lattice plane shown at the bottoms of Figs. 6.8 and 6.9. More electron charges in the NPs are found between the two nearest neighbors, but less around the lattice sites in the (000) plane (Fig. 6.8). The situation is different in the (0, 0, 0.2) plane, where a five-peak structure across the unit cell along the [110] crystallographic direction is seen in the difference pattern of the (0, 0, 0.2) plane (Fig. 6.9) but a three-peak structure is revealed in the (000) plane (Fig. 6.8). This spatially uneven change of the ECD over the crystallographic directions cannot be associated only with the redistribution of the s electrons but requires the redistribution of the d or p electrons as well.

Fig. 6.8

Difference in ECD in (000) lattice plane between 3.5 nm Ag assembly and 2 mm Ag ingot at 6 K. Color-filled regions indicate locations having a positive difference charge density, where the charge density of the NPs is higher than that of the 2 mm ingot. The projection of the ECD onto the lattice plane is shown at the bottom

Fig. 6.9

Difference in electron charge density in (0,0,0.2) lattice plane between 3.5 nm Ag assembly and 2 mm Ag ingot at 6 K. Color-filled regions indicate locations having a positive difference charge density, where the charge density of the NPs is higher than that of the 2 mm ingot. The projection of the ECD onto the lattice plane is shown at the bottom

It is known that the inner electrons in the core (1s to 4d electrons) of each Ag ion in a crystallized face-centered cubic structure extend from the lattice site to cover a spatial region with a radius of approximately 7.5% of a lattice unit, where the 4d orbital extends to the outermost area of the inner core region and the 5s orbital is slightly within. Interestingly, the electron density of the inner core is noticeably lower in the NPs, and this region of fewer electrons in the NPs extends into the 5s orbital. Remarkably, reducing the size of Ag to the nanometer scale results in more electrons being distributed in the central regions of the two nearest neighbors, up to a spatial region of approximately 10% of a lattice constant below and above the lattice plane. Further away from this the electron density in the NPs becomes less intense. It is clear that the spatially extended distribution of the electron charge in the NPs is not isotopically extended in all crystallographic directions, but rather a portion of the electrons shifts from specific regions to the others. The redistribution involves not only spherically distributed 5s electrons but also includes directional 4d electrons. It is known that although the band structure of Ag can be separated into 5 narrow 4d bands and one broad 5s band to accommodate the 11 outer electrons, at some values of wave vector all 6 electron bands are closer together [1]. Apparently, the disruption of lattice periodicity at the Ag NP surfaces results in a greater degree of mixture between the 4d and 5s bands and the electrons are distributed toward the center locations of the neighboring atoms, especially in between the nearest neighbors.

6.5 Superspin Magnetism

6.5.1 Spontaneous Magnetic Moment

Three components may be anticipated to appear in the magnetization of an Ag NP assembly: a Langevin component M _L that describes the alignment of the superspins of Ag NPs by the applied magnetic field H _a, a Brillouin component M_B from H _a-induced Zeeman splitting near the Fermi level that appears when the Kubo splitting from quantum confinement is significant, and a diamagnetic component M _D from the Lenz responses to the application of H _a. These components have all been observed in Au [35] and Cu [37] NPs. They are visible in the isothermal magnetization curves M(H _a) of the present Ag NP assemblies as well. Several features are seen in the isothermal M(H _a) curves of the representative 2.5 nm Ag NP assembly shown in Fig. 6.10. (1) In the low-H _a regime, M increases rapidly with increasing H _a, revealing the appearance of an M _L that becomes saturated at H _a ∼3 kOe; M _L is clearly visible even at 300 K; it appears that the thermal agitations at 300 K only slightly affect the strength of the superspins, showing a critical temperature that is much higher than 300 K for the superspins in 2.5 nm Ag NPs. (2) In addition to M _L being saturated above 3 kOe, at 2 K, M continues to increase with increasing H _a, showing the appearance of M _B. This component is largely reduced at 10 K, showing that the thermal populations from the down-spin state to the up-spin state have nearly decompensated for the H _a-induced magnetization. (3) Lenz diamagnetic responses are clearly revealed in the high-H _a regime in the M(H _a) curves above 15 K, such that M decreases linearly with increasing H _a. Stronger diamagnetic responses are seen at higher temperatures, reflecting that the mean square distance of the core electrons from the nucleus becomes larger at higher temperatures. Note that the thermal increase rate of the diamagnetic response becomes smaller as the temperature is increased.

Fig. 6.10

Field profile of magnetization of 2.5 nm Ag NP assembly, taken in field-increasing loops at nine representative temperatures. The Langevin profile is seen in the M(H _a) curves at all temperatures. The Lenz diamagnetic components are clearly revealed in the M(H _a) curves taken above 15 K. An additional Zeeman Brillouin component appears in the high H _a regime of the M(H _a) curves taken below 15 K. The solid curves indicate the results of fits for a Langevin profile plus a Brillouin profile plus a Lenz profile

A macroscopic amount of the monodispersed NP assembly is barely available. Results of size dispersion in the NP assembly must be accounted for when analyzing the M(H _a) curves measured for an NP assembly [46]. The solid curves in Fig. 6.10 indicate the results of the fits for M(H _a, T) = M _L(H _a, T) + M _B(H _a, T) + χ _D H _a, using the size distribution of the assembly obtained from the X-ray diffraction [solid curve in Fig. 6.2b] and assuming a log-normal type of particle moment dependency on the particle size (Eq. (6.8)), with αμ _pm, d _c, w, and χ_D being the fitting parameters. Unfortunately, the permeability α and maximum particle moment μ _pm cannot be separated in this fit since they are coupled parameters in the Langevin expression. Good agreement between the observations and fits is obtained at all the temperatures studied from 2 to 300 K. The size dependencies of the particle moments at various temperatures obtained from the fits are shown in Fig. 6.11. Note that αμ _p of Ag NPs with sizes other than 2.5 nm can also be extracted from the analysis, which is a direct consequence of the assumption made that the variation of superspin moment with particle diameter can be expressed by an analytical function. The intrinsic superspins of Ag NPs are represented by the T = 2 K curve (inset in Fig. 6.11), where thermally induced magnetization [47,48,49,50] does not severely affect the superspin moments. Accordingly, the maximum superspin moment of Ag will appear in the 2.6 nm NP with αμ _p = 50μ _B, and αμ _p drops to below 1μ _B for particles larger than 25 nm in diameter. We remark that the M(H _a) curves fit well to a Langevin profile without considering the size-dispersed nature of the assembly but gives αμ _p = 39μ _B at 2 K. This is the average αμ _p for the assembly, ignoring the uneven nature of the number fractions. The μ _p obtained when ignoring the size dispersion is 22% smaller.

Fig. 6.11

Size dependence of αμ _p obtained from M(H _a) curve of 2.5 nm Ag NP assembly at 2 K, where α is the dimensionless permeability and μ _p the average particle moment. The inset shows the curve at 2 K using an expanded scale for clarity of presentation

6.5.2 Thermally Induced Magnetization

It is interesting to see that the superspin moment μ _p of Ag NPs increases with increasing temperature for all sizes (Fig. 6.11). Generally speaking, the reduced coordination number and the cluster symmetry are the two fundamental factors for the onset of magnetism in small bare NPs. No sign of severe structural distortion is identified in the present face-centered cubic Ag NPs. The reduction of coordination number of the Ag ions on the particle surface, namely from the small size effect, is the main source for the development of superspins in Ag NPs. The electron charge redistribution that enhances the band mixture near the Fermi level, triggered by small size effect, has been discussed (Figs. 6.8 and 6.9). It is very likely that the developments of superspins in Ag NPs are closely linked to the enhanced band mixture near the Fermi level. However, it is difficult to account for the increase of the superspin moments by a factor of more than two orders of magnitude upon warming from 2 to 300 K (Fig. 6.11) owing solely to the thermally induced band mixture that may occur upon lattice expansion on warming.

Nevertheless, thermally induced magnetization [47,48,49,50] can be used to understand the extremely large increases of the superspin moment through thermal excitations. In this scenario, a ferrimagnetic-like alignment of the core macromoment m _c and the surface macromoment m _s is needed. This structure of separated macromoments for the core and surface ions can be justified since their coordination numbers are different. In addition, if the core and surface ions of an NP gather the same number of electrons, the Fermi energy of the surface electrons is then slightly higher than that of the core electrons because the surface ions are more closely packed owing to the appearance of surface stress, which deforms the surface of the NP into a curved one. Electron transfer from the surface region into the core can be anticipated for matching the Fermi energy of the two regions, which can result in noticeably different electron densities in the core and surface regions. This transfer of charges from the surface ions to the core has been found to be energetically favorable to stabilizing the core [49,50,51]. Thermal excitations of spin-precession modes in these ferrimagnetic-like NPs will result in a decrease in the difference between the moment directions of m _c and m _s , which in turn gives rise to an increase in μ _p [47, 52], as illustrated in Fig. 6.12.

Fig. 6.12

Schematic illustration of configurations of surface and core superspin moments at finite temperatures

6.5.3 Surface and Core Saturation Magnetizations

The intrinsic magnetic moments of NPs are expressed in the Langevin magnetization (Eq. (6.8)), where the saturation magnetization M _S may be obtained by

$$ {M}_{\mathrm{S}}=\sum_i{n}_i{\mu}_{\mathrm{p}i}, $$

(6.10)

using the parameters n _i and μ _pi extracted from the fits of the X-ray diffraction pattern (Fig. 6.2) and M(H _a) curves (Fig. 6.10). This M _S marks the saturation magnetization of the NP assembly, where the size-dispersed nature of the assembly has been accounted for. M _S will in general be different from one assembly to the next since every NP assembly has its own size-dispersion characteristics. Two components are clearly revealed in the temperature dependence of M _S of the 2.5 nm Ag NP assembly, as illustrated in Fig. 6.13. M _S drops rapidly with increasing temperature below 50 K, above which the thermal reduction rate of M _S is largely reduced. Interestingly, M _S reduces by only 2% upon warming from 50 to 300 K, showing that the transition temperature of the superspin is significantly higher than 300 K. The large difference observed in the thermal reduction rates below and above 50 K shows that they are associated with different origins. It is known that the coordination numbers of the Ag ions on the surface of an NP are different from those in the core. It can be anticipated that the superspin moments developed on the surface of an Ag NP will be different in strength from those developed in the core. In addition, it can be anticipated that the superspin moments on the surface will be weaker than those in the core, leading to a higher thermal reduction rate and a lower transition temperature for the surface superspins than for the core superspins. It is likely that the thermal profile of M _S at low temperature mainly reflects the thermal characteristics of the surface superspins, whereas the high-temperature profile is linked to the Ag ions in the core. The sharp turn at 50 K in the M _S(T) curve (Fig. 6.13) separates the effects resulting from the surface superspins from those of the core superspins.

Fig. 6.13

Temperature dependencies of saturation spontaneous magnetization of 2.5 nm Ag NP assembly. The solid curves indicate the results of fits for the expression listed in the plot

It has been suggested that the thermal excitations of surface superspins can be described by the exponential reduction profile of exp(−T/T _f) for the magnetization characterized by the surface superspin freezing temperature T _f [53, 54]. On the other hand, the thermal excitations of core superspins are frequently described by taking the power law of [1 − (T/T _C)^b] for magnetization, where T _C is the transition temperature and the exponent b is linked to the type of spin ordering [55]. Accounting for the contributions from the surface superspins as well as from the core superspins, the saturation magnetization can be expressed as

$$ {M}_{\mathrm{S}}(T)={M}_{\mathrm{S}0} \exp \left(-\frac{T}{T_{\mathrm{f}}}\right)+{M}_{\mathrm{C}0}\left[1-{\left(\frac{T}{T_{\mathrm{C}}}\right)}^b\right], $$

(6.11)

where M _S0 and M _C0 are the saturation magnetizations of the surface and core superspins at zero temperature. In this expression the saturation magnetization at zero temperature is M _S = M _S0 + M _C0. Unfortunately, the nearly flat thermal reduction rate observed in M _S(T) above 50 K prevents conclusive extraction of T _C and b for the core superspins in the 2.5 nm Ag NP assembly. The solid curve in Fig. 6.13 indicates the results of the fits of M _S(T) for Eq. (6.11), giving M _S0 = 0.0057(3) emu/g, T _f = 10(1) K, and M _C0 = 0.0329(2). Note that we choose not to call the values obtained for T _C and b since large uncertainties result for the two parameters as the direct results of lack of data at higher temperatures.

A field-induced magnetization M _B as large as 0.13 emu/g is revealed for the 2.5 nm Ag NP assembly at 2 K (Fig. 6.14). This M _B at 2 K is 3.4 times larger than the saturation magnetization M _S. M _B becomes hard to detect at 15 K, which indicates that at this temperature the thermal population from the down-spin states onto the up-spin states has decompensated for the Zeeman magnetization induced by H _a. It is known that the thermal reductions of M _B are linked to the creation of thermal magnons. The large reduction rate of M _B upon warming at low temperatures indicates small excitation energies for the associated thermal magnons.

Fig. 6.14

Temperature dependence of Brillouin saturation magnetization of 2.5 nm Ag NP assembly. The Brillouin component disappears above 15 K. The solid curve is a guide for the eye only

6.5.4 Size Dependence

It is clear that both the intrinsic (Langevin) and field-induced Zeeman (Brillouin) magnetizations depend strongly on the particle size. The critical particle size for the appearance of field-induced Zeeman magnetization can be estimated using the Kubo formalism (Eq. (6.1)). Unfortunately, there is no theoretical basis available for estimating the critical particle size for the development of spontaneous magnetic moments in Ag NPs. Experimentally, the dependency of the superspin moment on particle diameter μ _p(d) obtained from the M(H _a) curves of the 2.5 nm NP assembly (Fig. 6.11) shows that the maximum superspin moment will appear in 2.6 nm Ag particles. Figure 6.15 displays the M(H _a) curves of four representative Ag NP assemblies at 2 K. Comparing the M(H _a) curves of the 2 and 2.5 nm NP assemblies reveals that the particle superspin moment (dM/dH _a in the low-field regime) of the 2.5 nm NP assembly is larger, while the Zeeman moment (dM/dH _a in the high-field regime) of the 2 nm NP assembly is larger. A small but visible Zeeman moment can still be seen in the 8 nm NP assembly at 2 K (inset in Fig. 6.15). A Kubo gap of Δ = 0.45 meV is expected for the 8 nm Ag NPs when estimated using the Kubo formula (Eq. (6.1)), assuming the same electron density as for bulk Ag for the NPs. Apparently, the thermal energy at 2 K may be enough to equally populate the up-spin and down-spin states in the 8 nm Ag NPs.

Fig. 6.15

Isothermal M(H _a) curves of four representative Ag NP assemblies at 2 K. The inset shows the 4.5 and 8 nm assemblies using an expanded scale for clarity of presentation. Field-induced Brillouin magnetization is revealed even in the 8 nm assembly. The solid curves indicate the results of fits for the expression discussed in the text

The magnetization, on the other hand, indicates the total magnetic moment per unit mass of the assembly, where both the superspin moments (Eq. (6.9)) and the numbers of NPs (Eq. (6.5)) in the assembly must be accounted for. Generally speaking, the magnetizations of two multidispersed NP assemblies of the same mean particle diameter but having different size distributions will be different. The intrinsic magnetic moments of ultrasmall Ag NPs can still be seen even at 300 K (Fig. 6.16), where larger Lenz diamagnetic responses for the 2.5 nm assembly than for the 2 nm assembly are also visible. The solid curves in Fig. 6.16 indicate the results of the fits for M(H _a, T) = M _L(H _a, T) + χ _D H _a. Good agreements between the observations and the fits are obtained for all sets of NP assemblies. It is remarkable to find that the size dependencies of the superspin moment thus obtained from the four sets of NP assemblies agree very well. A direct comparison of the representative αμ _p(d _i ) curves obtained from the M(H _a) curves of 2.5 and 8 nm assemblies at 300 K can be made in Fig. 6.17. The superspin moment will be reduced to below 350μ _B in the 20 nm Ag NPs, which is barely detectable using conventional means.

Fig. 6.16.

Isothermal M(H _a) curves of four representative Ag NP assemblies at 300 K. Spontaneous magnetization is clearly revealed in all assemblies. The solid curves indicate the results of fits for the expression discussed in the text

Fig. 6.17

Direct comparison of size dependence of μ _p obtained from M(H _a) curves of 2.5 nm (solid curve), 4.5 nm (dashed curve), and 5 nm (dotted curve) particle assembly at 300 K. The three μ _p(d) curves match reasonably well

6.6 Concluding Remarks

In this chapter, we focused on identifying the intrinsic magnetic moments that developed in nanosized bare Ag NPs. Eleven sets of bare Ag NP assemblies were fabricated employing the gas condensation method, adopting a physical process involving the self-nucleation of atoms to form capping-free Ag NPs. The mean particle diameters and size distributions of the NP assemblies were extracted from the line profiles of the X-ray diffraction peaks. Lattice relaxation is clearly revealed in the Ag NPs with diameters smaller than 12 nm, reflecting that lattice interaction in bulk Ag extends to at least over 6 nm, which corresponds to 15 unit cells long. It is the small size effect that governs the lattice relaxation in Ag NPs since the Kubo gap opening near the Fermi level of a 12 nm Ag particle is only 0.13 meV, which is invisible at 300 K with a thermal energy of 25 meV. The disruption of lattice periodicity at the particle surface causes a significant change in the distribution of the electron charge of the silver, in such a way that the electron charges are more extensively distributed toward the central regions of two nearest neighbors. The extension of the electron charge distribution is not isotopic in all crystallographic directions, revealing that redistribution involves not only the spherically distributed 5s electrons but also includes the directional 4d electrons. Apparently, the small size effect results in a higher degree of mixture between the 4d and 5s bands of the ultrasmall silver NPs.

The diamagnetic responses from the filled narrow d band that are stronger than the Pauli paramagnetic responses from the half-filled free electron s band in Cu, Ag, and Au give rise to a diamagnetic character for these noble-metal elements in their bulk forms. A spontaneous magnetic moment, described using particle superspin, develops in particles when their sizes are reduced to several nanometers in diameter. The isothermal magnetization of superspins can be described by the Langevin field profile. Contributions from the differently sized particles in the NP assemblies to the magnetization are considered when analyzing the M(H _a) curves, which allows us to extract the dependency of the particle moment on the particle diameter μ _p(d). The μ _p(d) curves obtained from different sets of Ag NP assemblies match nicely, showing that the analysis is reasonably sound. Accordingly, the maximum superspin moment of Ag will appear in 2.6 nm particle with a superspin moment of αμ _p = 139 μ_B at 2 K. Thermal variation of the saturation magnetization of the superspin moments displays very different thermal reduction rates at temperatures below and above 50 K, revealing that the superspin moments that develop on the surface of an Ag NP are different in strength from those developed in the core. In addition, magnetic field–induced Zeeman magnetization from the quantum confined Kubo gap opening near the Fermi level was also observed in Ag NPs smaller than 8 nm in diameter. Isothermal Zeeman magnetization can be described by the Brillouin field profile. The large reduction rate of Zeeman magnetization upon warming indicates small excitation energies for the associated thermal magnons.

The general picture established so far for the development of magnetic moments in polymer-capped Au NPs is based on the occurrence of electron charge transfer, triggered by the strong chemical affinity between the capping molecules and Au atoms. This creates localized 5d holes in the surface region of the NP. Ferromagnetism is thus associated only with the atoms on the surface. In this picture, coupling between the capping molecules and atoms on the particle surface is a prerequisite for the appearance of spin-polarized moments in noble-metal NPs. The present study demonstrates further that magnetic moments do develop in bare Ag NPs, and both surface atoms and core atoms contribute to superspin moments. Clearly, the sources for the development of magnetic moments in capping-free bare Ag NPs are fundamentally different from those developed in polymer-capped NPs. It is known that if the surface and core atoms of an NP gather the same number of electrons, the Fermi energy of the surface electrons will be higher than that of the core electrons because the surface atoms are more closely packed. Electron transfer from the surface region to the core can be anticipated for matching the Fermi energy of the two regions from the small size effect. Although the superspin moments developed in Ag NPs are relatively weak, localized 4d holes do exist, which reveals ferromagnetism. The present observations of the existence of superspins in Ag NPs involve both conduction 5s electrons and localized 4d holes. This can happen only when the 5s and 4d bands in Ag NPs are energetically close to each other.