New Integrality Gap Results for the Firefighters Problem on Trees

Abstract

In the firefighter problem on trees, we are given a tree $G=(V,E)$ together with a vertex $s \in V$ where the fire starts spreading. At each time step, the firefighters can pick one vertex while the fire spreads from burning vertices to all their neighbors that have not been picked. The process stops when the fire can no longer spread. The objective is to find a strategy that maximizes the total number of vertices that do not burn. This is a simple mathematical model, introduced in 1995, that abstracts the spreading nature of, for instance, fire, viruses, and ideas. The firefighter problem is NP-hard and admits a $(1-1/e)$ approximation via LP rounding. Recently, a PTAS was announced in [1].(The $(1-1/e)$ approximation remained the best until very recently when Adjiashvili et al. [1] showed a PTAS. Their PTAS does not bound the LP gap.)

The goal of this paper is to develop better understanding on the power of LP relaxations for the firefighter problem. We first show a matching lower bound of $(1-1/e+\epsilon )$ on the integrality gap of the canonical LP. This result relies on a powerful combinatorial gadget that can be used to derive integrality gap results in other related settings. Next, we consider the canonical LP augmented with simple additional constraints (as suggested by Hartke). We provide several evidences that these constraints improve the integrality gap of the canonical LP: (i) Extreme points of the new LP are integral for some known tractable instances and (ii) A natural family of instances that are bad for the canonical LP admits an improved approximation algorithm via the new LP. We conclude by presenting a 5 / 6 integrality gap instance for the new LP.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Consider the following graph-theoretic model that abstracts the fire spreading process: We are given graph $G=(V,E)$ together with the source vertex s where the fire starts. At each time step, we are allowed to pick some vertices in the graph to be saved, and the fire spreads from burning vertices to their neighbors that have not been saved so far. The process terminates when the fire cannot spread any further. This model was introduced in 1995 [13] and has been used extensively by researchers in several fields as an abstraction of epidemic propagation.

There are two important variants of the firefighters problem. (i) In the maximization variant (Max-FF), we are given graph G and source s, and we are allowed to pick one vertex per time step. The objective is to maximize the number of vertices that do not burn. And (ii) In the minimization variant (Min-FF), we are given a graph G, a source s, and a terminal set ${\mathcal {X}}\subseteq V(G)$, and we are allowed to pick b vertices per time step. The goal is to save all terminals in ${\mathcal {X}}$, while minimizing the budget b.

In this paper, we focus on the Max-FF problem. The problem is $n^{1-\epsilon }$ hard to approximate in general graphs [2], so there is no hope to obtain any reasonable approximation guarantee. Past research, however, has focused on sparse graphs such as trees or grids. Much better approximation algorithms are known on trees: The problem is NP-hard [15] even on trees of degree at most three, but it admits a $(1-1/e)$ approximation algorithm. For more than a decade [2, 5, 6, 10, 14, 15], there was no progress on this approximability status of this problem, until a PTAS was recently discovered [1].

Besides the motivation of studying epidemic propagation, the firefighter problem and its variants are interesting due to their connections to other classical optimization problems:

• (Set cover) The firefighter problem is a special case of the maximum coverage problem with group budget constraint (MCG) [7]: Given a collection of sets ${\mathcal {S}}= \{S_1,\ldots , S_m\}: S_i \subseteq X$, together with group constraints, i.e. a partition of ${\mathcal {S}}$ into groups $G_1,\ldots , G_{\ell }$, we are interested in choosing one set from each group in a way that maximizes the total number of elements covered, i.e. a feasible solution is a subset ${\mathcal {S}}' \subseteq {\mathcal {S}}$ where $|{\mathcal {S}}' \cap G_j| \le 1$ for every j, and $|\bigcup _{S_i \in {\mathcal {S}}'} S_i|$ is maximized. It is not hard to see that Max-FF is a special case of MCG. We refer the readers to the discussion by Chekuri and Kumar [7] for more applications of MCG.

• (Cut) In a standard minimum node-cut problem, we are given a graph G together with a source-sink pair $s,t \in V(G)$. Our goal is to find a collection of nodes $V' \subseteq V(G)$ such that $G \setminus V'$ has s and t in distinct connected components. Anshelevich et al. [2] discussed that the firefighters’ solution can be seen as a “cut-over-time” in which the cut must be produced gradually over many timesteps. That is, in each time step t, the algorithm is allowed to choose vertex set $V'_t$ to remove from the graph G, and again the final goal is to “disconnect” s from t.¹ This cut-over-time problem is exactly equivalent to the minimization variant of the firefighter problem. We refer to [2] for more details about this equivalence.

1.1 Our Contributions

In this paper, we are interested in developing a better understanding of the Max-FF problem from the perspective of LP relaxation. The canonical LP relaxation has been used to obtain the known $(1-1/e)$ approximation algorithm via straightforward independent LP rounding (each node is picked independently with probability proportional to its LP-value). So far, it was not clear whether an improvement was possible via this LP, for instance, via sophisticated dependent rounding schemes.² Indeed, for the corresponding minimization variant, Min-FF, Chalermsook and Chuzhoy designed a dependent rounding scheme for the canonical LP in order to obtain $O(\log ^* n)$ approximation algorithm, improving upon an $O(\log n)$ approximation obtained via independent LP rounding. In this paper, we are interested in studying this potential improvement for Max-FF.

Our first result refutes such possibility for Max-FF: we show that the integrality gap of the standard LP relaxation can be arbitrarily close to $(1-1/e)$.

Theorem 1

For any $\epsilon >0$, there is an instance (G, s) (whose size depends on $\epsilon$) such that the ratio between optimal integral solution and fractional one is at most $(1- 1/e+ \epsilon )$.

Our techniques rely on a powerful combinatorial gadget that can be used to prove integrality gap results in some other settings studied in the literature. In particular, in the b-Max-FF problem, the firefighters can pick up to b vertices per time step, and the goal is to maximize the number of saved vertices. We provide an integrality gap of $(1-1/e)$ for the b-Max-FF problem for every constant $b \in {\mathbb N}$, thus matching the algorithmic result of [9]. In the setting where an input tree has degree at most $d \in [4,\infty )$, we show an integrality gap result of $(1-1/e + O(1/\sqrt{d}))$. The best known algorithmic result in this setting was previously a $(1-1/e+ \varOmega (1/d))$ approximation due to [14].

Motivated by the aforementioned negative results, we search for a stronger LP relaxation for the problem. We consider adding a set of valid linear inequalities, as suggested by Hartke [12]. We show the following evidences that the new LP is a stronger relaxation than the canonical LP.

• Any extreme point of the new LP is integral for the tractable instances studied by Finbow and MacGillivray [11]. In contrast, we argue that the canonical LP does not satisfy this integrality property of extreme points.

• A family of instances, capturing the integrality gap instances of Theorem 1, admits a better than $(1-1/e)$ approximation algorithm via the new LP.

• When the LP solution is near-integral, e.g. for half-integral solutions, the new LP is provably better than the old one.

Our results are the first rigorous evidences that Hartke’s constraints lead to improvements upon the canonical LP. All the aforementioned algorithmic results exploit the new LP constraints in dependent LP rounding procedures. In particular, we propose a two-phase dependent rounding algorithm, which can be used in deriving the second and third results. We believe the new LP has an integrality gap strictly better than $(1-1/e)$, but we are unable to analyze it.

Finally, we show a limitation of the new LP by presenting a family of instances, whose integrality gap can be arbitrarily close to 5 / 6. This improves the known integrality gap ratio [12], and puts the integrality gap answer somewhere between $(1-1/e)$ and 5 / 6. Closing this gap is, in our opinion, an interesting open question.

Organization: In Sect. 2, we formally define the problem and present the LP relaxation. In Sect. 3, we present the bad integrality gap instances. We present the LP augmented with Hartke’s constraints in Sect. 4 and discuss the relevant evidences of its power in comparison to the canonical LP. Some proofs are omitted for space constraint, and are presented in the full version.

Related Results: King and MacGillivray showed that the firefighter problem on trees is solvable in polynomial time if the input tree has degree at most three, with the fire starting at a degree-2 vertex. From exponential time algorithm’s perspective, Cai et al. showed $2^{O(\sqrt{n} \log n)}$ time, exact algorithm. The discrete mathematics community pays particularly high attention to the firefighter problem on grids [10, 16], and there has also been some work on infinite graphs [13].

The problem also received a lot of attention from the parameterized complexity perspectives [3, 5, 8] and on many special cases, e.g., when the tree has bounded pathwidth [8] and on bounded degree graphs [4, 8].

Recent Update: Very recently, Adjiashvili et al. [1] showed a polynomial time approximation scheme (PTAS) for the Max-FF problem, therefore settling the approximability status. Their results, however, do not bound the LP integrality gap. We believe that the integrality gap questions are interesting despite the known approximation guarantees.

2 Preliminaries

A formal definition of the problem is as follows. We are given a graph G and a source vertex s where the fire starts spreading. A strategy is described by a collection of vertices ${\mathcal {U}}= \{u_{t}\}_{t=1}^n$ where $u_t \in V(G)$ is the vertex picked by firefighters at time t. We say that a vertex $u \in V(G)$ is saved by the strategy ${\mathcal {U}}$ if for each path $P=(s=v_0,\ldots , v_z =u)$ from s to u, we have $v_i \in \{u_1,\ldots , u_{i}\}$ for some $i=1,\ldots , z$. A vertex v not saved by ${\mathcal {U}}$ is said to be a burning vertex. The objective of the problem is to compute ${\mathcal {U}}$ so as to maximize the total number of saved vertices. Denote by $\text{ OPT }(G,s)$ the number of vertices saved by an optimal solution.

When G is a tree, we think of G as being partitioned into layers $L_1,\ldots , L_{\lambda }$ where $\lambda$ is the height of the tree, and $L_i$ contains vertices whose distance is exactly i from s. Every strategy has the following structure.

Proposition 1

Consider the firefighters problem’s instance (G, s) where G is a tree. Let ${\mathcal {U}}=\{u_1,\ldots , u_n\}$ be any strategy. Then there is another strategy ${\mathcal {U}}'=\{u'_t\}$ where $u'_t$ belongs to layer t in G, and ${\mathcal {U}}'$ saves at least as many vertices as ${\mathcal {U}}$ does.

We remark that this structural result holds only when G is a tree.

LP Relaxation: This paper focuses on the linear programming aspect of the problem. For any vertex v, let $P_v$ denote the (unique) path from s to v, and let $T_v$ denote the subtree rooted at v. A natural LP relaxation is denoted by (LP-1): We have variable $x_v$ indicating whether v is picked by the solution, and $y_v$ indicating whether v is saved.

Let $\mathsf{LP}(T,s)$ denote the optimal fractional LP value for an instance (T, s). The integrality gap $\mathsf{gap}(T,s)$ of the instance (T, s) is defined as $\mathsf{gap}(T,s) = \mathsf{OPT}(T,s)/\mathsf{LP}(T,s)$. The integrality gap of the LP is defined as $\inf _T \mathsf{gap}(T, s)$.

Firefighters with Terminals: We consider a more general variant of the problem, where we are only interested in saving a subset ${\mathcal {X}}$ of vertices, which we call terminals. The goal is now to maximize the number of saved terminals. An LP formulation of this problem, given an instance $(T,v, {\mathcal {X}})$, is denoted by (LP-2). The following lemma argues that these two variants are “equivalent” from the perspectives of LP relaxation.

Lemma 1

Let $(T, {\mathcal {X}}, s)$, with $|{\mathcal {X}}| > 0$, be an input for the terminal firefighters problem that gives an integrality gap of $\gamma$ for (LP-2), and that the value of the fractional optimal solution is at least 1. Then, for any $\epsilon >0$, there is an instance $(T',s')$ that gives an integrality gap of $\gamma + \epsilon$ for (LP-1).

We will, from now on, focus on studying the integrality gap of (LP-2).

3 Integrality Gap of (LP-2)

We first discuss the integrality gap of (LP-2) for a general tree. We use the following combinatorial gadget.

Gadget: A $(M, k, \delta )$-good gadget is a collection of trees ${\mathcal T}= \{T_1,\ldots , T_M\}$, with roots $r_1, \ldots , r_M$ where $r_i$ is a root of $T_i$, and a subset ${\mathcal {S}}\subseteq \bigcup V(T_i)$ that satisfy the following properties:

• (Uniform depth) We think of these trees as having layers $L_0,L_1,\ldots , L_h$, where $L_j$ is the union over all trees of all vertices at layer j and $L_0 = \{r_1, \ldots , r_m\}$. All leaves are in the same layer $L_h$.

• (LP-friendly) For any layer $L_j$, $j\ge 1$, we have $|{\mathcal {S}}\cap L_j| \le k$ (and $|{\mathcal {S}}\cap L_0| = 0$). Moreover, for any tree $T_i$ and a leaf $v \in V(T_i)$, the unique path from $r_i$ to v must contain exactly one vertex in ${\mathcal {S}}$.

• (Integrally adversarial) Let ${\mathcal {B}}\subseteq \left\{ r_1,\ldots , r_M \right\}$ be any subset of roots. Consider a subset of vertices ${\mathcal {U}}= \{u_j\}_{j=1}^h$ such that $u_j \in L_j$. For $r_i \in {\mathcal {B}}$ and a leaf $v \in L_h\cap V(T_i)$, we say that v is $({\mathcal {U}}, {\mathcal {B}})$-risky if the unique path from $r_i$ to v does not contain any vertex in ${\mathcal {U}}$. There must be at least $(1-1/k - \delta ) \frac{|{\mathcal {B}}|}{M} |L_h|$ vertices in $L_h$ that are $({\mathcal {U}},{\mathcal {B}})$-risky, for all choices of ${\mathcal {B}}$ and ${\mathcal {U}}$.

We say that vertices in ${\mathcal {S}}$ are special and all other vertices are regular.

Lemma 2

For any integers $k\ge 2$, $M \ge 1$, and any real number $\delta >0$, a $(M,k ,\delta )$-good gadget exists. Moreover, the gadget contains at most $(k/\delta )^{O(M)}$ vertices.

We first show how to use this lemma to derive our final construction. The proof of the lemma follows later.

Construction: Our construction proceeds in k phases, and we will define it inductively. The first phase of the construction is simply a $(1,k,\delta )$-good gadget. Now, assume that we have constructed the instance up to phase q. Let $l_1,\ldots , l_{M_q} \in L_{\alpha _p}$ be the leaves after the construction of phase q that all lie in layer $\alpha _q$. In phase $q+1$, we take the $(M_q, k, \delta )$-good gadget $({\mathcal T}_q, \{r_q\},{\mathcal {S}}_q)$; recall that such a gadget consists of $M_q$ trees. For each $i =1,\ldots , M_q$, we unify each root $r_i$ with the leaf $l_i$. This completes the description of the construction.

Denote by $\bar{{\mathcal {S}}}_q= \bigcup _{q' \le q} {\mathcal {S}}_{q'}$ the set of all special vertices in the first q phases. After phase q, we argue that our construction satisfies the following properties:

• All leaves are in the same layer $\alpha _q$.

• For every layer $L_j$, $|L_j \cap \bar{{\mathcal {S}}}_q| \le k$. For every path P from the root to $v \in L_{\alpha _i}$, $|P \cap \bar{{\mathcal {S}}}_q| = q$.

• For any integral solution ${\mathcal {U}}$, at least $|L_{\alpha _q}| \left( \left( 1-1/k\right) ^q-q\delta \right)$ vertices of $L_{\alpha _q}$ burn.

It is clear from the construction that the leaves after phase q are all in the same layer. As to the second property, the properties of the gadget ensure that there are at most k special vertices per layer. Moreover, consider each path P from the root to some vertex $v \in L_{\alpha _{q+1}}$. We can split this path into two parts $P = P' \cup P''$ where $P'$ starts from the root and ends at some $v' \in L_{\alpha _{q}}$, and $P''$ starts at $v'$ and ends at v. By the induction hypothesis, $|P'\cap \bar{S}_{q}| = q$ and the second property of the gadget guarantees that $|P'' \cap {\mathcal {S}}_{q+1}| = 1$.

To prove the final property, consider a solution ${\mathcal {U}}=\{u_1,\ldots , u_{\alpha _{q+1}}\}$, which can be seen as ${\mathcal {U}}'\,\cup \,{\mathcal {U}}''$ where ${\mathcal {U}}' = \{u_1,\ldots , u_{\alpha _q}\}$ and ${\mathcal {U}}'' = \{u_{\alpha _{q}+1}, \ldots , u_{\alpha _{q+1}}\}$. By the induction hypothesis, we have that at least $\left( (1-1/k)^{q} - q \delta \right) |L_{\alpha _q}|$ vertices in $L_{\alpha _q}$ burn; denote these burning vertices by ${\mathcal {B}}$. The third property of the gadget will ensure that at least $(1-1/k- \delta )\frac{|{\mathcal {B}}|}{M_{q}} |L_{\alpha _{q+1}}|$ vertices in $L_{\alpha _{q+1}}$ must be $({\mathcal {U}}'', {\mathcal {B}})$-risky. For each risky vertex $v \in L_{\alpha _{q+1}}$, a unique path from the root to $v' \in {\mathcal {B}}$ does not contain any vertex in ${\mathcal {U}}'$, and also the path from $v'$ to v does not contain a vertex in ${\mathcal {U}}''$ (due to the fact that it is $({\mathcal {U}}'', {\mathcal {B}})$-risky.) This implies that such vertex v must burn. Therefore, the fraction of burning vertices in layer $L_{\alpha _{q+1}}$ is at least $(1-1/k-\delta )|{\mathcal {B}}|/M_q \ge (1-1/k - \delta )((1-1/k)^q- q\delta )$, by induction hypothesis. This number is at least $(1-1/k)^{q+1} - (q+1) \delta$, maintaining the invariant.

After the construction of all k phases, the leaves are designated as the terminals ${\mathcal {X}}$. Also, $M_{q+1} \le (k/\delta )^{2M_q}$, which means that, after k phases, $M_k$ is at most a tower function of $(k/\delta )^2$, that is, $(k/\delta )^{2(k/\delta )^{\cdots }}$ with $k-1$ such exponentiations. The total size of the construction is $\sum _q (k/\delta )^{2M_q} \le (k/\delta )^{2M_k} = O(M_{k+1})$.

For an example construction ($k=2$), refer to the full version.

Theorem 2

A fractional solution, that assigns $x_v = 1/k$ to each special vertex v, saves every terminal. On the other hand, any integral solution can save at most a fraction of $1-(1-1/k)^k + \epsilon$.

3.1 Proof of Lemma 2

We now show that the $(M, k,\delta )$-good gadget exists for any value of $M \in {\mathbb N}$, $k \in {\mathbb N}, k\ge 2$ and $\delta \in {\mathbb R}_{>0}$. We first describe the construction and then show that it has the desired properties.

Construction: Throughout the construction, we use a structure which we call spider. A spider is a tree in which every node except the root has at most one child. If a node has no children (i. e. a leaf), we call it a foot of the spider. We call the paths from the root to each foot the legs of the spider.

Let $D=\lceil 4/\delta \rceil$. For each $i = 1,\ldots , M$, the tree $T_i$ is constructed as follows. We have a spider rooted at $r_i$ that contains $kD^{i-1}$ legs. Its feet are in $D^{i-1}$ consecutive layers, starting at layer $\alpha _i = 1 + \sum _{j<i}D^{j-1}$; each such layer has k feet. Denote by ${\mathcal {S}}^{(i)}$ the feet of these spiders. Next, for each vertex $v \in {\mathcal {S}}^{(i)}$, we have a spider rooted at v, having $D^{2M-i+1}$ feet, all of which belong to layer $\alpha =1 + \sum _{j\le M}D^{j-1}$. The set ${\mathcal {S}}$ is defined as ${\mathcal {S}}= \bigcup _{i=1}^M {\mathcal {S}}^{(i)}$. This concludes the construction. We will use the following observation:

Observation 1

For each root $r_i$, the number of leaves of $T_i$ is $k D^{2M}$.

Analysis: We now prove that the above gadget is $(M, k,\delta )$-good. The construction ensures that all leaves are in the same layer $L_{\alpha }$.

The second property also follows obviously from the construction: For $i \ne i'$, we have that ${\mathcal {S}}^{(i)} \cap {\mathcal {S}}^{(i')} = \emptyset$, and that each layer contains exactly k vertices from ${\mathcal {S}}^{(i)}$. Moreover, any path from $r_i$ to the leaf of $T_i$ must go through a vertex in ${\mathcal {S}}^{(i)}$.

The third and final property is established by the following two lemmas.

Lemma 3

For any $r_i \in {\mathcal {B}}$ and any subset of vertices ${\mathcal {U}}= \{u_j\}_{j=1}^h$ such that $u_j \in L_j$, a fraction of at least $(1-1/k-2/D)$ of ${\mathcal {S}}^{(i)}$ are $({\mathcal {U}},{\mathcal {B}})$-risky.

Lemma 4

Let $v \in {\mathcal {S}}^{(i)}$ that is $({\mathcal {U}}, {\mathcal {B}})$-risky. Then at least $(1-2/D)$ fraction of descendants of v in $L_{\alpha }$ must be $({\mathcal {U}}, {\mathcal {B}})$-risky.

Combining the above two lemmas, for each $r_i \in {\mathcal {B}}$, the fraction of leaves of $T_i$ that are $({\mathcal {U}}, {\mathcal {B}})$-risky are at least $(1- 1/k- 2/D)(1-2/D) \ge (1-1/k - 4/D)$. Therefore, the total number of such leaves, over all trees in ${\mathcal T}$, are $(1- 1/k - \delta )|{\mathcal {B}}||L_{\alpha }|/M$.

We extend the construction to other settings in the full version.

4 Hartke’s Constraints

Due to the integrality gap result in the previous section, there is no hope to improve the best known algorithms via the canonical LP relaxation. Hartke [12] suggested adding the following constraints to narrow down the integrality gap of the LP.

$$ \sum _{ u\in P_v \cup (T_v \cap L_j)} x_u \le 1 \text{ for } \text{ each } \text{ vertex } v \in V(T) \text{ and } \text{ layer } L_j \text{ below } \text{ the } \text{ layer } \text{ of } \text{ v } $$

We write the new LP with these constraints below:

Proposition 2

Given the values $\left\{ x_v \right\} _{v \in V(T)}$ that satisfy the first set of constraints, then the solution (x, y) defined by $y_v = \sum _{u \in P_v} x_v$ is feasible for (LP’) and at least as good as any other feasible $(x,y')$.

In this section, we study the power of this LP and provide three evidences that it may be stronger than (LP-1).

4.1 New Properties of Extreme Points

In this section, we show that Finbow et al. tractable instances [11] admit a polynomial time exact algorithm via (LP’) (in fact, any optimal extreme point for (LP’) is integral.) In contrast, we show that (LP-1) contains an extreme point that is not integral.

We first present the following structural lemma.

Lemma 5

Let $(\mathbf{x},\mathbf{y})$ be an optimal extreme point for (LP’) on instance T rooted at s. Suppose s has two children, denoted by a and b. Then $x_a, x_b \in \left\{ 0,1 \right\}$.

Finbow et al. Instances: In this instance, the tree has degree at most 3 and the root has degree 2. Finbow et al. [11] showed that this is polynomial time solvable.

Theorem 3

Let (T, s) be an input instance where T has degree at most 3 and s has degree two. Let (x, y) be a feasible fractional solution for (LP’). Then there is a polynomial time algorithm that saves at least $\sum _{v \in V(T)} y_v$ vertices.

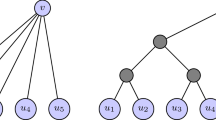
Bad Instance for (LP-1): We show in Fig. 1 a Finbow et al. instance as well as a solution for (LP-1) that is optimal and an extreme point, but not integral.

Fig. 1.

Instance with a non-integral extreme point for (LP-1). Gray vertices: $x_v=1/2$; otherwise: $x_v = 0$.

4.2 Rounding 1 / 2-Integral Solutions

We say that the LP solution (x, y) is (1 / k)-integral if, for each v, we have $x_v = r_v/k$ for some integer $r_v \in \{0,\ldots ,k\}$. By standard LP theory, one can assume that the LP solution is (1 / k)-integral for some polynomially large integer k.

In this section, we consider the case when $k=2$ (1 / 2-integral LP solutions). From Theorem 2, (LP-1) is not strong enough to obtain a $3/4+\epsilon$ approximation algorithm, for any $\epsilon > 0$. Here, we show a 5 / 6 approximation algorithm based on rounding (LP’).

Theorem 4

Given a solution (x, y) for (LP’) that is 1 / 2-integral, there is a polynomial time algorithm that produces a solution of cost $5/6\,\sum _{v \in V(T)} y_v$.

We believe that the extreme points in some interesting special cases will be 1 / 2-integral.

Algorithm’s Description: Initially, ${\mathcal {U}}= \emptyset$. Our algorithm considers the layers $L_1,\ldots , L_n$ in this order. When the algorithm looks at layer $L_j$, it picks a vertex $u_j$ and adds it to ${\mathcal {U}}$, as follows. Consider $A_j \subseteq L_j$, where $A_j = \left\{ v \in L_j: x_v >0 \right\}$. Let $A'_j \subseteq A_j$ contain vertices v such that there is no ancestor of v that belongs to $A_{j'}$ for some $j' <j$, and $A''_j = A_j \setminus A'_j$, i.e. for each $v \in A''_j$, there is another vertex $u \in A_{j'}$ for some $j' <j$ such that u is an ancestor of v. We choose the vertex $u_j$ based on the following rules:

• If there is only one $v \in A_j$, such that v is not saved by ${\mathcal {U}}$ so far, choose $u_j=v$.

• Otherwise, if $|A'_j| =2$, pick $u_j$ at random from $A'_j$ with uniform probability. Similarly, if $|A''_j| =2$, pick $u_j$ at random from $A''_j$.

• Otherwise, we have the case $|A'_j| = |A''_j| = 1$. In this case, we pick vertex $u_j$ from $A'_j$ with probability 1 / 3; otherwise, we take from $A''_j$.

4.3 Ruling Out the Gap Instances in Sect. 3

In this section, we show that the integrality gap instances for (LP-1) presented in the previous section admit a better than $(1-1/e)$ approximation via (LP’). To this end, we introduce the concept of well-separable LP solutions and show an improved rounding algorithm for solutions in this class.

Let $\eta \in (0,1)$. Given an LP solution (x, y) for (LP-1) or (LP’), we say that a vertex v is $\eta$-light if $\sum _{u \in P_v \setminus \left\{ v \right\} } x_u < \eta$; if a vertex v is not $\eta$-light, we say that it is $\eta$-heavy. A fractional solution is said to be $\eta$-separable if for each layer j, either all vertices in $L_j$ are $\eta$-light, or they are all $\eta$-heavy. For an $\eta$-separable LP solution (x, y), each layer $L_j$ is either an $\eta$-light layer that contains only $\eta$-light vertices, or $\eta$-heavy layer that contains only $\eta$-heavy vertices.

Observation 2

The LP solution presented in Sect. 3 is $\eta$-separable for all values of $\eta \in \left\{ 1/k, 2/k, \ldots , 1 \right\}$.

Theorem 5

If the LP solution (x, y) is $\eta$-separable for some $\eta$, then there is an efficient algorithm that produces an integral solution of cost $(1-1/e + f(\eta ))\sum _{v} y_v$, where $f(\eta )$ is some function depending only on $\eta$.

Algorithm: Let T be an input tree, and (x, y) be a solution for (LP’) on T that is $\eta$-separable for some constant $\eta \in (0,1)$. Our algorithm proceeds in two phases. In the first phase, it performs randomized rounding independently for each $\eta$-light layer. Denote by $V_1$ the (random) collection of vertices selected in this phase. Then, in the second phase, our algorithm performs randomized rounding conditioned on the solutions in the first phase. In particular, when we process each $\eta$-heavy layer $L_j$, let $\tilde{L}_j$ be the collection of vertices that have not yet been saved by $V_1$. We sample one vertex $v \in \tilde{L}_j$ from the distribution $\left\{ \frac{x_v}{x(\tilde{L}_j)}\right\} _{v \in \tilde{L}_j}$. Let $V_2$ be the set of vertices chosen from the second phase. This completes the description of our algorithm.

4.4 Integrality Gap for (LP’)

In this section, we present an instance where (LP’) has an integrality gap of $5/6+\epsilon$, for any $\epsilon > 0$. Interestingly, this instance admits an optimal $\frac{1}{2}$-integral LP solution.

Fig. 2.

Gadget used to get 5 / 6 integrality gap. Special vertices are colored gray.

Gadget: The motivation of our construction is a simple gadget represented in Fig. 2. In this instance, vertices are either special (colored gray) or regular. This gadget has three properties of our interest:

• If we assign an LP-value of $x_v= 1/2$ to every special vertex, then this is a feasible LP solution that ensures $y_u = 1$ for every leaf u.

• For any integral solution ${\mathcal {U}}$ that does not pick any vertex in the first layer of this gadget, at most 2 out of 3 leaves of the gadget are saved.

• Any pair of special vertices in the same layer do not have a common ancestor inside this gadget.

Our integrality gap instance is constructed by creating partially overlapping copies of this gadget. We describe it formally below.

Construction: The first layer of this instance, $L_1$, contains 4 nodes: two special nodes, which we name a(1) and a(2), and two regular nodes, which we name b(1) and b(2). We recall the definition of spider from Sect. 3.1.

Let $\alpha = 5\left\lceil 1/\epsilon \right\rceil$. The nodes b(1) and b(2) are the roots of two spiders. Specifically, the spider $Z_1$ rooted at b(1) has $\alpha$ feet, with one foot per layer, in consecutive layers $L_2,\ldots , L_{\alpha +1}$. For each $j \in [\alpha ]$, denote by $b'(1,j)$, the $j^{th}$ foot of spider $Z_1$. The spider $Z_2$, rooted at b(2), has $\alpha ^2$ feet, with one foot per layer, in layers $L_{\alpha +2}, \ldots , L_{\alpha ^2+\alpha +1}$. For each $j \in [\alpha ^2]$, denote by $b'(2,j)$, the $j^{th}$ foot of spider $Z_2$. All the feet of spiders $Z_1$ and $Z_2$ are special vertices.

For each $j \in [\alpha ]$, the node $b'(1,j)$ is also the root of spider $Z'_{1,j}$, with $\alpha ^2$ feet, lying in the $\alpha ^2$ consecutive layers $L_{2+\alpha + j \alpha ^2},\ldots , L_{1+\alpha + (j+1) \alpha ^2}$ (one foot per layer). For $j' \in [\alpha ^2]$, let $b''(1,j,j')$ denote the $j'$-th foot of spider $Z'_{1,j}$ that lies in layer $L_{1+\alpha +j\alpha ^2 +j'}$. Notice that we have $\alpha ^3$ such feet of these spiders $\left\{ Z'_{1,j} \right\} _{j=1}^{\alpha }$ lying in layers $L_{2+\alpha +\alpha ^2}, \ldots , L_{1+\alpha +\alpha ^2+\alpha ^3}$. Similarly, for each $j \in [\alpha ^2]$, the node $b'(2,j)$ is the root of spider $Z'_{2,j}$ with $\alpha ^2$ feet, lying in consecutive layers $L_{2+\alpha +\alpha ^3 + j\alpha ^2}, \ldots , L_{1+\alpha + \alpha ^3 + (j+1)\alpha ^2}$. We denote by $b''(2,j,j')$ the $j'$-th foot of this spider.

The special node a(1) is also the root of spider $W_1$ which has $\alpha + \alpha ^3$ feet: The first $\alpha$ feet, denoted by $a'(1,j)$ for $j \in [\alpha ]$, are aligned with the nodes $b'(1,j)$, i.e. for each $j \in [\alpha ]$, the foot $a'(1,j)$ of spider $W_1$ is in the same layer as the foot $b'(1,j)$ of $Z_1$. For each $j \in [\alpha ], j' \in [\alpha ^2]$, we also have a foot $a''(1,j,j')$ which is placed in the same layer as $b''(1,j,j')$. Similarly, the special node a(2) is the root of spider $W_2$ having $\alpha ^2 + \alpha ^4$ feet. For $j \in [\alpha ^2]$, spider $W_2$ has a foot $a'(2,j)$ placed in the same layer as $b'(2,j)$. For $j \in [\alpha ^2], j' \in [\alpha ^2]$, $W_2$ also has a foot $a''(2,j,j')$ in the layer of $b''(2,j,j')$. All the feet of both $W_1$ and $W_2$ are special vertices.

Finally, for $i \in \left\{ 1,2 \right\}$, and $j \in [\alpha ^i]$, each node $a'(i,j)$ has $\alpha ^{5-i}$ children, which are leaves of the instance. For $j \in [\alpha ], j' \in [\alpha ^2]$, the nodes $b''(i,j,j')$, $a''(i,j,j')$ have $\alpha ^{3-i}$ children each which are also leaves of the instance. The set of terminals ${\mathcal {X}}$ is simply the set of leaves.

Proposition 3

We have $|{\mathcal {X}}| = 6 \alpha ^5$. Moreover, (i) the number of terminals in subtrees $T_{a(1)} \cup T_{b(1)}$ is $3 \alpha ^5$, and (ii) the number of terminals in subtrees $T_{a(2)} \cup T_{b(2)}$ is $3 \alpha ^5$.

Fractional Solution: Our construction guarantees that any path from root to leaf contains 2 special vertices: For a leaf child of $a'(i,j)$, its path towards the root must contain $a'(i,j)$ and a(i). For a leaf child of $a''(i,j,j')$, its path towards the root contains $a''(i,j,j')$ and a(i). For a leaf child of $b''(i,j,j')$, the path towards the root contains $b''(i,j,j')$ and $b'(i,j)$.

Lemma 6

For each special vertex v, for each layer $L_j$ below v, the set $L_j \cap T_v$ contains at most one special vertex.

Notice that, there are at most two special vertices per layer. We define the LP solution x, with $x_v =1/2$ for every special vertex v and $x_v = 0$ for all other vertices. It is easy to verify that this is a feasible solution.

Integral Solution: We argue that any integral solution cannot save more than $(1+5/\alpha ) 5 \alpha ^5$ terminals. The following lemma is the key to our analysis.

Lemma 7

Any integral solution ${\mathcal {U}}: {\mathcal {U}}\cap \left\{ a(1), b(1) \right\} =\emptyset$ saves at most $(1+5/\alpha ) 5 \alpha ^5$ terminals.

Lemma 8

Any integral solution ${\mathcal {U}}: {\mathcal {U}}\cap \left\{ a(2), b(2) \right\} =\emptyset$ saves at most $(1+5/\alpha ) 5 \alpha ^5$ terminals.

Since nodes a(1), a(2), b(1), b(2) are in the first layer, it is only possible to save one of them. Therefore, either Lemma 7 or Lemma 8 apply, which concludes the analysis.

5 Conclusion and Open Problems

In this paper, we settled the integrality gap question for the standard LP relaxation. Our results ruled out the hope to use the canonical LP to obtain better approximation results. While a recent paper settled the approximability status of the problem [1], the question whether an improvement over $(1-1/e)$ can be done via LP relaxation is of independent interest. We provide some evidences that Hartke’s LP is a promising candidate for doing so. Another interesting question is to find a more general graph class that admits a constant approximation algorithm. We believe that this is possible for bounded treewidth graphs.