Keywords

1 Introduction

Three attractive inventions of Professor Leon Chua: the Chua’s circuit (Matsumoto 1984), the Cellular Neural/Nonlinear Networks (CNNs) (Chua and Yang 1988a, b), and the memristor (Chua 1971; Chua and Kang 1976) are considered as the major breakthroughs in the literature of the nonlinear science. While Chua’s circuit and CNNs have been studied and applied in various areas, such as secure communications, random generators, signal processing, pattern formation of modelling of complex systems (Arena 2005; Chua 1994, 1998), studies on memristor have only received significant attention recently after the realization of a solid-state thin film two-terminal memristor at Hewlett-Packard Laboratories (Strukov et al. 2008).

After this realization, a considerable number of potential memristor-based applications have been reported because memristor can be applied in different potential areas. The more important of them are related with spiking neural network, high-speed computing, synapses of biological systems, flexible circuits, nonvolatile memory, adaptive filter, pattern recognition systems, artificial intelligence, modeling of complex systems or low power devices and sensing (Adhikari et al. 2012; Ascoli et al. 2013; Ascoli and Corinto 2013; Corinto et al. 2012; Driscoll et al. 2010; Joglekar and Wolf 2009; Shin et al. 2011; Tetzlaff 2014). Interestingly, the intrinsic nonlinear characteristic of memristor has been exploited in implementing novel chaotic oscillators with complex dynamics (Bo-Cheng et al. 2011; Buscarino et al. 2012a, b; Corinto et al. 2012; Corinto and Ascoli 2012; Driscoll et al. 2011; Itoh and Chua 2008; Muthuswamy 2010).

Furthermore, the study of control of a chaotic system investigates methods for designing feedback control laws that globally or locally asymptotically stabilize or regulate the outputs of a chaotic system. Many methods have been developed for the control and tracking of chaotic systems such as active control (Chen 1999; Mahmoud et al. 2007; Nbendjo et al. 2003; Nbendjo and Woafo 2007), adaptive control (Chen 2011; Zheng 2011; Lin 2008; Luo et al. 2010; Vaidyanathan and Volos 2016a, b), backstepping control (Laoye et al. 2009; Lin 2010; Yassen 2006) and sliding mode control (Bartoszewicz and Patton 2007; Edwards and Spurgeon 1998; Utkin 1993, 2004; Utkin et al. 2009; Young et al. 1999).

Furthermore, chaos synchronization problem deals with the synchronization of a couple of systems called the master or drive system and the slave or response system. To solve this problem, control laws are designed so that the output of the slave system tracks the output of the master system asymptotically with time. The study of chaos in the last decades had a tremendous impact on the foundations of science and engineering and one of the most recent exciting developments is the discovery of chaos synchronization, which possibility was first reported by Fujisaka and Yamada and later by Pecora and Carroll (Fujisaka and Yamada 1983; Pecora and Carroll 1990). Because of the “butterfly” effect, the synchronization of chaotic systems is a challenging problem in the chaos literature even when the initial conditions of the master and slave systems are nearly identical because of the exponential divergence of the outputs of the two systems in the absence of any control. Different types of synchronization such as complete synchronization (Landsman and Schwartz 2007; Lin and He 2005; Liu 2002; Mahmoud and Mahmoud 2010; Pecora and Carroll 1990), antisynchronization (Kim et al. 2003; Li and Zhou 2007; Wang 2009; Wedekind and Parlitz 2002; Zhang and Sun 2004), hybrid synchronization (Barajas-Ramírez et al. 2003; Karthikeyan and Sundarapandian 2014; Xie 2002), lag synchronization (Li et al. 2005; Rosenblum et al. 1997; Shahverdiev et al. 2002; Taherion and Lai 1999), phase synchronization (Pikovsky et al. 1997; Rosenblum et al. 1996, 2001), anti-phase synchronization (Astakhov et al. 2000; Cao and Lai 1998; Liu et al. 2006), generalized synchronization (Kocarev and Parlitz 1996; Rulkov et al. 1995; Wang and Guan 2006; Yang and Duan 1998), projective synchronization (Li and Xu 2004; Mainieri and Rehacek 1999), generalized projective synchronization (Li 2007; Sarasu and Sundarapandian 2011; Yan and Li 2005), have been studied in the chaos literature.

Since the discovery of chaos synchronization, different approaches have been proposed to achieve it, such as PC method (Pecora and Carroll 1990), active control method (Agiza and Yassen 2001; Idowu et al. 2009; Vaidyanathan and Rajagopal 2011; Vincent 2008), adaptive control method (Chen and Lü 2002a, b; Vaidyanathan and Rajagopal 2012), backstepping control method (Huang 2005; Tan 2003; Yassen 2007) and sliding mode control method (Tavazoei and Haeri 2008; Yau 2004; Zhang and Xu 2010).

In this chapter, adaptive control and synchronization schemes for a memristor-based chaotic system have been developed. The proposed system is a modified Shinriki nonlinear circuit, in which its nonlinear positive conductance has been replaced with a first order memristive diode bridge. All the main adaptive results in this chapter are proved using Lyapunov stability theory. Simulation results prove the effectiveness of the proposed control and synchronization schemes.

The rest of this chapter is organized as follows. Related works are summarized in Sect. 2. Section 3 provides the mathematical model of the memristor-based Shinriki system, while the dynamics and properties of the system are presented in Sect. 4. The adaptive control scheme of the memristor-based Shinriki system is introduced in Sect. 5, while the adaptive synchronization scheme between two coupled memristor-based Shinriki system is presented in Sect. 6. Finally, conclusions are drawn in Sect. 7.

2 Related Works

Based on the complex dynamical behavior that memristive systems present, in the last five years many interesting control and synchronization schemes in those systems have been proposed. These schemes are presented in details in this section.

Firstly, in 2012, Wu et al. proposed some sufficient conditions for guarantying the exponential synchronization of the coupled memristor-based recurrent neural on drive-response concept (Wu et al. 2012).

Two different types of anti-synchronization algorithms are presented by Wu and Zeng in order to achieve the exponential anti-synchronization of coupled memristive recurrent neural networks (Wu and Zeng 2013). Huang and his co-workers investigated the problem of intermittent control of a memristor-based Chua’s oscillator and presented the oscillator as the T-S fuzzy model system (Huang et al. 2013). Also, in 2013, a novel kind of compound synchronization between four memristor chaotic oscillator systems was investigated, where the drive systems have been conceptually divided into two categories: scaling drive systems and base drive systems (Sun et al. 2013).

In 2014, Zhang and Shen have investigated the exponential synchronization of coupled memristor-based chaotic neural networks with both time-varying delays and general activation functions (Zhang and Shen 2014). In the same year, the problem of global exponential synchronization for a class of memristor-based Cohen–Grossberg neural networks with time-varying discrete delays and unbounded distributed delays was studied (Yang et al. 2014). The problem of exponential lag synchronization control of memristive neural networks via the fuzzy method and its application in pseudorandom number generators has been presented in Wen et al. (2014a). In Wang et al. (2014) the synchronization control of memristor-based recurrent neural networks with impulsive perturbations or boundary perturbations is studied. Also, in 2014, the synchronization problem of memristive systems with multiple networked input and output delays via observer-based control has been investigated (Wen et al. 2014b).

Pham et al. 2015, studied the case of anti-synchronization between coupled memristor-based hyperchaotic systems with hidden attractors (Pham et al. 2015). The global robust synchronization of multiple memristive neural networks with nonidentical uncertain parameters is presented in Yang et al. (2015). Wen and his co-workers studied the problem of circuit design and global exponential stabilization of memristive neural networks with time-varying delays and general activation functions (Wen et al. 2015). By using the parallel-memristors connection corresponding to the capacitors and memristors synaptic connection in usual recurrent neural networks, general delayed memristive recurrent neural networks are proposed in Zhang et al. (2013). The investigation of synchronization for memristor-based neural networks with time-varying delay via an adaptive and feedback controller is studied in Li and Cao (2015). Mathiyalagan and his co-workers formulated and investigated the impulsive synchronization of memristor based bidirectional associative memory neural networks with time varying delays (Mathiyalagan et al. 2015).

In Mathiyalagan et al. (2016) the mixed H∞ and passivity based synchronization criteria for memristor-based recurrent neural networks with time-varying delays has been investigated. The impulsive synchronization of stochastic memristor-based recurrent neural networks with time delay is studied in Chandrasekar and Rakkiyappan (2016). Li and Cao presented the lag synchronization problem of memristor-based coupled neural networks with or without parameter mismatch using two different algorithms (Li and Cao 2016). A memristor-based complex Lorenz system and its modified projective synchronization have been introduced in Wang et al. (2016). Wen and his co-workers presented the sliding-mode control scheme of uncertain memristive Chua’s circuits via the aforementioned method (Wen et al. 2016). Finally, a new memristor-based hyperchaotic complex Lü system and its adaptive complex generalized synchronization are presented in Wang et al. (2016).

3 Model of the Memristor-Based Shinriki’s System

In this section, the memristor-based chaotic oscillator obtained by replacing the nonlinear positive conductance of the Shinriki’s et al. (1981) circuit with a first order memristive diode bridge is considered, as it proposed by Kengne et al. (2015). The original Shinriki’s oscillator, which is a modified van der Pol oscillator, has been introduced by Shinriki and co-workers in 1981 (Fig. 1). It consists of a resonant circuit and two nonlinear conductances, one negative, which is approximated by

Fig. 1
figure 1

The schematic of the original Shinriki’s circuit

Full size image
$$ i_{\text{a}} \text{(}v_{1} \text{)} = - a_{1} v_{1} + a_{3} v_{1}^{3} , \, a_{1} > 0, \, a_{3} > 0 $$
(1)

and another positive, which is approximated by

$$ i_{\text{d}} \text{(}v_{2} - v_{1} \text{)} = b_{1} \text{(}v_{2} - v_{1} \text{)} + b_{3} \text{(}v_{2} - v_{1} \text{)}^{3} , \, b_{1} > 0, \, b_{3} > 0 $$
(2)

These approximations are quite reasonable from the qualitative viewpoint.

The state equation of the Shinriki’s circuit is written as:

$$ \left\{ {\begin{array}{*{20}l} {C_{0} \frac{{dv_{1} }}{dt} = - G_{1} v_{1} + a_{1} v_{1} - a_{3} v_{1}^{3} + b_{1} \text{(}v_{2} - v_{1} \text{) + }b_{3} \text{(}v_{2} - v_{1} \text{)}^{3} } \hfill \\ {C\frac{{dv_{2} }}{dt} = - i_{L} - G_{2} v_{2} - b_{1} \text{(}v_{2} - v_{1} \text{) - }b_{3} \text{(}v_{2} - v_{1} \text{)}^{3} } \hfill \\ {L\frac{{di_{L} }}{dt} = v_{2} } \hfill \\ \end{array} } \right. $$
(3)

with (v 1, v 2, i L )∈R3.

Shinriki and his co-workers showed that the circuit of Fig. 1 can generate oscillations with a random waveform or a periodic waveform depending on the chosen parameters.

In 1984, the dynamical behavior of the circuit of Fig. 1 has been further investigated in the work (Freire et al. 1984). The circuit is shown to develop a great variety of dynamical behaviors (equilibrium points, periodic oscillations, chaotic motions etc.) and the analysis proceeded to catalog all of them through a bifurcation study (pitchfork and Hopf bifurcations, flip bifurcations etc.). This study pointed out the interest devoted to the Shinriki’s system (3).

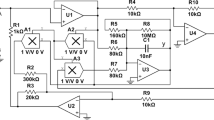
Furthermore, in 2015 a novel memristor-based oscillator, obtained from Shinriki’s circuit of Fig. 1, by substituting the nonlinear positive conductance with a first order memristive diode bridge, with a first order parallel RC filter, has been introduced (Kengne et al. 2015). The schematic diagram of the memristor-based Shinriki’s circuit, which is an autonomous nonlinear circuit belonging to the memristive Chua’s circuit family, is depicted in Fig. 2.

Fig. 2
figure 2

The schematic of the memristor-based Shinriki’s circuit

Full size image

The mathematical model of the proposed memristor is given by the following equations:

$$ i_{m} = g\text{(}v_{Cm} ,v\text{)}v = 2I_{S} \text{exp(} - kv_{Cm} \text{)sinh(}kv_{m} \text{)} $$
(4)
$$ \frac{{dv_{Cm} }}{dt} = f\text{(}v_{Cm} ,v\text{)} = \frac{{2I_{S} \text{exp(} - kv_{Cm} \text{)cosh(}kv_{m} \text{)}}}{{C_{m} }} - \frac{{v_{Cm} }}{{R_{m} C_{m} }} - \frac{{2I_{S} }}{{C_{m} }} $$
(5)

where k = 1/2nV T, while I S , n, V T denote the reverse current, the emission coefficient and the thermal voltage of the diode, respectively. Also, v m , i m represent the input voltage and current of the memristor, and v Cm is the voltage of the capacitor C m . The proposed memristor has been proved in Bao et al. (2014) that exhibits the three characteristic fingerprints for identifying a memristor (Adhikari et al. 2013).

By using the aforementioned memristor model, the Shinriki’s system (3) has became a fourth order dynamical system described by the following set of differential equations:

$$ \left\{ {\begin{array}{*{20}l} {C\frac{{dv_{C} }}{dt} = - i_{L} - \frac{{v_{C} }}{{R_{5} }} - 2I_{S} \text{e}^{{ - kv_{Cm} }} \text{sinh(}kv_{C} - kv_{Co} \text{)}} \hfill \\ {C_{0} \frac{{dv_{Co} }}{dt} = \left( {\frac{1}{{R_{3} }} - \frac{1}{{R_{4} }}} \right)v_{Co} + 2I_{S} \text{e}^{{ - kv_{Cm} }} \text{sinh(}kv_{C} - kv_{Co} \text{)}} \hfill \\ {L\frac{{di_{L} }}{dt} = v_{C} } \hfill \\ {C_{m} \frac{{dv_{Cm} }}{dt} = - \frac{{v_{Cm} }}{{R_{m} }} + 2I_{S} \text{e}^{{ - kv_{Cm} }} \text{cosh(}kv_{C} - kv_{Co} \text{)} - \text{2}I_{S} } \hfill \\ \end{array} } \right. $$
(6)

Normalizing the system (6), by using the following change of variable and parameters:

$$ \begin{aligned} x_{1} & = \frac{{v_{C} }}{{V_{ref} }},x_{2} = \frac{{v_{Co} }}{{V_{ref} }},x_{3} = \frac{{\rho i_{L} }}{{V_{ref} }},x_{4} = \frac{{v_{Cm} }}{{V_{ref} }},\tau = \frac{t}{{\sqrt {LC} }}, \\ V_{ref} & = 2\eta V_{T} ,\rho = \sqrt {{L \mathord{\left/ {\vphantom {L C}} \right. \kern-0pt} C}} ,\eta_{1} = \frac{C}{{C_{o} }},\eta_{2} = \frac{C}{{C_{m} }}, \\ \alpha & = \frac{\rho }{{R_{4} }},\beta = \frac{\rho }{{R_{3} }},\gamma = \frac{{2\rho i_{L} }}{{V_{ref} }},\delta = \frac{\rho }{{R_{5} }},\sigma = \frac{\rho }{{R_{m} }} \\ \end{aligned} $$
(7)

The dimensionless circuit’s system is defined as:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = - x_{3} - \delta x_{1} - \gamma \text{e}^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)}} \hfill \\ {\dot{x}_{2} = \eta_{1} \left[ {\text{(}\beta - \alpha \text{)}x_{2} + \gamma \text{e}^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)}} \right]} \hfill \\ {\dot{x}_{3} = x_{1} } \hfill \\ {\dot{x}_{4} = \eta_{2} \left[ { - \sigma x_{4} + \gamma \text{e}^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - \gamma } \right]} \hfill \\ \end{array} } \right. $$
(8)

where the over dots denotes differentiation with respect to the dimensionless time τ. Finally, for simplifying the system (8) further, it can be written as:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = - x_{3} - dx_{1} - ce^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)}} \hfill \\ {\dot{x}_{2} = \text{(}b - a\text{)}x_{2} + pe^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)}} \hfill \\ {\dot{x}_{3} = x_{1} } \hfill \\ {\dot{x}_{4} = - lx_{4} + me^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - m} \hfill \\ \end{array} } \right. $$
(9)

where, a = η 1 α, b = η 1 β, c = γ, d = δ, p = η 1 γ, l = η 2 σ and m = η 2 γ.

4 Dynamics of the Memristor-based Shinriki’s System

The detailed analysis of the memristor-based Shinriki’s system (8), regarding its fixed point’s analysis, system’s symmetry and numerical study, can be found in (Kengne et al. 2015). However, in this section the system’s chaotic behavior will be explored, in order to study, in the next sections, its chaos control and synchronization schemes.

For this reason the system (9) is solved numerically using the classical fourth-order Runge-Kutta integration algorithm with time step Δt = 0.005 and the calculations are performed using variables and constants parameters. Also, the system is integrated for a sufficiently long time and the transient is cancelled. Two indicators are substantially exploited to define the type of scenario giving rise to chaos. The bifurcation diagram stands as the first indicator, while the second indicator is the graph of the Lyapunov exponents.

Furthermore, the numerical analysis is performed with the following values of circuit components: L = 225 mH, C o = 10 nF, C = 100 nF, C m  = 940 nF, R 1 = 5.6 kΩ, R 2 = 5.6 kΩ, R 3 = 10 kΩ, R 4 = 50 kΩ, R 5 = 20 kΩ, R m —tuneable, 1N4148 diodes, with η = 1.9, V T  = 26 mV and I S  = 2.682 nA. With this set of components values, the system’s dimensionless parameters values are fixed to: a = 0.3, b = 1.5, c = 8.143724 × 10−5, d = 0.075, p = 8.143724 × 10−4, and m = 8.6635298 × 10−4, while l is the control parameter. The choice of l as a control parameter is done, because it is related with the memristor (via R m ). So, it is preferable as a control parameter, in order to see how a memristor’s parameter affects system’s behavior.

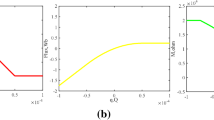
As it is known, the bifurcation diagram provides a useful tool in nonlinear science because it shows the change of system’s dynamical behavior. So, the bifurcation diagram of Fig. 3a has been obtained by plotting the value of variable x 1, when the trajectory intersects the section plane x 3 = 0, with \( \dot{x}_{3} > 0 \), in terms of the bifurcation parameter l that is increased with step Δl = 0.002 in the range of 0 ≤ l ≤ 2. From the observation of this diagram, the reader can see a period doubling route to chaos as the bifurcation parameter l is increased. The extended chaotic region is interrupted by tiny windows of periodic behavior sandwiched in the chaotic bands.

Fig. 3
figure 3

a Bifurcation diagram of x 1 versus the parameter l and b the respective diagram of Lyapunov exponents versus the parameter l

Full size image

Also, it is well known, that Lyapunov exponents measure the exponential rates of the divergence and convergence of nearby trajectories in the phase space of the chaotic system (Strogatz 1994). In order to have detailed view of the memristor-based Shinriki system (9), the Lyapunov exponents (λ i , with i = 1, 2, 3, 4) have been calculated using the algorithm in Wolf et al. (1985) and are depicted in Fig. 3b. In fact, Fig. 3b presents only the three largest Lyapunov exponents because the fourth Lyapunov exponent (λ 4) is very low. Briefly recall that for periodic orbits, the system has λ 1 = 0 and λ 2, λ 3, λ 4 ≤ 0, for quasiperiodic orbits λ 1 = λ 2 = 0 and λ 3, λ 4 ≤ 0, while for chaotic attractors λ 1 ≥ 0, λ 2 = 0, and λ 3, λ 4 ≤ 0, and for hyperchaotic attractors λ 1 ≥ λ 2 ≥ 0, λ 3 = 0 and λ 4 ≤ 0. It can be seen that the bifurcation diagram of Fig. 3a well coincide with the spectrum of the Lyapunov exponents (Fig. 3b). Note that, the system is simply chaotic (and not hyperchaotic), although it is a fourth order nonlinear system.

Finally, for the aforementioned set of parameters, various numerical phase portraits in (x 2 − x 1) planes are depicted (Figs. 4, 5, 6 and 7).

Fig. 4
figure 4

Phase portrait of x 2 versus x 1, for l = 0.2 (period-2 state)

Full size image
Fig. 5
figure 5

Phase portrait of x 2 versus x 1, for l = 1 (chaotic state)

Full size image
Fig. 6
figure 6

Phase portrait of x 2 versus x 1 for l = 1.4 (period-6 state)

Full size image
Fig. 7
figure 7

Phase portrait of x 2 versus x 1 for l = 2 (chaotic state)

Full size image

5 Adaptive Control of the Memristor-Based Shinriki’s System

From the results of the aforementioned simulation process, it is obvious that the nature of the memristor add an extra complexity to system’s dynamical behavior. So, it is useful to see if the proposed memristor-based Shinriki’s system can be controlled by using the adaptive control method, in order to derive an adaptive feedback control law for globally stabilizing the system with memristor’s unknown parameters.

Thus, we consider the memristor-based Shinriki’s system given by

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = - x_{3} - dx_{1} - ce^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} + u_{1} } \hfill \\ {\dot{x}_{2} = \text{(}b - a\text{)}x_{2} + pe^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} + u_{2} } \hfill \\ {\dot{x}_{3} = x_{1} + u_{3} } \hfill \\ {\dot{x}_{4} = - lx_{4} + me^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - m + u_{4} } \hfill \\ \end{array} } \right. $$
(10)

In (10), x i , (i = 1, …, 4) are the states and u i , (i = 1, …, 4) are the adaptive controls to be determined using estimates \( \hat{c}(t), \, \hat{p}(t), \, \hat{l}(t), \, \hat{m}(t) \) for the unknown memristor’s parameters c, p, l, m, respectively.

We consider the adaptive feedback control laws

$$ \left\{ {\begin{array}{*{20}l} {\dot{u}_{1} = x_{3} + dx_{1} + \hat{c}e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{1} x_{1} } \hfill \\ {\dot{u}_{2} = - \text{(}b - a\text{)}x_{2} - \hat{p}e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{2} x_{2} } \hfill \\ {\dot{u}_{3} = - x_{1} - k_{3} x_{3} } \hfill \\ {\dot{u}_{4} = \hat{l}x_{4} - \hat{m}e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{) + }\hat{m} - k_{4} x_{4} } \hfill \\ \end{array} } \right. $$
(11)

where k i , (i = 1, …, 4) are positive gain constants.

Substituting (11) into (10), we get the closed-loop plant dynamics as:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = - \text{(}c - \hat{c}\text{)}e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{1} x_{1} } \hfill \\ {\dot{x}_{2} = \text{(}p - \hat{p}\text{)}e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{2} x_{2} } \hfill \\ {\dot{x}_{3} = - k_{3} x_{3} } \hfill \\ {\dot{x}_{4} = - \text{(}l - \hat{l}\text{)}x_{4} \text{ + (}m - \hat{m}\text{)}e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - \text{(}m - \hat{m}\text{)} - k_{4} x_{4} } \hfill \\ \end{array} } \right. $$
(12)

The parameter estimation errors are defined as:

$$ \left\{ {\begin{array}{*{20}l} {e_{c} \text{(}t\text{) = }c - \hat{c}(t)} \hfill \\ {e_{p} \text{(}t\text{) = }p - \hat{p}(t)} \hfill \\ {e_{l} \text{(}t\text{) = }l - \hat{l}(t)} \hfill \\ {e_{m} \text{(}t\text{) = }m - \hat{m}(t)} \hfill \\ \end{array} } \right. $$
(13)

In view of (13), we can simplify the plant dynamics (12) as:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = - e_{c} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{1} x_{1} } \hfill \\ {\dot{x}_{2} = e_{p} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{2} x_{2} } \hfill \\ {\dot{x}_{3} = - k_{3} x_{3} } \hfill \\ {\dot{x}_{4} = - e_{l} x_{4} \text{ + e}_{m} e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - e_{m} - k_{4} x_{4} } \hfill \\ \end{array} } \right. $$
(14)

Differentiating (13) with respect to t, we obtain

$$ \left\{ {\begin{array}{*{20}l} {\dot{e}_{c} \text{(}t\text{) = } - \dot{\hat{c}}(t)} \hfill \\ {\dot{e}_{p} \text{(}t\text{) = } - \dot{\hat{p}}(t)} \hfill \\ {\dot{e}_{l} \text{(}t\text{) = } - \dot{\hat{l}}(t)} \hfill \\ {\dot{e}_{m} \text{(}t\text{) = } - \dot{\hat{m}}(t)} \hfill \\ \end{array} } \right. $$
(15)

We use adaptive control theory in order to find an update law for the parameter estimates. We consider the quadratic candidate Lyapunov function defined by

$$ V\text{(}\varvec{x},e_{c} ,e_{p} ,e_{l} ,{\text{e}}_{m} ) = \frac{1}{2}(x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + x_{4}^{2} ) + \frac{1}{2}(e_{c}^{2} + e_{p}^{2} + e_{l}^{2} + e_{m}^{2} ) $$
(16)

Differentiating V along the trajectories of (14) and (15), we obtain

$$ \begin{aligned} \dot{V} & = x_{1} \dot{x}_{1} + x_{2} \dot{x}_{2} + x_{3} \dot{x}_{3} + x_{4} \dot{x}_{4} + e_{c} \dot{e}_{c} + e_{p} \dot{e}_{p} + e_{l} \dot{e}_{l} + e_{m} \dot{e}_{m} \\ & = - k_{1} x_{1}^{2} - e_{c} x_{\text{1}} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{2} x_{2}^{2} + e_{p} x_{2} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} \\ & \quad - k_{3} x_{3}^{2} - k_{4} x_{4}^{2} - e_{l} x_{4}^{2} \text{ + e}_{m} x_{4} e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - e_{m} x_{4} \\ & \quad - e_{c} \dot{\hat{c}} - e_{p} \dot{\hat{p}} - e_{l} \dot{\hat{l}} - e_{m} \dot{\hat{m}} \\ \end{aligned} $$
(17)

or

$$ \begin{aligned} \dot{V} & = - k_{1} x_{1}^{2} - k_{2} x_{2}^{2} - k_{3} x_{3}^{2} - k_{4} x_{4}^{2} + e_{c} \left[ { - x_{\text{1}} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - \dot{\hat{c}}} \right] \\ & \quad + e_{p} \left[ {x_{2} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - \dot{\hat{p}}} \right]{ + }e_{l} \left[ { - x_{4}^{2} - \dot{\hat{l}}} \right] \\ & \quad - \text{e}_{m} \left[ {x_{4} e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - x_{4} - \dot{\hat{m}}} \right] \\ \end{aligned} $$
(18)

In view of (18), we take the parameter update law as

$$ \left\{ {\begin{array}{*{20}l} {\dot{\hat{c}} = - x_{\text{1}} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)}} \hfill \\ {\dot{\hat{p}} = x_{2} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)}} \hfill \\ {\dot{\hat{l}} = - x_{4}^{2} } \hfill \\ {\dot{\hat{m}} = x_{4} e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - x_{4} } \hfill \\ \end{array} } \right. $$
(19)

Next, we state and prove the main result of this section.

Theorem 1

The states x i , (i = 1, …, 4) of the memristor-based Shinriki’s system ( 5 ) with unknown system parameters are globally and exponentially stabilized for all initial conditions to the desired constant values c, p, l, m, respectively, by the adaptive control law ( 11 ) and the parameter update law ( 19 ), where k 1 , k 2 , k 3, k 4 are positive gain constants.

Proof

This result will be proved by applying Lyapunov stability theory (Khalil 2001).

The quadratic Lyapunov function defined by (16), which is clearly a positive definite function on R8 is considered.

By substituting the parameter update law (19) into (18), the time derivative of V is obtained as:

$$ \dot{V} = - k_{1} x_{1}^{2} - k_{2} x_{2}^{2} - k_{3} x_{3}^{2} - k_{4} x_{4}^{2} $$
(20)

From (20), it is clear that dV/dt is a negative semi-definite function on R8. Thus, the state vector x(t) and the parameter estimation error can be concluded that are globally bounded, i.e. \( \left[ {x_{1} \, x_{2} \, x_{3} \, x_{4} \, e_{c} (t ) { }e_{p} (t ) { }e_{l} (t ) { }e_{m} (t )} \right]^{T} \in {\mathbf{L}}_{\infty } \).

If k = min{k 1, k 2, k 3, k 4}, then it follows from (20) that

$$ \dot{V} \le - k\left\| {\varvec{x}(t)} \right\|^{2} $$
(21)

Thus

$$ k\left\| {\varvec{x}(t)} \right\|^{2} \le - \dot{V} $$
(22)

Integrating the inequality (22) from 0 to t, as:

$$ k\int\limits_{0}^{t} {\left\| {\varvec{x}(\tau )} \right\|^{2} } d\tau \le V\text{(}0\text{)} - V\text{(}t\text{)} $$
(23)

From (23), it follows that \( \varvec{x} \in {\mathbf{L}}_{2} \). Using (14), \( \dot{\varvec{x}} \in {\mathbf{L}}_{\infty } \) can be concluded.

Also, by using Barbalat’s lemma (Khalil 2001), the x(t) → 0 exponentially as t → ∞ for all initial conditions \( {\varvec{x}}(0) \in {\mathbf{R}}^{4} \) can be concluded. Hence, it follows that the states x i , (i = 1, …, 4) of the memristor-based Shinriki’s system (5) with unknown memristor’s parameters c, p, l, m are globally and exponentially stabilized for all initial conditions, by the adaptive control laws (11) and the parameter update law (19).

This completes the proof. ■

For the numerical simulations, the classical fourth-order Runge-Kutta method with step size h = 10−8 is used to solve the systems (10) and (19), when the adaptive control laws (11) are applied. The parameter values of the memristor-based Shinriki’s system (9) are taken as in the chaotic case, viz. a = 0.3, b = 1.5, c = 8.143724 × 10−5, d = 0.075, p = 8.143724 × 10−4, m = 8.6635298 × 10−4 and l = 2. Also, we take the positive gain constants as k i  = 5 for i = 1, …, 4. Furthermore, as initial conditions of the memristor-based Shinriki’s system (5), we take x 1(0) = −0.2, x 2(0) = 0.3, x 3(0) = −0.3 and x 4(0) = 1. Furthermore, as initial conditions of the parameter estimates \( \hat{c}(t),\hat{p}(t),\hat{l}(t),\hat{m}(t) \), we take \( \hat{c}(t) = 10^{ - 5} , \, \hat{p}(t) = 10^{ - 4} , \, \hat{l}(t) = 0.1, \, \hat{m}(t) = 8.143724 \cdot 10^{ - 5} \). In Fig. 8, the exponential convergence of the controlled states of the memristor-based Shinriki’s system (10) is depicted.

Fig. 8
figure 8

Time-series of the states x i , (i = 1,…, 4)

Full size image

6 Adaptive Synchronization of Identical Coupled Memristor-Based Shinriki’s Systems

In this section, we derive an adaptive control law for globally and exponentially synchronizing the identical chaotic systems with unknown memristor’s parameters. Thus, the master system is given by the chaotic memristor-based Shinriki’s system (9), while the slave system is given by the following system dynamics.

$$ \left\{ {\begin{array}{*{20}l} {\dot{y}_{1} = - y_{3} - dy_{1} - ce^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} + u_{1} } \hfill \\ {\dot{y}_{2} = \text{(}b - a\text{)}y_{2} + pe^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} + u_{2} } \hfill \\ {\dot{y}_{3} = y_{1} + u_{3} } \hfill \\ {\dot{y}_{4} = - ly_{4} + me^{{ - y_{4} }} \text{cosh(}y_{1} - y_{2} \text{)} - m + u_{4} } \hfill \\ \end{array} } \right. $$
(24)

where y i , (i = 1, …, 4) are the states and u i , (i = 1, …, 4) are the adaptive controls to be determined. In (9) and (24), the memristor’s parameters c, p, l, m, are unknown and the design goal is to find adaptive feedback controls u i that uses estimates \( \hat{c}(t), \, \hat{p}(t), \, \hat{l}(t), \, \hat{m}(t) \) for the parameters c, p, l, m respectively, so as to render the states of the systems (9) and (24) fully synchronized asymptotically.

The synchronization error between the chaotic systems (9) and (24) is defined as:

$$ \left\{ {\begin{array}{*{20}l} {e_{1} = y_{1} - x_{1} } \hfill \\ {e_{2} = y_{2} - x_{2} } \hfill \\ {e_{3} = y_{3} - x_{3} } \hfill \\ {e_{4} = y_{4} - x_{4} } \hfill \\ \end{array} } \right. $$
(25)

Thus, the synchronization error dynamics is obtained as:

$$ \left\{ {\begin{array}{*{20}l} {\dot{e}_{1} = - e_{3} - de_{1} - ce^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} + ce^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} + u_{1} } \hfill \\ {\dot{e}_{2} = \text{(}b - a\text{)}e_{2} + pe^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} - pe^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} + u_{2} } \hfill \\ {\dot{e}_{3} = e_{1} + u_{3} } \hfill \\ {\dot{e}_{4} = - le_{4} + me^{{ - y_{4} }} \text{cosh(}y_{1} - y_{2} \text{)} - me^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} + u_{4} } \hfill \\ \end{array} } \right. $$
(26)

We take the adaptive control laws defined by

$$ \left\{ {\begin{array}{*{20}l} {u_{1} = e_{3} + de_{1} + \hat{c}e^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} - \hat{c}e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{1} e_{1} } \hfill \\ {u_{2} = - \text{(}b - a\text{)}e_{2} + \hat{p}e^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} + \hat{p}e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{2} e_{2} } \hfill \\ {u_{3} = - e_{1} - k_{3} e_{3} } \hfill \\ {u_{4} = \hat{l}e_{4} - \hat{m}e^{{ - y_{4} }} \text{cosh(}y_{1} - y_{2} \text{)} + \hat{m}e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - k_{4} e_{4} } \hfill \\ \end{array} } \right. $$
(27)

where k i , (i = 1, …, 4) are positive gain constants.

Substituting (27) into (26), we obtain the closed-loop error dynamics as:

$$ \left\{ {\begin{array}{*{20}l} {\dot{e}_{1} = - \text{(}c - \hat{c}\text{)}e^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} + \text{(}c - \hat{c}\text{)}e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{1} e_{1} } \hfill \\ {\dot{e}_{2} = \text{(}p - \hat{p}\text{)}e^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} - \text{(}p - \hat{p}\text{)}e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{2} e_{2} } \hfill \\ {\dot{e}_{3} = - k_{3} e_{3} } \hfill \\ {\dot{e}_{4} = - \text{(}l - \hat{l}\text{)}e_{4} + \text{(}m - \hat{m}\text{)}e^{{ - y_{4} }} \text{cosh(}y_{1} - y_{2} \text{)} - \text{(}m - \hat{m}\text{)}e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - k_{4} e_{4} } \hfill \\ \end{array} } \right. $$
(28)

The parameter estimation errors are defined as:

$$ \left\{ {\begin{array}{*{20}l} {e_{c} \text{(}t\text{) = }c - \hat{c}(t)} \hfill \\ {e_{p} \text{(}t\text{) = }p - \hat{p}(t)} \hfill \\ {e_{l} \text{(}t\text{) = }l - \hat{l}(t)} \hfill \\ {e_{m} \text{(}t\text{) = }m - \hat{m}(t)} \hfill \\ \end{array} } \right. $$
(29)

Differentiating (29) with respect to t, we obtain

$$ \left\{ {\begin{array}{*{20}l} {\dot{e}_{c} \text{(}t\text{) = } - \dot{\hat{c}}(t)} \hfill \\ {\dot{e}_{p} \text{(}t\text{) = } - \dot{\hat{p}}(t)} \hfill \\ {\dot{e}_{l} \text{(}t\text{) = } - \dot{\hat{l}}(t)} \hfill \\ {\dot{e}_{m} \text{(}t\text{) = } - \dot{\hat{m}}(t)} \hfill \\ \end{array} } \right. $$
(30)

By using (29), we rewrite the closed-loop system (28) as:

$$ \left\{ {\begin{array}{*{20}l} {\dot{e}_{1} = - e_{c} e^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} + e_{c} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{1} e_{1} } \hfill \\ {\dot{e}_{2} = e_{p} e^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} - e_{p} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - k_{2} e_{2} } \hfill \\ {\dot{e}_{3} = - k_{3} e_{3} } \hfill \\ {\dot{e}_{4} = - e_{l} e_{4} + e_{m} e^{{ - y_{4} }} \text{cosh(}y_{1} - y_{2} \text{)} - e_{m} e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - k_{4} e_{4} } \hfill \\ \end{array} } \right. $$
(31)

We consider the quadratic Lyapunov function given by

$$ V(\varvec{e},e_{c} ,e_{p} ,e_{l} ,e_{m} ) = \frac{1}{2}(e_{1}^{2} + e_{2}^{2} + e_{3}^{2} + e_{4}^{2} ) + \frac{1}{2}(e_{c}^{2} + e_{p}^{2} + e_{l}^{2} + e_{m}^{2} ) $$
(32)

Differentiating V along the trajectories of the systems (31) and (30), we obtain the following.

$$ \begin{aligned} \dot{V} & = - k_{1} e_{1}^{2} - k_{2} e_{2}^{2} - k_{3} e_{3}^{2} - k_{4} e_{4}^{2} + e_{c} \left[ { - e_{\text{1}} e^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} + e_{1} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - \dot{\hat{c}}} \right] \\ & \quad + e_{p} \left[ {e_{2} e^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} - e_{2} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)} - \dot{\hat{p}}} \right] + e_{l} \left[ { - e_{4}^{2} - \dot{\hat{l}}} \right] \\ & \quad \text{ + e}_{m} \left[ {e_{4} e^{{ - y_{4} }} \text{cosh(y}_{1} - y_{2} \text{)} - e_{4} e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)} - \dot{\hat{m}}} \right] \\ \end{aligned} $$
(33)

In view of (33), we take the parameter update law as follows.

$$ \left\{ {\begin{array}{*{20}l} {\dot{\hat{c}} = - e_{\text{1}} e^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} + e_{1} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)}} \hfill \\ {\dot{\hat{p}} = e_{2} e^{{ - y_{4} }} \text{sinh(}y_{1} - y_{2} \text{)} - e_{2} e^{{ - x_{4} }} \text{sinh(}x_{1} - x_{2} \text{)}} \hfill \\ {\dot{\hat{l}} = - e_{4}^{2} } \hfill \\ {\dot{\hat{m}} = e_{4} e^{{ - y_{4} }} \text{cosh(y}_{1} - y_{2} \text{)} - e_{4} e^{{ - x_{4} }} \text{cosh(}x_{1} - x_{2} \text{)}} \hfill \\ \end{array} } \right. $$
(34)

Next, we establish the main result of this section.

Theorem 2

The memristor-based Shinriki’s systems ( 9 ) and ( 24 ) with unknown parameters are globally and exponentially synchronized for all initial conditions by the adaptive feedback control law ( 27 ) and the parameter update law ( 34 ), were k i , (i = 1, …, 4) are positive constants.

Proof

We prove this result via Lyapunov stability theory. We consider the quadratic Lyapunov function V defined by (32), which is positive definite on R8. Next, by substituting the parameter update law (34) into (33), we obtain the time derivative of V as:

$$ \dot{V} = - k_{1} e_{1}^{2} - k_{2} e_{2}^{2} - k_{3} e_{3}^{2} - k_{4} e_{4}^{2} $$
(35)

Thus, it is clear that \( \dot{V} \) is a negative semi-definite function on R8.

From (35), it follows that the synchronization error vector e(t) = (e 1(t), e 2(t), e 3(t), e 4(t)) and the parameter estimation error (e c (t), e p (t), e l (t), e m (t)) are globally bounded. We define k = min(k 1, k 2, k 3, k 4).

Then it follows from (35) that

$$ \dot{V} \le - k\left\| {\varvec{e}(t)} \right\|^{2} $$
(36)

Thus

$$ k\left\| {\varvec{e}(t)} \right\|^{2} \le - \dot{V} $$
(37)

Integrating the inequality (37) from 0 to t, as:

$$ k\int\limits_{0}^{t} {\left\| {\varvec{e}(\tau )} \right\|^{2} } d\tau \le V(0) - V(t) $$
(36)

From (36), it follows that \( \varvec{e} \in {\mathbf{L}}_{2} \), while from (28), it can be deduced that \( \dot{\varvec{e}} \in {\mathbf{L}}_{\infty } \). Thus, using Barbalat’s lemma (Khalil 2001), we can conclude that e(t) → 0 exponentially as t → ∞ for all initial conditions.

This completes the proof. ■

For numerical simulations, the classical fourth-order Runge-Kutta method with step size h = 10−8 is used to solve the system of differential Eqs. (9), (24) and (34), when the adaptive control laws (27) are applied.

The parameter values of the memristor-based Shinriki’s systems (9) and (24) are taken as in the chaotic case of the previous section. The gain constants are taken as k i  = 10, for i = 1, 2, 3, 4.

Furthermore, as initial conditions of the master system (9), we take x 1(t) = −0.2, x 2(t) = 0.3, x 3(t) = −0.3 and x 4(t) = 1, while the initial conditions of the slave system (24), are y 1(0) = 0.5, y 2(0) = −0.2, y 3(0) = −0.1 and y 4(0) = 0.7.

Also, as initial conditions of the parameter estimates, we take \( \hat{c}(t) = 10^{ - 5} , \, \hat{p}(t) = 10^{ - 4} , \, \hat{l}(t) = 0.1, \, \hat{m}(t) = 8.143724 \cdot 10^{ - 5} \). In Figs. 9, 10, 11 and 12, the synchronization of the states of the master system (9) and slave system (24) are depicted, when the adaptive control law (27) and parameter update law (34) are implemented. In Fig. 13, the time-history of the synchronization errors e 1(t), e 2(t), e 3(t) and e 4(t) is depicted.

Fig. 9
figure 9

Synchronization of the states x 1(t) and y 1(t)

Full size image
Fig. 10
figure 10

Synchronization of the states x 2(t) and y 2(t)

Full size image
Fig. 11
figure 11

Synchronization of the states x 3(t) and y 3(t)

Full size image
Fig. 12
figure 12

Synchronization of the states x 4(t) and y 4(t)

Full size image
Fig. 13
figure 13

Time-series of the synchronization errors e i (t), (i = 1, 2, 3, 4)

Full size image

7 Conclusion

In this chapter a memristor-based chaotic system as well as its control and synchronization problems were mainly investigated. As a chaotic system, a modified Shinriki’s nonlinear circuit, in which its nonlinear positive conductance has been replaced with a first order memristive diode bridge, was used. The study of its dynamics and especially of its chaotic behavior, was done by using well-known tools from nonlinear theory, such as the bifurcation diagram, Lyapunov exponents and phase portraits.

In addition, global control and global chaos synchronization of such memristor-based Shinriki’s systems, with unknown memristor’s parameters were achieved by using an adaptive controller. The main adaptive results were proved using Lyapunov stability theory. Finally, the simulation results confirmed the effectiveness of the proposed control and synchronization schemes.

So, this work is a step forward on the direction of studying the methods of control and synchronization of this new class of memristive chaotic systems, which have raised the interest of the research community due to memristor’s intrinsic nonlinear characteristic.