Comparison of Three Different Synchronization Schemes for Fractional Chaotic Systems

Abstract

The importance of synchronization schemes in natural and physical systems including communication modes has made chaotic synchronization an important tool for scientist. Synchronization of chaotic systems are usually conducted without considering the efficiency and robustness of the scheme used. In this work, performance evaluation of three different synchronization schemes: Direct Method, Open Plus Closed Loop (OPCL) and Active control is investigated. The active control technique was found to have the best stability and error convergence. Numerical simulations have been conducted to assert the effectiveness of the proposed analytical results.

1 Introduction

Strogatz [40] defined chaos as the aperiodic long term behaviour in a deterministic system that exhibit sensitive dependence on initial conditions. Using Lyapunov exponents, a chaotic system is one with at least one positive Lyapunov exponent. A system with more than one positive Lyapunov exponent is referred to as an hyperchaotic system. Since the proposition of the first chaotic system by Lorenz [19], the study of chaos has evolved due to development of high computing resources and mathematical procedures for analysis [39]. Chaotic systems has been developed in the form of maps, ordinary differential equations, partial differential equations and fractional order differential equations and presence of chaos investigated. Due to complex nature of natural systems, the study of chaos has been extended to time series analysis in natural systems with the development of appropriate tools [25]. The sensitivity of chaotic system to initial conditions implies that two more systems with different initial conditions will exhibit different dynamics. However, with the addition of appropriate functions, trajectories of similar or different chaotic systems can be made to coincide [24]. This is referred to as synchronization.

Synchronization of chaos refers to a process wherein two (or many) chaotic systems (either equivalent or nonequivalent) adjust a given property of their motion to a common behavior due to a coupling or to a forcing (periodical or noisy) [5]. The first evidence of synchronization phenomenon was given by Huygen’s pendulum clocks [17] while the first synchronization of chaotic system was proposed by Pecora and Carroll [37]. Since the pioneering work of Pecora and Carroll [37], the study of chaos synchronization has gained a lot of interest because of its applications. Several methods of secure communication and encryption has been proposed based on chaos synchronization [30]. The principle assumes that communication between two persons X and Y embedded in a chaotic signal can only be retrieved if the right system parameters (keys) are known. A practical demonstration of secure communication is presented in Strogatz [40].

As the study of chaos synchronization evolves, several types of synchronization such as generalized synchronization [35], lag synchronization [20], complete synchronization, phase synchronization and projective synchronization [32], modified and function projective synchronization [18], etc. have been discovered. In order to achieve any of these type of synchronization, different synchronization techniques such as backstepping [31], active control, direct method [42], Open Plus Close Loop (OPCL) [16] etc. have been developed and implemented. Early studies of different types of synchronization using any of the mentioned techniques on dynamical systems usually involves two systems. Over the years, real life applications of synchronization requires the synchronization of different systems and a given number of systems higher than the traditional two systems. This has given rise to reduced and increased order synchronization [24, 35], combination synchronization [26, 33, 34], combination-combination synchronization [27, 29] and compound combination synchronization [28].

The Caputo’s definition of fractional order differ-integral equations are given as

$$\begin{aligned} ^C_aD^\alpha _tf(t) = \frac{1}{\varGamma (\alpha -m)} \int _a^t \frac{f^{(m)}\tau }{(t-\tau )^{\alpha +1-m}} d\tau \end{aligned}$$

(1)

where $m-1 < \alpha \le m\; \varepsilon \; \mathbb {N}$ and $\alpha \; \varepsilon \;\mathbb {R}$ is a fractional order of the differ-integral of the function f(t) [10]. Applications of fractional order are found in transmission line theory, chemical analysis of aqueous solutions, design of heat-flux meters, rheology of soils, growth of intergranular grooves on metal surfaces, quantum mechanical calculations, and dissemination of atmospheric pollutants [7]. Analysis of football player’s motion has been analysed using fractional calculus [9]. Several chaotic fractional order systems have been proposed, these include: fractional order Lorenz system, fractional order Chua system, fractional order memristor based system, fractional order Duffing system, fractional order Chen system etc. There is a growing interest in fractional order systems due to its many applications in control and natural systems.

The use of Grunwald-Letnikov’s definition for solving fractional order differential equations is described by Concepcion et al. [8] and stated here.

Using the approximation

$$\begin{aligned} \mathfrak {D}^\alpha f(t)&\approx \varDelta ^\alpha _h f(t)\end{aligned}$$

(2)

$$\begin{aligned} \varDelta ^\alpha _h f(t)|_{t=kh}&= h^{-\alpha }\sum _{j=0}^k (-1)^{\,j}\begin{pmatrix} \alpha \\ j \\ \end{pmatrix} f(kh - jh). \end{aligned}$$

(3)

For a system given by $a\mathfrak {D}^\alpha u(t) + bu(t) = q(t)$, with $a=1$ and zero initial conditions

$$\begin{aligned} h^{-\alpha } \sum _{j=0}^k w_j^{(\alpha )} y_{k-j} + by_k = q_k \end{aligned}$$

(4)

where $t_k = kh,\; y_k = y(t_k),\; y_0 = 0,\; q_k=q(t_k),\;k=0,1,2,\cdots$, and

$$\begin{aligned} w_j^{(\alpha )} = (-1)^{\,j}\begin{pmatrix} \alpha \\ j \\ \end{pmatrix} \end{aligned}$$

(5)

the numerical solution is then obtained using

$$\begin{aligned} y_k = -bh^\alpha y_{k-1} - \sum _{j=1}^k w_j^{(\alpha )} y_{k-j} + h^\alpha q_k \end{aligned}$$

(6)

Synchronization of fractional order systems have been conducted by many researchers. Synchronization of a system consisting of multiple drive and one response was carried out in Zhou et al. [44]. Design, realization, control and synchronization of a novel 4D hyperchaotic fractional order system was carried out using time-delayed feedback control [11]. Generalized synchronization of a novel fractional order chaotic system in different order and dimension has been investigated with success using nonlinear feedback control [43].

In realization of chaos synchronization for real life application such as communication systems, it is intuitive to choose a method and technique which will minimize cost and error while giving the desired robust outputs. Ojo et al. [31] compared the backstepping and active control technique for complete synchronization of chaotic systems. From their results, active control transient error dynamics convergence and synchronization time are achieved faster via the backstepping than that of the active control technique but the control function obtained via the active control is simpler with a more stable synchronization time and hence, it is more suitable for practical implementation. There is the need to investigate an efficient and robust method of synchronization in light of growing interest in fractional order chaotic systems. The aim of this chapter is to compare the performance of three different techniques for complete synchronization of an hyperchaotic fractional order chaotic system. System performance will be investigated using both linear and nonlinear tools.

2 Related Work

Comparison of two different synchronization scheme was carried out on integer order chaotic systems [31]. Recent advances in synchronization of fractional chaotic systems has seen results such as hybrid synchronization [36], exponential synchronization with mixed uncertainties [22], combination-combination synchronization [21], synchronization of nonidentical systems using modified active control [13], synchronization of fractional order switching chaotic system [15], synchronization of fractional order hyperchaotic systems using a new adaptive sliding mode control [23], combination synchronization using nonlinear feedback control method [3], reduced order synchronization of fractional order systems using adaptive control [2], fuzzy adaptive synchronization [6] and robust methods [36] have been reported. Circuit realization of a fractional order chaotic systems has also been implemented [11].

3 Synchronization Methods

A mathematical definition of synchronization was proposed by Wu and Chua [42]. Two systems $\dot{x} = f(x,y,t)$ and $\dot{y} = g(x,y,t)$ are uniform-synchronized with error bound $\varepsilon$ if there exist $\delta > 0$ and $T\ge 0$ such that

$$\begin{aligned} \Vert x_{i,j}(t_0) - y_{k,l}(t_0) \Vert \le \delta \end{aligned}$$

(7)

In order to achieve this, several techniques have been proposed. In the following subsections, three of the popular techniques are discussed.

3.1 Direct Method

The mathematical definition of Lyapunov Direct Method was given by Wu and Chen [42] and is stated here. Consider the systems $\dot{x} = f(x,t)$ and $\dot{y} = f(y,t)$. Supposed that there exist a Lyapunov function V(t, x, y) such that for all $t\ge t_0$

$$\begin{aligned} a(\Vert x-y \Vert )\le V(t,x,y) \le b(\Vert x - y \Vert ) \end{aligned}$$

where $a(\cdot )$ and $b(\cdot )$ are functions. Supposed that there exist $\mu > 0$ such that for all $t>t_0$ and $\Vert x - y \Vert \ge \mu$

$$\begin{aligned} \dot{V}(t,x,y) \le -c \end{aligned}$$

for some constant $c>0$ where $\dot{V}(t,x,y)$ is the generalized derivative of V along the trajectories of the systems Wu and Chua [42]. The Lyapunov direct method has been used successfully for the synchronization of ...., anti-synchronization etc.

3.2 Open Plus Closed Loop (OPCL)

The method of Open Plus Closed Loop was proposed by Grosu [16]. The method has been used for robust synchronization [14].

Consider a drive system $\dot{y} = F(y)$ and a response system given by $\dot{x} = F(x) + D(x,g)$ where $x,y \varepsilon \mathfrak {R}^n$ and $g=\alpha y$, $\alpha$ is a constant. The goal is to satisfy the condition

$$\begin{aligned} \lim _{t \rightarrow \infty }(x(t) - g(t)) = 0 \end{aligned}$$

From the OPCL theory, there exist an open-loop action, H given by

$$\begin{aligned} H(g,dg/dt,t) = \frac{dg}{dt} - F(g,t) \end{aligned}$$

and a linear feedback (closed-loop), K given as

$$\begin{aligned} K(g,x,t) = \left( \frac{dF}{dg} - A \right) [g(t) - x(t)] \end{aligned}$$

where $g(t) \varepsilon \mathfrak {R}^n$ is an arbitrary smooth function and A is an arbitrary constant Hurwitx matrix with negative real part [14]. The driving term D, can be written as the sum of the open-loop and closed-loop as

$$\begin{aligned} D = \frac{dg}{dt} - F(g,t) + \left( \frac{dF}{dg} - A \right) [g(t) - x(t)] \end{aligned}$$

(8)

3.3 Active Control

The Active Control method of synchronization was proposed by Bai and Lonngren [4]. Considering a drive system $\dot{x} = f(x)$ and a response defined as $\dot{y} = f(y) + u(t)$, where u(t) are the control functions. Defining the error function as

$$\begin{aligned} \lim _{t\rightarrow \infty } \Vert e(t)\Vert = \lim _{t\rightarrow \infty } \Vert f(x) - f(y)\Vert = 0 \end{aligned}$$

(9)

we define a subcontroller $v(t) = -\mathbb {K}e$, where $\mathbb {K}$ is a linear controller gain for control of response feedback strength. The error term can be written as

$$\begin{aligned} \dot{e}(t) = A_i e(t) + v(t) \end{aligned}$$

where $A_i$ are residuals of the system parameters. Substituting the values of v(t)m, we obtain

$$\begin{aligned} \dot{e}(t) = Z e(t) \end{aligned}$$

(10)

where $Z = (A_i - K)$. If all the eigenvalues of the matrix Z have negative real parts, it is an Hurwitz matrix, which implies that the zero solution of the closed loop system is globally asymptotically stable [1].

4 System Description

The Lorenz system was proposed by Lorenz [19] and can be regarded as the first deterministic system. It is a 3D autonomous system given by

$$\begin{aligned} \begin{aligned} \dot{x}_1&= a(x_2 - x_1) \\ \dot{x}_2&= cx_1 - x_2 - x_1x_3\\ \dot{x}_3&= x_1x_2 - bx_3 \end{aligned} \end{aligned}$$

(11)

The system has been found to be chaotic when $a = 10,\, b = 8/3, \, c = 28$ with Lyapunov exponents $1.49,\, 0, \, -22.46$ indicating a strange attractor. Chaotic synchronization of the Lorenz system has been done using different techniques such as increased and reduced order using Active control [24], complete synchronization using OPCL [14].

Gao et al. [12] introduced the 3D fractional order chaotic Lorenz system with order 0.98.

$$\begin{aligned} \begin{aligned} \frac{d^{q_1}x_1}{dt^{q_1}}&= a(x_2 - x_1) \\ \frac{d^{q_2}x_2}{dt^{q_2}}&= cx_1 - x_2 - x_1x_3\\ \frac{d^{q_3}x_3}{dt^{q_3}}&= x_1x_2 - bx_3\\ \end{aligned} \end{aligned}$$

(12)

By adding a nonlinear term $\dot{x}_4 = -x_2x_3 + rx_4$ to Eq. 11, a new system given by

$$\begin{aligned} \begin{aligned} \dot{x}_1&= a(x_2 - x_1) + x_4 \\ \dot{x}_2&= cx_1 - x_2 - x_1x_3\\ \dot{x}_3&= x_1x_2 - bx_3\\ \dot{x}_4&= -x_2x_3 + rx_4 \end{aligned} \end{aligned}$$

(13)

was obtained. The system was found to be hyperchaotic when $r = -1$.

A 4D hyperchaotic fractional system developed based on Eqs. (12) and (13) system will be used in this paper

$$\begin{aligned} \begin{aligned} \frac{d^{q_1}x_1}{dt^{q_1}}&= a(x_2 - x_1) + x_4 \\ \frac{d^{q_2}x_2}{dt^{q_2}}&= cx_1 - x_2 - x_1x_3 \\ \frac{d^{q_3}x_3}{dt^{q_3}}&= x_1x_2 - bx_3 \\ \frac{d^{q_4}x_4}{dt^{q_4}}&= -x_2x_3 + rx_4 \end{aligned} \end{aligned}$$

(14)

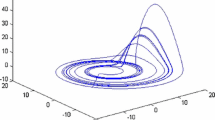
where the parameters are chosen as $a = 10,\, b = 8/3, \,c = 28, \,r = -1$. The system has Lyapunov exponents $\lambda _1 = 0.3362,\, \lambda _2 = 0.1568,\, \lambda _3 = 0,\, \lambda _4 = -15.172$ when the order of the system is 0.98 [38, 41]. The attractor of the fractional order Lorenz system is shown in Fig. 1 and the uncontrolled time series in Fig. 2.

Fig. 1

Phase space of the system

Fig. 2

(2) Time series of each component of the system ($x_1,x_2,x_3,x_4$) against time

5 Synchronization of Chaos in Fractional Order Lorenz System Using Direct Method

5.1 Design of Controllers

Let the drive system of the 4D fractional order Lorenz system be as described in Eq. 14 and the response system as

$$\begin{aligned} \begin{aligned} \frac{d^{q_1}y_1}{dt^{q_1}}&= a(y_2 - y_1) + y_4 + u_1(t)\\ \frac{d^{q_2}y_2}{dt^{q_2}}&= cy_1 - y_2 - y_1y_3 + u_2(t) \\ \frac{d^{q_3}y_3}{dt^{q_3}}&= y_1y_2 - by_3 + u_3(t)\\ \frac{d^{q_4}y_4}{dt^{q_4}}&= -y_2y_3 + ry_4 + u_4(t) \end{aligned} \end{aligned}$$

(15)

where $u_i(t) (i=1,2,3,4)$ is the control function to be determined. We define the error function of the form

$$\begin{aligned} \begin{aligned} e_1&= y_1 - \alpha _1 x_1 \\ e_2&= y_2 - \alpha _2 x_2 \\ e_3&= y_3 - \alpha _3 x_3 \\ e_4&= y_4 - \alpha _4 x_4 \end{aligned} \end{aligned}$$

(16)

where $\alpha _i (i=1,2,3,4)$ are scaling parameters.

Definition 1

If the scaling factors $\alpha _i (i=1,2,3,4)$ are chosen such that

$$\begin{aligned} \alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 1 \end{aligned}$$

complete synchronization of the drive-response system is achieved.

Definition 2

If the scaling factors $\alpha _i (i=1,2,3,4)$ are chosen such that

$$\begin{aligned} \alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = -1 \end{aligned}$$

complete anti-synchronization of the drive-response system is achieved.

Definition 3

If the scaling factors $\alpha _i (i=1,2,3,4)$ are chosen such that

$$\begin{aligned} \alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = p \end{aligned}$$

where $p \ne 0 \, \text {or} \, 1$ projective synchronization of the drive-response system is achieved.

Definition 4

The drive-response system is said to experience projective antisynchronization if the scaling factors $\alpha _i (i=1,2,3,4)$ are chosen such that

$$\begin{aligned} \alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = -p \end{aligned}$$

where $p \ne 0 \, \text {or}\, 1$.

Definition 5

The drive-response system is said to experience modified projective antisynchronization if the scaling factors $\alpha _i (i=1,2,3,4)$ are chosen such that

$$\begin{aligned} \alpha _1 \ne \alpha _2 \ne \alpha _3 \ne \alpha _4\ne -p \end{aligned}$$

where $p \ne 0 \, \text {or} \, 1$.

Definition 6

If $\alpha _1 = \alpha _3 = 1$ and $\alpha _2 = \alpha _4 = -1$, hybrid synchronization is achieved.

Definition 7

If $\alpha _1 = \alpha _3$ and $\alpha _2 = \alpha _4 = p$, where $p \ne 0,\pm 1$ projective hybrid synchronization is achieved.

Definitions (1)–(7) can be obtained from any of the synchronization method described in this chapter.

The error system is then obtained as

$$\begin{aligned} \begin{aligned} D^qe_1&= a(e_2 - e_1) + e_4 + u_1\\ D^qe_2&= ce_1 - e_2 - (y_1y_3 - \alpha _2x_1x_3) + u_2\\ D^qe_3&= -be_3 + y_1y_2 - \alpha _3x_1x_2 + u_3\\ D^qe_4&= re_4 - (y_2y_3 - \alpha _4x_2x_3) + u_4 \end{aligned} \end{aligned}$$

(17)

Choosing a quadratic Lyapunov function of the form

$$\begin{aligned} V = \frac{1}{2}\sum _{i=1}^4 e_i^2 \end{aligned}$$

(18)

Its derivative is obtained as

$$\begin{aligned} \dot{V} = \sum _{i=1}^4 e_i D^qe_i \end{aligned}$$

(19)

Applying this to the system,

$$\begin{aligned} \dot{V} = e_1[a&(e_2 - e_1) + e_4 + u_1] + e_2[ce_1 - e_2 - (y_1y_3 - \alpha _2 x_1x_3) + u_2]\nonumber \\&\,\,\,+ e_3[-be_3 + y_1y_2 - \alpha x_1 x_2 + u_3] + [re_4 - (y_2y_3 - \alpha _4 x_2x_3) + u_4)] \end{aligned}$$

(20)

If,

$$\begin{aligned} \begin{aligned} u_1&= -ae_2 - e_4 \\ u_2&= -ce_1 + (y_1y_3 - \alpha x_1 x_3)\\ u_3&= -y_1y_2 + \alpha x_2 x_3\\ u_4&= -r e_4 + (y_2y_3 - \alpha _4 x_2x_3) - ke_4 \end{aligned} \end{aligned}$$

(21)

Then,

$$\begin{aligned} \dot{V} = -ae_1^2 - e_2^2 - be_3^2 - ke_4^2 < 0 \end{aligned}$$

(22)

since a, b, k are positive numbers. We assume $k=1$.

5.2 Numerical Simulation Results

To verify the effectiveness of the synchronization between the drive and response systems using the Lyapunov Direct Method, we used Eq. (6) with the initial conditions $x_i(i=1,2,3,4)$ and $y_i(i=1,2,3,4)$ taken as $(-80\,\,\,\, 50\,\,\,\, 50\,\,\,\, 100)$ and $(0.08\,\,\,\, {-}0.5\,\,\,\, 1\,\,\,\, 0)$ respectively. The order of the system is taken to be 0.98. A time step of 0.005 was used the systems parameters used are $a = 10,\, b = 8/3, \,c = 28, \,r = -0.99$ to ensure chaotic dynamics of the state variables. Solving the drive (Eq. 14) and response (Eq. 15) with the control defined in Eq. (21). The results are shown in Figs. 3, 4, 5, 6 and 7 for the different scaling parameters ($\alpha = 1,-1,2,-2$). The drive and response systems could be seen to achieve synchronization as indicated by the convergence of the error state variables to zero (i.e. $e_i(1,2,3,4) \rightarrow 0$). From the results obtained, the effectiveness of the controller was confirmed.

Fig. 3

Error dynamics between Slave and Master system using direct method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 1$

Fig. 4

Error dynamics between Slave and Master system using direct method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = -1$

Fig. 5

Error dynamics between Slave and Master system using direct method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 2$

Fig. 6

Error dynamics between Slave and Master system using direct method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = -2$

Fig. 7

Error dynamics between Slave and Master system using direct method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 1$

6 Synchronization of Chaos in Fractional Order Lorenz System Using OPCL

6.1 Design of Controllers

If the drive system is taken as Eq. 14 and the response as Eq. 15, then the error state of the system can be written as

$$\begin{aligned} \begin{aligned} e_1&= y_1 - g_1 \\ e_2&= y_2 - g_2 \\ e_3&= y_3 - g_3 \\ e_4&= y_4 - g_4 \end{aligned} \end{aligned}$$

(23)

where

$$\begin{aligned} \begin{bmatrix} g_1 \\ g_2 \\ g_3 \\ g_4 \\ \end{bmatrix} = \begin{bmatrix} \alpha _1x_1 \\ \alpha _2x_2 \\ \alpha _3x_3 \\ \alpha _4x_4 \\ \end{bmatrix} \,\,\, \text {and}\,\,\, \begin{bmatrix} \dot{g_1} \\ \dot{g_2} \\ \dot{g_3} \\ \dot{g_4} \\ \end{bmatrix} = \begin{bmatrix} \alpha _1\dot{x_1} \\ \alpha _2\dot{x_2} \\ \alpha _3\dot{x_3} \\ \alpha _4\dot{x_4} \\ \end{bmatrix} \end{aligned}$$

Defining the drive system as a function of g

$$\begin{aligned} f(g) = \begin{bmatrix} a(g_2 - g_1) + g_4 \\ cg_1 - g_2 - g_1g_3 \\ g_1g_2 - bg_3 \\ -g_2g_3 + rg_4 \\ \end{bmatrix} \end{aligned}$$

(24)

Also, the Jacobian is obtained as

$$\begin{aligned} \frac{\partial f_g}{\partial g} = \begin{pmatrix} -a &{} a &{} 0 &{} 1 \\ (c-g_3) &{} -1 &{} -g &{} 0 \\ g_2 &{} g_1 &{} -b &{} 0 \\ 0 &{} -g_3 &{} -g_2 &{} r \\ \end{pmatrix} \end{aligned}$$

(25)

To ensure the stability of the system, we choose as Hurwitz matrix

$$\begin{aligned} H= \begin{pmatrix} -1 &{} 0 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 0 &{} -1 \\ \end{pmatrix} \end{aligned}$$

(26)

Using the OPCL theory, the controller is defined as

$$\begin{aligned} U = \dot{g} - f(g) + \left[ H - \frac{\partial f_g}{\partial g} \right] e \end{aligned}$$

(27)

The control $u_i(i=1,2,3,4)$ is then obtained as

$$\begin{aligned} \begin{aligned} u_1&= \alpha _1 \dot{x}_1 - a(g_2 - g_1) - g_4 + (a-1)e_1 -a_2e_2 - e_4\\ u_2&= \alpha _2 \dot{x}_2 - [cg_1 - g_2 - g_1g_3] - (c-g_3)e_1 + g_1e_3\\ u_3&= \alpha _3 \dot{x}_3 - [g_1g_2 - bg_3] - g_2e_1 - g_1e_2 + (b - 1)e_3 \\ u_4&= \alpha _4 \dot{x}_4 - [rg_4 - g_2g_3] + g_3e_2 + g_2e_3 - (1 + r)e_4 \end{aligned} \end{aligned}$$

(28)

6.2 Numerical Simulation Results

To verify the effectiveness of the synchronization between the drive and response systems using the OPCL method, we used Eq. (6) with the initial conditions $x_i(i=1,2,3,4)$ and $y_i(i=1,2,3,4)$ taken as $(-80\,\,\,\, 50\,\,\,\, 50\,\,\,\, 100)$ and $(0.08\,\,\,\, {-}0.5\,\,\,\, 1\,\,\,\, 0)$ respectively. The order of the system is taken to be 0.98. A time step of 0.005 was used the systems parameters used are $a = 10,\, b = 8/3, \,c = 28, \,r = -0.99$ to ensure chaotic dynamics of the state variables. Solving the drive (Eq. 14) and response (Eq. 15) with the control defined in Eq. (28). The results are shown in Figs. 8, 9, 10, 11 and 12 for the different scaling parameters ($\alpha = 1,-1,2,-2$). The drive and response systems could be seen to achieve synchronization as indicated by the convergence of the error state variables to zero (i.e. $e_i(1,2,3,4) \rightarrow 0$). From the results obtained, the effectiveness of the controller was confirmed.

Fig. 8

Error dynamics between Slave and Master system using OPCL method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 1$

Fig. 9

Error dynamics between Slave and Master system using OPCL method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = -1$

Fig. 10

Error dynamics between Slave and Master system using OPCL method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 2$

Fig. 11

Error dynamics between Slave and Master system using OPCL method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = -2$

Fig. 12

Error dynamics between Slave and Master system using OPCL method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 1$

7 Synchronization of Chaos in Fractional Order Lorenz System Using Active Control

7.1 Design of Controllers

If the drive system is taken as Eq. 14, the response as Eq. 15, then the error state of the system as Eq. 16, in line with the method of Active Control, we can eliminate terms which cannot be expressed as linear terms in $e_1,e_2,e_3,e_4$ as

$$\begin{aligned} \begin{aligned} u_1&=v_1(t) \\ u_2&=y_1y_3 - \alpha _2x_1x_3 + v_2(t)\\ u_3&= -y_1y_2 + \alpha _3x_1x_2 + v_3(t)\\ u_4&= y_2y_3 - \alpha _4 x_2x_3 + v_4(t) \end{aligned} \end{aligned}$$

(29)

the parameter $v_i(t)(i=1,2,3,4)$ will be obtained later. Substituting Eq. (29) into Eq. (17) yields

$$\begin{aligned} \begin{aligned} D^q e_1&= a(e_2 - e_1) + e_4 + v_1(t) \\ D^q e_2&= ce_1 - e_2 + v_2(t)\\ D^q e_3&= -be_3 + v_3(t)\\ D^q e_4&= re_4 + v_4(t) \end{aligned} \end{aligned}$$

(30)

Using the Active Control method, a constant matrix D is chosen which will control the error dynamics (Eq. 30) such that the feedback matrix is

$$\begin{aligned} \begin{pmatrix} v_1(t) \\ v_2(t) \\ v_3(t) \\ v_4(t) \\ \end{pmatrix} = D \begin{pmatrix} e_1 \\ e_2 \\ e_3 \\ e_4 \\ \end{pmatrix} \end{aligned}$$

where D is a $4\times 4$ matrix. There are various choices of the feedback D which can be chosen to control the error dynamics but we optimize this choice so that the problem of controller complexity is significantly reduced [31]. Hence, D is chosen to be of the form

$$\begin{aligned} D = \begin{pmatrix} (a-\lambda _1) &{} -a &{} 0 &{} -1 \\ -c &{} (1-\lambda _2) &{} 0 &{} 0 \\ 0 &{} 0 &{} (b-\lambda _3) &{} 0 \\ 0 &{} 0 &{} 0 &{} -(r + \lambda _4) \\ \end{pmatrix} \end{aligned}$$

(31)

The eigenvalues $\lambda _i(i=1,2,3,4)$ are chosen to be negative in order to achieve a stable synchronization between the drive and response system.

Fig. 13

Error dynamics between Slave and Master system using active control method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 1$

Fig. 14

Error dynamics between Slave and Master system using active control method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = -1$

Fig. 15

Error dynamics between Slave and Master system using active control method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 2$

Fig. 16

Error dynamics between Slave and Master system using active control method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = -2$

Fig. 17

Error dynamics between Slave and Master system using active control method for $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 1$

7.2 Numerical Simulation Results

To verify the effectiveness of the synchronization between the drive and response systems using the Active control method, we used Eq. (6) with the initial conditions $x_i(i=1,2,3,4)$ and $y_i(i=1,2,3,4)$ taken as $(-80\,\,\,\, 50\,\,\,\, 50\,\,\,\, 100)$ and $(0.08\,\,\,\, {-}0.5\,\,\,\, 1\,\,\,\, 0)$ respectively. The order of the system is taken to be 0.98. A time step of 0.005 was used the systems parameters used are $a = 10,\, b = 8/3, c = 28, \,r = -0.99$ to ensure chaotic dynamics of the state variables. Solving the drive (Eq. 14) and response (Eq. 15) with the control defined in Eq. (31). The results are shown in Figs. 13, 14, 15, 16 and 17 for the different scaling parameters ($\alpha = 1,-1,2,-2$). The drive and response systems could be seen to achieve synchronization as indicated by the convergence of the error state variables to zero (i.e. $e_i(1,2,3,4) \rightarrow 0$). From the results obtained, the effectiveness of the controller was confirmed.

8 Comparison of Direct Method, OPCL and Active Control Techniques

The performance of the three different synchronization scheme is to be compared. The error components for the system and error magnitude are presented in Figs. 18 and 19 respectively. From Fig. 18, apart from the top-left figure, the convergence of the synchronization technique in order of increasing speed is: active control, Lyapunov Direct Method and OPCL. The same trend and order could be observed in the error magnitude as shown in Fig. 19. The behaviour of the error dynamics before achieving convergence is important. The speed of convergence is referred to as synchronization time [24, 31]. From Fig. 18, the active control technique was found to have minimal variations before attaining convergence while the two other techniques show different behaviours in fluctuation. From the dynamics of the error dynamics, it could be observed that the OPCL method showed the highest variation in error amplitude before convergence while the active control has the lowest amplitude variation.

Fig. 18

Error dynamics between Slave and Master system for each component of the system for each of the synchronization techniques under consideration when $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 2$

Fig. 19

Error dynamics between Slave and Master system for the three synchronization techniques when $\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = 1$

9 Conclusion

The synchronization of chaotic fractional order Lorenz system has been investigated using three techniques: active control, Lyapunov direct method and OPCL. In each of the synchronization scheme, control functions have been achieve for the complete synchronization between the drive and response systems. Numerical simulations have been conducted to assert the effectiveness of the proposed analytical results. Comparing the three techniques, active control offers the best stability and fast convergence of error terms. The synchronization dynamics of fractional order systems under periodic driving force can be investigated. There is the need to study the performance of the different synchronization schemes considered here under different types of noise and noise strength to test their reliability. This study can be extended to maps and integer order systems. Practical realization using electronic simulations and/or circuit for communication can be investigated to determine efficiency and practicability of these results under field scenario. In real life applications of synchronization schemes for secure communication, there is interaction between multiple users, hence, further work can be carried out to study the best scheme under multiple drive and multiple response system with applications to secure communication systems.